симметричная задача на примере балки с двумя опорами

Расчет реакций относится к разделу физики с названием «Статика», которая рассматривает структуру и системы, находящиеся в покое.

Силой реакции опоры называется усилие противодействия опоры действующему на нее объекту, при этом она равна по модулю и противоположна по направлению усилию, с которым объект действует на опору, согласно третьему закону Ньютона.

Система между некоторой структурой и опорой, которая препятствует линейному или угловому перемещению этой структуры, называется системой опоры. Существует несколько типов опор:

• Шарнир (валик) — опора первого порядка, ограничивающая смещение в пространстве в одном измерении и обладающее реакцией опоры перпендикулярной основанию.
• Плоская опора — опора второго порядка, которая ограничивает перемещение в пространстве в двух измерениях (горизонтальном и вертикальном) и разрешает только движение вращения структуры.

Расчет равновесных систем связан с вычислением результирующего динамического момента. В ньютоновской (классической) механике момент силы определяется как векторное произведение усилия, действующего на опору, на вектор, образованный между точкой опоры и точкой приложения этого усилия. Момент силы также называют динамическим моментом или просто моментом.

Далее в статье приводится пример расчета реакции для наиболее распространенной задачи: балки с двумя опорами.

Содержание:

• Решение задачи о реакции опоры балки
  • Первый способ: через моменты
  • Второй способ: через силы
• Видео

Решение задачи о реакции опоры балки

Как было сказано выше, балка с двумя опорами является типичной и наиболее простой задачей статики. Задача состоит в расчете реакций в точках А и В ввиду действующих на балку усилий.

Знание этих величин необходимо для правильного понимания диаграмм моментов и диаграмм сил данной системы, и является важной частью статики в школьных и университетских курсах.

Существует компьютерная программа SkyCiv, которая предоставляет мощный инструмент по расчету таких реакций для различных равновесных систем.

Возвращаясь к поставленной выше задаче, напомним, что основным ее условием является статическое состояние, то есть отсутствие каких-либо линейных перемещений и вращений объектов. В простой физике последний факт означает, что сумма векторов всех усилий равна нулю (то есть сумма усилий, направленных вверх, равна таковым, направленным вниз). Вторым условием равновесия системы является равенство нулю динамических моментов, приложенных относительно определенной точки опоры.

Чтобы определить реакции подпорок балки, следуйте нижеизложенным двум способам решения задачи:

• используя равенство нулю суммы динамических моментов;
• используя равенство нулю суммы действующих усилий.

Первый способ: через моменты

Для начала нужно положить, что сумма всех моментов относительно точки реакции равна нулю, то есть ΣMi = 0, где Мi — момент усилия. Расчет таких моментов для нашей задачи очень прост, и состоит в перемножении действующих усилий на расстояния от точки их приложения до точки реакции.

Будем считать, что наша балка имеет длину 4 метра и расположена на двух подпорках А и В. Посредине балки вертикально вниз действует усилие в 20 кН, и нужно рассчитать реакции каждой подпорки, то есть Ay и By . Описанная задача представлена на рисунке.

Например, рассчитаем сумму всех динамических моментов относительно точки реакции В, учитывая ее равенство нулю в равновесии. Выбор точки В, относительно которой будет проводиться расчет, является произвольным, точно так же можно выбрать точку А. Таким образом, просуммируем все динамические моменты относительно точки В, полагая эту сумму равной нулю:

ΣMв = 0 = 20*2 — A y * 4 ==> A y = 10 кН.

Отметим, что в формуле выше мы выбрали положительное направление для моментов, действующих против часовой стрелки, и отрицательное направление для моментов, действующих по часовой стрелке. Такой выбор знаков моментом является наиболее общим, однако, вы можете выбрать и наоборот. Необходимо помнить, что всегда нужно использовать одно и то же соглашение на знак моментов, начиная сначала и следуя ему на протяжении всего решения конкретной задачи.

Таким образом, мы получили нашу первую формулу, из которой определили силу реакции опоры в точке А. Аналогичная формула запишется для определения реакции в точке В. В нашем случае, ввиду симметричности действующего вертикально вниз усилия в 20 кН относительно точек подпорок, реакция в точке В будет равна таковой в точке А, то есть 10 кН.

Второй способ: через силы

Для существования равновесия сумма всех вертикальных сил должна быть равна нулю, то есть ΣF y = 0, где индекс Y определяет конкретную вертикальную силу в системе. Помните, что в данном случае мы должны включать в расчет все действующие в системе силы. Принимая во внимание последний факт, проводим суммирование всех вертикальных сил, в итоге получаем следующую формулу:

ΣF y = 0 = A y + В y — 20 кН, откуда 0 = 10 кН + В y — 20 кН, и В y = 10 кН.

Так же, как и в случае моментов сил, силы являются векторными величинами и имеют знак, здесь мы приняли за положительные силы те, которые действуют вверх, и за отрицательные те, которые действуют вниз. Выбор знака остается за вами, однако, напоминаем, что этот выбор не должен изменяться в процессе решения задачи. Отметим, что в формуле выше мы использовали результат, полученный в предыдущем пункте, когда вычислили силу реакции Ay.

Таким образом, мы решили, поставленную в начале этого параграфа задачу о расчете сил реакций опоры балки, используя при этом две системы уравнений, уравнения момента силы и уравнения силы, и получили ответы: силы реакции в точках А и В равны между собой и составляют 10 кН. Напоминаем, что физический смысл полученного равенства заключается в том, что действующая на балку внешняя сила приложена точно посередине балки. В случае ее приложения в другой точке, приведенные формулы также будут действительны и процесс расчета остается тем же самым.

Видео

Эта видеоподборка поможет вам лучше разобраться в теме и закрепить полученные знания.

Определение реакций опор

Схема нагружения быстроходного вала.

Горизонтальная плоскость XOZ:

Знак минус говорит о том, что сила направлена в противоположную сторону.

Проверка:

Строим эпюру изгибающих моментов в характерных точках относительно оси Х:

Вертикальная плоскость YOZ:

Проверка:

Строим эпюру изгибающих моментов в характерных точках от носитель оси Y:

Строим эпюру крутящих моментов:

Определяем суммарные реакции опор для расчета подшипников

Схема нагружения тихоходного вала.

Горизонтальная плоскость XOZ [3]:

Знак минус говорит о том, что сила направлена в противоположную сторону.

Проверка:

Строим эпюру изгибающих моментов в характерных точках относительно оси Х:

Вертикальная плоскость YOZ:

Знак минус говорит о том, что сила направлена в противоположную сторону.

Проверка:

Строим эпюру изгибающих моментов в характерных точках от носитель оси Y:

Строим эпюру крутящих моментов:

Определяем суммарные реакции опор для расчета подшипников

Предварительно назначенный подшипник для быстроходного вала роликовые конические однорядные средней серии №7304А [3].

Таблица 4.1 – Размеры и характеристика выбранного подшипника.

№	d, мм	D, мм	B, мм	Cr, кН	C0, кН	е	Y
7304	20	52	15	31,9	20	0,30	2,00

Определяем осевые составляющие

(4. 10)

(4.11)

Так как и , находим осевые силы нагружающие подшипники по следующим формулам

(4.12)

Отношение для опоры А

(4.13)

Что меньше е=0,30 и для опоры А Х=1 Y=0.

Отношение для опоры В

(4.14)

Что больше е=0,30 и для опоры В Х=0,4 Y=2,03.

Эквивалентные динамические нагрузки при коэффициенте динамичности нагрузки для всех типов редукторов К_Б=1,5 и температурном коэффициенте К_Т=1, т. к. t_раб.<100^оС [3].

Опора А

(4.15)

Опора В

(4.16)

Расчетный ресурс более нагруженного подшипника опоры В, при обычных условиях нагружения а₂₃=0,6.

(4.17)

где

(4.18)

Подшипник 7304A пригоден, т.к. расчетный ресурс больше требуемого .

Предварительно назначенный подшипник для тихоходного вала легкой серии №7207А.

Таблица 4.2 – Размеры и характеристика выбранных подшипников.

№

d, мм

D, мм

B, мм

Cr, кН

C0, кН

е

Y

Продолжение таблицы 4.2

7207А

35

72

17

58,3

40,0

0,37

1,60

Определяем осевые составляющие [3]

(4. 19)

(4.20)

Так как и , находим осевые силы нагружающие подшипники по следующим формулам

(4.21)

Отношение для опоры С

(4.22)

Что меньше е=0,37 и для опоры А Х=1 Y=0.

Отношение для опоры D

(4.23)

Что больше е=0,37 и для опоры В Х=0,4 Y=1,62.

Эквивалентные динамические нагрузки при коэффициенте динамичности нагрузки для всех типов редукторов К_Б=1,5 и температурном коэффициенте К_Т=1, т. к. t_раб.<100^оС.

Опора C

(4.24)

Опора D

(4.25)

Расчетный ресурс более нагруженного подшипника опоры В, при обычных условиях нагружения а₂₃=0,6.

(4.26)

Подшипник 7304A пригоден, т.к. расчетный ресурс больше требуемого .

Механика для людей — Расчет реакций поддержки в кадре

Сочинения и письменные задания, выполненные для вас

Получите помощь с любым заданием — от школьного эссе до докторской диссертации

Расчет реакций поддержки в статически обнаруживаемая рама

Пример определения реакций в опорах плоской рамы, нагруженной силой, моментом и распределенной нагрузкой.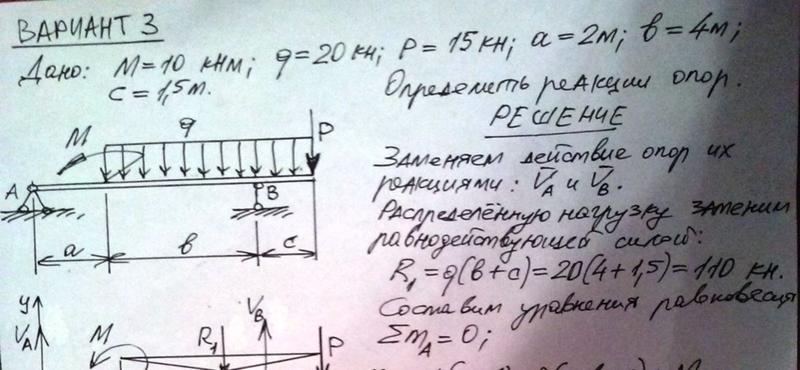

под действием нагрузки системы:

размер а=3м.

Расчет реакции

Перед началом решения задачи численные данные нагрузок переносим на расчетную схему и обозначаем характерные точки (сечения) рамы буквами А, В, С, Г и E.

Опорные реакции рамы будем определять из условия равновесия плоской системы сил.

Наш краткий видеоурок по расчету реакций балочных опор:

В шарнирно-неподвижной опоре (точка А) могут возникать две составляющие реакции — горизонтальная Н _А и вертикальная R _А , а в шарнирно-подвижной опоре (точка А) только одна реакция — вертикальная R _В .

О реакциях в шарнирных опорах

На данном этапе решения эти реакции могут быть направлены произвольно, например:

Для нахождения трех неизвестных сил нужны три уравнения статики: два уравнения суммы моментов относительно контрольных точек и суммы проекций всех сил на горизонтальную ось X, которая должна быть равна нулю.

Записываем их:

Из каждого уравнения выражаем и находим соответствующее значение опорной реакции:

Знак «-» реакции R _B указывает на то, что произвольно выбранное направление оказалось неверным, и его необходимо перенаправить в обратную сторону, при этом поменяв знак на положительный.

В задачах такого рода после расчета реакций в опорах настоятельно рекомендуется проверять полученные значения, так как даже небольшая ошибка в дальнейших расчетах может привести к неверному результату.

Проверка реакции

Проведем арифметическую проверку реакций, записав сумму моментов относительно, например, середины поперечины CD (точка К):

Тождество выполнено, значит реакции выполнены определены правильно.

После расчета и проверки опорных реакций можно приступать к построению диаграмм факторов внутренних сил в рамах.

Эссе и письменные задания для вас

Получите помощь с любым заданием — от школьного эссе до кандидатской диссертации

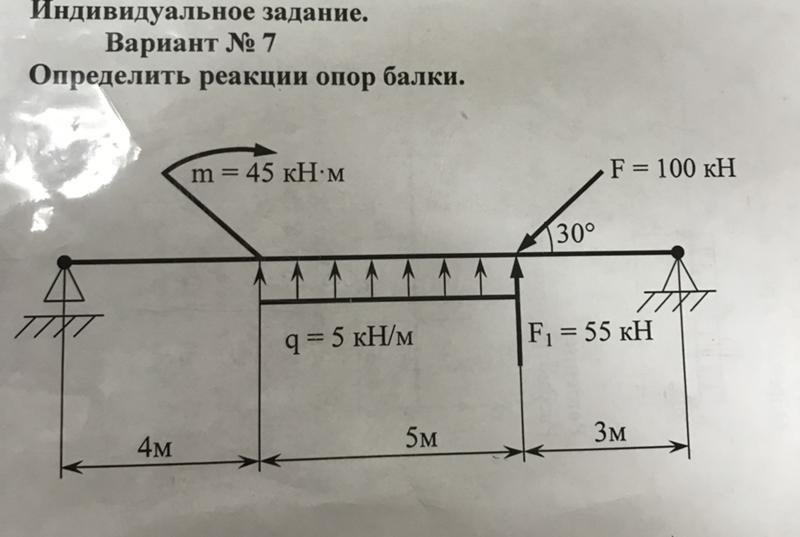
Как рассчитать реакции в балке с помощью уравнения равновесия — пример расчета реакции балки

Как рассчитать реакции в балке с помощью уравнения равновесия — реакция балки Расчет Пример

• Категория: Машиностроение
• Подкатегория: Физика

• как рассчитать опорные реакции в балках
• Пример расчета реакций в балке
• лучевые реакции
• как рассчитать реакции сплошной балки
• Расчет реакции в свободно опертых балках
• как рассчитать реакцию балки
• уравнения равновесия
• силы реакции на опорах
• как рассчитать реакции
• как найти реакцию луча

25 просмотров

Нет лайков

Нет не нравится

Нет Комментарии

Добро пожаловать на мой канал, состоящий из полных лекций по механике твердого тела, структурному анализу и RCD в виде плейлистов по порядку.