Расчет балки на прогиб: формулы и пример расчета
Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Виды балок
Независимо от того, какой должна быть конструкция, материал для изготовления балок выбирают прочный и надежный. Отличаются они друг от друга лишь по своим параметрам:
- длине;
- форме;
- сечению.

Чаще всего, для изготовления балок используется дерево и металл. Расчет балки на изгиб напрямую зависит от выбранного материала. В данном случае большое значение имеют такие показатели как однородность и структура.
Балки из дерева
Конструкции из дерева используются в одноэтажных домах или небольших домиках. Они отлично подходят как для потолка, так и пола. Для расчета прогиба балки берут следующие величины:
- Тип материала. Каждое дерево отличается прочностью, твердостью и гибкостью.
- Геометрические показатели, в которые включается как форма изделия, так и его сечение.
- Предполагаемые нагрузки, которые будут давить на материал.
На то, как будет изгибаться балка учитывается не только реальное давление, но и все возможные силы воздействия.
Стальные балки
Эти изделия очень сложные не только по сечению, но и по составу. Так как из выливают из нескольких видов металла. Производя расчет нагрузки на балку, необходимо принимать во внимание насколько она жесткая, а так же прочно ли она соединена.
Балки из стали используют для строительства многоэтажных домов Источник i0.photo.2gis.com
Конструкция из металла между собой соединяется с помощью:
- сваривания;
- склепывания;
- с помощью соединителей, имеющих резьбу.
Прочные металлические балки используются для строительства домов в несколько этажей. В таких конструкциях вся нагрузка равномерно распределяется по всей балке.
Смотрите также: Каталог проектов домов с террасой.
Прочность и жесткость балки
Балки в доме
Современные строительные технологии, применяемые для просчета стройконструкций, называемых также стержневыми, по качествам прочности и жесткости дают уникальную возможность на первом же этапе проектировки вычислить величину прогиба.
Кроме этого, можно, опираясь на рассчитанные данные, составить заключение о вероятности использования строительной конструкции.
Какой вопрос позволяет решать указанная далее формула для расчета жесткости? Данные, полученные таким путем, говорят о самых больших изменениях в геометрии детали, что могут возникнуть в строительной конструкции.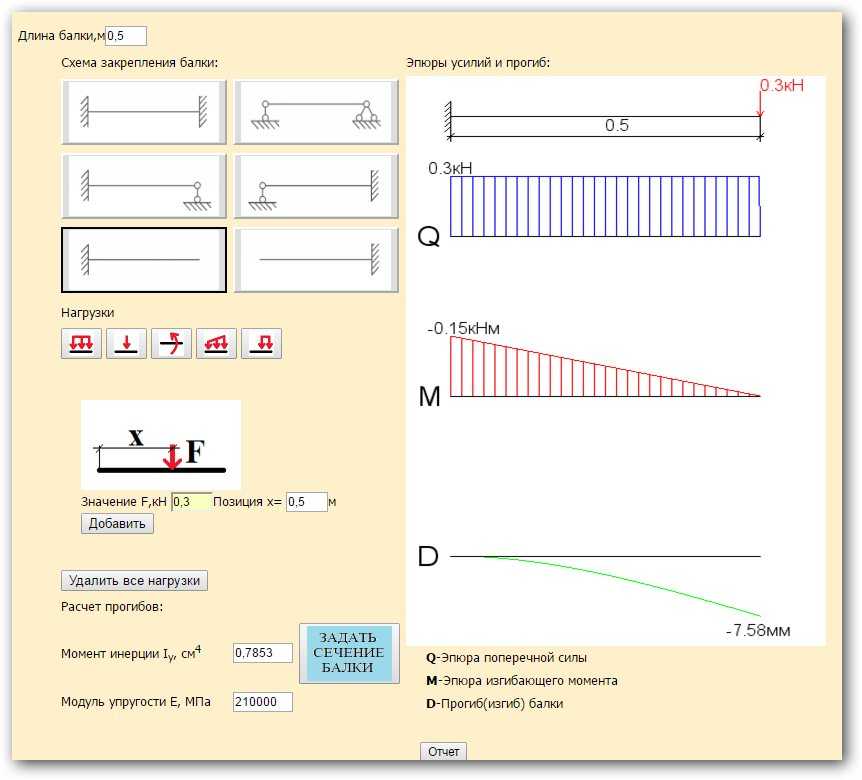
Несмотря на некоторую бюрократизацию методик для вычисления прогиба, используются опытные формулы, а если воздействие реальных нагрузок отличается от идеальных или усредненных, вопрос решается введением дополнительных коэффициентов для запаса прочности. Понятия «жесткость» и «прочность» связаны и абсолютно неразделимы.
Хотя некоторые различия все-таки есть. Но только в том случае, если рассматривать данные показатели в автомашинах. В стройконструкциях главное нарушение конструкции объектов случается потому, что снижаются или нивелируются полностью вопросы, связанные с запасом прочности, вследствие чего здания нельзя эксплуатировать.
Деревянные балки из древесины хвойных пород
На сегодня в таких предметах изучения, как «Сопромат» и другие, приняты 2 метода для расчета прочности и жесткости:
- Простой. При просчитывании показателей на основе этого метода используют увеличенный коэффициент.
- Точный. Тут используются не только коэффициенты, показывающие запас прочности, но также осуществляется вычисление пограничного состояния (какую нагрузку может выдержать балка).

Как добиться прочности конструкции
Согласно нормам, балка, используемая на эстакаде должна иметь изгиб не больше одного см при ее длине в полтора метра. При этом, в других конструкциях этот показатель меняется. В индивидуальном доме, балки чердака могут прогибаться на один см, при длине 2 м, а в многоэтажных домах тот же сантиметр должен припадать на длину в 2,5 м.
Для того, чтобы постройка была надежной и прочной, расчеты нужно проводить еще в процессе планирования здания. Именно в этот момент и определяется такой показатель, как изгиб балки. Ведь чем меньше прогибается балка, тем выше прочность дома. Таким образом потолок получает равномерное распределение веса и сохраняет устойчивость дома. Если же балки сильно прогибаются, то и весь потолок будет ненадежным и со временем происходит разрыв соединений и здание рушится.
Перед началом расчета, составляют схему давления на балку – макет будет кстати Источник pouznaval.ru
Расчеты проводятся с помощью одного из способов:
- Прибегнуть к помощи онлайн-калькулятора.
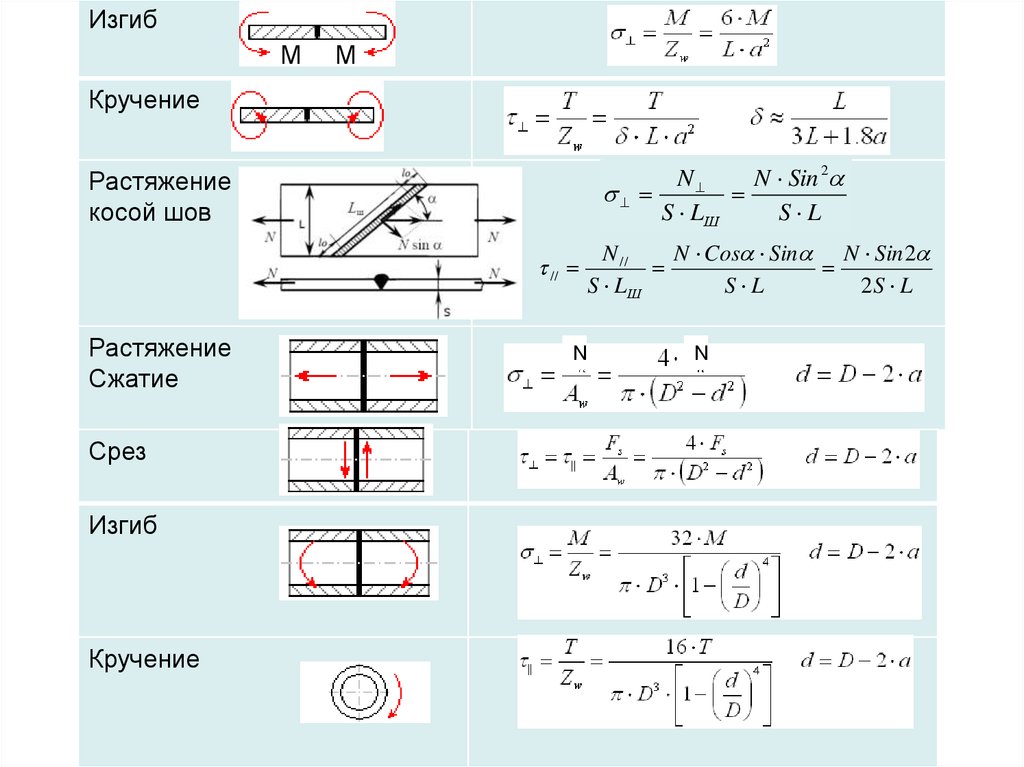 В данном инструменте запрограммированы стандартные данные.
В данном инструменте запрограммированы стандартные данные. - Воспользоваться справочником и, сравнив все параметры, произвести расчеты самостоятельно.
- Воспользоваться формулой и самостоятельно просчитать изгиб балок.
Важно! Просчитывать изгиб балки очень важно, чтобы на практике здание было прочным и надежным.
В помещении, которое используется уже не один год, определить насколько аварийным является его состояние, можно только после того, как будет определен уровень проседания балок.
Способы выполнить расчет и проверку на прогиб
Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.
Просчитать прогиб конструкции можно несколькими способами:
- Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
- Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
- Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.
К сведению! Чтобы реально представлять, почему так важно знать величину отклонения от первоначального положения, стоить понимать, что измерение величины прогиба является единственным доступным и достоверным способом определить состояние балки на практике.
Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.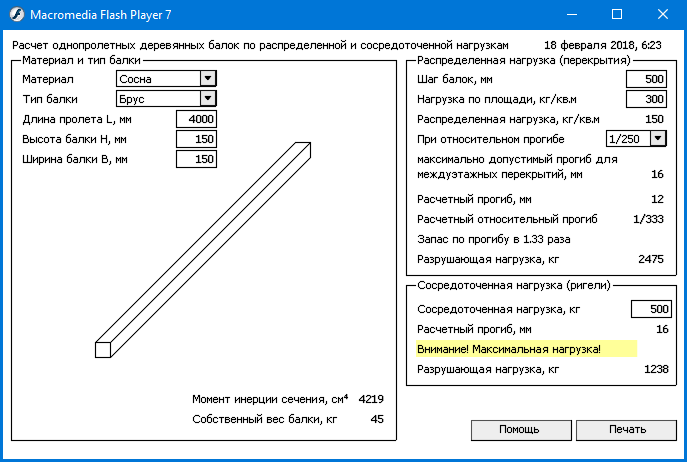
Формулы для определения изгиба балки
При расчете необходимо учесть силу сопротивления материала, из которого изготовлена конструкция. И только после этого рисуется схема, где указывается сила давления на балку.
Таким образом происходят измерения для вычисления изгиба Источник novainfo.ru
Смотрите также: Каталог компаний, что специализируются на монтаже печей и каминов.
Процесс расчета выглядит следующим образом:
- Используя формулу площади прямоугольной фигуры S=b*h, определяется сечение балки, а так же берется ко вниманию ее длина L;
- На балку воздействует сила давления Q, которая изгибает ее в центре, а ее концы образуют угол θ. Обязательно учитывается изначальное положение конструкции f;
- В схеме концы импровизированной балки установлены совершенно свободно, при этом опоры установлены стационарно. В этом случае нет реакции, как в случае горизонтального закрепления конструкции, и концы балки перемещаются в свободном направлении.

Изгиб предмета под давлением определяется формулой Е=R/Δ. В этом случае Е – это показатель, который берется из справочника, R – сила давления на предмет, Δ – это показатель, который получается в процессе изгиба.
Имея все необходимые показатели можно узнать, какой будет инерция, для этого используется формула:
Δ = Q/(S·Е)
Если же нагрузка будет равномерна по всей длине балки. То нужно использовать такую формулу:
Δ = q·h/(S·Е).
После всех этих вычислений, приходит черед к определению изгиба по системе Юнга. То есть, балку изгибают таким образом, что ее концы выворачиваются в разные стороны, при этом имеют разные куты изгиба. В таком случае в формуле обе части нужно умножить на число L и тогда получается следующее равенство:
Δ*L = Q·L/(b·h·Е)
Формулы можно найти в справочнике Источник pol-exp.com
Как вычислить вспомогательные величины
Для получения полной информации о значениях, необходимых для достижения конечной цели вычислений, нужно узнать, каков момент сопротивление сечения (формула № 2):
Wn(требуемое) = М мах / (Ry * Уc)
Необходимо обязательно уитывать ориентирование рассматриваемого балочного сечения, так как с уменьшением моментов инерций жесткость балок снижается, чего допускать нельзя. Для выяснения максимального значения нагрузки f, которое может выдержать балка, надо вычислить его по такой формуле № 3:
Для выяснения максимального значения нагрузки f, которое может выдержать балка, надо вычислить его по такой формуле № 3:
f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦], где
- L – продольный размер, в метрах
- E – коэффициент, показывающий упругость (для каждого материала или сплава он будет разным)
- J – момент инерции по сечению
- qn – это нагрузка, равномерно-распространенная, выражается в кг/м или в Н/м
Показатель J рассчитывается так:
J = b * h4 / 12
Обозначения:
- b – диаметр сечений
- h – вертикальный размер сечения
Примером для сечений, величиной 15 на 20 сантиметров:
J = 0,15 * (0,2)3 / 12 = 10 000 см4 или 0,0001 м4
Кроме указанных расчетных или табличных величин, среди важных факторов, которые нужно учитывать при определении максимальных нагрузок, выделяют такие: статические (которые действуют постоянно, независимо от переменных внешних факторов), периодические (действие ветра, вибрации, ударов).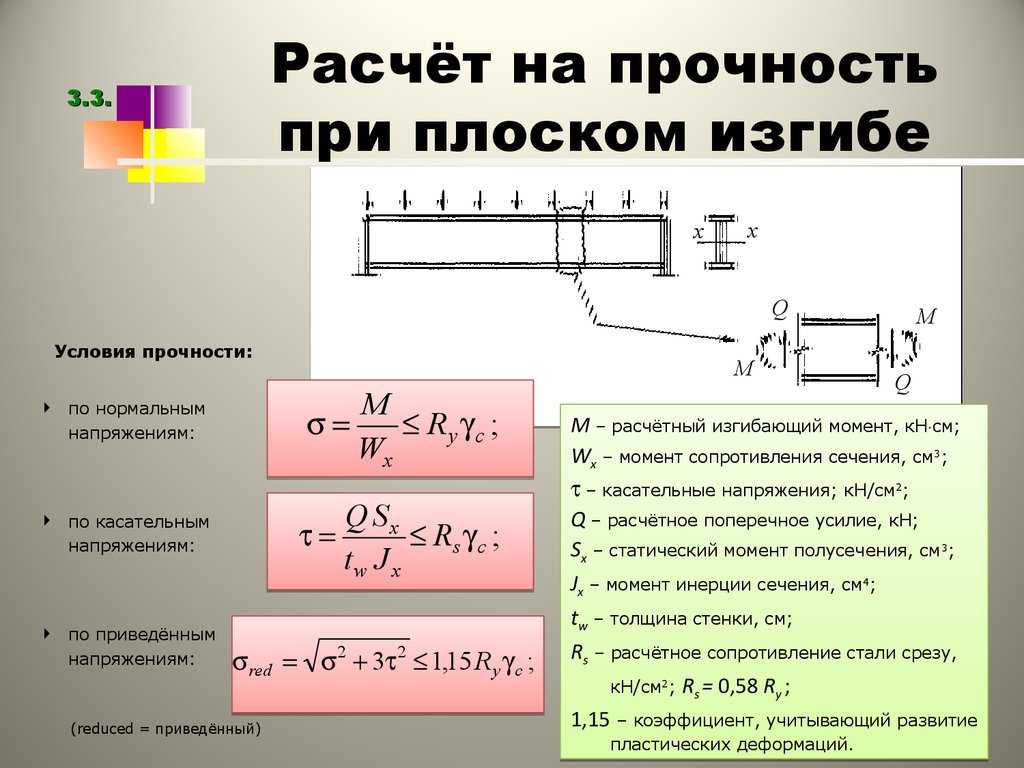
Дополнительные функции двутавра в частном домостроении
Сама перекрытие вовсе не обязательно должно состоять только из металлических двутавровых балок. Нередко их используют только в самых напряженных местах, а между металлическими частями устанавливают деревянные двутавры.
Почему так? Дело в том, что для сварки нужна высокая квалификация рабочих. Далее, в обычной литературе и интернет-сайтах нет того многообразия узлов и готовых схем конструкции для установки такого перекрытия, здесь действительно требуется грамотный инженер, и даже мы даем только рекомендации. Кроме того, металл обходится недешево. Да и качество сварки очень важно. Она должна работать долго, даже в условиях коррозии или перемены нагрузок.
Поэтому вот такой вариант не только имеет право на жизнь, но и достаточно практичен:
И, наконец, металлическая двутавровая балка нередко служит дополнительным функциональным элементов, который в любом хозяйстве имеет ценность:
Что собой представляет сварной двутавр?
По своему типу сечения двутавровые металлические балки сегодня принято делить на прокатные или составные, которые называются еще сварными. Сварная двутавровая балка – это особый вид фасонного металлического проката в форме наклонного или горизонтального бруса. Изготавливают ее сегодня из углеродистой и низколегированной стали, обязательно высокого качества.
Сварная двутавровая балка – это особый вид фасонного металлического проката в форме наклонного или горизонтального бруса. Изготавливают ее сегодня из углеродистой и низколегированной стали, обязательно высокого качества.
Давайте перечислим основные преимущества двутавровых сварных балок:
- Перекрывают большие пролеты со значительным нагрузками.
- Идеально перераспределяют горизонтальные и вертикальные нагрузки.
- Прекрасно работают на изгиб благодаря жесткости профиля балки.
- Не горят и не теряют свою несущую способность при нагревании даже достаточно высокими температурами.
- Устойчивы к биологическим воздействиям.
- Отлично подходят для строительства конструкции быстровозводимых зданий.
- Позволяют значительнее снизить массу всей конструкции, по сравнению с горячей корнями.
- Изготавливаются также с полностью ассиметричным сечением.
Вот почему такие сварные балки используются сегодня и в строительстве жилых домов, и для промышленных комплексов, и даже для мостов и тоннелей. Казалось бы, что такая балка будет слишком тяжелой для частного домостроительства, но на самом деле применение стальных двутавров позволяет в итоге сократить общий вес несущих конструкций. Но помните, что в отношении к перекрытию из сварных стальных двутавров существуют свои строгие требования:
Казалось бы, что такая балка будет слишком тяжелой для частного домостроительства, но на самом деле применение стальных двутавров позволяет в итоге сократить общий вес несущих конструкций. Но помните, что в отношении к перекрытию из сварных стальных двутавров существуют свои строгие требования:
Классические ошибки
Инженеры, не имеющие должного опыта, часто допускают некоторые ошибки при расчёте балок, а именно:
Слишком малое сечение, даже если оно и проходит по условиям прочности, может прогнуться больше нормативных значений, из-за чего перекрытие перестанет удовлетворять эксплуатационным требованиям.- Наоборот, слишком большое сечение приведёт к перерасходу материалов и повышенным затратам при строительстве.
- Неверно выбранное защемление балки повлияет на результат расчёта.
- При расчёте необходимо приводить все единицы к единому модулю, а, в противном случае, результат окажется далёким от истины.
Чтобы не совершать типичные ошибки, следует выполнять расчёт в соответствии с алгоритмом и фиксировать все промежуточные результаты. После выполнения расчёта следует несколько раз проверить результат. Если возникают сомнения, лучше сравнить подобранное сечение балки с аналогичными примерами.
После выполнения расчёта следует несколько раз проверить результат. Если возникают сомнения, лучше сравнить подобранное сечение балки с аналогичными примерами.
СОДЕРЖАНИЕ
- 1 Прогиб балки при различных нагрузках и опорах 1.1 Консольные балки 1.1.1 Консольные балки с торцевыми нагрузками
- 1.1.2 Равномерно нагруженные консольные балки
- 1.2.1 Простые балки с центральной нагрузкой
- 2.1 Международная система (SI)
Теория по методу начальных параметров
Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму.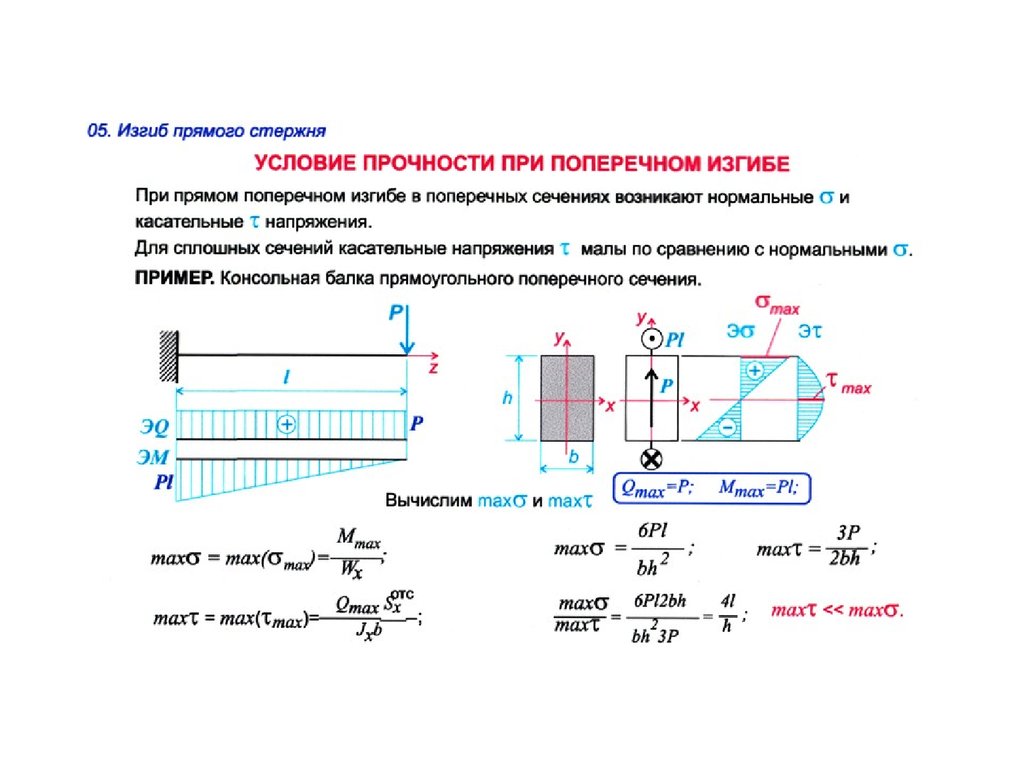 Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:
Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:
Выбор базы и обозначение системы координат
Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:
Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.
Универсальное уравнение прогибов для балки
После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:
- E – модуль упругости;
- I – момент инерции;
- Vk – прогиб сечения K;
- VO – прогиб сечения O;
- θO – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.
Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае Vk, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIVO:
Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθO всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.
Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.
Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:
В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.
Учет распределенной нагрузки
Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.
Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.
Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:
Правило знаков такое же, как и для сосредоточенных сил:
Граничные условия
Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: VK, VO и θO. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть VO=0 и θO=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.
Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах.
Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров.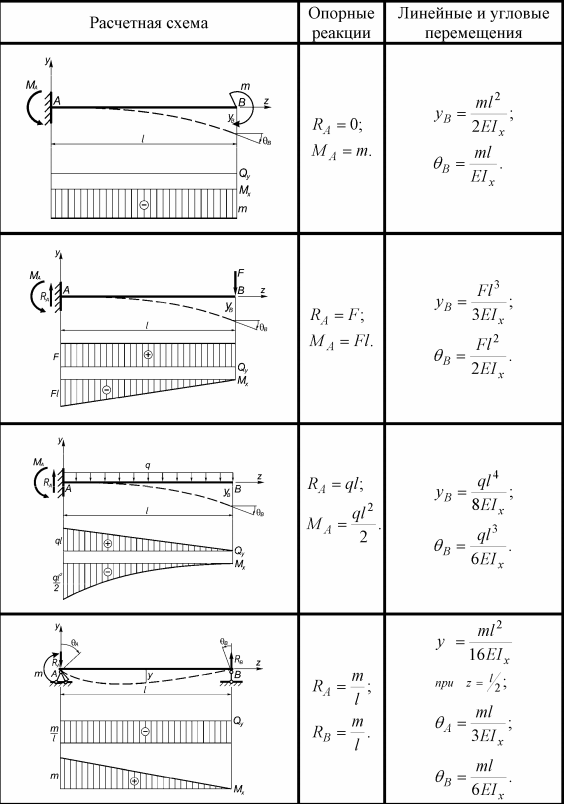 Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.
Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.
Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:
Пример 32. Расчет многопролетной балки
118 |
| на изгиб. |
| (Программа 32-n-opor2.mcd) | |
Если у многопролетной балки нет заделки на одном из ее концов, а есть только | ||
шарнирные опоры, то при работе в Mathcad расчет становится немного сложнее. Для | ||
грузовой и всех единичных систем потребуется определять опорные реакции. | ||
Условная схема расчета такой балки показана на рис. | ||
статически определимой системы возьмем балку на двух опорах. Оставляем крайние | ||
левую и правую опоры. Остальные отбрасываем и заменяем неизвестными | ||
реакциями | Xi . Грузовая и одна из единичных систем показаны на рис. 32П.2. | |
Исходные данные к расчету приведены на рис. 32П.3. | ||
y | M0 | q |
|
| F |
|
| x |
|
| q |
| aM |
|
| LRi |
|
| aF |
|
| aq |
|
|
| bq |
|
| x |
|
| L |
| Рис. | |
| Грузоваясистема |
y | q |
M 0 | |
| F |
| x |
| -q |
| aM |
| aF |
| aq |
| bq |
| x |
| L |
| i — яѝединичнаяѝсистема |
y |
|
| x |
LL | F = 1 |
| x |
| L |
Рис.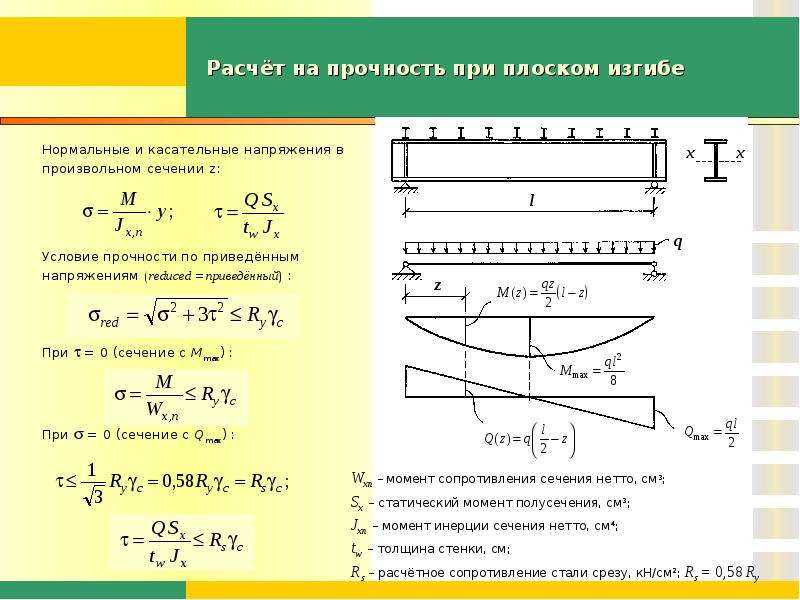 32П.2. Расчетные схемы для многопролетной балки
32П.2. Расчетные схемы для многопролетной балки
119
Рис. 32П.3. Исходные данные к расчету многопролетной балки
В примере12 (Определение внутренних усилий в балке на двух опорах)
опорные реакции определялись с помощью вычислительного блока Given-Find. При решении данной задачи этот блок вызывается тысячи раз и вычисление продолжается очень долго (больще 5 минут). Для ускорения процесса я решил вместо блока GivenFind вставить в программу формулы для определения реакций (рис. 32П.4). Реакции для грузовой системы вычисляются только один раз,. Там же на рис. 32П.4 показана эпюра изгибающих моментов для грузовой системы. а реакции единичной системы многократно, поэтому их определение оформлено в виде подпрограммы (рис. 32П.5), в которую вставлены конкретные формулы, полученные при преобразовании уравнений равновесия балки Замена вычислительного блока Given-Find на приведенную подпрограмму привело к уменьшению времени расчета примерно в сто раз.
Рис. 32П.4. Внутренние усилия в грузовой системе
120
Рис. 32П.5. Расчет многопролетной балки методом сил
32П.5. Расчет многопролетной балки методом сил
После определения внутренних усилий с учетом реакций последующие вычисления проводятся также как в примере 31 и приведены на рис. 32П.5 – 32П.7.
Рис. 32П.6. Результаты расчета многопролетной балки
121
Рис. 32П.7. Проверка правильности расчета многопролетной балки
| Пример 33. Подбор размеров сечения |
122 | сжатого стержня. |
(Программа 33-ustoi1.mcd)
Для стержня круглого поперечного сечения длиной L = 2 м, нагруженного силой F = 80 кН (рис. 33П.1), требуется определить диаметр стержня.
Рис. 33П.1. Схема нагружения стержня
Поскольку размеры сечения стержня неизвестны, а значит и гибкость стержня λ неизвестна, то расчет ведется итерационным методом.
Исходные данные для расчета стержня приведены на рис. 33П.1. На рис. 33П. 2 приведены справочные данные: зависимость коэффициента снижения допускаемого
напряжения ϕ от гибкости стержня λ . Для автоматизации расчета введена функция интерполяции и построен график зависимости ϕ от λ (рис. 33П.2).
Для автоматизации расчета введена функция интерполяции и построен график зависимости ϕ от λ (рис. 33П.2).
Рис. 33П.2. Зависимость коэффициента снижения допускаемого напряжения ϕ от гибкости стержня λ .
В справочниках приводятся значения коэффициента ϕ для λ ≤ 200. На всякий случай, в массивы данных введено ϕ = 0, 01 для λ =1000 ,так как в ходе
итерационного процесса могут появляться значения λ > 200. На графике это значение не показано.
Поскольку расчет выполняется многократно, он оформлен в виде программы (рис. 33П.3), состоящей из головной программы D , внутри которой многократно вызывается подпрограмма dλ определения диаметра и гибкости стержня.
123
Рис. 33П.3. Программа расчета диаметра сжатого стержня
В начале головной программы введены значения коэффициента ϕ : в начале ϕ1, в
конце итерации | ϕ2 и счетчик числа итераций | j . В нашем расчете для первой |
итерации взят | совершенно неправдоподобный | коэффициент ϕ1 = 0,9 , чтобы |
показать, что и в этом случае расчет сходится довольно быстро.
Затем следует итерационный цикл, начинающийся оператором while — повторять цикл до выполнения заданного критерия (пока расхождение между ϕ1 и ϕ2 не
станет меньше 0,1%).
Вся программа выделена длинной вертикальной чертой слева, итерационный цикл выделен второй вертикальной чертой.
В подпрограмме dλ последовательно вычисляются допускаемые напряжения на устойчивость σу , площадь сечения A , диаметр стержня d , момент инерции J ,
радиус инерции i и гибкость стержня λ .
В конце итерации определяется новое значение коэффициента ϕ с помощью функции интерполяции ϕ(λ), показанной на рис. 33П.2.
Для начала следующей итерации вычисляется усредненное новое значение ϕ1.
Далее следует возврат к началу цикла итерации, но перед этим организуется вывод результатов расчета каждой итерации.
Значения ϕ, λ, d на каждой итерации записываются в массивы ϕϕ, λλ,dd .
Поскольку программа выводит численные значения последнего оператора, то в качестве последнего оператора поставлен составной массив: вектор, содержащий три вложенных массива и записанный в виде строки для экономии места в программе.
При отладке программ в составной массив можно включать результаты любых внутренних операторов программы.
Рис. 33П.4. Результаты расчета на каждой итерации
Результаты расчета показаны на рис.33П.4. Несмотря на высокую точность расчета (0,1%) четырех итераций оказалось достаточно для достижения указанной точности.
| Пример 34. Определение критических |
124 | нагрузок энергетическим методом. |
(Программа 34-ustoi2.mcd)
Пример 1
Для схемы Эйлера (рис. 34П.1) определим критическую силу энергетическим методом.
Рис. 34П.1. Результаты расчета на каждой итерации
В общем случае изогнутую ось стержня будем аппроксимировать полиномом степени m
m
u(x) = C0 +C1x + C2 x2 + C3 x3 +… = ∑Ci xi .
i=0
Значения коэффициентов Ci определяем из граничных условий (условий
закрепления стержня), решая систему уравнений с помощью вычислительного блока given – find (рис. 34П.2). Поскольку в программе нумерация коэффициентов начинается с 1 (ORIGIN=1), вид выражения полинома отличается от написанного выше.
34П.2). Поскольку в программе нумерация коэффициентов начинается с 1 (ORIGIN=1), вид выражения полинома отличается от написанного выше.
Рис. 34П.2. Определение коэффициентов аппроксимирующего полинома
Для стержня шарнирно закрепленного с двух концов граничными условиями
являются равенство нулю | прогиба на опорах u(0) = 0 | и u(L) = 0 , | а также | |||
равенство нулю изгибающих моментов на концах стержня M (0) = 0 и M (L) = 0 . | ||||||
Но изгибающий момент | пропорционален второй | производной от | прогиба | |||
′′ |
| ′′ | = 0 | и u | ′′ |
|
M = EJu (x) , следовательно, на концах стержня u | (0) | (L) = 0 . |
| |||
ПРИМЕЧАНИЕ
Внутри блока given – find нельзя использовать в качестве условий производные. Граничные условия не могут вычисляться внутри блока given – find, поэтому каждой производной в программе присваивается имя функции, а в вычислительный блок записывается значение функции от заданного аргумента, например, для
второй производной u2(0, C) = 0 .
В рассмотренном примере используется полином четвертой степени, имеющий 5 неизвестных коэффициентов, следовательно, в вычислительный блок надо подставить 5 граничных условий. Однако в виду симметрии системы пятое условие
125(равенство нулю угла поворота сечения посередине балки) выполняется автоматически.
Кроме того, в формулу Рэлея входят лишь первая и вторая производные от прогиба, поэтому в расчете используются не 5, а 4 коэффициента. Кроме того, два коэффициента оказались равны нулю.
В общем, подбирая степень полинома, смотрите на его график. Главное, чтобы выполнялись граничные условия. Помните, что решение мы ищем приближенное, что подбираемый «на глазок» полином никак не учитывает различие в форме и размерах сечений по длине стержня.
Помните, что решение мы ищем приближенное, что подбираемый «на глазок» полином никак не учитывает различие в форме и размерах сечений по длине стержня.
Решение системы нелинейных алгебраических уравнений требует использования нелинейных методов решения. Щелкните правой кнопкой мыши на имени функции find и в открывшемся контекстном меню выберите метод решения Nonlinear.
На рис. 34П.3 приведен вектор коэффициентов полинома и графики прогиба стержня и его первой и второй производных.
Рис. 34П.3. Графики аппроксимирующего полинома и его первой и второй производных
Рис. 34П.4. Формула Рэлея определения критической силы
На рис. 34П.4 записана формула Рэлея и приведено расчетное значение Pкр .
Выведено численное значение критической силы для заданного стержня и числовой коэффициент при буквенном выражении.
На том же рисунке предлагается проверить другой вид аппроксимации уравнения изогнутой оси стержня. При выводе формулы Эйлера использовалась синусоида для описания изогнутой оси.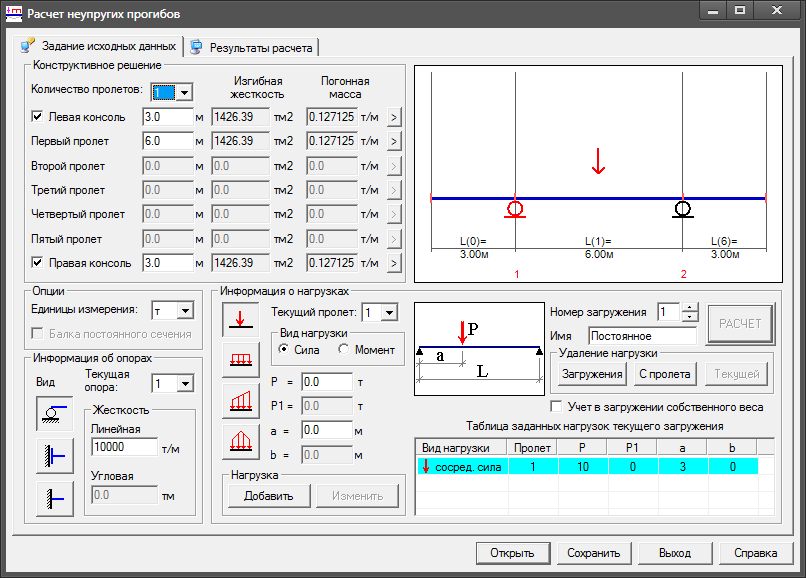 Включите выражение синусоиды и убедитесь, что результаты расчета совпадают для обоих видов аппроксимации изогнутой оси стержня.
Включите выражение синусоиды и убедитесь, что результаты расчета совпадают для обоих видов аппроксимации изогнутой оси стержня.
Пример 2
Определить нагрузку, соответствующую потере устойчивости для ступенчатого стального стержня с двумя заделками и промежуточной шарнирной опорой, нагруженного двумя силами (рис. 34П.5).
126
Рис. 34П.5. Схема нагружения ступенчатого стального стержня
Нижняя заделка неподвижная, верхняя подвижная. Промежуточная шарнирная опора установлена на границе нижней (толстой) части стержня и верхней (тонкой). Поскольку ищем нагрузку, то задано лишь соотношение сил на свободном конце и на
границе участков F1 = 2F2 . Исходные данные для расчета приведены на рис. 34П.6.
Рис. 34П.6. Исходные данные для расчета на устойчивость ступенчатого стержня
Граничными условиями для изогнутой оси стержня являются равенство нулю прогибов в заделках и шарнирной опоре и равенство нулю углов поворота в заделках. Имеем 5 граничных условий.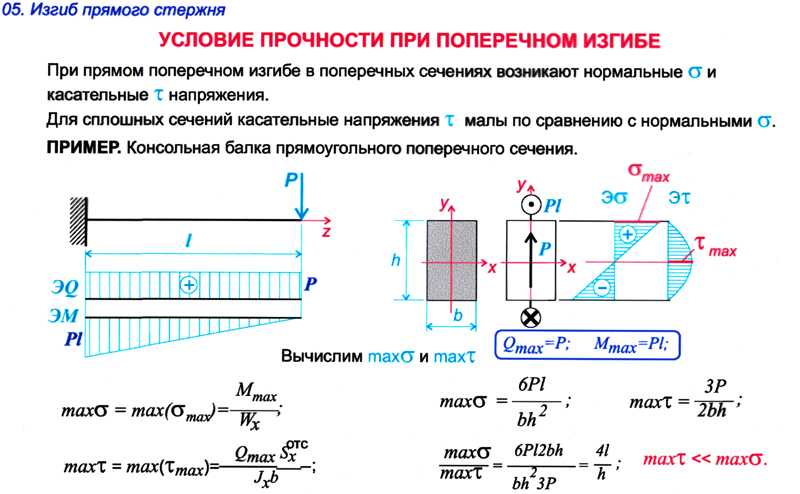 Ищем полином 5-й степени (рис.34П.7). Графики полинома и его первой и второй производных показаны на рис. 34П.8. Критические
Ищем полином 5-й степени (рис.34П.7). Графики полинома и его первой и второй производных показаны на рис. 34П.8. Критические
значения сил F1 и F2 приведены на рис. 34П.9.
Рис. 34П.7. Подбор коэффициентов аппроксимирующего полинома
127
Рис. 34П.8. Графики аппроксимирующего полинома и его производных
Рис. 34П.9. Определение критических нагрузок на ступенчатый стержень
Приведенная программа позволяет приближенно определять критическую нагрузку при действии нескольких сил и нескольких участках различной формы сечения. Степень полинома определяем, исходя из числа граничных условий и «на глазок» по виду графика полинома и его производных.
Калькулятор прогиба балки с простой опорой
Танвеш
Магистр строительных конструкций | Научный интерес — искусственный интеллект и машинное обучение в гражданском строительстве | Ютубер | Учитель | В настоящее время работает научным сотрудником в NIT Goa
.
 Содержание
СодержаниеСвяжитесь с нами:
Если вы обнаружите какую-либо ошибку в этом калькуляторе, мы будем очень признательны за ваши отзывы.
Пожалуйста, напишите по адресу [email protected]
Калькулятор прогиба балки с простой опорой для точечной нагрузки, udl, uvl, трапециевидной, треугольной нагрузки для прогиба, наклона, изгиба, фиксированного конечного момента и формулы сдвига.
Расчет балки на простой опоре
Прочие калькуляторы
Что такое свободно опертая балка
Если балка закреплена при перемещении в обоих направлениях на одном конце и только в одном направлении на другом конце и не закреплена против вращения на обоих концах, называется свободно опертой балкой.
Проще говоря, один конец шарнирный, другой конец роликовый, однако это определение может быть изменено, и оба конца, являющиеся шарнирной опорой, также могут рассматриваться как свободно опертая балка.
Как пользоваться калькулятором
Этот вычислитель трапециевидной нагрузки на свободно опертой балке запрограммирован для расчета профиля прогиба, уклона, диаграммы поперечной силы (sfd), диаграммы изгибающего момента (bmd) и осевых реакций.
Требуются: модуль Юнга (E) материала, длина (L) балки, момент инерции площади (I), интенсивность нагрузки (w1), расстояние, на котором действует w1 ‘a’, интенсивность нагрузки w2 и расстояние при который w2 действует как ‘b’.
Свободно опертая балка с трапециевидной нагрузкой может быть преобразована в udl при сохранении интенсивности нагрузки w1=w2. Та же самая нагрузка может быть преобразована в udl, если оставить любой из них равным нулю.
Свободно опертая балка с трапециевидной нагрузкой
Свободно опертая балка с трапециевидной нагрузкойВыдерживаемое расстояние a=b=0 и расстояние c=d=L; пусть интенсивность 1 будет w1, а интенсивность 2 будет w2.
Параметр
Значения
Реакция в A
V_{A}=\left(w_{1} * L\right)+\left(\frac{\left(w_{2}-w_{1}\right) * L}{2 }\справа)-V_{B} 9{3}}{30}
Свободно опертая балка с udl
Свободно опертая балка с udl может быть проанализирована с помощью «Калькулятора 1», выбрав тип нагрузки как «UDL».
Свободно опертая балка, несущая половину udl, будет иметь расстояние «a» = 0, расстояние «b» = L/2 или расстояние «a» = L/2 и расстояние «b» = L.
Для свободно опертой балки при равномерно распределенной нагрузке по всей длине расстояние ‘a’ = 0, а расстояние ‘b’ = L.
Все единицы могут быть изменены пользователем.
Свободно опертая балка будет иметь реакцию момента на обоих концах, равную 0, и вертикальную реакцию на обоих концах. Уклон на обоих концах не будет равен 0.
Свободно опертая балка с формулой udl
Свободно опертая балка с udlПараметр
Значения
Реакция в A
V_{A}=\left(w * L\right) -V_{B}
Реакция в B
V_{B}=\left(\frac{w L}{2}\right)
Уравнение момента
9{3}}{30}Свободно опертая балка с UVL
Для свободно опертой балки с uvl используйте «Калькулятор 1» и выберите тип нагрузки «Треугольный».
Свободно опертая балка с uvl (левосторонней) формула
Свободно опертая балка с uvl левостороннейПараметр
Значения
Реакция в A
V_{A}=\left(\frac{w * L}{2}\right)-V_{B}
Реакция в B
V_{B}=\frac{w*L}{3} 9{3}}{30}
Свободно опертая балка с точечной нагрузкой
Для свободно опертой балки с точечной нагрузкой используйте «Калькулятор 2» с типом нагрузки «Точечная нагрузка».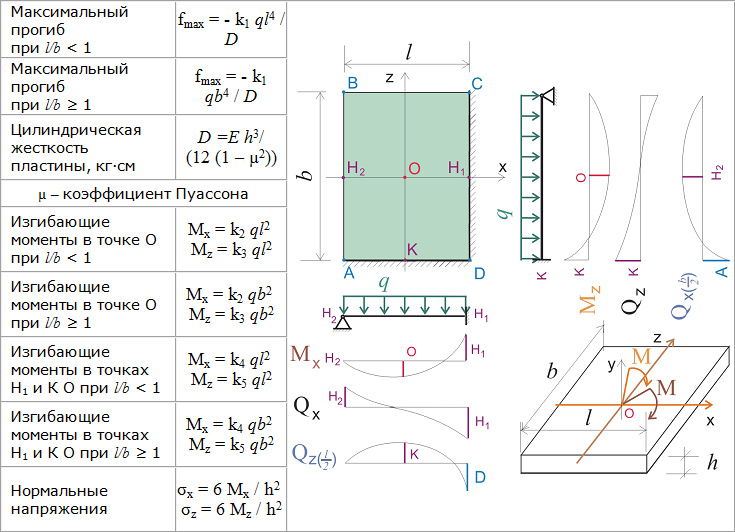
Точечная нагрузка считается идеализацией в инженерной механике, так как любая физическая нагрузка с очень малой площадью контакта может быть идеализирована как точечная нагрузка.
Ниже представлен случай для свободно опертой балки с точечной нагрузкой, действующей в центре или в середине пролета. Для этого расстояние «а» = L/2. 9{2}}{48}
Свободно опертая балка с моментом
Для свободно опертой балки с моментом используйте калькулятор 2 и выберите тип нагрузки как Момент.
Случай 1: Для свободно опертой балки с моментом в центре положить расстояние «a» = L/2.
Случай 2: Для свободно опертой балки с моментной нагрузкой на одном конце введите расстояние «a» = 0 или расстояние «a» = L.
Случай 3: Для свободно опертой балки с моментом на обоих концах вы можете алгебраически сложить результаты случая 2, сохраняя расстояние ‘a’ = 0 и расстояние ‘a’ = L соответственно. 9{2}}{2 л}
Последние сообщения
Просто поддерживаемая балка: ручной расчет момента и сдвига
Последнее обновление: 30 декабря 2022 г. самые основы проектирования конструкций и делать ручные расчеты.
самые основы проектирования конструкций и делать ручные расчеты.
Начав эту новую серию стоек с консольной балкой, мы продолжим наше путешествие с, вероятно, наиболее используемой статической системой — 92/8$$
и как рассчитать изгибающие моменты и поперечные силы для различных ситуаций нагрузки.
Не будем долго говорить, давайте начнем.
🙋♀️ Что такое свободно опертая балка?
Штифтовая и роликовая опора.Свободно опертая балка — это статическая система, действующая как элемент балки при изгибе и сдвиге, а в некоторых случаях также при сжатии или растяжении под действием осевых сил. Он характеризуется наличием двух опор, роликовой и шарнирной опоры. Эти опоры допускают вращение.
В повседневной жизни нас окружают свободно опертые балки.
Вот 7 примеров свободно опертых балок в реальной жизни
- Однопролетная сборная железобетонная балка
- Однопролетная сборная железобетонная плита
- Настил однопролетного моста, опирающийся на подшипники
- Деревянная плоская крыша с второстепенными балками
- Однопролетная стальная балка
- Стропильные балки, опирающиеся на 2 прогона
- Скамейки с опорой на обоих концах (пример ниже)
Свободно опертая балка в большинстве случаев представляет собой горизонтальную балку с роликом и шарнирной опорой на концах. Балка может воспринимать нормальные и поперечные силы, а также изгибающие моменты.
Балка может воспринимать нормальные и поперечные силы, а также изгибающие моменты.
Давайте посмотрим на статическую систему.
Статическая система свободно опертой балкиИз рисунка видно, что шарнирная опора (а) воспринимает
- вертикальную силу реакции $V_a$ и
- горизонтальная сила реакции $H_a$
Роликовая опора (b) воспринимает
- вертикальную реактивную силу $V_b$
🏢 Свободно опертая балка, применяемая к реальным конструкциям
Понимание статической системы конструкции, вероятно, является одной из самых сложных частей статики и проектирования конструкций в начале.
По моему опыту, этому также плохо учат в университете, да и информации о нем в сети очень мало, не так ли?
Итак, давайте рассмотрим несколько прикладных примеров.
- Второстепенные балки плоской крыши. Обратите внимание, что основные балки также могут просто поддерживаться. В нашем примере просто поддерживаются только второстепенные балки.
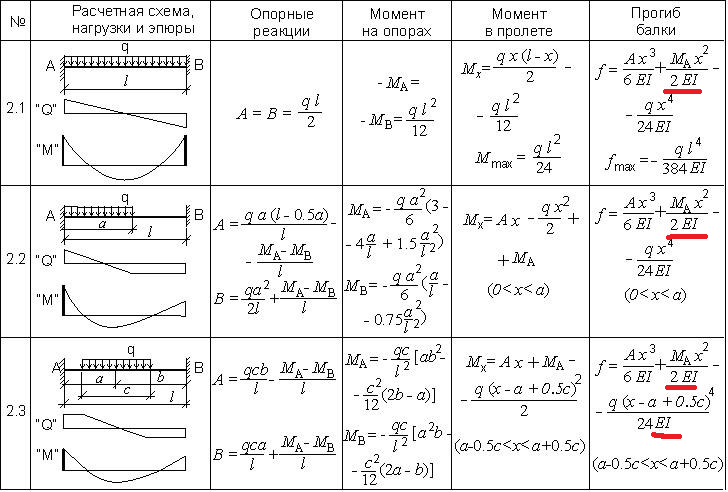
- Деревянные балки/панели этой скамьи просто поддерживаются.
⬇️ 2 примера ситуаций загрузки
Мы хотим, чтобы в этом блоге было немного радостно и реалистично, верно? Итак, давайте посмотрим на сценарии загрузки, к которым мы все можем относиться.
🧍 Я сижу и медитирую на скамейке — Точечная нагрузка
Давайте рассмотрим пример, где человек — в данном случае я😊 — сидит на скамейке и медитирует🧘♂️. Предположим, я немного прибавил в весе по сравнению с прошлым уроком, и теперь я вешу 76 кг.
Я медитирую на простой скамье.Этот вес 76 кг можно напрямую перевести в 0,745 кН.
Теперь, поскольку я сижу прикладом в определенной точке, нагрузка сосредоточена, и поэтому 0,745 кН можно приблизительно определить как точечную нагрузку на свободно опертую балку(и).
❗Поэтому всегда помните о своих приближениях и думайте, применимы ли они к тому, чего вы хотите достичь.
Поскольку мы хотим продемонстрировать «реальный» пример точечной нагрузки, эта точечная нагрузка не является на 100% реалистичной.
Однако «100% правильных» точечных нагрузок почти не бывает, и человек, сидящий на скамье, подходит достаточно близко к точечной нагрузке, приложенной к скамье, для определения толщины и ширины деревянной балки.
Хорошо, вернемся к модели луча.
3 балки скамьи равны 1 балке, когда мы вычисляем моменты и поперечные силы с помощью этого простого подхода.
Таким образом, мы можем применить точечную нагрузку к статической системе свободно опертой балки.
Точечная нагрузка, приложенная к скамейке.🏋️ Собственный вес деревянной балки – Линейная нагрузка
Итак, деревянная балка имеет собственный вес, верно? Я думаю, каждый может представить это, когда вы пытаетесь поднять его.
В проектировании конструкций мы также называем это постоянной нагрузкой , и он всегда одинаково/равномерно распределен для горизонтальных элементов.
Для деревянной второстепенной балки собственный вес на $м$ рассчитывается как
$\mbox{Плотность} \, \rho \cdot \mbox{Площадь поперечного сечения A} \,$
Плотность деревянных балок находится либо в таблицах производителей в Интернете, либо в Стандартах.
Площадь поперечного сечения деревянной балки взята из предыдущей статьи, где мы проектировали плоскую крышу и ее балки.
92 = 0,11 \mbox{кН/м}$Теперь всегда помогает перевести кН на нетехнический язык. $0,11$ кН/м также составляет 10,9 кг на $м$.
Это примерно столько же, сколько французского бульдога , но за метр и за пучок! Таким образом, в случае с нашей деревянной балкой, где у нас есть пролет в 5 миллионов долларов, собственная нагрузка на древесину равна 5 собакам🐕.
Статическая нагрузка вторичной деревянной балки примерно равна 5 французским бульдогам. Эта линейная нагрузка (кН/м) — или эти 5 собачек — теперь также может быть применена к просто поддерживаемая балка.
🧮 Ручной расчет изгибающего момента и поперечных сил – свободно опертая балка
Теперь, чтобы рассчитать толщину и свойства материала скамьи, второстепенной балки или любой другой свободно опертой конструкции, силы и моменты, действующие в балке, должны быть быть рассчитаны.
Как правило, статически определяемые конструкции, такие как консольные или свободно опертые балки, должны удовлетворять трем условиям равновесия:
- Горизонтальное равновесие $\sum H = 0$: Сумма всех горизонтальных нагрузок и реакций равна 0.
- Вертикальное равновесие $\sum V = 0$: Сумма всех вертикальных нагрузок и реакций равна 0.
- Момент равновесия $\sum M = 0$: Сумма всех моментов равна 0.
Давайте продолжим с двумя ситуациями нагружения, с которыми мы уже знакомы — точечной и линейной нагрузкой.
🔎 Изгибающий момент и поперечные силы балки – Точечная нагрузка на скамью
1. Первое, что мы всегда рассчитываем в детерминированных конструкциях, это силы реакции/момент . В нашем случае это $V_a, H_a$ на опоре (a) и $V_b$ на опоре (b) в силу условий равновесия.
Первое, что мы всегда рассчитываем в детерминированных конструкциях, это силы реакции/момент . В нашем случае это $V_a, H_a$ на опоре (a) и $V_b$ на опоре (b) в силу условий равновесия.
$\sum H = 0: H_a = 0$
$\sum V = 0: V_a + V_b – 0,745 \mbox{kN}= 0 =$ -> $V_a = V_b = \frac{0,745}{2} \mbox{kN} = 0,3725 \mbox{kN}$
$\sum M = 0: M_a = 0$
2. Расчет распределения сдвига и момента вдоль балки за счет сил реакции. Параметр x вводится как длина между точкой a и любой точкой на балке.
Параметр x 3. Перерезывающие силы и изгибающие моменты можно рассчитать в зависимости от x. Сделаем первый разрез в точке между опорой и точечной нагрузкой 0 Как и при расчете силы реакции, условия равновесия используются для расчета момента и поперечной силы в точке x $\sum H = 0: H_a = 0$ $ \сумма V = 0: 0,3725 \mbox{кН} – V_x = 0$ -> $V_x = 0,3725 \mbox{кН}$ $\sum M = 0: M_x – 0,3725 \mbox{кН} \cdot x = 0$ -> $M_x = 0,3725 \mbox{кН} \cdot x$ Как мы видим, поперечная сила постоянна и не зависит от параметра x. $M_{1,0м} = 0,3725 \mbox{кН} \cdot 1,0м = 0,3725 \mbox{кНм}$ В зависимости от x и точечной нагрузке Q = 0,745 кН общую формулу для изгибающего момента свободно опертой балки при 0 $M_{x} = 1/2 \cdot Q \cdot x$ Возможно, вы уже встречались с формулой, когда мы устанавливали x=l/2 $M_{max} = 1/2 \cdot Q \cdot l/2 = 1/4 \cdot Ql$ 4. Разрез в точке между точечной нагрузкой и конечной точкой 1,0м Условия равновесия приводят к $\sum H = 0: H_a = 0$ $\sum V = 0: 0,3725 кН – V_x – 0,745 кН = 0$ -> $V_x = -0,3725 кН$ $\sum M = 0: M_x – 0,3725 кН \cdot x + 0,745 кН \cdot (x-1,0м) = 0$ 0,3725 кН \cdot x + 0,745 кНм$ 5. Диаграммы изгибающего момента и поперечной силы Диаграммы можно построить с помощью инструмента, такого как Excel, с использованием приведенных выше формул или нарисованы от руки, если известна геометрическая форма распределения. Диаграмма поперечной силы – свободно опертая балка Диаграмма изгибающего момента – свободно опертая балка 1.Что касается точечной нагрузки, сначала мы вычисляем силы реакции $V_a, H_a$ и момент $M_a $ в детерминированной конструкции – свободно опертой балке – из-за условий равновесия. $\sum H = 0: H_a = 0$ $\sum V = 0: V_a + V_b – 0,11 \mbox{кН/м} \cdot 5,0m = 0$ -> $V_a = 0,5 \cdot 0,11 \ mbox{кН/м} \cdot 5\mbox{м} = 0,275 \mbox{кН}$ $\sum M = 0: M_a = M_b = 0$ 2. Расчет распределения сдвига и момента вдоль балки за счет сил реакции. 3. Перерезывающие силы и изгибающие моменты можно рассчитать в зависимости от x. Сделаем разрез в точке между опорой а и опорой b 0 Формула для максимальной поперечной силы в свободно опертой балке $ql/2$ Что касается изгибающего момента, мы заменяем значения нагрузки и реакции на переменные. В качестве q используется линейная нагрузка 0,11 кН/м, а сила реакции $V_a$ равна ql/2. $V_{x} = q \cdot l/2 – q \cdot x $ Теперь максимальное усилие сдвига действует непосредственно рядом с опорами, поэтому x устанавливается равным 0 или l $V_{ 0} = q \cdot l/2 – 0 $ $V_{0} = 0,11 \mbox{кН/м} \cdot 5\mbox{м}/2 = 0,275\mbox{кН}$ 4. Диаграммы изгибающего момента и поперечной силы Диаграммы могут быть построено с помощью инструмента, такого как Excel, с использованием приведенных выше формул или нарисовано вручную, если известно геометрическую форму распределения.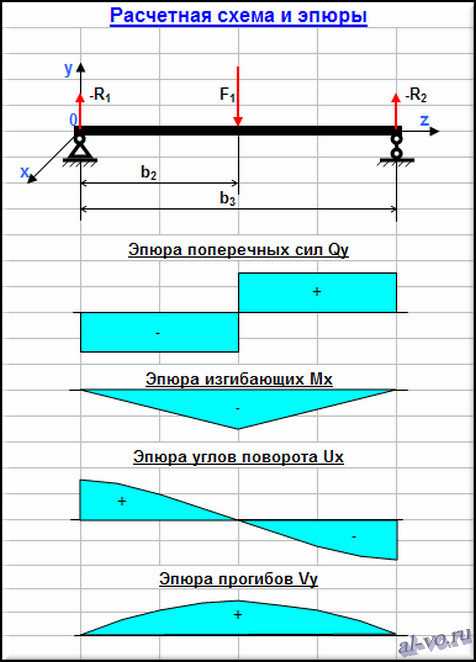 Положим x = 1,0м и посмотрим, какие результаты мы получим для изгибающего момента:
Положим x = 1,0м и посмотрим, какие результаты мы получим для изгибающего момента:
👨🏫 Изгибающий момент и поперечные силы балки – Линейная нагрузка на второстепенную балку крыши
 Параметр x вводится как длина между точкой a и любой точкой на балке.
Параметр x вводится как длина между точкой a и любой точкой на балке.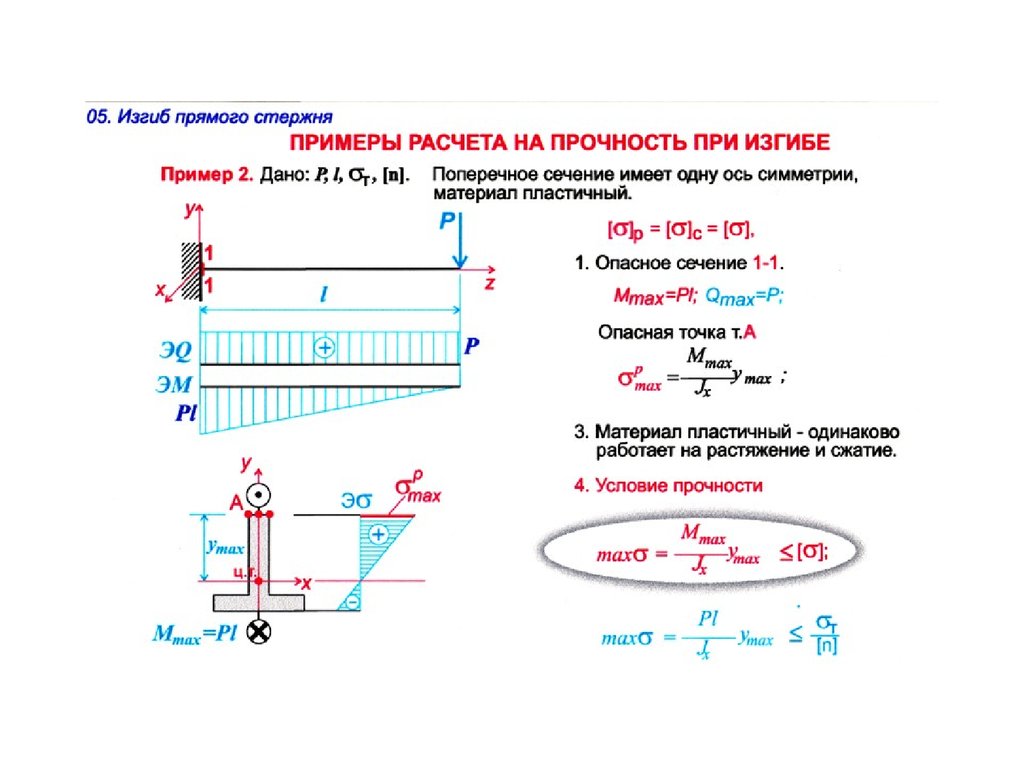
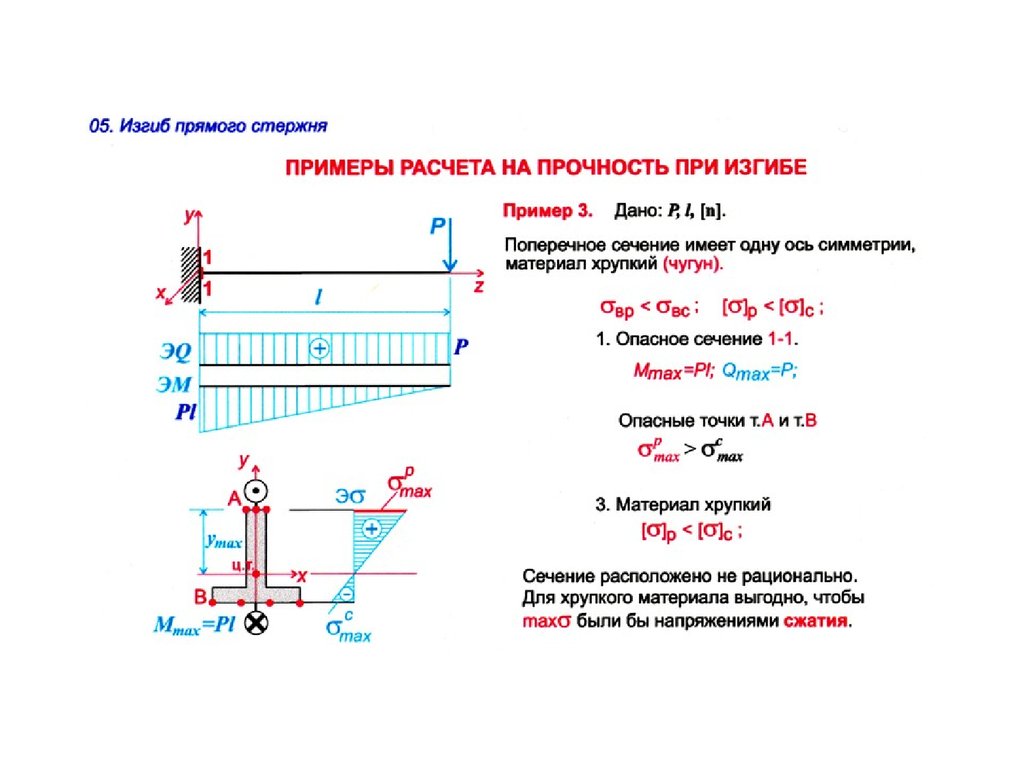 32П.1. В качестве основной
32П.1. В качестве основной 32П.1. Условная схема нагружения многопролетной балки
32П.1. Условная схема нагружения многопролетной балки