Расчет плит на упругом основании методом последовательных аппроксимаций
Список источников диссертации и автореферата по механике, кандидата технических наук, Исматов, Махмуд Хасанович, Москва
1. Абовский Н.П., Енджиевский Л.В. К расчету пластинчатых систем дискретными методами строительной механики.-Известия Вузов. Строительство и архитектура, 1966, № 12, с.40-43.
2. Альберг Дж., Нильсон Э., Уолш Дж. Теория сплайнов и ее приложения. Перевод с англ. М., Мир, 1972, 318с.
3. Александров А.В. Дискретная модель для расчета ортотропных пластин и оболочек.-Груды ШИТ, вып. 364, М., 1971, с.3-10.
4. Александров А.В. Численное решение линейных дифференциальных уравнений при помощи матрицы дифференцирования.-Труды МИИТ, вып. 131, М., 1961, с.253-266.
5. Александров А.В.Дащеников Б.Я., Шапошников Н.Н., Державин Б.П. Применение метода перемещений для расчета плит на упругом основании.-Труды МИИТ, вып.
371, М., 1971, с.66-93.
6. Аргирис Дж. Энергетические теоремы и расчет конструкций.
7. В кн.: Современные методы расчета сложных статически неопределимых систем. Сб. статей, перевод с англ. под ред. цроф. Филина А.П., Судцромгиз, Л., 1961, с.37-110.
8. Атаров Н.М. Некоторые вопросы расчета конструкций, взаимодействующих с упругим основанием.-Автореферат кандидатской диссертации. М., МИСИ, 1971, 13с.
9. Атаров Н.М., Леонтьев Н.Н. Расчет жесткой балки на комбинированном основании.-Сб. трудов МИСИ, 1,1., 1978, М56, с.57-64.
10. Бабанов В.В. Исследование напряженно деформированного состояния конструкций на упругом основании методом конечных элементов.-Автореферат кандидатской диссертации. Л., ЛИСИ, 1975, 22с.
11. Барвашов В.А. Комбинированные модели грунтового основания.-Основания, фундаменты и механика грунтов, 1976, is I, с.34-36.
12. Бобрицкий Г.М. Численный метод расчета фундаментных плит на неоднородном сжимаемом основании. НИИСК Госстроя УССР, Киев,- 17b 1970, 53c.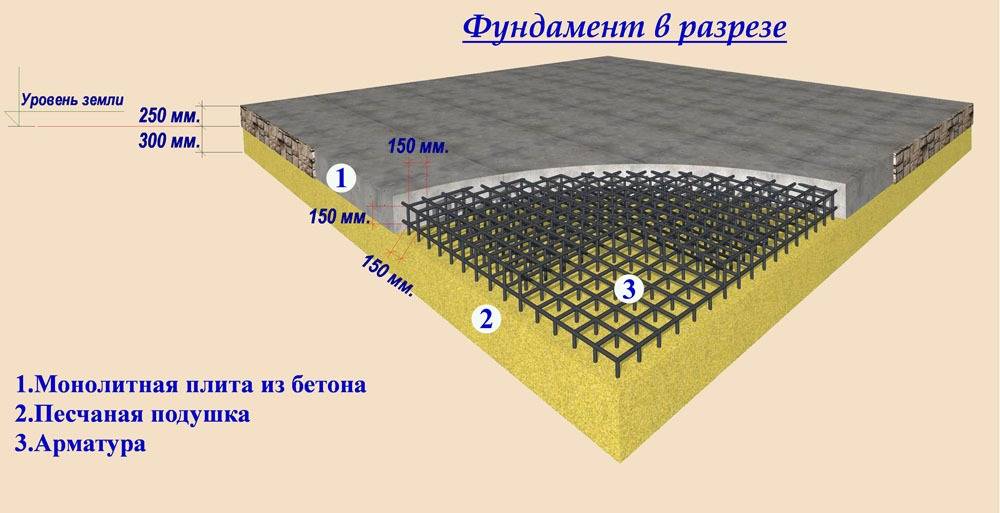
13. Болотин В.В. Об упругих деформациях подземных трубопроводов, прокладываемых в статистически неоднородном грунте.-Строительная механика и расчет сооружений, 1965, № I, с.4-8.
14. Вайнберг Д.В., Геращенко В.М., Ройтфорб И.З., Синявский АЛ. Вывод сеточных уравнений изгиба пластин вариационным методом. -Сопротивление материалов и теория сооружений, вып. I, Киев, «Будьвельник», 1965.
15. Вайнберг Д.В., Ворошко П.П., Геращенко В.М., Ройтфарб И.З., Синявский А.Л. Разностные уравнения контактной задачи изгиба пластин.-Сопротивление материалов и теории сооружений, вып.З, Киев, «Будьвельник», 1965, с.27-40.
16. Вайнберг Д.В. Справочник по прочности, устойчивости и колебаниям пластин. Киев, «Будьвельник», 1973, 488с.
17. Варвак А.П. Прямоугольные плиты переменной жесткости на упругом основании.-Доклады АН УССР, № 10, 1963, с.1318-1320.
18. Варвак А.П. Расчет плит на упругом основании и сваях.-Строительство и архитектура, вып.8, Киев,изд.Госстроя УССР, 1963, с.
33-36.
19. Варвак П.М. Развитие и приложение метода сеток к расчету пластинок, ч. I, 1949; ч. 2, 1952, 116с.
20. Варвак П.М., Губерман И.О., Мирошниченко М.М., Предтеченс-кий Н.Д. Таблицы для расчета прямоугольных плит. Киев, Изд-во АН УССР, 1959., 419с.
21. Варвак П.М., Варвак А.П. Метод сеток в задачах расчета строительных конструкций. Стройиздат, М., 1977, 160с.
22. Вахитов М.Б., Сафариев М.С. Применение метода прямых для расчета пластин.-Труды КЛИ, вып.143, Казань, 1972,с.59-67.
23. Вахитов М.Б., Борисов М.В. Расчет прямоугольных пластин с помощью интегрирующих матриц.-В сб.: Вопросы расчета прочности конструкции летательных аппаратов, вып.1, Казань,1976, с.7-11.
24. Винокуров Л.П. Расчет плит на упругом полупространстве с применением инженерно-дискретного метода.-Вестник инженеров и техников, }£ 4, 1951, с.166-171.
25. Владимиров В.Ф. Эффективность метода конечного элемента для решения задач об изгибе плит.-Кандидатекая диссертация,1. ГЛ., 1973, 150 л.
с ил.
26. Власов В.З., Леонтьев Н.Н. Техническая теория расчета фундаментов на упругом основании. -Труды 1.1ИСИ, J3 14, 1956,с.12-31.
27. Власов В.З., Леонтьев Н.Н. Балки, плиты и оболочки на упругом основании. М., Физматгиз, I960, 491с.
28. Высоковский В.Л., Соломин В.И., Сытник А.С. Расчет фундаментных плит сложной конфигурации.-Строительная механика и расчет сооружений, 1977, В 2, с.39-41.
29. Габбасов Р.Ф. 0 численно-интегральном методе решения краевых задач строительной механики для дифференциальных уравнений в частных производных.-Исследования по теории сооружений . М., Стройиздат, 1976, вып.22, с.27-32.
30. Габбасов Р.Ф. Об одном численном методе расчета пологих оболочек.-Строительная механика и расчет сооружений, 1976, № 3, с.15-18.
31. Габбасов Р.Ф. Применение численно-интегрального метода к расчету плит на упругом основании.-Прикладная механика, 1976, т.12, вып.10, с.21-26.
32. Габбасов Р.Ф., Щрамко В.В. 0 расчете пологих оболочек методом последовательных аппроксимаций.
-Известия вузов. Строительство и архитектура, 1977, №. 9, с.35-42.
33. Габбасов Р.Ф. Об интегральной и дифференциальной формах численного метода последовательных аппроксимаций.-Строительная механика и расчет сооружений, 1978, № 3, с.26-30.
34. Габбасов Р.Ф. Применение теории сплайнов к задачам строительной механики.-Сб. трудов МИСИ, ГЛ., 1978, J,’ 156,с.65-76.
35. Габбасов Р.Ф. О разностных формах метода последовательных аппроксимаций.-Б кн.: Численные методы решения задач строительной механики, Киев, изд. КИСИ, 1978, с.121-126.
36. Габбасов Р.Ф. Расчет плит с использованием разностных уравнений метода последовательных аппроксимаций.-Строительная механика и расчет сооружений, 1980, № 3, с.27-30.
37. Габбасов Р.Ф. К расчету стержней и стержневых систем методом последовательных аппроксимаций.- Известия вузов. Строительство и архитектура, 1980, № 4, с.30-35.
38. Габбасов Р.Ф., Кандалов Б.П. Разностные уравнения метода последовательных аппроксимаций в задачах устойчивости пластин.
-Известия вузов. Строительство и архитектура, 1981,1. В II, с.58-62.
39. Габбасов Р.Ф. Применение разностных уравнений МПА к плоской задаче теории упругости.-Строительная механика и расчет сооружений, 1982, № 4, с.23-26.
40. Габбасов Р.Ф. О разностных уравнениях в задачах прочности и устойчивости плит.-Прикладная механика, 1982, т.18, $ 9, с.63-67.
41. Габбасов Р.Ф., Исматов М.Х. Расчет изгибаемых плит методом последовательных аппроксимаций.-Известия вузов. Строительство и архитектура, 1984, й 2.
42. Габбасов Р.Ф., Исматов М.Х. Об учете закруглений, входящих углов при расчете изгибаемых плит.-Рукопись депонирована ВБИИС Госстроя СССР, 1983, № Ш*, 12с.
43. Галин Л.А. Контактные задачи теории упругости. М., ГТТИ, 1953, 264с.
44. Герсеванов Н.М. О применении теории упругости к расчетуоснований.-Труды ШИТ, выпб, 1927, с.19-28.
45. Герсеванов Н.М., Мачерет Я.А. К вопросу о бесконечно длин-i ной балке на упругой почве, нагруженной силой Р.-Сб.трудов ШС БИОС, }Ь 8, ОНТИ, М.
-Л., 1937, с.11-62.
46. Гильман А.С. К вопросу об определении напряжений на поверхности упругой среды.-Труды ЛИИПС, вып.1, 1934, с.35-60.
47. Горбунов-Посадов М.И. Точный расчет фундаментов из перекрестных лент.-Проект и стандарт, JG 5, 1935, с.23-27.
48. Горбунов-Посадов М.И. Таблицы для расчета тонких плит на упругом основании. Госстройиздат, М., 1959, 98с.
49. Горбунов-Посадов М.И. Современное состояние научных основ фундаментостроения. М., «Наука», 1967, 68с.
50. Горбунов-Посадов М.И., Маликова Т.А. Расчет конструкций на упругом основании. М., Стройиздат, 1973, 628с.
51. Горлов A.M., Серебряный Р.Б. Автоматизированный расчет прямоугольных плит на упругом основании. Стройиздат, М., 1968, 208с.
52. Григорьев А.С. Изгиб балок на упруго-пластическом основании? Труды ЦАГИ, вып.600, 1946, 30с.
53. Давыдов С.С. Расчет и проектирование подземных конструкций. Стройиздат, М., 1950, 376с.
54. Давыдов С.С. Расчет инженерных конструкций на упругом основании.
(Учебное пособие). МИИТ, 1967, 23с.
55. Даль Ю.М. Об изгибе упругой консольной пластины переменной толщины.-Расчет пространственных конструкций, 1974, 16,с.169-178.
56. Даревский Б.М. Изгиб прямоугольной пластинки со свободными краями, лежащей на упругом основании.-Изв.АН СССР. Механика твердого тела, 1977, JS I, с.79-90.
57. Державин Б.П. Применение полиномов Чебышева в задачах строительной механики.-Труды МИИТ, вып.194, М., 1966, с.99-110.
58. Деркач В.Ф. Расчет тонких плит ступенчато-переменной толщины на упругом полупространстве.-В кн.: Расчет конструкций подземных сооружений. Изд. Еудisельник, Киев, 1976, с.47-55.
59. Дидов Б.В. О расчете плит на упругом основании.-Сб.трудов лаборатории оснований и фундаментов ВОДГЕО, $ 9, M.-JI., 1938, с.82-112.
60. Дойхен Ю.М. Применение обобщенного вариационного метода Власова-Канторовича к расчету плит на упругом основании.-Сб. трудов ШСИ, 1970, 84, с.236-243.
61. Дутов Г.Д. 0 расчете балок на упругом основании.
«Кубуч», Л., 1929, 90с.
62. Егоров К.Е. К вопросу деформации основания конечной толщины. -Сб. трудов НИИОСП «Механика грунтов», В 34, М., Гос-стройиздат, 1958, с.5-33.
63. Егоров К.Е. 0 деформации основания конечной толщины.-Основания, фундаменты и механика грунтов, № I, 1961, с.4-6.
64. Елсукова К.П. Применение метода конечных элементов к расчету плит на упругом основании.-Автореферат диссертации на соискание ученой степени к.т.н., JI., 1976, 20с.
65. Еемочкин Б.Н., Синицын А.П. Практические методы расчета фундаментных балок и плит на упругом основании. М., Гос-стройиздат, 1962, 240с.
66. Зарецкий Ю.К. К расчету ленточных фундаментов на нелинейно-деформируемом основании.-Основания, фундаменты и механика грунтов, 1965, & I, с. 10-14.
67. Зенкевич O.K., Ченг Ю.К. Метод конечных элементов в задачах строительной механики, перевод с англ., Г0НТИ, № I, 1971, 358с.
68. Зенкевич O.K. Метод конечных элементов в механике. Перевод с англ., Мир, М., 1975, 541с.
69. Игнатов В.П. Расчет прямоугольных плит на статически неоднородном основании.-Основания, фундаменты и механика грунтов, 1970, JS 4, с.37-38.
70. Исматов М.Х. Применение 1ДПА к расчету балок и плит на упругом основании.-Рукопись депонирована ВНИИС Госстроя СССР, 1983, В 4226, 15с.
71. Исматов М.Х. Применение МПА к расчету прямоугольных плит на упругом полупространстве.-Рукопись депонирована ВНИИС Госстроя СССР, 1983, № Шб , 12с.
72. Ишкова А.Г., Коренев Б.Г. Изгиб пластинок на упругом основании.-Труды II Всесоюзного съезда по теоретической и прикладной механике, вып.З, «Механика твердого тела», М., «Наука», 1966, с.157-177.
73. Каноненко Е.С. Приближенный расчет плит на упругом основании: -Исследования по теории сооружений, вып.12, М., 1963, с.197-211.
74. Караманский Т.Д. Численные методы строительной механики. Перевод с болг. М., Стройиздат, 1981, 436с.
75. Киселев В.А. Балки и рамы на упругом основании. Глав. ред. строит, лит. ОНТИ, М.-Л., 1936, 228с.
76. Китовер К.А. К расчету прямоугольных плит на упругом основании. -С б. трудов общетехнических кафедр Ленинградского технологического института холодильной промышленности, вып.8, 1955, с.66-70.
77. Клейн Г.К. Учет неоднородности, разрывности деформаций и .других механических свойств грунта при расчете сооружений на сплошном основании.-Сб. трудов МИСИ, 1956, $ 14,с.169-180.
78. Клейн Г.К., Скуратов Л.Ф. Расчет балок на нелинейно деформируемом основании.-В кн.: Строительная механика, М., Стройиздат, 1966, с.109-117.
79. Клейн Г.К., Дураев А.Е. К расчету балок, лежащих на грунтовом основании с учетом переменности по глубине модуля деформации.-Сб. трудов МИСИ, 1971, J£ 79, c.I-IO.
80. Клепиков С.Н. Расчет конструкций на упругом основании. Буд«велышк, Киев, 1967, 184с.
81. Клубин П.К. Расчет балочных и круглых плит на упругом основании. «Инженерный сборник», ИМ АН СССР, т.12, 1952,с.95-135.
82. Клубин П.И. Балки и плиты на упругом основании.-Докторская диссертация, М.
, 1952, 230 л. с ил.
83. Коренев Б.Г. Вопросы расчета балок и плит на упругом основании. М., Госстройиздат, 1954, 232с.
84. Коренев Б.Г., Черниговская Е.И. Расчет плит на упругом основании. М., Госстройиздат, 1962, 355с.
85. Коренев Б.Г. Конструкции, лежащие на упругом основании.
86. В кн.: Строительная механика в СССР I9I7-I967r.r. М., Госстройиздат, 1969, с.112-134.
87. Корунский B.C. Расчет прямоугольных плит, лежащих на упругом основании.-Труды Киевского автодорожного института, вып.7, I960, с.69-86.
88. Кривошеев Н.И., Корнишин М.С. Изгиб прямоугольных пластин ступенчато переменной жесткости.-В сб.: Исследования по теории пластин и оболочек, J5 5, Казань, изд. КРУ, 1967, с.314-326.
89. Крылов А.Н. О расчете балок, лежащих на упругом основании. АН СССР, М., 1930, 127с.
90. Кузнецов В.И. Упругое основание. М., Госстройиздат, 1952, 296с.
91. Лащеников Б.Я. Применение тригонометрического интерполирования в задачах строительной механики.
-Труды МИИТ, М., 1961, вып.131, с.276-295.
92. Леонтьев Н.Н., Атаров Н.М. К расчету балки на упругом слоепеременной толщины.-Сб. трудов МИСИ. М., 1971, № 79,c.II-2I.
93. Леонтьев Н.Н. О расчете прямоугольной плиты на упругом основании. Известия вузов. Строительство и архитектура, 1970,6, с.68-73.
94. Мягальник С.М. Об оценке точности расчета плит на грунтовом основании методом разбивки на систему перекрестных балок.-Основания, фундаменты и механика грунтов, 1978, Je 6,с.22-24.
95. Мак-Кракен Д., Дорн У. Численные методы и программирование на ФОРТРАНе. Пер. с англ. М., «Мир», 1977, 584с.
96. Маликова Т.А., Румянцева И.А. Программа МРП-I для расчета на ЭВМ «Урал-4» прямоугольных фундаментных плит, НИИОСП, М., 1968, 68с.
97. Манвелов Л.И., Бартошевич Э.С. О выборе расчетной модели упругого основания.-Строительная механика и расчет сооружений, 1961, № 4, с.14-18.
98. Манвелов Л.И., Бартошевич Э.С. Расчет прямоугольной плиты на упругом основании.-Строительная механика и расчет сооружений, 1963, № 5, с.
12-16.
99. Масленников A.M. Матричный расчет статически неопределимых систем, исследования по строительной механике.-Труды ЛИСИ, вып.190, 1962.
100. Масленников A.M. Расчет тонких плит методом конечных элементов. -Труды ЛИСИ, вып.57, 1968, с.186-193.
101. Мачерет Я.А. К вопросу об изгибе конечной балки на упругом основании, нагруженной равномерной нагрузкой.-Сб. трудов НИС ШОС № 8, ОНТИ, М.-Л., 1937, с.104-116.
102. Метод конечных элементов в строительной механике и механике сплошных сред. Реф. обзор, ШИИТ, Л., 1971, 160с.
103. Механика в СССР за тридцать лет. М.-Л., Гостехиздат, 1950, 416с.
104. Мещеряков Ю.М. Перечень опубликованных в СССР работ по расчетам плит и балок на сжимаемом основании (обзор за 19171967 г.г.), М., 1967, 95с.
105. Низомов Д. Численное решение динамических задач по расчету балок, плит и оболочек.-Автореферат кандидатской диссертации. М., ШСИ, 1982, 18с.
106. Палатников Е.А. Прямоугольные плиты на упругом основании, М.
, Стройиздат, 1964, 236с.
107. Палатников Е.А., Кириллина В.П. Программа расчета на ЭЦШ «Минск-32» изотропных плит на упругом основании.-Труды Гицронииавиапрома, вып.З, 1968, с.55-86.
108. Папкович П.Ф. Строительная механика корабля, ч.2, 1л., Гос-стройиздат, 1941, 960с.
109. Пастернак П.Л. Основы нового метода расчета фундаментов на упругом основании при помощи двух коэффициентов постели. I/I., Госстройиздат, 1954, 56с.
110. Подгородецкий А.Э. Решение некоторых задач об изгибе прямоугольных пластин методом Бубиова-Галеркина.-Кандидатская диссертация, Запорожье, 1972, 160 л. с ил.
111. Попов Г.Я. Изгиб полубесконечной плиты, лежащей на линейно деформируемом основании. БММ, 1961, 25, вып.2, с.342-355.
112. Попов Г.Я. Изгиб полубесконечной плиты на комбинированном упругом основании.-Доклады АН СССР, 1959, т.126, 3,с.534-537.
113. Нузыревский Н.П. Расчеты фундаментов.-ПГ. Студенческая библиотека и И.П.С., 1923, 440с.
114. Развитие теории контактных задач в СССР (отв.
вельник, Киев, 1967, 304с.
119. Розин Л.А. Расчет гидротехнических сооружений на ЭЦВМ. Метод конечных элементов. «Энергия». Л., 1971.
120. Розин Л.А. Современное состояние метода конечных элементов в строительной механике.-Известия вузов. Строительство и архитектура, 1981, II, с.41-54.
121. Серебряный Р.В. Об изгибе тонкой полубеоконечной плиты, опирающейся на упругий слой конечной толщины.-Доклады АН СССР, т.125, № 4, 1959, с.752-755.
122. Серебряный Р.В. Расчет тонких шарнирно-соединенных плит на упругом основании. М., Госстройиздат, 1962, 64с.
123. Симвулиди И.А. Расчет сложных фундаментов на упругом основании. ВЗИСИ, М., 1969, 52с.
124. Симвулиди И.А. Расчет инженерных конструкций на упругом основании. М., Ейсшая школа, 1978, 480с.
125. Симвулиди И.А., Магальник С.И., Репников Л.Н. Расчет плит произвольного сечения и очертания в плане на грунтовом основании.-Известия вузов. Строительство и архитектура, 1978, № I, с.37-41.
126. Смирнов А.
Ф. Устойчивость и колебания сооружений. М., Трансжелдориздат, 1958, 571с.
127. Смирнов В.А. Численный метод решения некоторых краевых задач теории упругости для дифференциальных уравнений в частных производных.-Исследования по теории сооружений, вып.17, М., Госстройиздат, 1969, c.III-121.
128. Смирнов В.А. Расчет пластин сложного очертания.
129. М., Стройиздат, 1978, 300с.
130. Справочник по теории упругости, Киев, «Буд1вельник». 1971, 418с.
131. Справочник проектировщика, расчетно-теоретический, М., Госстройиздат, 1973, кн.1, 600с., кн.2, 416с.
132. Соболев Д.Н. К расчету конструкций, лежащих на статистически неоднородном основании.-Строительная механика и расчет сооружений, 1965, № I, с.1-4.
133. Соломин В.И. Расчет балок на упругом основании методом конечных разностей.-Труды УПИ, № 102, 1961, с.157-169.
134. Соломин В.И. Расчет прямоугольных пластин на упругом полупространстве методом сеток.-Строительная механика и расчет, сооружений, I960, № 6, с.
12-17.
135. Соломин В.И. К расчету фундаментных плит при нагрузке, приложенной вблизи угла.-Строительная механика и расчет сооружений, 1963, № 2, с.6-11.
136. Соломин В.И., Широков В.И., Комаров З.А. Расчет прямоугольных плит, опирающихся на упругий слой конечной мощности. -О снования, фундаменты и механика грунтов, 1968, № 4, с. 34-36.
137. Соломин В.И., Сытник А.С. К расчету фундаментных плит сложной конфигурации и переменной жесткости.-Основания, фундаменты и механика грунтов, 1974, № 5, с.16-19.
138. Страгонова С.М. Изгиб четвертьбесконечных плит на комбинированном основании.-Строительная механика и расчет сооружений, 1983, № 2, с.30-33.
139. Сухотерин М.В. Итерационный метод решения задачи об изгибе прямоугольной консольной пластины.-Прикладная механика, 1982, 18, № 5, с.121-125.
140. Травуш В.И. К задаче об изгибе полубесконечной плиты, лежащей на упругом основании.-Известия АН СССР, Механика, 1965, № 2, с.144-147.
141. Травуш Б.И. Изгиб неизолированных плит, лежащих на линейно-деформируемом основании общего типа.
-Исследования по теории сооружений, Стройиздат, М., 1969, вып.17, с.73-84.
142. Травуш В.И. Изгиб четвертьбесконечной плиты, лежащей на упругом основании.-Известия АН СССР, Механика твердого тела, 1971, $ 2, с.69-73.
143. Тимошенко С.П. Теория упругости. Изд. 2-е, пер. с англ. ivl.-Л., ОНТИ, 1934, 451с.
144. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. М., «Наука», 1966, 636с.
145. Уманский А.А. О расчете балок на упругом основании. Л., Ленгострансиздат, 1933, 48с.
146. Урисман B.C. Разработка расчета прямоугольных частично-ребристых конструктивно ортотропных фундаментных плит с применением ЭВМ.-Кандидатская диссертация, Москва-Харьков, 1976, 167 л. с ил.
147. Ухов С.Б. Расчет сооружений и оснований методом конечных элементов. Изд. МИСИ, М., 1973, П8с.
148. Фаянс Б.Л. Расчет прямоугольных плит на основании с переменным коэффициентом постели.-Основания, фундаменты и механика грунтов, 1967, А»! 2, с.32-34.
149. Филоненко-Еородич М.
М. Простейшая модель упругого основан ния, способная распределять нагрузку.-Труды МЭМИИТ, вып.53, Трансжелдориздат, 1945, с.92-110.
150. Филоненко-Бородич М.М. и др. Курс сопротивления материалов. ч.П, Гостехстройиздат, 1956, 644с.
151. Флорин В.А. Основы механики грунтов, т.1. Госстройиздат, 1959, 357с.
152. Флорин В.А. Расчет оснований гидротехнических сооружений.- 1»U
153. М., Стройиздат, 1948, 188с.
154. Хаяси К. Теория расчета балки на упругом основании в применении к фундаментостроению. М., Гостехиздат, 1930, 24с.
155. Цытович Н.А. Механика грунтов. М., Госстройиздат, 1963,636с.
156. Цытович Н.А. О методе расчета балок на сжимаемом основании. Труды ШСИ, № 14, 1956, с .5-11.
157. Черкасов И.И. Механические свойства грунтовых оснований. М., Автотрансиздат, 1958, 156с.
158. Чинилин Ю.Ю. Расчет конструкций элеваторных сооружений, взаимодействующих с деформируемым основанием.-Кандидатская диссертация, М., 1982, 198л. Л ил.
159.
Шапиро Е.С. Изгиб полубеоконечной плиты, лежащей на упругом основании. ПММ, т.7, вып.4, АН., М.-Л., 1943,с.316-320.
160. Шапошников Н.Н. Расчет пластинок на изгиб по методу конечного элемента.-Труды МИИТ, вып.260, М., 1968, с.134-144.
161. Шехтер О.Я., Винокурова А.В. Расчет плит на упругом основании. ОНТИ, М.-Л., 1936, 226с.
162. Шехтер О.Я. Расчет бесконечной фундаментной плиты, лежащей на упругом основании конечной и бесконечной мощности и нагруженной сосредоточенной силой.-В сб. трудов НИИ треста глубинных работ, № 10, Госстройиздат, 1939, с.133-139.
163. Шехтер О.Я. К расчету фундаментных плит на упругом слое грунта конечной мощности.-В сб. трудов НИИ Министерства строительства военных и военно-морских предприятий, № II, Стройвоенмориздат, 1948, с.139-151.
164. Ширинкулов Т.Ш. О расчете балочных плит на упругом основании, модуль упругости которого является функцией глубины.-Доклады АН Узб.ССР, № 9, 1967, с.9-12.
165. Ширинкулов Т.Ш. Расчет инженерных конструкций на упругом неоднородном основании.
.3, /932, s.
Задание граничных условий (связей) для фундаментных плит в горизонтальной плоскости
Теги: #ЛИРА-САПР #фундамент #связи
Фундаментные плиты зданий, как правило, моделируются в виде пластинчатых элементов на упругом основании. Роль вертикальной связи выполняют граничные условия виде коэффициентов постели. Для обеспечения геометрической неизменяемости здания в горизонтальных направлениях (вдоль осей X и Y) следует наложить граничные условия в плоскости фундаментной плиты. Как известно, для обеспечения геометрической неизменяемости тела на плоскости достаточно наложить 3 связи, не пересекающиеся в одной точке. Бывает, что на практике расчетчики закрепляют фундаментную плиту в только трех узлах. Подобное закрепление может привести к резким всплескам усилий в местах наложения связей, а соответственно и армирования:
Если фундаментная плита имеет оси симметрии, то связи лучше задавать по линиям симметрии. Для линии параллельной оси X следует запретить перемещение по направлению оси Y и наоборот.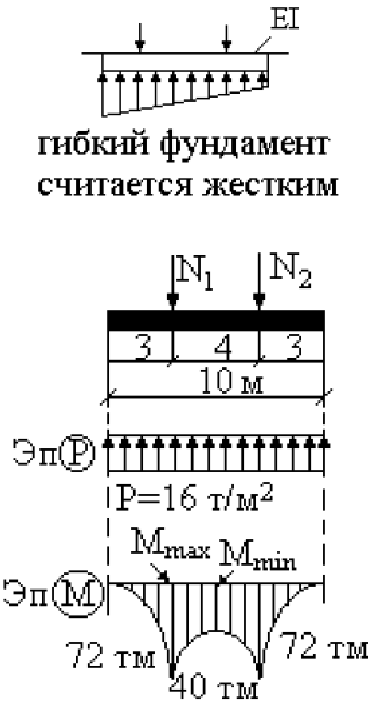
Наложенные таким образом связи не будут приводить к всплескам усилий в конечных элементах фундаментной плиты, а плита при этом остается неподвижной в горизонтальной плоскости. При этом при подборе армирования также будет учтена мембранная группа усилий.
Другой вариант задания граничных условий — применения связей конечной жесткости КЭ 56. При использовании данного варианта во все узлы фундаментной плиты вводятся одноузловые конечные элементы 56 типа. В описании типа жесткости данного конечного элемента следует задать жесткостные характеристики в горизонтальном направлении — Rx и Ry:
Значения Rx и Ry можно определить, зная количество n элементов 56 типа (равно количеству узлов фундаментной плиты, в которые вводятся эти элементы) и величину сдвиговой жесткости основания Kx/y:
Rx/y = Kx/y*A/n
Жесткость основания в горизонтальной плоскости Kx/y может быть определена из решения статической задачи о штампе на упругом основании [1] стр.
25:
где А — площадь фундамента; Е — модуль деформаций грунта основания; ν — коэффициент Пуассона грунта основания, ωz и ωx — коэффициенты, зависящие от соотношения сторон фундамента a и b.
Другой подход к определению Kx/y базируется на решении задачи о колебаниях штампа на упругом основании [2] стр. 97:
Kx/y = 0.7Kz = 0.7CzA
где А — площадь фундамента, Cz — коэффициент упругого равномерного сжатия.
Этот подход включен в нормы на проектирования [3].
Используемая литература
- С. Н. Клепиков «Расчет конструкций на упругом основании». Киев, Будивельник, 1967.
- М.Ф. Барштейн, Н. М. Бородачев, Л. Х. Блюмина и др.; Под ред. Б.Г. Коренева, И.М. Рабиновича. «Динамический расчет зданий и сооружений». М., Строиздат, 1984.
- СП 26.13330.2012 «Фундаменты машин с динамическими нагрузками».
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.
- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Торговые выгоды и экологические издержки ГСКС: пример БРИКС()
Сяохун Юй, Цзяцзя Фан, Ихан Луо, Сяоюань Чжу, Юйчен Чжан, Сяофэй Лонг
DOI: 10.4236/ajcc.2023.121003 10 загрузок 102 просмотра
Оценка корицы с помощью твердотельного ЯМР с использованием релаксометрии()
Педро Пауло Мерат, Роберто Кучинелли Нето, Витор Сантос Рамос, Мария Инес Бруно Таварес
Материаловедение и приложения Том 14 № 3, 6 марта 2023 г.
DOI: 10.4236/MSA.2023.143009 16 загрузок 64 просмотров
- Экспериментальная оценка физических, механических свойств и долговечности бетонов на основе натуральных, переработанных и комбинированных заполнителей()
Этьен Мальбила, Арба А.
Т. Уэдраого, Николас Кагамбега, Гилберт Г. Нана, Сие Кам, Дэвид Ю. К. ТогуениМатериаловедение и приложения Том 14 №3, 6 марта 2023 г.
DOI: 10.4236/MSA.2023.143008 8 загрузок 49 просмотров
Демонстрация оценки однородности центральной оси и модернизации для повышения эффективности использования воды()
Юнсук Донг, Линдон Келли, Эрик Андерсон
Журнал водных ресурсов и охраны Том 15 №3, 6 марта 2023 г.
DOI: 10.4236/jwarp.2023.153005 4 загрузки 28 просмотров
Воздействие и ведение при экстракорпоральном кровообращении пациента с почечной недостаточностью на диализе с высокопоточной артериовенозной фистулой в кардиохирургическом отделении клинической больницы Анже о случае и обзоре литературы()
Абдулай Канте, Брехима Кулибали, Мамаду Диаките, Мамаду А.
Кейта, Бакари Кейта, Дрисса Траоре, Нухум Онгоиба, Патрис Бинуани, Кристоф БофретонОткрытый журнал торакальной хирургии Том 13 № 1, 6 марта 2023 г.
DOI: 10.4236/оц.2023.131001 2 загрузки 19 просмотров
Обеспечение качества фантома кольцевого вихревого потока в режиме реального времени()
Алана С. Мэтьюз, Кельвин Симатво, Эндрю Нарракотт, Симона Амброджо, Адриан Уокер, Джон В. Феннер
Открытый журнал медицинской визуализации Том 13 № 1, 6 марта 2023 г.
DOI: 10.4236/ojmi.2023.131002 6 загрузок 32 просмотров
Т. Уэдраого, Николас Кагамбега, Гилберт Г. Нана, Сие Кам, Дэвид Ю. К. Тогуени
Кейта, Бакари Кейта, Дрисса Траоре, Нухум Онгоиба, Патрис Бинуани, Кристоф БофретонПодпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2023 Scientific Research Publishing Inc. Все права защищены.
ВершинаКак рассчитать фундаментную балку
Конструктивные расчеты зданий и инфраструктуры часто выполняются с использованием моделей, которые в упрощенном виде представляют ограничения в основании конструкции. Даже во многих случаях конструкция крепится к основанию с помощью жесткого крепления .
Однако такой подход не позволяет анализировать фактическое напряженное состояние фундаментов, а в некоторых случаях может привести к некорректной оценке реакции конструкций надземных сооружений.
Использование пружинный ограничитель может быть эффективным способом преодоления этих проблем и получения более точного прогноза поведения конструкции.
Основные преимущества использования пружинных ограничителей при моделировании конструкций
Моделирование фундаментных опор с пружинными ограничителями дает несколько преимуществ. Среди них можно выделить три основных преимущества:
реалистичные ограничения описание
У вас есть возможность выбрать жесткость пружины в зависимости от типа грунта основания. Кроме того, можно задавать пружины с разной жесткостью на разных участках граничной зоны. Наконец, вы можете определить ограничения поворотной пружины, которые полезны, например, для моделирования поворота цоколя у основания колонны.
повышенная точность модели
Использование пружинных зависимостей позволяет оценить правильный размер пиков деформации и их положение. Кроме того, он позволяет правильно рассчитать силы, действующие на фундаментные конструкции, и, следовательно, правильно определить их размеры.
Что не менее важно, можно учесть взаимодействие грунт-конструкция и получить реалистичный отклик надземных конструкций.
выше Надежность конструкции
Можно анализировать реакцию конструкции, оценивая различные значения жесткости грунта и элементов фундамента, получая огибающие действующие силы. Таким образом можно учесть возможные неопределенности модели , связанные с неопределенностью в знании типа почвы и ее изменчивости.
Моделирование фундаментов в виде балок Винклера
Модель Винклера основана на предположении, что грунт в общей точке деформируется пропорционально действующей на него нормальной силе. Деформация не зависит от деформации других точек и линейно зависит от приложенной силы.
Константа пропорциональности, называемая константой почвы , является физической характеристикой почвы и должен измеряться на месте.
| soil type | [MPa/mm] |
|---|---|
| Sand | 0. 02 ÷ 0.03 |
| Clay | 0.08 ÷ 0.12 |
| Gravel | 0.10 ÷ 0.30 |
Модель Винклера особенно полезна для моделирования поведения упругих фундаментных балок, часто используемых в качестве фундаментных конструкций в тех случаях, когда фундаментный цоколь не предполагается. Если фундаментные балки рассчитываются с учетом колонны как жестких ограничений и давления грунта как распределенной нагрузки, полученные изгибающие моменты и поперечные силы обычно приводят к превышению размеров фундаментных балок.
Использование упругих пружинных ограничителей на основе постоянной грунта Винклера позволяет получить более точные результаты. На рисунке ниже представлено схематическое изображение балочного фундамента Винклера. Жесткость пружины представляет собой постоянную грунта, умноженную на ширину балки.
Схема фундамента WinklerРасчет фундаментной балки с использованием грунтовой крепи Winkler
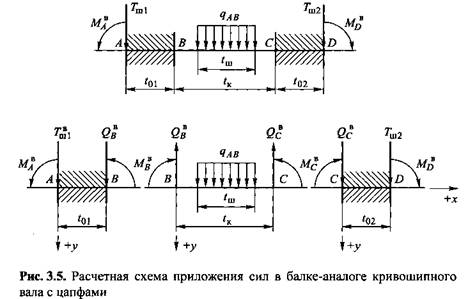
Здесь показан пример расчета фундаментной балки с использованием грунтовой крепи Winkler.
Исследуемая система показана на рисунке ниже. Балка подвержена распределенному действию из-за постоянных нагрузок. Кроме того, колонны испытывают сосредоточенные сдвигающие действия и изгибающие моменты на некоторых участках балки. Пример взят из работы Колаянни и др. [1].
Модель построена и решена с использованием WeStatiX . Если вы хотите узнать, как создать модель балки Винклера, взгляните на этот и другие примеры и руководство.
После моделирования геометрии балки были приложены распределенная и узловая нагрузки. Опора Винклера была вставлена путем применения ограничений упругих элементов. При этом, как только была выполнена дискретизация балки, код применил узловое ограничение с жесткостью в узлах балки. Диаграммы значимых результатов представлены ниже:
В частности, диаграмма вертикальных перемещений:
Вертикальные смещения фундаментной балки Видно, что вертикальные смещения не являются постоянными, а представляют собой пики, интенсивность которых можно точно оценить с помощью этой стратегии моделирования.
Диаграмма поперечной силы:
Диаграмма действия сдвига для фундаментной балкиДиаграмма изгибающего момента:
Диаграмма изгибающего момента для фундаментной балкиЗная точное распределение сдвигающих и изгибающих усилий в балке, принимаются правильные решения по проектированию, которые не нужны. можно избежать чрезмерного размера. Кроме того, можно выполнить несколько расчетов для оценки реакции конструкции с учетом неопределенности жесткости грунта, чтобы получить огибающую значений воздействия для фундаментной балки.
Полученные результаты согласуются с аналитическими решениями, представленными в [1]. Вы можете проверить точность решения WeStatiX , взглянув на проверочный тест опор Winkler.
В WeStatiX вы можете найти другие применения эластичных ограничителей! Например, вы хотите научиться моделировать глубокие фундаменты на упругих опорах или промышленные полы из фибробетона? Вы можете найти эти и другие приложения по адресу WeStatiX 9.