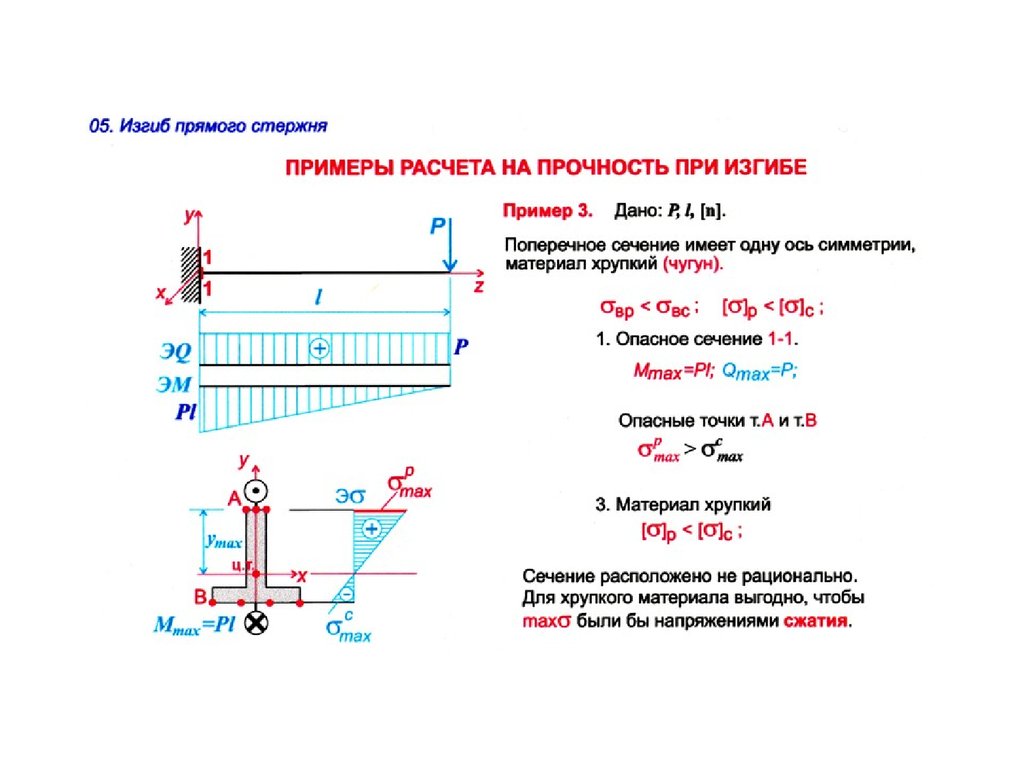
Расчёт на внецентренное сжатие простенка из керамического кирпича
Теги: #ЛИРА-САПР #кирпич #каменные_конструкции #верификация
Исходные данные
Материал – кирпич керамический на ц.п. растворе. Марка кирпича М125, марка раствора М100. Расчётное сопротивление кладки сжатию R=20.3943=20.3943 кгс/см2. Размеры простенка b=100 см, h=38 см. Высота простенка l0=290 см. По результатам определения внутренних усилий в сечении простенка возникают следующие усилия: N=16.057 т, изгибающие моменты Мх=0.314 т*м, Му=0 т*м, поперечные силы, Qx=0 т, Qy=0.18 т;
Схема приложения нагрузок к простенку
Расчёт на внецентренное сжатие в плоскости изгиба
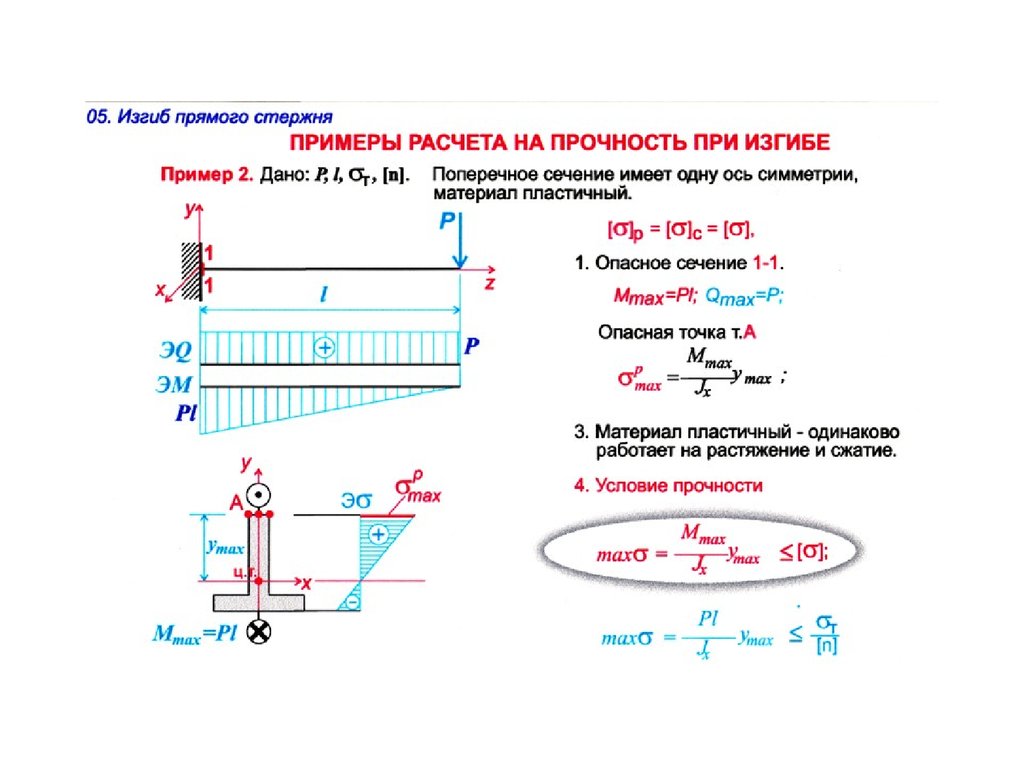
По п.7.7 Расчет внецентренно сжатых неармированных элементов каменных конструкций следует производить по формуле
N<=φ1*mg*R*Ac*ω
mg=1 — коэффициент, учитывающий влияние длительной нагрузки и определяемый по формуле (16). При толщине стены более 30 см, принимается равным 1.
При толщине стены более 30 см, принимается равным 1.
φ1x=(φx+φcx)/2
φ — коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый по расчетной высоте элемента l0
Для l0=290 см, ix=0.289*38=10.982 см, α=1000, по таблице 19, при λ=l0/ix=290/10.982=26.407, φ=0.92910
| αn | ||
| 1000 | ||
| λn | 21 | 0.96 |
| λi | 26.407 | 0.92910 |
| λn+1 | 28 | 0.92 |
φс — коэффициент продольного изгиба для сжатой части сечения, определяемый по фактической высоте элемента Н по таблице 18 в плоскости действия изгибающего момента при гибкости:
λiс=H/iс
где hс и iс — высота и радиус инерции сжатой части поперечного сечения Ас в плоскости действия изгибающего момента.
Площадь сжатой части сечения определяется по формуле:
A=b*h=3800 см2 — площадь поперечного сечения простенка;
e0x=Mx/N=0.314/16.057=1.955533 см – эксцентриситет расчётной силы N относительно центра тяжести сечения;
ev=0 см — случайный эксцентриситет продольной силы, для несущих стен толщиной 25 см и более не учитывается.
Высота сжатой части сечения h
Радиус инерции сжатой части сечения icx=0.289*hcx=0.289*34.0889=9.8517 см, λcx=l0/icx=290/9.8517=29.4365, φcx=0.91179
| αn | ||
| 1000 | ||
| λn | 28 | 0.92 |
| λi |
29. 4365 4365
|
0.91179 |
| λn+1 | 35 | 0.88 |
φ1x=(φx+φcx)/2=(0.92910+0.911792)/2=0.92045
Коэффициент ω=1+(ex+ev)/h=1+(1.955533+0)/38=1.051461 — для кладки из керамического кирпича.Подставляя данные в формулу прочности простенка, получаем:
N=16.057 т<=φ1x*mg*R*Ac*φx=0.92045*20.3943*1*3408.8934*1.051461=67.284588 т
Коэффициент запаса 67.284588/16.057=4.190358573
Расчёт на центральное сжатие из плоскости изгиба
По п.7.1 Расчет внецентренно сжатых неармированных элементов каменных конструкций следует производить по формуле (10):
N<=φy*mg*R*A
Определение коэффициента продольного изгиба
Для l0=290 см, iy=0. 289*100=28.9 см, α=1000, по таблице 19, при λ= l0/iy=29028.9=10.03, φ1.
289*100=28.9 см, α=1000, по таблице 19, при λ= l0/iy=29028.9=10.03, φ1.
Подставляя значения в формулу (10), получаем:
N=16.057 т<=φy*mg*R*A=1*1*20.3943*3800=77.4983 т
Коэффициент запаса 77.4983/16.057=4.826452.
Характеристики материалов каменных конструкций, заданных для расчёта в программе
Расчёт выполняется по СП 15.133330.2012, алгоритмом строго по нормам.
Характеристики кладки
Условия раскрепления
Сравнение результатов ручного расчёта с программным счётом
Сравнение выполним в табличной форме
| Параметр для сравнения | Результат расчёта | Погрешность | |
| Ручной расчёт | ЛИРА-САПР | ||
| Коэффициент запаса прочности кладки при сжатии |
4. 190358573 190358573
|
4.19 | 0.01 % |
Коэффициент запаса прочности кладки при сжатии
|
« Предыдущая часть …, что и пояс. При этом гвозди в ребрах жесткости ставят конструктивно, обычно в 2 ряда. Ширина опорных ребер = ширине поясов. Пролет до 13 м (исходя из 6,5 типовых материалов). Позволяют перекрывать пролеты под очень тяжелые нагрузки. Рассчитываем: брусья поясов воспринимают нормальные усилия, работают на растяжение сжатие. Усилия находим формуле: NП =MMAX / h0 ( Mmax – изгиб-й момент, h0 – расстояние между центрами тяжести верхнего и нижнего бруса.) Стенка работает на сдвигающие усилия, кот. возникают между стенкой и поясами при изгибе балки, сдвигающая сила определяется T= Q / h Гвозди, соединяющие пояс со стенкой, рассчитывают на сдвигающее усилие, равное на единицу длинны пояса: а) в балках с параллельным поясами: T= Q / h0. б) в балках с наклонным поясом: T = Q\h0 (-\+) Mtgα / h20.
15. Клееные деревянные балки. 1. Дощатоклееные балки. «+» работают как монолитные; их можно изготовить с поперечным сечением большой высоты; в балках длиной более 6м отдельные доски стыкуют по длине с помощью зубчатого шипа и → балки не будут иметь стыка, ослабляющего сечение. Для пролетов 6-24м применяют балки, склеиваемые из досок плашмя. Высоту балок принимают в пределах 1/8 – 1/12l. Ширину балок берут минимальной и определенной из условия опирания панелей покрытия и обеспечения монтажной жесткости. Уклон верхней грани 2скатных балок принимают 2,5-10%.
При склеивании можем изогнуть древесину любой формы, но наиболее часто встречающиеся кф балки имеют следующие фасадные формы: постоянной высоты, двускатная, односкатная, двускатная балка постоянной высоты с клеевой вставкой. Двускатные и односкатные балки для уменьшения расхода материала обычно выклеиваются следующим образом: нижняя часть из плетей постоянной длины, верхняя из плетей ступенчато-уменьшенной длинны. Поперечное сечение кд чаще всего выполняется в виде прямоугольника, однако при этом для экономии можем использовать древесину плетей разного сорта. Самые большие напряжения в верхней и нижней части – древесина более высокого сорта, в середине – древесина более низкого сорта, причем при расчете говорим, что сечение все из древесины первого сорта. Если балки большого пролета, делают двутаврового сечения из отдельно выполненных пакетов (стенку и полки), которые впоследствии склеиваются. Если балки большие и под тяжелую нагрузку, располагаем плети пастями параллельно поясам, если не очень большая нагрузка – располагаем вертикально, тем более что пакет мы можем выклеить шириной больше, чем ширина одной доски. Правда, при выклеивании большого пакета требуется перевязка швов на ширину, не менее ширины одной доски. Алгоритм расчета: по 1 предел. сост. а) по нормальным напряжениям σи = Mmax / W ≤ mб mсл Rи здесь коэф-т условия работы mб учитывает влияние размеров поперечного сечения, mсл – толщину слоев. б) по скалыванию (скалывающ-е напряжения проверяют в сечении с максимальной поперечной силой Q) τ = QS/Jb≤RСК (S-стаич-й момент брутто сдвигаемой части поперечного сечения эл-та, J- момент инерции, b – ширина балки, расчетное сопротивление скалыванию при изгибе для клееных эл-в). !!! В 2скатных балках при равномерно распределенной нагрузке сечение с максимальным нормальным напряжением не совпадает с положением максимального момента. Это сечение находится из общего выражения для нормальных напряжений, его дифференцируют и приравнивают к нулю, откуда получают, что указанное сечение отстоит от опоры на расстоянии → х=lhОП / 2hСР. !!! Для балок прямоугольного сечения из пакета досок необходимо производить расчет на устойчивость плоской формы деформирования: σИ = М/φМ Wбр φМ = 140 (b2 / lph)Kф.- коэф-т устойчивости. lp-расстояние между опорными сечениями балки, а при закреплении сжатой кромки балки в промежуточных точках от смещения из плоскости – расстояние между этими точками b – ширина поперечного сечения h – максимальная высота поперечного сечения на участке lp, Кф – коэф-т, зависящий от формы эпюры изгибающих моментов на участке lp. по 2 предел. сост. Наибольший прогиб шарнирно опертых и консольных балок постоянного и переменного сечений. f/l ≤ [f/l] где f = f0 / k [1+c (hо/l)2]. f0 – прогиб балки максимальной постоянной высоты по формулам строительной механики, h – наибольшая высота сечения, l – пролет балки, k – коэф-т учит-й влияние переменности высоты сечения, принимаемый 1 для балок постоянного сечения, с – коэф-т учит-й влияние деформаций сдвига от поперченной силы.
16. Клеефанерные балки. Общие положения. Ребристые конструкции.
Клеедостчатые имеют достаточно массивные стенки, а хотелось бы что-нибудь полегче – фанера, которая лучше работает на скалывание. Древесину заменяем на фанеру. Прочность на растяжение сжатие примерно такая же, как у древ, но за счет расположения слоев шпона прочность на скалывание увеличивается примерно в 10 раз. 7-12 мм толщина фанерного слоя. В зависимости от профиля здания, фанерные балки применяют с параллельными поясами (с плоской и волнистой стенками) и двускатные (с плоской стенкой) – с прямолинейным или криволинейным верхним поясом. Балка с криволинейным верхним поясом наиболее выгодна, так как ее очертания более всего соответствует эпюре изгибающих моментов. Клеефанерная балка является облегченной версией клеедощатой, в которой отсутствует древесина в центре, практически не участвующая в работе конструкции. Характеристики сечений балок с плоской стенкой:
1)двутавровое Проще всего по технологии самое экономичное по расходу материала, неплохо передает нагрузку, но имеет малый момент инерции на кручение при потере устойчивости – не обеспечивает большой несущей способности, те может использоваться только для не сильно загруженных балок небольшого пролета 2)коробчатое Имеет гладкую фасадную поверхность (не скапливается пыль), но кроме сдвига возникает также отдирающий момент. 3)двутаврово-коробчатое Наиболее выгодное: равнодействующая направлена прямо по стенке, те отдирающего момента не возникает; несущая способность при удачном подборе элементов может быть в 4 раза выше, чем в коробчатом сечении. Но не очень удобны для химически агрессивных сред. Пояса работают на растяжение (нижний) и на сжатие (верхние), воспринимают нормальные напряжения. Доски /слои/ в пакетах поясов располагаются вертикально и стыкуются зубчатым шипом до производства балок. В поясах балок коробчатого сечения допускается применять горизонтальное расположение слоев. Если высота поясов превышает 100 мм, во избежание появления в швах значительных дополнительных напряжений от возможной усушки древесины в поясах следует выполнять горизонтальные пропилы 5-10мм со стороны стенок. Стенки балок выполняют из водостойкой фанеры толщиной не менее 1/130 высоты стенки, но не менее 8 мм. Фанеру располагают волокнами рубашек, либо перпендикулярно к поясам, либо параллельно. В первом случае она воспринимает только касательные напряжения, лучше работает на скалывание между шпонами и на срез. Но вертикальные стыки её могут устраиваться только с помощью фанерных накладок. Во втором случае фанера воспринимает как касательные, так и часть нормальных напряжений, лучше работает на сжатие и растяжение при изгибе балки, а стыки легко выполняются склеиванием листов на «ус». При больших сосредоточенных грузах, фанеру располагают волокнами рубашек перпендикулярно к поясам. Фанерная стенка имеет сопротивление скалыванию примерно в 10 раз превышающее сопротивление древесины(тк приходится перерезать волокна в части слоев шпона), что позволяет уменьшить ее толщину. Поперечная устойчивость плоской фанерной стенки обеспечивают дощатыми ребрами, которые ставят по длине балки на расстоянии 1/8 – 1/10 её пролета (таким образом уменьшая поле фанерной стенки, способное потерять устойчивость). Опорные ребра принимают такой же ширины, как пояса (воспринимают опорную реакцию), а промежуточные вдвое уже. Ребра устанавливают на равных расстояниях, а у опор их при необходимости ставят чаще, но не ближе, чем на расстоянии, равном высоте стенки. Возможно укрепление фанеры в опорной панели диагональным ребром. Ребра должны совпадать со стыками фанерной стенки и располагаться в местах приложения сосредоточенных нагрузок (например, если в покрытии есть прогоны, то опорные ребра следует размещать под ними). Ребра приторцовывают к поясам балки и приклеивают. В целом вся конструкция работает на изгиб. Схема конструктивного расчета балок с плоской стенкой, волокна рубашек, расположенных вдоль поясов. Принятое сечение проверяют на:
по нормальным сжимающим напряжениям: δсж = Mрасч/Wпр ≤ Rс×γ, где γ – коэффициент продольного изгиба сжатого стержня из плоскости изгиба, зависит от гибкости пояса. При этом максимальный изгибающий момент возникает не в середине пролета, как в балках постоянного сечения, а на некотором расчетном расстоянии от опоры. Это связано с тем, что в месте, где момент должен достигать своего наибольшего значения (в середине балки), высота балки так же наибольшая => момент сопротивления повышается, и эпюра моментов становится похожей на лифчик =)
τ=Qmax×Sпр/Iпр×Σhп×n≤ Rф.ск, где n – число вертикальных швов 4.прочность фанерной стенки на действие главных растягивающих напряжений в местах приложения сосредоточенных нагрузок, либо в местах одновременного действия больших τ и δ: где
где Rф.рα – расчетное сопротивление фанеры сжатию под углом α τст и δст – нормальные и касательные напряжения в стенке на уровне внутренней кромки поясов 5.местная устойчивость фанерной стенки
τст и δст – нормальные и касательные напряжения в расчетном сечении стенки на уровне внутренней кромки поясов Kи; Kτ- коэффициенты, определяемые по СНиПу hрасч — расчетная высота стенки hст -расстояние между внутренними кромками поясов Проверка выполняется в панели, где действует максимальная поперечная сила, и в панели, где нормальные и касательные напряжения одновременно достигают больших значений (например, если в пределах границ панели приложена сосредоточенная сила). 6.жесткость (прогиб балки)
где правая часть – предельный относительный прогиб Наиболее экономична балка с криволинейным верхним поясом, так как ее форма повторяет форму эпюры моментов. Пропилы через 10 см. уменьшают площадь склеивания – уменьшают равнодействующие усадочные напряжения.
17. Балки с волнистой стенкой, основы расчета. Технология изготовления. Относятся к разряду малогабаритных конструкций (до 9 м), поэтому поперечное сечение имеет обычно двутавровую форму, с двумя стенками встречаются редко. Балки достаточно технологичны, что позволяет изготавливать их на поточных линиях. Пояса принимают либо цельными (из брусьев), либо клееными (из горизонтально уложенных досок). Воспринимают нормальные напряжения и работают на растяжение-сжатие. Вследствие придания волнистости стенке обеспечивается ее жесткость, лучше сопротивляется потере устойчивости (нет необходимости в укреплении ее ребрами жесткости; ставятся только опорные ребра, промежуточные отсутствуют). Толщину фанеры принимают не менее δф≥6мм. Фанерной стенке придают волнистую форму по синусоиде с высотой волны не менее bп/3 . По длине балки проектируют целое число полуволн с соотношением hв/lв = 1:12 – 1:18. Волокна рубашек фанеры в балке располагаются под углом 90 или 45 градусов к поясам. Листы стыкуются на «ус». Выбранное сечение проверяют на:
растянутого пояса по формуле σ = M/Wрасч ≤ Rр. 4. Прочность клеевого соединения волнистой стенки с поясами на действие касательных напряжений (скалывание): τш =Qmax*Sп/(Iх*Σhш) ≤ Rф. ск., где hш ≥ 2,5 δф – глубина паза. Проверку балки по наибольшим сдвигающим усилиям производят, как правило, в опорном сечении. При этом определяют сдвигающие напряжения в соединении стенки с полками. 5. Фанерную стенку на срез (по касательным напряжениям) с учетом местной потери устойчивости в опорном сечении: τ=Qmax*Sп/(Ix* δф) ≤ φф*Rф. ср 6. Прогиб балки: f ≤ fпр (аналогично балке с плоскими стенками + момент инерции умножается на коэффициент, уменьшающий жесткость из-за податливости стенки)
Технологии изготовления: 1) Брусья поясов распиливаем по шаблону, склеиваем картину фанерной стенки, зажимаем ее между распиленными брусьями поясов, смазываем клеем и запрессовываем. 2) Выбиваем в деревянных поясах пазы по лекалу, в эти пазы устраиваем фанерную картину и распираем с помощью деревянных бобышек, пазы заполняем эпоксидным компаундом. 3) По лекалу в брусьях поясов выбиваем узкий трапециевидный паз, ставим под него жесткую опору, пригружаем края => брус изогнется, и тогда можно затащить в паз фанерную картину => снимаем нагрузку. Глубину пазов принимают по расчету, но не менее hш ≥ δф.
18. армированные клееные балки.
Для уменьшения отрицательного влияния природных и технологических недостатков древесины (обезопашивает балку от влияния дефектов, выходящих на верхнюю и нижнюю кромку), уменьшения строительной высоты (или увеличения несущей способности при той же высоте), понижения материалоемкости клееной балки – производят армирование металлом, стеклопластиком и др, т.е. вклеивают эти материалы в наиболее напряженные зоны конструкции. Эффективны при больших пролетах и значит. нагрузках. Арматура в деревянных балках может быть продольной и поперечной. В качестве продольной арматуры используется стальная арматура периодического профиля, в качестве поперечной – деревянные цилиндры из более твердых пород. Клееные балки, как правило, армируются в растянутых и сжатых зонах (двойное симметричное армирование). Одиночное армирование – распределение арматуры только в растянутой зоне, дает незначительный эффект, поэтому нецелесообразно. Процент армирования колеблется от 1% до 3%. Арматуру укладывают в профрезерованные пазы прямоугольной или полукруглой формы на 5 мм шире диаметра арматуры. Пазы выбиваются во вторых от кромок досках (доски, выходящие на кромку, защищают арматуру от коррозии). Ширина древесины между пазами берется не менее 2.4 ширины паза, а расстояние от грани балки до крайних пазов – 1.2 ширины паза, но не менее 20 мм. В пазы заливают клей, а затем укладывают арматуру и производят запрессовку. Для вклеивания арматуры обычно используют эпоксидно-цементный безусадочный клей или эпоксидный компаунд (в эпоксидную смолу добавляют песок). Эпоксидный клей обладает хорошей адгезией, как к древесине, так и к стали; обеспечивает надежную совместную работу арматуры и дерева, при полимеризации не требует повышенных давлений, объем его почти не уменьшается. Расчет армированных балок ведется по схеме расчета изгибаемых элементов. Поперечное сечение армированной деревянной конструкции рассматривают как цельное, а учет совместной работы клееной древесины и арматуры выполняется с помощью использования приведенных геометрических характеристик, при этом материал арматуры приводиться к древесине. Геометрические характеристики приведенного сечения: основное сечение — древесина, а основные геометрические характеристики арматуры умножаем на отношение модулей упругости. Fсеч = Fдрев + Fарм*αпр, где αпр= Ест/Еар – коэф. приведения модуля упругости арматуры к модулю упругости древесины. Проверка принятого сечения проводится аналогично проверке обычной клеедощатой балки: 1) Проверяют прочность принятого поперечного сечения по формулам: Для простого изгиба δр = M/Wрасч ≤ Rи, где M – расчетный изгибающий момент, Wрасч – расчетный момент сопротивления сечения, Rи(ск) – расчетное сопротивление материала изгибу(скалыванию) По касательным напряжениям τ=Q×Sбр/Iбр×bрасч ≤ Rск(ср), где Q –расчетная поперечная сила, Sбр – статический момент брутто сдвигаемой части сечения относительно нейтрального слоя поперечного сечения, bрасч – расчетная ширина сечения элемента. 2) Прогиб по формуле: f = f0 / k [1+c (h/l)2] ≤ fпр, где f0 – прогиб балки постояннго сечения, h – наибольшая высота сечения, l – пролет балки, k – коэф- т учит-й влияние переменности высоты сечения, принимаемый 1 для балок постоянного сечения, с – коэф-т учит-й влияние деформаций сдвига от поперченной силы. 3) Устойчивость плоской формы деформирования по формулам, в которых значения геометрических характеристик принимают приведенными к древесине: σИ = М/φМ Wбр ≤ RИ mб mсл, φМ = 140 (b2 / lph)Kф.- коэф-т устойчивости. lp-расстояние между опорными сечениями балки, а при закреплении сжатой кромки балки в промежуточных точках от смещения из плоскости – расстояние между этими точками b – ширина поперечного сечения h – максимальная высота поперечного сечения на участке lp, Кф – коэф-т, зависящий от формы эпюры изгибающих моментов на участке lp. + 4) Прочность клеевого шва, соединяющего арматуру с древесиной: τ =Q*Sа.пр/(Iпр*Σhш) ≤ Rск, где Σhш – поверхность сдвига арматуры, равная половине периметра клеевого шва, который соединяет арматуру с древесиной. |
Анализ железобетона
Расчет железобетона выполняется в заданном сечении либо на осевую силу и изгибающий момент, либо на поперечные сдвигающие нагрузки. Анализ осевой силы и изгибающего момента обычно идеализирует поведение напряжения и деформации бетона с прямоугольным блоком напряжения для упрощения расчетов. Более подробный анализ моментной кривизны может быть выполнен с более сложными зависимостями между напряжением и деформацией.
- Осевая сила и изгибающий момент
- Пример конструкции с чистым изгибом
- Анализ кривизны моментов
Осевая сила и изгибающий момент:
Анализ железобетона на осевую силу
и изгибающий момент обычно выполняется
путем принятия заданного значения деформации в волокне с предельным сжатием с
линейное распределение деформации по глубине сечения. Стресс
распределение обычно предполагает прямоугольный блок напряжений глубиной
равной некоторой доле глубины нейтральной оси и величине, равной
часть прочности бетона на сжатие.
Стресс
распределение обычно предполагает прямоугольный блок напряжений глубиной
равной некоторой доле глубины нейтральной оси и величине, равной
часть прочности бетона на сжатие.
Параметры конструкции:
Стресс и деформация
- Глубина до нейтральной оси = c
- Максимальная деформация бетона = e
- Прочность бетона на сжатие = f ‘ c
- Предел текучести арматуры = f y
Блок стресса
- Коэффициент среднего напряжения бетона = a 1
- Коэффициент глубины блока напряжения = b 1
Понижающие коэффициенты (американский, ACI 318)
- Понижающий коэффициент армирования для растяжения и изгиба = f
- Понижающий коэффициент армирования для комплекции и изгиба = f
Примечание.
Коэффициенты снижения прочности используются в американских нормах как при расчете предельной прочности, так и при расчете коэффициента сопротивления нагрузке. Эти коэффициенты применяются к расчетной прочности на основе вида разрушения.
Факторы резистентности (канадский, CSA A23.3)
- Коэффициент сопротивления бетона = f c
- Коэффициент сопротивления арматуры = f r
Примечание. Коэффициенты сопротивления используются в канадских нормах и применяются непосредственно к прочности материала без учета вида разрушения.
Пример конструкции Pure Flexure:
Определить сопротивление изгибающему моменту прямоугольной балки с арматура на растяжение и отсутствие осевых нагрузок.
Глубина до армирования = d = 21 дюйм
Ширина балки = b = 12 дюймов
Площадь армирующей стали = A s = 3,0 дюйма 2
Прочность бетона на сжатие = f 706 3
Предел текучести арматуры = f y = 60000 psi
- Определение допустимого момента по ACI 318
Максимальная деформация бетона = e = 0,003
Понижающий коэффициент для изгиба = f = 0,90
Отношение среднего напряжения бетона = a 1 = 0,85
Отношение глубины блока напряжения = b 1 = 0,85
- Решить с помощью SF = 0,
A s f y = a b a 1 f ‘ c
3,0(60000) = a (12)(0,85)(4000)
а = 4,41 дюйма
- Определить момент от сила пару
ф М н = ф А с ф у (д — а / 2)
f M n = 0,9(3,0)(60)(21 — 4,41 / 2) / 12
f M n = 254 тыс.футов
- Определение допустимого момента согласно CSA A23.3
Максимальная деформация бетона = e = 0,0035
Коэффициент сопротивления бетона = f c = 0,60
Коэффициент сопротивления арматуры = f r = 0,85
Коэффициент среднего напряжения бетона = a 1 = 0,81
Коэффициент глубины блока напряжений = b 1 = 0,9
- Найдите «а» с помощью SF = 0,
f r A s f y = a b a 1 f c f ‘ c
0,85(3,0)(60000) = a (12)(0,81)(0,6)(4000)
a = 6,56 дюйма
- Определить момент от сила пару
М р = ф р А с ф у (д — а / 2)
M r = 0,85(3,0)(60)(21 — 6,56/2) / 12
M r = 226 килофутов
Параметрический анализ сейсмических характеристик соединения балки-колонны из сборного железобетона
На этой странице представлены соединения балка-колонна. Подробные экспериментальные результаты десяти полумасштабных гибридных соединений с ограниченной сейсмической детализацией обсуждались в другой статье. Тем не менее, из-за присущей сложности HPHS соединения балки-колонны и уникальных особенностей испытанных образцов, экспериментальное исследование не было достаточно полным. Новая деталь соединения (HPHS), предложенная в этом исследовании, характеризуется пластичным соединением, стальными соединителями и инженерным цементным композитом (ECC), который представляет собой разновидность высокоэффективного фиброцементного композита с множественными мелкими трещинами (HPFRCC). Поэтому в этой статье результаты анализа КЭ сравниваются с экспериментальными результатами циклических испытаний двух образцов (RC и PC) для оценки точности модели, а также представлены подробные описания модели, включая определение жесткости и прочности. Критическими параметрами, влияющими на поведение соединения, являются осевая нагрузка на колонну, длина стальной пластины соединения балки, вклад напряжения внутреннего болта и площадь пластического шарнира.
Подробные экспериментальные результаты десяти полумасштабных гибридных соединений с ограниченной сейсмической детализацией обсуждались в другой статье. Тем не менее, из-за присущей сложности HPHS соединения балки-колонны и уникальных особенностей испытанных образцов, экспериментальное исследование не было достаточно полным. Новая деталь соединения (HPHS), предложенная в этом исследовании, характеризуется пластичным соединением, стальными соединителями и инженерным цементным композитом (ECC), который представляет собой разновидность высокоэффективного фиброцементного композита с множественными мелкими трещинами (HPFRCC). Поэтому в этой статье результаты анализа КЭ сравниваются с экспериментальными результатами циклических испытаний двух образцов (RC и PC) для оценки точности модели, а также представлены подробные описания модели, включая определение жесткости и прочности. Критическими параметрами, влияющими на поведение соединения, являются осевая нагрузка на колонну, длина стальной пластины соединения балки, вклад напряжения внутреннего болта и площадь пластического шарнира.
1. Введение
Сборный железобетон не нашел широкого применения в качестве каркасной системы для зданий, расположенных в нескольких сейсмических регионах. Сборные железобетонные соединения между сборными элементами имеют некоторые проблемы. Соединения, в частности соединения балки с колонной, являются важной частью сборного железобетона. Чтобы удовлетворить структурным требованиям всей рамы, каждое соединение должно иметь возможность безопасно передавать вертикальный сдвиг, поперечный горизонтальный сдвиг, осевое растяжение и сжатие, а иногда и изгибающий момент и кручение между одним сборным элементом и другим. Передача сил между компонентами и, в конечном счете, поведение рам определяются характеристиками соединений. Однако на практике поведение сборных соединений недостаточно хорошо установлено и не полностью изучено для выполнения требований, необходимых при проектировании и разработке технологии сборных железобетонных изделий [1–3].
Современные технологии широко доступны для удовлетворения растущих потребностей инженеров в обеспечении населения превосходными структурными характеристиками во время землетрясения. По мере того, как в области сейсморазведки делается больше достижений, доступные технологии становятся более конкурентоспособными по стоимости по сравнению с традиционной практикой строительства: дополнительные финансовые выгоды могут быть связаны с улучшенной реакцией системы с учетом сейсмического риска, применяемого в течение срока службы конструкции. Высокопроизводительные системы будут спроектированы так, чтобы работать более эффективно, поскольку они настроены на прямое применение. В результате сейсмические требования к конструкции (максимальные смещения и ускорения) могут быть значительно снижены, что снижает материальные затраты и время строительства. Однако при разработке этой новой технологии требуются рекомендации по проектированию, чтобы обеспечить ее надлежащее использование.
По мере того, как в области сейсморазведки делается больше достижений, доступные технологии становятся более конкурентоспособными по стоимости по сравнению с традиционной практикой строительства: дополнительные финансовые выгоды могут быть связаны с улучшенной реакцией системы с учетом сейсмического риска, применяемого в течение срока службы конструкции. Высокопроизводительные системы будут спроектированы так, чтобы работать более эффективно, поскольку они настроены на прямое применение. В результате сейсмические требования к конструкции (максимальные смещения и ускорения) могут быть значительно снижены, что снижает материальные затраты и время строительства. Однако при разработке этой новой технологии требуются рекомендации по проектированию, чтобы обеспечить ее надлежащее использование.
В этом документе основное внимание уделяется пониманию поведения HPHS (высокопроизводительной гибридной системы) в условиях сейсмического воздействия. Пригодность системы HPHC была продемонстрирована серией экспериментальных испытаний, которые подтвердили хорошие характеристики системы при боковой нагрузке. Для применения HPHS к реальной конструкции необходимо оценить сейсмические характеристики одиночных соединений для нескольких первичных переменных. В этом исследовании было проведено параметрическое исследование для соединения HPHS на основе теста и анализа методом конечных элементов. Исследуемые параметры включают (1) осевую нагрузку на колонну, (2) длину стальной пластины соединения балки, (3) вклад напряжения внутреннего болта и (4) площадь пластического шарнира. Поэтому данная работа направлена на разработку и калибровку нелинейной КЭ-модели и дальнейшее ее использование для исследования поведения ВДГС путем варьирования основных параметров управления [4].
Для применения HPHS к реальной конструкции необходимо оценить сейсмические характеристики одиночных соединений для нескольких первичных переменных. В этом исследовании было проведено параметрическое исследование для соединения HPHS на основе теста и анализа методом конечных элементов. Исследуемые параметры включают (1) осевую нагрузку на колонну, (2) длину стальной пластины соединения балки, (3) вклад напряжения внутреннего болта и (4) площадь пластического шарнира. Поэтому данная работа направлена на разработку и калибровку нелинейной КЭ-модели и дальнейшее ее использование для исследования поведения ВДГС путем варьирования основных параметров управления [4].
2. Соединение предыдущей разработки и результаты испытаний
Новая деталь соединения, предложенная в этом исследовании, характеризуется пластичным соединением, стальными соединителями и инженерным цементным композитом (ECC), который представляет собой разновидность высокоэффективного фиброцементного композита с несколькими мелкие трещины (HPFRCC) и используются для улучшения технологичности соединения и эффективной передачи напряжения между снятыми с производства сборными элементами. Изготовление стального соединителя состоит из скрепления болтами стальных труб и стальных пластин, которые обычно размещаются внутри сборной колонны и балки, и заливки ЭСС к некоторым частям балки и соединения в полевых условиях (см. рис. 1 и 2) [1–3]. .
Изготовление стального соединителя состоит из скрепления болтами стальных труб и стальных пластин, которые обычно размещаются внутри сборной колонны и балки, и заливки ЭСС к некоторым частям балки и соединения в полевых условиях (см. рис. 1 и 2) [1–3]. .
Размеры и детали армирования образцов показаны на рисунке 3, а другие экспериментальные параметры перечислены в таблицах 1 и 2. Неоднородность напряжения между элементами, связанными со стальными соединителями и ECC, не наблюдалась, а нагрузка эффективно переносится на балку и сустав. Деталь соединения, разработанная и предложенная в этом исследовании, которая включает эластичное соединение и соединитель из стальных пластин, удовлетворяла требованиям, предписанным в руководстве по строительству ACI, и, таким образом, была проверена на предмет обеспечения отличных сейсмических характеристик (см. рис. 4) [1–3].
3. Аналитическая модель
Предлагаемая система соединения (СВД) имеет различные типы конструктивных элементов, таких как бетон, стальной лист и ЭСС. Очень сложно исследовать эксперимент с проектными переменными, поэтому на основе результатов эксперимента был проведен нелинейный анализ методом конечных элементов. Чтобы улучшить понимание предложенной системы соединения местного поведения напряжения-деформации и прочности соединения вблизи соединения балки с колонной, были приняты и проанализированы в общей сложности три конкретные модели. В этих инновационных высокопроизводительных гибридных системах (HPHS) используются сталь, болтовые секции и ECC в области соединения балки с колонной для облегчения соединения сборных элементов. В ходе экспериментального исследования были испытаны два монолитных и десять поликарбонатных образцов, конфигурации соединений которых незначительно отличались друг от друга. Однако из-за уникальных особенностей испытанных образцов и неоднородности материала было трудно понять сложное сейсмическое поведение соединений балки-колонны. Кроме того, влияние нескольких влияющих параметров, таких как коэффициент прочности на изгиб и осевая нагрузка, не может быть изменено в ограниченном числе экспериментов.
Очень сложно исследовать эксперимент с проектными переменными, поэтому на основе результатов эксперимента был проведен нелинейный анализ методом конечных элементов. Чтобы улучшить понимание предложенной системы соединения местного поведения напряжения-деформации и прочности соединения вблизи соединения балки с колонной, были приняты и проанализированы в общей сложности три конкретные модели. В этих инновационных высокопроизводительных гибридных системах (HPHS) используются сталь, болтовые секции и ECC в области соединения балки с колонной для облегчения соединения сборных элементов. В ходе экспериментального исследования были испытаны два монолитных и десять поликарбонатных образцов, конфигурации соединений которых незначительно отличались друг от друга. Однако из-за уникальных особенностей испытанных образцов и неоднородности материала было трудно понять сложное сейсмическое поведение соединений балки-колонны. Кроме того, влияние нескольких влияющих параметров, таких как коэффициент прочности на изгиб и осевая нагрузка, не может быть изменено в ограниченном числе экспериментов.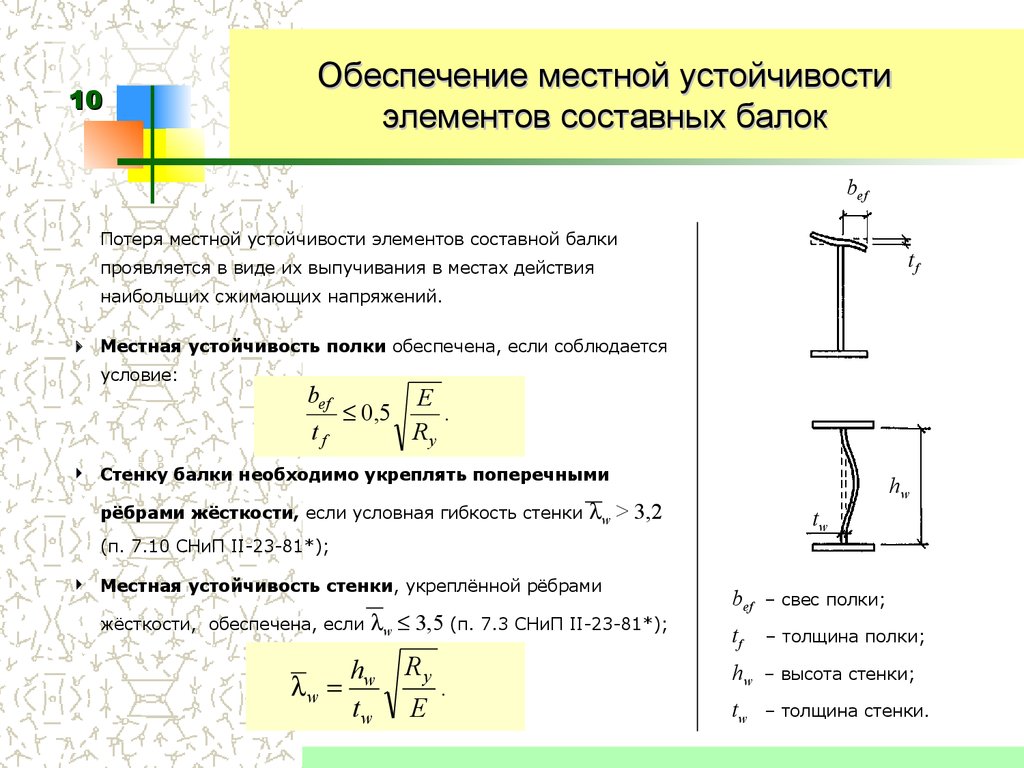 ABAQUS (версия ABAQUS 6.6-1, 2006 г.) конечно-элементный код был использован для анализа предлагаемых сборных соединений балки-колонны. Эти численные модели состояли из комбинации элементов, пружин и условий ограничения. Среди них были уточненные двухмерные элементы плоского напряжения, включающие полные нелинейные свойства материала/геометрические элементы, контактные элементы, взаимодействие поверхности с трением, условия ограничения с использованием точек уравнения, условия трещин в бетоне и упругие пружины фундамента. Эти передовые методы моделирования были предназначены для обеспечения детального и точного понимания общего поведения соединений, включая распределение напряжений на контактных поверхностях, несмотря на высокие вычислительные затраты, обычно связанные с этим типом данных [4, 5].
ABAQUS (версия ABAQUS 6.6-1, 2006 г.) конечно-элементный код был использован для анализа предлагаемых сборных соединений балки-колонны. Эти численные модели состояли из комбинации элементов, пружин и условий ограничения. Среди них были уточненные двухмерные элементы плоского напряжения, включающие полные нелинейные свойства материала/геометрические элементы, контактные элементы, взаимодействие поверхности с трением, условия ограничения с использованием точек уравнения, условия трещин в бетоне и упругие пружины фундамента. Эти передовые методы моделирования были предназначены для обеспечения детального и точного понимания общего поведения соединений, включая распределение напряжений на контактных поверхностях, несмотря на высокие вычислительные затраты, обычно связанные с этим типом данных [4, 5].
3.1. Свойства материала
Продольная арматура балки и колонны представляла собой деформированные стержни с пределом текучести 437 МПа и 508 МПа, а хомуты балки и поперечные связи колонны применялись с пределом текучести 475 МПа и 400 МПа. Величина осадки бетонной смеси составила 75 ± 25 мм. Средняя прочность бетона на сжатие, рассчитанная по цилиндрическим испытаниям, составила 27,5 МПа (площадь шва ECC = 40,5 МПа). Было подтверждено, что стальной соединитель, использованный при изготовлении образцов, изготовлен из нержавеющей стали SS400. Средние значения свойств стального профиля были получены по образцам образцовых испытаний на растяжение. Однако для широкого круга параметрических исследований использовались предложенные уравнения и сравнивались с результатами испытаний. Используемые модели напряжения-деформации бетона представляли собой модифицированную модель Кента-Парка и модель Коллинза, учитывающую ограничивающий эффект стальной трубы, встроенной в колонну. Кроме того, модель пластичности поврежденного бетона была предоставлена компанией ABAQUS; для этого требуется истинное логарифмическое соотношение между напряжением и деформацией для растяжения и сжатия. Поэтому в данном исследовании использовалась эквивалентная одноосная определяющая модель для бетона при растяжении, предложенная Торресом [6].
Величина осадки бетонной смеси составила 75 ± 25 мм. Средняя прочность бетона на сжатие, рассчитанная по цилиндрическим испытаниям, составила 27,5 МПа (площадь шва ECC = 40,5 МПа). Было подтверждено, что стальной соединитель, использованный при изготовлении образцов, изготовлен из нержавеющей стали SS400. Средние значения свойств стального профиля были получены по образцам образцовых испытаний на растяжение. Однако для широкого круга параметрических исследований использовались предложенные уравнения и сравнивались с результатами испытаний. Используемые модели напряжения-деформации бетона представляли собой модифицированную модель Кента-Парка и модель Коллинза, учитывающую ограничивающий эффект стальной трубы, встроенной в колонну. Кроме того, модель пластичности поврежденного бетона была предоставлена компанией ABAQUS; для этого требуется истинное логарифмическое соотношение между напряжением и деформацией для растяжения и сжатия. Поэтому в данном исследовании использовалась эквивалентная одноосная определяющая модель для бетона при растяжении, предложенная Торресом [6].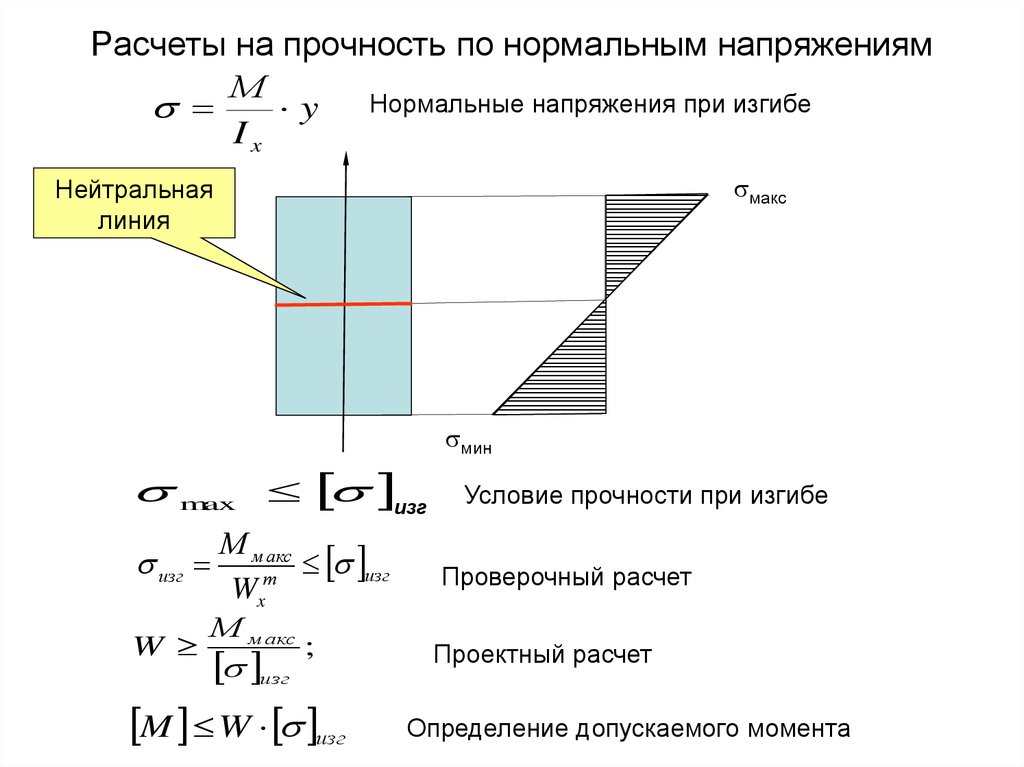 Это также показано на рис. 5. Свойства стального материала для стальной плиты и трубы колонны были смоделированы по образцу SS400 с полностью нелинейными изотропными характеристиками. По той же причине, что и бетон, сталь была смоделирована для упрощенного твердеющего материала, как показано на рисунках 6 и 7. Кривая напряжения-деформации арматуры также была определена в ходе испытаний. Тем не менее, коэффициент изгибающего момента является важной переменной для расчета моментной рамы, и для других элементов арматуры потребуется соотношение между напряжением и деформацией. Поэтому мы также используем соотношение напряжение-деформация для арматуры различного диаметра (см. рис. 6). В таблице 3 указаны коды входных материалов для пластичности бетона при повреждении для ABAQUS.
Это также показано на рис. 5. Свойства стального материала для стальной плиты и трубы колонны были смоделированы по образцу SS400 с полностью нелинейными изотропными характеристиками. По той же причине, что и бетон, сталь была смоделирована для упрощенного твердеющего материала, как показано на рисунках 6 и 7. Кривая напряжения-деформации арматуры также была определена в ходе испытаний. Тем не менее, коэффициент изгибающего момента является важной переменной для расчета моментной рамы, и для других элементов арматуры потребуется соотношение между напряжением и деформацией. Поэтому мы также используем соотношение напряжение-деформация для арматуры различного диаметра (см. рис. 6). В таблице 3 указаны коды входных материалов для пластичности бетона при повреждении для ABAQUS.
Последним набором свойств материала является ECC при сжатии и растяжении. Как обсуждалось ранее, ECC имеет очень большую способность к растяжению. Используя данные испытаний по напряжению-деформации, для моделирования материала при растяжении было использовано эквивалентное идеально пластичное поведение материала (см. рис. 8). А доступные тестовые данные использовались для сжатия.
рис. 8). А доступные тестовые данные использовались для сжатия.
3.2. Моделирование методом конечных элементов
В настоящем исследовании образцы анализировались с использованием программного обеспечения ABAQUS. Двумерные (2D) плоские напряженные элементы были применены для моделирования бетонных и стальных пластин, а арматурные стержни были смоделированы как элементы фермы. При моделировании материалов модели бетона основывались на нелинейных механизмах разрушения для учета растрескивания, а модели пластичности использовались для бетона при сжатии и стальной арматуре. Код конечных элементов ABAQUS (версия ABAQUS 6.10-1, 2010 г.) использовался для анализа влияния переменных предлагаемой системы соединения (см. рис. 9).).
Как правило, в композитной конструкции возникает много проблем с площадью контакта бетона и стали. Таким образом, все интерфейсы между двумя контактными поверхностями были ограничены друг другом. Общая формулировка контакта, используемая в ABAQUS, включает алгоритм ведущий-ведомый.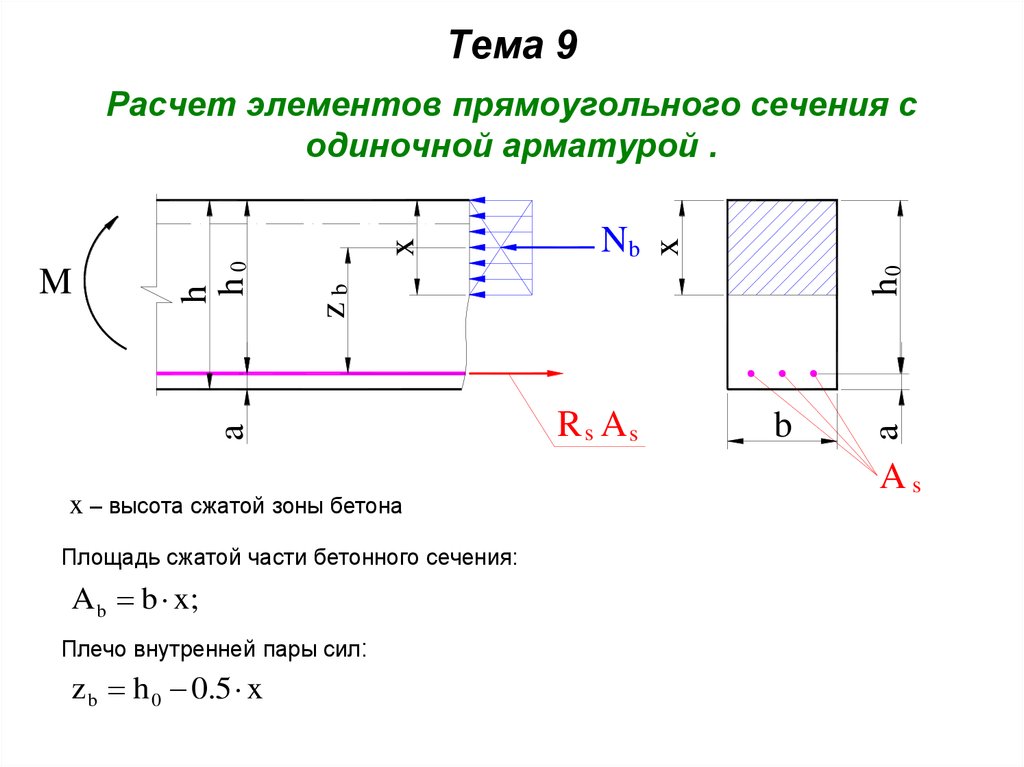 Эта формулировка учитывает жесткий контакт для нормального направления каждой поверхности и поведение фрикционного контакта для тангенциального направления. Поверхностные взаимодействия и ограниченная область показаны на рисунке 10. Граничные условия для сгенерированной модели показаны на рисунке 11. Нижняя часть колонны поддерживалась штифтом, а конец балки поддерживался роликом. Эти граничные условия были определены из тестовых допущений. Конец балки фиксировался только роликом, а низ колонны фиксировался шарниром. КЭ модели загружались в два этапа. Осевая нагрузка была приложена на первом этапе к колонне, а боковая нагрузка была приложена к тому же месту на втором этапе циклически. Циклическая нагрузка применялась путем управления перемещением, что показано на рис. 12.9.0003
Эта формулировка учитывает жесткий контакт для нормального направления каждой поверхности и поведение фрикционного контакта для тангенциального направления. Поверхностные взаимодействия и ограниченная область показаны на рисунке 10. Граничные условия для сгенерированной модели показаны на рисунке 11. Нижняя часть колонны поддерживалась штифтом, а конец балки поддерживался роликом. Эти граничные условия были определены из тестовых допущений. Конец балки фиксировался только роликом, а низ колонны фиксировался шарниром. КЭ модели загружались в два этапа. Осевая нагрузка была приложена на первом этапе к колонне, а боковая нагрузка была приложена к тому же месту на втором этапе циклически. Циклическая нагрузка применялась путем управления перемещением, что показано на рис. 12.9.0003
3.3. Результаты анализа КЭ
Для проверки конечно-элементной модели аналитические результаты сравнивались с экспериментальными. Образцы были смоделированы с элементами фермы и оставшимися двумерными элементами плоского напряжения.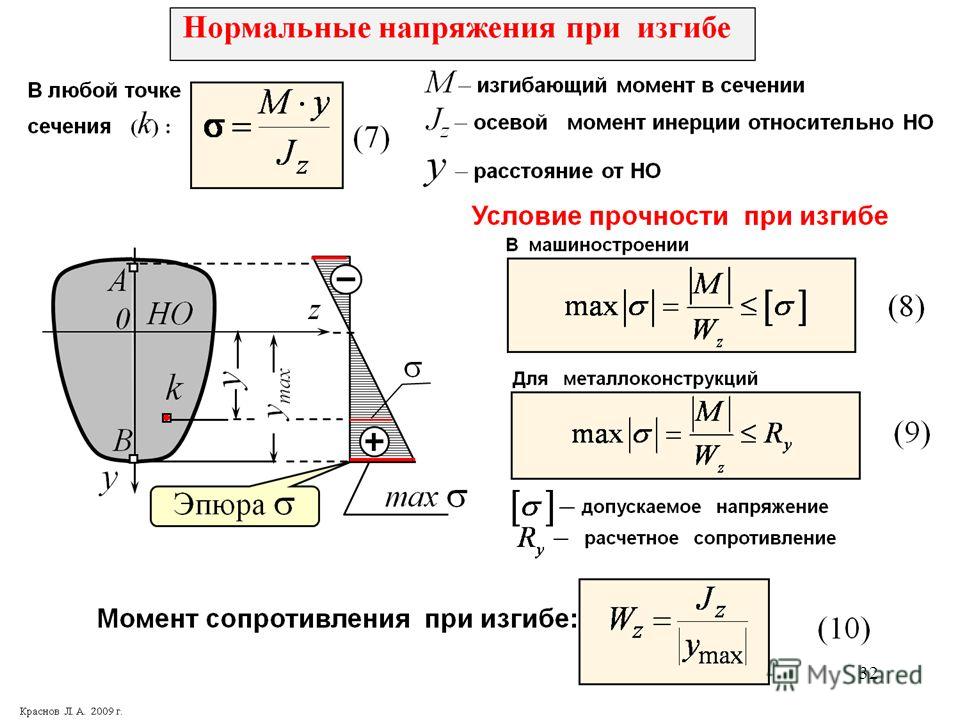 Бетон был смоделирован с использованием двумерных плоских элементов напряжения, которые были изопараметрическими элементами. С другой стороны, арматурные стальные стержни были смоделированы как двухузловые элементы фермы. В центральной области соединения площадь элементов фермы вблизи границы была соответственно увеличена, чтобы смоделировать их соответствующие вклады площади стали. Нижние стержни балки были прекращены на лице колонны. Стальные пластины, которые использовались для соединения в стыке, проходили внутрь балки с одной стороны и упирались в торец колонны с другой стороны. Эти пластины моделировались как двумерные плоские напряженные элементы. Этим элементам были присвоены толщина стального листа и свойства его материала. Бетон на передней и задней стороне этих элементов не учитывался при анализе, так как он был залит после того, как соединения были закреплены. Четыре ряда двумерных элементов в нижней части стыка считались соединенными стальными пластинами, а их эквивалентная площадь была перенесена на основные стержни колонны и поперечные звенья.
Бетон был смоделирован с использованием двумерных плоских элементов напряжения, которые были изопараметрическими элементами. С другой стороны, арматурные стальные стержни были смоделированы как двухузловые элементы фермы. В центральной области соединения площадь элементов фермы вблизи границы была соответственно увеличена, чтобы смоделировать их соответствующие вклады площади стали. Нижние стержни балки были прекращены на лице колонны. Стальные пластины, которые использовались для соединения в стыке, проходили внутрь балки с одной стороны и упирались в торец колонны с другой стороны. Эти пластины моделировались как двумерные плоские напряженные элементы. Этим элементам были присвоены толщина стального листа и свойства его материала. Бетон на передней и задней стороне этих элементов не учитывался при анализе, так как он был залит после того, как соединения были закреплены. Четыре ряда двумерных элементов в нижней части стыка считались соединенными стальными пластинами, а их эквивалентная площадь была перенесена на основные стержни колонны и поперечные звенья.
Предсказанная и наблюдаемая реакции образцов представлены на рисунке 13. Из рисунка 13(a) образца RC-контроль видно, что аналитическая модель предсказала хороший отклик по сравнению с экспериментальными наблюдениями. Хотя смещения аналитической модели для нескольких начальных циклов были несколько выше, предсказанные результаты более поздних циклов хорошо согласовывались с экспериментальными аналогами. Контрольный образец RC достиг коэффициента пластичности смещения () около 2,8, и в петлях наблюдалось защемление. Петли были тонкими и очень похожими на экспериментальные результаты. На этом этапе наблюдалась большая деформация ядра сустава. На рис. 13(б) показано сравнение аналитических и экспериментальных результатов для образца ПК-И50-0,2. Из результатов эксперимента видно, что образец демонстрировал большое начальное смещение в течение многих циклов. Образец достиг хорошего рассеяния энергии примерно до 2,8. Общая деформированная форма образца, соответствующая 1,5, приведена на рисунке 13 (б). На рисунке видна умеренная деформация ядра соединения, верхней и нижней частей колонны. Образец I-ECC25 достиг примерно 2,9, несколько меньше по сравнению с его экспериментальными значениями. Хотя экспериментальные петли показывали большие начальные смещения, их аналитические аналоги всегда отображали устойчивые смещения на всем протяжении. Это может быть связано с тем, что соединения могли иметь некоторые начальные зазоры в стальном соединителе, где крепились гайки и болты, которые могли проскальзывать после приложения нагрузки, что приводило к большим начальным смещениям.
На рисунке видна умеренная деформация ядра соединения, верхней и нижней частей колонны. Образец I-ECC25 достиг примерно 2,9, несколько меньше по сравнению с его экспериментальными значениями. Хотя экспериментальные петли показывали большие начальные смещения, их аналитические аналоги всегда отображали устойчивые смещения на всем протяжении. Это может быть связано с тем, что соединения могли иметь некоторые начальные зазоры в стальном соединителе, где крепились гайки и болты, которые могли проскальзывать после приложения нагрузки, что приводило к большим начальным смещениям.
Сравнение аналитических и экспериментальных результатов всех образцов показало, что боковые петли гистерезиса нагрузки-смещения, полученные из анализов КЭ, были очень похожи на экспериментальные наблюдения. Кроме того, режимы разрушения и предельная пластичность хорошо коррелировали с экспериментальными результатами. КЭ анализы также показали, что результаты деформаций и шаблонов растрескивания хорошо согласуются с экспериментальными наблюдениями. Исходя из вышеупомянутых наблюдений и прогнозов как глобального, так и локального поведения с использованием анализа КЭ, использование методов моделирования КЭ может быть расширено для изучения совместной работы путем изменения различных параметров.
Исходя из вышеупомянутых наблюдений и прогнозов как глобального, так и локального поведения с использованием анализа КЭ, использование методов моделирования КЭ может быть расширено для изучения совместной работы путем изменения различных параметров.
4. Параметрические исследования
4.1. Влияние осевых нагрузок на поведение соединений балка-колонна
Осевая нагрузка является критическим параметром при исследованиях соединений балка-колонна, но ее влияние на сейсмические характеристики соединений балки-колонны до конца не изучено. Предыдущие исследования показали, что осевая сила благотворно влияет на сопротивление сдвигу сустава [3]. Поскольку глубина нейтральной оси в колонне увеличивается с осевой сжимающей нагрузкой, можно предположить, что большая часть сил связи от балочных стержней передается на диагональную стойку. Следовательно, конкретный вклад в совместное сопротивление сдвигу будет увеличен. В [7] авторы экспериментально исследовали два непластичных внутренних соединения балки-колонны с различными уровнями осевой нагрузки. Тем не менее, оба этих образца не удалось из-за вытягивания закладных балки нижних баров вместо совместной разрушения сдвига.
Тем не менее, оба этих образца не удалось из-за вытягивания закладных балки нижних баров вместо совместной разрушения сдвига.
Исследования Lin и Restreop [8] показали, что чрезмерное осевое сжатие оказывает вредное воздействие на суставы. В исследовании, проведенном Fu et al. [9] было указано, что если сдвиг был небольшим, увеличение осевых нагрузок было благоприятным для суставов, тогда как при высоких сдвигах увеличение осевых нагрузок было неблагоприятным. Ли и др. [10] обнаружили, что для прямоугольного соединения осевая нагрузка меньше, чем была полезна для соединения, в то время как осевая сжимающая нагрузка в диапазоне от нуля улучшала работу соединения для глубоких соединений колонн, подобных стене.
В этом исследовании исследуется влияние осевой нагрузки на сейсмические характеристики гибридных сталебетонных соединений. Осевая нагрузка была приложена на первом этапе к колонне, а боковая нагрузка была приложена к тому же месту на втором этапе циклически. Были применены те же истории нагружения, что и при анализе образцов без осевой нагрузки, и для образца PC-I50-0,2 были построены графики зависимости поперечной силы от горизонтального смещения, соответствующие различным уровням осевой нагрузки. Можно видеть, что серия образцов между сериями достигла оптимального значения окончательного сдвига истории, когда отношение осевой нагрузки было . Таким образом, результаты анализа показали, что осевая нагрузка благотворно влияет на работу суставов. Однако было обнаружено, что отношение осевой нагрузки вредно, так как оно снижает сдвиг по этажу и рассеивание энергии соединения (см. рис. 14).
Можно видеть, что серия образцов между сериями достигла оптимального значения окончательного сдвига истории, когда отношение осевой нагрузки было . Таким образом, результаты анализа показали, что осевая нагрузка благотворно влияет на работу суставов. Однако было обнаружено, что отношение осевой нагрузки вредно, так как оно снижает сдвиг по этажу и рассеивание энергии соединения (см. рис. 14).
4.2. Формирование пластикового шарнира
При проектировании железобетонной рамы наиболее важным фактором при проектировании является соотношение силы момента балки и колонны и расположение пластикового шарнира. Кроме того, стальные пластины были бы очень важным конструктивным параметром, поскольку этот параметр определяет прочность и жесткость балок.
Коэффициент прочности при моменте определяется как отношение суммы номинальных сил моментов колонны над и под стыком к сумме номинальных моментов всех балок в одной плоскости, обрамляющих стык. Теоретически, коэффициент силы момента больше единицы должен привести к формированию пластичных шарниров в балках, а не в колонне. Однако строительные нормы и правила ACI318 [2] и комитет ASCE-ACI 352 рекомендуют, чтобы коэффициент прочности на момент был больше или равен 1,2 и 1,4 соответственно. Для балки отказа предлагаемого соединения, образцы были разработаны, чтобы иметь коэффициент силы момента как 1,6. Для более экономичного проектирования предлагаемой системы соединения необходимо тщательно изучить длину и толщину пластины. Поэтому в этом разделе были исследованы КЭ модели. Исследуемый диапазон деталей соединения определялся по соотношению моментов прочности 1 к 1,6.
Однако строительные нормы и правила ACI318 [2] и комитет ASCE-ACI 352 рекомендуют, чтобы коэффициент прочности на момент был больше или равен 1,2 и 1,4 соответственно. Для балки отказа предлагаемого соединения, образцы были разработаны, чтобы иметь коэффициент силы момента как 1,6. Для более экономичного проектирования предлагаемой системы соединения необходимо тщательно изучить длину и толщину пластины. Поэтому в этом разделе были исследованы КЭ модели. Исследуемый диапазон деталей соединения определялся по соотношению моментов прочности 1 к 1,6.
В результате анализа методом конечных элементов прочность образца соединения балки с колонной в большинстве случаев может быть определена по прочности балки. Тем не менее, режим разрушения пучка к колонне образца для случая коэффициента мощности момента 1 показал отказ соединения балки. Другие испытательные образцы с пределом прочности при моменте 1,2 ∼ 1,6 продемонстрировали режим разрушения балки. По мере увеличения коэффициента мощности пластический шарнир смещался к внешней стороне сустава. Причем трещины были более сосредоточены на пластиковом шарнире. Он показан на рисунках 15 и 16.
Причем трещины были более сосредоточены на пластиковом шарнире. Он показан на рисунках 15 и 16.
Распределение деформации является очень важной информацией для определения местоположения пластикового шарнира; из информации о деформации результатов МКЭ четко наблюдалось расположение пластического шарнира. Все образцы испытали текучесть арматуры. Однако уменьшение отношения моментов к прочности снижает напряжение в области пластического шарнира. При низком уровне отношения моментов к прочности податливость арматуры была показана позже, чем у других образцов. Это показано на рисунке 17. Кроме того, чтобы проверить вклад стальной пластины и определить местонахождение области пластического шарнира, были выполнены дополнительные анализы КЭ. Как описано выше, жесткость сечения балки является основным параметром для определения местоположения области пластического шарнира. В результате КЭ-анализа картина трещин каждой модели КЭ с разной длиной соединительной пластины явно различается. Расположение пластического шарнира четко определялось по длине пластин. Это показано на рисунке 18.
Это показано на рисунке 18.
5. Рассмотрение конструкции
Для определения допустимого момента болтового соединения необходимо исследовать распределение деформации болтов и соединительных пластин. Поскольку деформация болта не может быть измерена в ходе испытания, был проведен трехмерный анализ методом конечных элементов. Поскольку для компенсации деталей предлагаемой системы соединения требовалось слишком много компонентов, анализ проводился только при монотонной нагрузке. Конечно-элементная модель состояла из 3 частей: бетонных частей, стальных частей и арматуры. Для реальности конечно-элементного моделирования каждая деталь моделировалась отдельно. А арматура была встроена в бетонные компоненты. Эти модели показаны на рисунке 19.. Граничные условия и другие ограничения создаются с помощью того же метода двумерного анализа методом конечных элементов.
В результате конечно-элементного анализа были получены контур напряжений и поле деформации. В частности, были исследованы напряжение и деформация компонентов болтов для распределения результирующих усилий по площади соединения. Распределение напряжения показано на рисунке 20. В области соединения большая часть напряжения была сосредоточена в конце пластины. Поскольку напряжение шло вдоль нормального направления площади контакта, концентрация напряжения в бетоне была показана в концевой части стальной пластины. Однако бетон колонны оставался в диапазоне упругости. Для определения пластического шарнира балочных элементов было исследовано распределение напряжений арматуры. В основном напряжение концентрировалось на конце стальной пластины. Следовательно, при использовании предложенной системы соединения пластиковый шарнир можно было регулировать по длине пластины. Это показано на рис. 21. Для целей проектирования потребуется распределение напряжения соединительной стальной пластины. Используя информацию о распределении напряжения в центре элемента болта, описанную в этом разделе, можно рассчитать результирующую силу. Это также показано на рисунке 22.
Распределение напряжения показано на рисунке 20. В области соединения большая часть напряжения была сосредоточена в конце пластины. Поскольку напряжение шло вдоль нормального направления площади контакта, концентрация напряжения в бетоне была показана в концевой части стальной пластины. Однако бетон колонны оставался в диапазоне упругости. Для определения пластического шарнира балочных элементов было исследовано распределение напряжений арматуры. В основном напряжение концентрировалось на конце стальной пластины. Следовательно, при использовании предложенной системы соединения пластиковый шарнир можно было регулировать по длине пластины. Это показано на рис. 21. Для целей проектирования потребуется распределение напряжения соединительной стальной пластины. Используя информацию о распределении напряжения в центре элемента болта, описанную в этом разделе, можно рассчитать результирующую силу. Это также показано на рисунке 22.
Нейтральная ось сформирована на третьем болте от сжимающего крайнего волокна. Поскольку жесткость можно было увеличить за счет воздействия композита на сжимающую область, площадь сжимающего напряжения была больше, чем растягивающая. Приведенное напряжение показано в таблице 4.
Поскольку жесткость можно было увеличить за счет воздействия композита на сжимающую область, площадь сжимающего напряжения была больше, чем растягивающая. Приведенное напряжение показано в таблице 4.
6. Заключение
Модели КЭ, использованные в этом исследовании, хорошо предсказывают поведение испытуемых образцов. Однако первоначальные проблемы с жесткостью, с которыми сталкивается модель встроенной фермы, должны быть решены для более широкого параметрического исследования, такого как проверка работоспособности в процессе проектирования.
По данным параметрического исследования исследовано влияние осевой нагрузки. Существует снижение сдвига истории и предельного количества циклов после увеличения коэффициента осевой нагрузки за пределы 0,3 (т.е. ). Таким образом, результаты анализа показали, что осевая нагрузка положительно влияет на работу сустава. Однако было обнаружено, что отношение осевой нагрузки вредно, так как оно уменьшает сдвиг по этажу и рассеивание энергии сустава.
Пластиковая область шарнира является очень важным критерием конструкции рамы. По результатам параметрического исследования место пластического шарнира определяется соотношением сил и моментов и длиной пластины. Как правило, пластический шарнир формировался вдали от торца колонны с увеличением коэффициента прочности. Это было выяснено путем исследования распределения напряжений в арматуре. При низком значении коэффициента прочности арматура трудно поддается деформации, а пластический шарнир не может быть легко сформирован в зоне установки пластины. Однако длина пластин является важным параметром для расположения пластикового шарнира. Исследование с помощью теста и модели КЭ показало, что пластический шарнир возникает на концах стальных пластин. Таким образом, при использовании предложенной соединительной системы расположение пластиковых петель может регулироваться конструкторами.
Сложная 3D-модель предлагаемой соединительной системы будет использоваться для расчета расчетной прочности соединения. Распределение напряжений в болтовых элементах аналогично распределению напряжений, полученному с помощью методов совместимости деформаций. Следовательно, предлагаемое соединение может быть спроектировано с использованием обычных методов проектирования.
Распределение напряжений в болтовых элементах аналогично распределению напряжений, полученному с помощью методов совместимости деформаций. Следовательно, предлагаемое соединение может быть спроектировано с использованием обычных методов проектирования.
Доступность данных
Данные, использованные для поддержки результатов этого исследования, включены в статью. Любые дополнительные данные, относящиеся к статье, могут быть запрошены у соответствующего автора.
Конфликт интересов
Автор заявляет об отсутствии конфликта интересов.
Благодарности
Это исследование было поддержано грантом Университета Кённам, 2016 г.
Ссылки
H.-K. Чой, Ю.-К. Чой и К.-С. Чой, «Разработка и испытания соединений сборных железобетонных балок и колонн», Engineering Structures , vol. 56, стр. 1820–1835, 2013.
Посмотреть по адресу:
Сайт издателя | Академия Google
Х.
 -К. Чой, Ю.-К. Чой и К.-С. Чой, «Гистерезисное поведение и сейсмостойкость соединений сборных железобетонных балок и колонн», Журнал Общества сейсмостойких инженеров Кореи , том. 14, нет. 4, стр. 61–71, 2010.
-К. Чой, Ю.-К. Чой и К.-С. Чой, «Гистерезисное поведение и сейсмостойкость соединений сборных железобетонных балок и колонн», Журнал Общества сейсмостойких инженеров Кореи , том. 14, нет. 4, стр. 61–71, 2010.Посмотреть по адресу:
Сайт издателя | Google Scholar
К.-С. Чой, С.-Х. Ким, Ю.-К. Чой и Х.-К. Чой, «Аналитическое исследование соединений балок и колонн из гибридного сборного железобетона», Журнал Корейского института бетона , том. 25, нет. 6, стр. 631–639, 2013 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. А. Кулкарни, Б. Ли и В. К. Йип, «Конечно-элементный анализ сборных железобетонных соединений гибридной стали при циклической нагрузке», Journal of Constructional Steel Research , vol. 64, нет. 2, стр. 190–201, 2008 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж.
 Ху, «Проектирование и моделирование интеллектуальных систем соединения PR-CFT», в Smart Connection Systems , Taylor & Francis Group, Milton, England, 2015.
Ху, «Проектирование и моделирование интеллектуальных систем соединения PR-CFT», в Smart Connection Systems , Taylor & Francis Group, Milton, England, 2015.Просмотр по адресу:
Google Scholar изгибаемые бетонные элементы с трещинами», ASCE , vol. 130, нет. 8, pp. 1242–1251, 2004.
Просмотр по адресу:
Google Scholar
М. Аттила Б., С. П. Пессики, Р. Н. Уайт и П. Гергели, «Последствия экспериментов по сейсмическому поведению гравитационной нагрузки разработанных железобетонных соединений балки с колонной», Спектры землетрясений , vol. 12, нет. 2, стр. 185–198, 1996.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. М. Лин и Дж. И. Рестреоп, «Сейсмическое поведение и расчет железобетонных внутренних соединений балки-колонны», Бюллетень Новой Зеландии для Общества сейсмостойкого строительства , том.
 35, нет. 2, стр. 108–128, 2002 г.
35, нет. 2, стр. 108–128, 2002 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. П. Фу, Т. Чен, З. Ван и С. Бай, «Влияние коэффициента осевой нагрузки на сейсмические характеристики внутренних соединений балки и колонны», в Proceedings of the 12WCEE 2000 , стр. 1–5, Окленд, Новая Зеландия, февраль 2000 г. поведение соединений балки-колонны из высокопрочного бетона при осевой нагрузке колонны», ASCE , том. 141, нет. 9, стр. 1842–1853, 2004.
Посмотреть по адресу:
Google Scholar
Copyright
Copyright © 2020 H.-K. Чой. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.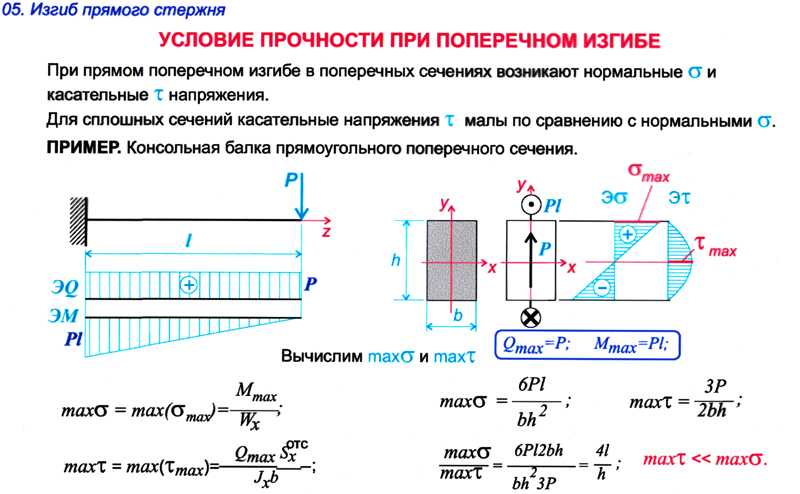


 (l-пролет, hОП –высота на опоре, hСР – в середине пролета)
(l-пролет, hОП –высота на опоре, hСР – в середине пролета)
 Модуль упругости примерно в 20 раз ниже – те устойчивость значительно выше, чем у двутавровых. Теперь на стенку передается нагрузка с половины верхнего пояса, равнодействующая расположена посередине – отрывающие усилия.
Модуль упругости примерно в 20 раз ниже – те устойчивость значительно выше, чем у двутавровых. Теперь на стенку передается нагрузка с половины верхнего пояса, равнодействующая расположена посередине – отрывающие усилия.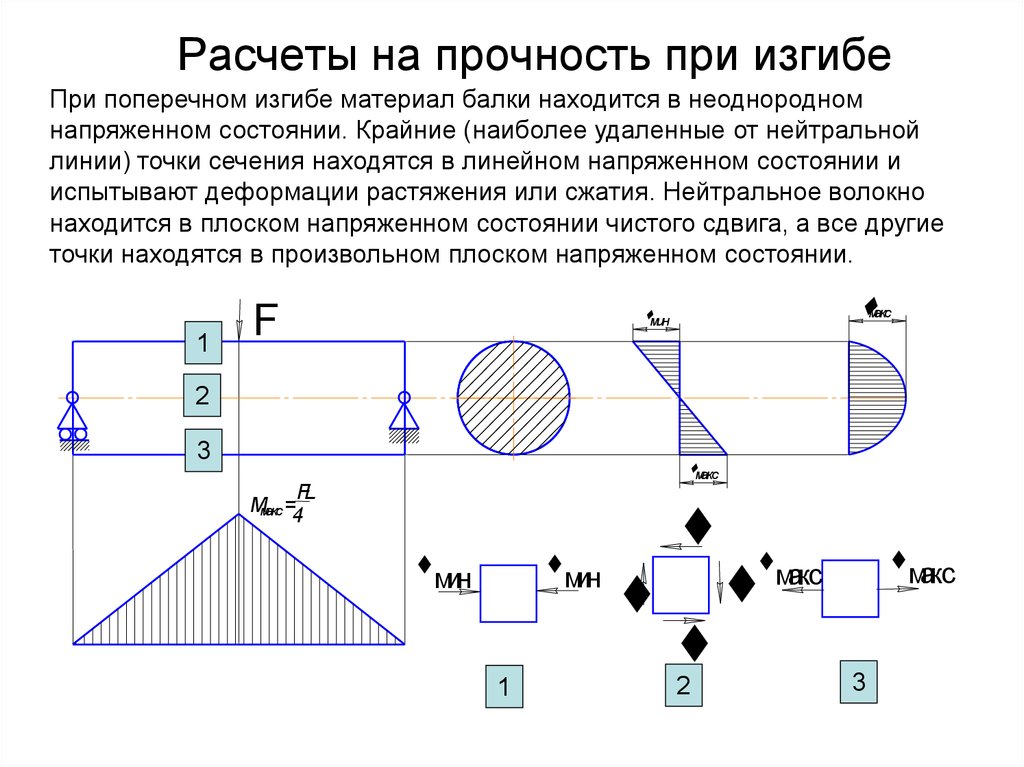 Так как сопротивление растяжению-сжатию у фанеры не сильно превышает сопротивление растяжению-сжатию древесины, делать пояса из фанеры нецелесообразно.
Так как сопротивление растяжению-сжатию у фанеры не сильно превышает сопротивление растяжению-сжатию древесины, делать пояса из фанеры нецелесообразно. Но это приводит к тому, что при изгибе балки тонкая фанерная стенка теряет местную устойчивость.
Но это приводит к тому, что при изгибе балки тонкая фанерная стенка теряет местную устойчивость. Балки, составленной из двух материалов (древесины и фанеры) рассчитывают по приведенным геометрическим характеристикам поперечных сечений. Приведение осуществляется к тому материалу, в котором проверяют напряжения.
Балки, составленной из двух материалов (древесины и фанеры) рассчитывают по приведенным геометрическим характеристикам поперечных сечений. Приведение осуществляется к тому материалу, в котором проверяют напряжения. ср.
ср.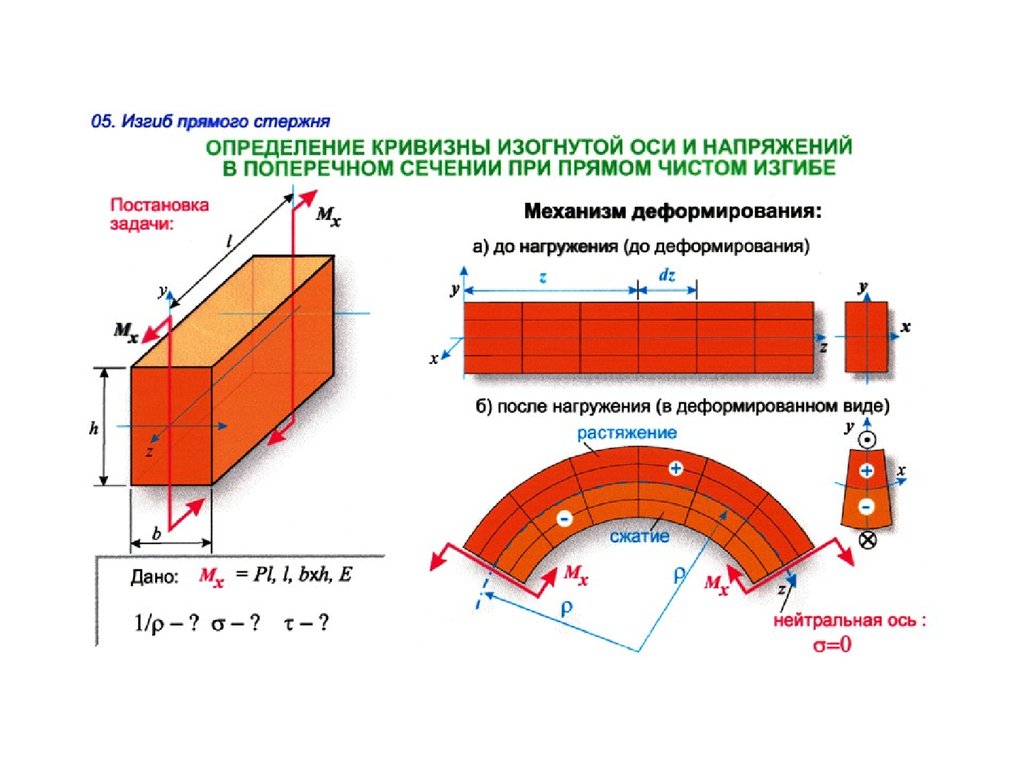 Геометрические характеристики и расчетные напряжения определяются для сечения, расположенного в середине длинны панели.
Геометрические характеристики и расчетные напряжения определяются для сечения, расположенного в середине длинны панели.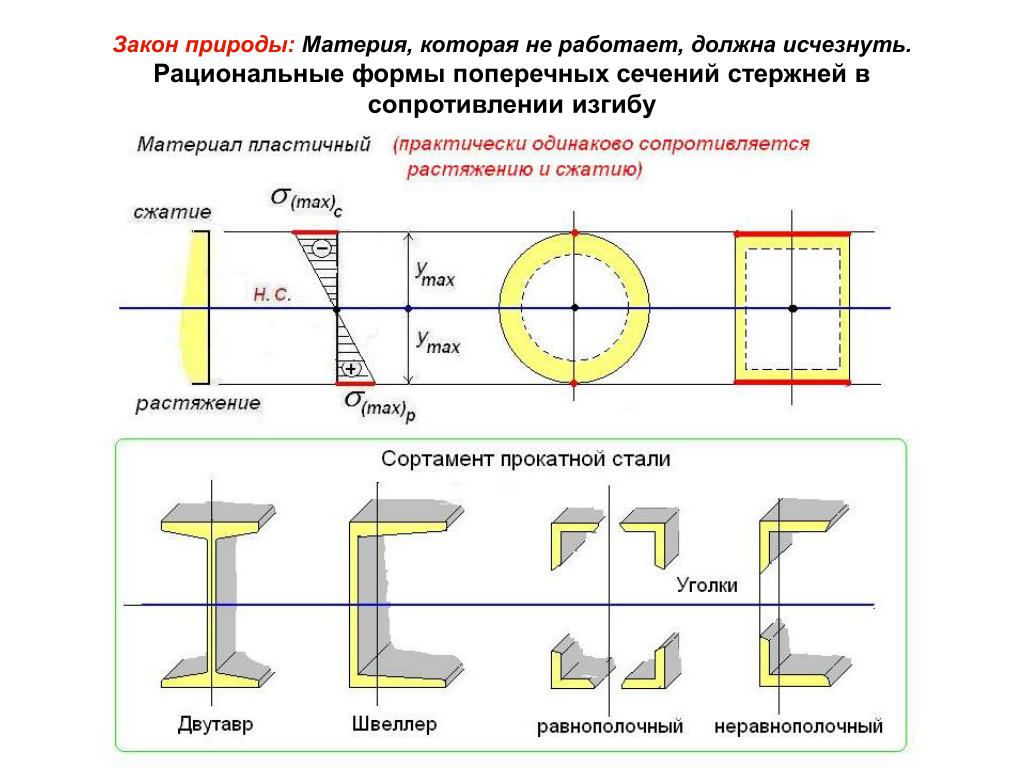 Волнистая фанерная стенка практически не воспринимает нормальные напряжения, так как при изгибе балки она способна складываться, или распрямляться, те обладает податливостью. В результате податливости волнистой фанерной стенки полки балки будут упруго сдвигаться относительно друг друга. Поэтому на основании исследований балку с волнистой стенкой следует рассчитывать как составную на податливых связях, где роль податливых связей играет волнистая стенка. В расчете податливость фанерной стенки учитывают, вводя специальные коэффициенты.
Волнистая фанерная стенка практически не воспринимает нормальные напряжения, так как при изгибе балки она способна складываться, или распрямляться, те обладает податливостью. В результате податливости волнистой фанерной стенки полки балки будут упруго сдвигаться относительно друг друга. Поэтому на основании исследований балку с волнистой стенкой следует рассчитывать как составную на податливых связях, где роль податливых связей играет волнистая стенка. В расчете податливость фанерной стенки учитывают, вводя специальные коэффициенты. ; сжатого пояса по формуле: σ = M/(φу*Wбр) ≤ Rс,
; сжатого пояса по формуле: σ = M/(φу*Wбр) ≤ Rс,



