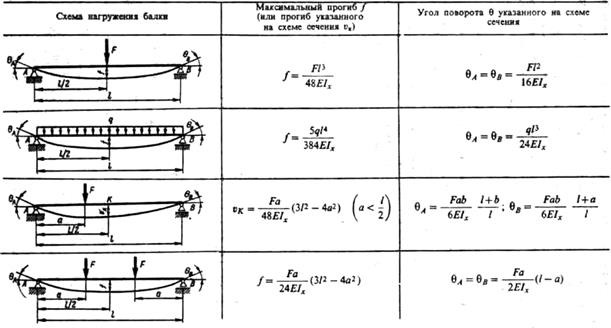
Расчет двутавра на прогиб и изгиб
Чаще всего для расчета высоты подпорки прибегают к помощи онлайн калькулятора, который автоматически проводит расчет всех необходимых параметров. Чтобы правильно подобрать тип кровельного элемента, нужно указать некоторые данные, а именно:
- сфера использования;
- шаг между элементами кровли;
- требуемая длина;
Затем вычисляется расчетная нагрузка согласно каркасному элементу:
- Система стропил – 220 кг/кв.м.
- Двутавровая балка перекрытия – 400 кг/кв.м.
Цена изделия варьируется от габаритов балки и материала, из которого создана полка (натуральное дерево, брус LVL).
Монтажный процесс
Чаще всего наиболее приемлемым способом установки деревянных двутавров является фиксация на специальные кронштейны, со специальной симметричной конструкцией. На противоположных сторонах изделие снабжено крепежным приспособлением и пластиной, фиксирующейся напротив аналогичного крепежного элемента.
Схема сборки перекрытия из двутавровой балки
Учитывая габариты, а если быть уж совсем точными, высоту комбинированной балки из дерева и стружечной плиты, элемент конструкции может комплектоваться крепежами разной длины.
Правила техники безопасности
Выполняя монтажные работы по установке двутавровых балок, изначально их нужно закрепить при помощи временных элементов, которые затем меняют на постоянные стационарные фиксаторы. По технике безопасности категорически запрещается начинать эксплуатацию балок, пока мастера не снабдят их обвязкой, и не будут сняты временные держатели.
Демонтаж можно проводить лишь после того, как мастера удостоверятся в наличие обвязки на балках. Закрепленные исключительно временными фиксаторами, двутавровые перекрытия способны выдержать только вес рабочих и монтажного оборудования. Очень важно знать, бракованные или деформированные балки не ремонтируются собственноручно или на производстве и не могут быть установлены на свои посадочные места, ни при каких обстоятельствах.
Перевозка и хранение
Во время перемещения перекрытия, его ни в крем случае нельзя пригружать по малой оси, иначе материал может прогнуться и искривиться. При погрузке балок их нельзя бросать, а только аккуратно складывать. Хранятся опоры под навесами и в крытых складах. Если нет такой возможности, и конструкционные элементы лежат на улице под небом, для этого их нужно защитить от попадания ультрафиолета и осадков специальным материалом.
Начало статьи в предыдущей статье.
Расчет нагрузки двутавровой балки: На прочность, на прогиб
Чтобы сделать прочные, надежные перекрытия, необходимо запастись подходящими балками. В частном строительстве вместо стальных элементов обычно используют деревянные. Но какие балки приобрести, на какой размер ориентироваться?
Выбираем оптимальную длину
Приобретая под заказ двутавровые балки перекрытия деревянные, расчет определяется несколькими важными моментами. Прежде всего, балка должна перекрыть пролет с небольшим запасом, чтобы в дальнейшем ее можно было заделать в стенку.
Возможны вариации. Например, вы хотите задействовать двутавры в создании ската крыши. Значит, их придется вывести наружу примерно на полметра. При использовании дополнительных элементов длина балки должна быть такой же, как расстояние от одной стены до другой. Самый оптимальный вариант расчета, когда балка перекрывает расстояние 2,5 – 4 метра. При большей длине ее прочности может оказаться недостаточно. В длинных пролетах применяется клееный брус, устанавливаются колонны, служащие опорами.
Определяем нагрузку
Важно соблюдать техусловия, когда устанавливаешь балки перекрытия деревянные двутавровые. Желательно задействовать специальный калькулятор для более точного расчета балочной конструкции. К этому вопросу мы еще вернемся, а пока рассмотрим основные способы определения нагрузки.
Какая именно нагрузка действует на двутавры? В первую очередь, это вес самих деталей.
Во-вторых, эксплуатационная нагрузка. Она бывает как временной, так и постоянной. Делать точный расчет деревянных элементов непросто – даже когда под рукой есть специальный онлайн-калькулятор. Впрочем, высчитать точные размеры двутавровых балок можно с помощью упрощенной формулы.
Например, вы планируете перекрывать чердак без возможности хранения вещей. Значение 50 кг/м2 примем за регулярную нагрузку. Чтобы высчитать эксплуатационную нагрузку, достаточно умножить 70 на 1,3 = 90 кг/м2. Первая цифра – нормативное значение, вторая – запас. Для определения общей нагрузки суммируем 50 и 90 = 140 кг/м
Приведенные выше расчеты предполагают, что бригада намерена перекрывать чердак с использованием легкого утеплителя. Применение материалов с другим весом автоматически влияет на нагрузку. Которая повышается с базовых 50 кг/м2 до 150 кг/м2. Даже не имея под рукой калькулятор, несложно догадаться, что конечное значение равно 150 х 1,3 + 50 = 245 кг/м2.
Округляем это значение и получаем 250.
Когда нужно высчитать нагрузку мансарды, учитывайте дополнительный вес самого пола и покрытия, а также мебели, находящихся на мансарде людей. Рекомендуемая нагрузка будет равна 350-400 кг/м2.
Сечение, шаг балок
Если известна длина, выполнены расчеты нагрузки, узнать размеры сечения, шаг гораздо проще. Подойдет прямоугольное сечение, соотношение ширины/высоты 1 к 1,4 соответственно. Размеры бывают разными: ширина порядка 4-20 см, высота – 10-30 см. Подбирайте высоту, дабы укладка утеплителя была удобной.
Не последнюю роль при выборе сечения деревянных балок перекрытия играет шаг укладки. Как правило, он варьируется в диапазоне 60-100 см. Однако возможны отклонения от заданной величины в пределах 30-120 см. Шаг может подбираться с ориентиром на ширину плиты теплоизоляционного материала. Чтобы в точности проверить размеры и произвести все необходимые расчеты двутавровых балок, воспользуйтесь специальной программой.
Благо, в интернете представлено немало приложений, позволяющих выполнить нужные расчеты быстро и точно.
Что еще нужно знать о нагрузках?
Когда возводится многоэтажное здание, перекрытие является потолком одного этажа, полом другого, расположенного выше. Существует опасность, что после меблировки возникнет перегруз. Особенно если шаг между балками очень существенный, и в процессе строительства было принято решение отказаться от лагов. Половые доски настилают на брус. Калькулятор здесь не поможет, ведь расстояние между двумя поперечинами будет зависеть от диаметра досок. Например, при значении 28 мм доска не должна быть длиннее 50 см. Установка лагов позволяет сделать 1-метровый промежуток между балками.
Также очень важно грамотно рассчитать прогиб. Это позволит обеспечить высокую надежность всей конструкции. Стойкости брусов бывает недостаточно для длительной эксплуатации, так как со временем из-за сильной нагрузки прогиб способен увеличиваться. И дело не только в том, что прогиб может испортить эстетичное восприятие перекрытия.
Как только этот параметр превысит показатель 1/250 общей длины элемента, вероятность обрушения вырастет в десятки раз.
Заключение
Всегда начинайте строительство с чертежей, точного расчета нагрузки. Для этого можно обратиться к специалистам или использовать специальный калькулятор. С его помощью можно высчитать прогиб, несущую способность, другие параметры. Вам не придется прибегать к формулам и сложным подсчетам.
Как рассчитать нагрузку стальной двутавровой балки
Двутавровая балка является фасонным прокатом, у которого есть поперечное сечение в форме «Н». Данный вид металлопроката имеет высокие прочностные характеристики. За счет всех параметров изделие широко распространено в строительстве многоэтажек с большими пролетами. Точно выбрать подходящий номер проката могут специалисты благодаря расчетам, где учтены нагрузки двутавра во время эксплуатационного периода.
Крепление Н-образного профиля по схеме
Для удобства расчета максимальной нагрузки на двутавровую балку все способы эксплуатации профиля сводятся к нескольким типовым схемам, различающихся по типу крепления и нагрузкой:
- 2 шарнирные опоры на концах балки: с равномерной нагрузкой и со сосредоточением на центр;
- Консоль.
Нагрузка на двутавр равномерно или сосредоточенно; - 2 шарнирные опоры с вылетом с равномерной по всей длине или сосредоточенной в центре нагрузкой;
- 2 жестко защемленные опоры с разными видами усилий;
Нагрузка на двутавр равномерно или сосредоточенно;Сбор нагрузок на балку осуществляется после выбора формальной схемы.
Сбор нагрузок на двутавр
Чтобы произвести расчеты на предельную прочность и прогиб, определяются все усилия, воздействующие на двутавровую балку:
- Постоянные. Наличие собственного веса металлического профиля и перекрытия;
- Временные. К ним относятся 3 вида усилий: длительные (масса временных перегородок), кратковременные (вес людей, ветер, снег и др.), особые (взрывные, вулканические).
В сооружениях с углом ската, превышающим 60°, снеговой покров не входит в расчет. Есть еще одна классификация усилий: расчетные и нормативные. Они определяются нормативными актами.
Выбор номера двутавровой балки
При подборе по предельному состоянию между 2-мя номерами делают выбор в пользу изделия, имеющего более массивное сечение.
Примеры выбора двутавровой балки по номеру:
- 10-ый – пролет 3-4 м, шаг 1 м, воздействие – 300 кг/пм;
- 16-ый – пролет 6 м, шаг 1 м, нагрузка– 300 кг/пм;
- 20-ый пролет 3-4 м, шаг 1,1 / 1,2 м, усилие – 400-500 кг/м.
Чтобы определить номер профиля посредством онлайн-калькулятора, кроме значения типовой схемы крепления двутавра, воздействия усилий и нагрузка, следует указать параметр длины пролета, материал изделия.
Читайте интересное
| Двутавровая балка ICJ-300L | Брус сухой строганный деревянный 100х240 мм | Цельный прямоугольный LVL брус 69х260 |
|---|---|---|
| Характеристики: Момент инерции 9 476,5 см4 Момент сопротивления 631,8 см3 Модуль упругости 12 000 МПа Расчетное сопротивление 22,0 МПа | Характеристики: Момент инерции 11 520,0 см4 Момент сопротивления 960,0 см3 Модуль упругости 9 000 МПа Расчетное сопротивление 14,0 МПа | Характеристики: Момент инерции 8 788,0 см4 Момент сопротивления 676,0 см3 Модуль упругости 14 000 МПа Расчетное сопротивление 26,5 МПа |
|
Производим расчет по первому предельному состоянию: (где, R — расчетное сопротивление изгибу, M-максимальный момент (M=q*L2/8; M=160*5,82/8=672,8 кНм), W-момент сопротивления) | ||
| R=M/W R=672,8 кНм/631,8*10-6 см3= 1,06 кНм2 = 10,6 МПа < Rрасч =22 МПа Выполнено. | R=M/W R=672,8 кНм/960*10-6 см3= 0,7 кНм2 = 7 МПа < Rрасч =14 МПа Выполнено. | R=M/W R=672,8 кНм/676*10-6 см3= 0,99 кНм2 = 9,9 МПа < Rрасч =26,5 МПа Выполнено. |
|
Производим расчет по второму предельному состоянию: (f/L < fпред/L | ||
| f/L=5*160*5,83 / (384*12000*105*9476,5*10-8)=0,00358 <fпред/L=0,004 Выполнено. | f/L=5*160*5,83/ (384*9000*105*11520*10-8)= 0,00392 <fпред/L=0,004 Выполнено. | f/L=5*160*5,83/ (384*9000*105*8788*10-8)= 0,00392 <fпред/L=0,004 Выполнено. |
Вывод: все 3 материала с данными геометрическими характеристиками примерно равны по своей несущей способности и удовлетворяют условиям прогибов. | ||
| Сравним цены и эксплуатационные характеристики | ||
|
|
|
С помощью данного калькулятора Вы можете подобрать балку, которая выдержит необходимую нагрузку по одной из нижеуказанных схем. Блок: 1/5 | Кол-во символов: 161 Содержание
Балка на двух шарнирных опорах
Блок: 2/5 | Кол-во символов: 180 Блок: 2/3 | Кол-во символов: 73 Консольная балка
Блок: 3/5 | Кол-во символов: 150 Исходные данные Расчетная схема: Длина пролета (L) — минимальное расстояние между двумя крайними опорами или длина консоли. Расстояния (A и B) — расстояния от опор до мест приложения нагрузок. Для 3 схемы А равна длине консоли балки, опирающейся на 2 опоры. Нормативная и расчетная нагрузки — нагрузки, на которые рассчитывается квадратная труба. Рассчитать их можно с помощью следующих материалов: Fmax — максимально возможный прогиб согласно таблицы E.1 СНиПа «Нагрузки и воздействия». Некоторые из них выписаны в таблицу 1. Количество двутавров — этот показатель введен на случай, если балку перекрытия придется усилить еще такой же, положив ее рядом. То есть, если у вас одна балка, то указывается «один», если две рядом, то необходимо выбрать «две». Расчетное сопротивление Ry— для каждой марки стали он свой. Наиболее распространенные значения приведены в таблице 2. Размер двутавра — здесь следует выбрать профиль двутавра по тому или иному ГОСТу. РезультатWтреб — требуемый момент сопротивления профиля. Fmax — максимальный прогиб в сантиметрах, в зависимости от указанных в исходных данных ограничениях. Вес балки — масса одного погонного метра того или иного двутавра. Расчет по прочности: Wбалки — момент сопротивления выбранной трубы по ГОСТ 30245-2003. Если Wбалки > Wтреб, значит прочность балки обеспечена. Запас — если в данной графе значение с минусом (-), то балка по прочности не проходит, а если с плюсом (+), то здесь показано, на какой процент балка имеет запас прочности. Расчет по прогибу: Fбалки — прогиб, возникающий у рассчитываемой балки под действием нормативной нагрузки. Здесь стоит отметить, что если он превышает допустимый Fmax,то это не значит, что двутавр сломается. Просто прогнутая балка может выглядеть некрасиво. Главное, чтобы выполнялось условие по прочности. Запас — то же самое, что и по отношению к моменту сопротивления. Блок: 3/3 | Кол-во символов: 2329 Балка с вылетом на двух шарнирных опорах
Блок: 4/5 | Кол-во символов: 171 Другие виджеты разработчика:
Блок: 4/4 | Кол-во символов: 1953 Балка с жестким защемлением на опорах
| Не забудь поделиться с друзьями |
1 Другие виджеты разработчика:
1.0.13 Расчет теплопотерь дома онлайн
ru/building-onlayn-calculators/293-raschet-dvutavra-na-progib-i-izgib.html
ru/index.php?app=goods&act=qa&id=8254307Расчет сечения двутавровой балки, веса, нагрузки
Стальная двутавровая балка – вид фасонного проката, поперечное сечение которого имеет форму буквы «Н».
Чаще всего применяется в многоэтажном жилом и промышленном строительстве. Для подбора сечения двутавровой балки производят расчеты на прогиб и прочность с помощью формул или онлайн-калькулятора. В качестве исходных данных используют планируемую схему крепления, длину свободного пролета, нагрузки, материал изготовления двутавра.
Расчет прочности двутавровых балок с помощью онлайн-калькуляторов
Онлайн-калькуляторы по результатам вычислений предлагают прокат: с уклоном полок (ГОСТ 8239) или с параллельными внутренними гранями полок (ГОСТ 26020 или СТО АСЧМ 20-93). При расчете сварной балки двутаврового сечения учитывают, что изделие в реальных условиях эксплуатации должно подвергаться прогибу, составляющему не более 80% от расчетного.
Для определения сортамента двутаврового профиля с помощью калькулятора требуется введение исходных данных:
- характеристик предварительно выбранной металлической балки;
- условий эксплуатации профиля;
- длины пролета.
В результате вычислений получают момент сопротивления, минимально возможный в заданных условиях. Расчеты могут быть упрощенными (формальными), произведенными с использованием укрупненных коэффициентов, и уточненными. Используя полученный момент сопротивления, по таблицам, имеющимся в ГОСТах, выбирают номер профиля.
Схемы крепления двутаврового профиля
Сегодня все вычисления на прогиб и прочность формализованы и сведены для удобства к достаточно простым расчетным схемам, различающимся по типу крепления концов двутавра и виду приложения нагрузки:
- двутавр на двух шарнирных опорах с равномерно распределенной или сосредоточенной по центру нагрузкой;
- консольная балка с равномерно распределенной или сосредоточенной нагрузкой;
- двутавровый профиль на двух шарнирных опорах с вылетом с равномерно распределенным усилием и сосредоточенной нагрузкой;
- жесткозащемленный двутавр с сосредоточенной или равномерно распределенной нагрузкой.
Определение нагрузок
Перед началом расчета собирают все нагрузки, которые будут действовать на балку. К ним относятся постоянные нагрузки, включающие вес самого конструктивного элемента и опирающихся на него конструкций, например, перекрытий. Следующий тип нагрузок – временные, которые разделяются на кратковременные и длительные. К кратковременным относятся: вес людей, ветровые нагрузки, снеговые, ледовые. Длительные: вес временно установленных перегородок, слоя воды. Еще один вид воздействий – особые (взрывы, сейсмическая активность, деформация основания).
Советы! Для высоких кровель с углом наклона ската 60° и более снеговая нагрузка не учитывается. Нормативная нагрузка в квартирах принимается равной 150 кг/м2. Расчет веса двутавровой балки осуществляется по таблицам ГОСТов 8239, 26020 или СТО АСЧМ 20-93.
Двутавр прочность на изгиб. Вес двутавровой балки – важный фактор несущей способности
Технические характеристики металлического профиля необходимы, чтобы их правильно применять в строительстве, ведь несмотря на большое разнообразие сфер применения, суть остается одна – создать надежную несущую конструкцию.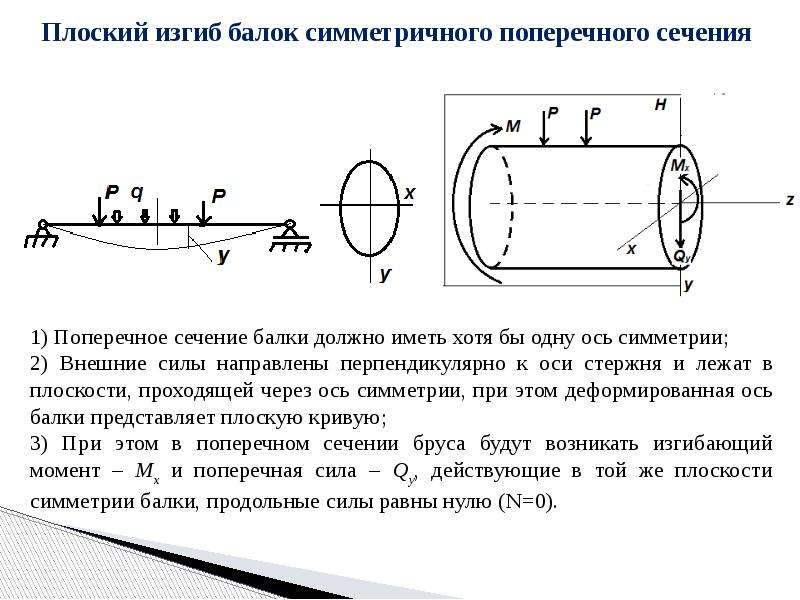
Она позволяет преобразовывать архитектуру сооружений:
- увеличивает ширину пролетов зданий;
- значительно, примерно на 35%, уменьшить массу несущих конструкций;
- существенно увеличить рентабельность проектов.
Говоря о достоинствах конструкции, нельзя не отметить и минусы, хотя их немного. Основные из них – это
- необходимость применять при создании ребер жесткости дополнительную арматуру;
- достаточно существенные трудозатраты, которые нужны для ее изготовления.
Однако, следует отметить, что с другой стороны дополнительные ребра жесткости дают возможность:
- уменьшить общую металлоемкость сварной металлоконструкции, так как ощутимо уменьшают толщину стенок. Таким образом удается понизить ее стоимость, но целиком сохранить механические характеристики;
- помимо этого облегченная конструкция экономична и с точки зрения устройства фундамента, поскольку после снижения общей массы можно использовать фундамент под БМЗ (быстровозводимые здания).
Чтобы найти двутавр, подходящий для конкретного случая, требуется произвести некоторые расчеты. Обычно для этого используют таблицы или онлайн калькуляторы. В их основе лежат заданные два параметра: расстояние от одной стены до другой и будущая нагрузка на строительную конструкцию.
Прочность двутавровой балки определяется такими параметрами, как:
- длина,
- метод закрепления,
- форма,
- площадь поперечного сечения.
Большее распространение получили изделия с буквой «Н» в сечении.
Жесткость металлической конструкции двутавра в 30 раз превышает жесткость квадратного профиля, а прочность, соответственно, в 7 раз.
Длина данной металлоконструкции бывает разной, к примеру, в случае ГОСТ 8239-89 это 4 –12 метров, то есть в зависимости от сортамента размеры и вес балки двутавровой отличаются. Помимо длины величина веса определяется толщиной металла и размерами граней. Поэтому для выполнения различных расчетов было введено понятие «вес метра балки двутавровой».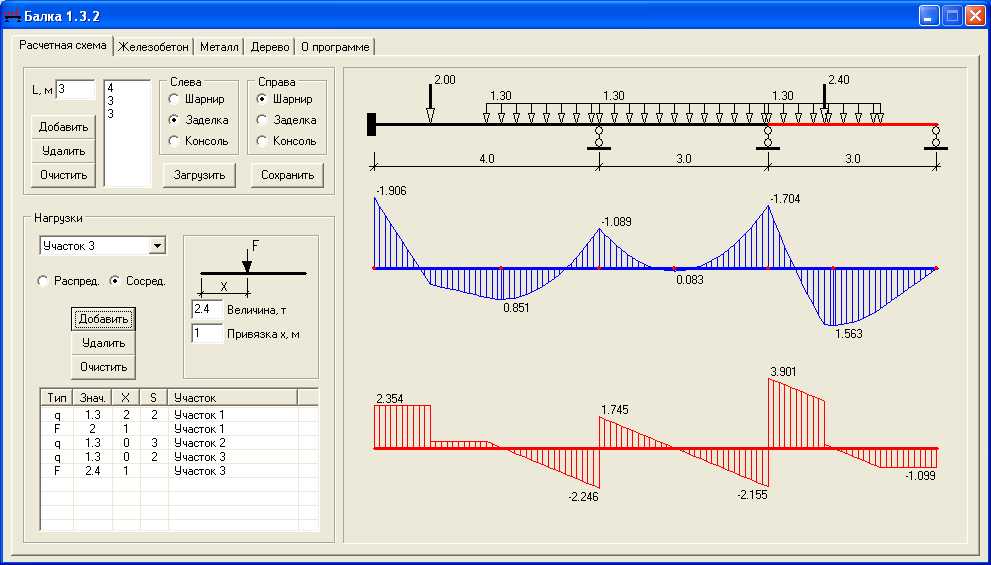
При покупке сварной конструкции обязательно требуется расчет на прочность, а для конкретного использования еще и расчет на прогиб. Грамотный расчет нагрузки на двутавровую балку позволит обеспечить устойчивость конструкции к проектным воздействиям, то есть способность воспринимать их без разрушения.
Нагрузка собственного веса
Чтобы определить в случае необходимости вес двутавровой балки пользуются специальными таблицами, где расписаны ее характеристики, к примеру, габариты, марка стали и т. д. В таблице представлена теоретическая масса 1 м профиля.
балка двутавровая размеры и вес (ГОСТ 8239-89)
Пример расчета двутавра
Предположим необходимо рассчитать вес двутавра № 12 длиной в 3 метра . Согласно таблице условная масса погонного метра данного профиля равна 11,50 кг. Если перемножить полученные значения, то получим величину общей массы – 34,5 кг.
Точнее значение веса сварной металлоконструкции можно посчитать, используя специальные онлайн калькуляторы.
В калькуляторе выбирают соответствующий номер двутавра и вводят необходимый метраж. Как видите, полученное значение больше рассчитанного нами на 0,12 кг.
Несущая способность
Среди всех типов балок двутавровая имеет наибольшую прочность, более того, она устойчива к температурным перепадам. Допустимая нагрузка на двутавр бывает указана на маркировке, как размер. Чем больше число, указанное в его наименовании, тем большую нагрузку может воспринимать балка.
Любой расчет предполагает изначальное знание размеров прокатного или сварного профиля, его длины и ширины. Проясним смысл значения ширины на примере самой популярной балочной опоры – колонны.
Предположим, что в сечении колонны лежит квадрат со стороной 510 мм, тогда на нее можно будет опереть профиль, для которого ширина не может превышать 460 мм. Это связано с тем, что двутавр придется приваривать к железобетонной подушке, а для сварочных швов понадобится запас, по крайней мере, в 40 мм.
После определения ширины переходят к выбору профиля и расчету нагрузки, воздействующей на профиль. Она представляет собой совокупность воздействий от перекрытия, а также воздействий временного и постоянного характера.
Нагрузку, выражающую величину нормативной нагрузки, собирают на длину 1 м профиля.
Но, расчет несущей способности двутавровой балки предполагает учет другого воздействия. Чтобы получить расчетную нагрузку, рассчитанное нормативное воздействие умножается на так называемый коэффициент прочности по нагрузке. Остается к результату прибавить уже подсчитанную массу изделия и найти его момент сопротивления.
Полученных данных достаточно, чтобы из сортамента подобрать профиль, необходимый для изготовления сварного профиля. Как правило, с учетом прогиба конструкции рекомендуется выбирать профиль выше на два порядка.
Сварная металлическая конструкция должна использовать примерно 70–80% от максимально допустимого прогиба.
Усиление
Если несущая способность двутавра оказывается недостаточной, то возникает необходимость ее усиления.
Для различных элементов сварной конструкции этот вопрос решается по-разному.
К примеру, для элементов, воспринимающих нагрузки типа растяжения, сжатия или изгиба, используют такой вариант усиления: увеличивают сечение, иначе говоря, повышают жесткость, скажем, приварив дополнительные детали.
Теоретически – это один из лучших вариантов усиления, однако, при его реализации не всегда удается получить требуемый результат. Дело в том, что элементы в процессе сварочных работ нагреваются, а это несет за собой уменьшение несущей способности.
В какой степени можно ожидать такого понижения зависит от размеров двутавра и режима и направления сварочных работ. Если для продольных швов максимальное понижение оказывается в пределах 15%, то для швов в поперечном направлении оно может достичь и 40%.
Поэтому при усилении двутавра под нагрузкой категорически запрещено накладывать швы в направлении, поперечном к элементу.
Расчетно и экспериментально было доказано, что оптимального результата усиления под нагрузкой можно получить при максимальном напряжении в 0,8 R y , то есть 80% расчетного сопротивления стали, которая была использована для изготовления двутавра.
01.10.2010, 11:47
расчет:
1) брус 200*200*6000 через 0,5М =22 т.р (прогиб 20 мм)
2) двутавр 20Б ч/з 1,2м =27 т.р. (прогиб 20 мм)
По весу 1) -90 кг брус, 2)- 120 кг балка
В теории решения очень похожи. интересует практика что все таки лучше?
Зеленый Кот
01.10.2010, 11:55
Брус.
Железом вообще не стоит делать любые несущие конструкции ибо при пожаре дерево держится до последнего, а железо — хрясь и готово.
01.10.2010, 15:55
Температура при которой пойдет деформирования двутавр с жизнью несовместима. Тем более если снизу это все будет обшито гипсокартоном.
Если все же решите делать деревом, то советую 200х60х6000 с шагом 600 мм.
01.10.2010, 16:55
«хрясь и готово» — а не все ли равно уже будет)))
Оно может деформироваться в одном месте, и прилететь в другое, где еще остались условия для жизни… 🙂 но в целом вы правы.
+Дерево само по себе будет поддерживать горение, а железо нет…
Зеленый Кот
01.
10.2010, 17:41
Температура при которой пойдет деформирования двутавр с жизнью несовместима.
Неправильно.
Одно дело когда он сам по себе, а другое, когда он под нагрузкой.
До недавнего времени вообще было запрщено использовать в качестве стропил мет. профиль, теперь же смотрю делают вовсю.
Советую 200х60х6000 с шагом 600 мм
Малавато будет, малавато — смотрим какулятор.
01.10.2010, 20:32
У меня в одном помещении пролет получился 5,7 метров, перекрытие между 1 и 2 этажом. Я выбрал двутавр 20Б через 1,3 метра, вроде по расчету двутавр был крепче, чем дерево. Стоит учесть что дерево можно найти 6,5 метров, а длина двутавра 11,7 метра или 12 метров (для перекрытия пролета 6 метров надо как минимум 15 см на сторону) . Правильнее было бы уложить плиты, но у меня не получилось. Разница между деревом и двутавром была гдето 10-12%. При кладке стен устанавливал между вырезом в газоблоке и двутавром пенопласт 3 см.
На счет пожара-надо предохроняться.
02.
10.2010, 00:47
А я на 6 м пролет положил 5,8 метровую жб плиту и ни о чем больше не задумываюсь. Не горит, не плавится, не гнется…
02.10.2010, 09:00
Спасибо всем, я все таки склоняюсь к двутавру,поскольку он прочнее, я на перекрытие хочу стены внутренние из пеноблока 100 см поставить. (хотя наверное можно было по 2 бруса под стену положить)
то wawan001 пролет 6М это по осям стен, то есть по 15 см с каждой стороны опора будет.
то Кот, я предполагаю если засыпать негорючий утеплитель аля керамзит то гореть там вообще нечему будет (дом из пеноблока).
И еще вопрос если перекрывать двутавром можно ли вместо крайних балок использовать деревянную скажем 50-ку закрепленную к боковым стенам??
02.10.2010, 18:30
Есть другой вариант.
02.10.2010, 19:12
Есть другой вариант.
Делаете несущую балку (пускай из двутавра), на которую укладываете простые деревянные балки перекрытия. Это гораздо дешевле выйдет.
Двутавров понадобится один-два, но мощных.
По цене все равно выйдет дешевле.
Я так себе сделал
02.10.2010, 20:01
dengt , у меня эта идея приходила в голову с точки зрения технологичности устройства в будущем полов, если деревянные перекрытия устанавливать внутрь двутавра, а по верх делать контробрешетку (балки по расчету). Расстояние от края балки до двутавра 40 см- надежно. Ведь по расчетам на крайнии балки нагрузка меньше раза в 2 чем на соседнию, можно положить балку 150х200 или взять 2 штуки доски 50х200 и между ними установить отрезки доски того же размера длиной 1,5 метра, а 50-ка думаю хлипковата, хотя если к стене притянуть может и нормально будет. Если уверен в крепеже то наверное да.
04.10.2010, 05:57
Я перекрывал пролет 5м брусом 150*150 сложенным вдвое и стянутым шпильками, т.е. получилась балка 150*300. Получилось довольно жестко, но я бы все равно сделал из бетона, если бы была возможность:(
05.10.2010, 09:32
[
я так себе сделал
пролет 11 на 6, разделил на три части двумя двутаврами и уложил деревянные балки, а что бы не увеличивать толщину перекрытия уложил их внутрь тавра.
Предварительно приварил уголки к тавру и закрепил балки на болты.
Я так понимаю двутавры 6-ти метровые были?
тут уже 25Б2 минимум нужен, это на 5 см толще перекытие, вроде не смертельно.
По поводу закрепления боковых балок к стенам меня беспокоит то, что все остальные балки будут прогибаться а крайние нет, тогда перекытие прогнется «»пузырем»? к чему это приедет?
05.10.2010, 10:11
двутавр 6-ти меровый 20Б1 — две штуки поперек длины, получилось 3 зоны, две с опиранием балок одной стороны на стену, а второй на двутавр, и одна зона с балками зажатыми между двутаврами. Прогибания не заметил, двутавр на такой длине не ходит.
06.10.2010, 13:06
06.10.2010, 13:47
смотря как грузить, если по теории 400 кг/м то в вашем случае 20Б1 прогнется на 77 мм
Интересно как Вы это посчитали?
Балка 20 . Применение. Виды. Расчёт двутавра .
Двутавровая балка — прокат, имеющий сечение буквы Н и означающий с латинского языка — «двурогая» с двух сторон («тавр» — бык).
Расстояние между полками называют высотой, у двутавра 20го высота составляет около 200 мм или 20 см. Двутавр — это металлопрокат фасонного типа, изготавливаемый из строительной стали — ст3 и низколегированной стали 09Г2С.
Балка двутавровая 20 наиболее распространена в применении у строителей и монтажников, в первую очередь при устройстве каркасов с большими пролётами в зданиях, для перераспределения нагрузки с перекрытий на несущие конструкции. Её используют для мостостроительства, изготовления кранов, автомобилей, трубопроводов, самолётных ангаров, в железнодорожном строительстве и т. д. 20й профиль производят по 8239 ГОСТ двутавры стальные , госстандарту 26020-83, двутавр гост 19425-74 и техническим условиям СТО АСЧМ 20-93.
Двутавр 20й подразделяют по СТО АСЧМ 20 на нормальную балку 20Б с параллельными гранями полок, широкополочную балку 20Ш и 20К — для колонн. Двутавр СТО АСЧМ 20-93 с высотой 20 см имеет грани полок, которые параллельны.
СТО двутавр производится НЛМК, который и разработал данный стандарт. По такому стандарту производится также балка 09Г2С , которая также подразделяется на нормальную балку, колонную и широкополочную. Металлопрокат из низколегированной стали может употребляться как при очень низкой температуре, так и при высоких температурах, не подвергаясь деформации.
Двутавр стальной 20Б1 имеет массу метра — 21,3 килограмм. Масса 20Ш1 составляет 30,6 кг в метре, вес колонной балки 20К1 — 41,4 кг, вес двутавра 20К2 — 49,9 кг. Параметры двутавра 20Б1: высота (h)- 200 мм, ширина полки (b)- 100 мм, толщина стенки (s) — 5,5 мм, толщина полки (t)- 8,0 мм. Широкополочный 20й профиль 20Ш1 имеет следующие характеристики: h — 194 мм, b- 150 мм, s — 6 мм, t — 9 мм. Колонная балка 20К1 обладает h 196 мм, b стенки — 199 мм, s стенки — 6,5 мм, t полки — 10, 0 мм.
Балка 20 по стандарту 19425 может быть монорельсовой (обозначается буквой М) и спец. (именуется буквой С). Этот ГОСТ распространяется на горячекатаные двутавры с полками, имеющими наклон внутренней поверхности полок.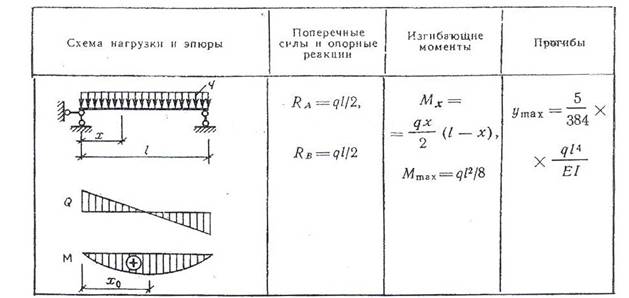
Монорельсовый двутавр, известный как кран балка, предназначена для крановых путей, как несущий мост в козловом или мостовом кранах, как подрельсовая балка. Такое изделие характеризуется высокой прочностью и способно противостоять большим нагрузкам, давлению, скручиванию. Специальная балка применима в стволе конструкций, которые обеспечивают движение подъёмных стволов, то есть для армирования стволов шахт, а также в сооружении лестниц и прокладке инженерных коммуникаций, креплении водоотливов.
Специальный профиль 20С имеет следующие параметры — двутавр размеры : высоту — 200мм, ширину полки — 100 мм, толщину стенки — 7 мм, толщину полки — 11,4 мм. Масса 1 м такого двутавра составляет 27,9 кг. Вес погонного метра балки в таблицах теоретический, он нужен для того,чтобы рассчитать самостоятельно вес целой балки или необходимое количество метров и штук двутавра. Итак, если балка 20 на складе металлоторгующей компании имеется длиной 12м, то чтобы выяснить вес одного хлыста, нужно двутавр вес 1 метра 27,9 умножить на 12м.
Зная общее количество метров балки, легко можно посчитать общий вес необходимого металлопроката. На практике это лучше всего выяснить, уточнив у менеджеров компании АО «Металлоторг», которые кроме того подскажут стоимость металла, двутавр цена за метр, выпишут счёт, чтобы двутавр купить , и решат все текущие вопросы по загрузке и доставке.
Двутавр ГОСТ 8239 89 — на сортамент двутавров , имеющий отличие — наклон внутренних поверхностей полок. Такая балка с расстоянием между полками 200 мм имеет ширину этих полок — 100 мм, толщину металла посередине высоты — 5,2 мм, толщину полок 8,4 мм.
Какой двутавр лучше? Горячекатаный двутавр или сварной?
Чтобы выбрать между горячекатаной балкой 20 и сварным профилем с похожими параметрами, вычиляют момент сопротивления. Для этого учитывают нагрузку на перекрытие, непрерывную и краткосрочную нагрузку, используют табличные данные — коэффициент прочности и допустимый прогиб для несущих конструкций.
Похожие статьи
Отклонение луча: как рассчитать
В приложениях, связанных с перемещением, существует множество ситуаций, когда линейная направляющая или привод не полностью поддерживается по всей своей длине. В этих случаях прогиб (из-за собственного веса компонента и из-за приложенных нагрузок и сил) может повлиять на ходовые качества подшипников и вызвать плохую работу в виде преждевременного износа и заедания.
Изделия, которые могут быть смонтированы только с концевыми опорами, такими как линейные валы или приводы в сборе, или в консольной ориентации, например телескопические подшипники, обычно имеют спецификацию на максимально допустимый прогиб.Важно проверить приложение и убедиться, что этот максимальный прогиб не превышен. К счастью, большинство линейных направляющих и приводов можно смоделировать как балки, а их отклонение можно рассчитать с помощью обычных уравнений отклонения балки.
Соображения, касающиеся материалов и конструкции
При расчете прогиба необходимо знать свойства направляющей или привода и условия приложенной нагрузки.
Что касается направляющей или привода, важными критериями являются модуль упругости и планарный момент инерции компонента.Модуль упругости является мерой жесткости материала, и его обычно можно найти в каталоге продукции. Момент инерции описывает сопротивление объекта изгибу и иногда предоставляется производителем компонента. Если момент инерции не указан, его можно разумно аппроксимировать, используя уравнение момента инерции для сплошного или полого цилиндра (для линейного круглого вала) или прямоугольника (телескопический подшипник или линейный привод).
Модуль упругости, также известный как модуль Юнга или модуль упругости при растяжении, может быть определен как отношение напряжения (силы на единицу площади) на оси к деформации (отношение деформации по длине) вдоль этой оси.
Планарный момент инерции (также называемый вторым моментом площади или моментом инерции площади) определяет, как точки области распределяются относительно произвольной плоскости и, следовательно, ее сопротивление изгибу.
С точки зрения применения и конструкции критериями, влияющими на прогиб балки, являются тип опоры на концах направляющей или привода, приложенная нагрузка и длина без опоры. Когда компонент является консольным, его можно смоделировать как фиксированную балку, а когда он поддерживается с обоих концов, он обычно может быть смоделирован как балка с простой опорой.Для консольных балок максимальное отклонение будет происходить, когда нагрузка находится на свободном конце балки, в то время как для балок с простой опорой максимальное отклонение будет иметь место, когда нагрузка находится в центре балки.
При определении общего отклонения имейте в виду, что будут иметь две нагрузки, , которые вызывают отклонение: вес направляющей или самого привода и приложенная нагрузка. Собственный вес компонента почти всегда можно смоделировать как равномерно распределенную нагрузку, оценивая приложенную нагрузку как точечную нагрузку в месте максимального прогиба (на свободном конце консольной балки или в центре балки с простой опорой).
обычно обеспечивает наихудший сценарий полного прогиба.
Прогиб консольных балок
Телескопические подшипники часто являются консольными, а некоторые конфигурации декартовых роботов приводят к консольному приводу на оси Y или Z. В этом случае вес балки, который достаточно однороден по длине, вызывает максимальный прогиб на конце балки.
Изображение предоставлено: wikipedia.orgЭтот прогиб рассчитывается как:
Где:
q = сила на единицу длины (Н / м, фунт-сила / дюйм)
L = длина без опоры (м, дюйм)
E = модуль упругости (Н / м 2 , фунт-сила / дюйм 2 )
I = планарный момент инерции (м 4 , дюйм 4 )
Для создания наихудшего сценария прогиба мы рассматриваем приложенную нагрузку как точечную нагрузку (F) на конце балки, и результирующий прогиб можно рассчитать как:
Сложив прогиб из-за равномерной нагрузки и прогиб из-за приложенной (точечной) нагрузки, получаем общий прогиб на конце балки:
Прогиб свободно опертых балок
Линейные валы и приводы часто закрепляются на концах, оставляя длину без опоры, как у балки с простой опорой.
Равномерная нагрузка на балку (собственный вес вала или привода) вызовет максимальный прогиб в центре балки, который можно рассчитать как:
Поскольку это балка с простой опорой, приложенная нагрузка может быть смоделирована как точечная нагрузка в центре балки для наихудшего сценария.
Изображение предоставлено: wikipedia.orgПрогиб из-за приложенной нагрузки в этом состоянии рассчитывается как:
Полный прогиб в центре балки:
Прогиб валов с двумя подшипниками
Когда два подшипника используются на балке с простой опорой, как это обычно бывает с круглыми направляющими вала, приложенная нагрузка распределяется между двумя подшипниками, и максимальное отклонение происходит в двух местах: в положении на каждом подшипнике , когда подшипниковый узел (иногда называемый кареткой или столом) находится в середине вала.
Изображение предоставлено: Thomson LinearРасчет отклонения балки для этого условия:
Опять же, мы должны добавить прогиб из-за собственного веса балки плюс прогиб из-за приложенной нагрузки, чтобы получить общий прогиб:
Существуют дополнительные сценарии монтажа и нагружения, которые могут возникнуть в некоторых приложениях, например, в приводе с фиксированной опорой на обоих концах. Но, как и в приведенных выше примерах, их можно оценить с помощью стандартных уравнений отклонения балки.Полный список сценариев опор балки и уравнений отклонения можно найти на этой странице Корнельского университета.
Изображение предоставлено: wikipedia.org
| КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ УЧАСТНИКОВ | |
| Калькулятор | Определение |
| Расчет элементов сжатия (продольного изгиба колонны) | |
| ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГНОЗА | |
| Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами | |
| Балка с простой опорой и сосредоточенной нагрузкой в любой точке | |
| Просто поддерживаемая балка с двумя Точечные нагрузки | |
| Балка с простой опорой и частично распределенной промежуточной нагрузкой | |
| Балка с простой опорой и двумя частично распределенными промежуточными нагрузками | |
| Балка с простой опорой и моментом | |
| Балка с простой опорой и двумя моментами | |
| КАНТИЛЬНЫЙ БАЛК КАЛЬКУЛЯТОРЫ ПРОБЕГА | |
| Консольная балка с множественными точечными / распределенными нагрузками и моментами | |
| Консольная балка с одинарной нагрузкой | |
| Распределенная нагрузка консольной балки | |
| Консольная балка с одним моментом | |
| КАЛЬКУЛЯТОРЫ ПРОГИБА ФИКСИРОВАННОЙ ЛУЧИ | |
| Фиксированный -Фиксированная балка с множественными точечными / распределенными нагрузками и моментами | |
| Фиксированная — фиксированная балка с одинарной нагрузкой | |
| Фиксированный — Неподвижная балка с распределенной нагрузкой | |
| Фиксированная — фиксированная балка с одним моментом | |
Лучшее руководство по определению прогиба в балках с переменным поперечным сечением — опытный инженер
Таблицы балок дают информацию и предполагают, что прогиб расчет основан на постоянном сечении.Итак, что делать, если у нашей балки есть крест сечение, которое меняется по длине балки?
Чтобы определить величину отклонения в балка переменного сечения, необходимо интегрировать формулу прогиба балки с моментом инерции, являющимся переменной по отношению к длине и применить граничные условия. Луч Формула отклонения: v ’’ = M (x) / [E * I (x)].
Непрерывное или дискретное — Есть два типа секций балки: непрерывные и дискретные.Большинство балок представляют собой непрерывных балок и имеют либо постоянное сечение, либо сечение, которое постепенно изменяется по длине балки. Кровельные балки в больших стальных зданиях — отличный пример непрерывной переменной балки. Балка относительно короткая на концах и очень высокая посередине.
Дискретные балки балки которые имеют внезапные разрывы в разрезе. Вы не поверите, но иногда это проще для расчета, потому что дискретные участки обычно постоянны, что приводит к более легкий расчет.
Формула отклонения балки является универсальной формула, которая позволяет настраивать несколько нагрузок и балку разделы. Предупреждаю, что чем больше чем точнее должны быть ваши расчеты, тем сложнее будет выполнить математику. Упрощение здесь сэкономит много времени и усилия. Как упоминалось ранее, формула:
в ’’ = M (x) / [E * I (x)]
Где v ’’ — вторая производная отклонения ( ускорение прогиба), M — момент, который обычно является функцией положение по длине балки, x. E — модуль упругости, I — момент инерции поверхности луч. Все табличные балки будут считайте это постоянной величиной и, следовательно, ни одна из формул прогиба может быть использован.
Теперь, когда мы проинтегрируем приведенное выше уравнение, мы будем выполнение неопределенного интеграла, что означает, что мы должны добавить константу, C n, к многочлену каждый раз, когда мы интегрируем. Поскольку мы будем интегрировать уравнение два раза, мы получим две константы. Если у нас есть дискретный В этом случае у нас будет два или более уравнений.
Граничные условия — это требования, которым должна соответствовать формула прогиба балки, когда она находится в окончательном виде. Окончательная форма приходит только тогда, когда мы используем граничные условия для решения констант образованный неопределенным интегралом. Общий случаи: концы балки с опорой должны быть равны 0 (дюймы, мм и т. д.) или наклон консольной балки должен быть 0 радиан.
В этой статье мы рассмотрим три примера распространенных балок переменного сечения.
- Двухсекционная консольная балка с точечной нагрузкой на конце.
- Двухсекционная балка, свободно поддерживаемая собственным весом.
- Постоянно изменяющаяся неразрезная балка с простой опорой и постоянной распределенной нагрузкой.
Эта проблема состоит из 100-дюймового консольная стальная балка с нагрузкой 500 фунтов на конец. 4.
Теперь мы определим момент и дважды проинтегрируем уравнение прогиба балки, каждый раз добавляя переменную для неопределенного интеграла. Я решил, что моя система координат (переменная x) начинается с основания. Это немного усложняет интегрирование, но переменные C 1 и C 2 будут уравновешиваться из-за граничных условий 1 и 2. Вы увидите через секунду.
Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I 1 на I 2 в уравнениях.Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте установим граничные условия. Нам нужно, чтобы положение и наклон на фиксированном конце балки составляли 0 дюймов и 0 радиан. Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этом положении должны быть одинаковыми.
Решим граничные условия 1 и 2
Как упоминалось выше, я предвидел, что переменные C1 и C2 будет равно 0, когда я выберу, чтобы система координат начиналась с база.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Обратите внимание на чек, который я поставил в блок поиска, чтобы чтобы мы могли проверить, что v 1 = v 2 и s 1 = s 2 на 50 дюймовЭто подтверждает что положение и наклон в этой точке будут непрерывными.
Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. Как видите, линии пересекаются и касаются друг друга на расстоянии 50 дюймов. Кроме того, v 1 не имеет прогиба или наклона в основании.
Наконец, мы объединим два графика вместе, образуя окончательное уравнение для отклонения нашей консольной балки. 4.
Теперь определим момент и проинтегрируем уравнение отклонения балки дважды каждый раз, добавляя переменную. Я выбрал две системы координат. Координата x идет слева направо и координата y идет справа налево. Их связывает:
г = L-x
Я выбрал эту систему координат так, чтобы C 2 и C 4 будет сокращаться, когда мы решаем граничные условия 1 и 2. Это также упрощает математические вычисления. чрезвычайно.Вы увидите через секунду.
Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I 1 на I 2 и w 1 на w 2 в уравнениях. В уравнениях правого сечения я также заменю «y» на «x». Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте установим граничные условия.Нам нужно, чтобы концы балки были отклонены на 0 дюймов (BC 1 и 2). Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этой позиции должны быть такими же, как и в месте соединения сегментов.
Решим граничные условия 1 и 2
Как упоминалось выше, я предвидел, что переменные C 2 и C 4 будет равно 0, если я выберу координату система запускается на базе.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Обратите внимание на чек, который я поставил в блок поиска, чтобы чтобы мы могли проверить, что v 1 = v 2 и s 1 = с 2 при 200 дюйм. Это подтверждает что положение и наклон в этой точке будут непрерывными.
Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине.Мы ищем четыре граничных условия, которые должны быть выполнены.
Ой, что случилось !? Линии определенно пересекаются на расстоянии 200 дюймов, а на каждом конце 0 дюймов. прогиб, но они не касаются на пересечении. Я не только показываю силу график решения для точности, но также демонстрируя, что с помощью двух разные системы координат создают проблему. Согласно уравнениям склоны приближаются к месту расположения стык на нисходящем склоне равной величины.Однако сделать эту работу одной из склонов на самом деле нужно подойти. Мы можем исправьте эту проблему, внеся одно небольшое изменение.
с 1 = -s 2
Давайте внесем это изменение и приступим к решению.
Да, намного лучше! Наконец, мы объединим два графика вместе, образуя окончательное уравнение для отклонения нашей консольной балки.
Как и ожидалось, более длинная и жесткая секция меньше прогибается.
Пример 3: Постоянно изменяющаяся неразрезная балка с простой опорой и постоянной распределенной нагрузкой.Эта проблема состоит из стальной балки с простой опорой длиной 300 дюймов и распределенной нагрузки 1000 фунтов / дюйм поперек балки. Сечение начинается на высоте 10 дюймов, линейно увеличивается к центру, где достигает высоты 24 дюйма. Затем он снова сужается до 10 дюймов.
Чтобы определить, как момент инерции изменяется по отношению к x, мы будем моделировать в Solidworks и делать сечения каждые 30 дюймов. Мы сведем эти данные в таблицу и подгоним к ним линию.
Вы, наверное, заметили, что я сделал таблицу только для значений от 0 до 150 дюймов. Это потому, что я собираюсь использовать симметрию, чтобы упростить эту сложную задачу. Мы можем использовать симметрию, потому что и нагрузка, и сечение балки симметричны относительно середины балки. Из-за симметрии нам нужно, чтобы конечная точка имела прогиб 0 дюймов, а наклон в середине балки был 0 градусов. Затем мы можем отразить это, чтобы получить непрерывное отклонение луча. В этом случае координата x будет идти слева направо.
Здесь вы можете видеть, что вычисленные значения I (x) точно соответствуют тому, что указано в таблице выше. Я назвал вторую производную от положения «а1» (ускорение). Как видите, верхняя и нижняя части имеют переменную «x», и интегрировать это будет очень весело. Итак, вам нужно знать обо мне одну вещь. У меня есть ограничения относительно того, что я не буду делать. Интеграция — одна из таких вещей. Вот почему у нас есть MathCAD!
Как видите, очень утомительная работа по интеграции была замалчена, и мы смогли напрямую решить для нашей границы условия.В уравнениях s (x) и v (x), на самом деле были натуральные бревна и каким-то образом появилась обратная касательная (не показано). Я все еще не жалею позволяя MathCAD делать всю работу.
Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине. Мы ищем, чтобы наши граничные условия были выполнены. Как видите, отклонение при x = 0 дюймов составляет 0 дюймов, а наклон кажется плоским при x = 150 дюймов.
Наконец, мы отразим графики вместе, образуя окончательное уравнение для отклонения нашей консольной балки.
Как видите, отклонение составляет 0 дюймов в конечных точках и имеет максимальное отклонение в центре.
ЗаключениеВ этой статье рассматриваются три популярных варианта нагружения, когда балка имеет переменное поперечное сечение. Хотя это действительно связано с исчислением, часто это очень легко сделать вручную, потому что это многочлены. Если нет, то будьте благодарны за такие надежные программы, как MathCAD, которые сделают это за вас. Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа подобных балок.Если ваша балка не загружена именно так, вы всегда можете найти расчет момента в таблице и интегрировать свое сердце.
СвязанныеКалькулятор прочности и прогиба балки
Балка или стержень — это любой элемент конструкции, длина которого значительно превышает ширину или глубину. Однако термин «существенно» означает разные вещи для разных людей. Некоторые люди считают, что длина в два раза больше, другие считают, что длина в пять раз больше, чем длина, и поэтому считают такой элемент пластиной, рамой или конструкцией.Процедуры расчета балок не накладывают таких ограничений или различий.
Балки обычно используются для несения нагрузки, в то время как пролетные опоры находятся на достаточном расстоянии друг от друга, например, пол (см. Калькулятор этажей CalQlata). При выборе балки вы должны определить ее максимальную грузоподъемность (то есть ее прочность) и максимально допустимый прогиб.
Прочность и жесткость балки
Прочность балки зависит от предела текучести материала, из которого изготовлена балка, тем самым определяя максимальную нагрузку, которая может быть приложена до того, как она будет деформироваться (или сломаться, если она сделана из хрупкого материала), и
, его жесткость зависит от второго момента площади поперечного сечения балки (например,грамм. Канал, двутавровая балка, двутавровая балка, угол и т. Д.) Вместе с модулем Юнга материала, тем самым определяя ожидаемый прогиб балки для любой заданной нагрузки
Обе вышеуказанные характеристики определяют поведение балки под нагрузкой.
Спроектировать балку
Предположим, у вас есть равномерно распределенная нагрузка в 4000 Н на длине балки 4 м (1 Н / мм) и максимально допустимый прогиб, скажем, 1/200 длины балки (20 мм).
Используя Beams, вы вводите информацию, которую знаете, и изменяете второй момент площади (I), пока не получите желаемое отклонение (20 мм в середине балки, где ее отклонение будет наибольшим), что в этом случае дает вам значение для I около 800000 мм².
Предполагая, что вы планируете использовать секцию канала, путем сортировки каналов в базе данных CalQlata Steel Sections вы обнаружите, что размер вашей балки должен быть сечением «3×6», которое является наименьшим сечением балки со значением I выше 800000 мм², и найдите значение для « y ‘(расстояние от нейтральной оси балки до внешней части ее сечения), которое в данном случае составляет 38,1 мм.
Вы возвращаетесь в раздел «Балки», вводите правильное значение для I (863 264 мм²), а также вводите значение 38,1 мм для «d», чтобы установить максимальное напряжение в материале балки, которое в данном случае составляет 88 Н / мм².
Если это значение находится в пределах требований вашего запаса прочности, то ваш луч приемлем. Если нет, но вы должны работать с данным материалом, вам следует изменить (увеличить) сечение балки, тем самым уменьшив допустимый прогиб до тех пор, пока напряжение не станет приемлемым.
Калькулятор прогиба балки — Техническая помощь
Рис. 1. Диаграмма нагрузки на балку
Предполагается, что любая нагрузка в калькуляторе прочности балок одинаково распространяется через плоскость или сечение балки во всех направлениях, перпендикулярных (другими словами, под углом 90 ° к) к ее продольной оси.
Если нагрузка локализована в поперечном сечении балки (т. Е. Неравномерно распределена по ней), могут потребоваться дополнительные расчеты для определения локальных (сосредоточенных) реакций и напряжений (см. Калькуляторы CalQlata Plates and Sheets).
Напряжение изгиба
Изгибающие напряжения в балках применяются к балке на заданном расстоянии (d) от ее нейтральной оси. Эта входная переменная (‘d’) используется только в расчетах для напряжения (σx) и деформации (ex). Если вы оставите поле пустым или установите его на ноль, балки не будут вычислять напряжение или деформацию в указанном вами месте вдоль балки (рис. 1 ‘x’).Никакие другие результаты не будут затронуты.
Условия одновременной / множественной нагрузки
Если у вас есть балка с более чем одной приложенной нагрузкой, вы просто складываете результаты вместе в указанном месте.
Пример расчета прочности балки (рис. 2):
Детали балки:
L = 2000 мм
I = 1.2E + 08 мм⁴
E = 2.07E + 05 Н / мм²
y = 200 мм
Условия нагрузки 1:
wA & wB = 450 Н / мм
l = 0
Условия нагрузки 2:
F = 150000 N
l = 700 мм
Расстояние вдоль балки до выхода:
x = 1000
Шаг 1:
Введите данные для балки и условия нагрузки 1 (простая фиксированная / распределенная нагрузка), установив wA (/ L) и wB (/ L) на 450 ‘скопируйте список данных и вставьте в электронную таблицу.
Шаг 2:
Введите условие нагрузки 2 (простая фиксированная / точечная нагрузка), установив значение F на 150000, скопируйте список данных и вставьте в ту же электронную таблицу.
Шаг 3:
Добавьте результаты обоих калькуляторов, и вы получите условия в нужном месте.
Рис. 2. Процедура расчета нагрузки смеси
Ограничения
Эти расчеты действительны только в том случае, если материал по всей длине и толщине сечения подчиняется закону Гука.
Результаты остаются действительными для этого калькулятора, если прогиб таков, что на длину балки существенно не влияют условия нагрузки.
Калькулятор больших отклоняющих балок CalQlata (гибкие балки) следует использовать, когда длина балки изменяется более чем на 5% в результате приложенной нагрузки.
Дополнительная литература
Дополнительную информацию по этому вопросу можно найти в справочных публикациях (2, 3 и 4)
Расс ЭллиотБлагодарности : Существует ряд стандартных работ, касающихся принципов отклонения балки.Особенно хорошее изложение, на котором основаны приведенные здесь уравнения, содержится в Механика материалов (четвертое издание SI) Дж. М. Гира и С. П. Тимошенко, Стэнли Торнса, ISBN 0 7487 3998 X. Следует сделать ссылку на эта работа для вывода уравнений. ВведениеПрогиб пружинной балки зависит от ее длины, формы поперечного сечения, материала, места приложения отклоняющей силы и того, как балка поддерживается. Уравнения, приведенные здесь, относятся к однородным, линейно упругим материалам, в которых вращение балки невелико. В следующих примерах рассматриваются только нагрузки, действующие в одной точке или отдельных точках — точка приложения силы F на диаграммах предназначена для обозначения рупорного блока модели локомотива (или буксы транспортного средства), способного перемещаться вертикально. в рупорной направляющей и действуя против силы пружинной балки, прикрепленной к локомотиву или основным шасси транспортного средства или переносимых ими.Доля общего веса, действующего на каждую ось локомотива или транспортного средства, будет зависеть от положения его центра тяжести по отношению к оси (или точек крепления уравновешивающих балок шасси, если они используются). Приложение для моделирования рожковых блоков локомотивовКак видно из уравнений, толщина материала ( h или d ) очень важна, и, следовательно, увеличивающиеся размеры в диапазоне доступных гитарных струн делают их очень привлекательными для использования в качестве пружинные балки.Также существует значительная разница в прогибе балки для данной силы, в зависимости от того, как она поддерживается и фиксируется, а также от того, поддерживается ли она только на одном конце или на обоих концах. Предполагается, что конструкция должна быть основана на заданном прогибе рогового блока, а затем определить, какая длина, толщина и стиль балки наиболее подходят для конкретной силы, которая должна восприниматься каждой осью. Для локомотивов, вес которых составляет от 4 до 6 граммов на тонну прототипа, массы, поддерживаемые каждым отдельным роговым блоком локомотива, вероятно, будут находиться в диапазоне от 30 до 60 граммов (что соответствует нагрузке прототипа от 14 до 20 тонн на тонну). ось). Выбор значения отклоненияДля разумного мелкого пути в масштабе 4 мм рекомендуемое значение прогиба рогового блока, δ , при конечной нагрузке локомотива составляет 0,5 мм. Известно, что вышеупомянутая рекомендация является чрезмерно упрощенной и, возможно, неверным предположением о том, каким должно быть расчетное значение прогиба, и вызвала серьезные споры. Приветствуется любой опыт применения этой рекомендации в реальной практике моделирования шасси — цель этой статьи — начало обсуждения, а не его заключение.Щелкните здесь, чтобы ознакомиться с вопросами по этому поводу. Момент инерции,I
Все приведенные ниже уравнения содержат I , момент инерции балки, который является константой, определяемой формой и толщиной поперечного сечения балки.Момент инерции не зависит от длины или материала балки. Здесь рассматриваются только прямоугольные и круглые цельные сечения. Пояснения к схемам прогиба и обозначениям
L = длина балки Уравнения и диаграммы прогибаПримечание к схемам и уравнениям .Приведенные здесь диаграммы были перевернуты по сравнению с их обычным описанием в учебниках, чтобы отразить их применение для моделей локомотивов и букс транспортных средств. Однако, хотя уравнения для отклонения были согласованы с их учебным представлением, нормальное соглашение о знаках (+ или -, чтобы указать отклонения по вертикальной оси y от опорной линии балки) было проигнорировано, поскольку мы здесь обеспокоены только с абсолютной величиной прогиба балки.
Значения модуля Юнга,E
Следует отметить, что это теоретические значения. Типичное значение для стальной гитарной струны можно принять как 205 ГПа. Значения, указанные для фосфористой бронзы, различаются: кажется, что они будут зависеть от материала типа «пружинный» или «экстрапружинный», состоящий из фосфористой бронзы 92% Cu / 8% Sn. обычно используется в переключателях с защелкой. 1 Шигли, инженер-конструктор машиностроения, 1980, McGraw Hill Примечания к единицам и размерам1 Па = 1 Н · м -2 = 10 -6 Н · мм -2 = 10 -6 кг · м · с -2 · мм -2 = 1 г · мм -1 · с -2 Чтобы получить силу F в приведенных выше уравнениях, массу нужно умножить на гравитационную постоянную g (9.81 м · с -2 , или, что нам удобнее, 9810 мм · с -2 ) Размеры модуля Юнга E составляют ML -1 T -2 © Расс Эллиотт , впервые опубликовано 19 апреля 2000 г .; |
% PDF-1.3 % 790 0 объект> эндобдж xref 790 87 0000000016 00000 н. 0000003638 00000 н. 0000002077 00000 н. 0000003742 00000 н. 0000003768 00000 н. 0000003814 00000 н. 0000004206 00000 н. 0000004286 00000 п. 0000004366 00000 н. 0000004446 00000 н. 0000004526 00000 н. 0000004606 00000 н. 0000004686 00000 п. 0000004766 00000 н. 0000004846 00000 н. 0000004926 00000 н. 0000005006 00000 н. 0000005086 00000 н. 0000005166 00000 н. 0000005246 00000 н. 0000005326 00000 н. 0000005405 00000 н. 0000005484 00000 н. 0000005563 00000 н. 0000005642 00000 н. 0000005721 00000 н. 0000005800 00000 н. 0000005879 00000 п. 0000005958 00000 н. 0000006037 00000 н. 0000006116 00000 п. 0000006195 00000 н. 0000006274 00000 н. 0000006353 00000 п. 0000006432 00000 н. 0000006511 00000 н. 0000006590 00000 н. 0000006669 00000 н. 0000006748 00000 н. 0000006827 00000 н. 0000006906 00000 н. 0000006985 00000 п. 0000007064 00000 н. 0000007143 00000 н. 0000007222 00000 н. 0000007301 00000 п. 0000007380 00000 н. 0000007459 00000 н. 0000007538 00000 н. 0000007616 00000 н. 0000007694 00000 п. 0000007772 00000 н. 0000008144 00000 п. 0000012271 00000 п. 0000012850 00000 п. 0000013048 00000 н. 0000013549 00000 п. 0000019289 00000 п. 0000019998 00000 п. 0000020324 00000 п. 0000020906 00000 н. 0000027647 00000 н. 0000028472 00000 п. 0000028889 00000 п. 0000028957 00000 п. 0000029405 00000 п. 0000030554 00000 п. 0000030916 00000 п. 0000031438 00000 п. 0000032252 00000 п. 0000032281 00000 п. 0000032366 00000 п. 0000032798 00000 п. 0000033385 00000 п. 0000034526 00000 п. 0000034622 00000 п. 0000034714 00000 п. 0000035389 00000 п. 0000036044 00000 п. 0000036678 00000 п. 0000036774 00000 п. 0000037386 00000 п. 0000038153 00000 п. 0000038785 00000 п. 0000039357 00000 п. 0000039385 00000 п. 0000003444 00000 н. трейлер ] >> startxref 0 %% EOF 792 0 obj> поток xb«b`tg`
Отклонение луча
Балка — конструктивный элемент, способный выдерживать большие нагрузки при изгибе.В случае небольших прогибов форму балки можно описать линейным дифференциальным уравнением четвертого порядка.
Рассмотрим вывод этого уравнения. Для изгибающейся балки угол \ (d \ theta \) появляется между двумя соседними секциями, расположенными на расстоянии \ (dx \) (рисунок \ (1 \)).
Рис. 1.Деформация \ (\ varepsilon \) в каждой точке пропорциональна координате \ (y, \), которая отсчитывается от нейтральной линии. 2}}} {2}} = {0.4}}} = q. \]
Это уравнение при соответствующих граничных условиях определяет прогиб нагруженной балки.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.