4 .3. Расчет вала на изгиб с кручением.
Задача решается по принципу суперпозиции, т.е. рассматриваются отдельно вертикальная и горизонтальная плоскости, определяются реакции в опорах А и В, строится эпюра изгибающего момента в той и другой плоскости, значения и геометрически суммируются, строится эпюра изгибающего момента. (рис. 6).
Для определения реакций используются три уравнения статики:
1) дает значение RB
2) дает значение RA
3) используется для проверки равновесия балки
Опасное сечение балки определяется по наибольшему суммарному изгибающему моменту:
В этом сечении определяется диаметр вала.
Вопросы для самопроверки:
Чем отличается вал от оси?
Классификация валов.

Материалы валов.
Порядок проектирования валов.
Какова принимаемая расчетная схема для вала?
Какие нагрузки действуют на валы в редукторах?
Что такое ориентировочный расчет вала на прочность?
Как определяются линейные размеры валов?
На какой вид деформаций рассчитывают валы?
Какие эпюры необходимо построить для проектировочного расчета вала?
Для определения расчетного
момента при совместном действии
изгиба и кручения используется
третья теория
прочности. Третья
Третья
теория прочности (как известно)
дает завышенный результат, но с
Рис. 6. учетом сложной работы вала и ответственности этой детали использование третьей теории прочности оправдано, ибо это повышает запас прочности.
Расчетный момент по третьей теории прочности в опасном сечении записывается так:
Вследствие вращения вала напряжения изгиба в нем изменяются по симметричному циклу, даже при постоянной величине нагрузки
 7)
7)Рис.7.
Н апряжения кручения изменяются пропорционально изменению крутящего момента (рис. 8).
В большинстве случаев трудно установить действительный цикл нагрузки машины в условиях эксплуатации. Тогда расчет выполняется условно по номинальной нагрузке, а цикл напряжений кручения прини- мается отнулевым (пульсационным), рис.8.
В ыбор пульсационного цикла для нап- ряжений кручения обосновывается тем, что большинство машин работает с переменным крутящим моментом, а знак момента изменяется только у реверсивных машин. Таким образом, если вал вращается в одну сторону (не реверсивное вращение), то изменение и показано на рис. 9.
Рис.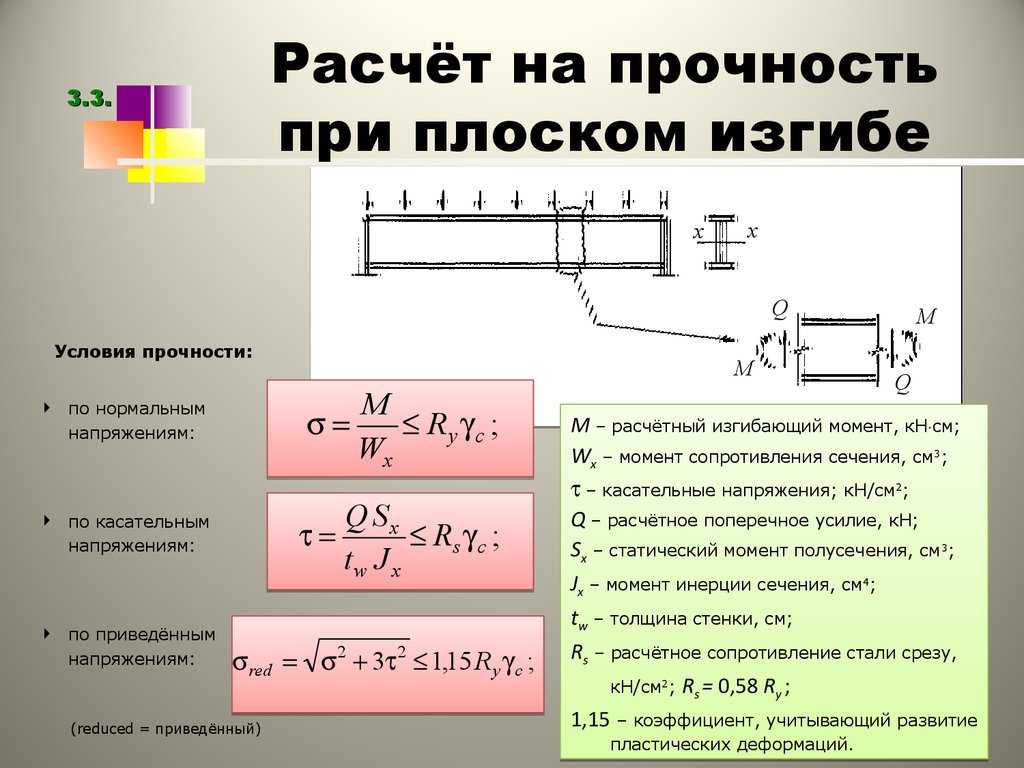 9.
9.
, где — коэффициент, учитывающий разные циклы
изменения напряжений от изгиба и кручения.
При реверсивном вращении вала изменение напряжений от изгиба и кручения принимаются по симметричному циклу (рис.10).
Рис. 10.
Тогда коэффициент .
Запишем условие прочности на изгиб с кручением:
,
здесь — осевой момент сопротивления
, откуда
dв уточняется по ГОСТу.
О пределение допускаемого нормального напряжения при симметричном цикле.
а) б) в)
Рис. 11
11
На рис.11 изображены:
а) закон изменения нормальных напряжений при статической нагрузке;
б) при пульсирующей;
в) при симметричной.
Экспериментально получено отношение допускаемых напряжений при этих законах изменения напряжений.
Тогда ; но , где — предел прочности материала
Окончательно
Так, для стали 45 и
5.5. Расчет валов на жесткость
HomeСОПРОМАТ 5.5. Расчет валов на жесткость
5.5. РАСЧЕТ ВАЛОВ НА ЖЕСТКОСТЬ
За меру жесткости принимают относительный угол закручивания, то есть угол, приходящийся на единицу длины вала Условие жесткости: ≤ [θ] где [θ] имеет размерность рад/м. Чаще пользуются условием Допускаемое значение угла [θ°] закручивания зависит от назначения вала. Принимают [θ°] = (0,3–1,0) град/м. При расчете валов на прочность и жесткость часто задают мощность N, передаваемую валом и частоту его вращения n. Для вычисления крутящего момента по этим данным удобно воспользоваться таблицей Пример 5.1. Расчета вала на прочность и жесткость I. Определение внутренних усилий Значение ведущего момента Мвед определим из условия равновесия вала: Σ Мх = 0; Мвед – М1 – М2 – М3 = 0, откуда Мвед = М1 + М2 + М3 = 5 + 7 + 6 = 18 кН·м. Для расчетов на прочность и жесткость необходимо найти положение опасных сечений и величины крутящих моментов, действующих в этих сечениях вала (рис. 5.3, а). Воспользовавшись методом сечений определим внутренние усилия и построим эпюру крутящих моментов (рис. 5.3, б). Опасными являются все сечения на участке II, где действует Тmax = 12 кН·м. II. Проектный расчет валов сплошного и полого сечений Предварительно найдем допускаемое касательное напряжение, связанное с допускаемым нормальным напряжением.
Принимают [θ°] = (0,3–1,0) град/м. При расчете валов на прочность и жесткость часто задают мощность N, передаваемую валом и частоту его вращения n. Для вычисления крутящего момента по этим данным удобно воспользоваться таблицей Пример 5.1. Расчета вала на прочность и жесткость I. Определение внутренних усилий Значение ведущего момента Мвед определим из условия равновесия вала: Σ Мх = 0; Мвед – М1 – М2 – М3 = 0, откуда Мвед = М1 + М2 + М3 = 5 + 7 + 6 = 18 кН·м. Для расчетов на прочность и жесткость необходимо найти положение опасных сечений и величины крутящих моментов, действующих в этих сечениях вала (рис. 5.3, а). Воспользовавшись методом сечений определим внутренние усилия и построим эпюру крутящих моментов (рис. 5.3, б). Опасными являются все сечения на участке II, где действует Тmax = 12 кН·м. II. Проектный расчет валов сплошного и полого сечений Предварительно найдем допускаемое касательное напряжение, связанное с допускаемым нормальным напряжением.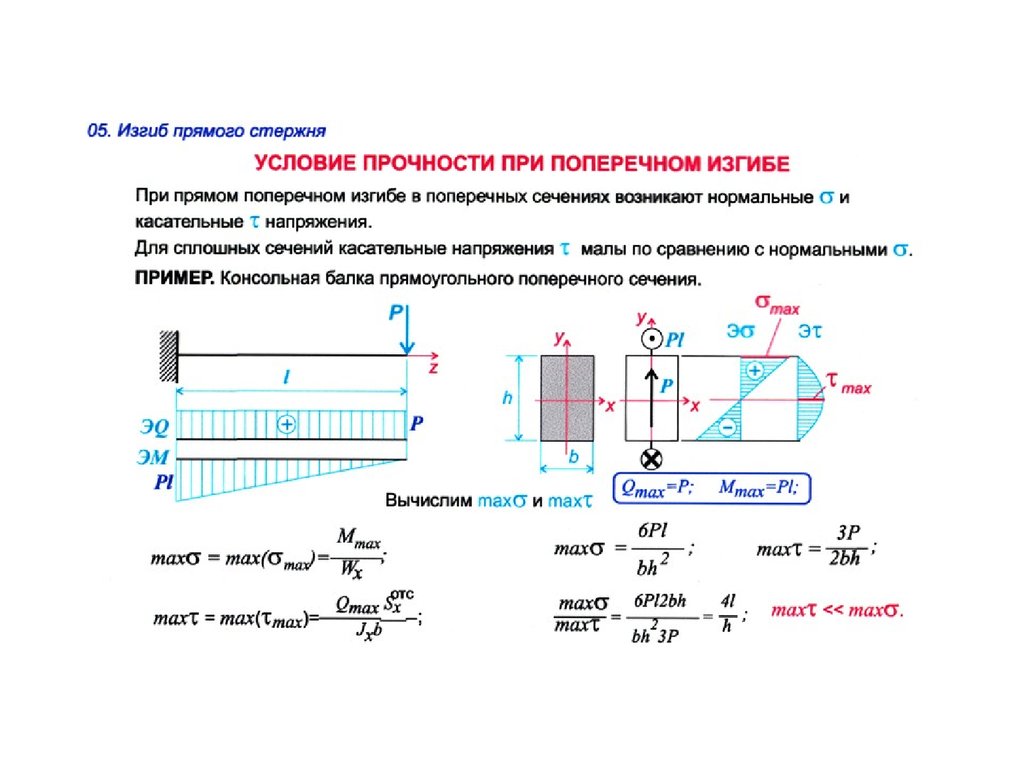
 Поэтому целесообразно убирать неработающий материал из этой области. Конструкции из полого сечения созданы природой: камыш, тростник, бамбук, злаковые культуры, трубчатые кости птиц и млекопитающих. В авиации и космонавтике используют полые валы, в строительстве – пустотные плиты перекрытий.
Поэтому целесообразно убирать неработающий материал из этой области. Конструкции из полого сечения созданы природой: камыш, тростник, бамбук, злаковые культуры, трубчатые кости птиц и млекопитающих. В авиации и космонавтике используют полые валы, в строительстве – пустотные плиты перекрытий.
НАШИ УСЛУГИ
Примеры решения задач по электротехнике
Типовые задания
Наши статьи
Расчетные формулы и калькулятор трансмиссионного вала
Связанные ресурсы: калькуляторы
Расчетные формулы и калькулятор трансмиссионного вала
Проектирование и проектирование силовой трансмиссии
Расчетные формулы вала силовой передачи и калькулятор для напряжения кручения, напряжения изгиба и напряжения растяжения или сжатия.
Конструкция вала заключается, прежде всего, в определении правильного диаметра вала для обеспечения достаточной прочности и жесткости, когда вал передает мощность в различных условиях эксплуатации.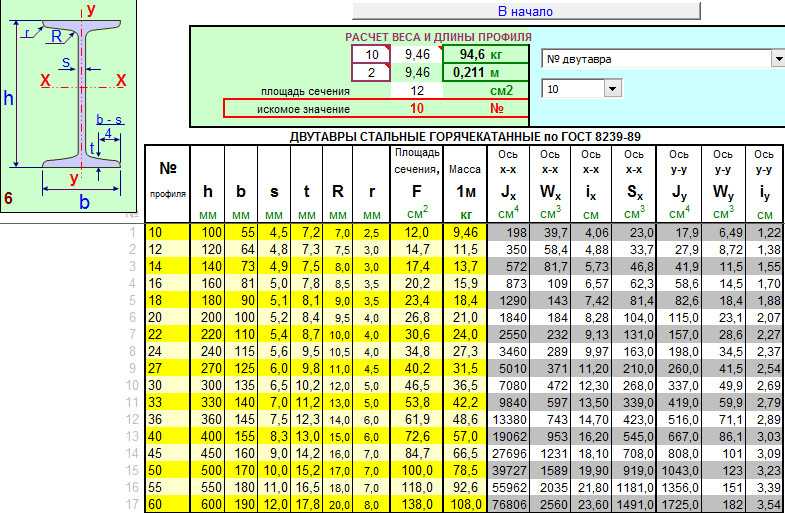 Вал обычно имеет круглое сечение и может быть как полым, так и сплошным.
Вал обычно имеет круглое сечение и может быть как полым, так и сплошным.
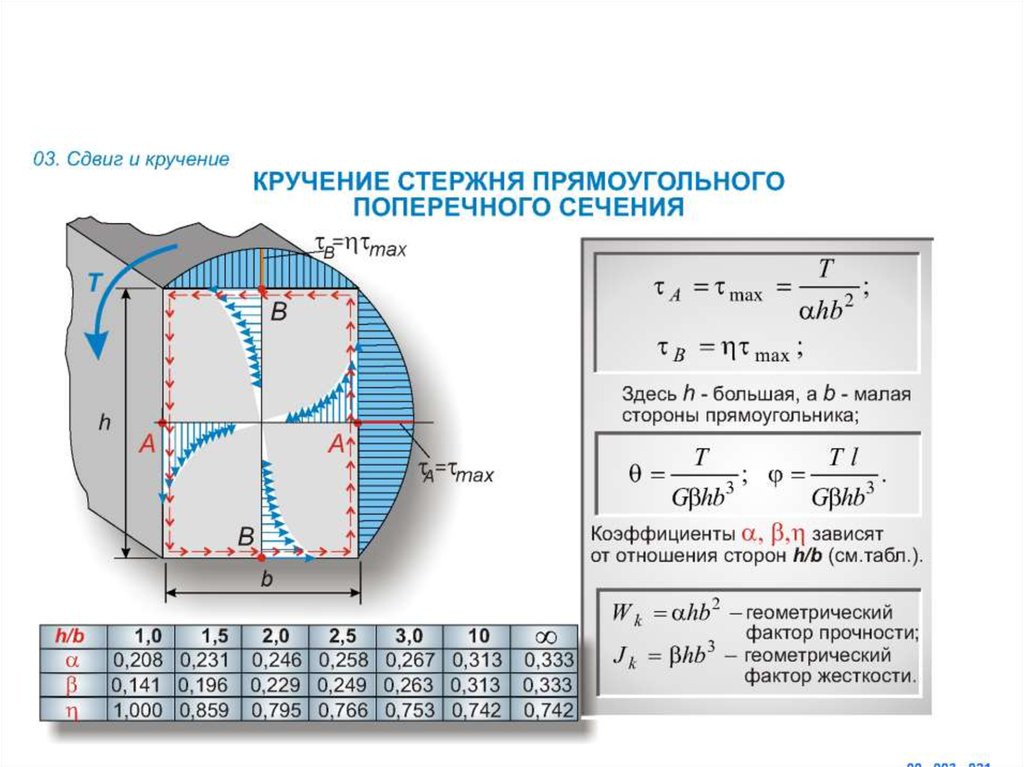
Расчет валов из пластичных материалов на основе прочности контролируется теорией максимального сдвига. В основе лежат валы из пластичного материала и круглого сечения. Вал из хрупкого материала будет спроектирован на основе теории максимального нормального напряжения. Вал обычно подвергается кручению, изгибу и осевой нагрузке. Для скручивающих нагрузок напряжение кручения составляет:
для сплошных валов, уравнение. 1
τ xy = M t r / J = 16 M t / π d 3
для полых валов, ур. 2
τ xy = 16 M t d o / π ( d o 4 — d i 4 )
Для изгибающих нагрузок напряжение изгиба (растяжение или сжатие )
для сплошных валов, экв. 3
s b = M b r / J = 32 M b / π d 3
для полых валов, ур. 4
4
s b = 32 M b d o / π ( d o 4 — d i 4 ) 9 0028
Для осевых нагрузок, растягивающих или сжимающих напряжений
Для твердых валы , экв. 5
s a = 4 F a / π d 2
для полых валов, уравнение 6
s a = 4 F a / π ( d o 4 — d i 4 )
Где:
τ xy = напряжение сдвига при кручении, фунт/кв. дюйм
M t = крутящий момент, дюйм-фунт 20 b = Изгибающий момент, дюйм-фунт
F a = осевая нагрузка, фунты
s b = напряжение изгиба (растяжение или сжатие), фунт/кв. дюйм
s a = осевое напряжение (растяжение или сжатие), фунт/кв. 9 д о = наружный диаметр полого вала, дюйм
d i = внутренний диаметр полого вала, в
d = диаметр сплошного вала, в
J = полярный момент инерции круглого сечения, в 4
π = pi = 3. 14159265
14159265
Связанный:
- Изгиб поперечного вала при кручении, уравнение напряжения и калькулятор
- Прочность и механика материалов
- ASME Расчет допустимого напряжения и диаметра вала, уравнения и калькуляторы
- Уравнения и калькулятор жесткости при кручении сплошного вала
- Калькулятор силы торсионной пружины и формула
- Расчет универсального шарнира грузовика и легкового автомобиля и инженерное уравнение
- Комбинированная нагрузка на круглый вал в уравнениях прямого сжатия и кручения и калькуляторе
Ссылки:
- Контурная теория Шаума и проблемы проектирования машин —
- Макгроу Хилл (1968),
- Аллен С. Холл, Альфред Р. Холовенко,
- Герман Г. Лафлин
Калькулятор изгибающего напряжения в валу
✖Изгибающий момент — это реакция, возникающая в элементе конструкции, когда к элементу прилагается внешняя сила или момент, вызывающий изгиб элемента. | Грамм-сила СантиметрКилограмм-сила-метрКилоньютон-метрМикроньютон-метрМиллиньютон-метрНьютон-метрНьютон-миллиметрфунт-футфунт-дюймфунт-сила фут-тонна-сила (длинная) метр-тонна-сила (метрическая) метр-тонна-сила (короткий) Метр | +10% -10% | |
✖ Диаметр вала -это диаметр внешней поверхности вала, который является вращающимся элементом в системе передачи для передачи. [d вал ] | AlnAngstromArpentАстрономическая единица Аттометр AU длиныЯчменьМиллиард световых летBohr RadiusCable (International)Cable (UK)Cable (US)CalibreCentimeterChainCubit (греческий)Cubit (Long)Cubit (UK) )DecameterDecimeterEarth Расстояние от MoonEarth Расстояние от SunEarth Экваториальный радиусEarth Полярный радиусЭлектронный радиус (классический)EllExameterFamnFathomFemtometerFermiFinger (ткань)BreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMile Миля (римская) Миля (исследование США) Миллиметр Миллион светового года Гвоздь (ткань) Нанометр Морская лига (внутренняя) Морская лига Великобритании Морская миля (Международная) Морская миля ( Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (Длинный)РодРоман АктусВеревкаРусский АрчинПротяженность (Ткань)Солнце РадиусТераметрТвипВара КастелланаВара КонукераВара Де ТареаЯрдЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
✖Напряжение при изгибе — это нормальное напряжение, возникающее в точке тела, на которое воздействуют нагрузки, вызывающие его изгиб. | Атмосфера ТехническаяАттопаскальБарБарьеСантиметр ртутного столба (0 °C)Сантиметр водяного столба (4 °C)СантипаскальДекапаскальДеципаскальДин на квадратный сантиметрЭксапаскальФемтопаскальФут морской воды (15 °C)ФемтопаскальФут морской воды (15 °C)ФемтопаскальФут морской воды (60 °F)ГигапаскальГрамм силы на квадратный сантиметрГектопаскальДюйм ртутного столба (32 ° F) Дюйм ртутного столба (60 °F) Дюйм водяного столба (4 °C) Дюйм водяного столба (60 °F) Килограмм-сила на квадратный сантиметр Килограмм-сила на квадратный метрКилограмм-сила на квадратный миллиметрКилоньютон на квадратный метрКилопаскальКилофунт на квадратный дюймКип-сила на квадратный дюймМегапаскальМетр Морская водаметр воды (4 °C)микробармикропаскальмиллибармиллиметр ртутного столба (0 °C)миллиметр воды (4 °C)миллипаскальнанопаскальньютон на квадратный сантиметрньютон на квадратный метрньютон на квадратный миллиметрпаскальпетапаскальпикопаскальпьезафунт на квадратный дюймфунт на квадратный футфунт-сила на квадратный футфунт-сила на квадратный дюймфунты на квадрат Футы стандартной атмосферы Терапаскаль-тонна-сила (длинная) на квадратный фут-тонна-сила (длинная) на квадратный дюйм-тонна-сила (короткая) на квадратный фут-тонна-сила (короткая) на квадратный дюйм-торр | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Изгибающее напряжение в валу Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Изгибающий момент: 53 ньютон-метра —> 53 ньютон-метра Преобразование не требуется
Диаметр вала: 1200 мм —> 1,2 Метр (Проверьте преобразование здесь)
ШАГ 2: Вычисление формулы
ШАГ 3: Преобразование результата в единицу измерения
312,415258661869 Паскаль —> Преобразование не требуется
< 11 Калькуляторы основ проектирования машин 92)))Допустимая прочность на растяжение для двойного поперечного углового соединения
Идти Напряжение растяжения в поперечном угловом сварном шве = нагрузка на двойной поперечный угловой сварной шов/(1,414*длина сварного шва*половина сварного шва)
Прочность стыкового сварного соединения
Идти Растягивающее напряжение в поперечном угловом сварном шве = Растягивающее усилие на сварных пластинах / (толщина сварного шва * длина сварного шва)
Начальная скорость
93))Передаваемая мощность
Идти Мощность на валу = (2*pi*скорость вращения*приложенный крутящий момент)
Плотность энергии деформации
Идти Плотность энергии деформации = 0,5*основное напряжение*основная деформация
Коэффициент запаса прочности при предельном напряжении и рабочем напряжении
Идти Коэффициент запаса прочности = напряжение разрушения/рабочее напряжение
Толщина шплинтового соединения
Идти Толщина шплинта = 0,31*диаметр стержня шплинта 93))
Что такое изгибающее напряжение в валу?
Это номинальное напряжение, когда вал подвергается нагрузке, вызывающей изгиб и усталость.

 ⓘ Изгибающий момент [M b ]
ⓘ Изгибающий момент [M b ]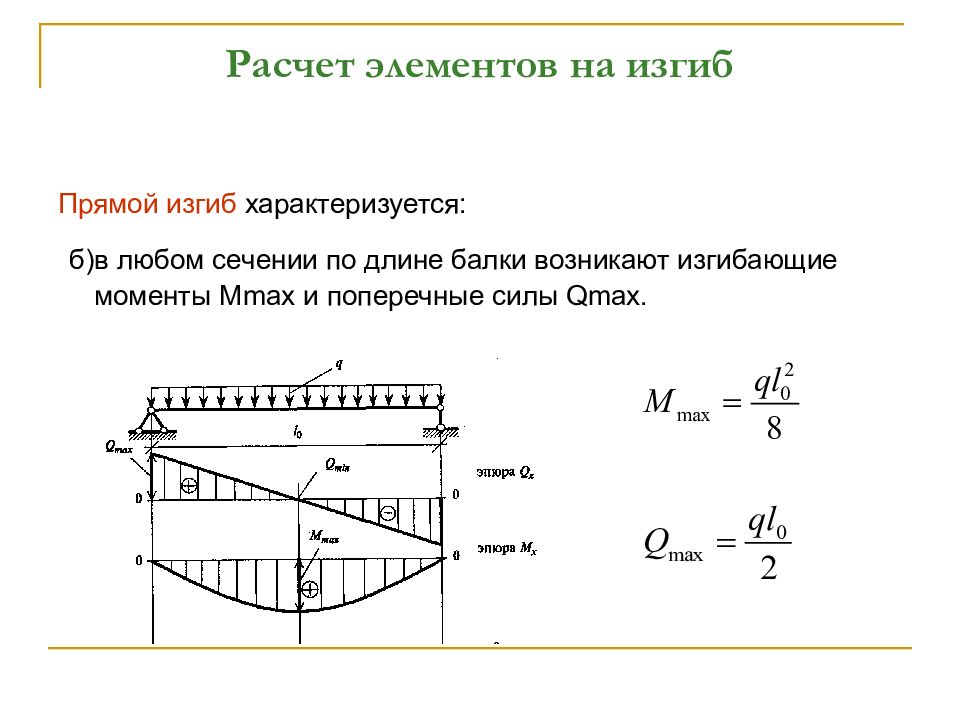 ⓘ Напряжение изгиба в валу [σ b ]
ⓘ Напряжение изгиба в валу [σ b ]