Расчет на изгиб консольной балки: Расчет консольной балки на изгиб пример

Проверка консольной балки на прочность

Пример решения задачи по проверке на прочность стальной консольной балки нагруженной силой, моментом и равномерно распределенной нагрузкой.

Задача

Проверить на прочность консольную балку, закрепленную в жесткой заделке.

Другие примеры решений >
Помощь с решением задач >

Решение

Приложим к балке систему внешних нагрузок:

  • Сосредоточенную поперечную силу F
  • Изгибающий момент m
  • Равномерно распределенную нагрузку q

Укажем величину заданных усилий и продольные размеры участков балки.

Это расчетная схема для решения задачи.

Проверим эту балку на прочность при следующих данных:

  • Сечение балки — двутавр №24;
  • Допустимые напряжения для материала балки [σ]=160МПа.

Прежде чем приступить к решению проанализируем задачу.

Чтобы проверить балку на прочность надо определить величину максимальных напряжений σ

max в ее сечениях и сравнить их с допустимыми [σ].

В случае если максимальные напряжения окажутся меньше, либо равны допустимым (т.е. σmax≤[σ]) прочность балки будет обеспечена.

Если же найденные напряжения превысят величину допустимых (т.е. σmax>[σ]) значит балка не прочная.

Условие прочности при плоском поперечном изгибе:

Здесь
Mx – внутренний изгибающий момент,
Wx – осевой момент сопротивления сечения балки.

У балки постоянного сечения, форма и размеры сечения одинаковы по всей ее длине, следовательно, Wx=const.

Тогда очевидно, что наибольшими напряжения окажутся в сечении, где будет максимальный изгибающий момент Mx.

Определить максимальный изгибающий момент Mx max в балке можно только по его эпюре.

Для построения эпюр сначала надо определить опорные реакции.

Ниже приведены ссылки на каждый этап решения данной задачи.

Порядок проверки балки на прочность при изгибе:

  1. Рассчитываются опорные реакции балки,
  2. Строятся эпюры Qy и Mx,
  3. Определяется опасное сечение балки,
  4. Рассчитываются максимальные нормальные напряжения,
  5. Полученные напряжения сравниваются с допустимыми, и делается заключение о прочности балки,
  6. В случае если прочность не обеспечена, подбираются новые размеры сечения, обеспечивающие прочность.

Другие примеры решения задач >

Сохранить или поделиться с друзьями


Вы находитесь тут:


На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее


Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями


Заказать решение

Поиск формул и решений задач

    Особенности расчета на прочность составных балок из неоднородных материалов 9789855502044

    Table of contents :
    Пустая страница

    Citation preview

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ Белорусский национальный технический университет Кафедра «Сопротивление материалов машиностроительного профиля»

    ОСОБЕННОСТИ РАСЧЕТА НА ПРОЧНОСТЬ СОСТАВНЫХ БАЛОК ИЗ НЕОДНОРОДНЫХ МАТЕРИАЛОВ Учебно-методическое пособие

    Минск БНТУ 2013

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ Белорусский национальный технический университет

    Кафедра «Сопротивление материалов машиностроительного профиля»

    ОСОБЕННОСТИ РАСЧЕТА НА ПРОЧНОСТЬ СОСТАВНЫХ БАЛОК ИЗ НЕОДНОРОДНЫХ МАТЕРИАЛОВ Учебно-методическое пособие для студентов специальности 1-36 01 03 «Технологическое оборудование машиностроительного производства» Рекомендовано учебно-методическим объединением в сфере высшего образования Республики Беларусь по образованию в области машиностроения

    Минск БНТУ 2013 1

    УДК 620. 172.251.224(075.8) ББК 34.41я7 О-75 Авторы: А. И. Дудяк, А. А. Хмелев, Т. А. Сахнович, О. И. Гурковская Рецензенты: зав. кафедрой «Теоретическая механика» БГАТУ, д-р техн. наук, профессор А. Н. Орда; зав. кафедрой «Машины и технология обработки металлов давлением» БНТУ, д-р техн. наук, профессор К. Е. Белянин

    Особенности расчета на прочность составных балок из неодноО-75 родных материалов : учебно-методическое пособие для студентов специальности 1-36 01 03 «Технологическое оборудование машиностроительного производства» / А. И. Дудяк [и др.]. – Минск : БНТУ, 2013. – 27 с. ISBN 978-985-550-204-4. В данном пособии рассмотрена теоретическая задача расчета на прочность стержней, состоящих из двух разнородных материалов, прочно соединенных между собой и работающих на изгиб как единое целое. Установлены зависимости для определения местоположения нейтрального слоя и показана методика по определению нормальных и касательных напряжений, возникающих в поперечных сечениях стержня. УДК 620.172. 251.224(075.8) ББК 34.41я7

    ISBN 978-985-550-204-4

    2

    © Белорусский национальный технический университет, 2013

    Введение Во многих областях техники применяют стержни, составленные из различных материалов. Типичным примером являются стержни биметаллических пар, составленные из металлов с разными значениями модулей Юнга и работающие на изгиб как консольные или двухопорные балки. Другим примером являются конструкции или детали, изготовленные из композитных материалов. Идея здесь состоит в том, что при создании комбинированного материала основу армируют большим количеством тонких нитей из другого материала, более прочного и жесткого. В результате получают стержень, имеющий в наиболее нагруженных частях сечения материал с повышенными упругими и прочностными характеристиками. В итоге сечение такой балки является составленным из двух и более материалов с соотношениями модулей упругости Е1 ≠ Е2. При этом обе части указанных стержней на всей длине надежно соединены между собой либо за счет сил сцепления, либо создания специальных устройств в виде упоров, отгибов и т. п. Поэтому они работают при продольных деформациях стержня совместно, как единое монолитное сечение, и к такому составному стержню применима гипотеза плоских сечений, считая при этом справедливой гипотезу ненадавливания продольных волокон друг на друга в поперечном направлении. Однако расчеты на прочность составных балок из неоднородных материалов имеют и существенные отличия от классических методов расчета балок из однородных материалов. Покажем это на примерах расчетов составных консольных и двухопорных балок из неоднородных материалов при Е1 ≠ Е2.

    3

    1. Теоретический расчет нормальных напряжений Рассмотрим случай чистого изгиба консольной балки прямоугольного сечения составленного из двух неоднородных материалов, обладающих различными значениями модулей упругости, т. е. E1 > E2 при неравных площадях их сечений A1

    a

    Рис. 1. Схема нагружения (а) и форма сечения балки (б)

    Для упрощения расчетов условно примем, что нейтральная ось сечения не совпадает с главной центральной осью х1, а проходит по границе раздела двух материалов (рис. 1, б). Составляющие сечения балки площади А1 и А2, не равные между собой, соединены жестко и работают как единое целое. Рассмотрим напряженно-деформированное состояние участка балки длинной dZ (рис. 2). В результате деформации верхние слои участка будут растянуты, а нижние сжаты, правое сечение балки этого участка повернется относительно левого сечения на угол d. Относительные деформации верхнего и нижнего слоев сечения будут 1  4

    y1 a y c  , 2   2   ,    

    где  – радиус кривизны нейтрального слоя; y1, y2 – расстояния от нейтрального слоя до верхнего и нижнего слоев сечения соответственно; a и с – толщина слоев составного сечения.

    Рис. 2. Деформированное состояние участка dZ длины балки

    По закону Гука напряжения растяжения и сжатия в этих слоях будут  z1  E1

    y1 y , z2  E 2 .  

    (1)

    Сумма элементарных сил  dA равна значению элементарной силы в сечении, которая при чистом изгибе равна нулю, поэтому

    N z   E1 A1

    y1 y dA1   E2 2 dA2  0.   A 2

    Учитывая, что

     y1dA1  S X 1,

    A1

     y2dA2  S X 2 

    A2

    5

    статические моменты верхней и нижней частей площади сечения, получим

    E1S X 1  E 2 S X 2  0,

    (2)

    a2 c2 и SX 2  b . 2 2 Подставив значения SX1 и SX2 в уравнение (2), получим

    где S X 1  b

    E1a 2  E2c 2  0 .

    (3)

    Учитывая, что c = h – a, и решая уравнение (3) относительно величины «а», определим его значение, считая, что центральный слой совпадает с границей раздела двух материалов: h a 1

    E2 E1 E2 E1

    или a 

    h n , 1 n

    (4)

    где n = E2 / E1. При значении n = 1 для сечения составной балки, состоящей из двух половин одного и того же материала, нейтральная h ось будет проходить при значении a  , что соответствует 2 положению центра тяжести площади сечения. В случае, если n отлично от единицы, то нейтральная ось будет смещена от центра тяжести площади сечения. Эпюра распределения напряжений по высоте сечения балки при совпадении нейтральной оси с линией раздела двух материалов приведена на рис. 3. 6

    Рис. 3. Распределение напряжений по сечению балки

    Из рис. 3 следует, что значение угла α1 > α2 если E1 > E2. Общий случай распределения напряжений по высоте сечения консольных балок для варианта, когда E1 > E2, а нейтральная ось проходит по площади материала с большим значением Е, приведен на рис. 4. Откуда следует, что при определении напряжений по формулам (1) на границе раздела двух материалов получается разрыв эпюры, так как в точках соприкосновения материалов напряжения будут отличатся в n раз. а

    б z, МПа

    Рис. 4. Напряжения в составной балке при E1 > E2

    7

    Из рис. 4 следует, что в большинстве случаев составных балок нейтральная ось сечения не будет совпадать с главной центральной осью xc, а будет смещаться, оставаясь параллельной оси xc, в сторону материала с большим значением модуля Юнга. В связи с этим для определения значения осевого момента инерции площади сечения балки следует применять метод его определения при параллельном переносе осей. Для данного сечения представим, что нейтральный слой проходит через ось x. В итоге новая главная ось х делит площадь сечения на три части, для которых надо определить значения статических моментов SX1, SX2, SX3 и осевых моментов инерции IX1, IX2, IX3. Определим значение a1 как расстояние от верхней кромки сечения до оси х. Из условия равенства нулю продольной силы Nz в сечении балки при чистом изгибе имеем N z   E1 A1

    y1 y y dA1   E1 2 dA2   E2 3 dA3  0 .    A A 2

    3

    После ряда преобразований получим E1S X 1  E1S X 2  E 2 S X 3  0,

    (5)

    h (  a1 )2 h h h и S X 3  b (  (  a1 )). где S X 1  b ; S X 2  b 2 2 4 2 2 2 Подставив значения статических моментов площадей в формулу (5), получим

    a12

    E1

    8

    h b(  a1 )2 h h h  E1 2  E2b (  (  a1 ))  0. 2 2 2 4 2

    ba12

    После ряда преобразований получим

    a1 

    h( E1  3E2 ) h(1  3n)  .                            (6) 4( E1  E2 ) 4(1  n)

    Значение а1 определяет место положения нейтрального слоя. Известно, что значение изгибающего момента в сечении z записывается в виде M z    z ydA, A

    которое для общего случая составного сечения балки можно записать в виде M z   E1 A1

    y1 y y y1dA1   E1 2 y2dA2   E2 3 y3dA3  0.    A A 2

    Учитывая, что

    3

    2  y dA  I x – момент инерции площади се-

    A

    чения, получим Mz 

    E1 E E I X 1  1 I X 2  2 I X 3,   

    откуда определим значение

    1 : 

    1 Mz  ,  E1I X 1  E1I X 2  E2 I X 3

    (7) 9

    где

    I X1 

    IX2

    ba13 a  ba1( 1 )2 , 12 2

    h h  a1 b(  a1 )3 h 2 2   b(  a1 )( )2 , 12 2 2

    h b( )3 h h h I X 3  2  b (  (  a ))2 . 12 2 4 2 В этом случае напряжения в точках верхнего участка сечения балки относительно нейтральной оси с модулем упругости ‫ܧ‬ଵ определим по формуле

    Z 1 

    M z E1 y1. E1I X 1  E1I X 2  E2 I X 3

    (8)

    На участке сечения балки с модулем Юнга Е1, расположенного ниже нейтральной оси, напряжение определяют по формуле

    Z 2  

    M z E1 y2 . E1I X 1  E1I X 2  E2 I X 3

    (9)

    На третьем нижнем участке сечения балки с модулем упругости Е2 напряжение определим по формуле

    Z 3  

    M z E2 y3. E1I X 1  E1I X 2  E2 I X 3

    (10)

    Эпюра напряжений и разрыв значений напряжений на границе раздела материалов приведены на рис. 4. 10

    2. Касательные напряжения при плоском поперечном изгибе   При плоском поперечном изгибе в поперечных сечениях балки действуют два внутренних силовых фактора: поперечная сила Qz и изгибающий момент Mz. Схема нагружения составной консольной балки прямоугольного сечения и эскиз ее сечения приведены на рис. 5.

    Рис. 5. Схема нагружения и форма сечения балки

    В сечениях балки действуют нормальные напряжения z и касательные напряжения zy. Значения касательных напряжений проще всего вычислить через значения парных напряжений yz, возникающих в продольных сечениях балки. Рассмотрим элемент длины балки dZ (рис. 6), когда модуль упругости материала верхнего слоя балки E1 > E2 нижнего слоя балки. В этом случае нейтральная ось сечения балки должна проходить по площади сечения верхнего материала балки, см. формулу (4).

    11

    а

    б

    Рис. 6. Распределение нормальных напряжений z, касательных напряжений τzy и τyz выше нейтрального слоя х по высоте сечения составной балки

    Равнодействующая сил, вызванная действием нормальных напряжений z и касательных напряжений τzy, должна быть равна нулю, что можно представить следующим образом:

     ( z  d z ) dA    z dA   yz bdz  0.

    A

    A

    Данные уравнение приводим к виду  yz bdz   d z dA.

    (11)

    A

    С учетом уравнения (8), полученного для значения z, производная для  z1 будет иметь вид

    d z1  12

    dM z E1 . E1I X 1  E1I X 2  E2 I X 3

    (12)

    Совместное решение уравнений (11) и (12) дает  yz bdz 

    dM z E1  y1dA1, E1I X 1  E1I X 2  E2 I X 3 A

    где  y1dA1  S Xотс1 – статический момент отсеченной площади A

    сечения, т. е. площади, лежащей выше прямой AB (рис. 6, б). Значение касательных напряжений, действующих выше нейтрального слоя балки, с учетом статического момента отсеченной площади можно выразить следующим образом:

     yz  Так как

    dM z E1S Xотс1 . dz b( E1I X 1  E1I X 2  E2 I X 3 )

    (13)

    dM z  Qz , уравнение (13) получает вид dz

     yz

    Qz S Xотс1 E1 ,  b( E1I X 1  E1I X 2  E2 I X 3 )

    (14)

    a1  y1 ). 2 Для определения касательных напряжений на участке сечения, расположенного между нейтральным слоем и линией раздела материалов, необходимо учитывать значение касательных напряжений, действующих на третьем участке балки: где S Xотс1  b( a1  y1 )( y1 

     yz 

    Qz ( S Xотс3 E2  S Xотс2 E1 ) , b( E1I X 1  E1I X 2  E2 I X 3 )

    где S Xотс2  b( c  a1  y2 )( y2 

    (15)

    c  a1  y2 d ), S Xотс3  bd (c  a1  ). 2 2 13

    На участке сечения ниже раздела двух материалов

     yz

    Qz S Xотс4 E2 ,  b( E1I X 1  E1I X 2  E2 I X 3 )

    (16)

    h  a1  y3 ). 2 По формулам (14), (15) и (16) построена эпюра касательных напряжений (рис. 7) по высоте сечения балки h. где S Xотс4  b( h  a1  y3 )( y3 

    Рис. 7. Распределение касательных напряжений по высоте сечения балки

    Из рис. 7 следует, что максимальные касательные напряжения в сечении балки действуют на уровне расположения нейтрального слоя х, что подтверждает известную классическую закономерность их распределения. 3. Пример расчета составной консольной балки с разными значениями модуля Юнга

    На рис. 8 приведена расчетная схема и сечение консольной составной балки со значениями Е1 = 2·105 МПа, а Е2 = 1·105 МПа. Сечение балки прямоугольное, состоящее из двух одинаковых по высоте частей, равных 50 мм. Ширина балки b = 50 мм, а высота ее сечения h = 100 мм. 14

    Рис. 8. Расчетная схема и эскиз сечения составной балки

    Требуется определить значения нормальных и касательных напряжений в характерных точках сечения и построить эпюры этих напряжений. На рис. 8 условно нейтральная ось сечения балки совпадает с центром тяжести площади сечения, но так как Е1 > Е2 по условию задачи, нейтральная ось (н. о.) будет проходить по площади материала балки со значением Е1, т. е. выше условно принятого положения оси ХС. По формуле (6) определим положение нейтральной оси, обозначив его значением а1, отсчитывая его положение от верхней кромки общего сечения балки: а1 

    h ( E1  3E2 ) 100(2  105  3  1  105 )   41, 67 мм. 4( E1  E2 ) 4(2  105  1  105 ) 15

    Тогда расстояние до нейтральной оси сечения от центральной оси ХС составит l

    h 100 a   41,67  8,33 мм. 2 2

    Отложим полученные значения на эскизе площади сечения (рис. 9). а

    б

    Рис. 9. Положение нейтральной оси в сечении (а) балки и эпюры нормальных и касательных напряжений (б)

    Из рис. 9 следует, что нейтральная ось сечения разделила это сечение на три участка, которые пронумерованы 1, 2, 3 соответственно. Для каждого из этих участков определим значения осевых моментов инерции относительно нейтральной оси (н. о.) с учетом параллельного переноса осей:

    16

    50  41,673 41,67 2 I X1   50  41,67( )  12,06  105 мм4 ; 12 2 IX 2 

    50  8,333 8,33 2  50  8,33  ( )  9,63  103 мм4 ; 12 2

    50  503 IX3   50  50(25  8,33)2  32,98  105 мм4 .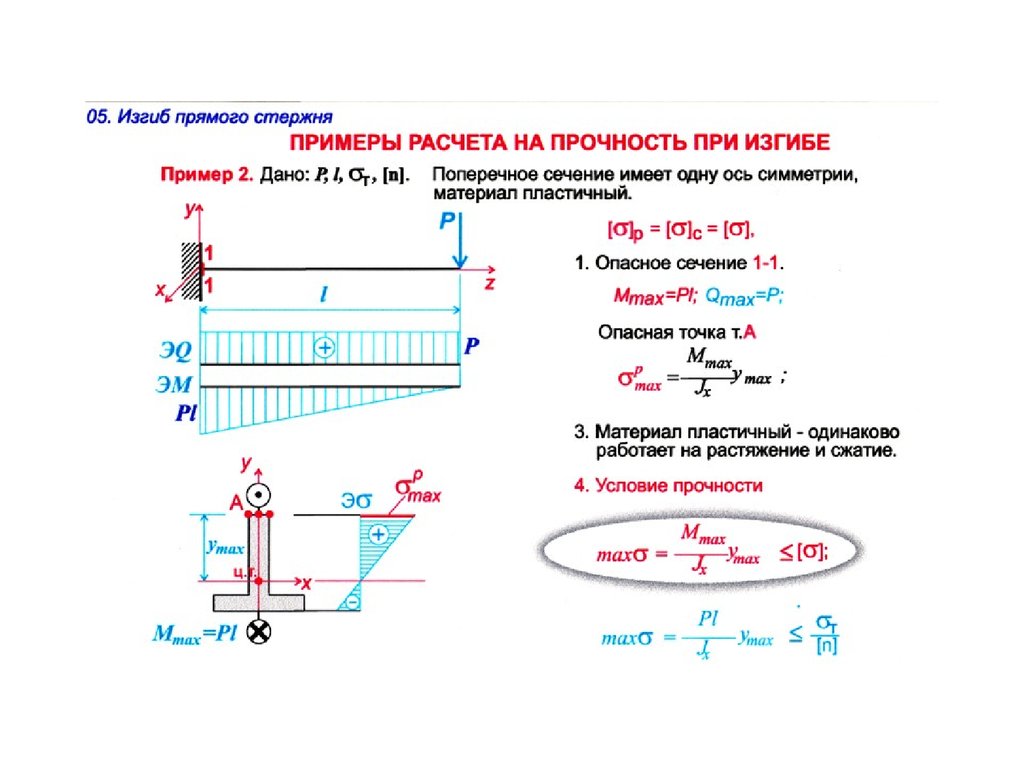 12 Значение 1/ρ определим по формуле (7):

    1 Mz    E1I X 1  E1I X 2  E2 I X 3 

    Mz Mz .  3 5 5 2  10 (12,06  10  9,63  10 )  1  10  32,98  10 57, 29  1010 5

    5

    Напряжение в точке А (рис. 9) определим по формуле  Z ( A)  

    M z E1  yA  E1I X 1  E1I X 2  E2 I X 3

    10  106  2  105  41,67  2  105  12,06  105  2  105  0,96  105  1  105  32,98  105 20  106  41,67   145,5 МПа. 57, 29  105

    Напряжения в точке B, расположенной на нейтральной линии, равны нулю. На границе раздела материалов в точке D в материале с модулем упругости E1 напряжение  z определяется из выражения (9): 17

    Z ( D )  

    M z E1 yD  E1I X 1  E1I X 2  E2 I X 3

    10  106  2  105 8,33  29,08 МПа.  57, 29  1010 На границе раздела материалов в точке D в материале с модулем упругости E2 напряжение  z определим из выражения (9): Z ( D)  

    Mz E2  yD  E1I X1  E1I X 2  E2I X 3

    10 106 1105   8,33  14,54 МПа.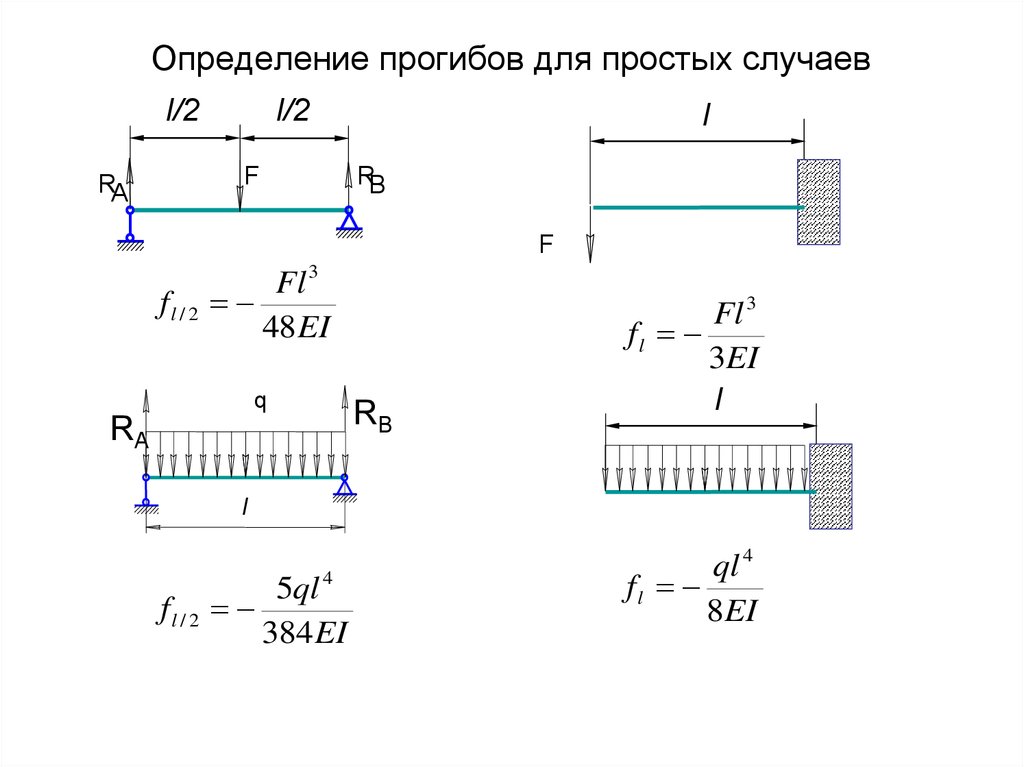 57,29 1010 Напряжение в точке К определим по формуле (10) при yk = 58,33 мм:

    Z ( K )   

    M z E2  yК  E1I X 1  E1I X 2  E2 I X 3

    10  106  1  105  58,33  101,81 МПа. 57, 29  1010

    Эпюра нормальных напряжений по высоте сечения балки приведена на рис. 9, где на границе раздела материалов получаем скачок напряжений, равный n = E1 / E2 = 2 ·105/(1·105) = 2, что подтверждает правильность решения задачи. Определяем значения касательных напряжений в характерных точках по высоте сечения балки (рис. 9). Напряжения в точках А и К равны нулю. Касательные напряжения в точке B определим по формуле (14): 18

     yz ( B )  отс где S XB  50  41,67 

     yz ( B ) 

    отс Qz S XB E2 , b( E1I X 1  E1I X 2  E2 I X 3 )

    41,67  0, 434  105 мм3; 2

    10  103  0, 434  105  1  105  3,03 МПа. 50  57, 29  1010

    Напряжение в точке D определим по формуле (15):

     yz ( D )  отс где S XD  50  50  (

     yz ( D )

    отс Qz S XD E2 , b( E1I X 1  E1I X 2  E2 I X 3 )

    50  8,33)  83325 мм3; 2

    10  103  83325  2  105   2,9 МПа. 50  57,29  105

    Эпюра касательных напряжений по высоте сечения балки приведена на рис. 9. 4. Нормальные напряжения при плоском изгибе прямого стержня, возникающие в результате надавливания волокон друг на друга

    В данной работе приводится доказательство, что в продольных сечениях бруса при поперечном изгибе, вызванным действием сосредоточенной силы, возникают нормальные напряжения в результате надавливания волокон друг на друга. Из курсов «Сопротивление материалов» и «Теория упругости» известно, что при таком изгибе в поперечных сечениях бруса 19

    возникают только нормальные напряжения в поперечном направлении, а в перпендикулярном поперечном направлении они отсутствуют. Рассмотрим двухопорную балку прямоугольного сечения, нагруженную сосредоточенной силой на середине пролета (рис. 10). ‫ݕ‬ 

    Рис. 10. Схема нагружения и форма сечения балки

    Из курса «Сопротивление материалов» расчетные формулы для определения нормальных и касательных напряжений в сечениях балки, без учета гипотезы о надавливании волокон в поперечном направлении, имеют вид z 

    Mz  y, Ix

    Qz  S xотс  zy  , Ix b

    (17)

    (18)

    где h h 1 h bh3 4 y2 b Sxотс  A  yc  b(  y)  (  (  y))  (1  2 )  (h3  4 y 2 ).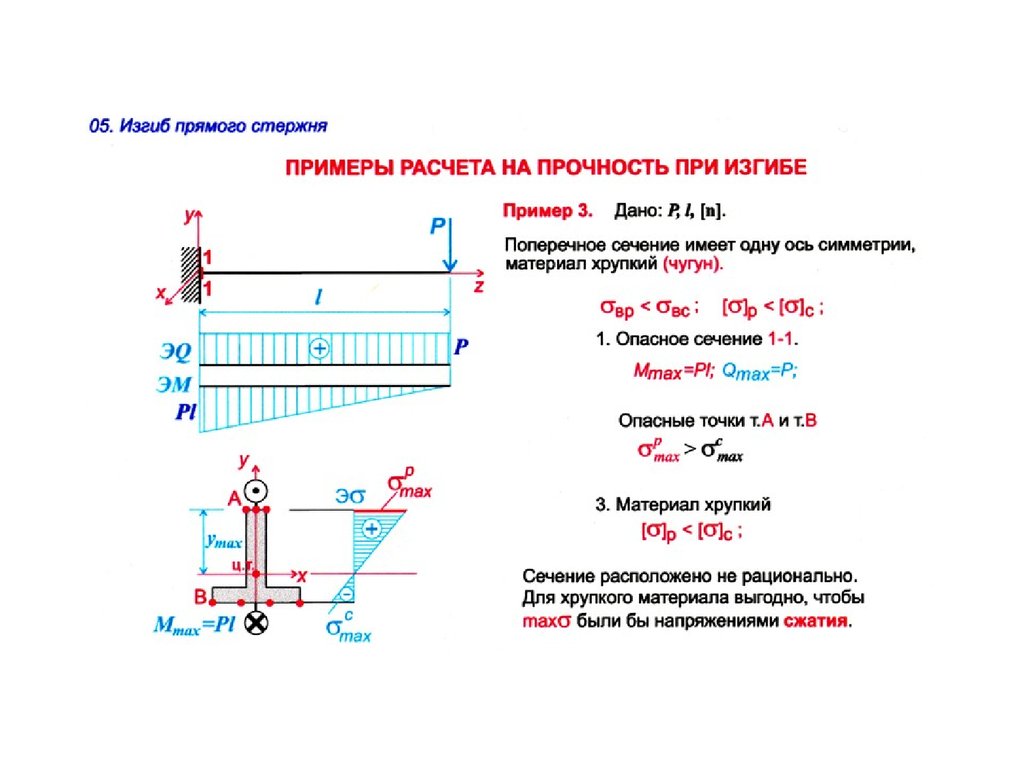 2 2 2 2 8 8 h 20

    Подставив значение S xотс  в формулу (18), получим  zy

    b Qz  ( h 2  4 y 2 ) Qz ( h 2  4 y 2 ) 8 .   8I X IXb

    (19)

    Уравнения равновесия для плоской задачи без учета компонента объемных сил имеют вид  y

     zy

      0 y z  .  yz  z   0  y z 

    (20)

    Из первого уравнения системы уравнений (20) следует, что  zy   yz   

     z y  c1, z

    (21)

    тогда, используя уравнение (17), получим  z M z y Qz     y. z z I x I x

    (22)

    Решая совместно уравнения (22) и (21), получим  zy   

    Qz yy  c1. Ix

    (23)

    Постоянную интегрирования определим из граничных усh ловий при y   , zy = 0: 2

    Qz h 2 Q h3   c1  0 и c1  z . 2I x 4 8I x

    (24) 21

    Совместное решение (23) и (24) дает  zy 

    Qz 2 ( h  4 y 2 ). 8I x

    (25)

    Выражение для zy полностью совпадает с уравнением (19), полученным с помощью методов сопротивления материалов.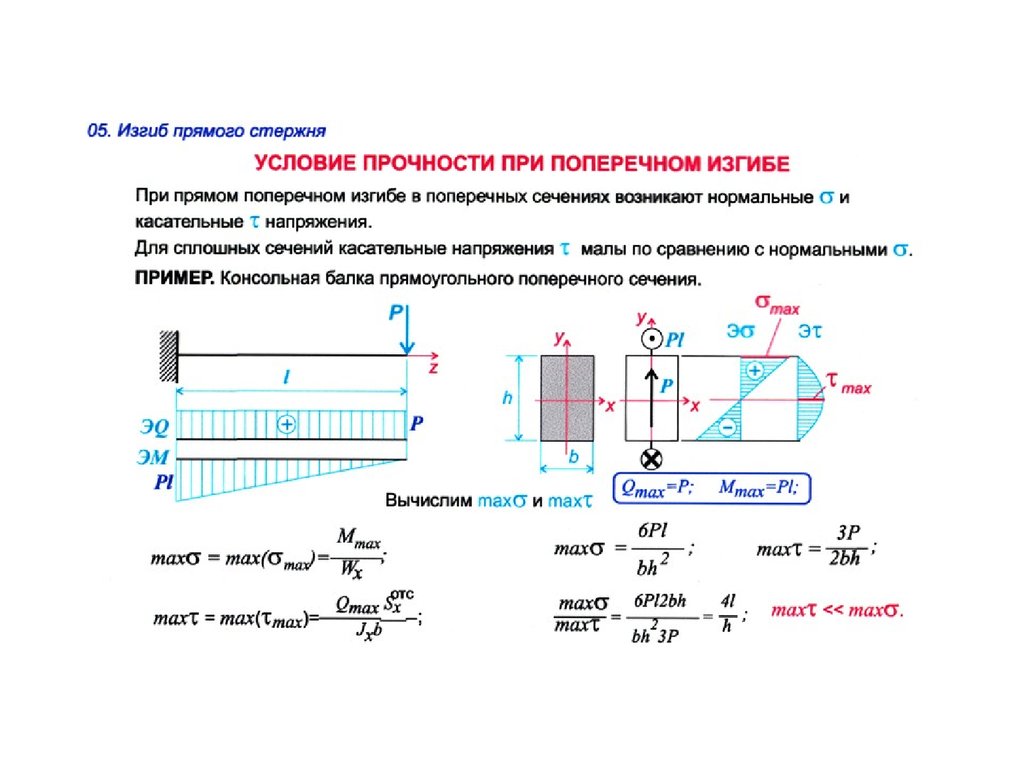 Из второго уравнения системы уравнений (20) следует, что  y  

     zy z

     zy z

    y  c2 ,

    q Qz 1 (h 2  4 y 2 )  z (h 2  4 y 2 ),  8I x z 8 I x

    (26)

    (27)

    где qz – интенсивность распределенной нагрузки в рассматриваемом слое изгибаемой балки, значение которой можно рассматривать как величину касательных напряжений zy в данном слое (рис. 11).

    Рис. 11. Вариант эквивалентности zy и qz

    22

    Решая совместно уравнения (25) и (26) получим  y  

    qz 2 ( h  4 y 2 ) y  c2 , 8I x

    y  

    qz 2 4 ( h y  y 3 )  c2 . 8I x 3

    С учетом того, что в рассматриваемом слое qz   zy , получим y  

    Qz 2 1 4 (h  4 y 2 )  ( h 2 y  y 3 )  c2 . 8I x 8I x 3

    После ряда преобразований получим y  

    Qz 4 ( h 2  4 y 2 )( h 2 y  y 3 )  c2 . 2 3 64 I x

    Значение постоянной с2 определим из граничного условия h y   , y = 0  с2 = 0. 2 В итоге получаем окончательное уравнение для определения нормальных напряжений в сечениях балки, вызванных надавливанием горизонтальных слоев балки при плоском поперечном изгибе: y 

    Qz 4 ( h 2  4 y 2 )( y 3  h 2 y ).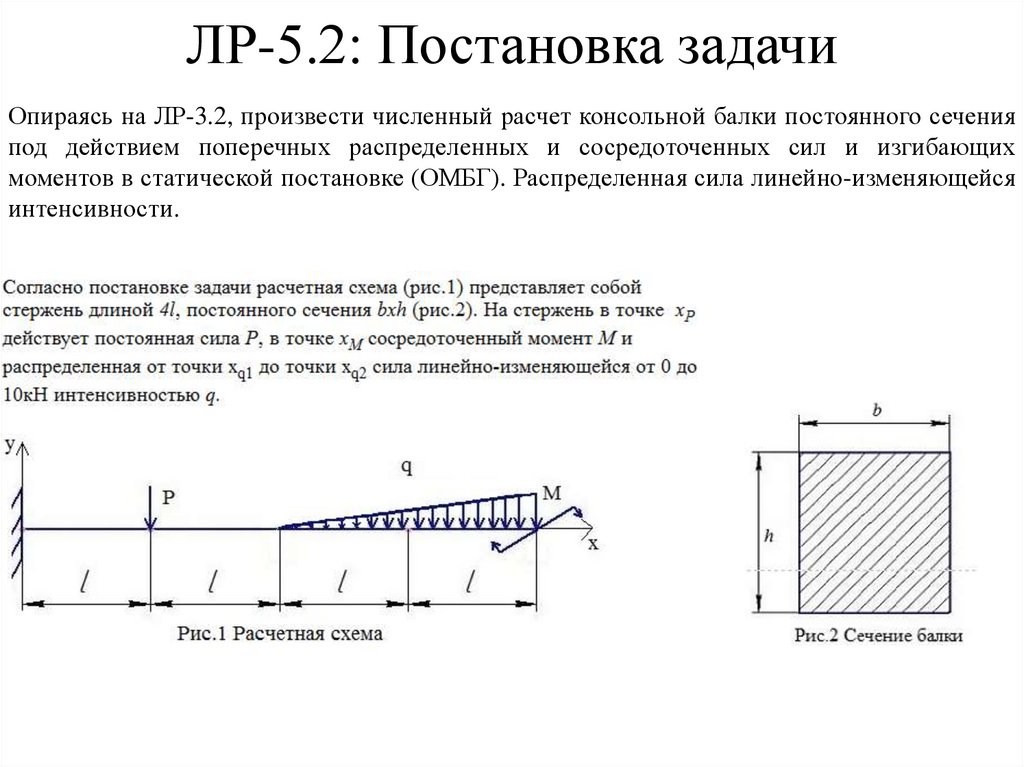 2 3 64 I x

    (28)

    Эпюры распределения нормальных и касательных напряжений по высоте сечения балки, полученные по формулам (25) и (28) приведены на рис. 12 для положительного значения поперечной силы Qz. 23

    Рис. 12. Распределение касательных и нормальных напряжений по высоте сечения балки

    Из приведенных на рис. 12 эпюр следует, что при y = 0 и при y = ±h / 2 нормальные напряжения в продольных волокнах стержня y будут равны нулю и достигают своего максимального значения при y = ±h / 4. Изменения этих напряжений по высоте бруса описывается кубической параболой в соответствии с формулой (28).

    24

    Список литературы

    1. Феодосьев, В. И. Сопротивление материалов / В. И. Феодосьев. – М. : Наука, 1972. – 541 с. 2. Сопротивление материалов / Г. С. Писаренко [и др.]. – Киев : Технiка, 1967. – 783 с. 3. Тимошенко, С. П. Теория упругости / С. П. Тимошенко, Дж. Гудьер. – М. : Наука, 1972 – 559 с.

    25

    Содержание

    Введение …………………… ………………………………………………………. 3 1. Теоретический расчет нормальных напряжений ………………. 4 2. Касательные напряжения при плоском поперечном изгибе……………………………………………………………. 11 3. Пример расчета составной консольной балки с разными значениями модуля Юнга …………………………………. 14 4. Нормальные напряжения при плоском изгибе прямого стержня, возникающие в результате надавливания волокон друг на друга …………………………………. 19 Список литературы …………………………………………………………… 25

    26

    Учебное издание

    ДУДЯК Александр Иванович ХМЕЛЕВ Александр Афанасьевич САХНОВИЧ Татьяна Александровна ГУРКОВСКАЯ Ольга Игоревна ОСОБЕННОСТИ РАСЧЕТА НА ПРОЧНОСТЬ СОСТАВНЫХ БАЛОК ИЗ НЕОДНОРОДНЫХ МАТЕРИАЛОВ Учебно-методическое пособие для студентов специальности 1-36 01 03 «Технологическое оборудование машиностроительного производства» Редактор Т. А. Зезюльчик Компьютерная верстка Н. А. Школьниковой Подписано в печать 19.06.2013. Формат 6084 1/16. Бумага офсетная. Ризография. Усл. печ. л. 1,57. Уч.-изд. л. 1,23. Тираж 100. Заказ 350. Издатель и полиграфическое исполнение: Белорусский национальный технический университет. ЛИ № 02330/0494349 от 16.03.2009. Пр. Независимости, 65. 220013, г. Минск.

    27

    Расчет конструкций. Изгиб консольной балки

    $\begingroup$

    Каким образом изгиб консольной балки может быть отрицательным, если некоторые статические методы говорят об обратном, при условии, что я применяю их правильно?

    1. Когда я использовал метод функций сингулярности, я получил положительную изгиб на фиксированном конце.
    2. Опять же, используя уравнения равновесия, я выяснил, что изгиб при фиксированный конец положительный.

    Теперь, соблюдая концепцию, изгиб считается положительным всякий раз, когда возникает сжатие в верхних волокнах балки и растяжение в нижних волокнах балки, и наоборот.

    1. Учитывая искривленную форму консольной балки, видно, что верхние волокна балки удлиняются, а нижние волокна укорачиваются. Следовательно, изгиб должен быть отрицательным.
    2. Кроме того, при использовании графического метода гибка начинается положительно, если предположить, что подход, который я избрал, правильный, но как он может равна нулю на свободном конце, если разность (полученная из площади СФО положительный? Другими словами, [+Ma +(+разница)] должно быть положительным значением, а не нулем.
    3. Наконец, анализируя концепцию о том, что БМД является интегралом СФД, при интегрировании SFD или кривой должен быть положительный результат не негатив.

    Возможная интерпретация, которую я получил, состоит в том, что я предположил противоположный смысл мгновенной реакции.

    • структурный анализ

    $\endgroup$

    $\begingroup$

    «. ..изгиб считается положительным, когда возникает сжатие верхних волокон балки и растяжение нижних волокон балки и наоборот.»

    Из приведенного выше утверждения делаем вывод, что изгибающий момент на консольной балке может быть только положительным или отрицательным, поскольку изогнутая форма консоли обычно образует «единую кривизну», для которой знак остается постоянным по всей ее длине .

    Обратите внимание, что «система координат» может искажать результаты и давать разные знаки моменту. Но путаницы не должно возникнуть, если использовать согласованную систему координат и придерживаться соглашения о знаках, указанного в самом начале.

    $\endgroup$

    Зарегистрируйтесь или войдите в систему

    Зарегистрируйтесь с помощью Google

    Зарегистрироваться через Facebook

    Зарегистрируйтесь, используя электронную почту и пароль

    Опубликовать как гость

    Электронная почта

    Требуется, но не отображается

    Опубликовать как гость

    Электронная почта

    Требуется, но не отображается

    Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

    .

    Анализ консольных лучей при изгибной нагрузке

    Исполнительные программы

    Семинары

    Проекты

    Карьера

    Найдите рабочие места

    для бизнеса / университеты

    Най. Все курсы

    Выберите категорию

    Загрузка…

    Все курсы

    Все курсы

    Расчет консольных балок под действием изгибающей нагрузки один конец к (обычно вертикальной) опоре, из которой он выступает; это соединение также может быть перпендикулярно плоской вертикальной поверхности, такой как стена. Консоли также могут…

    Детали проекта

    Загрузка…

    Оставить комментарий

    Спасибо, что решили оставить комментарий. Пожалуйста, имейте в виду, что все комментарии модерируются в соответствии с нашей политикой комментариев, и ваш адрес электронной почты не будет опубликован по соображениям конфиденциальности. Пожалуйста, оставьте личный и содержательный разговор.

    Пожалуйста, войдите, чтобы добавить комментарий

    Другие комментарии…

    Комментариев пока нет!
    Оставьте первый комментарий

    Подробнее Проекты Пранава Паранджапе (49о`. Обратите внимание на характерные схемы потока в каждой конфигурации. Определить изменение коэффициента аэродинамического сопротивления при изменении угла наклона.…

    03 января 2021 г. 19:45 IST

    Подробнее

    Численный анализ квазиодномерного потока через сужающееся расходящееся сопло с использованием метода МакКормака

    Цель:

    Аннотация Численный анализ одномерного дозвукового сверхзвукового изоэнтропического течения через сужающееся-расширяющееся сопло выполнен с использованием метода Мака Кормака с использованием MATLAB. Численное исследование проводится при двух методах формулировки, т. е. консервативной форме и неконсервативной форме. В…

    17 дек. 2020 03:40 IST

    • MATLAB

    Подробнее

    Анализ обтекания двумерного цилиндра Механика жидкости. Целью данного моделирования является анализ характеристик обтекания двумерного цилиндра и изучение формирования вихревой дорожки фон Кармана для различных чисел Рейнольдса в переходных условиях. Симуляция завершена…

    03 сентября 2020 г. 12:43 IST

    Подробнее

    Затухающие колебания простого маятника

    Цель:

    https://projects.skill-lync.com/projects/Damped-Simple-Pendulum-4

    15 января 2020 г. 02:19 AM IST

    Читать Подробнее

    Анализ данных с использованием Python

    Цель:

    Анализ данных, используя введение Python. Когда выполняется большое моделирование, он генерирует огромное количество данных, в которых поиск необходимых данных. становится практически невозможным. Чтобы упростить…

    15 января 2020 г. 02:19 AM IST

    • Python

    Читать Подробнее

    Решение оды второго порядка для демпфированных колебаний простых маятников

    Объектива:

    Решение второго порядка для затухающей осме Простой маятник. В механике и физике простое гармоническое движение – это особый тип периодического движения колебаний при котором возвращающая сила прямо пропорциональна перемещению и действует в направлении, противоположном …

    15 января 2020 г. 02:19 IST

    • MATLAB

    Читать далее

    Моделирование обтекания аэродинамическим профилем

    Цель:

    /Flow-Skill-projects/com-projects. skills.s://projects.ss://projects.s.s.s. over-an-Airfoil-16924

    15 января 2020 г. 02:19 IST

    Подробнее

    Простой затухающий маятник

    Цель:

    Решение ОДУ второго порядка для затухающих колебаний простого маятника и в механике простое гармоническое движение — это особый тип периодического движения колебаний, при котором возвращающая сила прямо пропорциональна смещению и действует в направлении, противоположном…

    15 января 2020 г. 02:19 IST

    • MATLAB

    Подробнее

    Анализ системы планетарной передачи

    Цель:

    /Alysis-nalysis-ofc.com/projects-lynofc.skill-lyn Planetary-Gear-System-084429

    15 января 2020 г. 02:19 AM IST

    Читать Подробнее

    Подгонка кривой с использованием Python

    Объектива:

    Подгонка Кривая Кривая. , который лучше всего подходит для ряда точек данных, возможно, с учетом ограничений. Подгонка кривой может включать интерполяцию,…

    15 января 2020 г. 02:19 IST

    Подробнее

    Обтекание цилиндра

    Цель:

    Цель Целью этого проекта является выполнение анализа моделирования течения в цилиндре произвольного диаметра и длины при произвольном Число Рейнольдса, а затем выполните тот же анализ, увеличив число Рейнольдса на 20%, 40% и 100%, а затем сравнив результаты и наблюдения. Уравнение `R_e=(rho*V*d)/mu`…

    15 января 2020 г. 02:19 IST

    Подробнее

    2R МОДЕЛИРОВАНИЕ РУКОЯТКИ РОБОТА

    Цель:

    СИМУЛЯТОР РУКОЯТКИ 2R С ИСПОЛЬЗОВАНИЕМ ПРЯМОЙ КИНЕМАТИКИ ПРЯМАЯ КИНЕМАТИКА  Прямая кинематика относится к использованию кинематических уравнений робота для вычисления положения на основе заданных значений конечного эффектора. параметры сустава. Этот кинематический робот в основном представляет собой комбинацию…

    15 января 2020 г. 02:19 IST

    • MATLAB

    Подробнее

    ВИЗУАЛИЗАЦИЯ ЦИКЛА ОТТО — ИСПОЛЬЗОВАНИЕ PYTHON

    Цель:

     ВИЗУАЛИЗАЦИЯ ЦИКЛА ОТТО  ВВЕДЕНИЕ В СТАНДАРТНЫЙ ЦИКЛ ВОЗДУХА В газовом энергетическом цикле рабочая жидкость остается газом на протяжении всего цикла. Двигатели с искровым зажиганием и дизельные двигатели являются известными примерами устройств, работающих на газовых циклах. Во всех этих двигателях энергия обеспечивается за счет сжигания топлива и воздуха в замкнутом…

    15 Jan 2020 02:19 IST

    • PYTHON

    Подробнее

    Определение глобальных максимумов функции сталагмита

    Цель:

    Определение глобальных максимумов функции сталагмита Введение в генетический алгоритм Генетический алгоритм — это метод решения задач оптимизации с ограничениями и без ограничений, основанный на естественном отборе — процессе, управляющем биологической эволюцией. Генетический алгоритм многократно изменяет популяцию…

    15 января 2020 г. 02:19 IST

    • MATLAB

    Подробнее

    Моделирование клапанного механизма двигателя внутреннего сгорания

    Цель:

    Введение Двигатель внутреннего сгорания работает на управляемом сгорании топлива в цилиндре. Впуск топлива в цилиндр и выпуск отработавших газов из цилиндра допускается через впускной и выпускной клапаны, продолжительность открытия и закрытия которых специально рассчитана по времени, а его движение регулируется…

    15 января 2020 г. 02:19 IST

    Подробнее

    Анализ потери устойчивости в стенде циклонного сепаратора

    Задача:

    Введение Циклонные сепараторы или просто циклоны представляют собой сепарационные устройства (сухие скрубберы), которые используют принцип инерции для удаления твердых частиц из дымовых газов.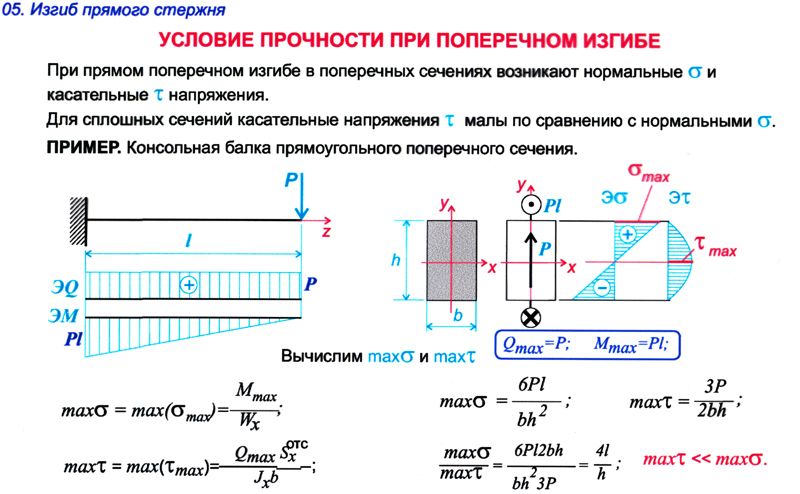 Циклонные сепараторы являются одним из многих устройств для контроля загрязнения воздуха, известных как предварительные очистители, поскольку они обычно удаляют более крупные частицы твердых частиц.…

    15 янв.

    Цель:

    https://projects.skill-lync.com/projects/Calculation-of-Global-Maximum-of-a-Stalagmite-Function-15276

    15 января 2020 г. 02:19 AM IST

    Читать Подробнее

    Votto Visualization с использованием Python

    Цель:

    https://projects.skill-lync.com/projects/otto-cycle-visualization-05960

    15 января 2020 г. 02:19 IST

    Читать дальше

    MBD моделирование узла поршня

    Цель:

    Введение Анализ движения поршня — это анализ узла поршня и кривошипа, состоящего из головки поршня, поршневого пальца и шатуна. , торцевая крышка и кривошип. Цель Спроектировать части узла поршня и кривошипа, собрать их и смоделировать их движение, ограничивая степени свободы каждого…

    15 января 2020 г. 02:19 IST

    Подробнее

    Моделирование течения в трубе

    Цель:

    Введение Когда жидкость течет по трубе, создается градиент скорости из-за коэффициента трения материала трубы и из-за вязкости жидкости. При диаметральном рассмотрении скорость потока жидкости постепенно увеличивается от одной поверхности, достигает максимума и…

    15 янв. 2020 02:19 IST

    Подробнее

    ВИЗУАЛИЗАЦИЯ ЦИКЛА ОТТО

    Цель:

                 ВИЗУАЛИЗАЦИЯ ЦИКЛА ОТТО   ВВЕДЕНИЕ В СТАНДАРТНЫЙ ЦИКЛ ВОЗДУХА В газовом энергетическом цикле рабочая жидкость остается газом на протяжении всего цикла. Двигатели с искровым зажиганием и дизельные двигатели являются известными примерами устройств, работающих на газовых циклах. Во всех этих двигателях энергия равна…

    15 Jan 2020 02:19 IST

    • MATLAB

    Подробнее

    Внутренний женевский колесный механизм

    Задача:

    https://projects.skill-lync.com/projects/Internal-Geneva-Mechanism-17310

    15 января 2020 г. 02:19 IST

    Подробнее

    Обтекание цилиндра 900 Объектив 900 :

    https://projects.skill-lync.com/projects/Flow-over-a-Cylinder-29886

    15 января 2020 г. 02:19 IST

    Подробнее

    Определение минимального давления методом Ньютона-Рафсона

    Цель:

    Разбивание льда с помощью транспортного средства на воздушной подушке. Определение минимального давления методом Ньютона-Рафсона. Введение в транспортное средство на воздушной подушке. и даже на суше в полярных странах. Этот автомобиль использует давление воздуха…

    15 янв. 2020 02:19 IST

    Подробнее

    Решение ОДУ второго порядка для затухающих колебаний маятника

    Цель:

    Решение ОДУ второго порядка для затухающих колебаний маятника и простого механического маятника В физике простое гармоническое движение – это особый тип периодического движения колебаний при котором возвращающая сила прямо пропорциональна смещению и действует в направлении, противоположном …

    15 января 2020 г. 02:19 IST

    • MATLAB

    Подробнее

    Внутренний женевский механизм

    Задача:

    Задача: Собрать ведущее и ведомое колеса и частично их собрать. Проанализируйте сборку при различных скоростях вращения и усилиях. Проанализируйте разницу в контактных усилиях с «Точным контактом» и без него. Наблюдайте за изменением угловой скорости во времени. Введение Женевский драйв или Мальта…

    15 января 2020 г. 02:19 IST

    Подробнее

    Анализ системы планетарной передачи

    Цель:

    Цель Построение системы планетарной передачи с четырьмя сателлитами, закрепленными на водиле, и анализ угловых скоростей входной и выходной шестерен. Введение Система планетарной трансмиссии (или эпициклическая система, как ее также называют) обычно состоит из солнечной шестерни с центральным поворотом, зубчатого венца и нескольких… ВЕЛОСИПЕД

    Цель:

    ПРОЕКТ: СИЛА СОПРОТИВЛЕНИЯ ВЕЛОСИПЕДА Введение Когда тело движется в жидкости или когда жидкость движется над телом, жидкость оказывает на тело некоторую силу.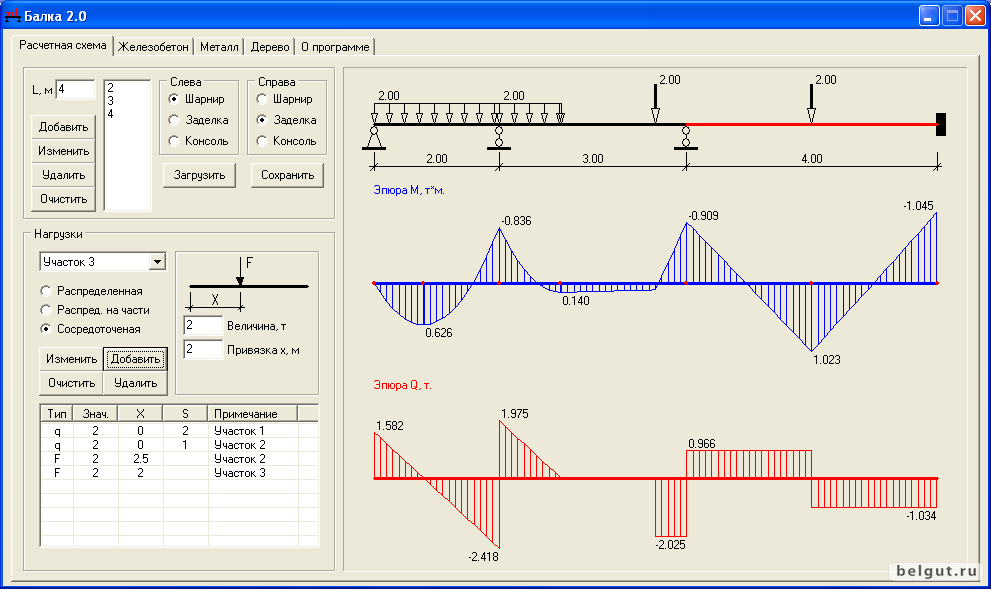 Суммарная сила, действующая на поверхность, будет перпендикулярна поверхности. Эта сила может быть разделена на две составляющие, одна из которых действует в направлении движения под названием «DRAG…»0003

    Цель:

    https://projects.skill-lync.com/projects/Frequency-Analysis-of-a-Rotating-Shaft-98142

    15 января 2020 г. 02:19 IST

    Подробнее

    ДАННЫЕ АНАЛИЗ С ИСПОЛЬЗОВАНИЕМ PYTHON

    Цель:

    https://projects.skill-lync.com/projects/DATA-ANALYSIS-USING-PYTHON-45949

    15 янв. далее

    Подбор кривой с использованием Python

    Цель:

    https://projects.skill-lync.com/projects/Curve-Fitting-Using-Python-62263

    15 января 2020 г. 02:19 IST

    Подробнее

    Анализ консольных балок под действием изгибающей нагрузки

    Цель :

    Анализ консольных балок под действием изгибающей нагрузки Введение Консоль — это жесткий конструктивный элемент, такой как балка или пластина, прикрепленный одним концом к (обычно вертикальной) опоре, из которой он выступает; это соединение также может быть перпендикулярно плоской вертикальной поверхности, такой как стена. Консоли также могут…

    15 янв. 2020 02:19 IST

    Подробнее

    РАСЧЕТ СИЛЫ СОПРОТИВЛЕНИЯ ВЕЛОСИПЕДА С ИСПОЛЬЗОВАНИЕМ PYTHON

    Цель:

    ПРОЕКТ: СИЛА СОПРОТИВЛЕНИЯ ВЕЛОСИПЕДА Введение Когда тело движется внутри Введение жидкость движется по телу, жидкость действует на тело с некоторой силой. Суммарная сила, действующая на поверхность, будет перпендикулярна поверхности. Эта сила может быть разделена на две составляющие, одна из которых действует в направлении движения, называемом «ТРАССИРОВАТЬ…»

    15 января 2020 г. 02:19AM IST

    • PYTHON

    Подробнее

    Проектирование и анализ центробежных насосов с помощью Solidworks

    Цель:

    https://projects. skill-lync.com/projects/Centrifugal-Apump-Design-and

    Затухающие колебания простого маятника представляет собой особый тип периодического движения колебаний, при котором возвращающая сила прямо пропорциональна смещению и действует в направлении, противоположном …

    15 января 2020 г. 02:19 IST

    • MATLAB

    Читать далее

    Моделирование и симуляция потока через Flowbench

    Цель:

    Цель:

    Цель проекта:

    и анализ двойной. Выполнение параметрического теста на сеточную зависимость анализа. После того, как определили лучшую сетку, проанализировали характеристики потока при различных подъемах клапанов с этой сеткой. Введение Поток…

    15 января 2020 г. 02:19 IST

    Подробнее

    Моделирование обтекания аэродинамического профиля

    Цель:

    Цель атаке и сравните подъемную силу и силу сопротивления при каждом угле атаки. Ссылка на текстовый файл аэродинамического профиля NACA-0017: https://drive.google.com/open?id=1LoEW9AmcWjdCEFWbrYi9Y1b16Vq8-pBi.0002 Читать далее

    2R Моделирование манипулятора робота с использованием Python

    Цель:

    2R СИМУЛЯТОР РОБОТО-РУКИ С ИСПОЛЬЗОВАНИЕМ ПРЯМОЙ КИНЕМАТИКИ. значения параметров соединения. Этот кинематический робот в основном представляет собой комбинацию…

    15 янв.0003

    Цель:

    https://projects.skill-lync.com/projects/Parsing-NASA-thermodynamic-data-57639

    15 января 2020 г. 02:19 IST

    Подробнее

    Моделирование клапана двигателя внутреннего сгорания train

    Задача:

    https://projects.skill-lync.com/projects/Simulation-of-IC-Engine-valve-train-88949

    15 января 2020 г. 02:19 IST

    Подробнее

    Разрушение льда на воздушной подушке. Транспортное средство. Определение минимального давления методом Ньютона-Рафсона

    Цель:

    https://projects.skill-lync.com/projects/Breaking-Ice-with-Air-cushion-Vehicle-Finding-minimum-pressure-with-Newton-Raphson-method-21445

    15 Январь 2020 г. 02:19 IST

    Подробнее

    MBD-анализ узла поршня

    Цель:

    https://projects.skill-lync.com/projects/MBD-simulation-of-Piston-assembly-63392 Ссылка на детали и сборку: https://drive.google.com/open?id=1DhdS6gK0X_AXWH-zE9pLmBK36PR41YsP

    15 янв. 2020 02:19 IST

    Подробнее

    Определение глобальных максимумов функции сталагмита

    Цель:

    Определение глобальных максимумов функции сталагмита Введение в генетический алгоритм и задачи неограниченной оптимизации, основанные на естественном отборе, процессе, управляющем биологической эволюцией. Генетический алгоритм многократно изменяет популяцию…

    15 Jan 2020 02:19AM IST

    • MATLAB

    Подробнее

    Частотный анализ вращающегося вала

    Цель:

    ВВЕДЕНИЕ Вал — это вращающийся элемент машины, обычно круглого сечения, который используется для передачи мощности от одной части. к другому или от машины, производящей энергию, к машине, поглощающей энергию. Материал, обычно используемый для обычных валов, представляет собой мягкую сталь. В основном они классифицируются…

    15 января 2020 г. 02:19 IST

    Подробнее

    Проектирование и анализ центробежного насоса с использованием Solidworks

    Цель:

    Цель Целью этого проекта является проектирование центробежного насоса, моделирование потока и анализ его производительности. Введение Центробежные насосы используются для транспортировки жидкостей путем преобразования кинетической энергии вращения в гидродинамическую энергию потока жидкости. Энергия вращения…

    15 янв. 2020 02:19 IST

    Подробнее

    Моделирование и симуляция потока через Flowbench

    Цель:

    https://projects.skill-lync.com/projects/Modelling-and-Simulation-of-flow-through-a-Flowbench-18272

    15 января 2020 г. 02:19 IST

    Читать Подробнее

    Кривая подгонка

    Цель:

    Подгонка кривой ввода. Кривая подгонка — это процесс построения кривой или математической функции, который наилучшим образом подходит для…

    15 января 2020 02:19 IST

    Подробнее

    0003

    Анализ термодинамических данных НАСА

    Цель:

    Анализ термодинамических данных НАСА   Введение   Для расчета термодинамических свойств определенных элементов или молекул НАСА разработало набор коэффициентов, которые очень хорошо подходят для определенного диапазона температур.