Расчет нагрузки двутавровой балки – максимальные значения + Видео
Расчет нагрузки двутавровой балки проводится для определения номера из списка сортамента при проектировании несущих конструкций зданий и сооружений. Расчет производится согласно формулам и таблицам, а полученные параметры влияют на процесс проектирования и строительства, а также дальнейшие эксплуатационные характеристики конструкции.
1 Применение двутавровой балки и основные параметры
Основная функция двутавра при проектировании различных зданий и сооружений – создание надежной и эффективной несущей конструкции. В отличии от бетонных вариантов несущих конструкций, использование двутавровой балки позволяет добиться увеличения ширины пролетов жилых или коммерческих зданий и уменьшить массу основных несущих конструкций. Таким образом, существенно повышается рентабельность строительства.
Двутавровое балки
Двутавровый швеллер выбирается, исходя из длины и веса. Балки могут быть горячекатаными стандартными или специальными и иметь параллельные или наклонные грани полок.
Масса двутавра рассчитывается согласно таблице сортамента, в которой указан конкретный номер и маркировка двутавровой балки, а также показатели ширины, высоты, толщины полок и средняя толщина стенок профиля. Таким образом, для определения массы, согласно таблице, необходимо знать нормативный вес одного погонного метра. Например, балка с номером 45, при весе погонного метра 66,5 кг, имеет длину 15,05 метров.
Помимо расчета массы, который можно провести, используя простой калькулятор, в процессе проектирования необходимо рассчитать максимальную и минимальную нагрузку на изгиб и прогиб (деформацию), чтобы выбрать подходящую под конкретные цели строительства двутавровую балку.
- минимальное и максимальное расстояние между полками (стенками) балки с учетом их толщины;
- максимальная нагрузка на будущую конструкцию перекрытия;
- тип и форма конструкции, метод крепления;
- площадь поперечного сечения.
В некоторых случаях для проведения расчетов может понадобиться и шаг укладки, то есть расстояние, через которое балки укладываются параллельно друг другу.
Расчет двутавровой балки, как правило, производится на прочность и прогиб. Для максимально точных расчетов в таблице сортамента и нормах ГОСТ прописаны и такие необходимые параметры, как момент сопротивления, который делится на статистический и осевые моменты. Помимо этого, иногда необходимо знать величину расчетного сопротивления, которая зависит от типа и марки стали, из которой изготовлена двутавровая балка, а также от типа производства (сварная или прокатная). В случае сварного профиля при расчете прочности прибавляется до 30 процентов к вычисленной несущей нагрузке профиля.
2 Выбор металлической балки по номеру и примеры расчета
В таблице сортамента все номера металлического двутавра указаны согласно нормам ГОСТ 823989. Таким образом, выбор номера должен осуществляться с учетом предполагаемой нагрузки на балку, длины пролетов, веса. Например, если максимальная нагрузка на двутавровую балку равна 300 кг/м.п, из таблицы выбирается балка номер 16, при этом пролет будет равен 6 метрам при шаге укладки от 1 до 1,2 метров. При выборе 20-го профиля максимальная нагрузка увеличивается до 500 кг/ м.п, а шаг может быть увеличен до 1,2 метра. Профиль с номерами 10 или 12 означает максимально допустимую нагрузку до 300 кг/м.п и сокращение пролета до 3-4 метров.
Применение балок в строительстве
Таким образом, расчет того, какую нагрузку выдерживает балка, производится так:
- определяется величина нагрузки, которая давит на перекрытие с учетом веса самого профиля (из таблицы), которая рассчитывается на 1 погонный метр профиля;
- полученная нагрузка, согласно формуле, умножается на показатель коэффициента надежности и упругости стали, который прописан в ГОСТ 823989;
- используя таблицу расчетных значений по ГОСТ, необходимо определить величину момента сопротивления;
- исходя из момента сопротивления, выбираем соответствующий номер из таблицы сортамента.
Рассчитывая несущую нагрузку при выборе профиля, рекомендуем выбирать номера балки на 1-2 пункта выше полученных расчетных значений. Несущая способность профиля также рассчитывается при определении нагрузки двутавровой балки на изгиб.
3 Как марки стали влияют на расчеты?
При расчете прочности несущей балки в обязательном порядке учитывается марка стали, которая использовалась в процессе производства, и тип производственного проката. Для сложных конструкций и возведения перекрытий жилых зданий, коммерческих помещений, мостов необходимо выбирать балки из максимально прочных марок стали. Изделия с более высокой прочностью обладают меньшими габаритными размерами, но при этом способны выдерживать большие нагрузки.
Балки на производстве
Таким образом, расчет на прочность рекомендуется проводить несколькими способами, а полученные данные сравнить для получения максимально точных результатов вычислений. При определении прочности необходимо знать нормативные и расчетные напряжения и учитывать такие параметры, как поперечные и продольные силы, а также крутящие моменты.
4 Как вычислить нагрузку на деформацию?
Для определения нагрузки балки на деформацию необходимо учитывать такие параметры, как:
- расчетная и нормативная нагрузка;
- длина и вес перекрытия;
- нормативное сопротивление.
Двутавровые балки для строительства
При этом для некоторых типов балок невозможно рассчитать нагрузку на прогиб, ввиду их формы и видов крепления при строительстве. Следует также понимать, что деформация балки (прогиб) возникает в поворотных углах. Поэтому она сильно зависит от габаритов конструкции, ее назначения, марки стали и других свойств и показателей. Существует несколько формул и вариантов для расчета балки на прогиб, использование которых зависит от расчета деформации внизу и вверху балки. Чаще всего для того, чтобы вычислить максимальную нагрузку на прогиб, специалисты используют универсальную формулу.
Модуль упругости вычисляется, исходя из конкретной марки стали, момент инерции прописан в ГОСТе по номеру выбранной балки. Полученное число необходимо умножить на коэффициент, равный 0,013. В том случае, если рассчитанный относительный коэффициент деформации больше или меньше, чем прописано в нормативе, то в строительной конструкции необходимо использовать двутавры большего или меньшего типоразмера из таблицы.
Следует понимать, что двутавровая балка, ввиду своей формы, конструкции и веса, довольно редко используется в частном строительстве. Обычно вместо балок применяются более легкие швеллеры или стальные уголки. Но если вы все же используете балку для строительства небольшого частного дома, дачи, то необязательно проводить сложные расчеты по всем видам деформации и нагрузок.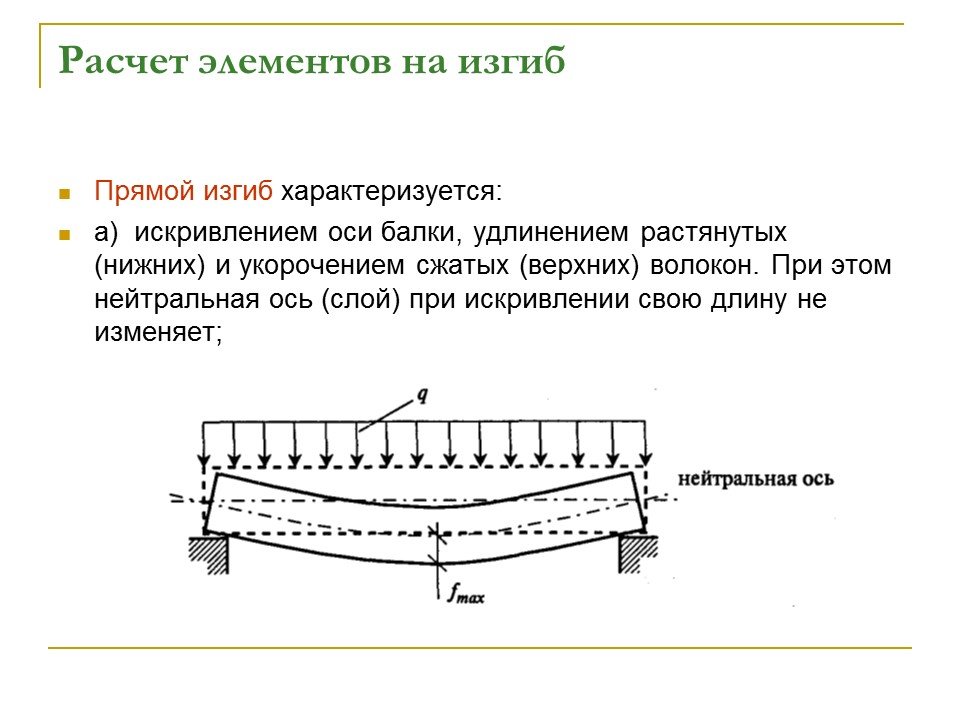
Для небольшой конструкции перекрытия достаточно рассчитать максимальную и минимальную нагрузку на изгиб.
Как построить — Выбор нужного двутавра
Благодаря своей особой Н-образной форме металлический двутавр является универсальным металлопрокатом, так как обладает повышенной степенью прочности и надежности. Двутавровые балки способны выдерживать существенные динамические и статические нагрузки и широко применяется при возведении строений в качестве вертикальных опор и горизонтальных перекрытий.
Классификация двутавровых балок по ГОСТу
Для двутавровых балок разработаны ГОСТы на основе теоретических и экспериментальных исследований по выявлению наиболее рациональных типов фасонных профилей и частоты их градации.
С возрастанием ширины пролета увеличивается высота стальных балок:
- прочность при шестиметровом пролете обеспечивает двутавр № 20 с высотой профиля 200 мм;
- при уменьшенном до 4 м расстоянии между стенами можно использовать двутавр № 16 с высотой 160 мм.
| Двутавр ГОСТ 8239-89 | Двутавр нормальный (Б) | Двутавр широкополочный (Ш) | Двутавр колонный (К) |
Классический двутавр с уклоном внутренних граней полок 6-12% (ГОСТ 8239-89) применяются главным образом в качестве элементов, работающих на изгиб, а также в составных сечениях колонн. Работа в качестве сжатых элементов (стоек, колонн) не эффективна ввиду малого момента инерции. Балки обозначаются в сортаменте по номерам, соответствующим высоте профиля в сантиметрах.
Двутавры с параллельными гранями полок (ГОСТ 26020-83, СТО АСЧМ 20-93) выпускаются трех основных типоразмеров:
- Нормальные балочные двутавры (Б), выпускаются высотой до 1000 мм, с шириной полок до 320 мм. Применяются для эксплуатация под средними нагрузками;
- Широкополочные двутавры (Ш), имеют высоту также до 1000 мм при максимальной ширине полок 400 мм. Могут использоваться для разрезки по продольной оси для получения таврогово профиля. Тавр укладывается на один пролет. Целый двутавровый профиль – на один или несколько пролетов. Эти металлоизделия очень массивны. Плюсом их использования является возможность использования в качестве самостоятельного элемента без применения усиливающих деталей;
- Колонные двутавры (К), их использование эффективно в колоннах зданий. Они имеют соотношение высоты к ширине полок 1:1 и максимальные размеры 400х400 мм. Это наиболее массивные профили. Имеют широкие, утолщенные полки и стенки. Применяются при устройстве большепролетных конструкций.
Применяются для эксплуатация под средними нагрузками;Типовые схемы расположения двутавра
Один из исходных параметров, учитываемых в расчетах, – схема закрепления балки и вид прилагаемой нагрузки. Большинство вариантов сводится к основным схемам:Расчет нагрузки
Перед началом расчета производят сбор сил, действующих на двутавровую балку.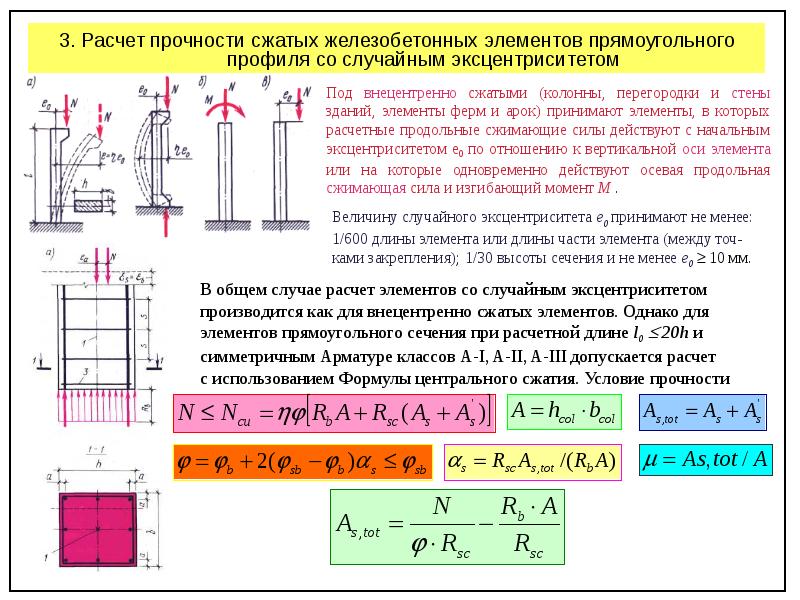
В зависимости от продолжительности воздействия, их разделяют на временные и постоянные. Расчет нагрузки на двутавровые балки представлен в таблице:
|
Постоянные |
Собственная масса балки и перекрытия. В упрощенном варианте вес межэтажного перекрытия без цементной стяжки с учетом массы балки принимают равным 350 кг/м2, с цементной стяжкой – 500 кг/м2 |
|
|
Длительные |
Полезные |
Зависят от назначения здания |
|
Кратковременные |
Снеговые, зависят от климатических условий региона |
|
|
Особые |
Взрывные, сейсмические. |
|
Для балок, работающих в стандартных эксплуатационных условиях, не учитываются. В онлайн-калькуляторах обычно не учитываются
Выделяют два типа нагрузки:
- Нормативные устанавливаются строительными нормами и правилами и расчетные;
- Расчетные равны нормативной величине, умноженной на коэффициент надежности.
При усилии менее 200 кг/м2 коэффициент обычно принимают равным 1,3, при более 200 кг/м2 – 1,2.
Шаг между балками принимают равным 1 м. В некоторых случаях, если это допустимо в конкретных эксплуатационных условиях, в целях экономии материалов его принимают равным 1,1 или 1,2 м.
При расчетах принимают во внимание марку стали. Для использования в условиях высоких нагрузок и при минусовых температурах востребованы двутавровые балки, изготовленные из низколегированных сталей.
Способы выбора оптимального размера сечения профиля
Наиболее точным вариантом подбора номера и типа двутаврового профиля является проведение профессиональных расчетов.
Именно этот способ применяется при проектировании ответственных крупногабаритных объектов. Для обеспечения надежности строения рекомендуется отдавать предпочтение профилю с большим номером.
Для примерного определения размера профиля можно воспользоваться таблицей соответствия номера двутавровой балки максимально допустимой нагрузке:
|
Общая нагрузка, кг/ м2 |
Длина пролета |
||||||||
|
3м при шаге: |
4 м при шаге: |
6м при шаге: |
|||||||
|
1м |
1,1м |
1,2м |
1м |
1,1м |
1,2м |
1м |
1,1м |
1,2м |
|
|
300 |
10 |
10 |
10 |
10 |
12 |
12 |
16 |
16 |
16 |
|
400 |
10 |
10 |
10 |
12 |
12 |
12 |
20 |
20 |
20 |
|
500 |
10 |
12 |
12 |
12 |
12 |
12 |
20 |
20 |
20 |
Из этой таблицы видно, что для двутавровой балки номер 10 максимальная длина пролета составляет 4 м при шаге 1,2 м, нагрузка – 400 кг/м2, для номера 16 длина пролета может достигать 6 м, нагрузка, которую он может выдержать, – 300 кг/м2, для профиля 20 – 6 м и нагрузка 400 кг/м2.
Рекомендованые товары
С помощью данного калькулятора Вы можете подобрать балку, которая выдержит необходимую нагрузку по одной из нижеуказанных схем. Блок: 1/5 | Кол-во символов: 161 Содержание
Балка на двух шарнирных опорах
Блок: 2/5 | Кол-во символов: 180 Блок: 2/3 | Кол-во символов: 73 Консольная балка
Блок: 3/5 | Кол-во символов: 150 Исходные данные Расчетная схема: Длина пролета (L) — минимальное расстояние между двумя крайними опорами или длина консоли. Расстояния (A и B) — расстояния от опор до мест приложения нагрузок. Для 3 схемы А равна длине консоли балки, опирающейся на 2 опоры. Нормативная и расчетная нагрузки — нагрузки, на которые рассчитывается квадратная труба. Рассчитать их можно с помощью следующих материалов: Fmax — максимально возможный прогиб согласно таблицы E.1 СНиПа «Нагрузки и воздействия». Некоторые из них выписаны в таблицу 1. Количество двутавров — этот показатель введен на случай, если балку перекрытия придется усилить еще такой же, положив ее рядом. То есть, если у вас одна балка, то указывается «один», если две рядом, то необходимо выбрать «две». Расчетное сопротивление Ry— для каждой марки стали он свой. Наиболее распространенные значения приведены в таблице 2. Размер двутавра — здесь следует выбрать профиль двутавра по тому или иному ГОСТу. РезультатWтреб — требуемый момент сопротивления профиля. Fmax — максимальный прогиб в сантиметрах, в зависимости от указанных в исходных данных ограничениях. Вес балки — масса одного погонного метра того или иного двутавра. Расчет по прочности: Wбалки — момент сопротивления выбранной трубы по ГОСТ 30245-2003. Если Wбалки > Wтреб, значит прочность балки обеспечена. Запас — если в данной графе значение с минусом (-), то балка по прочности не проходит, а если с плюсом (+), то здесь показано, на какой процент балка имеет запас прочности. Расчет по прогибу: Fбалки — прогиб, возникающий у рассчитываемой балки под действием нормативной нагрузки. Здесь стоит отметить, что если он превышает допустимый Fmax,то это не значит, что двутавр сломается. Просто прогнутая балка может выглядеть некрасиво. Главное, чтобы выполнялось условие по прочности. Запас — то же самое, что и по отношению к моменту сопротивления. Блок: 3/3 | Кол-во символов: 2329 Балка с вылетом на двух шарнирных опорах
Блок: 4/5 | Кол-во символов: 171 Другие виджеты разработчика:
Блок: 4/4 | Кол-во символов: 1953 Балка с жестким защемлением на опорах
| Не забудь поделиться с друзьями |
1.0.6 Онлайн калькулятор расчета веса и длины арматуры
ru/?view=calc/load_beam| Двутавровая балка ICJ-300L | Брус сухой строганный деревянный 100х240 мм | Цельный прямоугольный LVL брус 69х260 |
|---|---|---|
| Характеристики: Момент инерции 9 476,5 см4 Момент сопротивления 631,8 см3 Модуль упругости 12 000 МПа Расчетное сопротивление 22,0 МПа | Характеристики: Момент инерции 11 520,0 см4 Момент сопротивления 960,0 см3 Модуль упругости 9 000 МПа Расчетное сопротивление 14,0 МПа | Характеристики: Момент инерции 8 788,0 см4 Момент сопротивления 676,0 см3 Модуль упругости 14 000 МПа Расчетное сопротивление 26,5 МПа |
|
Производим расчет по первому предельному состоянию: (где, R — расчетное сопротивление изгибу, M-максимальный момент (M=q*L2/8; M=160*5,82/8=672,8 кНм), W-момент сопротивления) | ||
| R=M/W R=672,8 кНм/631,8*10-6 см3= 1,06 кНм2 = 10,6 МПа < Rрасч =22 МПа Выполнено. | R=M/W R=672,8 кНм/960*10-6 см3= 0,7 кНм2 = 7 МПа < Rрасч =14 МПа Выполнено. | R=M/W R=672,8 кНм/676*10-6 см3= 0,99 кНм2 = 9,9 МПа < Rрасч =26,5 МПа Выполнено. |
|
Производим расчет по второму предельному состоянию: (f/L < fпред/L | ||
| f/L=5*160*5,83 / (384*12000*105*9476,5*10-8)=0,00358 <fпред/L=0,004 Выполнено. | f/L=5*160*5,83/ (384*9000*105*11520*10-8)= 0,00392 <fпред/L=0,004 Выполнено. | f/L=5*160*5,83/ (384*9000*105*8788*10-8)= 0,00392 <fпред/L=0,004 Выполнено. |
| Вывод: все 3 материала с данными геометрическими характеристиками примерно равны по своей несущей способности и удовлетворяют условиям прогибов. | ||
| Сравним цены и эксплуатационные характеристики | ||
|
|
|
Расчет двутавра на прогиб и изгиб
Чаще всего для расчета высоты подпорки прибегают к помощи онлайн калькулятора, который автоматически проводит расчет всех необходимых параметров. Чтобы правильно подобрать тип кровельного элемента, нужно указать некоторые данные, а именно:
- сфера использования;
- шаг между элементами кровли;
- требуемая длина;
Затем вычисляется расчетная нагрузка согласно каркасному элементу:
- Система стропил – 220 кг/кв.м.
- Двутавровая балка перекрытия – 400 кг/кв.м.
Цена изделия варьируется от габаритов балки и материала, из которого создана полка (натуральное дерево, брус LVL).
Монтажный процесс
Чаще всего наиболее приемлемым способом установки деревянных двутавров является фиксация на специальные кронштейны, со специальной симметричной конструкцией. На противоположных сторонах изделие снабжено крепежным приспособлением и пластиной, фиксирующейся напротив аналогичного крепежного элемента.
Схема сборки перекрытия из двутавровой балки
Учитывая габариты, а если быть уж совсем точными, высоту комбинированной балки из дерева и стружечной плиты, элемент конструкции может комплектоваться крепежами разной длины.
Правила техники безопасности
Выполняя монтажные работы по установке двутавровых балок, изначально их нужно закрепить при помощи временных элементов, которые затем меняют на постоянные стационарные фиксаторы. По технике безопасности категорически запрещается начинать эксплуатацию балок, пока мастера не снабдят их обвязкой, и не будут сняты временные держатели.
Демонтаж можно проводить лишь после того, как мастера удостоверятся в наличие обвязки на балках. Закрепленные исключительно временными фиксаторами, двутавровые перекрытия способны выдержать только вес рабочих и монтажного оборудования. Очень важно знать, бракованные или деформированные балки не ремонтируются собственноручно или на производстве и не могут быть установлены на свои посадочные места, ни при каких обстоятельствах.
Перевозка и хранение
Во время перемещения перекрытия, его ни в крем случае нельзя пригружать по малой оси, иначе материал может прогнуться и искривиться. При погрузке балок их нельзя бросать, а только аккуратно складывать. Хранятся опоры под навесами и в крытых складах. Если нет такой возможности, и конструкционные элементы лежат на улице под небом, для этого их нужно защитить от попадания ультрафиолета и осадков специальным материалом.
Начало статьи в предыдущей статье.
Двутавр прочность на изгиб. Вес двутавровой балки – важный фактор несущей способности
Технические характеристики металлического профиля необходимы, чтобы их правильно применять в строительстве, ведь несмотря на большое разнообразие сфер применения, суть остается одна – создать надежную несущую конструкцию. Она позволяет преобразовывать архитектуру сооружений:
- увеличивает ширину пролетов зданий;
- значительно, примерно на 35%, уменьшить массу несущих конструкций;
- существенно увеличить рентабельность проектов.
Говоря о достоинствах конструкции, нельзя не отметить и минусы, хотя их немного. Основные из них – это
- необходимость применять при создании ребер жесткости дополнительную арматуру;
- достаточно существенные трудозатраты, которые нужны для ее изготовления.
Однако, следует отметить, что с другой стороны дополнительные ребра жесткости дают возможность:
- уменьшить общую металлоемкость сварной металлоконструкции, так как ощутимо уменьшают толщину стенок. Таким образом удается понизить ее стоимость, но целиком сохранить механические характеристики;
- помимо этого облегченная конструкция экономична и с точки зрения устройства фундамента, поскольку после снижения общей массы можно использовать фундамент под БМЗ (быстровозводимые здания).
Чтобы найти двутавр, подходящий для конкретного случая, требуется произвести некоторые расчеты. Обычно для этого используют таблицы или онлайн калькуляторы. В их основе лежат заданные два параметра: расстояние от одной стены до другой и будущая нагрузка на строительную конструкцию.
Прочность двутавровой балки определяется такими параметрами, как:
- длина,
- метод закрепления,
- форма,
- площадь поперечного сечения.
Большее распространение получили изделия с буквой «Н» в сечении.
Жесткость металлической конструкции двутавра в 30 раз превышает жесткость квадратного профиля, а прочность, соответственно, в 7 раз.
Длина данной металлоконструкции бывает разной, к примеру, в случае ГОСТ 8239-89 это 4 –12 метров, то есть в зависимости от сортамента размеры и вес балки двутавровой отличаются. Помимо длины величина веса определяется толщиной металла и размерами граней. Поэтому для выполнения различных расчетов было введено понятие «вес метра балки двутавровой».
При покупке сварной конструкции обязательно требуется расчет на прочность, а для конкретного использования еще и расчет на прогиб. Грамотный расчет нагрузки на двутавровую балку позволит обеспечить устойчивость конструкции к проектным воздействиям, то есть способность воспринимать их без разрушения.
Нагрузка собственного веса
Чтобы определить в случае необходимости вес двутавровой балки пользуются специальными таблицами, где расписаны ее характеристики, к примеру, габариты, марка стали и т. д. В таблице представлена теоретическая масса 1 м профиля.
балка двутавровая размеры и вес (ГОСТ 8239-89)
Пример расчета двутавра
Предположим необходимо рассчитать вес двутавра № 12 длиной в 3 метра . Согласно таблице условная масса погонного метра данного профиля равна 11,50 кг. Если перемножить полученные значения, то получим величину общей массы – 34,5 кг.
Точнее значение веса сварной металлоконструкции можно посчитать, используя специальные онлайн калькуляторы.
В калькуляторе выбирают соответствующий номер двутавра и вводят необходимый метраж. Как видите, полученное значение больше рассчитанного нами на 0,12 кг.
Несущая способность
Среди всех типов балок двутавровая имеет наибольшую прочность, более того, она устойчива к температурным перепадам. Допустимая нагрузка на двутавр бывает указана на маркировке, как размер. Чем больше число, указанное в его наименовании, тем большую нагрузку может воспринимать балка.
Любой расчет предполагает изначальное знание размеров прокатного или сварного профиля, его длины и ширины. Проясним смысл значения ширины на примере самой популярной балочной опоры – колонны.
Предположим, что в сечении колонны лежит квадрат со стороной 510 мм, тогда на нее можно будет опереть профиль, для которого ширина не может превышать 460 мм. Это связано с тем, что двутавр придется приваривать к железобетонной подушке, а для сварочных швов понадобится запас, по крайней мере, в 40 мм.
После определения ширины переходят к выбору профиля и расчету нагрузки, воздействующей на профиль. Она представляет собой совокупность воздействий от перекрытия, а также воздействий временного и постоянного характера.
Нагрузку, выражающую величину нормативной нагрузки, собирают на длину 1 м профиля.
Но, расчет несущей способности двутавровой балки предполагает учет другого воздействия. Чтобы получить расчетную нагрузку, рассчитанное нормативное воздействие умножается на так называемый коэффициент прочности по нагрузке. Остается к результату прибавить уже подсчитанную массу изделия и найти его момент сопротивления.
Полученных данных достаточно, чтобы из сортамента подобрать профиль, необходимый для изготовления сварного профиля. Как правило, с учетом прогиба конструкции рекомендуется выбирать профиль выше на два порядка.
Сварная металлическая конструкция должна использовать примерно 70–80% от максимально допустимого прогиба.
Усиление
Если несущая способность двутавра оказывается недостаточной, то возникает необходимость ее усиления. Для различных элементов сварной конструкции этот вопрос решается по-разному.
К примеру, для элементов, воспринимающих нагрузки типа растяжения, сжатия или изгиба, используют такой вариант усиления: увеличивают сечение, иначе говоря, повышают жесткость, скажем, приварив дополнительные детали.
Теоретически – это один из лучших вариантов усиления, однако, при его реализации не всегда удается получить требуемый результат. Дело в том, что элементы в процессе сварочных работ нагреваются, а это несет за собой уменьшение несущей способности.
В какой степени можно ожидать такого понижения зависит от размеров двутавра и режима и направления сварочных работ. Если для продольных швов максимальное понижение оказывается в пределах 15%, то для швов в поперечном направлении оно может достичь и 40%.
Поэтому при усилении двутавра под нагрузкой категорически запрещено накладывать швы в направлении, поперечном к элементу.
Расчетно и экспериментально было доказано, что оптимального результата усиления под нагрузкой можно получить при максимальном напряжении в 0,8 R y , то есть 80% расчетного сопротивления стали, которая была использована для изготовления двутавра.
01.10.2010, 11:47
расчет:
1) брус 200*200*6000 через 0,5М =22 т.р (прогиб 20 мм)
2) двутавр 20Б ч/з 1,2м =27 т.р. (прогиб 20 мм)
По весу 1) -90 кг брус, 2)- 120 кг балка
В теории решения очень похожи. интересует практика что все таки лучше?
Зеленый Кот
01.10.2010, 11:55
Брус.
Железом вообще не стоит делать любые несущие конструкции ибо при пожаре дерево держится до последнего, а железо — хрясь и готово.
01.10.2010, 15:55
Температура при которой пойдет деформирования двутавр с жизнью несовместима. Тем более если снизу это все будет обшито гипсокартоном.
Если все же решите делать деревом, то советую 200х60х6000 с шагом 600 мм.
01.10.2010, 16:55
«хрясь и готово» — а не все ли равно уже будет)))
Оно может деформироваться в одном месте, и прилететь в другое, где еще остались условия для жизни… 🙂 но в целом вы правы.
+Дерево само по себе будет поддерживать горение, а железо нет…
Зеленый Кот
01.10.2010, 17:41
Температура при которой пойдет деформирования двутавр с жизнью несовместима.
Неправильно.
Одно дело когда он сам по себе, а другое, когда он под нагрузкой.
До недавнего времени вообще было запрщено использовать в качестве стропил мет. профиль, теперь же смотрю делают вовсю.
Советую 200х60х6000 с шагом 600 мм
Малавато будет, малавато — смотрим какулятор.
01.10.2010, 20:32
У меня в одном помещении пролет получился 5,7 метров, перекрытие между 1 и 2 этажом. Я выбрал двутавр 20Б через 1,3 метра, вроде по расчету двутавр был крепче, чем дерево. Стоит учесть что дерево можно найти 6,5 метров, а длина двутавра 11,7 метра или 12 метров (для перекрытия пролета 6 метров надо как минимум 15 см на сторону) . Правильнее было бы уложить плиты, но у меня не получилось. Разница между деревом и двутавром была гдето 10-12%. При кладке стен устанавливал между вырезом в газоблоке и двутавром пенопласт 3 см.
На счет пожара-надо предохроняться.
02.10.2010, 00:47
А я на 6 м пролет положил 5,8 метровую жб плиту и ни о чем больше не задумываюсь. Не горит, не плавится, не гнется…
02.10.2010, 09:00
Спасибо всем, я все таки склоняюсь к двутавру,поскольку он прочнее, я на перекрытие хочу стены внутренние из пеноблока 100 см поставить. (хотя наверное можно было по 2 бруса под стену положить)
то wawan001 пролет 6М это по осям стен, то есть по 15 см с каждой стороны опора будет.
то Кот, я предполагаю если засыпать негорючий утеплитель аля керамзит то гореть там вообще нечему будет (дом из пеноблока).
И еще вопрос если перекрывать двутавром можно ли вместо крайних балок использовать деревянную скажем 50-ку закрепленную к боковым стенам??
02.10.2010, 18:30
Есть другой вариант.
02.10.2010, 19:12
Есть другой вариант.
Делаете несущую балку (пускай из двутавра), на которую укладываете простые деревянные балки перекрытия. Это гораздо дешевле выйдет.
Двутавров понадобится один-два, но мощных. По цене все равно выйдет дешевле.
Я так себе сделал
02.10.2010, 20:01
dengt , у меня эта идея приходила в голову с точки зрения технологичности устройства в будущем полов, если деревянные перекрытия устанавливать внутрь двутавра, а по верх делать контробрешетку (балки по расчету). Расстояние от края балки до двутавра 40 см- надежно. Ведь по расчетам на крайнии балки нагрузка меньше раза в 2 чем на соседнию, можно положить балку 150х200 или взять 2 штуки доски 50х200 и между ними установить отрезки доски того же размера длиной 1,5 метра, а 50-ка думаю хлипковата, хотя если к стене притянуть может и нормально будет. Если уверен в крепеже то наверное да.
04.10.2010, 05:57
Я перекрывал пролет 5м брусом 150*150 сложенным вдвое и стянутым шпильками, т.е. получилась балка 150*300. Получилось довольно жестко, но я бы все равно сделал из бетона, если бы была возможность:(
05.10.2010, 09:32
[
я так себе сделал
пролет 11 на 6, разделил на три части двумя двутаврами и уложил деревянные балки, а что бы не увеличивать толщину перекрытия уложил их внутрь тавра. Предварительно приварил уголки к тавру и закрепил балки на болты.
Я так понимаю двутавры 6-ти метровые были?
тут уже 25Б2 минимум нужен, это на 5 см толще перекытие, вроде не смертельно.
По поводу закрепления боковых балок к стенам меня беспокоит то, что все остальные балки будут прогибаться а крайние нет, тогда перекытие прогнется «»пузырем»? к чему это приедет?
05.10.2010, 10:11
двутавр 6-ти меровый 20Б1 — две штуки поперек длины, получилось 3 зоны, две с опиранием балок одной стороны на стену, а второй на двутавр, и одна зона с балками зажатыми между двутаврами. Прогибания не заметил, двутавр на такой длине не ходит.
06.10.2010, 13:06
06.10.2010, 13:47
смотря как грузить, если по теории 400 кг/м то в вашем случае 20Б1 прогнется на 77 мм
Интересно как Вы это посчитали?
Балка 20 . Применение. Виды. Расчёт двутавра .
Двутавровая балка — прокат, имеющий сечение буквы Н и означающий с латинского языка — «двурогая» с двух сторон («тавр» — бык). Расстояние между полками называют высотой, у двутавра 20го высота составляет около 200 мм или 20 см. Двутавр — это металлопрокат фасонного типа, изготавливаемый из строительной стали — ст3 и низколегированной стали 09Г2С.
Балка двутавровая 20 наиболее распространена в применении у строителей и монтажников, в первую очередь при устройстве каркасов с большими пролётами в зданиях, для перераспределения нагрузки с перекрытий на несущие конструкции. Её используют для мостостроительства, изготовления кранов, автомобилей, трубопроводов, самолётных ангаров, в железнодорожном строительстве и т. д. 20й профиль производят по 8239 ГОСТ двутавры стальные , госстандарту 26020-83, двутавр гост 19425-74 и техническим условиям СТО АСЧМ 20-93.
Двутавр 20й подразделяют по СТО АСЧМ 20 на нормальную балку 20Б с параллельными гранями полок, широкополочную балку 20Ш и 20К — для колонн. Двутавр СТО АСЧМ 20-93 с высотой 20 см имеет грани полок, которые параллельны. СТО двутавр производится НЛМК, который и разработал данный стандарт. По такому стандарту производится также балка 09Г2С , которая также подразделяется на нормальную балку, колонную и широкополочную. Металлопрокат из низколегированной стали может употребляться как при очень низкой температуре, так и при высоких температурах, не подвергаясь деформации.
Двутавр стальной 20Б1 имеет массу метра — 21,3 килограмм. Масса 20Ш1 составляет 30,6 кг в метре, вес колонной балки 20К1 — 41,4 кг, вес двутавра 20К2 — 49,9 кг. Параметры двутавра 20Б1: высота (h)- 200 мм, ширина полки (b)- 100 мм, толщина стенки (s) — 5,5 мм, толщина полки (t)- 8,0 мм. Широкополочный 20й профиль 20Ш1 имеет следующие характеристики: h — 194 мм, b- 150 мм, s — 6 мм, t — 9 мм. Колонная балка 20К1 обладает h 196 мм, b стенки — 199 мм, s стенки — 6,5 мм, t полки — 10, 0 мм.
Балка 20 по стандарту 19425 может быть монорельсовой (обозначается буквой М) и спец. (именуется буквой С). Этот ГОСТ распространяется на горячекатаные двутавры с полками, имеющими наклон внутренней поверхности полок. Монорельсовый двутавр, известный как кран балка, предназначена для крановых путей, как несущий мост в козловом или мостовом кранах, как подрельсовая балка. Такое изделие характеризуется высокой прочностью и способно противостоять большим нагрузкам, давлению, скручиванию. Специальная балка применима в стволе конструкций, которые обеспечивают движение подъёмных стволов, то есть для армирования стволов шахт, а также в сооружении лестниц и прокладке инженерных коммуникаций, креплении водоотливов.
Специальный профиль 20С имеет следующие параметры — двутавр размеры : высоту — 200мм, ширину полки — 100 мм, толщину стенки — 7 мм, толщину полки — 11,4 мм. Масса 1 м такого двутавра составляет 27,9 кг. Вес погонного метра балки в таблицах теоретический, он нужен для того,чтобы рассчитать самостоятельно вес целой балки или необходимое количество метров и штук двутавра. Итак, если балка 20 на складе металлоторгующей компании имеется длиной 12м, то чтобы выяснить вес одного хлыста, нужно двутавр вес 1 метра 27,9 умножить на 12м. Зная общее количество метров балки, легко можно посчитать общий вес необходимого металлопроката. На практике это лучше всего выяснить, уточнив у менеджеров компании АО «Металлоторг», которые кроме того подскажут стоимость металла, двутавр цена за метр, выпишут счёт, чтобы двутавр купить , и решат все текущие вопросы по загрузке и доставке.
Двутавр ГОСТ 8239 89 — на сортамент двутавров , имеющий отличие — наклон внутренних поверхностей полок. Такая балка с расстоянием между полками 200 мм имеет ширину этих полок — 100 мм, толщину металла посередине высоты — 5,2 мм, толщину полок 8,4 мм.
Какой двутавр лучше? Горячекатаный двутавр или сварной?
Чтобы выбрать между горячекатаной балкой 20 и сварным профилем с похожими параметрами, вычиляют момент сопротивления. Для этого учитывают нагрузку на перекрытие, непрерывную и краткосрочную нагрузку, используют табличные данные — коэффициент прочности и допустимый прогиб для несущих конструкций.
Похожие статьи
Изгибаемые элементы. Расчет на изгиб
Расчёт на прочностьРасчет на изгиб. Расчёт на прочность элементов (кроме балок с гибкой стенкой, с перфорированной стенкой и подкрановых балок), изгибаемых в одной из главных плоскостей, следует выполнять по формуле:
Значения касательных напряжений τ в сечениях изгибаемых элементов должны удовлетворять условию:
Расчёт на прочность разрезных балок сплошного сечения при изгибе в двух плоскостях и несущих статическую нагрузку следует выполнять по формуле:
где Сх –Су – коэффициенты, принимаемые по таблице
КОЭФФИЦИЕНТЫ ДЛЯ РАСЧЁТА НА ПРОЧНОСТЬ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ С УЧЁТОМ РАЗВИТИЯ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
Коэффициенты С (Сх ), Су , n
Расчет на устойчивостьРасчёт на устойчивость балок двутаврового сечения, изгибаемых в плоскости стенки, следует выполнять по формуле:
Wc – следует определять для сжатого пояса;
ϕb – коэффициент, определяемый по прил. 7
При определении значения ϕb за расчётную длину балки lef следует принимать расстояние между точками закреплений сжатого пояса от поперечных смещений.
Для балок двутаврового сечения с двумя осями симметрии для определения коэффициента ϕb необходимо вычислить коэффициент ϕ1 по формуле:
где значения ψ следует принимать по таблицам в зависимости от характера нагрузки и параметра α, который должен вычисляться по формулам:
а) для прокатных двутавров:
l ef – расчётная длина балки или консоли, определяемая согласно требованиям п. 5.15;
h – полная высота сечения;
J t – момент инерции сечения при кручении.
б) для сварных двутавров, составленных из трёх листов, а также для двутавровых балок с поясными соединениями на высокопрочных болтах:
где обозначено:
для сварных двутавров:
t – толщина стенки
b f и t 1 – ширина и толщина пояса балки;
h – расстояние между осями поясов;
a – размер, равный 0,5 h.
для двутавровых балок с поясными соединениями на высокопрочных болтах:
t – сумма толщин стенки и вертикальных поясных уголков;
b f – ширина листов пояса;
t 1 – сумма толщин листов пояса и горизонтальной полки поясного уголка;
h – расстояние между осями пакета поясных листов;
a – сумма толщины листов пояса и высоты вертикальной полки поясного уголка.
Значение коэффициента ϕb в формуле (7) необходимо принимать:
при ϕ 1 ≤ 0,85 ϕb = ϕ 1 ; при ϕ 1 > 0,85 ϕb = 0,68+0,21⋅ϕ1 , но не более 1,0.
Коэффициенты ψ для двутавровых балок с двумя осями симметрии
Коэффициенты ψ для жёстко заделанных консолей двутаврового сечения с двумя осями симметрии
Прогиб балокПрогиб балок следует проверять по формуле:
f пред – предельный прогиб от нормативной нагрузки, приведённый в таблице
p.s.: Расчет Центрально-растянутых и центрально-сжатых элементов смотрите ЗДЕСЬ
Поделиться ссылкой:
Похожее% PDF-1.3 % 1809 0 obj> эндобдж xref 1809 75 0000000016 00000 н. 0000003313 00000 н. 0000001836 00000 н. 0000003471 00000 н. 0000003499 00000 н. 0000003547 00000 н. 0000003673 00000 н. 0000004059 00000 н. 0000004144 00000 п. 0000004229 00000 п. 0000004312 00000 н. 0000004395 00000 н. 0000004478 00000 н. 0000004561 00000 н. 0000004644 00000 н. 0000004727 00000 н. 0000004810 00000 н. 0000004893 00000 н. 0000004976 00000 н. 0000005059 00000 н. 0000005142 00000 н. 0000005225 00000 н. 0000005308 00000 н. 0000005391 00000 п. 0000005474 00000 н. 0000005557 00000 н. 0000005640 00000 н. 0000005723 00000 п. 0000005806 00000 н. 0000005889 00000 н. 0000005972 00000 н. 0000006054 00000 н. 0000006136 00000 н. 0000006218 00000 н. 0000006300 00000 н. 0000006382 00000 п. 0000006745 00000 н. 0000010431 00000 п. 0000010978 00000 п. 0000011166 00000 п. 0000011806 00000 п. 0000011892 00000 п. 0000011919 00000 п. 0000012473 00000 п. 0000018402 00000 п. 0000019201 00000 п. 0000019589 00000 п. 0000019658 00000 п. 0000020148 00000 п. 0000021318 00000 п. 0000021664 00000 н. 0000022422 00000 п. 0000022686 00000 п. 0000023334 00000 п. 0000028354 00000 п. 0000028792 00000 п. 0000029204 00000 п. 0000029823 00000 п. 0000030993 00000 п. 0000031394 00000 п. 0000031939 00000 п. 0000032026 00000 п. 0000032066 00000 п. 0000033237 00000 п. 0000033324 00000 п. 0000033353 00000 п. 0000033452 00000 п. 0000034614 00000 п. 0000035778 00000 п. 0000036478 00000 п. 0000037185 00000 п. 0000037959 00000 п. 0000038616 00000 п. 0000039340 00000 п. 0000003100 00000 н. трейлер ] >> startxref 0 %% EOF 1811 0 obj> поток xb«b`π
Изгиб балки
Введение
На этой странице рассматривается классическая теория изгиба балок, которая является важным фактором почти во всех конструктивных решениях и анализы.Хотя это менее очевидно, оно также имеет отношение к изгибу колонны. также. И это на самом деле второй мотив этого страницы, чтобы заложить основу для предстоящего обсуждения теории продольного изгиба колонн.Цель не состоит в том, чтобы охватить все аспекты изгиба балки. В частности, такие темы, как определение нейтральной оси, теорема о параллельной оси и расчет прогибов балок не рассматривается.
Радиус кривизны
Радиус кривизны имеет фундаментальное значение для изгиба балки, поэтому он будет рассмотрено здесь.Обычно обозначается греческой буквой \ (\ rho \), и может рассматриваться как радиус круга, имеющего ту же кривизну, что и часть графика, изгиб дороги или любой другой путь. Когда путь прямой, \ (\ rho \) бесконечен, а когда путь имеет острый кривая в нем, \ (\ rho \) мала. В конечном итоге нам понадобится аналитическое выражение для радиуса кривизны,
так что он будет развиваться здесь. Начните с любой функции \ (y = y (x) \), как
показано на рисунке. Напомним, что длина дуги \ (s \) связана с
\ (\ rho \) через \ (\ rho \, \ theta = s \), где \ (\ theta \) — угол
дуги.{3/2}}
\]
Интересно, что любое выражение, включающее радиус кривизны, кажется, всегда имеет
появляются в знаменателе. И это не исключение, даже если это
определяющее уравнение.
Также интересен тот факт, что многие приложения механики включают гибку,
но в малых масштабах. Обсуждаемый здесь изгиб балки не является исключением. В таких случаях,
лучший подход — определить ось x вдоль луча так, чтобы
прогибы \ (y \) и, что более важно, деформированный уклон \ (y ‘\) будут
оба будут маленькими.3}
\]
где \ ({\ bf v} \) — вектор, определяемый параметрически как \ ({\ bf v} = {\ bf v} (x (t), y (t), z (t)) \),
\ ({\ bf v ‘} \) — его первая производная, \ ({\ bf v’ ‘} \) — его вторая производная, и
\ (| … | \) представляет длину вектора, то есть квадратный корень из суммы
квадраты его составляющих.
Деформации при изгибе
Напомним, что длина дуги \ (L \) связана с радиусом кривизны \ (\ rho \) через \ (L = \ rho \, \ theta \), где \ (\ theta \) — угол.Ситуация усложняется, если принять во внимание толщину. На рисунке ниже объект начальной длины \ (L_o \) изогнут. как показано. Поскольку он имеет конечную толщину, различные его части растягиваются, или сжатые, в разном количестве. Внешняя часть балки растягивается больше всего, потому что он дальше всего от этот центр. Математически все части изогнуты под одинаковым углом, \ (\ theta \), но \ (\ rho \) изменяется по толщине, поэтому количество \ (\ rho \, \ theta \) тоже меняется, и, следовательно, меняется и \ (L \).
Следующий шаг — принять осознанное решение, чтобы избежать путаницы, связанной с наличием множества разные радиусы кривизны по толщине изгибаемого объекта. Это выполняется в два этапа.
Сначала найдите тот \ (\ rho \), который удовлетворяет \ (\ rho \, \ theta = L_o \). Обратите внимание, что \ (\ rho \) — вычисленный результат здесь, а \ (\ theta \) и \ (L_o \) — входные данные. Также обратите внимание, что длина в уравнении равна \ (L_o \), исходная недеформированная длина, не деформированный. Этот шаг устанавливает одно уникальное значение \ (\ rho \) для поперечное сечение, а не иметь несколько значений, что может привести к большой путанице.
Нейтральная ось
Местоположение в поперечном сечении, где известно \ (\ rho \, \ theta = L_o \) как нейтральная ось . Это единственное место, где окончательная деформированная длина такая же, как и исходная недеформированная длина, поэтому растяжения не происходит … из-за изгиба. Не думайте, что нейтральная ось должна быть посередине. поперечного сечения объекта. Это не обязательно так, особенно если объект состоит из разных материалов с разными жесткости.Предупреждение «из-за изгиба» в предыдущем абзаце присутствует, потому что объект также может быть одновременно нагружен растяжением (или сжатием), которое его растягивает пока каждая точка в его поперечном сечении не будет длиннее (или короче, если сжато), чем исходная длина, \ (L_o \).
Второй шаг — ввести переменную \ (y \) как расстояние от нейтральной оси. с любым другим радиусом в поперечном сечении, как показано на рисунке ниже. В результате радиус кривизны при любом \ (y \) равно \ ((\ rho — y) \), а окончательная длина в любом \ (y \) определяется как \ [
L = (\ rho — y) \ тета
\]
Напомним, что \ (L_o = \ rho \, \ theta \).Теперь деформацию \ (\ epsilon \) можно выразить как
\ [
\ epsilon_x = {L — L_o \ над L_o} = {(\ rho — y) \ theta — \ rho \, \ theta \ over \ rho \, \ theta}
\]
, что упрощает
\ [
\ epsilon_x = — {y \ over \ rho}
\]
Это ключевой результат деформации объекта. Это показывает, что деформация равна нулю при \ (у = 0 \),
нейтральная ось, и линейно отклоняется от нее. Если объект толстый, то \ (y \) может принимать
на больших значениях, но не на тонких объектах. Вот почему толстые объекты
имеют большую жесткость на изгиб, чем тонкие предметы.
Кроме того, радиус кривизны в знаменателе учитывает многие эффекты изгиба. Когда объект не изогнут, тогда \ (\ rho \) бесконечно, а деформации, естественно, равны нулю. По мере изгиба объекта \ (\ rho \) уменьшается, и уравнение показывает, что деформации увеличиваются.
Наконец, обратите внимание, что деформация представляет собой нормальную деформацию и фактически является продольной, по длине балки. Обычно ось \ (x \) выравнивается по длина балки, создающая деформацию \ (\ epsilon_x \).
Напряжение изгиба
Теперь, когда у нас есть выражение для деформации, разработать выражение для стресса невозможно. будь проще. Умножьте деформацию на \ (E \), модуль упругости, для получения напряжения \ (\ sigma_x \). \ [
\ sigma_x = — {E \, y \ over \ rho}
\]
Хотя этот шаг был невероятно простым, на самом деле он довольно глубок в том,
пренебрегали простотой. Напомним со страницы на
Закон Гука о том, что каждая нормальная составляющая напряжения
зависит от всех трех компонентов нормальной деформации.Но здесь у нас просто
умножили деформацию на \ (E \), чтобы получить напряжение. Этот шаг имеет ключевое предположение
встроено в него … что на балку не действуют боковые нагрузки / напряжения.
В таких случаях уравнения «работают» так, что \ (\ sigma_x = E \, \ epsilon_x \) как в
одноосное растяжение. Это происходит в большинстве балок, потому что они тонкие по сравнению с
их длина.
Гибка пластин
В случае пластин этот этап будет более сложным, потому что пластина тонкая только в одном направление, а не два, относительно его длины.2)} \ epsilon_x \]где \ (\ nu \) — коэффициент Пуассона материалов. Понятно, что напряжение при заданном деформация в этом случае выше, чем при классическом одноосном растяжении.
Изгибающие моменты и напряжения
Изгибающий момент \ (M_z \) в поперечном сечении, создаваемый полем напряжений, вычисляется по формуле
\ [
M_z \; знак равно \ int_A r \ times dF \; знак равно — \ int_A y \, \ sigma_x dA
\]
где \ (y \) — плечо момента, а \ (\ sigma_x dA \) — сила.
Напомним, что \ (\ sigma_x = — E \, y / \ rho \) и вставьте в уравнение моментов, чтобы получить
\ [
M_z \; знак равно — \ int_A y \, \ left [{- E \, y \ over \ rho} \ right] dA
\; знак равно {E \ over \ rho} \ int_A y ^ 2 dA
\]
Оставшийся интеграл очень важен.2 дА
\]
Всегда помните, что значения \ (y \) измеряются от нейтральной оси, которая
соответствует \ (y = 0 \).
Уравнение изгибающего момента теперь можно записать как
\ [
M_z = {E \, I_ {zz} \ over \ rho}
\]
, что является очень важным уравнением.
Аппроксимация малого изгиба
Напомним, что мы обсуждали ранее, что когда уровень изгиба мал и \ (y ‘\ lt \ lt 1 \), тогда \ (\ rho \) может быть близко аппроксимируется \ (y » \). Это дает \ [
M_z = E \, I_ {zz} y » \ qquad (\ text {when} \; \; y ‘\ lt \ lt 1)
\]
, что является еще одним очень важным и полезным уравнением.
\ [
M_z = {E \, I_ {zz} \ over \ rho} \ qquad \ qquad \ text {и} \ qquad \ qquad \ sigma_x = — {E \, y \ over \ rho}
\]
и поймите, что оба содержат \ (E / \ rho \). Решение каждого уравнения для этого отношения дает
\ [
{E \ over \ rho} = {M_z \ over I_ {zz}} \ qquad \ qquad \ text {и} \ qquad \ qquad {E \ over \ rho} = — {y \ over \ sigma_x}
\]
Итак, приравняем эти два, чтобы получить одно из самых известных уравнений в машиностроении. 2 dA — {E \ over \ rho_z} \ int_A y \, z \, dA
\\
\\
\\
& & & = & {E \ over \ rho_y} I_ {yy} — {E \ over \ rho_z} I_ {yz}
\ end {eqnarray}
\]
А другой момент, \ (M_z \), вычисляется путем интегрирования
напряжение по поперечному сечению с \ (y \) в качестве плеча момента.2 dA — {E \ over \ rho_y} \ int_A y \, z \, dA
\\
\\
\\
& & & = & {E \ over \ rho_z} I_ {zz} — {E \ over \ rho_y} I_ {yz}
\ end {eqnarray}
\]
Уравнения можно компактно записать в матричной форме как
\ [
\оставил\{
\ matrix {
Мой
\\
\\
M_z
}
\верно\}
знак равно
\оставил[
\ matrix {
\; I_ {yy} & -I_ {yz} \\
\\
-I_ {yz} & \; I_ {zz}
}
\верно]
\оставил\{
\ matrix {
E / \ rho_y
\\
\\
E / \ rho_z
}
\верно\}
\]
Это показывает, что момент инерции на самом деле является тензором.2 \).
Наконец, если \ (I_ {yz} = 0 \), все значительно упростится до
\ [ \ sigma_x = {M_y \, z \ over I_ {yy}} — {M_z \, y \ over I_ {zz}} \]
Лучшее руководство по определению прогиба в балках переменного поперечного сечения — опытный инженер
Таблицы балок дают информацию и предполагают, что прогиб расчет основан на постоянном сечении. Итак, что нам делать, если у нашей балки есть крест сечение, которое меняется по длине балки?
Чтобы определить величину отклонения в балка переменного сечения, необходимо интегрировать формулу прогиба балки с моментом инерции, являющимся переменной по отношению к длине и применить граничные условия.Луч Формула отклонения: v ’’ = M (x) / [E * I (x)].
Непрерывный или дискретный — Есть два типа секций балки: непрерывная и дискретная. Большинство балок представляют собой непрерывные балки и имеют либо постоянное сечение, либо сечение, которое постепенно изменяется по длине балки. Кровельные балки в больших стальных зданиях — отличный пример непрерывной переменной балки. Балка относительно короткая на концах и очень высокая посередине.
Дискретные балки балки которые имеют внезапные разрывы в разрезе.Вы не поверите, но иногда это проще для расчета, потому что дискретные участки обычно постоянны, что приводит к более легкий расчет.
Формула отклонения балки является универсальной формула, которая позволяет настраивать несколько нагрузок и балку разделы. Предупреждаю, что чем больше чем точнее должны быть ваши расчеты, тем сложнее будет выполнить математику. Упрощение здесь сэкономит много времени и усилия. Как упоминалось ранее, формула:
в ’’ = M (x) / [E * I (x)]
Где v ’’ — вторая производная отклонения ( ускорение прогиба), M — момент, который обычно является функцией положение по длине балки, x. E — модуль упругости, I — момент инерции поверхности луч. Все табличные балки будут считайте это постоянной величиной, и поэтому ни одна из формул прогиба может быть использован.
Теперь, когда мы проинтегрируем приведенное выше уравнение, мы будем выполнение неопределенного интеграла, что означает, что мы должны добавить константу, C n, к полиному каждый раз, когда мы интегрируем. Поскольку мы будем интегрировать уравнение два раза, мы получим две константы. Если у нас есть дискретный В этом случае у нас будет два или более уравнений.
Граничные условия — это требования, которым должна соответствовать формула прогиба балки, когда она находится в окончательном виде. Окончательная форма приходит только тогда, когда мы используем граничные условия для решения для констант образованный неопределенным интегралом. Общий случаи: концы балки с опорой должны быть равны 0 (дюймы, мм и т. д.) или наклон консольной балки должен быть 0 радиан.
В этой статье мы рассмотрим три примера распространенных балок переменного сечения.
- Двухсекционная консольная балка с точечной нагрузкой на конце.
- Двухсекционная балка, свободно поддерживаемая собственным весом.
- Постоянно изменяющаяся непрерывная балка с простой опорой и постоянной распределенной нагрузкой.
Эта проблема состоит из 100-дюймового консольная стальная балка с нагрузкой 500 фунтов на конец. 4.
Теперь мы определим момент и дважды проинтегрируем уравнение прогиба балки, каждый раз добавляя переменную для неопределенного интеграла. Я решил, что моя система координат (переменная x) начинается с основания. Это немного усложняет интегрирование, но переменные C 1 и C 2 будут уравновешиваться из-за граничных условий 1 и 2. Вы увидите через секунду.
Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I 1 на I 2 в уравнениях.Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте установим граничные условия. Нам нужно, чтобы положение и наклон на фиксированном конце балки составляли 0 дюймов и 0 радиан. Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этом положении должны быть одинаковыми.
Решим граничные условия 1 и 2
Как упоминалось выше, я предвидел, что переменные C1 и C2 будет равно 0, когда я выберу, чтобы система координат начиналась с база.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Обратите внимание на проверку, которую я вставил в блок поиска, чтобы чтобы мы могли проверить, что v 1 = v 2 и s 1 = s 2 при 50in.Это подтверждает что положение и наклон в этой точке будут непрерывными.
Следующим шагом является проверка результатов. Это делается в два этапа. Первый — нанести каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. Как видите, линии пересекаются и касаются друг друга на расстоянии 50 дюймов. Кроме того, v 1 не имеет прогиба или наклона в основании.
Наконец, мы объединим два графика вместе, образуя окончательное уравнение для отклонения нашей консольной балки. 4.
Теперь определим момент и проинтегрируем уравнение отклонения балки дважды каждый раз, добавляя переменную. Я выбрал две системы координат. Координата x идет слева направо и координата y идет справа налево. Их связывает:
г = L-x
Я выбрал эту систему координат так, чтобы C 2 и C 4 будет сокращаться, когда мы решаем граничные условия 1 и 2. Это также упрощает математику. чрезвычайно.Вы увидите через секунду.
Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I 1 на I 2 и w 1 на w 2 в уравнениях. В уравнениях правого сечения я также заменю «y» на «x». Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте установим граничные условия.Нам нужно, чтобы концы балки были отклонены на 0 дюймов (BC 1 и 2). Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этой позиции должны быть такими же, как и в месте соединения сегментов.
Решим граничные условия 1 и 2
Как упоминалось выше, я предвидел, что переменные C 2 и C 4 будет равно 0, если я выберу координату система запускается на базе.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Обратите внимание на проверку, которую я вставил в блок поиска, чтобы чтобы мы могли проверить, что v 1 = v 2 и s 1 = s 2 при 200 дюйм. Это подтверждает что положение и наклон в этой точке будут непрерывными.
Следующим шагом является проверка результатов. Это делается в два этапа. Первый — нанести каждый сегмент по всей длине.Мы ищем четыре граничных условия, которые должны быть выполнены.
Ой, что случилось !? Линии определенно пересекаются на расстоянии 200 дюймов, и каждый конец имеет 0 дюймов. прогиб, но они не касаются на пересечении. Я не только показываю силу график решения для точности, но также демонстрируя, что с помощью двух разные системы координат создают проблему. Согласно уравнениям склоны приближаются к месту расположения стык на равном по величине нисходящем склоне.Однако сделать эту работу одной из склонов на самом деле нужно подойти. Мы можем исправьте эту проблему, внеся одно небольшое изменение.
с 1 = -s 2
Давайте внесем это изменение и приступим к решению.
Да, намного лучше! Наконец, мы объединим два графика вместе, образуя окончательное уравнение отклонения нашей консольной балки.
Как и ожидалось, более длинная и жесткая секция меньше прогибается.
Пример 3: Постоянно изменяющаяся неразрезная балка с простой опорой и постоянной распределенной нагрузкой.Эта проблема состоит из стальной балки с простой опорой длиной 300 дюймов с распределенной нагрузкой 1000 фунтов / дюйм поперек балки. Сечение начинается на высоте 10 дюймов, линейно увеличивается к центру, где достигает высоты 24 дюйма. Затем он снова сужается до 10 дюймов.
Чтобы определить, как момент инерции изменяется по отношению к x, мы будем моделировать в Solidworks и делать сечения каждые 30 дюймов. Мы сведем эти данные в таблицу и подгоним к ним линию.
Теперь вы, наверное, заметили, что я сделал таблицу только для значений от 0 до 150 дюймов. Это потому, что я собираюсь использовать симметрию, чтобы упростить эту сложную задачу. Мы можем использовать симметрию, потому что и нагрузка, и сечение балки симметричны относительно середины балки. Из-за симметрии нам нужно, чтобы конечная точка имела прогиб 0 дюймов, а наклон в середине балки был 0 градусов. Затем мы можем отразить это, чтобы получить непрерывное отклонение луча. В этом случае координата x будет идти слева направо.
Здесь вы можете видеть, что вычисленные значения I (x) точно соответствуют тому, что указано в таблице выше. Я назвал вторую производную от положения «а1» (ускорение). Как видите, верхняя и нижняя части имеют переменную «x», и интегрировать это будет очень весело. Итак, вам нужно знать обо мне одну вещь. У меня есть ограничения на то, что я не буду делать. Интеграция — одна из таких вещей. Вот почему у нас есть MathCAD!
Как видите, очень утомительная работа по интеграции была замалчена, и мы смогли напрямую решить для нашей границы условия.В уравнениях s (x) и v (x), на самом деле были натуральные бревна и каким-то образом появилась обратная касательная (не показано). Я до сих пор не жалею позволяя MathCAD делать всю работу.
Следующим шагом является проверка результатов. Это делается в два этапа. Первый — нанести каждый сегмент по всей длине. Мы ищем, чтобы наши граничные условия были выполнены. Как видите, отклонение при x = 0 дюймов составляет 0 дюймов, а наклон кажется плоским при x = 150 дюймов.
Наконец, мы отразим графики вместе, образуя окончательное уравнение для отклонения нашей консольной балки.
Как видите, отклонение составляет 0 дюймов в конечных точках и имеет максимальное отклонение в центре.
ЗаключениеВ этой статье рассматриваются три популярных варианта нагружения, когда балка имеет переменное поперечное сечение. Хотя это действительно связано с исчислением, часто это очень легко сделать вручную, потому что это многочлены. Если нет, то будьте благодарны за такие надежные программы, как MathCAD, которые сделают это за вас. Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа подобных балок.Если ваша балка не загружена именно так, вы всегда можете найти расчет момента в таблице и интегрировать свое сердце.
СвязанныеЛегкий прогиб стальной балки
Верулам, инженер-строитель Том. 70, No. 12, 16 июня 1992 г.
Легкое отклонение луча
Г-н А. Н. Бил из Лидса прислал нам записку с предложением простой процедуры приблизительного ручного расчета прогибов стальных балок.Хотя его вклад оказался слишком длинным, чтобы его можно было полностью включить в Verulam, его сокращенная версия может заинтересовать многих читателей. Г-н Бил отмечает, что, хотя расчет вручную изгибающих напряжений в балке обычно не является трудным, расчет прогибов может быть гораздо более трудоемким. Поскольку обычно нет необходимости знать прогиб с какой-либо большой степенью точности (в пределах 10%, вероятно, будет адекватным), предлагается следующий подход.
Пример балки с простой опорой, поддерживающей равномерную нагрузку, иллюстрирует подход.
Если мы возьмем формулу прогиба (Δ = 5WL³ / 384EI) и выразим ее через изгибающий момент (M = WL / 8), то получится Δ = 5ML³ / 48EI.
Теперь для стальной балки напряжение упругого изгиба fbt = M / Z, где Z = 2I / D, что дает fbt = MD / 2I.
(Z — модуль упругости, I — момент инерции, D — общая глубина сечения.)
Подставив это в формулу прогиба, мы получим Δ = 5 fbtL³ / 24ED. При E 210 кН / мм² это становится:
Δ (мм) = 0.992 фбтL² / сут. . . (1)
Здесь fbt, L и D выражены в их обычных единицах измерения: Н / мм², м и мм соответственно.
Для всех практических целей формула
Δ = fbtL² / D. . . (2)
удобен в использовании, легко запоминается и отличается точностью до 1%.
Г-н Бил затем переходит к рассмотрению других распределений нагрузки, аналогичным образом связывая центральный прогиб Δ с экстремальным напряжением волокна fbt, получая результаты, показанные в первом столбце результатов в таблице 1.Во втором столбце приведены значения для балок с фиксированными концами —
Наконец, г-н Бил показывает, как его методика может использоваться для сложных нагрузок, получая отклонение нагруженной балки с простой опорой, как показано на рис. 1:
Рис.1
Центральный изгибающий момент, рассчитанный как 444,3 кНм.
Для сечения балки Z = 2474 см³, D = 539,5 мм, что дает
фут = 179,6 Н / мм².
Простое приблизительное отклонение с использованием ур. (2) это
ΔAPP = 179,6 x 7² / 539,5 = 16,3 мм = L / 429 OK.
Для более точной оценки, учитывая, что большая часть момента создается центральной точечной нагрузкой, мы могли бы взять коэффициент, более близкий к значению точечной нагрузки, равному 0.8 (скажем, 0,85), что дает
Δ = 0,85 футов x L² / D = 13,9 мм
Для сравнения, точный компьютерный анализ той же балки дал отклонение 13,8 мм.
Таким образом, для большинства практических целей нам нужно запомнить только четыре простые формулы для прогиба прямошовных или непрерывных стальных балок, как показано в Таблице 2.
Эти формулы не только упрощают жизнь для простых равномерных и точечных нагрузок —
Есть желающие?
| Получение Знакомый | ||||||||||||||
| Расчет на изгиб балок был
освященный веками центральный элемент в раннем обучении «технической
механика «, с которым приходилось сталкиваться каждому начинающему инженеру и ученому.
через как своего рода обряд посвящения.Многие этого не сделали. Освоение
изгибание луча — это просто не то, что делается на обратной стороне конверта, в то время как
выпить пива или два. Вам действительно нужно приложить все усилия, чтобы сдать эти экзамены. Давайте сначала посмотрим на масштабность задачи, а затем разрежем ее на части. может справиться. На рисунке ниже показано, что это такое при довольно простом обстоятельства. У нас есть то, что иллюминаты называют «луч», прочно закреплен на одном конце. С таким же успехом это мог быть меч, увиденный с ребра.Некоторые силы воздействовать на нашу балку; в результате он гнется. Давайте посмотрим на основные моменты, связанные к этому один за другим: | ||||||||||||||
| ||||||||||||||
| Сначала , давайте уточним, что я имею в виду
со словом « балка ».«Луч» — это общее название любого длинного предмета с некоторыми
поперечное сечение везде одинаковое по длине l .
Причем длина l должна быть значительно больше, чем длина
размеры поперечного сечения. Поскольку поперечное сечение большинства мечей изменяется с длиной, эти мечи — это не правильных лучей, а в лучшем случае приблизительно лучей. | ||||||||||||||
| Второй , давай определить « гибка ».если ты изгибаете что-нибудь, в частности балку, механически деформируете. Что касается слово изгиб здесь касается, мы ограничиваем себя на чисто упругих деформаций в любом месте луча. Снимите силы, действующие на балку выше, и она должна снова будь совершенно прямым. | ||||||||||||||
| Третий , мы
посмотрите на силы , которые могут согнуть
луч. Мы допускаем любые силы, действующие в любом месте балки — до тех пор, пока
они действуют только в направлении z .В противном случае мы имеем две проблемы изгиба балки — изгиб в z — направление и в y — направление, перпендикулярное плоскости чертежа. Применение сил
в направлении x — будет означать испытание на растяжение (или сжатие), поэтому
мы им тоже не позволяем. Конечно, силы, действующие на настоящие балки или
мечи не заботятся об этих ограничениях, но я смотрю на простой луч
изгиб здесь. Силы могли быть баллов сил, как у заставить свой меч переживать, когда он ударяется лезвием другого меча, или распределил сил, как вы их получите, когда вы кладете на балку, например, груз, как показано выше. Наша балка должна гнуться, но иначе она не двинется. Он не будет вращаться и никуда не денется, а значит, сумма всех сил и моментов должен быть равен нулю по определению. Очевидно, что это не так на картинке выше.Что ж, мы забыли: | ||||||||||||||
| Четвертый г. граничные условия .
На картинке выше балка прочно закреплена в стене. Математически
это означает отклонение z ( x ) , величина изгиба по координате x или просто линия сгиба, равна нулю для x = 0 . Выражаясь математически, мы имеем в качестве граничного условия: z ( x = 0) = 0 , и, по понятным причинам, d z ( x = 0) / d x = 0 . Для математиков: производная d z / d x дает наклон кривой изгиба z ( x ) , который должен быть ноль (т.е. параллельно оси x ) рядом со стенкой Эти граничные условия могут быть выполнены только в том случае, если на балку действуют силы и моменты. при x = 0 , которые точно компенсируют силы и моменты внешние силы.Это неплохо, потому что нам не о чем беспокоиться об этом. Проще говоря, если вы каким-то образом обездвиживаете меч (поместив его в тиски) он не может двигаться или вращаться по определению, независимо от того, силы действуют на него где-то еще. | ||||||||||||||
| Пятый и
не забываем, луч может иметь произвольные поперечное сечение , в т.ч.
полые. Три показанных примера уже довольно особенные, так как они очень интересны. симметричный.Этого не требуется, тем не менее, мы будем рассматривать только сечения с некоторой симметрией из теперь дальше, чтобы не слишком запутывать ум. | ||||||||||||||
| Теперь рассмотрим поставленную задачу.
Мы хотим вычислить z ( x ) , кривую, которая
описывает форму гнутой балки. Допускается любая длина л и
формы поперечного сечения балки и все виды сил, силы
распределения и всевозможные (разумные) граничные условия. Даже если у вас такие математические проблемы, что вам пришлось заняться банковским делом, вы поймете, что это непростая задача. Как вы выражаете сечение № 2 выше (меч с долом) в уравнениях? Что бы граничные условия будут, если вы попытаетесь удерживать меч в фиксированном положении с помощью руки вместо того, чтобы заткнуть его в тиски? Если он поражен другим мечом, вы невозможно сохранить положение руки и меча полностью без изменений — в отличие от (очень сильный) порок. | ||||||||||||||
| Ну задача конечно непростая — но тоже не так сложно, как может показаться. Давайте сделаем это в два этапа и модули. Во-первых, в этом модуле я даю довольно простое описание специального ситуация, которую я затем использую, чтобы вывести несколько общих правил изгиба балки. Во втором модуле я дам более общее лечение. | ||||||||||||||
| Угадай Специальное решение | ||||||||||||||
| Хорошая новость в том, что я не математик.Если бы я был одним, я бы не смог нарисовать картинку выше потому что он уже содержит своего рода решение проблемы, поскольку он показывает (угадывая), как изгибается балка. Математики решают только задачи без какого-либо предварительного представления о результате, а это означает, что без милых маленьких фотографий. Вот почему они часто не решают настоящие проблемы, а только подробно обсудите, может ли проблема иметь решение, много решений — или, возможно, нет. | ||||||||||||||
| Все мы
не математики, однако, только знают , что
балка изгибается примерно так, как показано выше для данной ситуации.Мы знаем даже
более. Мы знаем, что если мы посмотрим на небольшую часть балки, мы сможем, по крайней мере,
в хорошем приближении, предположим, что изгиб локально, можно описать как круговой. Затем верхнюю и нижнюю поверхность луча можно нарисовать с помощью компаса, используя два радиуса, которые отличаются толщиной d . По сравнению с длиной недеформированной балки верхняя часть теперь немного длиннее, нижняя часть немного короче. Мы посмотрели на это раньше и там можно не сомневаться, что у нас всегда есть нейтральный ось внутри балки, длина которой не изменилась.В нашем простой пример у нас фактически есть нейтральный поверхность , но для более сложных сечений придерживается нейтральной оси (иногда также называемая нейтральной линией или центроидом ) лучше, поскольку она более общая. Этот нейтральная ось (а здесь и вся нейтральная поверхность) тоже, несомненно, будет в середину прямоугольной балки, как показано ниже. | ||||||||||||||
| ||||||||||||||
| Теперь, в процессе мысли, мы
«культивируйте» желтую часть изгиба балки. Чтобы держать его в форме
когда он еще был неотъемлемой частью балки, мы должны приложить силы.
Очевидно, что следует отметить, что только распределение сил, как показано на рис.
синий с правой стороны, и то же самое, отраженное на другом конце (не
показано) может вызвать деформацию, как показано.Всегда можно заменить раздачу на синего цвета
силы двумя точками F умным усреднением, и результат будет таким, как показано на
коричневый на левом конце нашей балочной части. Теперь мы видим, что суммарное действие сил заключается в создании крутящего момента или крутящий момент T с угадал звездную величину T = ½ Fd , так как расстояние между парой сил в предположении составляет d /2 , или половину балки толщина, как показано.´ (Если вы на самом деле все рассчитаете, расстояние будет 2d /3 ). | ||||||||||||||
| Пока я просто описываю
рисунок, генерируя первые уравнения по мере продвижения. Если вы продолжите смотреть на рисунок, вы поймете, что это еще не все. что можно описать простыми уравнениями. В частности, максимальная нагрузка справа вверху e t max = d /2 r ; это растяжение .В максимальная деформация справа внизу e b max = — d /2 r ; он сжимающий. | ||||||||||||||
| Почему? На картинке все видно. В
длина крайней части л 0 +
D л = л 0 + ½ d · Sina = l 0 + ( d ·
l 0 ) / 2r) .Отсюда получаем e max = [ l 0 + ( d · л 0 / 2r) — л 0 ] / л 0 = d /2 r . Вуаля! В равной степени, конечно, деформация линейно уменьшается от максимального значения на снаружи до нуля в нейтральной плоскости при движении внутри луча. | ||||||||||||||
| Вкл. в среднем , как мы предполагаем, верхняя или нижняя часть, таким образом, испытывает среднее значение деформация e av = ± d /4 r . | ||||||||||||||
| Пока мы рассматриваем только упругих деформаций , деформация e и напряжение s являются связанные: s = Y · e ; с Y = Янга модуль. | ||||||||||||||
| Среднее напряжение при нашей средней деформации — это среднее усилие F , деленное на половину
площадь поперечного сечения ш.д. .Другими словами: s = ( F ) / (½ bd ) = 2 F / bd = Y · e av = Y · d /4 r . Это дает нам для силы F = ( Y · d / 4 r ) · bd /2 = b · d 2 · Y /8 R | ||||||||||||||
| Теперь легко понять, что в конец это крутящий момент T = F · d /2 , вызывающий изгиб.Итак, давайте соотнесем крутящий момент T до радиуса кривизны r . С уравнением выше мы получаем окончательный результат : | ||||||||||||||
| ||||||||||||||
| Вычитание Немного Essentials | ||||||||||||||
| У нас есть красивое и простое уравнение.Мы много гадали, поэтому не можем ожидать, что это уравнение абсолютно
верный. Однако мы не сделали ничего вопиющего неправильно, так что этого не должно быть.
Совершенно неверно, но это весьма приличное приближение. Но что значит
уравнение означает? Во-первых, я скажу вам, что это определенно означает, несмотря на предположения. Затем я собираюсь обсудить недостатки этого простого подхода и то, как мы это можно исправить .. | ||||||||||||||
Мы можем сделать следующие основные выводы:
| ||||||||||||||
| ||||||||||||||
| На рисунке показан ряд
вещи.Прежде всего, это проясняет, что для показанной точечной силы локальная
изгиб наиболее силен вокруг зажима балки, потому что там у вас есть
самый высокий крутящий момент и, следовательно, наименьший радиус кривизны. Радиус кривизны
таким образом плавно изменяется по длине балки до места расположения
сила. Справа от силы изгиба в этом случае нет вообще
(имеется в виду бесконечный радиус кривизны). Обратите внимание, что мы еще не рассчитали кривую прогиба , а только увидели, как она
результат локальных искривлений. Не иллюстрируя это напрямую, мы можем вывести еще несколько моментов: | ||||||||||||||
| Если бы у нас не было точка силы, но некоторые распределены силы, мы все еще можем рассчитать крутящий момент
в любой момент путем суммирования или интегрирования по распределению сил. Как это
сделано не важно на данном этапе, все, что нам нужно знать, это то, что это может быть
Выполнено. Если бы мы применили точечную силу секунд где-то справа от показанного выше мы просто суммируем моменты силы. | ||||||||||||||
| Разве это не удивительно, сколько можно сделать выводы о сложной проблеме, не решая ее «с первого принципы «? Прежде чем я перейду дальше предположений, давайте посмотрим на проблемы, упущения и недостатки моего «гадательного» подхода. | ||||||||||||||
| Первое, что нужно сделать , — это маленькие кубики внутри нашего
опыт изгиба балки только одноосный нормальный
стрессы.Любой
маленький куб
внутри луч становится немного длиннее в направлении x ;
это показано
здесь в несколько ином контексте. Напряжение увеличивается линейно с увеличением
расстояние до нейтральной поверхности. Это приблизительное значение. Настоящие лучи испытают боковой сокращение в верхней половине и соответствующее расширение в нижней. Форма поперечного сечения изменится с прямоугольной на трапециевидную. Более того, внешние силы также вызывают некоторые компоненты сдвига в напряжении, которым мы пренебрегли.Понятно, что разобраться в этом будет непросто, так что позвольте мне сразу сообщить вам хорошие новости: Нам не нужно этого делать. Обработка изгиба балки с помощью только одноосных нормальных напряжений , конечно, не совсем правильно, его хватит почти на все практические случаи. | ||||||||||||||
| вторая точка более серьезная и откроет большую
банка червей. В нашем подходе к предположениям мы предположили, что прямоугольная
поперечное сечение, определяемое толщиной d раз больше ширины или
«широта» b .Мы догадались, что нейтральный самолет
прямо посередине. Если мы перепишем окончательное уравнение для радиуса
кривизна, как указано выше, мы можем выразить ее как r =
( b d 3 /16) · ( Y / T ) и
коэффициент ( bd 3 /16) содержит все информацию о поперечном сечении
геометрии, предположение о нейтральной плоскости (и, следовательно, о направлении
изгиб), плюс процедуры усреднения.Другими словами, он содержит всех возможных ошибок и недостатков
угадывающий подход. Поэтому неудивительно, что правильное значение этого фактора в результате правильных расчетов на самом деле: ( b d 3 /12) . Что ж, это очень плохо. Тем не менее, подход к предположениям был не таким уж Плохо и, конечно, стоит сделать для простого прямоугольного сечения. | ||||||||||||||
| Настоящая проблема в том, что для произвольные сечения, угадывание
подход не работает вообще больше для
вывод значения коэффициента перед Y / T который заботится о геометрии балки.Пока можно было сделать хорошее предположение
о положении нейтральной поверхности для
сечения, данные выше, вы
будет трудно, например, для треугольных сечений и многих других. Хуже того, вы не могли легко угадать средние значения по очевидным причинам. Так вы видите проблему: | ||||||||||||||
| ||||||||||||||
| Что ж, результат нашего предположения дает
ясный намек: мы можем сохранить общее соотношение r µ ( Y / T ) .Все что меняется, это то, что
константа пропорциональности ( b d 3 /16) в нашем
предположение) должны быть рассчитаны на основе реального сечения балки . На самом деле это не так
очень сложно сделать (при условии, что вы немного знаете об интеграции двух
Габаритные размеры). Результатом будет просто номер , который называется моментом инерции площади Я А .Если и было неправильное название, так это оно. В площадь момент инерции ничего не имеет что бы ни случилось с тем, что называется «моментом инерция «по уважительным причинам, когда вы рассчитываете, как тела вращаются вокруг некоторой оси. Единственная связь между ними заключается в том, что если вы запишете интегралы для вычисления этих моментов, математические выражения похожий. | ||||||||||||||
| Так все нам необходимо рассчитать момент инерции площади I для поперечное сечение и переписать наши основное уравнение как | ||||||||||||||
| ||||||||||||||
| Требуется вычислить положение нейтральной оси или центроид первый.Затем он определит система координат, так как мы центрируем ее на нейтральной оси. | ||||||||||||||
| Посмотрите на прямоугольную поперечный разрез на картинке ниже, чтобы получить это: красный кружок обозначает положение нейтральной оси (она проходит перпендикулярно плоскости изображения в x — направления, конечно). Поскольку изгибаясь о z — ось (приложив силу в направлении y — получить результаты изгиба различной формы относительно оси y ( прикладывая силу в направлении z ), нам нужно вычислить два момента инерции площади , I y и I y , чтобы учесть что. | ||||||||||||||
| Как центроид и
моменты площади I A определены, и как они
вычислено, является предметом другого модуля. Все, что нам нужно знать, это то, что
если кто-то рассчитывал это в прошлом, нам не нужно делать это самим. Мы
просто можно использовать сгенерированные числа. Вот несколько примеров; положение центра тяжести отображается красной точкой. | ||||||||||||||
| Красная точка обозначает нейтральную линию.Для тот же модуль Юнга Y , моменты площадей теперь дают сопротивление для гибки в y — или z — направлении ( I z или I y соответственно. ось, вокруг которой происходит изгиб). Что можно сразу оценить в том, что легкая трубка с несколько больший радиус, чем у тяжелого круглого сечения стержень может иметь одинаковый момент инерции и, следовательно, сопротивление изгибу.Вот почему у вас всегда есть полые балки (или и двойной фигурные) в любых структурное строительство. | ||||||||||||||
| Поперечное сечение меча, как правило, больше сложнее, чем приведенные выше, но с эллиптическим мы могли по крайней мере, сделай обоснованное предположение для мечей. Это позволяет нам оценить деформацию во внешних слоях в зависимости от изгиба, и это дает нам последний Важная информация: | ||||||||||||||
| Как только эта деформация e (или напряжение, связанное с s / e = Y ) достигает предел для пластической деформации или разрушения, все кончено.Поскольку мы должны предположим, что где-то вдоль лезвия может быть «слабое» место, все закончилось несколько раньше, чем мы рассчитывали. | ||||||||||||||
| Наконец, я просто скажу вам, что мы узнали, что здесь можно также перенести на «коробление балок» проблема, или эффект того, что ваш меч может погнуться, когда вы попытаетесь проткнуть прямо во что-то. Этим мы займемся в специальном модуле | .||||||||||||||
| Все это может показаться ошеломляющим, но это не так. Некоторые эксперты говорят, что инженерия — это на 80% логика и на 20% приложение. Некоторые могут обсудите это, но здесь мы предоставим вам основную инженерную информацию и приложения, которые не всегда доступны. Пока балки нагружаются по-разному.Балка с простой опорой — это обычно используемая балка (как показано выше). Ниже вам будет показано, как все это работает, и как спроектировать и выбрать балку (дерево или стали). Мы также коснемся выбора бетонной балки. В приведенных ниже примерах представлены шаги, необходимые для выбора и проектирования деревянного Луч. Если вы хотите выбрать и спроектировать стальную балку, шаги будут одно и тоже. Отличаются только свойства материала, например, напряжение изгиба в Материал (fb), момент инерции (I), модуль упругости (E) и сечение Модуль (S). Все остальные уравнения были бы такими же, если бы у вас были такие же нагрузка (W) и пролет (L). Обычные этапы проектирования балки:
Ниже приведены практические примеры нагрузок и расчетов, применяемых к прямоугольным стержням. Равномерно распределенная нагрузка (100 фунтов на фут) на 2 x 10 Пример простой опорной балки с равномерно распределенной нагрузкой Точечная сосредоточенная нагрузка (600 фунтов) на 2 x 12 Пример простой опорной балки с сосредоточенной нагрузкой Точечная сосредоточенная нагрузка (1200 фунтов) на 4 x 12 Пример простой опорной балки с сосредоточенной нагрузкой Бетонные балки: Для среднего домовладельца, который хочет построить дом или построить пристройку, наиболее распространенной используемой бетонной балкой является сборная балка или сборная перемычка. Эти балки или перемычки обычно производятся на фабрике с контролируемым качеством. У этих компаний обычно есть в наличии Руководства, в которых указана грузоподъемность и пролет балок или перемычек, которые они изготавливают. Это очень полезно и удобно, поскольку вам не нужно проводить фактические расчетные операции. Если вам нужна специальная балка с особыми условиями нагрузки, рекомендуется обратиться к инженеру для проектирования балки. |
Калькулятор и таблица веса двутавровой балки и двутавровой балки (бесплатно)
Что такое двутавровая балка
Двутавровая балка Сталь Двутавровая балка также называется стальной балкой (универсальная балка), которая представляет собой длинную стальную полосу с сечение двутавровое. Двутавровая балка делится на обыкновенную двутавровую и световую двутавровую.
Что такое двутавровая балка
Двутавровая балка разработана на основе оптимизации двутавровой стали. Название происходит от того факта, что его раздел совпадает с английской буквой H.Это экономичный высокоэффективный профиль с более разумным соотношением прочности и веса и более оптимизированным распределением площади поперечного сечения.
Каждая часть H-образной стали расположена под прямым углом, поэтому она обладает такими преимуществами, как сильное сопротивление изгибу, экономия затрат, простая конструкция и легкий вес во всех направлениях.
Он часто используется в больших зданиях, где требуется большая перехватывающая способность и хорошая стабильность поперечного сечения, например, в высотных зданиях и мастерских.Кроме того, он также широко используется на судах, мостах, подъемно-транспортном оборудовании, кронштейнах, фундаментах оборудования, фундаментных сваях и т. Д.
H-образная балка по сравнению с двутавровой балкой
Что касается разницы между двутавровой балкой и двутавровой балкой , вы можете обратиться к статье ниже.
Двутавровая балка по сравнению со сталью (14 анализ различий)
Расчет двутавровой балки и расчет веса двутавровой балки
В этой статье мы в основном обсуждаем, как рассчитать вес двутавровой и двутавровой балок.
Для удобства расчетов мы создали два калькулятора: калькулятор веса двутавровой балки и калькулятор веса двутавровой балки.
С помощью этих двух калькуляторов вы можете легко рассчитать вес двутавровой и двутавровой балок.
Конечно, чтобы узнать больше о расчетах веса различных металлов, вы можете обратиться к следующей статье.
Теоретическая формула расчета веса металла (30 типов металлов)
Кроме того, мы также сделали калькулятор тоннажа листогибочного пресса и калькулятор усилия прессования.Если вам интересно, вы можете воспользоваться им, перейдя по ссылке.
Теперь начните использовать калькулятор для расчета веса профиля.
Если вы устали от использования калькулятора для расчета веса двутавровой балки и двутавровой балки, вы можете обратиться к следующей таблице веса двутавровой балки и таблице веса двутавровой балки.