Расчет металлической балки перекрытия на прогиб и на жесткость

11.07.2016/в Плита перекрытия /от admin

Металлические балки двутавровые

Кроме повсеместно ведущегося строительства многоэтажных зданий с большим числом квартир, широкое распространение получило сооружение частных домов, причем не только небольших одноэтажных, но и довольно крупных, с двумя и более этажами, иногда и с мансардой наверху или обитаемым чердаком. Для таких домов уже не подходит каркасный метод; материалом часто служит, вместо дерева, кирпич или железобетон. Возведение крупных частных домов должно вестись по всем правилам строительной науки, так как ошибки при проектировании или воплощении проекта могут привести к нежелательным последствиям.

Если строящийся дом представляет собой капитальное здание – из бетона, кирпича, шлакоблока, то для потолочных перекрытий, межэтажных и чердачных, целесообразно применить железобетонные плиты. Наиболее подходящий тип каркаса, способный выдержать вес таких перекрытий, – это каркас, элементом которого является металлическая балка двутаврового профиля.

Именно этот вид проката, установленный своей стенкой вертикально, обладает наибольшей несущей способностью. Естественно, фундамент и стены дома при этом должны быть достаточной прочности, чтобы выдерживать дополнительный вес от 0,5 до 1 тонны – столько металла, в зависимости от количества балок и номера профиля может понадобиться для потолочного перекрытия.

Чтобы избежать лишних затрат и лишнего веса каркаса потолка, а также не допустить обрушения или значительного прогиба балок, необходимо заранее рассчитать их параметры и по результатам расчета подобрать нужный прокат. Расчет сводится к вычислению следующих величин: требуемого момента сопротивления и минимального момента инерции сечения балки, а исходя из последнего – максимального относительного прогиба.

Примечание

Расчет ведется по двум характеристикам – на прочность и на жесткость. По полученным значениям момента сопротивления и момента инерции в таблицах ГОСТ находят требуемый номер проката.

Исходные данные для расчетов

Для каркаса потолочных перекрытий малогабаритных частных домов обычно используется двутавр 10 – 20 номеров. Характеристики этих профилей приводятся в ГОСТ 8239-72 – их линейные размеры, площади сечения, максимальные моменты сопротивления по вертикали W_y и минимальные моменты инерции J_y.

Необходимо знать тип плит, которые будут опираться на балочный каркас, а также размеры несущего периметра дома. Можно применить пустотные железобетонные плиты ПК-12-10-8 (1180 х 990 мм, масса 380 кг), а размеры дома взять 4,5 х 6 м. Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см). Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.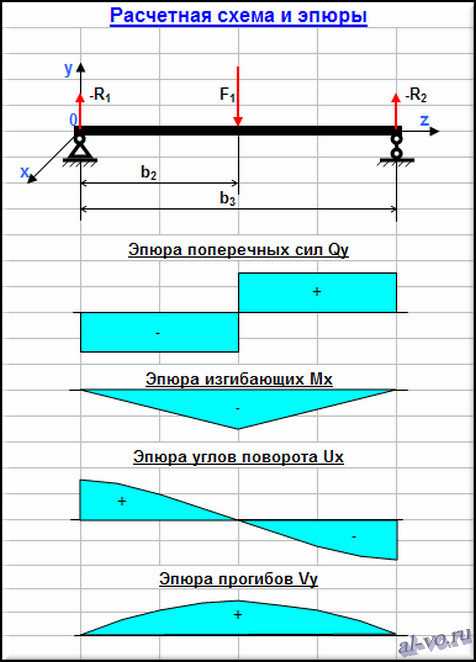

Распределенная нагрузка при таком типе плит будет равна 325 кгс / м². К этому надо добавить нагрузку возможных перегородок на верхней стороне перекрытия (75 кгс / м²) и возможную временную нагрузку (200 кгс / м²). В итоге нагрузка, распределенная по площади:

Q = 325 + 75 + 200 = 600 кгс / м²,

а линейная нагрузка

q = Q * p = 600 кгс / м = 6 кгс / см.

Эта величина используется в дальнейших расчетах.

Расчет на прогиб

Изгибающий момент для каждой балки вычисляется, исходя из величины линейной нагрузки q, шага укладки балок p и длины перекрываемого пролета L. Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).

Искомая величина момента, в таком случае:

M_y = (q * L²) / 8 = 6 * 450² / 8 = 151875 кгс * см.

Максимальный момент сопротивления сечения балки можно рассчитать, разделив изгибающий момент на расчетное сопротивление стали – например, марки С235, равное 2150 кгс / см²:

W_y = 151875 / 2150 = 70,6 см³.

Это полученное значение надо сравнить с величиной момента сопротивления сечения двутавровой балки. Из таблицы ГОСТ 8239-72 видно, что вычисленный показатель  примерно соответствует (с запасом) моменту сопротивления для профиля 14 (81,7 см

3). Следовательно, этот номер проката будет удовлетворять требованиям к прочности балок.

Расчет на жесткость

Жесткость балок характеризуется максимальной величиной прогиба при заданных исходных параметрах. В случае распределенной нагрузки прогиб вычисляется по формуле:

f = 5 * q * L⁴ / (384 * E * J_y), где

• q – линейная нагрузка на балку;
• L – длина пролета;
• E – модуль упругости материала, для стали С235 равный 2,1 * 10⁶ кгс / см²;
• J_y – минимальный момент инерции для данного профиля.

Для принятых ранее исходных данных, с учетом того, что из расчета на прочность наиболее подходящим профилем оказался № 14, для которого J_y, по табличным значениям ГОСТ, равен 572 см⁴, можно получить:

f = 2,6 см,

а в относительной мере, с учетом того, что длина пролета 450 см – 1 / 172. Это превышает максимально допустимый прогиб, принятый равным 1 / 250.

Поэтому расчет приходится повторить и вычислить прогиб для другого номера проката. Для № 16, у которого момент инерции равен 873 см⁴, абсолютный прогиб получается 1,74 см, а относительный – 1 / 256, что является приемлемым.

Данная страница не существует!

• О центре

  • История

  • Структура

  • Совет Директоров

  • Руководство

  • Специалисты

    • Помним

  • Дирекция специальных проектов

  • Дирекция научно-технических проектов и экспертиз

  • Вакансии

  • Научные школы

  • Партнеры

  • Технологическая платформа «Строительство и архитектура»

  • Членство в организациях

  • Лицензии

  • Раскрытие информации

    • Отчетность 2019

    • Непрофильные активы

  • Противодействие коррупции

  • Социальная ответственность

• Услуги

  • В сфере подземного строительства

    • Геологические изыскания

    • Инженерные изыскания

  • В сфере бетонного строительства

  • В высотном и уникальном строительстве

  • Проектирование

  • Управление проектами

    • Проект реконструкции

  • Экспертиза

    • Обследование зданий

  • Технологический и ценовой аудит (ТЦА)

  • Галерея проектов

  • Ультразвуковой контроль сплошности свай и ультразвуковой контроль сплошности стен в грунте

  • Акустическое обследование фундаментных плит

  • Сейсмоакустический контроль сплошности свай

  • Сейсмоакустический контроль сплошности фундаментов и плит, поиск дефектов и пустот

  • Динамические испытания свай по волновой теории удара

  • Статические испытания свай

  • Теплоконтроль сейсмичности при бетонировании свай

• Новости

  • Новости Центра

  • Новости отрасли

  • Календарь мероприятий

  • СМИ о нас

  • Отзывы организаций

  • Закупки

• Центр
  сертификации

• Заказчику

  • Оборудование

  • Контакты

• Научно —
  техническая
  деятельность

  • Научные и инновационные разработки в области строительства и их внедрение

  • Научно-исследовательские (теоретические, поисковые и прикладные) работы

  • Научно-технический совет (НТС)

  • Научно-техническое сопровождение

  • Нормативно-технические документы

    • Разработка СТУ

  • Сотрудничество

  • BIM-технологии

  • Интеллектуальная собственность

  • Корпоративные издания

• Научно —
  образовательная
  деятельность

  • Сведения об образовательной деятельности

  • Диссертационный совет

  • Информация о защитах диссертаций

  • Аспирантура

  • Подготовка диссертаций без освоения программы подготовки научно-педагогических кадров в аспирантуре

  • Прикрепление для сдачи кандидатских экзаменов

  • Докторантура

  • Повышение квалификации

  • Учебные программы Центра информационного моделирования

  • Психология личностного роста в профессиональной деятельности

  • ПК СТАРКОН. 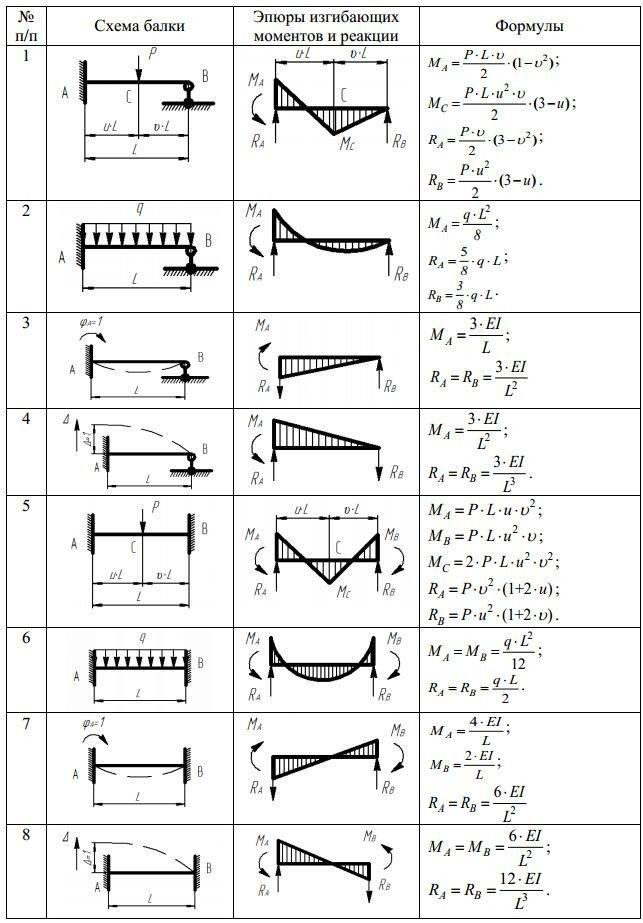Обучение.

  • Кафедра Иностранных языков и кафедра Философии

  • Кафедра Строительные сооружения, конструкции и материалы

• Вакансии

• Контакты

  • Обратная связь

Проверка стальной балки на прогиб

БЛОГ PROJECT TUTORIAL

 

Прогиб балки является одной из проверок, которые должны выполняться при расчете предельных состояний эксплуатационной пригодности. Прогиб — это смещение элемента конструкции под действием нагрузок, без учета смещения остальной части конструкции.

 

Рис. 1. Ограничение прогиба

 

 

 

 

Рис. 2. Предлагаемые пределы прогиба для элементов конструкции (Сравнение результатов анализа и результатов проектирования)

 

SW не просто использует результаты анализа, потому что прогиб в результате анализа представляет собой величину, включающую деформацию соседних элементов.

 

 

Результат проектирования консольной балки

Рисунок 3. Результаты проверки отклонения

Рисунок 4. Результаты анализа и конструкции

Как вычислять это на Hangual? (Пример — консоль)

 

Вычисление вручную дает приблизительное значение, поэтому ручное значение и значение результата Gen не могут совпадать.

Пожалуйста, обратитесь только к расчетной концепции и способу.

Рисунок 5. Пример кантилевера модели

Как вычислять деформацию кантилевера по ручным (единица: мм) — Пример

Δ = (Δ _E 4555559595

Δ = (Δ _{. E 4551515151515155959}

Δ = (δ _{4. –Δ C ) -θ 1 * L (добавьте это, чтобы удалить эффект по деформации столбца)}

= (0,846566 -(-0,039507)) -0,000473 * 1981,2

= -0510 мм

9000 2

= -0,0510 мм

= -0510 мм

= -0510 мм

0007

Результаты проверки отклонения

Рисунок 6. Результаты проверки отклонения — 1

Как рассчитать его по общению? (Пример — консольный)

Рисунок 7. Пример модели кантилевера с узелом A

θ 1 : роскошь деформацией колонны

0002 θ ₂ : угол линии, которая связывает деформированные точки

BEAM COLUND и первого узла, когда L разделяется на

1001 100. 100.

Δ _E : деформация конца луча (деформация на одном конце луча)

Δ _{C Δ C Δ C Δ C Δ C C .0153}

      beam)   

Node A : the first internal node when L is divided into 100 equal

              parts

L : Length of beam

 

 

 

 

 

Как рассчитать деформацию кантилевера в мидасе Gen (единица измерения: мм)

 

Gen использует θ ₂   рассчитывается внутренне. θ ₂ означает угол линии, соединяющей узлы колонны и ближайший к колонне деформированный узел при разделении балки на 100 равных частей и

θ ₂ = ( DZ AT Узел A = DZ AT NODE 1) / (L / 100153 AT NODE 1) / (L/15) AT NODE 1) / (L / 100) . ) / (1981.2/100)

    = 0.000425

δ = ( δ _E – δ _C ) – θ 2 *L

   = (0.846566 – (-0.039507)) – 0.000425* 1981.2

   = — 0.0436 mm

 

 

 

 

 

Deflection checking results

 

Рисунок 6. Результаты проверки отклонения – 1

 

 

Dz в узле A = -0,031082

Поскольку это внутреннее значение, оно не выводится отдельно.

 

 

 

Как рассчитать? (Example -Continous Beam)

 

Figure 8. Continuous Beam Example Model 

 

δ ₁ : Deformation at One end of beam

δ ₂ : Деформация на другом конце балки

δ _м : Деформация в средней точке балки

 

 

 

How to calculate the deformation of the cantilever by manual (unit : mm)

 

δ = δ _m – ( δ ₁ – δ ₂ )/2

   = 0.845448 – (0.039507 – 0.000) / 2

   = 0.8257 mm

Результаты проверки отклонения

Рисунок 9. Результаты проверки отклонения -2

Рекомендуйте прочитать эту статью. Склад с односкатной крышей».

 

• Последние
• Популярные

Подписаться на рассылку новостей S.O.S

Прогиб балок – формула, методы, вопросы

Что такое прогиб балок?

Прогиб измеряется от исходной нейтральной поверхности балки до нейтральной поверхности деформированной балки. Конфигурация, которую принимает деформированная нейтральная поверхность, известна как упругая кривая балки.

Прогиб балок Определение

Прогиб балок – это поперечная деформация, возникающая под действием поперечной силы и изгибающего момента. Прогиб балок под действием перерезывающей силы незначителен по сравнению с прогибом балок под действием изгибающего момента. Поэтому отклонение балок из-за поперечной силы не учитывается.

Давайте теперь кратко рассмотрим наклон и отклонение балок.

• Наклон луча : Наклон луча — это угол между отклоненным лучом и фактическим лучом в той же точке.
• Прогиб балки: Прогиб определяется как вертикальное смещение точки на нагруженной балке. Многие методы определяют наклон и прогиб в сечении нагруженной балки.

Максимальное отклонение происходит при нулевом наклоне. Положение максимального прогиба находится путем приравнивания уравнения наклона к нулю. Затем значение x подставляется в уравнение прогиба для расчета максимального прогиба. «Прогиб балок» является важной темой предмета «Сопротивление материалов».

Формула отклонения балок

Деформированная форма фасоли известна как упругая кривая. Ниже приведены формулы наклона и прогиба балок для некоторых стандартных случаев. Эти формулы можно использовать непосредственно для решения многих задач прогиба балок.

y — вертикальное отклонение балки. Цель балки определяется как форма, заданная формулой:

θ= dy/dx

Момент Уравнение кривизны используется для расчета отклонения балки.

1/R=M/EI

Где

• M = изгибающий момент
• R = радиус кривизны деформированной формы
• EI = жесткость балки на изгиб = кривизна
• 4/904 904

Deflection Differential Equation

d ² y/dx ² = M/EI

(a)

Θ _B = ML/EI

∆ _B = ML ² /2EI

(б)

θ _B = PL ² /2EI

∆ _B = PL ³ /3EI

(C)

θ _B = WL ^{, № . № . B= WL 4 /8EI}

DIFFERENTIAL EQUATION OF THE DEFLECTION CURVE OF BEAM

Deflection of Beams Formula for Cantilever Beams:

Deflection of Beams Formula for Simply supported Beams:

Методы определения прогиба балки

Существуют различные методы определения прогиба балки и конструкций в зависимости от типа нагрузки и характера балки. Некоторые важные методы определения отклонения балок:

• Метод двойного интегрирования
• Метод Маколея
• Метод площади момента
• Метод сопряженной балки

Метод двойного интегрирования 0002 Метод двойного интегрирования подходит для призматических балок с постоянным EI. Этот метод подходит, когда уравнение изгибающего момента остается постоянным по всей длине балки. Согласно методу двойной интеграции,

EID ² Y/DX ² = MX

, где

EI = Жесткость изгибного = ∫Mx+ c ₁

Это дает уравнение наклона, где dy/dxis наклон или вращение.

Интегрируя приведенное выше уравнение,

EI.y= ∬Mx+ ∫c ₁ + c ₂

Где y — прогиб.

Метод Маколея

Метод Маколея является усовершенствованием метода двойного интегрирования. Становится трудно решать отклонения балки, которые необходимо разделить на множество секций. Поэтому этот метод используется там, где нет необходимости разделять луч. Этот метод подходит для призматических стержней, имеющих разные изгибающие моменты в разных поперечных сечениях.

Рассмотрим приведенную выше балку, на которую воздействуют две точечные нагрузки L ₁ и L ₂ на расстоянии «a» и «b» от левой опоры. Рассмотрим сечение x-x на расстоянии x от левой опоры. Нахождение момента относительно х-х:

Mx= R _A x- L ₁ (x-a)- L ₂ (x-b)

EId ² y/dx 5 L 01 x ^{2 9051 ₁ (x-a)- L ₂ (x-b)}

Интегрируя приведенное выше уравнение,

EI y= R _A x ³ /6+ c ₁ x+ c ₂ -[L ₁ (x-a) ³ /6]- [L ₂ / 14 76 9095 905

Метод момент-площадь

Метод момент-площадь используется, когда нам нужно проанализировать балку, в которой мы заинтересованы в расчете наклона и отклонения балки в одном месте. Этот метод подходит для призматических и непризматических элементов. Этот метод основан на площади под диаграммой изгибающего момента.

Теорема 1

Изменение наклона от сечения A к сечению B B-A будет равно площади диаграммы M/EI между Θ _A и Θ _B . Теорема 2

Метод сопряженных балок

Сопряженная балка — это воображаемая балка, диаграмма нагрузки которой является диаграммой M/EI реальной балки. Метод сопряженных балок подходит как для призматических, так и для непризматических элементов; единственное требование — диаграмма M/EI не должна быть заполнена; должно быть легко определить площадь и центр тяжести диаграммы M/EI. Если диаграмма M/EI положительна, то нагрузка в сопряженной балке будет восходящей. Если диаграмма M/EI отрицательна, то нагрузка в сопряженной балке будет нисходящей.

Теорема 1

Уклон в любом сечении реальной балки становится поперечной силой в соответствующем сечении сопряженной балки. Диаграмма поперечной силы сопряженной балки представляет собой диаграмму наклона реальной балки.

Теорема 2

Прогиб на любом сечении реальной балки становится изгибающим моментом на соответствующем сечении сопряженной балки. Диаграмма изгибающего момента сопряженной балки представляет собой диаграмму прогиба реальной балки.

Метод суперпозиции: Метод суперпозиции, при котором приложенная нагрузка представлена ​​в виде ряда простых нагрузок, для которых доступны формулы прогиба. Затем вычисляется требуемый прогиб путем сложения вкладов компонентных нагрузок (принцип суперпозиции).

В вопросах используется самая прямая формула. Отсюда советуется искать формулу прогиба балки, которая прямо запрашивается из этой темы, а не пускаться в длинные выкладки.

Прогиб при общих нагрузках

1. Сосредоточенная нагрузка на свободном конце консольной балки (начало точки А):

Максимальный момент, M=−PL 7 Наклон

:θ=PL

² /2EI

Максимальный прогиб:δ=PL ³ /3EI

Уравнение прогиба (у положительное вниз): EIy = (Px ² )(3L−x)/6

2. Сосредоточенная нагрузка в любой точке пролета консольной балки

Максимальный момент: M = -WA

Наклон на конце: θ = WA ² /2EI

Максимум. )/6EI

Уравнение отклонения (у положителен вниз),
EIy = Px ² (3a−x)/6for0 EIy = Pa ² (3x−a)/6fora

3. Равномерно распределенная нагрузка по всей длине консольной балки

Максимум момента: M = −WL ² /2

Наклон на конце: θ = WL ³ /6EI

Максимум. Дефект: Δ = WL ^{4.9057 /80515 /} / /80515 /80515 / /9057 /80515 / / / / / /9057 /80515 / /9057 /80515 /9057 /

/9051. (у положителен вниз),
EIy=wx ² (6L ² −4Lx+x ² )/120L

4. Треугольная нагрузка, полная на фиксированном конце и ноль на свободном конце

Максимальный момент: M=−wL ² /6

Уклон на конце: θ = WL ³ /24EI

Максимальное отклонение, Δ = WL ⁴ /30EI

Уравнение отклонения: (y положительно),
EIY = WX ^{2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 (y является положительным). 10L 2 x+5Lx 2 −x 3 )/120L}

конец: θ=ML/EI

Максимальное отклонение: δ = мл ² / 2EI

Уравнение отклонения (Y положительный вниз),
EIY = MX ² /2

6. Connect Rated AT MIDAT

Максимальный момент: M = PL /4

Наклон на конце: θ _A = θ _B = WL ² /16EI

Maximum Devetuction: 15 /16EI

. 48EI

Уравнение отклонения (у положителен вниз),
EIy=Px{(3/4)L ² −x ² )}/12 для 0

7. Равномерно распределенная нагрузка по всему пролету простой балки

Maximum Moment: M = wL ² /8

The slope at the end: θ _L =θ _R =wL ³ /24EI

Maximum deflection: δ=5wL ⁴ /384EI

Уравнение прогиба (EIy=wx(L ³ −2Lx ² +x ³ )/24

9. Треугольная нагрузка с нулевой на одной опоре и полной на другой опоре простой балки

Максимальный момент: M = w _o L 5 / 90√ 3

Наклон на конце,

θ _L = 7WL ³ /360EI

θ _R = 8WL ³ /360515.60515.905.905.. 9515951595159159595951515959595951595159515151515151595159515951595159515951595159515951591595159159515915951595159515. _{. 4 /384EI при x = 0,519L}

Уравнение прогиба (у положителен вниз),
EIy = wx(7L ⁴ −10L ² x+3x)/360L

10. Треугольная нагрузка с нулевой нагрузкой на каждой опоре и полной в середине пролета простой балки

Максимум 95 9000 M = WL ² /12

Наклон на конце, θ _L = θ _R = 5WL ³ /192EI

Maximum Defluction: 5 /192EI

.

Уравнение отклонения (у положителен вниз),
EIY = W _O x (25L ⁴ −40L ² x ² +16x ⁴ )/960L для 010292915 . . . . . . . . ). Задача 1: Каковы уклон и направление консольной балки на свободном конце нагрузки, действующей на свободный конец?

Решение-

Дифференциальное уравнение прогиба

M= -Px

EId ² y/dx ² = -px

∫eid ² Y/DX ² = ∫-PX

EIDY/DX = -PX ² /2+ C _{1 9059}

9

9

9019

9

9

9

9

9

9

9

9

9

9

9

9

9

9

9

9

9

9

9

9

9

9. 9. x=L, dy/dx = 0,

c ₁ = PL ² /2

EIdy/dx= -Px ² /2+ PL ² /2

9000 Интегрируя это, мы получаем ,

EIy= -Px ³ /6+ PL ² x/2+ c ₂

Граничное условие x=L, y=0

c _{2 PL} = -0514 3 /3

EIy= -Px ³ /6+ PL ² x/2- PL ³ /3

Наклон и прогиб на свободном конце

4 PLdy/d Наклон /2EI

Прогиб y= PL ³ /3EI

Задача 2: Свободно опертая балка с пролетом 6 м нагружена, как показано на рисунке. I = 78 x 10 ⁶ мм ⁴ E = 2,1 x 10 ⁵ Н/мм ² . Найдите центральные прогибы.

Решение-

Мы знаем, что

y _C = WL ³ /48EI = 60 × 10 ³ × 5000 ^{14 3} 1515151515151515151415151515151515151515151515151515151515151515151515151515151.