Расчет с перераспределением моментов железобетонной неразрезной балки и экономией арматуры
Васильев Антон Владимирович1, Лукьянов Сергей Дмитриевич2, Назарова Дарья Сергеевна3, Переверзев Никита Александрович4
1Воронежский государственный технический университет, старший преподаватель кафедры строительных конструкций, оснований и фундаментов имени профессора Ю.М. Борисова
2Воронежский государственный технический университет, бакалавр 4 курса, направление «Промышленное и гражданское строительство»
3Воронежский государственный технический университет, бакалавр 4 курса, направление «Промышленное и гражданское строительство»
4Воронежский государственный технический университет, бакалавр 4 курса, направление «Промышленное и гражданское строительство»
Аннотация
Расчет неразрезной балки по упругой системе и с учетом перераспределения моментов.
Получение и сравнение результатов армирования балки.
Ключевые слова: железобетонная неразрезная балка, пластический шарнир, постоянный изгибающий момент, расчет с перераспределением моментов, экономия рабочей арматур
Библиографическая ссылка на статью:
Васильев А.В., Лукьянов С.Д., Назарова Д.С., Переверзев Н.А. Расчет с перераспределением моментов железобетонной неразрезной балки и экономией арматуры // Современные научные исследования и инновации. 2018. № 2 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2018/02/85807 (дата обращения: 07.04.2023).
Введение. В строительстве всегда есть резервы для экономии и оптимизации стоимости строительного производства. Снижение затрат для изгибаемых элементов возможно при исключении из растянутой зоны бетона, если это не снижает прочности конструкции в целом. Конструкция остается прочной, пока с увеличением предельно допустимой нагрузки не произойдет разрушение.
Разрушение в монолитных статически неопределимых конструкциях возможно только после потери геометрической неизменяемости всей системы с лишними связями с образованием пластических шарниров.
Цель: рассчитать железобетонную конструкцию по упругой системе и с учетом перераспределения моментов, выявить экономическую эффективность.
Задачи исследования:
1. Создание расчетной схемы позволяющей произвести расчет по упругой системе, преобразование ее с учетом перераспределения моментов с выявлением мест возникновения пластических шарниров и определением значений постоянного изгибающего момента в них.
Проверка по образованию, раскрытию трещин и деформациям.3. Сравнение результатов.
Создание расчетной схемы позволяющей произвести расчет по упругой системе и преобразование ее с учетом перераспределения моментов. В большинстве случаев инженер задает в ПК статически неопределимую конструкцию, и программный комплекс выделяет усилия, по которым инженер подбирает арматуру. При этом изменить значения моментов, подобранных по правилам строительной механики, казалось бы невозможно. Однако при введении в расчетную схему пластического шарнира [9], тем самым откорректировав ее, можно ограничить дальнейшее увеличение момента. Таким образом, инженер может снизить усилие от момента в рассматриваемом сечении.
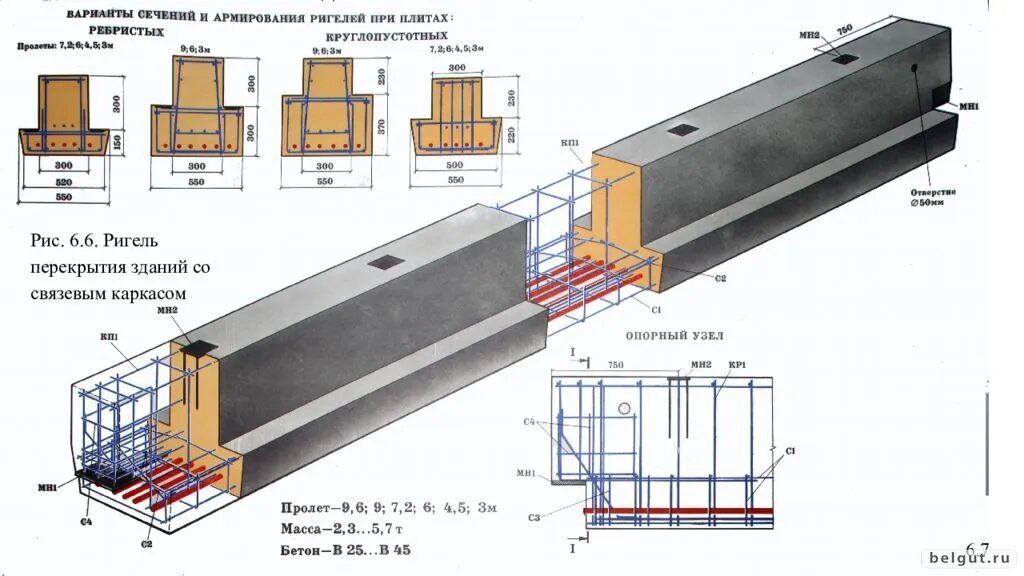
Рассмотрим неразрезную пяти пролетную железобетонную балку с равными пролетами 6 м (рис.1), с высотой сечения 0,4 м и шириной – 0,2 м. Бетон – класса В30. Продольная арматура класса А400. Нагружаем равномерно распределенной нагрузкой 25 кН/м. Моделируем расчетную схему в ПК и получаем усилия [10].
В большинстве случаев перекрытия рассчитываются под равномерно распределенную нагрузку, при этом экстремумы эпюры моментов возникают на опорах и в пролетах. Поэтому введение пластического шарнира желательно возле опор.[8]
Условие предельного равновесия, т.е. возможности образования пластических шарниров и развития достаточных местных деформаций при достижении конструкцией предельного равновесия, обеспечиваются соблюдением конструктивных требований:
1) сооружение или ее рассматриваемый элемент должны быть сконструированы так, чтобы причиной ее разрушения не могли быть срез сжатой зоной или раздавливание бетона от главных сжимающих напряжений;
3) следует применять арматурные стержни с площадкой текучести или сварные сетки из обыкновенной арматурной проволоки.
При условии возникновения пластического шарнира на опоре, необходимо задаться значением изгибающего момента.
Расчетную схему можно собрать иначе. Пластический шарнир разделяет неразрезную систему на отдельные балочные элементы. Узел упругой неразрезной системы, в котором планируется образование пластического шарнира, состоит из узлов на концах балочных элементы и узлом опоры. Опорный узел не имеет перемещений относительно опоры. Узлы на концах балочных элементов поворачиваются благодаря пластическим шарнирам. Поэтому в преобразовании обычной расчетной схемы в образовании пластического шарнира в одном узле упругой системы участвует группа узлов. Узлы, состоящие в группе, объединены в треугольный элемент между собой жесткими стержнями (жесткими вставками). Треугольный элемент представляет собой: верхний стержень численно равен ширине опоры, а расстояние от верхнего стержня до нижнего узла – половине высоты балки. Длина верхнего стержня не оказывает влияния на получаемые усилия. Поэтому в рассматриваемой пятипролетной балке для наглядности это значение принято 0,2 м. Два нижних стержня треугольного элемента имеют по концам шарниры на поворот по направлениям Uy и Uz.
Таким образом, изгибающий момент с балки не передается на нижние стержни треугольного элемента (рис.2).В расчетной схеме упругой неразрезной системы верхний стержень треугольного элемента делается без шарниров. В расчетной схеме с перераспределением моментов верхний стержень треугольного элемента делается с шарнирами на поворот по направлениям Uy и Uz,
Согласно методике расчета статически неопределимых железобетонных конструкций [2] из уравнения равенства виртуальных работ внутренних усилий и внешнего усилия при соответствующем прогибе для участка балки имеющем две опоры А и В имеем:
, (1)
где — пролетный момент, и — опорные моменты, и — расстояния от соответствующих концов А и В рассматриваемой балки до сечения с , — пролет балки, — момент от внешней нагрузки в статически определимой свободно лежащей балке пролетом .
Рассматривая только левую часть уравнения равновесия (1) получим уравнение для выравнивания моментов, где в левой части описываем моменты упругой системе, а в правой моменты необходимые при перераспределении моментов.
Для крайнего пролета и , при перераспределении моментов имеем:
(2)
Тогда с учетом и поправки знака пролетного момента получаем:
(3)
Для среднего пролета и , при перераспределении моментов имеем:
(4)
Тогда с учетом и поправки знака пролетного момента получаем:
(5)
Отклонение моментов с расчетной схемой составляет 0,4%.
В результате получаем выровненную эпюру моментов (рис.2).
После получения перераспределенного момента, произведем расчет по предельным состояниям второй группы.
Проверка по образованию, раскрытию трещин и деформациям. Рассмотрим наиболее характерное сечение 2-2.
Определим момент образования трещин с учетом неупругих деформаций растянутого бетона, получаем:
. (6)
То есть трещины образуются.
Принимаем коэффициент надежности по нагрузке равный единице, в результате чего изгибающий момент — .
Рассмотрим варианты:1) Если учесть работу растянутого бетона, защемленного между двумя рядами рабочей арматуры. Схема напряженно-деформированного состояния изгибаемой балки с трещинами при расположении растянутой арматуры в два ряда для сечения 2-2 представлена на рис.3а. Тогда:
— (7)
проверка выполняется.
2) Если расположить подобранную арматуру в один ряд (рис.3.б), тогда:
— (8)
проверка выполняется.3) Если учесть, что нагрузка всегда делится на продолжительно действующую и непродолжительно действующую нагрузки, и, предположив, что длительно действующая составляет 94 % и менее. Тогда:— (9)
проверка выполняется.
Рассмотрев варианты, можно сделать вывод, что проверка по раскрытию трещин удовлетворяется.
За счет шарнирного опирания неразрезной балки на первой и последней опорах, кривизна и прогиб в крайних пролетах больше, чем в средних. Поэтому рассматривать прогиб целесообразно в крайнем пролете с предельно допустимым, в нашем случае равным .
Определим, как изменяются значения прогибов по отношению к выбранным расчетным схемам (рис.1.а) и (рис.2.а), то есть наличием и отсутствием выгиба. Для этого рассмотрим расчетные схемы соответственно на (рис.4.а) и (рис.4.б), отличающиеся наличием следующих пролетов или заменой их шарниром с наложенным у окончания балки изгибающим моментом, соответствующим опорному моменту возникающим в неразрезной балке.
Определим наиболее неблагоприятное действие нагрузки на значение прогиба на примере балки по расчетной схеме согласно (рис.4.а) (соответствующий рис.1.а).
Допустим, что вся нагрузка непродолжительного действия, поэтому прогиб согласно [2, 4, 7] равен:
(10)
Если предположить, что вся нагрузка продолжительного действия, то прогиб, согласно [2], равен:
(11)
Заметим, что наиболее неблагоприятное действие нагрузки на значение прогиба – продолжительное действие нагрузки, поэтому сравнивать прогибы для разных расчетных схем будем при условии продолжительного действия нагрузки.
Определим значение прогиба балки по расчетной схеме согласно (рис.4.б). Изгибающий момент и коэффициенты армирования, так же как и в расчетной схеме по (рис.4.а).
Прогиб балки будет складываться из прогиба от равномерно распределенной нагрузки и прогиба от момента на опоре.
(12)
(13)
Находим экстремум при :
(14)
То есть при отсутствии выгиба в следующем пролете прогиб балки с расчетной схемой по (рис.4.б) увеличивается на 6,62 % по отношению к прогибу балки с расчетной схемой по (рис.4.а).
Определим значение прогиба балки с учетом перераспределения моментов по расчетной схеме согласно (рис.4.в). Прогиб балки будет складываться по (12) из прогиба от равномерно распределенной нагрузки и прогиба от момента на опоре:
(15)
Подставляя значения и складывая (12) и (15), получаем уравнение и находим экстремум при
(16)
Таким образом, отличие прогиба по расчетной схеме (рис.
4.в и соответственно рис.2.а) по отношению к прогибу по расчетной схеме (рис.4.а и соответственно рис.1.а) равно увеличению на 14,16 %.
Шарнир для расчетной схемы по (рис.2.а) будет не в явном виде, то есть для определения расчетных усилий с учетом перераспределения моментов, балка остается неразрезной и выгиб в следующем пролете возможен. С учетом выгиба увеличение прогиба по расчетной схеме (рис.4.в) по отношению к прогибу по расчетной схеме (рис.4.а) составит 6,60 %.
Таким образом, проверка по деформациям удовлетворяется.
Сравнение результатов. Для выявления экономии арматуры проведено сравнение расходов арматуры. Полное армирование пятипролетной балки, определенное по расчетной схеме в упругой системе получено 217,63 кг. Полное армирование пятипролетной балки определенное по расчетной схеме с учетом перераспределения моментов – 212,33 кг, что составляет экономию арматуры 2 % [6].
Рабочая арматура пятипролетной балки, определенная по расчетной схеме в упругой системе, имеет массу 156,08 кг.
Рабочая арматура пятипролетной балки, определенная по расчетной схеме с учетом перераспределения моментов, – 148,92 кг, что составляет экономию арматуры 5 %.
Однако, многопролетные системы, где пролетов более пяти, рекомендуется заменять пятипролетными системами. То есть наиболее характерным показателем будет значение массы рабочей арматуры в среднем пролете. Здесь рабочая арматура в среднем пролете для пятипролетной балки определенная по расчетной схеме в упругой системе имеет массу 26,68 кг. Рабочая арматура в среднем пролете для пятипролетной балки, определенная по расчетной схеме с учетом перераспределения моментов, – 23,24 кг, что составляет экономию арматуры 13 %.
Выводы
Снижение максимальных значений изгибающего момента в упругой системе возможно с преобразование ее, перераспределением моментов, при этом могут образоваться трещины, но проверки по раскрытию трещин и по деформациям удовлетворяются.
При использовании расчетной схемы неразрезной балки с учетом перераспределения моментов экономия рабочей арматуры в средних пролетах составляет 13 %.
Библиографический список
- СП 63.13330.2012 Бетонные и Железобетонные конструкции. Основные положения. – М.: Министерство регионального развития РФ, 2012. – 156 с.
- Руководство по расчету статически неопределимых железобетонных конструкций. – М., Стройиздат, 1975, – 192 с.
- Байков В.Н., Железобетонные конструкции. Общий курс: учебн. для вузов. – 5-е изд., перераб. и доп. / В.Н. Байков, Э.Е. Сигалов. – М.: Стройиздат, 1991. – 767 с.
- Бондаренко В.М., – Железобетонные и каменные конструкции. Учебн. для студентов вузов по спец. «Пром. и гражд. стр-во» / В.М. Бондаренко, Д.Г. Суворкин. – М.:Высш. шк.,1987. – 384с.
- Феодосьев В.И., Сопротивление материалов. Учебное пособие для студентов. – М.: МГТУ им. Баумана, 2016.-544 с.
- Тихонов И.Н., Армирование элементов монолитных железобетонных зданий. Пособие по проектированию. – НИИЖБ им. А.А. Гвордева, М. 2007. – 169 с.
- Габрусенко В.В., Основы расчета железобетона в вопросах и ответах.
Учебное пособие. – М: ACB, 2002. – 104 с. - Константинов И.А., Строительная механика. Учебник / И.А. Константинов,
- В.В. Лалин, И.И. Лалина. – М: Проспект, 2014. – 432 c.
- Шагисултанова Ю.Н., Строительная механика. Учебное пособие для студентов / Ю.Н. Шагисултанова, О.М.Иванова – Тюмень: РИО ФГБОУ ВПО “ТюмГАСУ”, 2014. – 86 с.
- Цай Т.Н. Строительные конструкции. Железобетонные конструкции. Учебник для студентов строительных специальностей / Т.Н. Цай, 2012. – 464 с.
Учебное пособие. – М: ACB, 2002. – 104 с.Количество просмотров публикации: Please wait
Все статьи автора «Назарова Дарья Сергеевна»
Расчет железобетонной балки сборно-монолитного перекрытия
РЕКЛАМА
Для ориентировочного расчета балки сборно-монолитного перекрытия удобно использовать программу-калькулятор. Файл Excel с программой-калькулятором можно скачать, если перейти по этой ссылке и выбрать в меню «Файл» — «Загрузить». К сожалению, найти фамилию автора программы мне не удалось.
Расчет начинают с определения величины желаемой полезной нагрузки. Для расчета сборно-монолитного перекрытия полезная нагрузка складывается:
- Из нормативной эксплуатационной нагрузки перекрытия с коэффициентом запаса (из СНиП). Например, для жилых помещений нормативная эксплуатационная нагрузка 150 кг/м2, коэффициент запаса 1,3, получаем эксплуатационную нагрузку 150 х 1,3=195 кг/м2.
- Из нагрузки от веса блоков, которыми заполняется межбалочное пространство. Например, блоки газобетонные плотностью 500 кг/м3 (D=500) толщиной 0,2 м. создадут нагрузку 500 х 0,2=100 кг/м2.
- Из нагрузки от веса армированной стяжки. Например, бетонная стяжка толщиной 0,05 м. при плотности бетона 2100 кг/м3 создаст нагрузку 2100 х 0,05=105 кг/м2 (вес арматурной сетки включен в показатель плотности бетона).
Итого желаемая полезная нагрузка на балку составит 195+100+105=400 кг/м2 Далее указываем длину перекрываемого пролета.
Например, длина пролета 4,6 м.
Шаг балок — это расстояние между центрами балок, определяется размерами блока и принятой шириной балки. Например, длина блока 0,61 м., ширина балки 0,12 м., шаг балок 0,61+0,12=0,73 м.
Ширина перекрываемого пролета, стоимость бетона и арматуры указываются для того, чтобы калькулятор расчитал количество и стоимость материалов для перекрытия. На расчет параметров армирования эти показатели не влияют.
В разделе «Параметры балки» в первых двух строчках указываются рекомендуемые размеры балки. Принимая во внимание рекомендуемые размеры, выбираем размеры балки исходя из конструктивных соображений. Поскольку используются блоки толщиной 200 мм. и толщина стяжки 50 мм., то принимаем высоту балки 0,25 м. Если стяжка будет заливаться бетоном не одновременно с балками, то высота балки должна приниматься без учета стяжки.
Выбираем количество прутков арматуры из конструктивных соображений.
Защитный слой бетона для арматуры должен быть не менее 20 мм., а расстояние между прутками должно превышать размер фракции щебня в бетоне.
На заключительном этапе анализируем результаты расчета и пытамся оптимизировать расходы на устройство перекрытия.
Подбирая число прутков арматуры стараемся уменьшить вес арматуры на балку. Увеличивая ширину балки пробуем избежать применения поперечной арматуры, при этом правда будет увеличиваться объем бетона на одну балку.
Товары для дома
⇆
Для нашего примера окончательно выбираем два прутка арматуры в один ряд. Диаметр стержня арматуры 12 мм. Поперечная арматура не нужна. Верхняя арматура также не нужна, так как балка заливается бетоном на месте.
Эта программа-калькулятор позволяет рассчитать перекрытие с равномерно распределенной нагрузкой. Она не применима, если на перекрытие, кроме распределенной, также воздействует значительная сосредоточенная нагрузка от веса каменных перегородок, печей, каминов и пр.
Следующая статья:
Расчет толщины утеплителя перекрытия или покрытия мансарды.
Предыдущая статья:
Опубликовано Автор Igor PazdnikovРубрики ПерекрытияСборно-монолитное перекрытие из легких каменных блоков
Расчетные модули > Балки > Бетонная балка
Нужно больше? Задайте нам вопрос
В этом разделе для каждой вкладки ввода мы рассмотрим только элементы, которые являются уникальными для типа материала БЕТОН. Нажмите здесь, чтобы просмотреть видео:
Общие данные
Модуль бетонных балок обрабатывает одно- и многопролетные балки, используя ОДНУ форму поперечного сечения.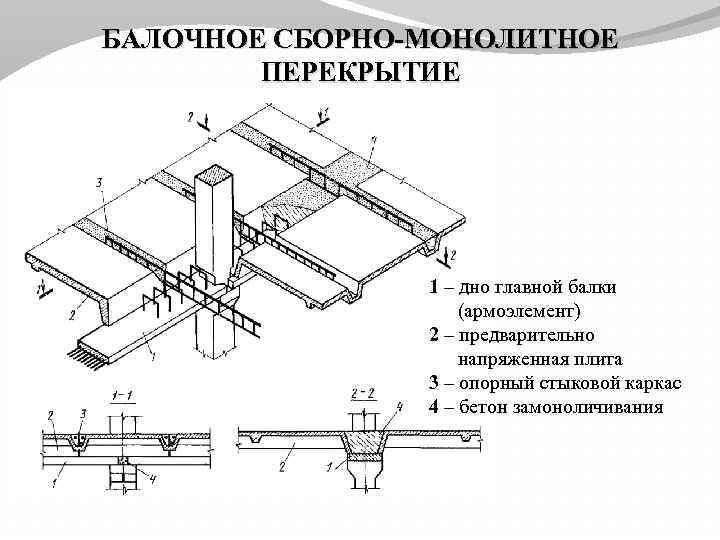
Эта форма может иметь до шести групп армирования на пролет, и армирование может варьироваться в зависимости от пролета.
Этот модуль также имеет вариант балки на упругом основании для однопролетных балок. На снимке экрана ниже вы можете увидеть два больших поля выбора. Выбор «Однопролетная балка на эластичном фундаменте» удалит возможность выбора условий торцевой опоры и предоставит ввод для модуля реакции грунтового основания поддерживающего грунта.
В правой части этой вкладки находятся все необходимые записи арматуры, прочности бетона и модуля упругости, данные хомута сдвига, коэффициенты снижения прочности и критерии прогиба для проверки.
ПРИМЕЧАНИЕ. Важно знать, как этот модуль работает с жесткостью балки вдоль пролета и как это влияет на многопролетные балки. Этот модуль делит каждый пролет на серию сегментов. Эффективный момент инерции для каждого сегмента (для каждой комбинации нагрузок) рассчитывается с использованием фактического нефакторизованного момента на этом сегменте.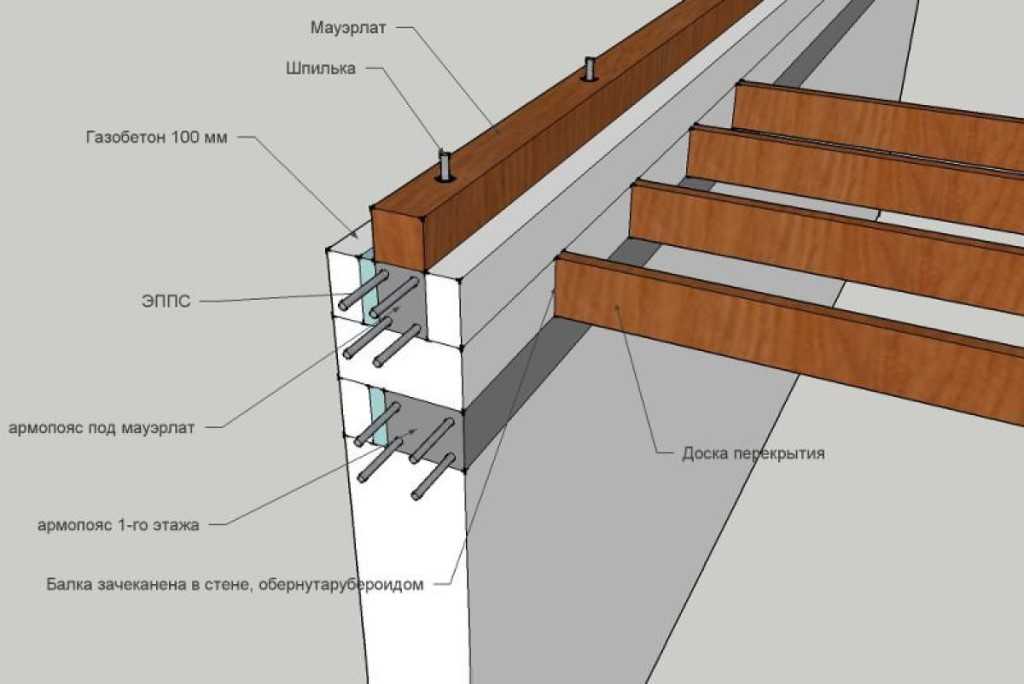
Таким образом, модуль создает очень точную модель переменной жесткости балки на основе фактических моментов. Для многопролетных балок это повлияет на относительную жесткость каждого пролета балки. Таким образом, распределение момента по нескольким пролетам будет выполнено надлежащим образом. Это повлияет на учитываемые моменты нагрузки и срезы, а также отклонения и реакции уровня эксплуатационной нагрузки.
Данные о пролете балки
На этой вкладке есть некоторые входные данные, которые являются постоянными для всех пролетов, а некоторые могут варьироваться в зависимости от пролета.
Форма и размеры поперечного сечения одинаковы для всех пролетов.
Если щелкнуть пролет (для многопролетных балок) в самой верхней части окна, длина пролета и компоновка арматурных стержней будут обновлены для отображения расположения, характерного для этого пролета.
В правой части этой вкладки можно указать до 6 наборов тактов (количество, размер, вертикальное расположение и конечные точки начала/конца).
Каждый набор стержней обозначен на эскизе цветом, показанным в виде точки слева от описания набора.
Столбец «Расстояние от центра стержня….от…», выделенный голубым цветом, показывает, как вы задаете вертикальное положение наборов стержней в балке. Когда вы посмотрите на верхний, вы можете прочитать его как «Верхний набор стержней находится в 3 дюймах от нижней части балки». Обратите внимание, что модуль будет знать, находятся ли стержни в растяжении или сжатии, и правильно обработает расчеты.
Элемент с меткой Bar Position Этот диапазон определяет начальное и конечное положение концов штрихов относительно левого конца каждого соответствующего диапазона. Данные на снимке экрана ниже показывают, что наборы стержней № 1 и № 2 проходят от левого конца (0,0 фута) до 25,0 фута от левого конца пролета 1. Используя эти начальные и конечные местоположения, вы можете точно настроить расположение стержней и концевые отсечки.
Примечание.
Модуль выдаст сообщение об ошибке, если окажется, что какие-либо сегменты балки полностью неармированы. Поэтому крайне важно, чтобы арматурный стержень был определен таким образом, чтобы исключить полностью неармированные сегменты. Сюда входят короткие сегменты на крайних концах балки, где обычно заканчиваются арматурные стержни. Помните, что этот модуль является инструментом анализа, а не инструментом детализации, поэтому не поддавайтесь искушению определить арматурный стержень как начинающийся или заканчивающийся за пределами физического конца балки. Кнопка с надписью «FL» рядом с каждым определением арматурного стержня была предоставлена как удобный способ указать программе, что выбранный арматурный стержень проходит по всей длине пролета.
Важно. Предполагается, что бары полностью эффективны в местах, где они определены. Это видно из диаграммы емкости. Таким образом, в ситуациях, когда необходимо учитывать развитие, пользователь должен понимать это поведение и соответствующим образом определять расположение полос.
Продольные нагрузки
Нет отличий от других материалов.
Все нагрузки на пролет
Нет отличий от других материалов.
Комбинации нагрузок
Нет отличий от других материалов.
Вкладки результатов
На этом наборе вкладок представлены подробные результаты текущего расчета. Вертикальные вкладки на левом краю экрана позволяют выбрать три основные области, доступные для просмотра: Расчеты, Эскиз и Диаграмма.
На вкладке «Расчеты» предлагаются следующие варианты результатов:
Сводные результаты содержат подробные сведения о сдвиге, моменте и прогибе для определяющих сочетаний нагрузок. Результаты сдвига здесь не показаны… они суммированы на отдельной вкладке, где указана необходимая компоновка хомута.
Макс. Комбинации предоставляют подробные результаты для каждого сегмента балки для каждой комбинации нагрузок.
Эти результаты представляют собой консолидацию очень подробных дополнительных результатов на вкладке Сводка M-V-D.
M-V-D Резюме — Комбинации LRFD/Strengt Stress показывает очень подробные результаты момента и сдвига для каждой балки и для каждой комбинации нагрузок. Для многопролетных балок, использующих автоматическое размещение несбалансированной динамической нагрузки, могут быть тысячи строк результатов.
Сводка M-V-D — Отклонения рабочей нагрузки показывает очень подробные результаты отклонения для всех сочетаний нагрузок. При расширении каждой комбинации нагрузок нажатием на значок [+] вы увидите прогибы по всей длине балки. Вы также увидите эффективный момент инерции, используемый в этом регионе. (Помните, что эффективный момент инерции рассчитывается на основе моментов уровня обслуживания во многих местах по длине каждого пролета.)
M-V-D Сводка – Значения поперечного сечения показывают значения момента и момента инерции для всех идентифицированных поперечных сечений. Модуль проверил все заданные вами пролеты и отыскал идентичные схемы армирования.
Дубликаты устранены, и для простоты здесь перечислены только уникальные усиленные поперечные сечения.
M-V-D Резюме. Расчетный сдвиг показывает требования к хомуту сдвига вдоль пролета (ов) в соответствии с требованиями управляющих комбинаций нагрузок, создающих наибольший сдвиг в каждой секции.
В столбце с надписью «Комментарий» указано кодовое условие ACI, определяющее требование к поперечной арматуре в каждом месте конструкции.
Реакции опор показывает реакции каждой опоры для каждого состояния нагрузки.
На вкладке Эскиз представлено графическое представление проектируемой балки:
0002 На вкладке «Диаграмма» можно просмотреть диаграммы сдвига, момента и прогиба для выбранных сочетаний нагрузок:
Расчетные модули > ENERCALC 3D > Расчет бетона — ACI 318-02/05/08/11/14 > Бетон Расчет балок
Общие сведения
Модуль бетонных балок рассчитывает бетонные прямоугольные или тавровые балки на огибающий изгиб вокруг сильной оси (локальная z) и огибающий сдвиг вдоль локальной оси y.
Осевая сила, изгиб вокруг слабой оси (локальная y) и кручение не учитываются. Кроме того, не рассматривается действие глубокого луча. Если нельзя пренебречь осевой силой или двухосным изгибом, рекомендуется использовать модуль проектирования колонн.
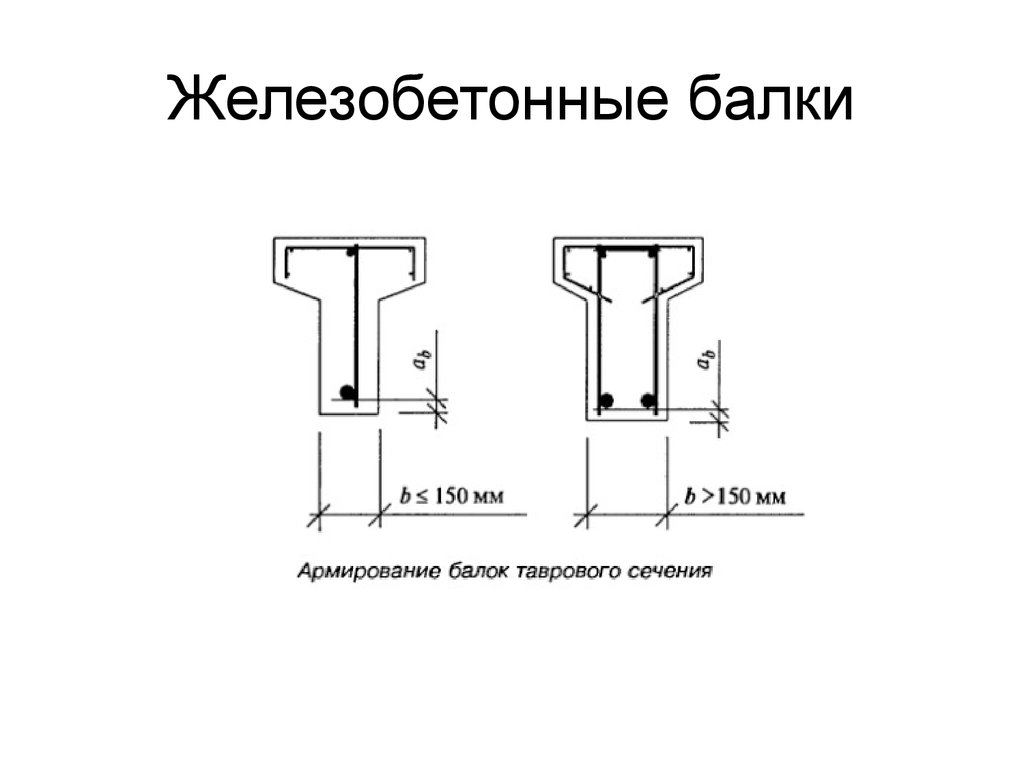
Армирование балки на изгиб
Армирование на изгиб верхней и нижней частей балки рассчитывается на каждой станции анализа по длине балки. Минимальное армирование рассчитывается для нижней стали. Программа рассчитывает каждую балку на положительный или отрицательный момент с помощью одного слоя натяжной стали с контролируемым натяжением. Для расчетов на изгиб критическое сечение опоры может быть принято на лицевой стороне опоры (но не более 0,175 * длины пролета от центра опоры). Программа предлагает возможность учета этих условий путем автоматического вычисления ширины опорных балок на основе критериев проектирования модели в разделе «Бетон» > «Критерии проектирования».
В следующем алгоритме предполагается один слой растянутой стали, то есть dt = d, глубина центроида растянутой стали.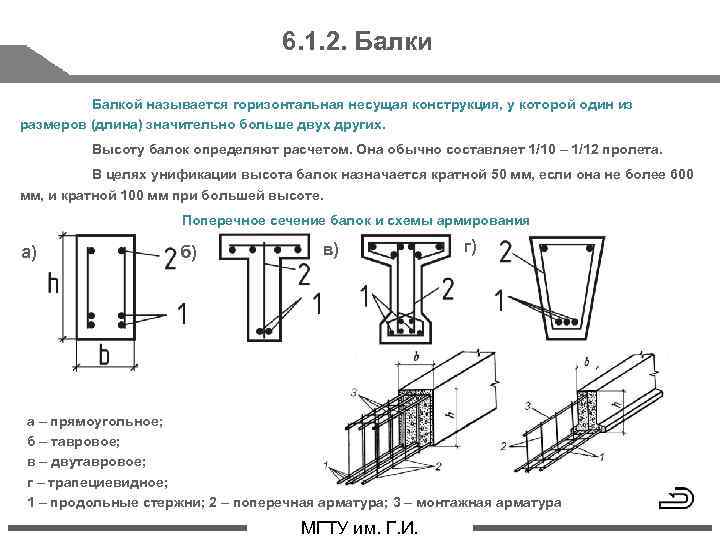
Это предположение сделано из-за его простоты и консервативного характера и является разумным, если только деформация стали при растяжении не очень близка к 0,005 — предельной деформации, контролируемой растяжением.
Результат расчета отражен на схемах верхней и нижней арматуры.
Алгоритм расчета изгиба прямоугольной балки
Учитывая b, d = dt, d’, fc, fy и Mu, найдите требуемое As (и As’, если необходимо)
Шаг 1: Определите максимальный момент без сжатия стали, используя предел, контролируемый растяжением, и .
Шаг 2: Если разрабатывать раздел как по отдельности, приведенном следующим образом:
(ACI 318-02/05 10.5.1)
(ACI 318-02/05 10.5.1)
Шаг 3: Если разрабатывать раздел как вдвойне, закрепленный следующим образом (все еще предполагая ограниченный натяжение и):
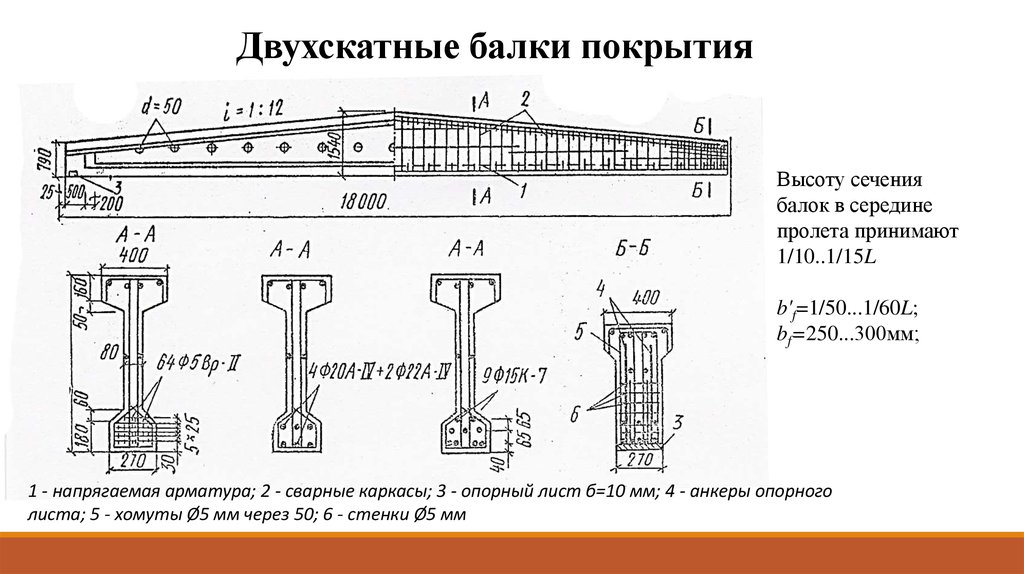
сталь на растяжение, необходимая для уравновешивания стали на сжатие, составляет
.
Алгоритм расчета изгиба тавровой балки
По данным b, bw, hf , d = dt, fc, fy и Mu найти требуемое As
Шаг а). Assuming a <= hf and tension-controlled section with
If a > hf, go to Step b)
Если , проект терпит неудачу.
Шаг b). a > hf и регулируемая натяжением секция с
,
Армирование балки на сдвиг
Армирование стержня на сдвиг (расстояние между хомутами) рассчитывается на каждой станции анализа по длине стержня. Размер хомута и количество ножек предполагаются одинаковыми по длине стержня как часть входных данных. При расчете на сдвиг секции, расположенные на расстоянии менее d от поверхности опоры, могут быть рассчитаны на Vu, рассчитанное на расстоянии d от опоры (ACI 318-02/05 11.