Расчет нагрузки на двутавр – актуальность выполнения и основные методики
Двутавровая балка – это вид металлопроката, особенностью которого является прием большого веса. При использовании продукции в строительстве необходимо выбрать нужный номер. Для этого на основе данных о длине пролета, виде закрепления рассчитывается прочность и прогиб.
Область применения двутавровой балки
Двутавр – это металлический продукт, который состоит из полок и стенки посередине. Зачастую двутавр используют при проектировании сооружений и создании качественной несущей конструкции. Благодаря изделию можно увеличить пролеты жилого или коммерческого здания, а также уменьшить массу несущих конструкций.
При выборе двутавра необходимо учитывать следующие характеристики:
высота профиля и средней стенки;
ширина полок;
толщина стенки, проката и граненых полок;
радиус закругления внутри изделия.
Основные параметры для расчета нагрузки
Стоит помнить, что все подсчеты осуществляются на основе справочных обозначений.
Так, одним из важных является инерционный момент, значение которого определяется таблицей сортамента, обозначенного в ГОСТах.
Учитывается также центробежный момент, который не внесен в таблицы, поскольку равняется 0.
Влияет на вычисление нагрузки и сопротивление. Данный показатель непосредственно зависит от маркировки стали.
Еще один из признаков – модуль упругости – выходит из особенностей материала, использованного для изготовления двутаврового металлического продукта. В частности речь идет о черном металлопрокате, при котором модуль упругости Е используется для двутавровой стальной балки.
Не нужно забывать о том, что конструкционные характеристики определенного объекта требуют и других параметров расчета, для которых берутся данные из таблицы.
Расчет нагрузки, прогиба и прочности
Для исчисления нагрузки разработаны таблицы, в которых номер балки вычисляется на основе:
Первая характеристика рассчитывается благодаря несущей способности.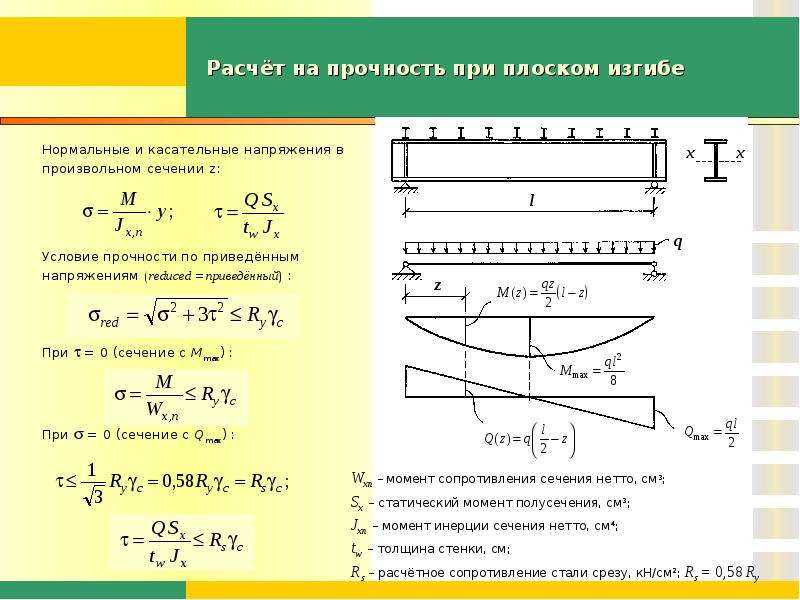
Стоит обращать внимание на технологию производства (горячекатаный, сварочный, клепаный). Например, при расчете максимальной нагрузки сварного двутавра прибавляется приблизительно 30% к прочности.
Давление на конструкцию рассчитывается с учетом ее веса. Эту цифру умножают на показатель надежности, выбирая момент сопротивления из табличных показаний. Уже в результате процесса определяется профильный номер.
Чтобы проверить двутавровую балку на прочность, нужно акцентировать внимание на нормативных напряжениях, воздействии сил, а также крутящих моментах.
Металл, из которого производится двутавр, имеет значение. Если в его основе содержится черный стальной прокат, то главный критерий – маркировка. Если древесина, то речь идет о породе. Важно знать, что прочность материала уменьшает габариты готового изделия. Вследствие этого снижается давление на конструкцию.
Для определения прочности материала нужно разложить по осям прилагаемую силу, после чего установить максимальные моменты вокруг каждой из них.
Для расчета прогиба выделяются такие параметры:
нагрузка;
пролет;
сопротивление.
При этом стоит обращать внимание на предназначение конструкции. Для того чтобы уменьшить величину прогиба, нужно изменить исходные параметры или уменьшить расстояние между опорными точками.
Компания «Металл Холдинг» предлагает клиентам широкий ассортимент двутавровых балок с указаниями марок, стандартов и габаритов.
Прочностной расчет. Сравнение
Сравним несущие способности 3-х видов балок: деревянная двутавровая балка ICJ (с полками из LVL бруса), деревянный брус, цельный LVL брус.
Расчет будем вести по 1 и 2 предельному состоянию (по потере эксплуатационных свойств и по прогибам). Важным и определяющим для нас будет расчет по 2 предельному состоянию (по прогибам). Именно значение прогиба под нагрузкой при равных условиях загружения будет для нас критерием сравнения.
Условия для расчета:
- Расчетная длина (расстояние в свету между соседними опорами) 5,8 м
- Нагрузка на м 2 перекрытия 400 кг
- Шаг балок 0,4 м
- Нагрузка на м.пог. балки 400кг/м2 х 0,4= 160 кг
| Двутавровая балка ICJ-300L | Брус сухой строганный деревянный 100х240 мм | Цельный прямоугольный LVL брус 69х260 |
|---|---|---|
| Характеристики: Момент инерции 9 476,5 см4 Момент сопротивления 631,8 см3 Модуль упругости 12 000 МПа Расчетное сопротивление 22,0 МПа | Характеристики: Момент инерции 11 520,0 см4 Момент сопротивления 960,0 см3 Модуль упругости 9 000 МПа Расчетное сопротивление 14,0 МПа | Характеристики: Момент инерции 8 788,0 см4 Момент сопротивления 676,0 см3 Модуль упругости 14 000 МПа Расчетное сопротивление 26,5 МПа |
|
Производим расчет по первому предельному состоянию: (где, R — расчетное сопротивление изгибу, M-максимальный момент (M=q*L2/8; M=160*5,82/8=672,8 кНм), W-момент сопротивления) | ||
| R=M/W R=672,8 кНм/631,8*10-6 см3= 1,06 кНм2 = 10,6 МПа < Rрасч =22 МПа Выполнено. | R=M/W R=672,8 кНм/960*10-6 см3= 0,7 кНм2 = 7 МПа < Rрасч =14 МПа Выполнено. | R=M/W R=672,8 кНм/676*10-6 см3= 0,99 кНм2 = 9,9 МПа < Rрасч =26,5 МПа Выполнено. |
|
Производим расчет по второму предельному состоянию: (f/L < fпред/L | ||
| f/L=5*160*5,83 / (384*12000*105*9476,5*10-8)=0,00358 <fпред/L=0,004 Выполнено. | f/L=5*160*5,83/ (384*9000*105*11520*10-8)= 0,00392 <fпред/L=0,004 Выполнено. | f/L=5*160*5,83/ (384*9000*105*8788*10-8)= 0,00392 <f Выполнено. |
Вывод: все 3 материала с данными геометрическими характеристиками примерно равны по своей несущей способности и удовлетворяют условиям прогибов. | ||
| Сравним цены и эксплуатационные характеристики | ||
|
|
|
По своим прочностным характеристикам равны:
| Двутавр ICJ-240W | Брус 80х200 | LVL брус 51х200 | |
|---|---|---|---|
| Цена | 244 р/м.пог | 216 р/м.пог | 306 р/м.пог |
| Вес | 3.52 кг | 7.2 кг | 4.6 кг |
| Геометрия | точная | плохая | точная |
| Качество | высокое | низкое | высокое |
| Двутавр ICJ-300W | Брус 75х250 | LVL брус 57х260 | |
|---|---|---|---|
| Цена | 264 р/м. пог | 253 р/м.пог | 444 р/пог |
| Вес | 3.87 кг | 8,4 кг | 7,4 кг |
| Геометрия | точная | плохая | точная |
| Качество | высокое | низкое | высокое |
| Двутавр ICJ-240L | Брус 100х240 | LVL брус 69х260 | |
|---|---|---|---|
| Цена | 332 р/м.пог | 232 р/м.пог | 397 р/пог |
| Вес | 3.63 кг | 9,0 кг | 6,0 кг |
| Геометрия | точная | плохая | точная |
| Качество | высокое | низкое | высокое |
| Двутавр ICJ-300L | Брус 100х240 | LVL брус 69х260 | |
|---|---|---|---|
| Цена | 352 р/м.пог | 324 р/м.пог | 538 р/пог |
| Вес | 3. 95 кг | 10.8 кг | 8.6 кг |
| Геометрия | точная | плохая | точная |
| Качество | высокое | низкое | высокое |
| Двутавр ICJ-360L | Брус 100х300 | LVL брус 75х300 | |
|---|---|---|---|
| Цена | 362 р/м.пог | 405 р/м.пог | 675 р/пог |
| Вес | 4.30 кг | 12 кг | 10.2 кг |
| Геометрия | точная | плохая | точная |
| Качество | высокое | низкое | высокое |
| Двутавр ICJ-400L | Брус 150х300 | LVL брус 90х360 | |
|---|---|---|---|
| Цена | 414 р/м.пог | 609 р/м.пог | 972 р/пог |
| Вес | 5,60 кг | 18 кг | 14,6 кг |
| Геометрия | плохая | точная | |
| Качество | высокое | низкое | высокое |
Формулы напряжения изогнутой двутавровой балки и калькулятор
Связанные ресурсы: калькуляторы
Формулы напряжения изогнутой двутавровой балки и калькулятор
Калькуляторы напряжения и прогиба балки с формулами
Формулы напряжения изогнутой двутавровой балки и калькулятор
Изгибающие напряжения в криволинейных балках не подчиняются той же линейной вариации, что и в прямых балках, из-за различий в длине дуги.
Несмотря на то, что для обоих типов используются одни и те же предположения, то есть плоское сечение, перпендикулярное оси балки, остается плоским после изгиба, а напряжение совершенно другое. На рис. 1.0 показано линейное изменение напряжения в прямой балке и гиперболическое распределение напряжения в изогнутой балке. Обратите внимание, что напряжение изгиба в изогнутой балке равно нулю в точке, отличной от оси центра тяжести. Также обратите внимание, что нейтральная ось расположена между осью гравитации и центром кривизны: это всегда происходит в криволинейных балках.
Предварительный просмотр расчета напряжения изогнутой двутавровой балки
Рисунок 1.0
Рисунок 2.0 Размеры двутавровой балки
Распределение напряжения из-за изгиба определяется по формуле:
Уравнение 1
s = M · γ / ( A · e · ( r n — y ) )
Где:
s = изгибающее напряжение, psi
M = изгибающий момент относительно центральной оси, дюйм-фунт
y = расстояние от нейтральной оси до рассматриваемой точки, дюймы (положительно для расстояний до центра кривизны, отрицательно для расстояний от центра кривизны)
A = площадь сечения в 2
e = расстояние от оси центра тяжести до нейтральной оси, дюймы
r n = радиус кривизны нейтральной оси, дюймы
Изгибающее напряжение внутри волокна определяется по формуле:
Уравнение 2
s = ( M · h i ) / ( A · e · r i )
Где:
h i = расстояние от центральной нейтральной оси до внутренней части волокна, дюймы ( h i = r n — r i )
r i
Напряжение изгиба на внешней стороне волокна определяется по формуле:
Уравнение 3
s = ( M · h o ) / ( A · e · r i )
Где:
h o = расстояние от центральной нейтральной оси до внутреннего волокна, дюймы ( ч о = r o — r i )
r o = radius of curvature on the outside fiber, inches
A = b i t i + b o t o + (H — T I — T O ) T
Стакулярная форма I -BEAM
R N = [B I — T) T I + (B O — т ) (т о ) + й ] / [ i лог E (( I + T I ) / R I ) + T LOG E ((R O — T O ) / (R I + T I )+ B O Log E (R O / (R O — T O ))]
E = R — R N
9002 R N 9002 7.
r i + [ (1/2) h 2 t + (1/2) t i 2 ( b i — t ) + ( b o — t ) ( t o ) ( h — (1/2) t o ) ( h — (1/2) t o ] / [ ( b i — t ) ( t i ) + ( b o — t ) ( t o ) — th ] Где:
b i = ширина полки двутавровой балки, в
b o = толщина полки двутавровой балки, в
t i = толщина стенки полки, в
t o = толщина стенки полки, в
t i = толщина стенки полки, дюйм
час = толщина стенки полки, дюймы
Балка с опорой на штифтахКаталожные номера:
- McGraw Hill Machine Design (1968)
Расчет сопротивления изгибу конструкционной стальной балки
Способность к изгибающему моменту — это, как правило, первое, с чего вы начинаете проектирование стального элемента. Он покажет вам, какой максимальный момент может выдержать выбранный вами элемент.
Всегда помните, что этот максимальный момент не может быть вашим худшим методом отказа. Всем моим существующим студентам, если вы не уверены, переходите к лекции «Как сталь выходит из строя» в курсе «Принципы проектирования стали», чтобы еще раз пройтись по этим методам отказа.
Прежде чем мы сможем определить емкость на данный момент, есть несколько ключевых сведений, которые нам нужны в первую очередь. Давайте кратко рассмотрим каждый.
Глядя на марку стали, вы, как правило, выбираете между сталью S275 или S355. Они указаны в МПа или Н/мм 2 . Сталь
марки 275 МПа чаще всего используется в балках, где прогиб является критическим случаем, поскольку более высокий предел текучести 355 МПа не требуется. Он также более пластичен, что может быть использовано в сейсмостойких конструкциях.
В бытовых конструкциях обычно все упирается в цену, сталь S275 может быть дешевле, чем S355. Это сильно колеблется. В настоящее время в Великобритании разница в цене незначительна, и я уже давно не указывал на балки S275.
Класс балки
Класс балки рассчитывается на основе гибкости полки и секций стенки, которые определяют, сможет ли балка достичь и сохранить пластическое сопротивление или только упругое сопротивление.
Для секций класса 1 и 2 можно использовать модуль пластического сечения, а в секции класса 3 необходимо использовать модуль упругости сечения.
Все секции универсальной балки (I), кроме одной, относятся к классу 3, поэтому вы почти всегда будете использовать модуль пластического сечения.
или
Модуль упругого и пластического сечения находится из справочных таблиц, подобных приведенной здесь: https://www.steelforlifebluebook.co.uk/ub/
Вы можете рассчитать его для каждого сечения, но я бы не рекомендовал этого делать! Сделайте это несколько раз, будучи студентом инженерного факультета, чтобы точно понять, что происходит, а затем используйте справочные таблицы.
Модуль сечения всегда будет в виде куба расстояния, например, 500см 3 .
Гамма — это особый коэффициент материала Еврокода, значение которого будет различным в каждой стране и указано в соответствующем национальном приложении. В Великобритании в Национальном приложении указано значение 1 (отлично подходит для обеспечения аккуратности и чистоты расчетов!)
Это закрывает все части, необходимые для завершения расчета, так как же они все сочетаются друг с другом.
Здесь мы имеем окончательный расчет. Вы умножаете модуль соответствующего сечения на предел текучести стали и применяете/делите частичный коэффициент материала. Довольно просто, если вы знаете, что означают все символы.
Взглянув на единицы измерения, вы получите куб расстояния, умноженный на напряжение, деленный на статическое значение. Немного сложно представить, поэтому давайте напишем это.
Из этого мы можем видеть, что квадрат расстояния от напряжения аннулирует два расстояния от модуля сечения, что оставит нас с силой, умноженной на расстояние, т.е. на момент!
Спасибо за внимание, увидимся в следующей статье!
PS. Если вы хотите бесплатно получать эти статьи обо всем, что связано со структурой, добавьте свой адрес электронной почты ниже, и вы будете в списке.
стр/с. Я ненавижу спам, поэтому будьте уверены, я буду посылать вам только информацию, непосредственно связанную с проектированием конструкций, с возможностью отказаться от подписки в любое время.