Армирование ростверка свайного фундамента: расчет
Ни один современный дом сейчас нельзя представить без фундамента. Именно фундамент собирает на себя все нагрузки от несущих конструкций, и передает их на грунты. Существуют разные типы фундаментов.
Монтаж опалубки для ленточного ростверка
В некоторых случаях уместно создавать ленточные монолитные фундаменты, в других же используют цельные монолитные конструкции. Мы же сейчас поговорим об особенностях свайного фундамента, а также ростверка на сваях и таком важном процессе, как армирование всех несущих конструкций фундамента.
Особенности и конструкция свайного фундамента
Свайный фундамент является одной из разновидностей несущих поддерживающих конструкций, на которые монтируют затем все остальное строение.
Так же, как и другие фундаменты, этот его тип проектируют и строят, используя СНИП и другую нормативную документацию. Однако чертеж, расчет и тип конкретных элементов буронабивного фундамента с ростверком будет немного отличаться от ленточного или цельного, так как и задачи у него немного другие.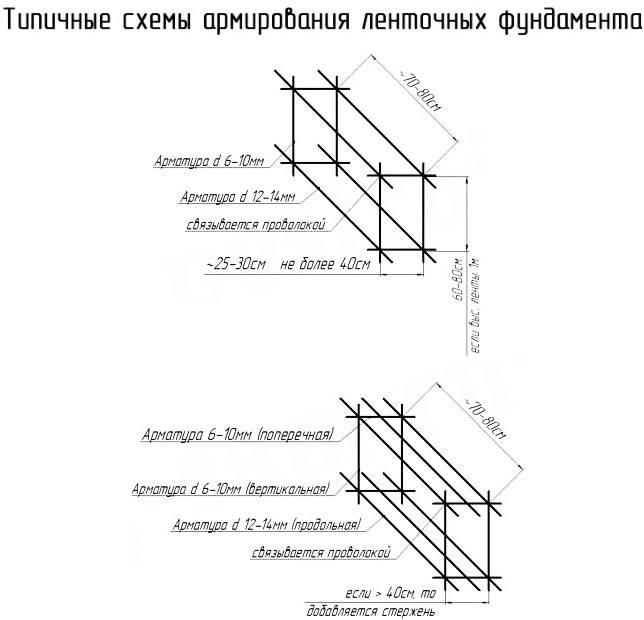
В отличие от ленточных несущих конструкций, у свайных оснований несущими элементами и основными передатчиками напряжений являются непосредственно сваи.
Они отлично подходят для использования, когда необходимо монтировать дом на слабых грунтах. В таких случаях крупная подошва ленточных моделей фундаментных оснований слишком дорога, а вот создание точечных свай считается более уместным.
При конструировании такой конструкции используются сваи буронабивной, забивной и нескольких других технологий изготовления. Их расчет и нормирование регулирует подходящий СНИП.
Полная последовательность действий по созданию ленточного ростверкового фундамента
Без учета нормативной документации создавать такие важные элементы будущего строения запрещено, так как это может привести к довольно неприятным последствиям. Причем не имеет значения, какой тип конструкции вам предстоит строить, в любом случае СНИП будет приоритетным документом.
Помимо свайного основания из нескольких десятков элементов ни одна конструкция свайного фундамента не обойдется без ростверка.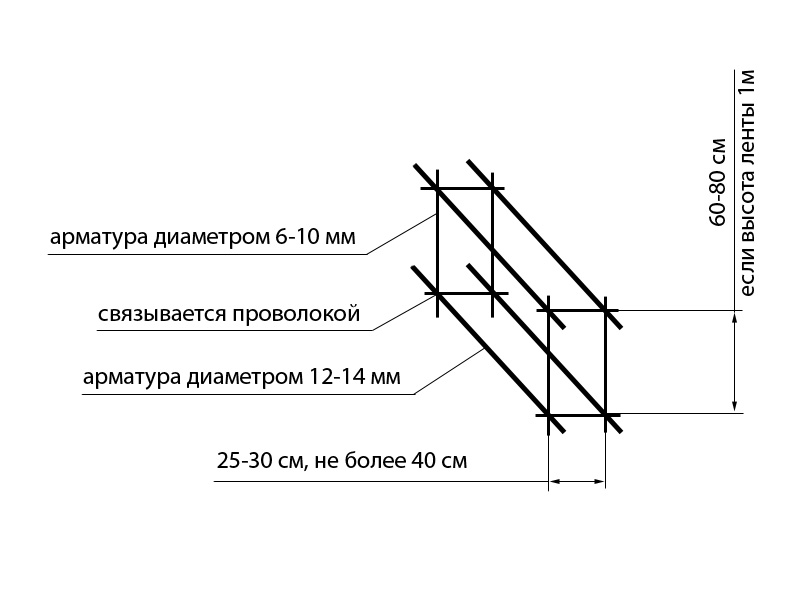 Стоит понимать, что тип свайного фундамента предусматривает установку непосредственно свай на расстоянии примерно 2-4 метров друг от друга.
Стоит понимать, что тип свайного фундамента предусматривает установку непосредственно свай на расстоянии примерно 2-4 метров друг от друга.
Читайте также: как происходит погружение металлических и железобетонных свай-оболочек?
Конкретное расстояние регулирует чертеж, СНИП, тип фундамента и еще несколько параметров. Но в любом случае оно будет достаточно внушительным.
Чтобы собрать всю эту конструкцию воедино и пользуются созданием ростверкового обвязывающего пояса или плиты. Причем не имеет значения, применяется ростверк для обвязки буронабивных или забивных свай. В любом случае его наличие просто необходимо.
Сам ростверк являет собой последовательную и довольно внушительную часть свайного фундамента, он может состоять из большого количества балок или монолитной плиты.
Именно на конструкцию ростверка ложится вся основная нагрузка от несущих конструкций дома, а он уже, в свою очередь, передает ее на сваи, которые давят на грунт и распределяют нагрузку по почве.
Для свайного фундамента характерно использование разных типов свай (буронабивных, забивных) и разных материалов. В данном случае мы рассматриваем только железобетонные сваи, как самые прочные, надежные и нуждающиеся в армировании.
Читайте также: технология армирования фундаментной плиты.
Армирование свай и непосредственно всего свайного фундамента – это совершенно необходимый процесс. Без армирования бетон хоть и выполняет свои функции, но не так хорошо.
Дело в том, что бетон сам по себе является довольно прочным материалом, однако любой СНИП, ГОСТ или результаты официальных исследований говорят о том, что при всей своей прочности он плохо работает на изгиб. А именно нагрузки на изгиб давят на конструкцию ростверкового свайного фундамента.
Заливка буронабивных свай монолитным раствором
Если не армировать все эти конструкции, то есть большой риск их разрушения или основательного повреждения. В таком случае весь дом придется признать аварийным, так как фундаментное основание – это едва ли не самая главная его часть.
Для осуществления качественного армирования используется конкретный расчет. Его же регулирует текущий чертеж конструкции, а также его тип и нормативная документация, что даст вам всю дополнительную информацию (СНИП, ГОСТ, справочники и т.д.).
Читайте также: особенности технологического процесса армирования разных типов фундаментов.
Для армирования используется сварные арматурные каркасы в виде сетки с определенным шагом. Конкретный тип металлической или стеклопластиковой арматуры, ее длина и все остальные параметры определяет расчет конструкции. Тип сечения армирования определяет то, как сварная сетка будет собираться.
к оглавлению ↑
Виды и отличия ростверковых фундаментов
Как мы уже упоминали выше, существует несколько разновидностей фундаментов ростверкового типа, а также конструкций ростверка и свай. Все они имеют довольно серьезное значение не только за счет особенностей своей конструкции, но и за счет того, как арматурная сварная сетка будет применяться для их армирования.
Совершенно очевидно, что ленточный ростверк по своей форме, габаритам и предназначению отличается от цельного. А значит и сварная сетка для армирования у них будет разной.
Фундаменты такого типа начинаются из свай. Сваи могут собирать и монтировать по:
- Буронабивной технологии;
- Забивной технологии.
Для буронабивной технологии обустройства характерно создание свай с мощной нижней подушкой. Формируют их по технологии погружения в грунт специальных инструментов и его вытеснения, а затем укладки арматурной сетки и бетонирования всей конструкции.
Арматура, выпущенная из забитых свай
У буронабивных свай есть преимущество за счет наличия подушки, возможности выбирать арматурную сетку по своему желанию и т.д.
Забивные сваи, как правило, уже готовы к применению, так как являются сборными железобетонными элементами. Их нижняя часть имеет заостренное или конусообразное сечение.
Выбор конкретной марки бетона и сечения таких элементов регулирует СНИП. Забивные конструкции, как можно понять из названия, устанавливают в грунт путем забивки специальными вибропрессами или другим подобным оборудованием.
Для ростверка тоже характерно применение нескольких популярных разновидностей. От их типа зависит весь чертеж конструкции. Ростверк по типу сечения делят на:
- Ленточный;
- Цельный.
Ленточный ростверк во многом повторяет все принципы, что применяются при устройстве ленточного фундамента. Он обвязывает непосредственно сваи, не распространяясь на остальную площадь дома.
Впрочем, этого и не требуется. Ленточный ростверк монтируется под несущие стены дома. Обходится он дешевле, чем цельный, а по своей эффективности и надежности редко ему уступает. Сечение ленточного ростверка напоминает укрупненную балку, а значит и чертеж его армирования по сути ничем от аналогичного у балок не отличается.
Читайте также: как делается ручная вязка арматуры для фундамента?
Для цельного ростверка характерно покрывать всю площадь дома.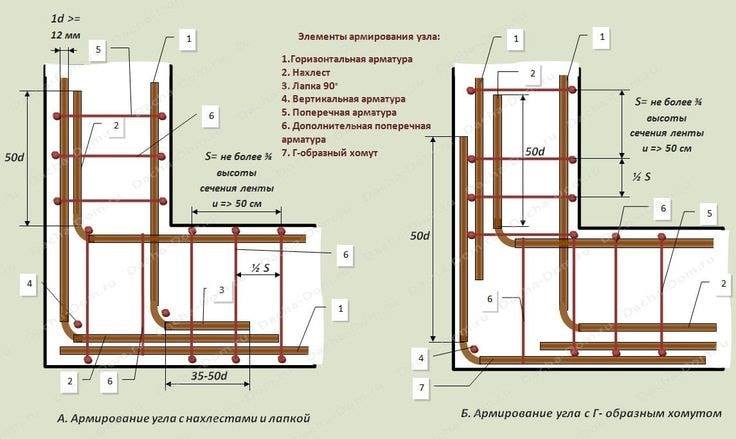
Арматурная сетка цельного ростверкового фундамента
Чертеж и вся сварная сетка в таком случае будет практически идентичной сетке, что используется для армирования плит перекрытий, особенно тех, что являются монолитными и размещаются на колоннах.
к оглавлению ↑
Расчет армирования сетки ростверка
Теперь перейдем к самому важному моменту – расчету арматурной сетки (каркаса). Сварная сетка для ростверка будет отличаться в первую очередь в зависимости от его типа.
Читайте также: вязка арматурных прутьев с помощью крючка: преимущества, особенности технологического процесса.
Использование буронабивных, забивных или других типов свай будет иметь второстепенное значение, так как от свай в данном случае требуется только выпустить наружу связующие арматурные штыри, к которым сетку ростверка и присоединят.
Расчет выполняется по чертежу конкретного типа ростверка. Так, линейный ростверк имеет форму крупной балки. Он обвязывает все сваи, образуя своеобразный пояс. По такой же схеме обвязывают колонны в несущих каркасных строениях.
Нижняя часть сетки будет собираться из более толстой арматуры диаметром от 20 мм. Верхняя же будет иметь сечение 8-15 миллиметров .
Так как основные нагрузки на поверхностный изгиб будут давить на ленту ростверка только в местах контакта со сваями, то серьезное усиление следует делать на участках ленты под сваями.
Причем достаточно всего лишь растянуть арматуру на 1,5-2 метра от центра сваи по ленте в обе стороны. В остальных же местах делать столь мощные конструкции верхней сетки рекомендуется, но вовсе не обязательно.
Сварная сетка-каркас в таком случае рассчитывается довольно легко. В учет берут ширину ленты и ее высоту. Арматуру нижнего уровня укладывают с шагом в 8-10 см. Как правило, на нижнюю сетку одной из лент ростверка уходит не меньше 4 стержней. На верхнюю может уходить от 6 стержней.
На верхнюю может уходить от 6 стержней.
Пример обвязки арматурных выводов из отверстия под скважину
Этот расчет касается лент шириной в 25 сантиметров. Если лента намного шире, то и арматуры на нее придется потратить больше. Также верхняя и нижняя сетки обвязываются и крепятся друг к другу упорными хомутами из прочной арматуры. Это тоже следует учитывать.
Таким образом, обсчитав длину и ширину лент ростверка, а также создав чертеж его сетки, можно выполнить полноценный расчет армирования, узнать количество необходимого материала, его стоимость и кучу других полезных моментов.
Здесь с шагом в 20-25 см необходимо укладывать арматуру минимальным диаметром от 20-25 мм. Арматуру укладывают крест-накрест, чтобы создать чрезвычайно прочное основание.
А вот верхняя сетка имеет интересные особенности. Далеко не всегда ее следует монтировать по всей площади. Это объясняется тем, что нижняя сетка арматуры гасит практически все нагрузки.
Любая же верхняя сетка должна гасить нагрузки на изгиб, которые приходятся от взаимодействия несущих конструкций и верхних элементов здания. А это значит, что ее нужно устанавливать только возле несущих элементов, что будут размещаться сверху или несущих элементов, что ее подпирают.
В каркасных монолитных домах верхняя арматурная сетка перекрытий покрывает только площадки в 2×2 или 3×3 квадратных метра, с центром в каждой подпирающей колонне. Все остальные места либо снабжаются страховочной сеткой из тонкой арматуры, либо вообще остаются без нее.
Если выполнить расчет габаритов цельного ростверка, а также его полезной площади, можно точно так же узнать всю необходимую вам информацию.
к оглавлению ↑
Технология армирования ростверка
Описать саму технологию армирования довольно легко, так как она, по сути, практически идентична во всех случаях.
Готовый ростверковый фундамент для легкого дома
Этапы работы:
- Собираем опалубку, следим за ее прочностью и надежностью.
- Собираем нижний каркас арматурной сетки.
- Монтируем хомуты, поддерживающие стойки и другие элементы.
- Собираем верхний арматурный каркас в нужных местах.
- Обвязываем и закрепляем все части армирования проволокой и дополнительными хомутами.
- Заливаем конструкцию бетоном, следим за тем, чтобы бетон заполнял опалубку без образования пустот, идеальным будет применение вибропресса.
- Ждем в течение недели, пока бетон окончательно не схватится.
Стоит заметить, что железобетонная конструкция набирает свою прочность в течение 27 дней. Ходить по ней, однако, можно будет уже через 4-8 дней, но возведение последующих несущих конструкций рекомендуется отложить на месяц.
к оглавлению ↑
Особенности и нюансы армирования ростверка (видео)
Расчет арматуры свайно ростверкового фундамента
Онлайн калькулятор расчета буронабивных свайно-ростверковых и столбчатых фундаментов
Информация по назначению калькулятора
Онлайн калькулятор монолитного буронабивного свайного и столбчатого ростверкого фундамента предназначен для расчетов размеров, опалубки, количества и диаметра арматуры и объема бетона, необходимого для обустройства данного типа фундамента. Для определения подходящего типа, обязательно обратитесь к специалистам.
Для определения подходящего типа, обязательно обратитесь к специалистам.
Все расчеты выполняются в соответствии со СНиП 52-01-2003 «Бетонные и железобетонные конструкции», СНиП 3.03.01-87 и ГОСТ Р 52086-2003
С вайный либо столбчатый фундамент – тип фундамента, в котором сваи либо столбы находятся непосредственно в самом грунте, на необходимой глубине, а их вершины связаны между собой монолитной железобетонной лентой (ростверком), находящейся на определенном расстоянии от земли. Главным отличием между столбчатым и свайным фундаментом является разная глубина установки опор.
О сновными условиями для выбора такого фундамента является наличие слабых, растительных и пучинистых грунтов, а так же большая глубина промерзания. В последнем случаем и при возможности забивания свай при любых погодных условиях, такой вид очень актуален в районах с суровым климатом. Так же к основным преимуществам можно отнести высокую скорость постройки и минимальное количество земляных работ, так как достаточно пробурить необходимое количество отверстий, либо вбить уже готовые сваи с использованием специальной техники.
С уществует различное множество вариаций данного типа фундамента, таких как геометрическая форма свай, материалы для их изготовления, механизм действия на грунт, методы установки и виды ростверка. В каждом индивидуальном случае необходимо выбирать свой вариант с учетом характеристик грунта, расчетных нагрузок, климатических и других условий. Для этого необходимо обращаться к специалистам, которые смогут произвести все необходимые замеры и расчеты. Попытки экономии и самостроя могут привести к разрушению постройки.
При заполнении данных, обратите внимание на дополнительную информацию со знаком Дополнительная информация .
Д алее представлен полный список выполняемых расчетов с кратким описанием каждого пункта. Вы так же можете задать свой вопрос, воспользовавшись формой справа.
Общие сведения по результатам расчетов
- О бщая длина ростверка — Периметр фундамента, с учетом длины внутренних перегородок.
- П лощадь подошвы ростверка — Соответствует размерам необходимой гидроизоляции.
- П лощадь внешней боковой поверхности ростверка — Соответствует площади необходимого утеплителя для внешней стороны фундамента.
- О бщий Объем бетона для ростверка и столбов — Объем бетона, необходимого для заливки всего фундамента с заданными параметрами. Так как объем заказанного бетона может незначительно отличаться от фактического, а так же вследствие уплотнения при заливке, заказывать необходимо с 10% запасом.
- В ес бетона — Указан примерный вес бетона по средней плотности.
- Н агрузка на почву от фундамента в местах основания столбов — Нагрузка на почву от веса фундамента в местах основания столбов/свай.
- М инимальный диаметр продольных стержней арматуры — Минимальный диаметр по СНиП, с учетом относительного содержания арматуры от площади сечения ленты.
- М инимальное кол-во рядов арматуры ростверка в верхнем и нижнем поясах — Минимальное количество рядов продольных стержней в каждом поясе, для предотвращения деформации ленты под действием сил сжатия и растяжения.
- М инимальный диаметр поперечных стержней арматуры (хомутов) — Минимальный диаметр поперечных и вертикальных стержней арматуры (хомутов) по СНиП.
- М инимальное кол-во вертикальных стержней арматуры для столбов — Количество вертикальных стержней арматуры на каждый столб/сваю.
- М инимальный диаметр арматуры столбов — Минимальный диаметр вертикальных стержней для столбов/свай.
- Ш аг поперечных стержней арматуры (хомутов) для ростверка — Шаг хомутов, необходимых для предотвращения сдвигов арматурного каркаса при заливке бетона.
- В еличина нахлеста арматуры — При креплении отрезков стержней внахлест.
- О бщая длина арматуры — Длина всей арматуры для вязки каркаса с учетом нахлеста.
- О бщий вес арматуры — Вес арматурного каркаса.
- Т олщина доски опалубки — Расчетная толщина досок опалубки в соответствии с ГОСТ Р 52086-2003, для заданных параметров фундамента и при заданном шаге опор.
- К ол-во досок для опалубки — Количество материала для опалубки заданного размера.

Калькулятор для расчета свайного фундамента
Дополнительная информация о калькуляторе
Онлайн-калькулятор для расчета монолитного буронабивного ростверкового фундамента поможет рассчитать размеры фундамента, опалубки, диаметр и общую длину арматуры и объём расходуемого бетона. Перед началом проектирования здания с таким фундаментом обязательно проконсультируйтесь у специалистов, насколько оправдан такой выбор.
Обратите внимание! Расчеты данного калькулятора основываются на нормативах, приведенных в ГОСТ Р 52086-2003, СНиП 3.03.01-87 и СНиП 52-01-2003 Бетонные и железобетонные конструкции .
Столбчатый и свайный фундамент – разновидности фундаментов, в которых используются столбы или сваи в качестве опор. Они погружаются в грунт на необходимую глубину, а их верхние части соединяются цельной железобетонной конструкцией (ростверком), которая не соприкасается с землёй. При столбчатом и свайном варианте ростверкового фундамента отличается глубина установки опор.
Ростверковая конструкция имеет смысл там, где грунт не пригоден для обычного размещения фундамента (слабый грунт, пучинистый, либо промерзающий на значительную глубину). Поскольку сваи забиваются при любых климатических условиях, ростверковый фундамент особенно актуален для регионов с низкими температурами и суровым климатом. Другие преимущества ростверковой технологии – высокая скорость возведения и низкая потребность в земляных работах. Достаточно пробурить отверстия и выполнить установку уже готовых свай.
Многие параметры ростверкового фундамента могут варьироваться. Это форма и материалы свай, способы действия на грунт, способы установки, форма ростверка. Каждый случай ростверкового фундамента должен учитывать расчётные нагрузки, климатические условия, специфику грунта и другие особенности местности и будущего сооружения. Чтобы уточнить все эти моменты, нужно провести необходимые замеры и расчёты, при необходимости – пригласить специалистов. Экономия на первоначальных расчётах может обернуться серьезными последствиями в будущем. Чтобы этого избежать, в первую очередь рекомендуем внимательно изучить данный калькулятор. В нем вы сможете определить будущие расходы и на примере стандартной конструкции определиться с составляющими планируемого фундамента.
Чтобы этого избежать, в первую очередь рекомендуем внимательно изучить данный калькулятор. В нем вы сможете определить будущие расходы и на примере стандартной конструкции определиться с составляющими планируемого фундамента.
Заполняя поля калькулятора, сверьтесь с дополнительной информацией, отображающейся при наведении на иконку вопроса .
Внизу страницы вы можете оставить отзыв, задать вопрос разработчикам или предложить идею по улучшению этого калькулятора.
Разъяснение результатов расчетов
Общая длина ростверка
Суммарный периметр фундамента, включая внутренние перегородки.
Площадь подошвы ростверка
Площадь нижней части ростверка, которая нуждается в гидроизоляции.
Площадь внешней боковой поверхности ростверка
Площадь боковых поверхностей наружной стороны фундамента, нуждающаяся в утеплении.
Объем бетона для ростверка и столбов
Общее количество бетона, которое понадобится для заливки фундамента заданных параметров.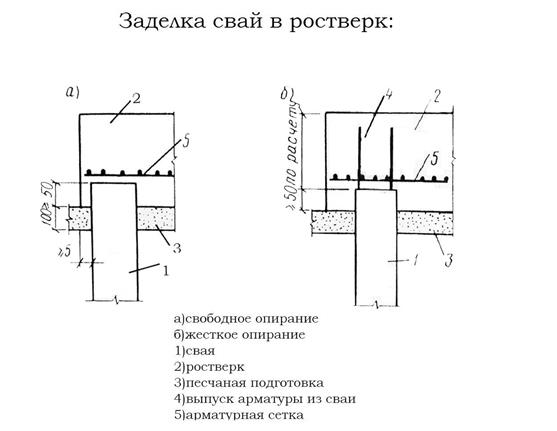 Фактическая потребность может оказаться выше из-за уплотнений при заливке, а объём фактически доставленного бетона может оказаться меньше заказанного. Поэтому рекомендуем заказывать бетон с 10-процентным запасом.
Фактическая потребность может оказаться выше из-за уплотнений при заливке, а объём фактически доставленного бетона может оказаться меньше заказанного. Поэтому рекомендуем заказывать бетон с 10-процентным запасом.
Вес бетона
Приблизительный вес бетона при средней плотности.
Нагрузка на почву от фундамента в местах основания столбов
При расчете берется во внимание полный вес конструкции.
Минимальный диаметр продольных стержней арматуры
Рассчитывается по нормативам СНиП. Учитывается относительное содержание продольной арматуры в сечении ленты ростверка.
Минимальное количество рядов арматуры ростверка
Для противодействия естественной деформации ленты ростверка под действием сил сжатия и растяжения, необходимо использовать продольные стержни в разных поясах ростверка (вверху и внизу ленты).
Общий вес арматуры
Вес стержней арматуры, вместе взятых.
Величина нахлеста арматуры
Для крепления стержней арматуры внахлёст, используйте данное значение.
Длина продольной арматуры
Общая длина арматуры включая нахлест.
Минимальное количество продольных стержней арматуры для столбов и свай
Необходимое количество продольных стержней арматуры для каждого столба или сваи.
Минимальный диаметр арматуры для столбов и свай
Минимально допустимый диаметр продольных стержней арматуры, обеспечивающих прочность столбов или свай.
Минимальный диаметр поперечной арматуры (хомутов)
Определяется, основываясь на нормативах СНиП.
Максимальный шаг поперечной арматуры (хомутов)
Рассчитывается таким образом, чтобы при заливке бетона арматурный каркас не был смещён или деформирован.
Общий вес хомутов
Суммарный вес хомутов, которые потребуются при строительстве всего фундамента.
Минимальная толщина доски при опорах через каждый метр
Необходимая толщина досок опалубки при заданных параметрах фундамента и заданном шаге опор. Рассчитывается исходя из ГОСТ Р 52086-2003.
Рассчитывается исходя из ГОСТ Р 52086-2003.
Количество досок для опалубки
Число досок стандартной длиной 6 метров, которые потребуются для возведения всей опалубки.
Периметр опалубки
Общая протяженность опалубки с учетом внутренних перегородок.
Объем и примерный вес досок для опалубки
Такой объем досок потребуется для возведения опалубки. Вес досок рассчитывается из среднего значения плотности и влажности хвойных пород дерева.
Раздел III. РАСЧЕТ СВАЙ И СВАЙНЫХ ФУНДАМЕНТОВ Глава 4. РАСЧЕТ РОСТВЕРКОВ СВАЙНЫХ ФУНДАМЕНТОВРостверки являются составной частью свайных фундаментов, объединяют головы свай н служат для передачи нагрузки от надземной части здания через сван на основание.
После размещения свай в плане и определения габаритов ростверка уточняют вертикальную нагрузку на отдельную сваю в фундаменте по формуле
Расчетную горизонтальную нагрузку Р, тс, на сваю определяют из условии равномерного распределения нагрузки на все сваи фундамента. При этом плита ростверка по отношению к сваям принимается бесконечно жесткой.
Ростверки ленточные и под отдельные колонны рассчитывают в соответствии с требованиями СНиП Ц-В.1—G2* по первому предельному состоянию (по несущей способности) на основное, дополнительное н особое сочетание расчетных нагрузок, а прн необходимости — по раскрытию трещин на основное и дополнительное сочетание нормативных нагрузок.
Проверка ширины раскрытия нормальных трещки производится при применении арматуры из стали класса А-Ш для армирования подошвы ростверка. Расчет по раскрытию трещин следует производить согласно указаниям п. 10.4 СНиП П-В.1—62*. Ширина раскрытия нормальных трещин йт должна быть не более 0,2 мм.
Расчет ростверков на сваях сплошного круглого сечения производят так же, как и на сваях квадратного сечения..
Сборные н монолитные железобетонные ростверки свайных фундаментов должны изготавливаться из бетона проектной марки ие ниже соответственно 200 и 150.
Высоту железобетонного ленточного свайного ростверка определяют расчетом. Рекомендуемая минимальная высота ростверка — 30, ширина — 40 см.
Размеры подошвы ростверка под колонны, ступеней И подколонника в плане нз условия унификации рекомендуется принимать кратными 300 мм. Высоту плнтной части, ступеней и подколонника следует принимать кратной 150 мм.
Арматуру для армирования ростверков применяют стержневую горячекатаную периодического профиля нз стали клвссов A-I1, А-1И и круглую класса A-I.
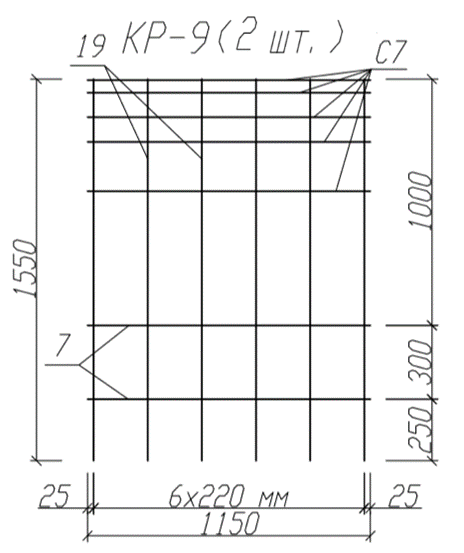
Плиты ростверка рекомендуется армировать в каждом направлении отдельными сварными сетками, у которых расстояние между рабочими стержнями равно 200 мм. Диаметр рабочей арматуры следует принимать ие менее 10 мм при длине стержней до 3 м и не менее 12 мм при длине более 3 м. Арматурные сетки должны быть сварены во всех точках пересечения стержней. Допускается часть пересечений связывать проволокой при условии обязательной сварки всех точек пересечений я двух крайних рядах по периметру сеток. Для обеспечения анкеровки рабочей арматуры по концам сеток ва расстоянии 25 мм от конца продольных стержней должны быть предусмотрены поперечные стержни вдвое меньшего диаметра, чем продольные.
В случае заделки верхних концов свай в ростверк иа глубину 50 мм арматурные сетки укладывают сверху на головы свай. При заделке свай в ростверк иа глубину более 50 мм стержни, попадающие на сваи, вырезают, а сетки укладывают с защитным слоем бетона 50 мм.
Стенки стакана ростверка подсборные железобетонные колонны армируют продольной н поперечной арматурой. Поперечное армирование стенок стакана следует выполнять в ниде сварных сеток с расположением стержней у наружных и внутренних поверхностей стенок. Диаметр арматурных стержней принимается по расчету, но не менее 0,25 диаметра продольной арматуры стенок. Расстояние между сетками принимается не более 0,25 глубины заделки колони н не более 200 мм.
В верхней части стакана рекомендуется устанавливать 2—3 сетки с шатоы 100 мм.
Диаметр продольной арматуры стенок стакана определяют расчетом.
Сетки, необходимые по расчету на смятие под торцами сборных железобетонных колонн, укладывают ке менее 2 шт. а под опорными плитами базы стальных колонн — не менее 4 шт. с расстоянием по высоте 50—100 мм.
Железобетонные монолитные, а также стальные колонны соединяются с монолитными ростверками так же, как и с монолитными фундаментами на естественном основании
Железобетонные ростверки. Устройство свайных ростверков
Верхние концы свай должны быть заделаны в ростверк на глубину, определяемую расчетом. учитывающим сейсмические нагрузки. Устройство безростверковых свайных.
www.bibliotekar.ru/spravochnik-127-fundamenty/57.htm
Источники: http://stroy-calc.ru/raschet-stolbchatogo-fundamenta, http://www.stroitelstvosovety.ru/raschet-stolbchatogo-fundamenta, http://www.bibliotekar.ru/spravochnik-160-svai-svaynye-fundamenty/51.htm
Комментариев пока нет!
17.Расчет ростверков
Принимаем материалы для изготовления ростверков:
— монолитный бетон класса по прочности В25, Rb= 14,5 МПа;Rbt= 1,05 МПа;γb2= 0,9;Rb= 13,05 МПа;Rbt= 0,945 МПа;Eb= 30000 МПа;
— арматура класса А-III,Rs=Rsc= 365 МПа;Es= 200000 МПа;
— арматура класса А-I,Rsw= 175 МПа;Es= 210000 МПа.
Ростверк фундамента ФС1.
Расчет на продавливание.
Поскольку ростверк является высоким, отпор грунта под его подошвой при расчете на продавливание не учитывается. Анализ опалубочного чертежа фундамента СВ1 (рис. 6) приводит к выводу, что рассчитываемый ростверк является балочным. В балочном ростверке пирамида продавливания вырождается в фигуру с двумя наклонными плоскостями, по которым происходит продавливание под колонной. Указанные плоскости пересекают ростверк в верхнем сечении по граням колонны, а в нижнем сечении по граням свай. Здесь имеется полная аналогия с разрушением балки по наклонному сечению при действии поперечной силы. Расчеты на продавливание выполняются по формуле (107) норм /6/:
где N– максимальная нагрузка на сваю, равная 1256,6 кН;α— коэффициент, принимаемый для тяжелого бетона равным 1,0;um– средняя линия боковой поверхности пирамиды продавливания, равная в нашем случае ширине ростверка 0,9 м;h0– высота пирамиды продавливания, равная в нашем случае высоте ростверка за вычетом защитного слоя бетона в нижней зонеa= 0,05 м,h0= 0,6 – 0,05 = 0,55 м.
Из опалубочного чертежа фундамента следует, что боковая грань пирамиды продавливания наклонена к горизонтали на угол, больший 450. При этом проекция ее высоты на горизонтальную плоскостьс= 0,25 м. Вычисляем минимальное значение этой проекции, учитываемое в расчетах на продавливание (п. 3.42 норм /6/):
Поскольку c>cmin, в качестве расчетного значения принимаемc= 0,25 м. При наклоне боковой грани пирамиды продавливания к горизонтали на угол, больший 450, расчетное сопротивление батонаFbумножают на коэффициент, равныйh0/c. С учетом сделанных замечаний расчет на продавливание ростверка выполняем по формуле:
Условие прочности при продавливании ростверка не выполняется. Увеличение несущей способности ростверка на продавливание может быть выполнено одним из следующих способов:
— применение поперечного армирования;
— увеличение толщины ростверка;
— увеличение класса бетона по прочности.
Недостаток несущей способности составляет 18,1 %. Несущая способность минимального расчетного поперечного армирования (п. 3.42 норм /6/) должно составлять не менее 50 % несущей способности бетонного сечения. В связи с этим способ повышения несущей способности ростверка на продавливание за счет применения поперчного армирования следует признать экономически нецелесообразным.
Принимаем толщину ростверка 0,7 м. Переопределяем величину cmin:
Поскольку c<cmin, в качестве расчетного значения принимаемc= 0,26 м.
Проверяем несущую способность ростверка на продавливание:
Условие прочности ростверка на продавливание выполнено. Корректируем по результатам расчета опалубочный чертеж фундамента ФС1 (рис. 7).
Вставить рис. 7, чертеж ФС1, окончательный вариант
Расчет на изгиб.
Нижнюю продольную арматуру в ростверке подбираем из расчета на изгиб нормального сечения по грани колонны. Отпор Pсо стороны сваи равен нагрузке на сваю и составляет 1256,6 кН. Плечо приложения силыlизмеряется от оси сваи до грани колонны и составляет 0,4 м. Изгибающий момент в расчетном сечении будет равен:
Находим предварительное сечение продольной арматуры:
Принимаем 4Ф28А-III,As= 0,002463 м2или 24,63 см2. Проверяем достаточность принятого армирования по нормам /6/:
Принятое армирование является достаточным.
Верхнюю продольную арматуру определяем из расчета на изгиб нормального сечения ростверка по грани колонны при действии изгибающего момента, передавемого колонной на ростверк, М= 179,0 кНм. При этом ростверк рассматривается как балка, свободно опертая на сваи и загруженная расчетным изгибающим моментом в центре пролета. Определяем по правилам строительной механики изгибающий момент в расчетном сечении ростварка:
где xi– расстояние от оси сваи до центра колонны или ростверка;lc— размер поперечного сечения колонны.
Находим предварительное сечение продольной арматуры:
Минимальное сечение растянутой арматуры по таб. 38 норм /6/ составляет 0,05 % от площади поперечного сечения b∙h0или 0,0002925 м2.
Принимаем 4Ф10А-III,As= 0,000314 м2или 3,14 см2. Проверяем достаточность принятого армирования по нормам /6/:
Принятое армирование является достаточным и удовлетворяет требованиям норм /6/ по минимальному армированию.
Поперечное армирование принимаем конструктивно с учетом требований п. 5.29 норм /6/ в виде замкнутых хомутов 4Ф6А-I, устанавливаемых с шагом 200 мм.
0
Ростверк фундамента ФС2.
Расчет на продавливание.
Поскольку ростверк является высоким, отпор грунта под его подошвой при расчете на продавливание не учитывается. Анализ опалубочного чертежа фундамента СВ2 (рис. 4) приводит к выводу, что рассчитываемый ростверк является плитным. В плитном ростверке пирамида продавливания имеет верхнее основание, совподающее с опорным сечением колонны, и нижнее основание в форме прямоугольника, углы которого совпадают с внутренними углами поперечных сечений свай. Расчеты на продавливание выполняются по формуле (107) норм /6/:
где N– максимальная нагрузка от колонны на ростверк, равная 3412,7 кН;α— коэффициент, принимаемый для тяжелого бетона равным 1,0;um– среднеарифметическое значение периметров верхнего и нижнего оснований пирамиды продавливания;h0– высота пирамиды продавливания, равная в нашем случае высоте ростверка за вычетом защитного слоя бетона в нижней зонеa= 0,05 м,h0= 0,6 – 0,05 = 0,55 м.
Из опалубочного чертежа фундамента следует, что боковые грани пирамиды продавливания наклонены к горизонтали на угол, больший 450. При этом проекция высоты боковой грани на горизонтальную плоскостьс= 0,1 м. Вычисляем минимальное значение этой проекции, учитываемое в расчетах на продавливание (п. 3.42 норм /6/):
Поскольку c<cmin, в качестве расчетного значения принимаемc= 0,22 м.
Вычисляем среднеарифметическое значение периметров оснований пирамиды продавливания:
При наклоне боковой грани пирамиды продавливания к горизонтали на угол, больший 450, расчетное сопротивление батонаFbумножают на коэффициент, равныйh0/c. С учетом сделанных замечаний расчет на продавливание ростверка выполняем по формуле:
Условие прочности при продавливании ростверка не выполняется. Увеличение несущей способности ростверка на продавливание может быть выполнено увеличение толщины ростверка.
Принимаем толщину ростверка 0,7 м. Переопределяем величину cmin:
Поскольку c<cmin, в качестве расчетного значения принимаемc= 0,26 м.
Проверяем несущую способность ростверка на продавливание:
Условие прочности ростверка на продавливание выполнено. Корректируем по результатам расчета опалубочный чертеж фундамента ФС2 (рис. 8).
Вставить рис. 8, чертеж ФС2, окончательный вариант
Расчет на изгиб.
Применяем для расчета пространственного ростверка упрощенную схему, в соответствии с которой он рассчитывается по балочной схеме в двух направлениях. Поскольку ростверк симметричен по геометрии и нагрузкам, расчет выполняем в одном направлении, а результаты этого расчета распространяем на оба направления. Нижнюю продольную арматуру в ростверке подбираем из расчета на изгиб нормального сечения по грани колонны. Отпор Pсо стороны свай равен сумме нагрузок на сваи, расположенные по одну сторону от колонны, и составляет 899,1∙2 = 1798,2 кН. Плечо приложения силыlизмеряется от оси сваи до грани колонны и составляет в соответствии с опалубочным чартежом (рис. 8) 0,25 м. Изгибающий момент в расчетном сечении будет равен:
Находим предварительное сечение продольной арматуры:
Принимаем 7Ф20А-III,As= 0,002199 м2или 21,99 см2. Проверяем достаточность принятого армирования по нормам /6/:
Принятое армирование является достаточным.
Верхнюю продольную арматуру определяем из расчета на изгиб нормального сечения ростверка по грани колонны при действии изгибающего момента, передавемого колонной на ростверк, М= 82,7 кНм. При этом ростверк рассматривается как балка, свободно опертая на сваи и загруженная расчетным изгибающим моментом в центре пролета. Определяем по правилам строительной механики изгибающий момент в расчетном сечении ростварка:
Находим предварительное сечение продольной арматуры:
Минимальное сечение растянутой арматуры по таб. 38 норм /6/ составляет 0,05 % от площади поперечного сечения b∙h0или 0,000585 м2.
Принимаем 8Ф10А-III,As= 0,000628 м2или 6,28 см2. Проверяем достаточность принятого армирования по нормам /6/:
Принятое армирование является достаточным и удовлетворяет требованиям норм /6/ по минимальному армированию.
Поперечное армирование принимаем по технологическим соображениям для фиксации в проектном положении продольной арматуры. Применяем отдельные стержни Ф10А-I, устанавливаемые с шагом в продольном и поперечном направлении 600 мм (по 4 стержня в каждом продольном и поперечном ряду).
Окончательно принимаем:
— нижняя продольная арматура в виде сетки Ф 20А-III по 7 стержней в каждом направлении;
— верхняя продольная арматура в виде сетки Ф 10А-III по 8 стержней в каждом направлении.
Рекомендуется 7 стержней верхней сетки разместить по аналогии с нижней арматурной сеткой, а 8-й стержень установить как спаренный в центре сечения. Это позволит систематизировать установку поперечной арматуры, стержни которой будут размещаться в узлах сеток и крепиться к продольной арматуре на сварке.
18.Анкеровка арматуры колонн
По проектному заданию в колонне применена арматура периодического профиля класса А-IIIс максимальным диаметром 25 мм. Вычисляем длину зоны анкеровки по формуле (186) норм /6/:
где входящие в формулу коэффициенты принимаются по таб. 37 норм /6/, а расчетное сопротивление бетона берется без учета коэффициента γb2. Поскольку расчетная длина анкеровки арматуры превышаетh0= 650 мм, требуется применение конструктивных мероприятий по обеспечению надежной анкеровки рабочей арматуры колонн в ростверке. Рекомендуется применить анкер в виде поперечного стержня (коротыша) диаметром 16 мм, который привариваетсы к рабочей арматуре на расстоянии 100 мм от конца, заделанного в ростверке (тип анкеровки № 5 по таб. 9 Рекомендаций /27/). При использовании такой анкеровки вводится понижающий коэффициент на расчетную длину анкеровки, равный 0,7. При этом получаем:
Надежность анкеровки рабочей арматуры колонны в ростверке обеспечена.
Онлайн-калькулятор расчета размеров, арматуры и количества бетона монолитного ленточного фундамента
ИНФОРМАЦИЯ ПО НАЗНАЧЕНИЮ КАЛЬКУЛЯТОРА
Онлайн калькулятор монолитного буронабивного свайного и столбчатого ростверкого фундамента предназначен для расчетов размеров, опалубки, количества и диаметра арматуры и объема бетона, необходимого для обустройства данного типа фундамента. Для определения подходящего типа, обязательно обратитесь к специалистам.
Свайный либо столбчатый фундамент – тип фундамента, в котором сваи либо столбы находятся непосредственно в самом грунте, на необходимой глубине, а их вершины связаны между собой монолитной железобетонной лентой (ростверком), находящейся на определенном расстоянии от земли. Главным отличием между столбчатым и свайным фундаментом является разная глубина установки опор. Дешевле ленточного фундамента.
Основными условиями для выбора такого фундамента является наличие слабых, растительных и пучинистых грунтов, а так же большая глубина промерзания. В последнем случаем и при возможности забивания свай при любых погодных условиях, такой вид очень актуален в районах с суровым климатом. Так же к основным преимуществам можно отнести высокую скорость постройки и минимальное количество земляных работ, так как достаточно пробурить необходимое количество отверстий, либо вбить уже готовые сваи с использованием специальной техники.
Существует различное множество вариаций данного типа фундамента, таких как геометрическая форма свай, материалы для их изготовления, механизм действия на грунт, методы установки и виды ростверка. В каждом индивидуальном случае необходимо выбирать свой вариант с учетом характеристик грунта, расчетных нагрузок, климатических и других условий. Для этого необходимо обращаться к специалистам, которые смогут произвести все необходимые замеры и расчеты. Попытки экономии и самостроя могут привести к разрушению постройки.
Далее представлен полный список выполняемых расчетов с кратким описанием каждого пункта. Вы так же можете задать свой вопрос, воспользовавшись формой в правом блоке.
ОБЩИЕ СВЕДЕНИЯ ПО РЕЗУЛЬТАТАМ РАСЧЕТОВ
Общая длина ростверка
• Периметр фундамента, с учетом длины внутренних перегородок.
Площадь подошвы ростверка
• Соответствует размерам необходимой гидроизоляции.
Площадь внешней боковой поверхности ростверка
• Соответствует площади необходимого утеплителя для внешней стороны фундамента.
Общий Объем бетона для ростверка и столбов
• Объем бетона, необходимого для заливки всего фундамента с заданными параметрами. Так как объем заказанного бетона может незначительно отличаться от фактического, а так же вследствие уплотнения при заливке, заказывать необходимо с 10% запасом.
Вес бетона
• Указан примерный вес бетона по средней плотности.
Нагрузка на почву от фундамента в местах основания столбов
• Нагрузка на почву от веса фундамента в местах основания столбов/свай.
Минимальный диаметр продольных стержней арматуры
• Минимальный диаметр по СНиП, с учетом относительного содержания арматуры от площади сечения ленты.
Минимальное кол-во рядов арматуры ростверка в верхнем и нижнем поясах
• Минимальное количество рядов продольных стержней в каждом поясе, для предотвращения деформации ленты под действием сил сжатия и растяжения.
Минимальный диаметр поперечных стержней арматуры (хомутов)
• Минимальный диаметр поперечных и вертикальных стержней арматуры (хомутов) по СНиП.
Минимальное кол-во вертикальных стержней арматуры для столбов
• Количество вертикальных стержней арматуры на каждый столб/сваю.
Минимальный диаметр арматуры столбов
• Минимальный диаметр вертикальных стержней для столбов/свай.
Шаг поперечных стержней арматуры (хомутов) для ростверка
• Шаг хомутов, необходимых для предотвращения сдвигов арматурного каркаса при заливке бетона.
Величина нахлеста арматуры
• При креплении отрезков стержней внахлест.
Общая длина арматуры
• Длина всей арматуры для вязки каркаса с учетом нахлеста.
Общий вес арматуры
• Вес арматурного каркаса.
Толщина доски опалубки
• Расчетная толщина досок опалубки в соответствии с ГОСТ для заданных параметров фундамента и при заданном шаге опор.
Кол-во досок для опалубки
• Количество материала для опалубки заданного размера.
Монолитный ростверк. Основные положения проектирования
Уроки по LIRA SAPR. Жмите>>>
Монолитный ростверк. Основные положения проектирования
Способы соединения ростверка со сваями
Защита ростверка от коррозии
Защита ростверка от морозного пучения
Металлический ростверк
План работ по проектированию ростверка:
Получить схемы свай и нагрузок на ростверк;
Вычерчивание контура ростверка;
Простановка размеров;
Расчет ростверка, определение площади арматуры;
Маркировка сечений;
Вычерчивание сечений по ростверку;
Оформление узлов сопряжения каркасов ростверка;
Подсчёт объёмов материалов. Заполнение спецификации;
Оформление текстовой части.
Возможные спорные вопросы и затруднения, которые могут возникнуть при проектировании ростверка:
Как рассчитать армирование в ленточном монолитном ростверке?
Ответ: Руководство по проектированию свайных фундаментов. Приложение 9 Расчёт железобетонных ленточных ростверков свайных фундаментов под кирпичные и крупноблочные стены
- Ростверки под стенами кирпичных и крупноблочных зданий, опирающиеся на железобетонные сваи, расположенные в один или в два ряда, должны рассчитываться на эксплуатационные нагрузки и на нагрузки, возникающие в период строительства.
- Расчет ростверка на эксплуатационные нагрузки следует вести из условия распределения нагрузки в виде треугольников с наибольшей ординатой р, тс/м, над осью сваи, которая определяется по формуле
p=qo*L / а
где L – расстояние между осями свай по линии ряда или рядов, м;
qo – равномерно распределенная нагрузка от здания на уровне низа ростверка (вес стен, перекрытий, ростверка и полезная нагрузка), тс/м;
а – длина полуоснования эпюры нагрузки, м, определяемая по формуле
a=3.14*√(Ер*Iр/Eк*bк)
где Ер – модуль упругости бетона ростверка, кгс/см2;
Iр – момент инерции сечения ростверка, см4;
Ек – модуль упругости кладки стены над ростверком, кгс/см2;
bк – ширина стены, опирающейся на ростверк (ширина цоколя), м.
- Наибольшую ординату эпюры нагрузки над гранью сваи р0, тс/м, можно определить по формуле
p=qo*Lp / а
Lp – расчетный пролет, м, принимаемый равным 1,05 Lсв, (где Lсв – расстояние между сваями в свету, м.)
Для различных схем нагрузок расчетные изгибающие моменты Моп и Мпр определяются по формулам, приведенным в табл. 1
Класс бетона, как правило, для фундаментов не должен превышать В15. Арматура для фундаментов, как правило, принимается минимум диаметром 12мм, даже если по расчёту получилось меньше.
Как армировать монолитный ленточный ростверк?
При проектировании обратить внимание на защитный слой бетона, таблица 10.1 СП 63.13330.2012, защитный слой не должен быть меньше той величины, но и не должен сильно её превышать, для экономии бетона. В зависимости от вида подготовки назначается толщина защитного слоя бетона нижней арматуры, соответственно 70 мм и 35 мм (п. 5.5 СНиП 2.03.01-84*).
Предусмотреть в углах и пересечениях лент дополнительное армирование для обеспечения жёсткой связи в соответствии с требованием п.8.9 СП 50-101-2004 (Сборно-монолитные и монолитные фундаменты всех стен должны быть жестко связаны между собой и объединены в систему перекрестных лент). Жёсткое соединение может быть выполнено по аналогии сопряжения между собой балок и колонн, схемы армирования углов смотреть в СП 63.13330.2012 п. 10.4.1. Применение предложенных решений в монолитном ростверке показано на рисунке.
Какую подготовку предусмотреть под монолитный ростверк? Сколько слоёв, из какого материала и какой толщины?
Подготовку под фундамент выполняют из уплотненного щебня или тощего бетона” – п. 13.2.22 СП 50-101-2004 “Проектирование и устройство оснований и фундаментов зданий и сооружений”. В каких случаях применять щебеночную или бетонную подготовку в нормативных документах не оговаривается.
Толщина щебеночной подготовки как правило принимается 150-200 мм, бетонной подготовки B15 100 мм. Какой из вариантов принять – зависит от конкретной задачи. Если речь идет о фундаментной плите или ростверке, армированных пространствнными каркасами, “тяжелыми” сетками, то по технологическим, конструктивным соображениям предпочтительнее предусматривать бетонную подготовку: на ней не деформируются каркасы и сетки фундаментной плиты, можно выполнить разметку осей , првязку к ним выпусков арматуры, не происходит утечка цементного молока с рабочей арматуры нижней плоскости плиты и т.д.
При щебеночной подгтовке необходимо предусматривать проливку ее битумом до полного насыщения или образования пленки, сложнее выставлять на фиксаторах каркасы и сетки, уменьшается рабочая высота КП и сеток и т.д.
При бетонировании в зимних условиях так-же предпочтительнее иметь бетонную подготовку – ее можно прогреть шнурами, тепляком,можно использовать бетон с противоморозными добавками, но гораздо больше проблем прогревать и проливать битумом промерзший щебень.
По сложившейся у нас практике в основном применяют бетонную подготовку – качество арматурных и бетонных работ в этом случае заметно повыше.
Руководство по конструированию бетонных и железобетонных конструкций из тяжелого бетона (без предварительного напряжения)
3.24. Под монолитными фундаментами независимо от грунтовых условий (кроме скальных грунтов) рекомендуется всегда предусматривать бетонную подготовку толщиной 100 мм из бетона марки М50, а под сборными – из среднезернистого песка слоем 100 мм.
При необходимости устройства фундаментов на скальных грунтах следует предусматривать выравнивающий слой по грунту из бетона марки М50.
Другие уроки по теме
Перекрытия в автокадеУроки по LIRA SAPR. Жмите>>> Многопустотные плиты перекрытия длиной 4.8–6.3 м (марки ПК) с шагом 0.3 м, шириной 1, 1,2 и 1,5 м и высотой 220 мм изготавливаются из тяжёлого бетона. Класс бетона по прочности определяется заводом–изготовителем. Армирование плиты в нижней (растянутой) зоне выполняется из высокопрочной проволоки периодического профиля диаметром 5 мм с выраженными анкерными головками, по граням контура […]
Вопросы и ответы по авторскому надзоруУроки по LIRA SAPR. Жмите>>> Узнай ещё: Авторский надзор опыт работы Может ли авторский надзор осуществлять другая организация (не выполнявшая проект)? В соответствии с СП 11-110-99 3.5 Проектировщик – физическое или юридическое лицо, разработавшее, как правило, рабочую документацию на строительство объекта и осуществляющее авторский надзор. Работы по авторскому надзору могут выполняться сторонней организация, т. е. следить […]
Как рассчитать свайно ростверковый фундамент
Обычно монолитный железобетонный ростверк располагается на самом фундаменте и равномерно распределяет на него нагрузку от здания. Прежде всего нужно определиться с типом фундамента который вам подойдёт он может быть столбчатый, свайный или ленточный фундамент с ростверком. При столбчатом и свайном фундаменте ростверк находится на вершинах свай соединяя их между собой, а на ленточном фундаменте он находится между фундаментом и несущими стенами. Так как несущими стенами могут быть не только наружные но внутренние стены то бетонный ростверк может иметь различную конфигурацию.
Определившись с типом фундамента можно сделать расчет ростверка. Столбчатый фундамент отличается от свайного фундамента в основном глубиной заложения поэтому рассчитать свайно ростверковый фундамент и столбчато ростверковый фундамент можно на одном и том же калькуляторе. Чтобы сделать расчет буронабивных свай с ростверком или расчет свайного ростверка, а также расчитать ленточно ростверковый фундамент можно воспользоваться онлайн калькулятором. Мне нравится делать расчет ростверкового фундамента калькулятором который находится на сайте stroy-calc.ru.
Прежде чем начать делать буронабивной фундамент с ростверком расчет нужно сделать
С помощью этого онлайн калькулятора можно рассчитать необходимый размер опалубки для ростверка, диаметр арматуры и её количество, а также объём бетона. Все расчёты производятся в соответствии со СНиП 52-01-2003 Бетонные и железобетонные конструкции, СНиП 3.03.01-87 и ГОСТ Р 52086-2003.
Чтобы произвести расчет свайно ростверкового фундамента в калькуляторе нужно указать: вид ростверка, марку бетона для ростверка, количество столбов или свай, диаметр и длину столба или сваи, диаметр и высоту расширения внизу столба или сваи если оно предусмотрено, ширину и длину заложения фундамента, высоту, размеры ростверка по длине и толщине, длину арматурного стержня, ширину, толщину и длину досок которые будут применяться при строительстве опалубки.
Указав эти параметры и нажав кнопку Рассчитать произойдёт расчет ростверка свайного фундамента и калькулятор покажет:
- Общую длину.
- Площадь подошвы и площадь внешней боковой поверхности.
- Необходимый объём бетона и вес этого бетона.
- Нагрузку передаваемую от фундамента на почву в местах основания столбов.
- Минимальный диаметр продольной и поперечной арматуры ростверка и столбов.
- Минимальное количество рядов арматуры ростверка и столбов.
- Расстояние между поперечными хомутами.
- Размер нахлёста арматуры.
- Общую длину и вес продольной арматуры.
- Общую длину хомутов ростверка и поперечной арматуры столбов и их вес.
- Количество досок необходимое для обустройства опалубки для ростверка.
- Максимальное расстояние между опорами опалубки.
Чтобы рассчитать ленточный ростверк для монолитного ленточного фундамента нужно указать: тип ростверка, марку бетона, ширину и длину фундамента, толщину и высоту ростверка, длину всех стержней арматуры, ширину, толщину и длину досок которые будут применяться для строительства опалубки.
указав эти параметры вы узнаете:
- Общую длину.
- Площадь подошвы и площадь внешней боковой поверхности.
- Вес и объём бетона необходимого для создания ростверка.
- Нагрузку передаваемую от фундамента на грунт.
- Минимальный диаметр продольных и поперечных стержней арматуры.
- Минимальное количество рядов арматуры.
- Расстояние между поперечными хомутами.
- Размер нахлёста арматуры.
- Общую длину и вес продольной арматуры.
- Общую длину и вес поперечной арматуры.
- Количество досок необходимое для обустройства опалубки.
- Максимальное расстояние между опорами опалубки.
Похожие записи:
Расчёт арматуры плиты ростверка — Студопедия
С1= 0,45–0,15=0,3м;
;
;
мм2,
Принимаем шаг 150 мм 9 Æ 12 А400, А=10,18 см2.
Расчёт поперечных сечений подколонника ростверка (подбор продольной арматуры подколонника для прямоугольного и коробчатого сечений подколонника), расчёт поперечной арматуры подколонника, а также расчёт подколонника ростверка на местное смятие под торцом колонны идентичны аналогичным расчётам подколонника фундамента на естественном основании (см. выше), ввиду идентичности нагрузок на подколонники, размеров и характеристик бетона подколонников.
Список литературы
1. ГОСТ 25100-95. Грунты. Классификация / Стандартинформ. – М.: 2013. – 38 с.
2. СП 22.13330.2011. Основания зданий и сооружений / Минрегион России. – М.: 2011. – 160 с.
3. СП 20.13330.2011. Свайные фундаменты. / Минрегион России. – М.: 2011. – 86 с.
4. СП 20.13330.2011. Нагрузки и воздействия. / Минрегион России. – М.: 2011. – 36 с.
5. СП 63.13330.2010 (СП 52-101-2003). Бетонные и железобетонные конструкции. Основные положения / Минрегион России. – М.: 2010. – 76 с.
6. Пособие по проектированию оснований зданий и сооружений (к СНиП 2.02.01-83). М.: Стройиздат, 1986. – 412 с.
7. Пособие по проектированию фундаментов на естественном основании под колонны зданий и сооружений (к СНиП 2.02.01-83 и СНиП 2.03.01-84). М.: Стройиздат, 1989. – 89 с.
8. Пособие по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СП 52-101-2003).
9. СНиП 23-01-99*. Строительная климатология.
10. СП 45.13330.2010. Земляные сооружения, основания и фундаменты.
11. СП 50-102-2003. Проектирование и устройство свайных фундаментов.
12. ГОСТ 21.302-96. Условные графические обозначения в документации по инженерно – геологическим изысканиям. / Минстрой России. – М.: ГУП ЦПП, 1996. – 38 с.
13. ГОСТ Р 21.1101-2013. Основные требования к проектной и рабочей документации.
14. ГОСТ 21.501-93. Правила выполнения архитектурно строительных рабочих чертежей.
15. Руководство по выбору рациональных конструкций фундаментов. М.: Стройиздат, 1981. – 125 с.
16. Руководство по проектированию свайных фундаментов. М.: Стройиздат, 1980. – 154 с.
17. Пономарев А. Б. Учебно-методическое пособие к выполнению курсового проекта по дисциплине «Основания и фундаменты». Перм. гос. тех. ун-т Пермь, 2002. – 75 с.
Сравнение расчета балочной ростверки с расчетом с использованием ортотропных плит
Изображение 01 — Автомобильный мост через L55 возле Шварцхайде, Германия
Например, [2] часто рекомендует определять балочный ростверк. Ростверк очень хорошо отображает двухосное структурное поведение бетонной плиты из композитной балки. Однако в этом случае требуется больше усилий по моделированию, и ростверк неточен в локальных дискретных точках.Ниже моделирование балочного ростверка сравнивается с моделированием ортотропной плиты.
Изображение 02 — «Редактировать жесткость поверхности — ортотропия» в RFEM
Сначала описывается определение балочного ростверка с использованием простой конструкции, а затем определяется ортотропная пластина. Наконец, объясняются результаты и отклонения.
Система
Изображение 03 — Структурная система
- Сталь поперечного сечения: HE-A 200
- Материал стали: S235
- Поперечное сечение бетона: d = 100 мм
- Материал бетон: C30 / 37
- Нагрузка: 5 кН / м²
Изображение 04 — Поперечное сечение, включая эффективную ширину
Составное поперечное сечение создается в SHAPE-MASSIVE и импортируется в RFEM с заданным эксцентриситетом поперечного сечения относительно бетонной плиты.Эффективная ширина поперечного сечения принята 60 см. Центр тяжести поперечного сечения немного смещен вверх на 0,8 см к стыку между бетоном и сталью. Поэтому стык опор учитывается. Опоры смещены вниз на 5 см.
Изображение 05 — Поддержка позиционирования
Сама схема опоры подобрана таким образом, чтобы не возникало ограничений из-за сдерживаемой деформации.
Нагрузка одинакова для обеих систем.
- LC1 = 5 кН / м²
- LC2 = 10 кН (направление x = середина пролета, направление y = внешний край)
Изображение 06 — Вариант нагружения 2
Конструкция балочного ростверка
Требования к балочному ростверку (из [1]):
- постоянная высота конструкции
- мост с прямой балкой
- Простое симметричное поперечное сечение
- Обе основные балки опираются на каждую опорную ось, которая перпендикулярно продольной оси моста.
- приблизительно жесткая поперечная распорка в опорных осях
- неограниченная деформация в опорных осях
- Программа проектирования конструкций для расчета фермы должна иметь возможность рассчитывать элементы стержня.
Расчетное значение жесткости на изгиб (из [2]):
Формула 1
(EI) I = EcIPlatte = Ec · b · d³12 · (1 — μ²) = 3,300 · 120 см · (10 см) ³12 · 0,8 = 20,6 · E06 кНсм²
Расчетное значение жесткости на кручение:
Формула 2
(GIT) I = k · (GIT) Gc = Ec2 · (1 μ) = 3.3002 · (1 0,2) = 1,375 кНсм²
Характеристики поперечного сечения:
- I T = 0 см 4
- I y = 6250 см 4
- A = 1000 см²
- A y = 833 см²
ввод осуществляется в программе с использованием свойств действующего сечения. Учитывается жесткость элементов на сдвиг.
Ортотропная пластинчатая конструкция
В ортотропной пластинчатой конструкции основные балки моделируются таким же образом, как и в балочном ростверке.Затем эти балки встраиваются в бетонный фланец. Жесткость полностью передается главными балками в продольном направлении и бетонной полкой в поперечном направлении. Размер ячейки FE определяется идентично расстоянию до вторичной балки в 50 см.
Матрица жесткости ортотропной пластины симметрична и применяется только к главным диагоналям. Жесткости на изгиб в продольном направлении плиты и кручение определены идентично поперечным стержням балочного ростверка с почти нулевым значением.
Расчетное значение жесткости на изгиб:
Формула 3
D22 = Ec · d³12 · (1 — μ²) = 206,000 кНсм / см
Расчетное значение жесткости на кручение:
Формула 4
D33 = Gxy · dx3 · dy312 = 13,8 кНсм / см
В программе данные вводятся с использованием значений жесткости, определенных пользователем.
Изображение 07 — Матрица жесткости плоскости плиты
Заключение
Изображение 08 — Сравнение результатов
Изображение 09 — Деформации при нагружении 2
Литература
| [1] | Unterweger, H.: Globale Systemberechnung von Stahl- und Verbundbrücken, Modellbildung und Leistungsfähigkeit verbesserter einfacher Stabmodelle. Грац: IBK при Технологическом университете Граца, 2007 |
| [2] | Standsicherheitsnachweise für Kunstbauten: Anforderungen an den Inhalt den Umfang und die Form. Бонн-Бад Годесберг: Федеральный министр транспорта, Департамент дорожного строительства, 1987 |
Grillage — обзор | Темы ScienceDirect
Требуется опора для стальной колонны с бетонной оболочкой, несущей 2000 тонн.Допустимая несущая способность породы 20 тсф. Стальная колонна поддерживается на опорной плите размером 24 дюйма × 24 дюйма. Решено делать ростверк, состоящий из двух ярусов двутавровых балок. Инженер решает иметь три двутавровых балки в верхнем слое и пять двутавровых балок в нижнем слое.
Разработайте верхний слой двутавровых балок.
Расчет нижнего слоя двутавровых балок.
Решение
Шаг 1: Требуемый размер фундамента = 2000 тонн / 20 тсф = 100 кв.футов
Используйте опору 10 футов × 10 футов
Допущения:
- •
Предположим, что балки имеют длину 10 футов. (На самом деле балки меньше 10 футов, поскольку размеры основания составляют 10 футов × 10 футов)
- •
Предположим, что опорная плита имеет размер 24 дюйма × 24 дюйма и нагрузка передается на верхний слой балок, как показано на рисунке 11.3.
Рисунок 11.3. Ростверк.
(а) Вид спереди. (б) Вид сбоку.
- •
Предположим, что нагрузка передается на участок длиной 30 дюймов (см. Рисунок 11.4).
Шаг 2: Нагрузки, действующие на три верхние балки, показаны на рисунке 11.4.
Рисунок 11.4. Погрузка на ростверк.
Общая нагрузка от опорной плиты = 2000 тонн.
Поскольку в верхнем слое есть три двутавровых балки, одна двутавровая балка выдержит нагрузку 666,67 (2000/3) тонны. Эта нагрузка распределяется по длине 30 дюймов.
Следовательно, распределенная нагрузка на балку составляет 666.67 / 2,5 = 266,67 цс.
Нагрузка от верхних балок распределяется на нижний слой двутавровых балок.
Нижний слой двутавровых балок вызывает восходящую реакцию на верхние двутавровые балки. Эта реакция считается однородной.
В действительности эта восходящая реакция ( U ) представляет собой пять концентрированных реакций, действующих на верхний слой двутавровых балок. Как вы знаете, в нижнем слое есть пять лучей, и каждый из них вызывает реакцию.
Равномерно распределенная нагрузка из-за реакций нижнего слоя = 666.67/10 = 66,7 тсф.
(Общая нагрузка, которую необходимо передать с одной верхней балки, составляет 666,67 тонны, и она распределяется по длине 10 футов).
Теперь задача состоит в том, чтобы найти максимальный изгибающий момент, возникающий в балке. После определения максимального изгибающего момента можно спроектировать двутавровое сечение.
Максимальный изгибающий момент возникает в центре балки. (См. Рисунок 11.5).
Рисунок 11.5. Половина секции ростверка.
Шаг 3: Найдите максимальный изгибающий момент в балке.
Реакция в центральной точке балки принята равной « R ».
Предположим, что изгибающий момент в центре равен « M ». Для этого типа нагружения максимальный изгибающий момент возникает в центре. (Возьмите моменты о центральной точке).
M = (66,67 × 5 × 2,5) −266,67 × 1,25 × 1,25 / 2 = 625 тонн. ft.
, где 66,67 × 5 представляет общую нагрузку, а 2,5 — расстояние до центра тяжести. Аналогично 266,67 × 1,25 представляет общую нагрузку и 1.25/2 представляет собой расстояние до центра тяжести.
Балка должна выдерживать этот изгибающий момент. Выберите I-образное сечение, которое может выдерживать изгибающий момент 625 тонн фут.
M = 625 тонн. футов = 2 × 625 = 1250 тысяч фунтов. фут
M / Z = σ
M = изгибающий момент
Z = модуль упругости
σ = напряжение в самом внешнем волокне балки
Используйте S-образное сечение с допустимым напряжением стали 36000 фунтов на квадратный дюйм.
σ = 36 тысяч фунтов / кв. Дюйм
Z = M / σ
Z = (1250 × 12) тыс. дюйм / 36 тысяч фунтов / кв. дюйм
Z = 417 дюймов 3 .
Используйте профиль W 36 × 135 с модулем упругости 439 дюймов 3 .
Шаг 4: Спроектируйте нижний слой балок.
Три верхние балки опираются на каждую балку нижнего яруса. Предположим, что верхние балки имеют длину 12 дюймов.врозь (рисунок 11.6).
Рисунок 11.6. Силы на нижний слой балок.
Каждая балка верхнего яруса несет нагрузку 666,67 тонны. Каждая из балок верхнего слоя опирается на 5 балок нижнего слоя. Таким образом, 666,67 тонны распределяются по 5 балкам нижнего яруса. Каждая балка нижнего яруса получает нагрузку 666,67 / 5 тонн (= 133,33) от каждой верхней балки.
Есть три балки верхнего слоя.
Следовательно, каждая балка нижнего яруса несет нагрузку 3 × 133,33 = 400 тонн.
Все балки нижнего слоя лежат на бетоне.Эту нагрузку необходимо передать бетону.
Реакция бетона считается равномерно распределенной.
W = Реакция бетона = 400/10 = 40 тонн на погонный фут
Шаг 5: Найдите максимальный изгибающий момент.
Максимальный изгибающий момент, возникающий в балках нижнего слоя, может быть вычислен (рисунок 11.7).
Рисунок 11.7. Половина разреза нижнего слоя ростверка.
Обрежьте балку по центру. Затем сосредоточенную нагрузку в центре нужно уменьшить вдвое, так как одна половина идет на другую часть.
Взгляните на точку «С».
M = 40 × 5 × 2,5 — 133,33 × 1 = 366,7 тонны. ft
Следовательно, максимальный изгибающий момент = 366,7 тонны. футов
M = 366,7 тонны. фут = 2 × 366,7 = 733,4 тысячи фунтов. фут
M / Z = σ
M = изгибающий момент; Z = модуль упругости сечения; σ = напряжение в самом внешнем волокне балки.
Используйте стальной профиль с допустимым напряжением стали 36 000 фунтов на квадратный дюйм.
σ = 36 тысяч фунтов / кв. Дюйм
Z = M / σ
Z = (733.4 × 12) кип. дюйм / 36 тысяч фунтов / кв. дюйм
Z = 244,4 дюйма 3 .
Используйте S 24 × 121 сечение с модулем упругости 258 дюймов 3 .
Моделирование и анализ балочных мостов
Большинство автомобильных мостов представляют собой балочные конструкции с однопролетными или непрерывными пролетами, а композитные мосты имеют форму многобалочных или лестничных настилов. Определение основных эффектов различных комбинаций нагрузок часто может быть достигнуто с помощью 2-мерной аналитической модели, но для более полного анализа необходима 3-мерная модель.В этой статье рассматриваются соответствующие методы анализа и моделирования типичных мостов из стали и композитных материалов в Великобритании.
Полная конечно-элементная модель
[вверху] Варианты моделирования типичного многолучевого моста
Типичный многобалочный мост из стального композитного материала
Овербридж Тринити на трассе A120
(Изображение любезно предоставлено Аткинсом)
Существует три варианта моделирования типичного многобалочного стального композитного моста:
Линейный луч — довольно грубый инструмент.Он не учитывает поперечное распределение, он не дает результатов для поперечного дизайна (например, плиты или распорки) и не учитывает эффекты перекоса. Его не рекомендуется использовать для детального проектирования, но это полезный инструмент для предварительного проектирования.
Использование ростверка подходит во многих ситуациях. Использование модели конечных элементов даст более подробные результаты, особенно для неоднородных балок.
Хотя анализ ростверка широко используется и по-прежнему считается наиболее подходящим для большинства мостовых настилов, признано, что программы анализа методом конечных элементов становятся все более доступными и более простыми в использовании.Кроме того, требования Еврокода для проверки бокового продольного изгиба при кручении могут сделать анализ продольного изгиба методом конечных элементов важным для проверки случая нагрузки мокрой бетонной конструкции.
Поперечный разрез Овербриджа Тринити
[вверх] Анализ ростков
[вверх] Анализ ростков: обзор
Изометрический вид ростверка, представляющего собой настил балки
Модель ростверка — это обычная форма расчетной модели для композитных настилов мостов.Его ключевые особенности:
- Это 2D модель
- Конструктивное поведение линейно-упругое
- Элементы балки выложены сеткой в одной плоскости, жестко соединены в узлах
- Продольные элементы представляют собой составные секции (т. Е. Основные балки с соответствующей плитой)
- Поперечные элементы представляют собой только плиту или составное сечение, в котором присутствуют поперечные стальные балки
[вверх] Анализ ростверка: план элемента
Предлагается следующее руководство по выбору планировки ростверка:
- Сохраняйте размеры сетки примерно квадратными
- Используйте четное количество шагов сетки
- Шаг сетки не более пролета / 8
- Кромки вдоль парапета для облегчения приложения нагрузки
- Вставьте дополнительные стыки для мест стыковки (обычно предполагается, что это 25% пролета от опор)
Для двухпролетного моста, как показано выше, подходящая компоновка будет такой, как показано ниже.
Типовая схема ростверка для двухпролетного многобалочного стального композитного моста
[вверх] Анализ ростверка: поэтапное применение загрузки
Для моделирования реакции конструкции на диапазон постоянных и переменных воздействий потребуются как минимум три различных модели ростверка:
- Модель «только сталь» : собственный вес стальных балок и вес влажного бетона во время строительства применяются к модели ростверка только из стали.Продольные элементы представляют собой только стальные балки, в то время как поперечные элементы обычно не требуются (они могут быть установлены как «фиктивные» элементы, чтобы сохранить то же расположение модели, что и составные модели).
- «Долговременная» композитная модель : Постоянные воздействия, применяемые к завершенной конструкции (в основном, наложенные постоянные нагрузки, такие как покрытие поверхности, и ограничение кривизны из-за усадки), применяются к долговременной композитной модели. Характеристики сечения продольных составных элементов и поперечных элементов, представляющих плиту, рассчитываются с использованием длительного модуля упругости бетона.Если плита находится в состоянии растяжения, могут потребоваться свойства сечения с трещинами.
- «Кратковременная» составная модель : Переходные воздействия (в основном вертикальные нагрузки, вызванные движением) применяются к краткосрочной составной модели. Свойства сечения рассчитываются так же, как и для долгосрочной модели, но с использованием краткосрочного модуля упругости. Опять же, свойства сечения с трещинами могут потребоваться там, где плита находится в состоянии растяжения.
Обратите внимание, что BS EN 1992-1-1 [1] дает несколько иной долгосрочный модуль упругости бетона при усадочной нагрузке, поэтому теоретически должна быть четвертая модель для анализа эффектов усадки.Однако модуль существенно не отличается от «обычного» долгосрочного значения, и разумно применить удерживающие моменты усадки к долгосрочной модели для определения вторичных моментов в балках. Однако соответствующие свойства сечения для усадки следует использовать для расчета напряжений, вызванных этими эффектами.
[вверх] Анализ ростков: свойства сечения
Свойства трансформируемого сечения элемента составной балки ростверка
Обычно все свойства сечения в «стальных элементах» рассчитываются с использованием преобразованной площади бетонной полки (разделить на коэффициент модульности n = E s / E c ).Следующие свойства сечения необходимы для каждого отдельного сечения:
- Только сталь: только свойства стальной балки
- Долговечный композит: бетонная поверхность, преобразованная в долгосрочную модульную конструкцию
- Кратковременный композит: бетонная поверхность, преобразованная для кратковременного модульного соотношения
- Свойства с трещинами (в областях коробления): площадь армирования принимается как эффективная только в сечении плиты.
Для свойств сечения без трещин армирование в плите может игнорироваться.
Типичный преобразованный разрез показан справа.
[вверх] Степень трещинности
Если соотношение длин соседних пролетов составляет не менее 0,6, поправка на растрескивание плиты в зонах коробления может быть сделана путем использования свойств сечения с трещинами для 15% пролета с каждой стороны промежуточных опор, как показано ниже. Это предусмотрено BS EN 1994-2 [2] , пункт 5.4.2.3.
Степень трещиностойкости элементов балки
[вверху] Задержка сдвига в бетонных полках
Эффективная ширина бетонных полок основана на ширине плиты, равной L e /8 за пределами внешней стойки, по обе стороны от балки, где L e — это расстояние между точками обратного прогиба.Это определение дано в BS EN 1994-2 [2] , пункт 5.4.1.2, где приведены приблизительные значения L e . Обратите внимание, что запаздывание сдвига необходимо учитывать как при ULS, так и при SLS (одинаковая эффективная ширина используется для обоих предельных состояний).
[вверх] Анализ ростверка: приложение нагрузок
Остаточные воздействия (собственный вес) распределяются между продольными стержнями с помощью простой статики. Графическое изображение типичных постоянных нагрузок, приложенных к модели ростверка, показано ниже (слева).
Загрузка трафика обычно определяется с помощью программ «автозагрузки», которые являются частью большинства аналитических программ. Эти программы используют поверхности влияния для определения степени равномерно распределенных нагрузок и положения тандемных систем и специальных транспортных средств. Типичная поверхность влияния для места изгиба в середине пролета показана ниже (справа).
Пользователь решает, какие положения на модели наиболее важны для проектирования (например, промежуточные участки, стыки и положения опор), и требует, чтобы для этих положений были созданы поверхности влияния; затем автопогрузчик определяет позиции, в которых применяется для наиболее обременительного эффекта.
Графическое изображение постоянных нагрузок, приложенных к модели
Типовая поверхность воздействия изгибающего момента в середине пролета двухпролетного четырехбалочного моста
[вверх] Анализ ростков: выход
Основная цель любого глобального анализа мостов — получение результатов, которые затем можно использовать при анализе и проектировании сечений. Обычно на выходе будут изгибающие моменты, поперечные силы и крутящие моменты (если они значительны) в главных балках.Прогибы также потребуются для расчетов из преамбула. Результат, вероятно, будет либо графическим, либо табличным, оба полезны. Графический вывод позволяет быстро установить на глаз пиковые моменты и сдвиги, а также позволяет проектировщику визуально проверить, ведет ли модель себя так, как ожидалось. Табличный вывод может быть полезен для постобработки в виде электронной таблицы и одновременного чтения сопутствующих эффектов нагрузки. Однако проектировщику следует принимать решения о том, где находятся критические места на конструкции, чтобы избежать чрезмерного количества выходных данных и постобработки.
Типовое графическое представление вывода изгибающего момента
Типичный результат анализа влияния нагрузки на ростверк
[вверх] Анализ ростков: прочие соображения
Графический вывод изгибающих моментов в элементах плиты в ростверке модели
Также необходимо учитывать следующее:
- Глобальные эффекты для расчета поперечных перекрытий : возьмите эффекты нагрузки на поперечные элементы из модели ростверка и добавьте к эффектам из локального анализа (например,грамм. Диаграммы Пучера. См. SCI 356). Любые нагрузки, приложенные к ростверку, следует прикладывать к швам только для этой цели, чтобы избежать неточного двойного учета местных эффектов.
- Распорка : Связь обычно моделируется с помощью гибкого на сдвиг элемента (консервативно для использования элемента, который не допускает гибкости при сдвиге) с эквивалентными свойствами, рассчитанными на основе модели плоской рамы. Модель плоской рамы также может использоваться для расчета распорок с использованием отклонений от модели ростверка, приложенных к модели плоской рамы, и при необходимости удерживающих сил.
- Опоры : Все опоры обеспечивают только вертикальное ограничение в 2D ростверке. Влияние невертикальных нагрузок необходимо оценивать вручную или с помощью альтернативной модели.
- Ручные проверки : Ручные проверки должны проводиться для проверки модели, например, проверка изгибающих моментов при равномерной нагрузке и проверка опорных реакций
- Комбинированное программное обеспечение для глобального анализа и проектирования сечений : Некоторое программное обеспечение предлагает комбинированный глобальный анализ и возможность проектирования сечений.Проектировщики должны убедиться, что они понимают теорию, лежащую в основе проектирования секций балки, и проводить проверки на выходе.
Модель плоской рамы для оценки жесткости (для элемента модели ростверка) и для определения эффектов от смещений из выходного
[вверх] Анализ ростков: варианты
[вверх] Мосты косые
Многие мосты имеют перекос в плане, и модель ростверка позволяет приспособить это расположение одним из нескольких способов.Рассмотрим типичный план косого моста, показанный ниже.
Для малых углов перекоса сетку можно выровнять с перекосом, как показано ниже.
перекос сетки (перекос не более 20 °)
Для больших углов перекоса поведение элементов перекоса становится неточным, и лучше вернуться к ортогональной сетке.На концах необходимо компенсировать перекос.
Ортогональная сетка для большего перекоса. (наклон более 20 °)
[вверх] Изогнутые мосты
Типовой изогнутый композитный мост
Это относительно обычное явление для мостов на развязках с разнесенными уровнями и в других местах, где пространство ограничено, чтобы иметь значительную кривизну в плане.
В таких ситуациях можно использовать изогнутые ростверки, хотя при выборе компоновки и рассмотрении результатов анализа необходимо соблюдать осторожность, поскольку крутильные эффекты в плите нелегко отделить от эффектов коробления в стальных балках. Кроме того, после анализа ростверка необходимо будет добавить влияние горизонтальных «радиальных» сил в стальных фланцах.
Модель изогнутого ростверка для 4-пролетного моста
[вверх] Балки переменной глубины
Балки переменной глубины, такие как показанные ниже, могут быть легко включены в модель ростверка путем изменения свойств сечения по длине продольных элементов.
Балки переменной глубины в двухпролетном мосту
(Изображение любезно предоставлено Аткинсом)
[вверху] Лестничные настилы
Лестничный мостик (этап строительства, со спусковой головкой)
Лестничные настилы, подобные показанному справа, можно смоделировать с помощью ростверков.
В модели ростверка для лестничной площадки:
- Основные лонжероны представляют собой сплошное составное сечение
- Промежуточные лонжероны представляют собой только плиту
- Поперечные элементы обычно представляют собой составное сечение, включая поперечные балки.Иногда могут быть включены только промежуточные элементы плиты между композитными поперечными элементами.
Вероятно, потребуется 3D-модель для моделирования взаимодействия между поперечными балками и главными балками, в частности, для определения жесткости U-образной рамы и воздействия на поперечные балки из-за местного применения специальных транспортных средств.
Трехмерная модель лестничного настила для взаимодействия поперечных балок и главных балок
[вверх] Мосты интегральные
Для интегрального моста можно использовать двухмерный ростверк с поворотными пружинными опорами на встроенных опорах в сочетании с двухмерной плоской моделью рамы для температурных воздействий.В качестве альтернативы можно использовать 3D-модель с участком ростверка для настила и вертикальными участками для примыкания и фундамента.
[вверху] Расчет критического изгиба на упругость для грузовой платформы «мокрый бетон»
Голые стальные балки в ожидании загрузки мокрого бетона
BS EN 1993-2 [3] не дает формулы для определения гибкости при продольном изгибе при кручении парных стальных балок с торсионными связями, когда пара балок склонна изгибаться как пара, сочувствуя друг другу, а не между ограничениями. .Это обычный сценарий для мокрой загрузки бетона. Можно рассмотреть два варианта:
- Расчет гибкости с помощью анализа критического продольного изгиба на упругость КЭ
- Используйте упрощенные правила гибкости ограничителей скручивания, взятые из BS 5400-3 [4] (они доступны в формате Еврокода в SCI P356).
Для анализа КЭ пользователю необходимо просмотреть режимы потери устойчивости, чтобы найти режим продольного изгиба при кручении — можно обнаружить, что формы продольного изгиба стенки или фланца возникают раньше, чем поперечные формы продольного изгиба при кручении.
Анализ КЭ, вероятно, даст значительные преимущества по сравнению с упрощенным подходом, который обсуждается при проектировании балки.
Дальнейшие инструкции по определению сопротивления продольному изгибу балок из стальных листов в композитных мостах во время строительства (голая стальная ступень) и в эксплуатации (когда плита настила действует как верхний фланец) доступны в ED008
[вверх] Конечно-элементное моделирование
Поскольку вполне вероятно, что для проверки упругой критической потери устойчивости потребуется модель конечных элементов, можно рассмотреть возможность использования полной модели конечных элементов для всего анализа.Это также будет иметь то преимущество, что структурный отклик потенциально лучше моделируется. Однако есть ряд недостатков, в том числе:
Полная конечно-элементная модель
- Более длинная установка
- Больше шансов на ошибку
- Больше времени для извлечения результатов
- Для уверенного использования требуется больше практики
- Отладка сложнее
- Пиковые опорные моменты могут быть недооценены
Если принято решение об использовании конечно-элементной модели, следующие рекомендации могут оказаться полезными:
- Крупная сетка, вероятно, будет достаточной
- Держите сетку как можно более квадратной
- Требуется более тщательное планирование
- Элементы толстой оболочки для балок и перекрытий, элементы балок в других местах (например,грамм. для распорки)
- В качестве альтернативы можно использовать балочные элементы для составных пластин стальных балок
- Требуется дополнительная проверка
- Необходимые анизотропные свойства в областях с трещинами
[вверх] Выводы
Ростверк — это обычно используемая модель мостовых настилов, и она относительно проста в использовании. Тем не менее, модель конечных элементов, скорее всего, по-прежнему потребуется для анализа упругого критического продольного изгиба стальных балок, поддерживающих влажную нагрузку бетона.Следовательно, модель конечных элементов может быть рассмотрена для всего анализа, что также будет иметь возможное преимущество в виде лучшего моделирования отклика конструкции. Однако у этого подхода есть некоторые недостатки, поэтому многие проектировщики используют ростверк для основного анализа и используют модель конечных элементов только там, где это абсолютно необходимо.
[вверх] Список литературы
- ↑ BS EN 1992-1-1: 2004 + A1: 2014 Еврокод 2. Проектирование бетонных конструкций. Общие правила и правила для зданий, BSI
- ↑ 2.0 2,1 BS EN 1994-2: 2005, Еврокод 4. Проектирование композитных стальных и бетонных конструкций. Общие правила и правила для мостов, BSI
- ↑ BS EN 1993-2: 2006, Еврокод 3. Проектирование стальных конструкций. Стальные мосты, BSI
- ↑ BS 5400-3: 2000 Стальные, бетонные и композитные мосты. Свод правил проектирования стальных мостов. BSI
[вверх] Ресурсы
[вверху] См. Также
[вверх] Внешние ссылки
Моделирование и анализ балочных мостов
Большинство автомобильных мостов представляют собой балочные конструкции с однопролетными или непрерывными пролетами, а композитные мосты имеют форму многобалочных или лестничных настилов.Определение основных эффектов различных комбинаций нагрузок часто может быть достигнуто с помощью 2-мерной аналитической модели, но для более полного анализа необходима 3-мерная модель. В этой статье рассматриваются соответствующие методы анализа и моделирования типичных мостов из стали и композитных материалов в Великобритании.
Полная конечно-элементная модель
[вверху] Варианты моделирования типичного многолучевого моста
Типичный многобалочный мост из стального композитного материала
Овербридж Тринити на трассе A120
(Изображение любезно предоставлено Аткинсом)
Существует три варианта моделирования типичного многобалочного стального композитного моста:
Линейный луч — довольно грубый инструмент.Он не учитывает поперечное распределение, он не дает результатов для поперечного дизайна (например, плиты или распорки) и не учитывает эффекты перекоса. Его не рекомендуется использовать для детального проектирования, но это полезный инструмент для предварительного проектирования.
Использование ростверка подходит во многих ситуациях. Использование модели конечных элементов даст более подробные результаты, особенно для неоднородных балок.
Хотя анализ ростверка широко используется и по-прежнему считается наиболее подходящим для большинства мостовых настилов, признано, что программы анализа методом конечных элементов становятся все более доступными и более простыми в использовании.Кроме того, требования Еврокода для проверки бокового продольного изгиба при кручении могут сделать анализ продольного изгиба методом конечных элементов важным для проверки случая нагрузки мокрой бетонной конструкции.
Поперечный разрез Овербриджа Тринити
[вверх] Анализ ростков
[вверх] Анализ ростков: обзор
Изометрический вид ростверка, представляющего собой настил балки
Модель ростверка — это обычная форма расчетной модели для композитных настилов мостов.Его ключевые особенности:
- Это 2D модель
- Конструктивное поведение линейно-упругое
- Элементы балки выложены сеткой в одной плоскости, жестко соединены в узлах
- Продольные элементы представляют собой составные секции (т. Е. Основные балки с соответствующей плитой)
- Поперечные элементы представляют собой только плиту или составное сечение, в котором присутствуют поперечные стальные балки
[вверх] Анализ ростверка: план элемента
Предлагается следующее руководство по выбору планировки ростверка:
- Сохраняйте размеры сетки примерно квадратными
- Используйте четное количество шагов сетки
- Шаг сетки не более пролета / 8
- Кромки вдоль парапета для облегчения приложения нагрузки
- Вставьте дополнительные стыки для мест стыковки (обычно предполагается, что это 25% пролета от опор)
Для двухпролетного моста, как показано выше, подходящая компоновка будет такой, как показано ниже.
Типовая схема ростверка для двухпролетного многобалочного стального композитного моста
[вверх] Анализ ростверка: поэтапное применение загрузки
Для моделирования реакции конструкции на диапазон постоянных и переменных воздействий потребуются как минимум три различных модели ростверка:
- Модель «только сталь» : собственный вес стальных балок и вес влажного бетона во время строительства применяются к модели ростверка только из стали.Продольные элементы представляют собой только стальные балки, в то время как поперечные элементы обычно не требуются (они могут быть установлены как «фиктивные» элементы, чтобы сохранить то же расположение модели, что и составные модели).
- «Долговременная» композитная модель : Постоянные воздействия, применяемые к завершенной конструкции (в основном, наложенные постоянные нагрузки, такие как покрытие поверхности, и ограничение кривизны из-за усадки), применяются к долговременной композитной модели. Характеристики сечения продольных составных элементов и поперечных элементов, представляющих плиту, рассчитываются с использованием длительного модуля упругости бетона.Если плита находится в состоянии растяжения, могут потребоваться свойства сечения с трещинами.
- «Кратковременная» составная модель : Переходные воздействия (в основном вертикальные нагрузки, вызванные движением) применяются к краткосрочной составной модели. Свойства сечения рассчитываются так же, как и для долгосрочной модели, но с использованием краткосрочного модуля упругости. Опять же, свойства сечения с трещинами могут потребоваться там, где плита находится в состоянии растяжения.
Обратите внимание, что BS EN 1992-1-1 [1] дает несколько иной долгосрочный модуль упругости бетона при усадочной нагрузке, поэтому теоретически должна быть четвертая модель для анализа эффектов усадки.Однако модуль существенно не отличается от «обычного» долгосрочного значения, и разумно применить удерживающие моменты усадки к долгосрочной модели для определения вторичных моментов в балках. Однако соответствующие свойства сечения для усадки следует использовать для расчета напряжений, вызванных этими эффектами.
[вверх] Анализ ростков: свойства сечения
Свойства трансформируемого сечения элемента составной балки ростверка
Обычно все свойства сечения в «стальных элементах» рассчитываются с использованием преобразованной площади бетонной полки (разделить на коэффициент модульности n = E s / E c ).Следующие свойства сечения необходимы для каждого отдельного сечения:
- Только сталь: только свойства стальной балки
- Долговечный композит: бетонная поверхность, преобразованная в долгосрочную модульную конструкцию
- Кратковременный композит: бетонная поверхность, преобразованная для кратковременного модульного соотношения
- Свойства с трещинами (в областях коробления): площадь армирования принимается как эффективная только в сечении плиты.
Для свойств сечения без трещин армирование в плите может игнорироваться.
Типичный преобразованный разрез показан справа.
[вверх] Степень трещинности
Если соотношение длин соседних пролетов составляет не менее 0,6, поправка на растрескивание плиты в зонах коробления может быть сделана путем использования свойств сечения с трещинами для 15% пролета с каждой стороны промежуточных опор, как показано ниже. Это предусмотрено BS EN 1994-2 [2] , пункт 5.4.2.3.
Степень трещиностойкости элементов балки
[вверху] Задержка сдвига в бетонных полках
Эффективная ширина бетонных полок основана на ширине плиты, равной L e /8 за пределами внешней стойки, по обе стороны от балки, где L e — это расстояние между точками обратного прогиба.Это определение дано в BS EN 1994-2 [2] , пункт 5.4.1.2, где приведены приблизительные значения L e . Обратите внимание, что запаздывание сдвига необходимо учитывать как при ULS, так и при SLS (одинаковая эффективная ширина используется для обоих предельных состояний).
[вверх] Анализ ростверка: приложение нагрузок
Остаточные воздействия (собственный вес) распределяются между продольными стержнями с помощью простой статики. Графическое изображение типичных постоянных нагрузок, приложенных к модели ростверка, показано ниже (слева).
Загрузка трафика обычно определяется с помощью программ «автозагрузки», которые являются частью большинства аналитических программ. Эти программы используют поверхности влияния для определения степени равномерно распределенных нагрузок и положения тандемных систем и специальных транспортных средств. Типичная поверхность влияния для места изгиба в середине пролета показана ниже (справа).
Пользователь решает, какие положения на модели наиболее важны для проектирования (например, промежуточные участки, стыки и положения опор), и требует, чтобы для этих положений были созданы поверхности влияния; затем автопогрузчик определяет позиции, в которых применяется для наиболее обременительного эффекта.
Графическое изображение постоянных нагрузок, приложенных к модели
Типовая поверхность воздействия изгибающего момента в середине пролета двухпролетного четырехбалочного моста
[вверх] Анализ ростков: выход
Основная цель любого глобального анализа мостов — получение результатов, которые затем можно использовать при анализе и проектировании сечений. Обычно на выходе будут изгибающие моменты, поперечные силы и крутящие моменты (если они значительны) в главных балках.Прогибы также потребуются для расчетов из преамбула. Результат, вероятно, будет либо графическим, либо табличным, оба полезны. Графический вывод позволяет быстро установить на глаз пиковые моменты и сдвиги, а также позволяет проектировщику визуально проверить, ведет ли модель себя так, как ожидалось. Табличный вывод может быть полезен для постобработки в виде электронной таблицы и одновременного чтения сопутствующих эффектов нагрузки. Однако проектировщику следует принимать решения о том, где находятся критические места на конструкции, чтобы избежать чрезмерного количества выходных данных и постобработки.
Типовое графическое представление вывода изгибающего момента
Типичный результат анализа влияния нагрузки на ростверк
[вверх] Анализ ростков: прочие соображения
Графический вывод изгибающих моментов в элементах плиты в ростверке модели
Также необходимо учитывать следующее:
- Глобальные эффекты для расчета поперечных перекрытий : возьмите эффекты нагрузки на поперечные элементы из модели ростверка и добавьте к эффектам из локального анализа (например,грамм. Диаграммы Пучера. См. SCI 356). Любые нагрузки, приложенные к ростверку, следует прикладывать к швам только для этой цели, чтобы избежать неточного двойного учета местных эффектов.
- Распорка : Связь обычно моделируется с помощью гибкого на сдвиг элемента (консервативно для использования элемента, который не допускает гибкости при сдвиге) с эквивалентными свойствами, рассчитанными на основе модели плоской рамы. Модель плоской рамы также может использоваться для расчета распорок с использованием отклонений от модели ростверка, приложенных к модели плоской рамы, и при необходимости удерживающих сил.
- Опоры : Все опоры обеспечивают только вертикальное ограничение в 2D ростверке. Влияние невертикальных нагрузок необходимо оценивать вручную или с помощью альтернативной модели.
- Ручные проверки : Ручные проверки должны проводиться для проверки модели, например, проверка изгибающих моментов при равномерной нагрузке и проверка опорных реакций
- Комбинированное программное обеспечение для глобального анализа и проектирования сечений : Некоторое программное обеспечение предлагает комбинированный глобальный анализ и возможность проектирования сечений.Проектировщики должны убедиться, что они понимают теорию, лежащую в основе проектирования секций балки, и проводить проверки на выходе.
Модель плоской рамы для оценки жесткости (для элемента модели ростверка) и для определения эффектов от смещений из выходного
[вверх] Анализ ростков: варианты
[вверх] Мосты косые
Многие мосты имеют перекос в плане, и модель ростверка позволяет приспособить это расположение одним из нескольких способов.Рассмотрим типичный план косого моста, показанный ниже.
Для малых углов перекоса сетку можно выровнять с перекосом, как показано ниже.
перекос сетки (перекос не более 20 °)
Для больших углов перекоса поведение элементов перекоса становится неточным, и лучше вернуться к ортогональной сетке.На концах необходимо компенсировать перекос.
Ортогональная сетка для большего перекоса. (наклон более 20 °)
[вверх] Изогнутые мосты
Типовой изогнутый композитный мост
Это относительно обычное явление для мостов на развязках с разнесенными уровнями и в других местах, где пространство ограничено, чтобы иметь значительную кривизну в плане.
В таких ситуациях можно использовать изогнутые ростверки, хотя при выборе компоновки и рассмотрении результатов анализа необходимо соблюдать осторожность, поскольку крутильные эффекты в плите нелегко отделить от эффектов коробления в стальных балках. Кроме того, после анализа ростверка необходимо будет добавить влияние горизонтальных «радиальных» сил в стальных фланцах.
Модель изогнутого ростверка для 4-пролетного моста
[вверх] Балки переменной глубины
Балки переменной глубины, такие как показанные ниже, могут быть легко включены в модель ростверка путем изменения свойств сечения по длине продольных элементов.
Балки переменной глубины в двухпролетном мосту
(Изображение любезно предоставлено Аткинсом)
[вверху] Лестничные настилы
Лестничный мостик (этап строительства, со спусковой головкой)
Лестничные настилы, подобные показанному справа, можно смоделировать с помощью ростверков.
В модели ростверка для лестничной площадки:
- Основные лонжероны представляют собой сплошное составное сечение
- Промежуточные лонжероны представляют собой только плиту
- Поперечные элементы обычно представляют собой составное сечение, включая поперечные балки.Иногда могут быть включены только промежуточные элементы плиты между композитными поперечными элементами.
Вероятно, потребуется 3D-модель для моделирования взаимодействия между поперечными балками и главными балками, в частности, для определения жесткости U-образной рамы и воздействия на поперечные балки из-за местного применения специальных транспортных средств.
Трехмерная модель лестничного настила для взаимодействия поперечных балок и главных балок
[вверх] Мосты интегральные
Для интегрального моста можно использовать двухмерный ростверк с поворотными пружинными опорами на встроенных опорах в сочетании с двухмерной плоской моделью рамы для температурных воздействий.В качестве альтернативы можно использовать 3D-модель с участком ростверка для настила и вертикальными участками для примыкания и фундамента.
[вверху] Расчет критического изгиба на упругость для грузовой платформы «мокрый бетон»
Голые стальные балки в ожидании загрузки мокрого бетона
BS EN 1993-2 [3] не дает формулы для определения гибкости при продольном изгибе при кручении парных стальных балок с торсионными связями, когда пара балок склонна изгибаться как пара, сочувствуя друг другу, а не между ограничениями. .Это обычный сценарий для мокрой загрузки бетона. Можно рассмотреть два варианта:
- Расчет гибкости с помощью анализа критического продольного изгиба на упругость КЭ
- Используйте упрощенные правила гибкости ограничителей скручивания, взятые из BS 5400-3 [4] (они доступны в формате Еврокода в SCI P356).
Для анализа КЭ пользователю необходимо просмотреть режимы потери устойчивости, чтобы найти режим продольного изгиба при кручении — можно обнаружить, что формы продольного изгиба стенки или фланца возникают раньше, чем поперечные формы продольного изгиба при кручении.
Анализ КЭ, вероятно, даст значительные преимущества по сравнению с упрощенным подходом, который обсуждается при проектировании балки.
Дальнейшие инструкции по определению сопротивления продольному изгибу балок из стальных листов в композитных мостах во время строительства (голая стальная ступень) и в эксплуатации (когда плита настила действует как верхний фланец) доступны в ED008
[вверх] Конечно-элементное моделирование
Поскольку вполне вероятно, что для проверки упругой критической потери устойчивости потребуется модель конечных элементов, можно рассмотреть возможность использования полной модели конечных элементов для всего анализа.Это также будет иметь то преимущество, что структурный отклик потенциально лучше моделируется. Однако есть ряд недостатков, в том числе:
Полная конечно-элементная модель
- Более длинная установка
- Больше шансов на ошибку
- Больше времени для извлечения результатов
- Для уверенного использования требуется больше практики
- Отладка сложнее
- Пиковые опорные моменты могут быть недооценены
Если принято решение об использовании конечно-элементной модели, следующие рекомендации могут оказаться полезными:
- Крупная сетка, вероятно, будет достаточной
- Держите сетку как можно более квадратной
- Требуется более тщательное планирование
- Элементы толстой оболочки для балок и перекрытий, элементы балок в других местах (например,грамм. для распорки)
- В качестве альтернативы можно использовать балочные элементы для составных пластин стальных балок
- Требуется дополнительная проверка
- Необходимые анизотропные свойства в областях с трещинами
[вверх] Выводы
Ростверк — это обычно используемая модель мостовых настилов, и она относительно проста в использовании. Тем не менее, модель конечных элементов, скорее всего, по-прежнему потребуется для анализа упругого критического продольного изгиба стальных балок, поддерживающих влажную нагрузку бетона.Следовательно, модель конечных элементов может быть рассмотрена для всего анализа, что также будет иметь возможное преимущество в виде лучшего моделирования отклика конструкции. Однако у этого подхода есть некоторые недостатки, поэтому многие проектировщики используют ростверк для основного анализа и используют модель конечных элементов только там, где это абсолютно необходимо.
[вверх] Список литературы
- ↑ BS EN 1992-1-1: 2004 + A1: 2014 Еврокод 2. Проектирование бетонных конструкций. Общие правила и правила для зданий, BSI
- ↑ 2.0 2,1 BS EN 1994-2: 2005, Еврокод 4. Проектирование композитных стальных и бетонных конструкций. Общие правила и правила для мостов, BSI
- ↑ BS EN 1993-2: 2006, Еврокод 3. Проектирование стальных конструкций. Стальные мосты, BSI
- ↑ BS 5400-3: 2000 Стальные, бетонные и композитные мосты. Свод правил проектирования стальных мостов. BSI
[вверх] Ресурсы
[вверху] См. Также
[вверх] Внешние ссылки
Моделирование и анализ балочных мостов
Большинство автомобильных мостов представляют собой балочные конструкции с однопролетными или непрерывными пролетами, а композитные мосты имеют форму многобалочных или лестничных настилов.Определение основных эффектов различных комбинаций нагрузок часто может быть достигнуто с помощью 2-мерной аналитической модели, но для более полного анализа необходима 3-мерная модель. В этой статье рассматриваются соответствующие методы анализа и моделирования типичных мостов из стали и композитных материалов в Великобритании.
Полная конечно-элементная модель
[вверху] Варианты моделирования типичного многолучевого моста
Типичный многобалочный мост из стального композитного материала
Овербридж Тринити на трассе A120
(Изображение любезно предоставлено Аткинсом)
Существует три варианта моделирования типичного многобалочного стального композитного моста:
Линейный луч — довольно грубый инструмент.Он не учитывает поперечное распределение, он не дает результатов для поперечного дизайна (например, плиты или распорки) и не учитывает эффекты перекоса. Его не рекомендуется использовать для детального проектирования, но это полезный инструмент для предварительного проектирования.
Использование ростверка подходит во многих ситуациях. Использование модели конечных элементов даст более подробные результаты, особенно для неоднородных балок.
Хотя анализ ростверка широко используется и по-прежнему считается наиболее подходящим для большинства мостовых настилов, признано, что программы анализа методом конечных элементов становятся все более доступными и более простыми в использовании.Кроме того, требования Еврокода для проверки бокового продольного изгиба при кручении могут сделать анализ продольного изгиба методом конечных элементов важным для проверки случая нагрузки мокрой бетонной конструкции.
Поперечный разрез Овербриджа Тринити
[вверх] Анализ ростков
[вверх] Анализ ростков: обзор
Изометрический вид ростверка, представляющего собой настил балки
Модель ростверка — это обычная форма расчетной модели для композитных настилов мостов.Его ключевые особенности:
- Это 2D модель
- Конструктивное поведение линейно-упругое
- Элементы балки выложены сеткой в одной плоскости, жестко соединены в узлах
- Продольные элементы представляют собой составные секции (т. Е. Основные балки с соответствующей плитой)
- Поперечные элементы представляют собой только плиту или составное сечение, в котором присутствуют поперечные стальные балки
[вверх] Анализ ростверка: план элемента
Предлагается следующее руководство по выбору планировки ростверка:
- Сохраняйте размеры сетки примерно квадратными
- Используйте четное количество шагов сетки
- Шаг сетки не более пролета / 8
- Кромки вдоль парапета для облегчения приложения нагрузки
- Вставьте дополнительные стыки для мест стыковки (обычно предполагается, что это 25% пролета от опор)
Для двухпролетного моста, как показано выше, подходящая компоновка будет такой, как показано ниже.
Типовая схема ростверка для двухпролетного многобалочного стального композитного моста
[вверх] Анализ ростверка: поэтапное применение загрузки
Для моделирования реакции конструкции на диапазон постоянных и переменных воздействий потребуются как минимум три различных модели ростверка:
- Модель «только сталь» : собственный вес стальных балок и вес влажного бетона во время строительства применяются к модели ростверка только из стали.Продольные элементы представляют собой только стальные балки, в то время как поперечные элементы обычно не требуются (они могут быть установлены как «фиктивные» элементы, чтобы сохранить то же расположение модели, что и составные модели).
- «Долговременная» композитная модель : Постоянные воздействия, применяемые к завершенной конструкции (в основном, наложенные постоянные нагрузки, такие как покрытие поверхности, и ограничение кривизны из-за усадки), применяются к долговременной композитной модели. Характеристики сечения продольных составных элементов и поперечных элементов, представляющих плиту, рассчитываются с использованием длительного модуля упругости бетона.Если плита находится в состоянии растяжения, могут потребоваться свойства сечения с трещинами.
- «Кратковременная» составная модель : Переходные воздействия (в основном вертикальные нагрузки, вызванные движением) применяются к краткосрочной составной модели. Свойства сечения рассчитываются так же, как и для долгосрочной модели, но с использованием краткосрочного модуля упругости. Опять же, свойства сечения с трещинами могут потребоваться там, где плита находится в состоянии растяжения.
Обратите внимание, что BS EN 1992-1-1 [1] дает несколько иной долгосрочный модуль упругости бетона при усадочной нагрузке, поэтому теоретически должна быть четвертая модель для анализа эффектов усадки.Однако модуль существенно не отличается от «обычного» долгосрочного значения, и разумно применить удерживающие моменты усадки к долгосрочной модели для определения вторичных моментов в балках. Однако соответствующие свойства сечения для усадки следует использовать для расчета напряжений, вызванных этими эффектами.
[вверх] Анализ ростков: свойства сечения
Свойства трансформируемого сечения элемента составной балки ростверка
Обычно все свойства сечения в «стальных элементах» рассчитываются с использованием преобразованной площади бетонной полки (разделить на коэффициент модульности n = E s / E c ).Следующие свойства сечения необходимы для каждого отдельного сечения:
- Только сталь: только свойства стальной балки
- Долговечный композит: бетонная поверхность, преобразованная в долгосрочную модульную конструкцию
- Кратковременный композит: бетонная поверхность, преобразованная для кратковременного модульного соотношения
- Свойства с трещинами (в областях коробления): площадь армирования принимается как эффективная только в сечении плиты.
Для свойств сечения без трещин армирование в плите может игнорироваться.
Типичный преобразованный разрез показан справа.
[вверх] Степень трещинности
Если соотношение длин соседних пролетов составляет не менее 0,6, поправка на растрескивание плиты в зонах коробления может быть сделана путем использования свойств сечения с трещинами для 15% пролета с каждой стороны промежуточных опор, как показано ниже. Это предусмотрено BS EN 1994-2 [2] , пункт 5.4.2.3.
Степень трещиностойкости элементов балки
[вверху] Задержка сдвига в бетонных полках
Эффективная ширина бетонных полок основана на ширине плиты, равной L e /8 за пределами внешней стойки, по обе стороны от балки, где L e — это расстояние между точками обратного прогиба.Это определение дано в BS EN 1994-2 [2] , пункт 5.4.1.2, где приведены приблизительные значения L e . Обратите внимание, что запаздывание сдвига необходимо учитывать как при ULS, так и при SLS (одинаковая эффективная ширина используется для обоих предельных состояний).
[вверх] Анализ ростверка: приложение нагрузок
Остаточные воздействия (собственный вес) распределяются между продольными стержнями с помощью простой статики. Графическое изображение типичных постоянных нагрузок, приложенных к модели ростверка, показано ниже (слева).
Загрузка трафика обычно определяется с помощью программ «автозагрузки», которые являются частью большинства аналитических программ. Эти программы используют поверхности влияния для определения степени равномерно распределенных нагрузок и положения тандемных систем и специальных транспортных средств. Типичная поверхность влияния для места изгиба в середине пролета показана ниже (справа).
Пользователь решает, какие положения на модели наиболее важны для проектирования (например, промежуточные участки, стыки и положения опор), и требует, чтобы для этих положений были созданы поверхности влияния; затем автопогрузчик определяет позиции, в которых применяется для наиболее обременительного эффекта.
Графическое изображение постоянных нагрузок, приложенных к модели
Типовая поверхность воздействия изгибающего момента в середине пролета двухпролетного четырехбалочного моста
[вверх] Анализ ростков: выход
Основная цель любого глобального анализа мостов — получение результатов, которые затем можно использовать при анализе и проектировании сечений. Обычно на выходе будут изгибающие моменты, поперечные силы и крутящие моменты (если они значительны) в главных балках.Прогибы также потребуются для расчетов из преамбула. Результат, вероятно, будет либо графическим, либо табличным, оба полезны. Графический вывод позволяет быстро установить на глаз пиковые моменты и сдвиги, а также позволяет проектировщику визуально проверить, ведет ли модель себя так, как ожидалось. Табличный вывод может быть полезен для постобработки в виде электронной таблицы и одновременного чтения сопутствующих эффектов нагрузки. Однако проектировщику следует принимать решения о том, где находятся критические места на конструкции, чтобы избежать чрезмерного количества выходных данных и постобработки.
Типовое графическое представление вывода изгибающего момента
Типичный результат анализа влияния нагрузки на ростверк
[вверх] Анализ ростков: прочие соображения
Графический вывод изгибающих моментов в элементах плиты в ростверке модели
Также необходимо учитывать следующее:
- Глобальные эффекты для расчета поперечных перекрытий : возьмите эффекты нагрузки на поперечные элементы из модели ростверка и добавьте к эффектам из локального анализа (например,грамм. Диаграммы Пучера. См. SCI 356). Любые нагрузки, приложенные к ростверку, следует прикладывать к швам только для этой цели, чтобы избежать неточного двойного учета местных эффектов.
- Распорка : Связь обычно моделируется с помощью гибкого на сдвиг элемента (консервативно для использования элемента, который не допускает гибкости при сдвиге) с эквивалентными свойствами, рассчитанными на основе модели плоской рамы. Модель плоской рамы также может использоваться для расчета распорок с использованием отклонений от модели ростверка, приложенных к модели плоской рамы, и при необходимости удерживающих сил.
- Опоры : Все опоры обеспечивают только вертикальное ограничение в 2D ростверке. Влияние невертикальных нагрузок необходимо оценивать вручную или с помощью альтернативной модели.
- Ручные проверки : Ручные проверки должны проводиться для проверки модели, например, проверка изгибающих моментов при равномерной нагрузке и проверка опорных реакций
- Комбинированное программное обеспечение для глобального анализа и проектирования сечений : Некоторое программное обеспечение предлагает комбинированный глобальный анализ и возможность проектирования сечений.Проектировщики должны убедиться, что они понимают теорию, лежащую в основе проектирования секций балки, и проводить проверки на выходе.
Модель плоской рамы для оценки жесткости (для элемента модели ростверка) и для определения эффектов от смещений из выходного
[вверх] Анализ ростков: варианты
[вверх] Мосты косые
Многие мосты имеют перекос в плане, и модель ростверка позволяет приспособить это расположение одним из нескольких способов.Рассмотрим типичный план косого моста, показанный ниже.
Для малых углов перекоса сетку можно выровнять с перекосом, как показано ниже.
перекос сетки (перекос не более 20 °)
Для больших углов перекоса поведение элементов перекоса становится неточным, и лучше вернуться к ортогональной сетке.На концах необходимо компенсировать перекос.
Ортогональная сетка для большего перекоса. (наклон более 20 °)
[вверх] Изогнутые мосты
Типовой изогнутый композитный мост
Это относительно обычное явление для мостов на развязках с разнесенными уровнями и в других местах, где пространство ограничено, чтобы иметь значительную кривизну в плане.
В таких ситуациях можно использовать изогнутые ростверки, хотя при выборе компоновки и рассмотрении результатов анализа необходимо соблюдать осторожность, поскольку крутильные эффекты в плите нелегко отделить от эффектов коробления в стальных балках. Кроме того, после анализа ростверка необходимо будет добавить влияние горизонтальных «радиальных» сил в стальных фланцах.
Модель изогнутого ростверка для 4-пролетного моста
[вверх] Балки переменной глубины
Балки переменной глубины, такие как показанные ниже, могут быть легко включены в модель ростверка путем изменения свойств сечения по длине продольных элементов.
Балки переменной глубины в двухпролетном мосту
(Изображение любезно предоставлено Аткинсом)
[вверху] Лестничные настилы
Лестничный мостик (этап строительства, со спусковой головкой)
Лестничные настилы, подобные показанному справа, можно смоделировать с помощью ростверков.
В модели ростверка для лестничной площадки:
- Основные лонжероны представляют собой сплошное составное сечение
- Промежуточные лонжероны представляют собой только плиту
- Поперечные элементы обычно представляют собой составное сечение, включая поперечные балки.Иногда могут быть включены только промежуточные элементы плиты между композитными поперечными элементами.
Вероятно, потребуется 3D-модель для моделирования взаимодействия между поперечными балками и главными балками, в частности, для определения жесткости U-образной рамы и воздействия на поперечные балки из-за местного применения специальных транспортных средств.
Трехмерная модель лестничного настила для взаимодействия поперечных балок и главных балок
[вверх] Мосты интегральные
Для интегрального моста можно использовать двухмерный ростверк с поворотными пружинными опорами на встроенных опорах в сочетании с двухмерной плоской моделью рамы для температурных воздействий.В качестве альтернативы можно использовать 3D-модель с участком ростверка для настила и вертикальными участками для примыкания и фундамента.
[вверху] Расчет критического изгиба на упругость для грузовой платформы «мокрый бетон»
Голые стальные балки в ожидании загрузки мокрого бетона
BS EN 1993-2 [3] не дает формулы для определения гибкости при продольном изгибе при кручении парных стальных балок с торсионными связями, когда пара балок склонна изгибаться как пара, сочувствуя друг другу, а не между ограничениями. .Это обычный сценарий для мокрой загрузки бетона. Можно рассмотреть два варианта:
- Расчет гибкости с помощью анализа критического продольного изгиба на упругость КЭ
- Используйте упрощенные правила гибкости ограничителей скручивания, взятые из BS 5400-3 [4] (они доступны в формате Еврокода в SCI P356).
Для анализа КЭ пользователю необходимо просмотреть режимы потери устойчивости, чтобы найти режим продольного изгиба при кручении — можно обнаружить, что формы продольного изгиба стенки или фланца возникают раньше, чем поперечные формы продольного изгиба при кручении.
Анализ КЭ, вероятно, даст значительные преимущества по сравнению с упрощенным подходом, который обсуждается при проектировании балки.
Дальнейшие инструкции по определению сопротивления продольному изгибу балок из стальных листов в композитных мостах во время строительства (голая стальная ступень) и в эксплуатации (когда плита настила действует как верхний фланец) доступны в ED008
[вверх] Конечно-элементное моделирование
Поскольку вполне вероятно, что для проверки упругой критической потери устойчивости потребуется модель конечных элементов, можно рассмотреть возможность использования полной модели конечных элементов для всего анализа.Это также будет иметь то преимущество, что структурный отклик потенциально лучше моделируется. Однако есть ряд недостатков, в том числе:
Полная конечно-элементная модель
- Более длинная установка
- Больше шансов на ошибку
- Больше времени для извлечения результатов
- Для уверенного использования требуется больше практики
- Отладка сложнее
- Пиковые опорные моменты могут быть недооценены
Если принято решение об использовании конечно-элементной модели, следующие рекомендации могут оказаться полезными:
- Крупная сетка, вероятно, будет достаточной
- Держите сетку как можно более квадратной
- Требуется более тщательное планирование
- Элементы толстой оболочки для балок и перекрытий, элементы балок в других местах (например,грамм. для распорки)
- В качестве альтернативы можно использовать балочные элементы для составных пластин стальных балок
- Требуется дополнительная проверка
- Необходимые анизотропные свойства в областях с трещинами
[вверх] Выводы
Ростверк — это обычно используемая модель мостовых настилов, и она относительно проста в использовании. Тем не менее, модель конечных элементов, скорее всего, по-прежнему потребуется для анализа упругого критического продольного изгиба стальных балок, поддерживающих влажную нагрузку бетона.Следовательно, модель конечных элементов может быть рассмотрена для всего анализа, что также будет иметь возможное преимущество в виде лучшего моделирования отклика конструкции. Однако у этого подхода есть некоторые недостатки, поэтому многие проектировщики используют ростверк для основного анализа и используют модель конечных элементов только там, где это абсолютно необходимо.
[вверх] Список литературы
- ↑ BS EN 1992-1-1: 2004 + A1: 2014 Еврокод 2. Проектирование бетонных конструкций. Общие правила и правила для зданий, BSI
- ↑ 2.0 2,1 BS EN 1994-2: 2005, Еврокод 4. Проектирование композитных стальных и бетонных конструкций. Общие правила и правила для мостов, BSI
- ↑ BS EN 1993-2: 2006, Еврокод 3. Проектирование стальных конструкций. Стальные мосты, BSI
- ↑ BS 5400-3: 2000 Стальные, бетонные и композитные мосты. Свод правил проектирования стальных мостов. BSI
[вверх] Ресурсы
[вверху] См. Также
[вверх] Внешние ссылки
Моделирование и анализ балочных мостов
Большинство автомобильных мостов представляют собой балочные конструкции с однопролетными или непрерывными пролетами, а композитные мосты имеют форму многобалочных или лестничных настилов.Определение основных эффектов различных комбинаций нагрузок часто может быть достигнуто с помощью 2-мерной аналитической модели, но для более полного анализа необходима 3-мерная модель. В этой статье рассматриваются соответствующие методы анализа и моделирования типичных мостов из стали и композитных материалов в Великобритании.
Полная конечно-элементная модель
[вверху] Варианты моделирования типичного многолучевого моста
Типичный многобалочный мост из стального композитного материала
Овербридж Тринити на трассе A120
(Изображение любезно предоставлено Аткинсом)
Существует три варианта моделирования типичного многобалочного стального композитного моста:
Линейный луч — довольно грубый инструмент.Он не учитывает поперечное распределение, он не дает результатов для поперечного дизайна (например, плиты или распорки) и не учитывает эффекты перекоса. Его не рекомендуется использовать для детального проектирования, но это полезный инструмент для предварительного проектирования.
Использование ростверка подходит во многих ситуациях. Использование модели конечных элементов даст более подробные результаты, особенно для неоднородных балок.
Хотя анализ ростверка широко используется и по-прежнему считается наиболее подходящим для большинства мостовых настилов, признано, что программы анализа методом конечных элементов становятся все более доступными и более простыми в использовании.Кроме того, требования Еврокода для проверки бокового продольного изгиба при кручении могут сделать анализ продольного изгиба методом конечных элементов важным для проверки случая нагрузки мокрой бетонной конструкции.
Поперечный разрез Овербриджа Тринити
[вверх] Анализ ростков
[вверх] Анализ ростков: обзор
Изометрический вид ростверка, представляющего собой настил балки
Модель ростверка — это обычная форма расчетной модели для композитных настилов мостов.Его ключевые особенности:
- Это 2D модель
- Конструктивное поведение линейно-упругое
- Элементы балки выложены сеткой в одной плоскости, жестко соединены в узлах
- Продольные элементы представляют собой составные секции (т. Е. Основные балки с соответствующей плитой)
- Поперечные элементы представляют собой только плиту или составное сечение, в котором присутствуют поперечные стальные балки
[вверх] Анализ ростверка: план элемента
Предлагается следующее руководство по выбору планировки ростверка:
- Сохраняйте размеры сетки примерно квадратными
- Используйте четное количество шагов сетки
- Шаг сетки не более пролета / 8
- Кромки вдоль парапета для облегчения приложения нагрузки
- Вставьте дополнительные стыки для мест стыковки (обычно предполагается, что это 25% пролета от опор)
Для двухпролетного моста, как показано выше, подходящая компоновка будет такой, как показано ниже.
Типовая схема ростверка для двухпролетного многобалочного стального композитного моста
[вверх] Анализ ростверка: поэтапное применение загрузки
Для моделирования реакции конструкции на диапазон постоянных и переменных воздействий потребуются как минимум три различных модели ростверка:
- Модель «только сталь» : собственный вес стальных балок и вес влажного бетона во время строительства применяются к модели ростверка только из стали.Продольные элементы представляют собой только стальные балки, в то время как поперечные элементы обычно не требуются (они могут быть установлены как «фиктивные» элементы, чтобы сохранить то же расположение модели, что и составные модели).
- «Долговременная» композитная модель : Постоянные воздействия, применяемые к завершенной конструкции (в основном, наложенные постоянные нагрузки, такие как покрытие поверхности, и ограничение кривизны из-за усадки), применяются к долговременной композитной модели. Характеристики сечения продольных составных элементов и поперечных элементов, представляющих плиту, рассчитываются с использованием длительного модуля упругости бетона.Если плита находится в состоянии растяжения, могут потребоваться свойства сечения с трещинами.
- «Кратковременная» составная модель : Переходные воздействия (в основном вертикальные нагрузки, вызванные движением) применяются к краткосрочной составной модели. Свойства сечения рассчитываются так же, как и для долгосрочной модели, но с использованием краткосрочного модуля упругости. Опять же, свойства сечения с трещинами могут потребоваться там, где плита находится в состоянии растяжения.
Обратите внимание, что BS EN 1992-1-1 [1] дает несколько иной долгосрочный модуль упругости бетона при усадочной нагрузке, поэтому теоретически должна быть четвертая модель для анализа эффектов усадки.Однако модуль существенно не отличается от «обычного» долгосрочного значения, и разумно применить удерживающие моменты усадки к долгосрочной модели для определения вторичных моментов в балках. Однако соответствующие свойства сечения для усадки следует использовать для расчета напряжений, вызванных этими эффектами.
[вверх] Анализ ростков: свойства сечения
Свойства трансформируемого сечения элемента составной балки ростверка
Обычно все свойства сечения в «стальных элементах» рассчитываются с использованием преобразованной площади бетонной полки (разделить на коэффициент модульности n = E s / E c ).Следующие свойства сечения необходимы для каждого отдельного сечения:
- Только сталь: только свойства стальной балки
- Долговечный композит: бетонная поверхность, преобразованная в долгосрочную модульную конструкцию
- Кратковременный композит: бетонная поверхность, преобразованная для кратковременного модульного соотношения
- Свойства с трещинами (в областях коробления): площадь армирования принимается как эффективная только в сечении плиты.
Для свойств сечения без трещин армирование в плите может игнорироваться.
Типичный преобразованный разрез показан справа.
[вверх] Степень трещинности
Если соотношение длин соседних пролетов составляет не менее 0,6, поправка на растрескивание плиты в зонах коробления может быть сделана путем использования свойств сечения с трещинами для 15% пролета с каждой стороны промежуточных опор, как показано ниже. Это предусмотрено BS EN 1994-2 [2] , пункт 5.4.2.3.
Степень трещиностойкости элементов балки
[вверху] Задержка сдвига в бетонных полках
Эффективная ширина бетонных полок основана на ширине плиты, равной L e /8 за пределами внешней стойки, по обе стороны от балки, где L e — это расстояние между точками обратного прогиба.Это определение дано в BS EN 1994-2 [2] , пункт 5.4.1.2, где приведены приблизительные значения L e . Обратите внимание, что запаздывание сдвига необходимо учитывать как при ULS, так и при SLS (одинаковая эффективная ширина используется для обоих предельных состояний).
[вверх] Анализ ростверка: приложение нагрузок
Остаточные воздействия (собственный вес) распределяются между продольными стержнями с помощью простой статики. Графическое изображение типичных постоянных нагрузок, приложенных к модели ростверка, показано ниже (слева).
Загрузка трафика обычно определяется с помощью программ «автозагрузки», которые являются частью большинства аналитических программ. Эти программы используют поверхности влияния для определения степени равномерно распределенных нагрузок и положения тандемных систем и специальных транспортных средств. Типичная поверхность влияния для места изгиба в середине пролета показана ниже (справа).
Пользователь решает, какие положения на модели наиболее важны для проектирования (например, промежуточные участки, стыки и положения опор), и требует, чтобы для этих положений были созданы поверхности влияния; затем автопогрузчик определяет позиции, в которых применяется для наиболее обременительного эффекта.
Графическое изображение постоянных нагрузок, приложенных к модели
Типовая поверхность воздействия изгибающего момента в середине пролета двухпролетного четырехбалочного моста
[вверх] Анализ ростков: выход
Основная цель любого глобального анализа мостов — получение результатов, которые затем можно использовать при анализе и проектировании сечений. Обычно на выходе будут изгибающие моменты, поперечные силы и крутящие моменты (если они значительны) в главных балках.Прогибы также потребуются для расчетов из преамбула. Результат, вероятно, будет либо графическим, либо табличным, оба полезны. Графический вывод позволяет быстро установить на глаз пиковые моменты и сдвиги, а также позволяет проектировщику визуально проверить, ведет ли модель себя так, как ожидалось. Табличный вывод может быть полезен для постобработки в виде электронной таблицы и одновременного чтения сопутствующих эффектов нагрузки. Однако проектировщику следует принимать решения о том, где находятся критические места на конструкции, чтобы избежать чрезмерного количества выходных данных и постобработки.
Типовое графическое представление вывода изгибающего момента
Типичный результат анализа влияния нагрузки на ростверк
[вверх] Анализ ростков: прочие соображения
Графический вывод изгибающих моментов в элементах плиты в ростверке модели
Также необходимо учитывать следующее:
- Глобальные эффекты для расчета поперечных перекрытий : возьмите эффекты нагрузки на поперечные элементы из модели ростверка и добавьте к эффектам из локального анализа (например,грамм. Диаграммы Пучера. См. SCI 356). Любые нагрузки, приложенные к ростверку, следует прикладывать к швам только для этой цели, чтобы избежать неточного двойного учета местных эффектов.
- Распорка : Связь обычно моделируется с помощью гибкого на сдвиг элемента (консервативно для использования элемента, который не допускает гибкости при сдвиге) с эквивалентными свойствами, рассчитанными на основе модели плоской рамы. Модель плоской рамы также может использоваться для расчета распорок с использованием отклонений от модели ростверка, приложенных к модели плоской рамы, и при необходимости удерживающих сил.
- Опоры : Все опоры обеспечивают только вертикальное ограничение в 2D ростверке. Влияние невертикальных нагрузок необходимо оценивать вручную или с помощью альтернативной модели.
- Ручные проверки : Ручные проверки должны проводиться для проверки модели, например, проверка изгибающих моментов при равномерной нагрузке и проверка опорных реакций
- Комбинированное программное обеспечение для глобального анализа и проектирования сечений : Некоторое программное обеспечение предлагает комбинированный глобальный анализ и возможность проектирования сечений.Проектировщики должны убедиться, что они понимают теорию, лежащую в основе проектирования секций балки, и проводить проверки на выходе.
Модель плоской рамы для оценки жесткости (для элемента модели ростверка) и для определения эффектов от смещений из выходного
[вверх] Анализ ростков: варианты
[вверх] Мосты косые
Многие мосты имеют перекос в плане, и модель ростверка позволяет приспособить это расположение одним из нескольких способов.Рассмотрим типичный план косого моста, показанный ниже.
Для малых углов перекоса сетку можно выровнять с перекосом, как показано ниже.
перекос сетки (перекос не более 20 °)
Для больших углов перекоса поведение элементов перекоса становится неточным, и лучше вернуться к ортогональной сетке.На концах необходимо компенсировать перекос.
Ортогональная сетка для большего перекоса. (наклон более 20 °)
[вверх] Изогнутые мосты
Типовой изогнутый композитный мост
Это относительно обычное явление для мостов на развязках с разнесенными уровнями и в других местах, где пространство ограничено, чтобы иметь значительную кривизну в плане.
В таких ситуациях можно использовать изогнутые ростверки, хотя при выборе компоновки и рассмотрении результатов анализа необходимо соблюдать осторожность, поскольку крутильные эффекты в плите нелегко отделить от эффектов коробления в стальных балках. Кроме того, после анализа ростверка необходимо будет добавить влияние горизонтальных «радиальных» сил в стальных фланцах.
Модель изогнутого ростверка для 4-пролетного моста
[вверх] Балки переменной глубины
Балки переменной глубины, такие как показанные ниже, могут быть легко включены в модель ростверка путем изменения свойств сечения по длине продольных элементов.
Балки переменной глубины в двухпролетном мосту
(Изображение любезно предоставлено Аткинсом)
[вверху] Лестничные настилы
Лестничный мостик (этап строительства, со спусковой головкой)
Лестничные настилы, подобные показанному справа, можно смоделировать с помощью ростверков.
В модели ростверка для лестничной площадки:
- Основные лонжероны представляют собой сплошное составное сечение
- Промежуточные лонжероны представляют собой только плиту
- Поперечные элементы обычно представляют собой составное сечение, включая поперечные балки.Иногда могут быть включены только промежуточные элементы плиты между композитными поперечными элементами.
Вероятно, потребуется 3D-модель для моделирования взаимодействия между поперечными балками и главными балками, в частности, для определения жесткости U-образной рамы и воздействия на поперечные балки из-за местного применения специальных транспортных средств.
Трехмерная модель лестничного настила для взаимодействия поперечных балок и главных балок
[вверх] Мосты интегральные
Для интегрального моста можно использовать двухмерный ростверк с поворотными пружинными опорами на встроенных опорах в сочетании с двухмерной плоской моделью рамы для температурных воздействий.В качестве альтернативы можно использовать 3D-модель с участком ростверка для настила и вертикальными участками для примыкания и фундамента.
[вверху] Расчет критического изгиба на упругость для грузовой платформы «мокрый бетон»
Голые стальные балки в ожидании загрузки мокрого бетона
BS EN 1993-2 [3] не дает формулы для определения гибкости при продольном изгибе при кручении парных стальных балок с торсионными связями, когда пара балок склонна изгибаться как пара, сочувствуя друг другу, а не между ограничениями. .Это обычный сценарий для мокрой загрузки бетона. Можно рассмотреть два варианта:
- Расчет гибкости с помощью анализа критического продольного изгиба на упругость КЭ
- Используйте упрощенные правила гибкости ограничителей скручивания, взятые из BS 5400-3 [4] (они доступны в формате Еврокода в SCI P356).
Для анализа КЭ пользователю необходимо просмотреть режимы потери устойчивости, чтобы найти режим продольного изгиба при кручении — можно обнаружить, что формы продольного изгиба стенки или фланца возникают раньше, чем поперечные формы продольного изгиба при кручении.
Анализ КЭ, вероятно, даст значительные преимущества по сравнению с упрощенным подходом, который обсуждается при проектировании балки.
Дальнейшие инструкции по определению сопротивления продольному изгибу балок из стальных листов в композитных мостах во время строительства (голая стальная ступень) и в эксплуатации (когда плита настила действует как верхний фланец) доступны в ED008
[вверх] Конечно-элементное моделирование
Поскольку вполне вероятно, что для проверки упругой критической потери устойчивости потребуется модель конечных элементов, можно рассмотреть возможность использования полной модели конечных элементов для всего анализа.Это также будет иметь то преимущество, что структурный отклик потенциально лучше моделируется. Однако есть ряд недостатков, в том числе:
Полная конечно-элементная модель
- Более длинная установка
- Больше шансов на ошибку
- Больше времени для извлечения результатов
- Для уверенного использования требуется больше практики
- Отладка сложнее
- Пиковые опорные моменты могут быть недооценены
Если принято решение об использовании конечно-элементной модели, следующие рекомендации могут оказаться полезными:
- Крупная сетка, вероятно, будет достаточной
- Держите сетку как можно более квадратной
- Требуется более тщательное планирование
- Элементы толстой оболочки для балок и перекрытий, элементы балок в других местах (например,грамм. для распорки)
- В качестве альтернативы можно использовать балочные элементы для составных пластин стальных балок
- Требуется дополнительная проверка
- Необходимые анизотропные свойства в областях с трещинами
[вверх] Выводы
Ростверк — это обычно используемая модель мостовых настилов, и она относительно проста в использовании. Тем не менее, модель конечных элементов, скорее всего, по-прежнему потребуется для анализа упругого критического продольного изгиба стальных балок, поддерживающих влажную нагрузку бетона.Следовательно, модель конечных элементов может быть рассмотрена для всего анализа, что также будет иметь возможное преимущество в виде лучшего моделирования отклика конструкции. Однако у этого подхода есть некоторые недостатки, поэтому многие проектировщики используют ростверк для основного анализа и используют модель конечных элементов только там, где это абсолютно необходимо.
[вверх] Список литературы
- ↑ BS EN 1992-1-1: 2004 + A1: 2014 Еврокод 2. Проектирование бетонных конструкций. Общие правила и правила для зданий, BSI
- ↑ 2.0 2,1 BS EN 1994-2: 2005, Еврокод 4. Проектирование композитных стальных и бетонных конструкций. Общие правила и правила для мостов, BSI
- ↑ BS EN 1993-2: 2006, Еврокод 3. Проектирование стальных конструкций. Стальные мосты, BSI
- ↑ BS 5400-3: 2000 Стальные, бетонные и композитные мосты. Свод правил проектирования стальных мостов. BSI
[вверх] Ресурсы
[вверху] См. Также
[вверх] Внешние ссылки
Модифицированная модель для расчета прогиба железобетонной балки с деформированной арматурой из стеклопластика
Авторы провели экспериментальные и аналитические исследования, чтобы оценить изгибную способность и соотношение момент-прогиб бетонных балок, армированных стержнями из стеклопластика.Предлагаемая модель для прогнозирования эффективного момента инерции для ж / б балки с стержнями из стеклопластика была разработана эмпирически на основе уравнения Брэнсона, чтобы иметь лучшую точность и знакомый подход инженеру-строителю. Для лучшего прогнозирования зависимости момент-прогиб до достижения предельной прочности также учитывался нелинейный параметр (). Этот параметр был введен, чтобы уменьшить влияние момента инерции трещин для железобетонного элемента, включая более низкий коэффициент усиления и модуль упругости стержня из стеклопластика.В сравнительном исследовании с использованием шести уравнений, предложенных другими, предложенная модель показала лучшее согласие с результатами экспериментальных испытаний. Было подтверждено, что эмпирическая модификация, основанная на уравнении Брэнсона, действительна для прогнозирования эффективного момента инерции R / C балок с стержнем из стеклопластика в этом исследовании. Чтобы оценить общность предложенной модели, было проведено сравнительное исследование с использованием результатов предыдущих тестов из литературы и результатов этого исследования. Было обнаружено, что предложенная модель имеет лучшую точность и знакома инженерам-строителям для прогнозирования и оценки поведения прогиба.
1. Введение
Срок службы железобетонных (ЖБИ) конструкций может быть уменьшен за счет ряда факторов, включая суровые условия окружающей среды и неожиданные чрезмерные внешние нагрузки. Одним из основных факторов, способствующих ухудшению состояния конструкции, является коррозия стальной арматуры. Следовательно, использование некоррозионной арматуры может быть эффективным решением для увеличения срока службы железобетонных конструкций. Во многих регионах стержни из армированного волокном полимера (FRP) представляют значительный интерес для инженеров-строителей (строителей) и инженеров-строителей для усиления и армирования бетона в качестве замены стальным стержням.Их высокое отношение прочности к весу, антикоррозионные свойства и простота обращения во время строительства считаются преимуществами для применения в строительных конструкциях. Многочисленные структурные исследования с использованием стержней из стеклопластика были выполнены в полевых условиях, и в настоящее время существуют рекомендации по проектированию и строительству бетона, армированного стержнями из стеклопластика, такие как Спецификация проектирования мостов AASHTO LRFD, рекомендации ACI 440 и Канадские нормы проектирования [1–1] 3].
Изгибная способность железобетонных элементов со стержнем из стеклопластика была проблемой при проектировании конструкций из-за относительно низкого модуля упругости, который вызывает больший прогиб и ширину трещин.Таким образом, поведение при изгибе железобетонных элементов с стержнем из стеклопластика должно быть дополнительно исследовано с точки зрения эксплуатационной пригодности. Прогнозирование прогиба — один из наиболее важных критериев при оценке и обеспечении работоспособности бетонного элемента. ACI 318-14 [4] использует уравнение момента инерции на основе уравнения Брэнсона [5] для расчета прогиба железобетонных балок. Недавно ACI 440.1R-15 [2] рекомендовал новую модель момента инерции для железобетонных элементов с стержнем из стеклопластика, которая не была основана на уравнении Брэнсона в отличие от ACI 440.1Р-06 [6]. Уравнение на основе Брэнсона уже давно знакомо большинству инженеров-строителей при проектировании изгибаемых бетонных элементов. Для железобетонных элементов с стержнем из стеклопластика уравнение Брэнсона было изменено для максимально точного прогнозирования прогиба. Существенные изменения заключались в корректировке мощности и добавлении параметра.
В этом исследовании мы предлагаем модифицированный эффективный момент инерции и провели сравнительное исследование поведения прогиба ж / б балок с стержнем из стеклопластика с экспериментальными испытаниями.Для сравнительного исследования были рассмотрены шесть уравнений, в том числе некоторые из индивидуальных исследований. Предлагаемая модель была разработана на основе уравнения Брэнсона, чтобы обеспечить знакомый подход к вычислению момента инерции для R / C балок с стержнем из стеклопластика. Эта модель была эмпирически изменена в соответствии с результатами испытаний шести образцов для испытаний с переменными коэффициентом усиления. Для лучшего прогнозирования прогиба до достижения предельной прочности был введен эмпирический нелинейный параметр, чтобы уменьшить влияние момента инерции трещины.Среди уравнений была проанализирована степень точности предсказания поведения отклонения для нового момента инерции, предложенная в этом исследовании, и обсуждалась предсказуемость.
2. Существующие и предлагаемые уравнения момента инерции для изгибаемых стержней из армированного стеклопластиком бетона
Уравнение Брэнсона обычно недооценивает прогиб балок из армированного стеклопластом бетона. Benmokrane et al. [7] изменили уравнение, чтобы сделать его более подходящим для оценки прогиба армированных FRP балок на основе экспериментальных данных.Уравнение выглядит следующим образом: где — полный момент инерции ( 4 мм), — момент инерции трансформированного участка с трещиной ( 4 мм), — момент растрескивания (Н · м) и — максимальное рабочий момент нагрузки в стержне (Н · м).
Заметная разница заключается в модификации и. отражает уменьшенное композитное действие между бетоном и стержнями FRP. Однако не имеет физического значения, потому что не было оснований для уменьшения. и были 0.84 и 7 соответственно.
ACI 440.1R-06 [6] рекомендовал уравнение для эффективного момента инерции на основе модели Брэнсона. Был дополнительный фактор для рассмотрения уменьшенной жесткости при растяжении армированных стеклопластиком бетонных элементов. Эта модель обычно использовалась для расчета момента инерции элементов из армированного стекловолокном бетона, чтобы можно было рассчитать прогиб секции с трещинами: где — коэффициент уменьшения, связанный с уменьшенной жесткостью при растяжении, проявляемой элементом R / C с FRP. bar () — коэффициент армирования стержня из стеклопластика и сбалансированный коэффициент армирования стержня из стеклопластика.
Toutanji и Saafi [9] эмпирически предложили уравнение для эффективного момента инерции для железобетонной балки с стержнем из стеклопластика. Их уравнение сосредоточено на коэффициенте модификации мощности в (1). Фактор был основан на применении коэффициента упругости к коэффициенту усиления стержня из стеклопластика. Изменяя только степень, традиционная форма уравнения, знакомая инженерам-строителям, была сохранена. Уравнение хорошо предсказало прогиб испытанных ж / б балок с GFRP.Посмотрим где.
Для канадских норм для железобетонных элементов с стержнем из стеклопластика CAN / CSA S806-12 [3] предлагает следующее уравнение (см. (4)) для расчета прогиба. Уравнение было основано на обычном уравнении для расчета прогиба при четырехточечной нагрузке. Он использует момент инерции при трещине, в то время как ACI 440.1R-15 [2] использует эффективный момент инерции. Однако были включены дополнительные члены уравнения, относящиеся к пролету сдвига, длине пролета и длине без трещин в половине балки.Это уравнение требует интенсивных вычислений, допускающих человеческую ошибку; таким образом, код также предоставляет уравнения в замкнутой форме для общих условий нагрузки и поддержки. Следовательно, где — пролет сдвига (мм), — общая приложенная нагрузка (Н), — длина пролета (мм), — длина без трещин в половине балки (мм) (), — это модуль упругости бетон (МПа),.
Недавно была предложена другая полуэмпирическая модель путем модификации уравнения Брэнсона в соответствии с экспериментальными результатами и методом генетического алгоритма [10].Для лучшего прогноза некоторые факторы были разработаны эмпирически. Модель, которая имеет два множителя и экспоненциальный фактор, была проанализирована с использованием экспериментальных данных для 55 армированных стеклопластиком балок для зависимости нагрузки от прогиба. Влияние модуля упругости стержней из стеклопластика, коэффициента армирования и уровня нагрузки на мощность в уравнении Брэнсона учитывается в (5) следующим образом: где, — модуль упругости стержня из стеклопластика (МПа), и — модуль упругости стального стержня (МПа).
ACI 440.1R-15 [2] предложил уравнение для расчета эффективного момента инерции для железобетонных балок с стержнем из стеклопластика. Это уравнение основано на подходе, предложенном Бишоффом, который представляет собой средневзвешенное значение гибкости (), как показано в (6). Сообщалось, что уравнение одинаково хорошо работает как для стальных, так и для армированных стеклопластиком элементов без эмпирического параметра [11]. Следовательно, где — параметр, учитывающий изменение жесткости по длине элемента при четырехточечном изгибе.Следовательно, Intelligent Sensing для инновационных конструкций [12] рекомендовал следующий (8) эффективный момент инерции для балок из армированного стержнем из стеклопластика. Это уравнение добавило дополнительные корректирующие члены в модифицированное уравнение Брэнсона с большим количеством экспериментальных данных. Обозначения введены выше в уравнениях от (1) до (6). Здесь
3. Экспериментальные испытания
3.1. Описание стержня из стеклопластика
Арматурный стержень из стеклопластика, используемый в этом исследовании, представляет собой развитую арматуру, имеющую внешнюю форму, аналогичную обычной стальной арматуре.Он состоит из непрерывных продольных стекловолокон с объемной долей 67% в термореактивной эпоксидной смоле. Был принят типичный процесс пултрузии. Чтобы повысить сопротивление сдвигу при склеивании, на сердечнике из стеклопластика были сформированы ребра из фрезерованного стекловолокна. Для формирования волоконных ребер в процессе отверждения использовалась стальная форма. Ребристая секция стержня из стеклопластика была изготовлена путем смешивания измельченного стекловолокна и эпоксидной смолы в соотношении 1: 1 по весу и отверждена в течение 15 минут при температуре выше 160 ° C. Детали внешней формы стержня из стеклопластика с волоконными ребрами были предоставлены Джу и О [8] (рис. 1 (б)).
(a) Детализация арматурного стержня GFRP
(b) Рисунок поверхности арматурного стержня GFRP
(a) Детализация арматурного стержня GFRP
(b) Рисунок поверхности арматурного стержня GFRP0002 GFRP0002 стержень, используемый для области растяжения, имел номинальный диаметр 9,53 мм. Испытания на растяжение проводились с восемью образцами для испытаний в соответствии с ACI 440.3R-04 [13]. Образцы на растяжение были загружены через толстые пластины на закрепленных концах. Использовалась универсальная испытательная машина (УТМ) грузоподъемностью 2000 кН, скорость нагружения составляла 17.8 кН / мин. Среди испытанных образцов максимальная прочность на разрыв составила 871,4 МПа. В таблице 1 приведены значения прочности на разрыв стержня из стеклопластика. Расчетный гарантированный предел прочности на разрыв со стандартным отклонением составил 616,0 МПа. Расчетная прочность на растяжение была рассчитана путем умножения фактора снижения воздействия окружающей среды (0,7, для внешнего воздействия) в соответствии с ACI 440.1R-15 [2], что дало 539,1 МПа. Модуль упругости оказался равным 42,9 ГПа в пределах общего диапазона модуля упругости стержней из стеклопластика.
3.2. Испытательная установкаДля стержня из стеклопластика обычная конструкция пластичности, используемая для стальных стержней, не подходит из-за отсутствия предела текучести. Три типа ж / б балок с стержнем из стеклопластика были разработаны в соответствии с ACI 440.1R-15 [2]: разрыв из стеклопластика (FB-1), сбалансированный (FB-2) и разрушение при раздавливании бетона (FB-3). Были использованы три различных количества продольного армирования стержня из стеклопластика: 2D10 для FB-2, 3D10 для FB-3 и 4D10 для FB-4.D указывает номинальный диаметр стержня из стеклопластика. Для уравновешенного FB-2 это можно рассматривать как разрушение FRP с дроблением бетона. Каждый образец состоял из двух одинаковых балок. Испытание на изгиб проводилось четырехточечным изгибом. На Рисунке 2 показаны испытательная установка и детали измерения. Размеры испытательных балок были следующими: ширина 180 мм, глубина 230 мм и длина 2000 мм. Чистый пролет составлял 1600 мм. Предел прочности на сдвиг, который может определять регулируемое поведение изгибной балки, был рассчитан между 3.7 и 3,9; таким образом, балка считалась подверженной изгибу. Чтобы контролировать структурное поведение балки, на нижней поверхности бетона в средней части были установлены линейные переменные дифференциальные трансформаторы (LVDT). Два тензодатчика электрического сопротивления были прикреплены к поверхности центрированного стержня из стеклопластика для FB-2 и внешнего стержня из стеклопластика для FB-1 и FB-3 в средней части. Две нагрузки были автоматически приложены к балке со скоростью 2 кН в минуту с помощью погрузочной машины MTS.Все данные (силы, деформации и отклонения) были собраны автоматизированной системой сбора данных. Для ширины трещины использовалась мера трещины, и ширина трещины исследовалась визуально на отдельном этапе нагружения. Для бетона средняя 28-дневная прочность на сжатие составила 27,0 МПа, а предел прочности при изгибе бетона был приблизительно 2,4 МПа. 3.3. Результаты испытаний на изгиб и их обсуждениеРазрушение при изгибе и структура трещин показаны на Рисунке 3.Образцы не выдержали типичного разрушения при изгибе. FB-1 показал растрескивающую нагрузку 12,0 кН. Разрушение было обусловлено разрывом стержней из стеклопластика. Максимальная ширина трещины в средней части была исследована визуально и составила 0,9 мм. Образец FB-2 изначально разрушился из-за раздавливания бетона, а затем окончательно разрушился из-за разрыва стержня из стеклопластика. Следовательно, разрушения показали разрушение при сжатии и растяжении с разрывом стержня из стеклопластика, а максимальная ширина трещины составила 0,7 мм. В случае образца FB-3 он показал обычное разрушение бетона при раздавливании без разрыва стержня из стеклопластика.Максимальная ширина трещины была измерена как 0,4 мм в средней части. Что касается прочности на изгиб, было обнаружено, что расчетные режимы разрушения представляют собой экспериментальные режимы разрушения, и ширина трещины была уменьшена по мере увеличения коэффициента усиления. Трещины в зоне изгиба преимущественно состояли из вертикальных трещин, перпендикулярных направлению максимального главного напряжения, вызванного чистым изгибающим моментом. Трещины возникли в середине пролета, а затем распространились по направлению к опорам. Со временем напряжение сдвига стало более важным и привело к появлению наклонных трещин. При достижении предела прочности трещины при изгибе распространялись по направлению к точкам нагрузки на сжимаемой поверхности балок. Все испытательные балки показали значительные изгибные трещины до того, как наклонные трещины присоединились к изгибным трещинам. Для аналитического подхода в отношении номинального изгибающего момента использовалось уравнение из ACI 440.1R-15 [2] с изменяющимся коэффициентом усиления. Когда контролирующим предельным состоянием является разрыв стержня из стеклопластика, и можно вычислить номинальную прочность на изгиб.На основе равновесия сил и совместимости деформаций можно получить (10). В противном случае, когда, расчетная прочность на растяжение () в (10) изменяется на напряжение в FRP () при растяжении (см. (9)). В таблице 2 показаны экспериментально и аналитически полученные значения прочности на изгиб R / C балок с стержнем из стеклопластика. Теоретическая сила момента была оценена и была примерно на 20% ниже, чем сила момента в экспериментальных испытаниях. Это может быть связано с отклонениями из-за небольшого количества образцов для испытаний.Тем не менее, расчетная моментная сила вполне может представлять конструктивную способность в качестве консервативного прогноза. Для жесткости конструкции, определенной путем деления средней нагрузки на средний прогиб при предельной прочности, FB-1, FB-2 и FB-3 показали значения 1,58, 1,65 и 2,78 соответственно. Было обнаружено, что жесткость конструкции увеличивалась в соответствии с увеличением степени армирования стержня из стеклопластика: где — номинальная прочность на изгиб (кН · м), — глубина эквивалентного прямоугольного блока напряжений (мм), — это напряжение в Бар из стеклопластика при растяжении (МПа), это расчетная прочность на растяжение стержня из стеклопластика (МПа), это расчетный или гарантированный модуль (МПа), это предельная деформация в бетоне (0.003), является эмпирическим фактором, представляет собой заданную прочность бетона на сжатие (МПа), представляет собой коэффициент армирования FRP и является сбалансированным коэффициентом армирования FRP, установленным Комитетом ACI 440 [2].
Предложенный прогиб 4. Сравнительный анализ прогиба 4. Существующие модели для расчета эффективного момента инерцииВ этой статье предлагается полуэмпирическая модель прогнозирования эффективного момента инерции. Модель основана на уравнении Брэнсона, а методология модификации следовала эмпирическому подходу Тутанжи и Саафи [9].Как показано на рисунке 4, на прогиб R / C балки со стержнями из стеклопластика повлиял коэффициент усиления стержней из стеклопластика, а также модуль упругости стержня из стеклопластика. Примечательным параметром, отражающим нелинейное поведение R / C балок с стержнем из стеклопластика, эмпирически считается, что он обеспечивает хорошее согласие с экспериментальными испытаниями в этом исследовании (см. (11)). Этот фактор был использован, чтобы уменьшить влияние момента инерции трещин для железобетонного элемента, включая более низкий коэффициент усиления и модуль упругости для стержня из стеклопластика.Этот рассматриваемый параметр является коэффициентом аппроксимации кривой. Его концепция была получена эмпирически путем исследования результатов зависимости момент-прогиб из уравнения, приведенного выше в этом исследовании. На рисунке 6 рассматриваемые уравнения показали жесткую кривую как билинейное поведение вплоть до разрушения испытуемого образца. Однако результат испытания показал нелинейное поведение вплоть до отказа, так что можно было оценить необходимость уменьшения коэффициента для хорошего соответствия кривой экспериментальным результатам.Это привело к уменьшению эффективного момента инерции, так что расчетный прогиб увеличивался в соответствии с увеличением приложенной нагрузки. Рисунок 4 иллюстрирует основную концепцию рассмотрения в предлагаемой модели. Используя, можно немного смягчить жесткость отклонения. Эта аналитическая концепция может быть более подходящей для бетонного элемента, армированного материалом с более низким коэффициентом армирования и модулем упругости: где и — нелинейный параметр. Всего было исследовано шесть кодов и разработанных уравнений для сравнительного исследования момента инерции и отклонения нагрузки в соответствии с экспериментальными испытаниями и моделью, предложенной в этом исследовании. Для этого репрезентативный образец для каждой группы армирования был рассмотрен для сравнительного исследования из-за их сходства с результатами испытаний. Есть некоторые исследования, показывающие, что оценка структурной способности FRP стержневой железобетонной балки с использованием только одного репрезентативного образца для каждой группы армирования была успешно проведена [14, 15].На рисунке 5 показаны результаты сравнительного исследования эффективного момента инерции. Существует заметное расхождение между экспериментом и уравнением, приближающееся к приложенному моменту 5 кН · м. Комитет ACI 440 [6], Toutanji и Saafi [9] и предложенная модель показали лучшее согласие с хорошим нелинейным предсказанием экспериментально полученного эффективного момента инерции после растрескивания бетона. Другие уравнения, например, ACI Committee 440 [2], ISIS Canada [12], Mousavi et al.[10] и Benmokrane et al. [7], показали большие падения полного момента инерции () после растрескивания бетона. Они плохо отражают поведение упрочнения экспериментальных результатов. Две модели прогнозирования, модифицированные на основе уравнения Брэнсона, показали хорошее согласие с экспериментальными результатами, в то время как две другие модели с модифицированными уравнениями Брэнсона показали относительно большие расхождения. Это было вызвано применением эмпирических параметров, таких как степень или постоянные умножения. На рис. 6 показана кривая момента и прогиба в середине пролета для образца FB-1, который состоял из двух ж / б балок с стержнем из стеклопластика. За исключением Toutanji и Saafi [9], ACI 440 Committee [6] и Benmokrane et al. [7], поведение пластичности было обнаружено после растрескивания. Эти уравнения недооценивают растрескивание образца FB-1, в то время как экспериментальные результаты показывают поведение упрочнения с приложенным моментом. Уравнение Мусави и др. [10] показали самую высокую жесткость при прогнозировании прогиба.Они использовали почти одинаковую постоянную умножения для полного и разорванного моментов инерции; однако мощность была иной, чем у Benmokrane et al. [7]. Это различие может сделать жесткость на изгиб при прогнозе отклонения более расслабленным, чем у Benmokrane et al. [7]. Комитет ACI 440 [6] и Тутанджи и Саафи [9] показали хорошее соответствие поведения отклонения примерно до половины приложенного момента; однако после стадии нагружения эти модели вели себя как линейно-зависимый прогноз прогиба.Таким образом, разница в прогнозе прогиба увеличивалась до конечного момента. Для предложенного уравнения с нелинейным параметром было обнаружено, что оно лучше всего предсказывает поведение отклонения в экспериментальных испытаниях до разрушения. На рисунках 7–10 аналитические кривые силы приложенного момента инерции и момент-прогиб, полученные из шести уравнений и предложенной модели, сравниваются с экспериментальными результатами для образцов FB-2 и FB-3. Тенденции в предсказании прогиба были аналогичны таковому для образца FB-1, где Комитет ACI 440 [6], Toutanji и Saafi [9], и предложенные модели все же показали лучшее согласие с хорошими нелинейными предсказаниями экспериментальных полученный эффективный момент инерции после растрескивания бетона.Экспериментальные кривые момент-прогиб FB-2 и FB-3 не показали хорошего согласия с аналитическими кривыми, полученными из шести рассмотренных здесь уравнений, но хорошо согласуются с предложенной моделью. Шесть уравнений оценивали реакцию на отклонение от момента, которая была линейной по сравнению с фактической реакцией образцов для испытаний после растрескивания до достижения предельной прочности. В отличие от ACI 440.1R-06 [6], Toutanji and Saafi [9] и предложенной модели, другие уравнения не отражали эффект жесткости при растяжении испытательных образцов примерно до половины предела прочности.Причина может заключаться в том, что уравнения оценивают эффективный момент инерции как намного меньший, чем у испытуемого образца до стадии нагружения, а затем они отвечают прогнозом линейного упрочнения до предела прочности. Предложенная модель, однако, хорошо представляла отклик на отклонение от момента, даже с нелинейным поведением, до предела прочности. 5. Сравнительное исследование для проверки предложенной моделиЧтобы оценить универсальность предложенной модели, были рассмотрены некоторые из предыдущих результатов испытаний: образец A1 от Aiello и Ombres [16], образец BC2HA от Thériault и Benmokrane [17] ], образец F1 из Pecce et al.[18], серия образцов 1 из Benmokrane et al. [7], а также образцы группы 2 из Al-Salloum et al. [19]. Кроме того, испытанные образцы, FB-1, FB-2 и FB-3, из этого исследования также сравнивались в соответствии с порядком вычисленного значения эквивалентного коэффициента усиления с коэффициентом модуля упругости. нормализовал отношение армирования стержня из стеклопластика к свойствам стального стержня и должен быть важным показателем для исследования валидации поведения момента отклонения с помощью предлагаемой модели. Критерии применения могут быть определены для оценки структурного поведения бетонных балок, армированных с различными соотношениями армирования.На рисунке 11 показаны результаты сравнительного исследования с использованием предложенной модели. Результаты показали, что предложенная модель разумно описывает поведение момента отклонения рассматриваемых испытательных образцов, когда он изменялся от 0,00068 до 0,006. Однако предложенная модель показала переоценку, так как она была увеличена, например, до 0,006 для группы 2, так что границы приложения должны быть исследованы дополнительно. Серия FB показала относительно хорошее согласие с экспериментальными испытаниями благодаря эталонным образцам, использованным в этом исследовании. Для других образцов восходящий тренд был хорошо описан экспериментальными результатами, и после появления трещин были обнаружены некоторые расхождения. Есть некоторые влияющие параметры, такие как свойства бетона, размерный эффект и тип стержня для свойства склеивания. В частности, характеристики сцепления стержня из стеклопластика в бетонной балке могут больше зависеть от изгибных нагрузок, чем от одноосной растягивающей нагрузки из-за различной обработки поверхности, включая свойства химической адгезии.Дальнейший точный анализ этого требует экспериментального и аналитического исследования. 6. ВыводыВ этом исследовании мы провели экспериментальные и аналитические исследования, чтобы оценить способность к изгибу и соотношение момент-прогиб бетонных балок, армированных стержнями из стеклопластика. Предлагаемая модель, предложенная для эффективного момента инерции R / C балок с стержнем из стеклопластика, могла бы разумно описать соотношение момент-отклонение. Сделанные выводы заключаются в следующем: (i) Это исследование предложило новое уравнение для эффективного момента инерции для бетонных балок, армированных стержнями из стеклопластика.Новое уравнение было модифицировано из уравнения Брэнсона, которое давно используется в этой области инженерами-строителями. Мощность была изменена на основе уравнения Тутанджи и Саафи [9], а также введен нелинейный параметр. Этот фактор использовался для уменьшения влияния момента инерции трещин для бетонного элемента, армированного с более низким коэффициентом армирования и материала с более низким модулем упругости. Для сравнения с экспериментальными испытаниями были спроектированы и испытаны три типа ж / б балок с стержнем из стеклопластика.Была оценена предсказуемость предложенной модели. (Ii) В сравнительном исследовании использовались шесть уравнений и предложенная модель для расчета эффективного момента инерции и зависимости приложенного момента, и было обнаружено, что уравнения ACI 440.1R-06 [6], Toutanji и Саафи [9], и предложенные модели показали лучшее согласие с экспериментальными результатами. Остальные три уравнения значительно занижали момент инерции сразу после растрескивания бетона. На основе этого результата было подтверждено, что эмпирическая модификация, основанная на уравнении Брэнсона, действительна для прогнозирования эффективного момента инерции и приложенного момента балок R / C с стержнем из стеклопластика.(iii) Для предсказания прогиба в экспериментальных испытаниях предложенная модель показала лучшую предсказуемость среди рассмотренных уравнений. Новая модель показала лучшее согласие с поведением прогиба балки из армированного стеклопластиком бетона до предела прочности, даже в отношении нелинейного поведения. Чтобы оценить универсальность предложенной модели, было проведено сравнительное исследование с использованием результатов предыдущих испытаний, а также результатов этого исследования в отношении отношения момент-прогиб.Для дальнейшего изучения, в отношении разницы в свойствах сцепления стержней из стеклопластика, предложенная модель могла бы разумно описать соотношение момент-прогиб для результатов испытаний, рассмотренных в предыдущих исследованиях, и результатов испытаний в этом исследовании. (Iv) Это исследование подтвердило предсказуемость предложенной модели по эффективному моменту инерции. Было обнаружено, что применима методология модификации с эмпирическим подходом. Что касается будущих исследований, важно провести сравнительное исследование с различными соотношениями армирования, связующими свойствами стержней из стеклопластика и размерными эффектами бетонных балок. Конкурирующие интересыАвторы заявляют, что у них нет конкурирующих интересов. БлагодарностиРабота поддержана грантом (2015R1A2A2A01005286) Национального исследовательского фонда Кореи (NRF) и грантом (16CTAP-C117247-01) программы НИОКР Министерства земли, инфраструктуры и транспорта Правительство Кореи. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

