Пропорция 1 к 5: Пропорция 1 к 5

Содержание

Как развести бензин для бензопилы: официальный сайт Echotool.

Почему нужно смешивать масло и бензин

Для нормальной работы любому двигателю внутреннего сгорания нужны, как минимум, две вещи:

Топливо — вернее топливовоздушная смесь, приготовленная карбюратором, попадает в камеру сгорания, воспламеняется, расширяется, и «толкает» поршень вниз, за счёт чего выполняется полезная работа.
Смазка — необходима для уменьшения силы трения между соприкасающимися деталями двигателя.

В первую очередь, масло нужно для того, чтобы исключить так называемое «сухое» трение металла о металл. Из-за него контактирующие детали подвергаются критическому износу — появляются задиры, царапины, уменьшается компрессия, снижается ресурс. Также масло нужно для уплотнения зазоров.

Почему же нужно смешивать масло с топливом для бензопилы?

Это требование напрямую связано с особенностями устройства и принципом работы двухтактных двигателей, которыми оснащается данный инструмент.

Смазка деталей кривошипно-шатунного механизма и цилиндропоршневой группы здесь выполняется исключительно за счёт масла, находящегося в горючем. Благодаря особому устройству двигателя, топливовоздушная смесь попадает не только в камеру сгорания, но и в картер, где находится коленвал с шатуном. Таким образом, смазываются все трущиеся детали.

Соотношение количества масла и бензина для топливной смеси

Чтобы двухтактный двигатель бензопилы работал в оптимальном для него режиме, масло с бензином необходимо смешивать в определённых пропорциях. Они обычно указываются в инструкции к инструменту, а также на упаковках со смазкой. Рассмотрим вкратце, что будет, если рекомендуемых соотношений не соблюдать, или нарушать их по ошибке (незнанию).

Если масла добавить в бензин слишком мало, его концентрации не хватит для эффективной смазки трущихся деталей. Двигатель будет издавать звенящие звуки, чрезмерно греться, и быстро выйдет из строя.

Много масла — тоже плохо, так как излишки не смогут полноценно сгорать. Это приведёт к образованию нагара на стенках цилиндра и поршне, загрязнению свечи зажигания, выхлопной системы. Также упадёт мощность, повысится расход топлива, и во время работы будет наблюдаться чрезмерная дымность выхлопа.

Чтобы этих проблем избежать, масло с бензином надо смешивать в рекомендуемых производителем пропорциях. Указываются они в виде соотношений — 1:50, 1:40, 1:25 и так далее. Любая из этих пропорций говорит о том, сколько масла нужно лить на объём топлива. Например, для приготовления смеси по пропорции 1:25 понадобится 1 литр масла на 25 литров бензина.

Важно не перепутать! Довольно часто указанные пропорции воспринимаются пользователями наоборот. К примеру, 1:50 понимается, как на 1 литр бензина 50 миллилитров масла. Это грубая ошибка, которая приведёт к повышенной концентрации масла в горючем. На самом деле при таком соотношении на 1 литр масла нужно всего 20 миллилитров масла.

Как не запутаться в пропорциях? Ведь мало кому надо готовить 50, или даже 25 литров топливной смеси для бензопилы. Тем более, что хранить смешанный с маслом бензин долго нельзя. Обычно готовят столько, сколько потребуется на день-два. А с учётом небольшого расхода бензопилы это 1-5 литров.

Есть три способа, как правильно развести бензин для бензопилы в небольших объёмах:

Поделить 1000 на вторую цифру в пропорции. К примеру, нужно приготовить смесь в соотношении 1:40. Делите 1000 на 40, получаете 25. Столько миллилитров масла льёте на 1 литр бензина.
Решить пропорцию, как в школе. Для этого требуемый объём бензина в литрах делим на вторую цифру в пропорции. В результате получаем нужный объём масла в литрах. Переводим литры в миллилитры для удобства. Допустим, вам нужно 3 литра смеси в пропорции 1:50. Решаем: 3/50=0,06 л. Чтобы превратить литры в миллилитры, переносим запятую на три знака вправо, и получаем 60 миллилитров.
Посмотреть в таблице. Это самый простой, быстрый и наглядный способ, если пропорции стандартные. Остальные два способа нужны для того, чтобы понять, почему при пропорции 1:50 нужно лить на литр бензина 20 миллилитров масла, а не 50.

Пропорция	Масла на 1 л бензина (мл)
1:20	50 мл
1:25	40 мл
1:30	33 мл
1:35	28 мл
1:40	25 мл
1:45	22 мл
1:50	20 мл

Теперь кратко о том, почему у разных производителей отличаются пропорции и нет какого-то единого стандарта. На это есть, как минимум, три причины. Во-первых, разные характеристики масел и бензина. Во-вторых, качество сборки двигателей (технологии, материалы) тоже отличается. В-третьих, режим эксплуатации инструмента. К примеру, для обкатки бензопил некоторых производителей рекомендуется добавлять в смесь на 20% больше масла.

Пошаговая инструкция по заправке

Для приготовления топливной смеси и заправки бензопилы понадобится:

мерная ёмкость;
чистый бензин с октановым числом 92;
специальное масло для двухтактных моторов с воздушным охлаждением;
ёмкость для готовой смеси;
воронка.

Для измерения объёмов можно использовать ёмкость, которыми обычно комплектуются бензиновые инструменты. Также можно купить специальные фирменные канистры с отделами и мерными приспособлениями.

Пошаговая инструкция:

Приготовьте ёмкость для готовой топливной смеси.

Её вместительности должно хватить и для бензина, и для масла.
Посчитайте пропорцию смазки и бензина, исходя из руководства по эксплуатации, и воспользовавшись одним из способов выше.
Отмерьте и налейте в ёмкость требуемый объём бензина.
При помощи мерного стакана, штатной бутылочки или шприца отмерьте и добавьте в бензин нужный объём масла.
Ёмкость для готовой смеси в итоге не должна быть полной под завязку.
Надёжно закройте ёмкость крышкой, и несколько раз переверните её для того, чтобы масло смешалось с бензином.
Заправьте приготовленную смесь в топливный бак бензопилы.

Вопреки гуляющему по Сети мнению, нет разницы, что первое заливать в ёмкость для приготовления смеси — бензин или масло. Главное, не забудьте тщательно перемешать. Вот чего на самом деле не стоит делать, так это готовить топливную смесь непосредственно в топливном баке бензопилы.

назад в блог

пропорция масла и бензина для бензопилы

Двигатель бензопилы — это «сердце» инструмента, поэтому очень важно использовать правильно приготовленную топливную смесь.

Топливная смесь для бензопилы готовится из двух составных — масла и бензина. Бензопилы оснащаются двухтактными двигателями, поэтому масло добавляется не в смазочную систему (как у четырехтактного двигателя), а непосредственно в бензин. При этом очень важно соблюдать верные пропорции ингредиентов и, конечно же, ни в коем случае не пытаться работать на чистом бензине, ведь таким образом, вы очень быстро «убьете» цепную пилу.

Масло обязательно должно быть предназначено для двухтактных двигателей садово-лесной техники (то есть ни в коем случае нельзя использовать масло для лодочных моторов или скутеров). Как показывает практика, такое масло можно купить в любом магазине или сервисном центре, где в продаже есть бензопилы или производиться их обслуживание.

Если говорить о том, какой бензин заливать в бензопилу, то оптимально будет использовать горючее с октановым числом А-95, в данном случае экономия на горючем может обернуться плачевно. Часто европейские производители указывают, что можно использовать бензин А-90 или А-92, но в постсоветских странах качество бензина уступает европейскому, поэтому в наших реалиях лучше использовать более качественный бензин.

Что касается самой пропорции бензо-масляной смеси, то здесь все просто: необходимо четко следовать инструкции к инструменту. Все производители бензопил указывают необходимое соотношение в руководстве по эксплуатации или в паспорте инструмента, кроме того, пропорции для заправки бензопилы могут отличаться в зависимости от модели цепной пилы. Как правило, пропорция масла и бензина к бензопиле именитых производителей это соотношение

1:40 или 1:50, что означает 1 часть масла на, например, 40 частей бензина.

Теперь арифметика — 1 л бензина = 1000 мл бензина, делим на 40 и получаем 25 мл масла. Если выполнить те же действия к соотношению 1:50, то получаем 20 мл масла на 1 л бензина.

Что касается бюджетных бензопил китайского производства, то ситуация немного иная. Соотношение бензина и масла для бензопилы made in China 1:25, то есть 1000 мл бензина делим на 25, получаем 40 мл масла. Все дело в том, что в фирменных бензопилах добротная сборка и расстояние между поршнями и цилиндрами в двигателе намного меньше, чем у китайских бензопил, поэтому и необходимое количество масла отличается практически в два раза.

Для того чтобы отмерить правильную порцию масла, воспользуйтесь обычным медицинским шприцем достаточного объема.

Еще одна тонкость — в сухую канистру для бензина сначала заливайте бензин, а потом масло. Процедура наоборот чревата топливной смесью низкого качества, ведь масло более плотное, прилипнет ко дну канистры. Поэтому о хорошем смешивания речь никак не может идти.

Обязательно готовьте топливную смесь в канистре и заливайте в бензобак уже готовое спецгорючее! Никогда не готовьте и не смешивайте ее непосредственно в топливном баке бензопилы!

Если с вопросом как разводить бензин для бензопилы разобрались, то и об условиях хранения и сроках годности топливной смеси стоит сказать несколько слов. Лучше всего и проще готовить бензомасленую смесь на 1 л бензина, делать это рекомендуется непосредственно перед работой с инструментом. Топливные баки бензопил имеют объем от 0,3 до 1 л. В условиях бытового использования за один сеанс редко используется весь объем приготовленной горючей смеси, поэтому остаток можно сохранить до следующего сеанса работы. Хранить топливную смесь необходимо в специальной канистре для бензина, в сухом темном месте. Оптимально рассчитывать, что срок хранения готовой смеси составит 7-10 дней

Дело в том, что масло представленное сейчас на рынке не синтетическое, а органическое, то есть натуральное. После 10 дней все смазочные свойства теряются, бензин попросту «съедает» масло. Естественно, использовать такое горючее уже нельзя, это может вызвать поломку и выход из строя бензопилы.

В конце работы необходимо слить топливную смесь и завести бензопилу — инструмент заглохнет (для того чтобы у пилы был сухой карбюратор) и теперь можно оставить ее до следующего сеанса эксплуатации.

Непригодную топливную смесь обязательно необходимо утилизировать!

Проверка пропорциональности | Purplemath

СоотношенияПропорцииРешение словесных задачПодобные фигурыСолнечные лучи / Части

Purplemath

Тема пропорций имеет некоторую специфическую терминологию, которую вам может понадобиться знать. Например, при следующем уравнении пропорции:

… значения в позициях « b » и « c » называются «средними» пропорциями, а значения в « a Позиции «» и « d » называются «крайними» пропорциями.

Основным определяющим свойством любой пропорции является то, что произведение средних равно произведению крайних значений. Другими словами, учитывая утверждение о пропорции:

Содержание продолжается ниже

MathHelp.com

Пропорции

… мы знаем, что должно быть верно, что ad равно bc . Этот факт о пропорциях, по сути, представляет собой перекрестное умножение, продемонстрированное на предыдущей странице. И этот факт перекрестного умножения произведений средних и крайних иногда превращается в домашнюю задачу, например:

Является ли
²⁴ / ₁₄₀ пропорциональным ³⁰ / ₁₇₆ ? Объясните, почему (или почему нет), не упрощая дроби.

Чтобы эти дроби (т. уравнение равно произведению крайних. Таким образом, я могу выяснить, действительно ли две дроби пропорциональны друг другу (без их упрощения), найдя эти два произведения.

Другими словами, указывая, что я должен , а не упростить дроби, они намекают, что хотят, чтобы я нашел произведение 140 и 30 (что означает, что я сохраняю дроби в одном и том же порядке, как они мне их дали) и произведение 24 и 176 (крайних), а затем посмотрите, равны ли эти произведения. Итак, я проверю:

140 × 30 = 4200

24 × 176 = 4224

Хотя эти значения близки, они не равны, поэтому я знаю, что исходные дроби не могут быть пропорциональны друг другу. Итак, мой ответ:

Дроби не пропорциональны, потому что произведение их средних не равно произведению их крайних значений.

Если бы я поменял местами дроби и использовал 176 и 24 как средние, а 30 и 140 как крайние значения, я получил бы те же произведения (только в обратном порядке) и, следовательно, тот же ответ (а именно, что дроби не пропорциональны). Так что не беспокойтесь о том, какая дробь «первая» или «вторая»; в любом случае будет работать.

Пропорционально ли 42/55 50/65? Обоснуйте свой ответ, не сокращая дроби.

Чтобы подтвердить пропорциональность (или опровергнуть ее), мне нужно составить пропорцию, умножить средние, умножить крайние значения и сравнить результаты. Или, что то же самое (но без составления уравнения, которое на самом деле может быть неверным), я умножу знаменатель одной дроби на числитель другой и наоборот:

(42)(65) = 2730

(55)(50) = 2750

Опять же, они близки, но не равны. Итак:

Дроби не пропорциональны, потому что произведение их средних не равно произведению их крайних значений.

Пропорциональны ли 42/273 и 170/1105? Объясните свой ответ, не сокращая дроби и не приводя к общему знаменателю.

I «перемножить» (имеется в виду в данном контексте умножение числителя одной дроби на знаменатель другой и наоборот):

(42)(1,105) = 46 410

(273)(170) = 46 410

Наконец, пара, в которой пропорциональна !

Дроби пропорциональны, потому что в виде пропорции произведение средних равно произведению крайних.

Пропорциональные средние

Другим техническим типом упражнения, основанным на терминологии пропорций, является нахождение «средней пропорциональной» между двумя числами. Средние пропорциональные — это особый класс пропорций, в которых средние пропорции равны между собой. Примером среднего пропорционального будет:

¹ / ₂ = ² / ₄

крайности равны 1 и 4. Это говорит нам о том, что число 2 является «средним пропорциональным» между числами 1 и 4. их.

Мне дали два числа и ключевое слово «пропорциональное среднему». Итак, я знаю, что мне нужно установить пропорцию, используя заданные значения как крайние значения, а затем я должен найти средние значения.

По определению «среднее пропорциональное» я знаю, что средние значения будут одинаковыми. Я позволю « x » быть тем единственным значением, которое я ищу. Я составлю уравнение пропорции, используя свою переменную для средних значений и два значения, которые они мне дали в качестве крайних значений:

Теперь я перемножу их, а затем найду значение x :

3 × 12 = х ²

36 = х ²

± 6 = x

Так как я ищу среднее пропорциональное 3 и 12, я должен был бы взять только положительное значение в качестве моего ответа, так что среднее пропорциональное будет просто 6 Однако, учитывая дроби, подойдет любое значение:

Если я проверю векторные произведения каждого уравнения, я получу равные результаты; другими словами, отрицательное значение также является допустимым результатом. Итак, на самом деле, есть две средние пропорциональные данному уравнению:

−6 и 6

Примечание. Ваша книга (или преподаватель) может потребовать, чтобы вы учитывали только положительное среднее, пропорциональное, поскольку положительное значение находится между 3 и 12. Фактически, ваша книга (или преподаватель) может определить » среднее пропорциональное» должно быть только и всегда положительным значением. Используйте определение, данное в вашей книге (или преподавателем), но имейте в виду, что вы можете встретить другие определения в других классах или контекстах.

Чтобы найти средние значения, я составлю уравнение и решу:

4/ x = x /25

4 × 25 = x ²

100 = 90 011 x ²

±10 = x

Поскольку указано что им нужно положительное среднее, мой ответ:

Вы, возможно, заметили, что в приведенных выше решениях я всегда получал квадратное значение, равное числу, а затем извлекал квадратный корень из каждого сторону уравнения. Это дает сокращенный метод для решения среднего пропорционального:

Они указали, что им нужно значение, которое находится «между» двумя заданными значениями, и эти значения положительны, поэтому я знаю, что им нужно положительное решение. Вместо того, чтобы составлять пропорцию, перемножать, чтобы создать квадратное уравнение, а затем решать, я перейду прямо к квадратному корню:

sqrt[8 × 50]

кв[400]

sqrt[16 &times 25]

4 × 5 = 20

И это окончательное значение является моим ответом:

(Кстати, хотя это и очень необычно, вы можете увидеть упражнение, в котором экстремумы пропорции (то есть заданные значения в «нахождении среднего пропорциональное» упражнение) оба отрицательны. Когда эти значения перемножаются, знаки «минус» сокращаются, и вы можете извлечь квадратный корень, как обычно.

(Однако невозможно экстремумы имеют противоположные знаки. Почему? Потому что произведение экстремумов с противоположными знаками будет отрицательным, и вы не можете извлечь квадратный корень из отрицательного значения. Если вас когда-нибудь попросят найти среднее, пропорциональное двум значениям с противоположным знаком, имейте в виду, что это вопрос с подвохом!)

То, что все примеры, которые мне приводили в учебнике, были целыми числами, не означает, что пропорция не может содержать дроби; он может. Я буду использовать упрощенный метод решения, умножая две крайние точки, а затем извлекая (положительный) квадратный корень:

(3/2) × (3/8) = 9/16

sqrt[9/16] = 3/4

Таким образом, среднее, пропорциональное двум дробям, является еще одной дробью:

Вы также можете услышать, что «среднее пропорциональное», называемое «средним геометрическим». Это потому, что это пропорциональное отношение возникает в геометрии прямоугольных треугольников. Если мы возьмем прямоугольный треугольник и проведем прямую из прямого угла к гипотенузе так, чтобы эта линия была перпендикулярна гипотенузе, то гипотенуза разделится на две части. Перпендикулярную линию можно рассматривать как линию, указывающую высоту » h «треугольника, когда гипотенуза является основанием. Две части помечены » x » и » y » на рисунке ниже:

Можно доказать, что высота h и две части, x и y , основания образуют пропорцию:

x / h = h / y

9 0003

В частности:

ч = sqrt [ ху ]

Это отношение можно превратить в упражнения, такие как:

Когда прямоугольный треугольник построен таким образом, с линией высоты, проведенной от прямого угла к гипотенузе, высота и две части основания образуют пропорцию в котором высота является средней пропорциональной двух частей. Итак, чтобы найти высоту, мне нужно найти среднее значение, пропорциональное двум значениям, которые они мне дали.

(132)(44) = 5,808

Тогда I фактор:

5,808 = (16)(121)(3)

Затем я извлекаю квадратный корень:

sqrt[(16)(121)(3)] = (4)(11) sqrt[3]

Затем, умножив это, я нахожу, что высота треугольника:

h = 44 sqrt[3]

URL: https://www. purplemath.com/modules/ratio3.htm

возраст 6Страница 7

6.3: Введение в пропорции — Mathematics LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 22496

Дэвид Арнольд
Колледж Редвудс

В разделе 6.1 мы ввели понятия соотношения и скорости. В этом разделе мы приравниваем эти отношения в конструкции, называемой пропорция .

Пропорции

Пропорция — это утверждение, которое уравнивает два соотношения или коэффициента.

Например, каждое из уравнений

\[\frac{1}{3} = \frac{2}{6}, ~ \frac{15 \text{ миль}}{2 \text{ часов}} = \frac{30 \text{ миль} }{4 \text{ часов}}, \text{ и } \frac{a}{b} = \frac{c}{d}\nonumber \]

сравнивает два соотношения или коэффициента и является пропорцией.

Пропорция

\[ \frac{1}{3} = \frac{2}{6}\номер \]

читается как «один к трем, как два к шести». Четыре числа, составляющие эту пропорцию, называются членами пропорции и упорядочены естественным образом.

Крайности и средние значения

Первый и четвертый члены называются крайними пропорциями. Второй и третий члены называются означает пропорции.

В пропорции

\[ \frac{a}{b} = \frac{c}{d},\nonnumber \]

термины a и d являются крайностями; термины b и c являются средними.

Если обе части пропорции умножить на общий знаменатель,

\[bd \left(\frac{a}{b} \right) = bd \left( \frac{c}{d} \right)\nonnumber \]

затем отменить,

\[ \cancel{b} d \left( \frac{a}{\cancel{b}} \right) = b \cancel{d} \left( \frac{c}{\cancel{d}} \ справа)\номер\]

получаем следующий результат.

\[объявление = до н. э.\номер\]

Это приводит к следующему наблюдению.

Произведение крайностей и средних

В пропорции

\[ \frac{a}{b} = \frac{c}{d}\nonumber \]

произведение средних равно произведению крайних. То есть

\[ad = bc.\nonumber \]

Мы можем получить эквивалентный результат, используя метод, называемый скрещиванием умножением .

Пример 1

Какая из следующих пропорций является допустимой: (a) $\frac{2}{3} = \frac{7}{12}$ или (b) $\frac{4}{9} = \фрак{12}{27}$.

Решение

(a) Перемножить

, чтобы получить

24 = 21.

Следовательно, произведение крайних значений не равно произведению средних, поэтому 2/3 =7/12 является , а не действительной пропорцией.

(b) Перемножить

, чтобы получить

108 = 108.

Следовательно, произведение крайних значений равно произведению средних, поэтому 4/9= 12/27 — это действительная пропорция.

Упражнение

Верна ли следующая пропорция? $\frac{4}{3} = \frac{16}{11}$

Ответ: №

Решение пропорций

У нас уже есть все инструменты, необходимые для решения пропорций. Начнем с первого примера.

Пример 2

Решите пропорцию для x : $\frac{3}{4} = \frac{x}{12}$.

Решение

Умножьте крест-накрест, затем решите полученное уравнение.

\[ \begin{align} \frac{3}{4} = \frac{x}{12} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ 4 \cdot x = 3 \cdot 12 ~ & \textcolor{red}{ \text{ Произведения средних и крайних равны.}} \\ 4x = 36 ~ & \textcolor{red}{ \text{ Упростить.}} \\ \frac{4x }{4} = \frac{36}{4} ~ & \textcolor{red}{ \text{ Разделить обе части на 4.}} \\ x = 9 ~ & \textcolor{red}{ \text{ Упростить. }} \end{выровнено}\номер \]

Проверить

Подставить 9 вместо x в исходную пропорцию и проверить.

\[ \begin{aligned} \frac{3}{4} = \frac{x}{12} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ \frac{3}{ 4} = \frac{9}{12} ~ & \textcolor{red}{ \text{ Замените 9 на } x.} \end{aligned}\nonumber \]

Перекрестное умножение.

Таким образом, решение 9 проверяется.

Упражнение

Решите пропорцию для n : $\frac{2}{3} = \frac{n}{9}$

Ответ: 6

Пример 3

Решите пропорцию для n : $\frac{3}{2} = \frac{24}{n}$.

Решение

Перемножить крест-накрест, затем решить полученное уравнение.

\[ \begin{align} \frac{3}{2} = \frac{24}{n} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ 3 \cdot n = 2 \cdot 24 ~ & \textcolor{red}{ \text{ Произведения средних и крайних равны.}} \\ 3n = 48 ~ & \textcolor{red}{ \text{ Упростить.}} \\ \frac{3n }{3} = \frac{48}{3} ~ & \textcolor{red}{ \text{ Разделить обе части на 3. }} \\ n = 16 ~ & \textcolor{red}{ \text{ Упростить. }} \end{выровнено}\номер \]

Проверить

Подставить 16 вместо n в исходную пропорцию и проверить.

\[ \begin{aligned} \frac{3}{2} = \frac{24}{n} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ \frac{3}{ 2} = \frac{24}{16} ~ & \textcolor{red}{ \text{ Замените 16 на } n.} \end{aligned}\nonumber \]

Перекрестное умножение.

Таким образом, решение 16 проверяется.

Упражнение

Решите пропорцию для м : $\frac{9}{6} = \frac{m}{4}$

Ответ: 6

Пример 4

Решите пропорцию для x : $\frac{2x + 1}{15} = \frac{1}{3}$.

Решение

Перемножить крест-накрест, затем решить полученное уравнение.

\[ \begin{align} \frac{2x+1}{15} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ 3(2x+ 1) = 15(1) ~ & \textcolor{red}{ \text{ Произведения f средние и крайние значения равны. }} \\ 6x+3 = 15 ~ & \textcolor{red}{ \begin{aligned} \text { Слева распределите.} \\ \text{ Справа умножьте.} \end{aligned}} \\ 6x+3-3=15-3 ~ & \textcolor{red}{ \text{ Вычтите 3 с обеих сторон.}} \\ 6x=12 ~ & \textcolor{red}{ \text{ Упростить.}} \\ \frac{6x}{6} = \frac{12}{6} ~ & \textcolor{ red}{ \text{ Разделить обе стороны на 6.}} \\ x = 2 ~ & \textcolor{red}{ \text{ Упростить обе стороны.}} \end{aligned}\nonumber \]

Проверить

Мы предоставим нашим читателям возможность проверить это решение.

Упражнение

Решите пропорцию для y : $\frac{6+2y}{18} = \frac{8}{9}$

Ответ: 5

Приложения

Ряд практических приложений включает в себя решение пропорции.

Пример 5

Если 5 апельсинов стоят 1,15 доллара, сколько будет стоить 15 апельсинов (при условии равного курса)?

Решение

Пусть x представляет стоимость 15 апельсинов. Предполагая, что курс 5 апельсинов по 1,15 доллара равен курсу 15 апельсинов по неизвестной стоимости x , мы устанавливаем следующую пропорцию.

\[ \frac{5}{1.15} = \frac{15}{x}\nonumber \]

Перемножить

, чтобы получить

\[5x = 17,25.\nonumber \]

Решить для х .

\[\begin{align} \frac{5x}{5} = \frac{17.25}{5} \\ x = 3.45 \end{align}\nonumber \]

Таким образом, 15 апельсинов стоят 3,45 доллара.

Упражнение

Если 7 яблок стоят 3,15 доллара, сколько будут стоить 10 яблок (при равном курсе)?

Ответить: 4,50 $

Чрезвычайно важно проверять единицы измерения

При составлении пропорции убедитесь, что оба числителя имеют одинаковые единицы измерения и оба знаменателя имеют одинаковые единицы измерения.

Например, в Примере 5 в обоих числителях используются «апельсины», а в обоих знаменателях — «доллары».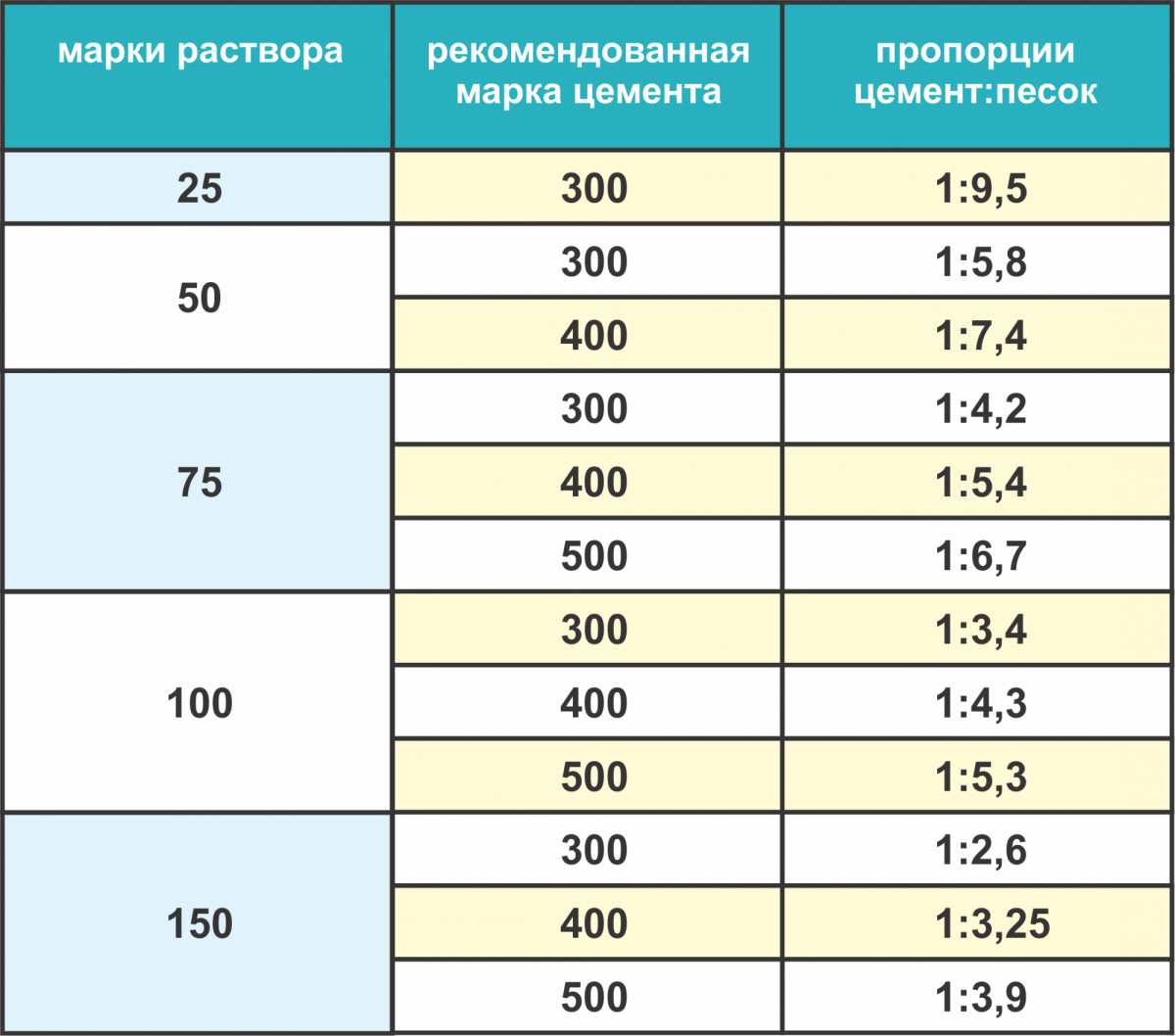

Эта пропорция составлена правильно, потому что оба числителя имеют одинаковые единицы измерения и оба знаменателя имеют одинаковые единицы измерения. С другой стороны, если бы мы неправильно установили пропорцию следующим образом,

, быстрая проверка единиц выявит ошибку; т. е. числители имеют разные единицы измерения, а знаменатели имеют разные единицы измерения. Проверка единиц помогает нам избежать ошибок!

Пример 6

Дилан и Дэвид планируют поход в национальный парк Йосемити. На их карте легенда указывает, что 1,2 сантиметра соответствуют 2 милям. Какова продолжительность их пути, если длина маршрута на карте составляет 10,6 см? Округлите ответ до ближайшей десятой мили.

Решение

Построим пропорцию в единицах.

\[\frac{1,2 \text{ см}}{2 \text{ми}} = \frac{10,6 \text{см}}{x \text{ми}}\номер\]

Обратите внимание, как включая единицы помогают в настройке пропорции. Теперь давайте отбросим единицы измерения и найдем x .

\[ \begin{align} \frac{1.2}{2} = \frac{10.6}{x} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ 1.2x = (2) (10.6) ~ & \textcolor{red}{ \text{ Перекрестное умножение.}} \\ 1,2x = 21,2 ~ & \textcolor{red}{ \text{ Упростить правую часть.}} \\ \frac{1.2 x}{1.2} = \frac{21.2}{1.2} ~ & \textcolor{red}{ \text{ Разделите обе части на 1.2.}} \\ x \приблизительно 17,66 ~ & \textcolor{red}{ \text{ Справа: Разделить.}} \end{aligned}\nonumber \]

Мы перенесли деление на один десятичный знак справа после десятых. Цифра округления — 6, а следующая проверочная цифра — 6. Добавьте 1 к цифре округления и усеките.

С точностью до десятой мили пеший маршрут составляет примерно 17,7 миль.

Упражнение

Элоиза и Сюзанна планируют поездку в национальный парк Секвойя. На их карте 3 дюйма соответствуют 50 милям. Какова продолжительность их поездки, если размер маршрута составляет $4 \frac{1}{2}$ дюймов на карте?

Ответить: 75 миль

Пример 7

Рецепт приготовления 2 дюжин печенья требует $1 \frac{3}{4}$ чашек муки, среди других ингредиентов. Если пекарь хочет испечь в два раза больше печенья, сколько потребуется муки?

Решение

Дважды 2 дюжины — это 4 дюжины печенья. Пусть x представляет собой количество муки, необходимое для 4 дюжин печенья. Принимая равноценную норму на 2 дюжины печенья (на 2 дюжины требуется 1 3 4 стакана муки), составим следующую пропорцию. Опять же, использование единиц помогает нам создать правильную пропорцию.

\[\frac{2 \text{дюжина}}{1 \frac{3}{4} \text{чашек}} = \frac{4 \text{дюжина}}{x \text{чашек}}\ nonumber \]

Обратите внимание, как включение единиц помогает в настройке пропорции. Теперь давайте отбросим единицы измерения и найдем x .

\[ \begin{aligned} \frac{2}{1 \frac{3}{4}} = \frac{4}{x} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ 2x = 1 \frac{3}{4} \cdot 4 ~ & \textcolor{red}{ \text{ Перекрестное умножение.}} \\ 2x = \frac{7}{4} \cdot 4 ~ & \ textcolor{red}{ \text{ Заменить на неправильную дробь.}} \\ 2x = 7 ~ & \textcolor{red}{ \text{ Умножить. }} \end{aligned}\nonumber \]

Разделите обе части уравнения на 2 и закончите.

\[ \begin{aligned} \frac{2x}{2} = \frac{7}{2} ~ & \textcolor{red}{ \text{ Разделить обе стороны на 2.}} \\ x = \ frac{7}{2} \end{aligned}\nonumber \]

Замените неправильную дробь на смешанную. Таким образом, для приготовления 4 дюжин печенья потребуется $3 \frac{1}{2}$ стаканов муки.

Упражнение

Тесто для 3 пицц требует $8 \frac{1}{2}$ чашек муки. Если пекарь хочет испечь 9 пицц, сколько чашек муки потребуется?

Ответить: $25 \frac{1}{2}$ чашек

Упражнения

Какое из следующих утверждений в упражнениях 1-12 является истинной пропорцией?

1. $\frac{9}{7} = \frac{27}{21}, ~ \frac{4}{3} = \frac{9}{7}, ~ \frac{7}{ 2} = \frac{8}{9}, ~ \frac{4}{8} = \frac{9}{6}$

2. $\frac{6}{7} = \frac{ 18}{21}, ~ \frac{2}{3} = \frac{8}{6}, ~ \frac{4}{3} = \frac{3}{2}, ~ \frac{8} {9} = \frac{3}{8}$

3. $\frac{7}{6} = \frac{28}{24}, ~ \frac{5}{6} = \frac {5}{4}, ~ \frac{9}{5} = \frac{7}{3}, ~ \frac{9}{2} = \frac{8}{9}$

4. $\frac{7}{6} = \ frac{2}{8}, ~ \frac{4}{5} = \frac{5}{7}, ~ \frac{3}{4} = \frac{15}{20}, ~ \frac{ 8}{4} = \frac{8}{7}$

5. $\frac{6}{5} = \frac{24}{20}, ~ \frac{7}{3} = \frac{2}{4}, ~ \frac{2}{4} = \frac{2}{6}, ~ \frac{5}{2} = \frac{2}{8}$

6. $\frac{9}{8} = \frac{4}{3}, ~ \frac{5}{7} = \frac{10}{14}, ~ \frac{8}{6} = \frac{5}{4}, ~ \frac{8}{5} = \frac{2}{6}$

7. $\frac{3}{5} = \frac{2} {8}, ~ \frac{3}{7} = \frac{6}{14}, ~ \frac{5}{6} = \frac{2}{4}, ~ \frac{7}{4} } = \фракция{5}{9}$

8. $\frac{7}{3} = \frac{7}{6}, ~ \frac{4}{7} = \frac{8}{14}, ~ \frac{ 5}{3} = \frac{7}{8}, ~ \frac{5}{7} = \frac{6}{9}$

9. $\frac{5}{4} = \frac{25}{20}, ~ \frac{9}{3} = \frac{9}{6}, ~ \frac{7}{4} = \frac{3}{6}, ~ \frac {3}{5} = \frac{9}{4}$

10. $\frac{7}{6} = \frac{6}{9}, ~ \frac{7}{3} = \frac{2}{5}, ~ \frac{6}{7} = \frac{30}{35}, ~ \frac{4}{7} = \frac{2}{8}$

11. $\frac{9}{7} = \frac{4}{3}, ~ \frac{9}{4} = \frac{7}{9}, ~ \frac{3}{5 } = \frac{6}{10}, ~ \frac{3}{9} = \frac{9}{5}$

12. $\frac{4}{3} = \frac{8}{7}, ~ \frac{2}{6} = \frac{5 {8}, ~ \frac{7}{2} = \frac{3}{6}, ~ \frac{9}{4} = \frac{36}{16}$

В упражнениях 13 -36, решите данную пропорцию.

13. $\frac{17}{3} = \frac{x}{18}$

14. $\frac{16}{5} = \frac{x}{20}$

15. $\frac{6x + 10}{6} = \frac{11}{3}$

16. $\frac{4x + 8}{12} = \frac{5}{ 3}$

17. $\frac{17}{9} = \frac{x}{18}$

18. $\frac{8}{9} = \frac{x}{18}$

19. $\frac{11}{2} = \frac{x}{8}$

20. $\frac{11}{4 } = \frac{x}{8}$

21. $\frac{7x + 15}{15} = \frac{10}{3}$

22. $\frac{7x + 3}{8} = \frac{5}{4}$

23. $\frac{11}{2} = \frac{x}{10}$

24. $\frac{ 19}{6} = \frac{x}{18}$

25. $\frac{5x + 8}{12} = \frac{2}{3}$

26. $\ frac{3x + 12}{6} = \frac{3}{2}$

27. $\frac{2}{15} = \frac{24}{x}$

28. \ (\ гидроразрыва {7} {8} = \ гидроразрыва {14} {x} \)

29. $\frac{3}{16} = \frac{6}{x}$

30. $\frac{4}{21} = \frac{12}{x}$

31. $\frac{5}{22} = \frac{20}{x}$

32. $\frac{3}{22} = \frac{21}{x}$

33. $\frac{2x + 10}{6} = \frac{14}{3}$

34. $\frac{2x + 9}{9} = \frac{13}{ 3}$

35. $\frac{7}{2} = \frac{21}{x}$

36. $\frac{2}{15} = \frac{18}{ x}$

37. Если 13 собачьих костей стоят 1,97 доллара, сколько будет стоить 7 собачьих костей (при условии равного курса)? Округлите ответ до копейки.

38. Если 2 арбуза стоят 3,89 доллара, сколько будет стоить 11 арбузов (при равном курсе)? Округлите ответ до копейки.

39. Если 7 бананов стоят 2,55 доллара, сколько будет стоить 14 бананов (при равном курсе)? Округлите ответ до копейки.

40. Если 2 яблока стоят 2,05 доллара, сколько будет стоить 8 яблок (при равном курсе)? Округлите ответ до копейки.

41. Если 13 апельсинов стоят 3,61 доллара, сколько будет стоить 11 апельсинов (при равном курсе)? Округлите ответ до копейки.

42. Если 3 арбуза стоят 1 доллар 05 центов, сколько будет стоить 9 арбузов (при равном курсе)? Округлите ответ до копейки.

43. Если 3 собачьи кости стоят 1,23 доллара, сколько будет стоить 13 собачьих костей (при равном курсе)? Округлите ответ до копейки.

44. Если 3 арбуза стоят 4,41 доллара, сколько будет стоить 7 арбузов (при равном курсе)? Округлите ответ до копейки.

45. Если 3 яблока стоят 3,24 доллара, сколько будет стоить 13 яблок (при равном курсе)? Округлите ответ до копейки.

46. Если 6 яблок стоят 3,43 доллара, сколько будет стоить 7 яблок (при условии равного курса)? Округлите ответ до копейки.

47. Если 4 собачьи кости стоят 1,03 доллара, сколько будет стоить 8 собачьих костей (при равном курсе)? Округлите ответ до копейки.

48. Если 4 апельсина стоят 4,28 доллара, сколько будет стоить 3 апельсина (при равном курсе)? Округлите ответ до копейки.

49. Два рулона. На Гаити две плоские булочки стоят 5 гурдов, около 12 центов. Сколько центов будут стоить 20 рулонов? Ассошиэйтед Пресс-Таймс-Стандарт 18.02.10 Гаитянские лагеря землетрясений превращаются в трущобы.

50. Турбины. Согласно предложению, проект Shell Wind Energy состоит из 25 коньковых турбин, которые могут генерировать до 50 мегаватт, чего достаточно для снабжения электроэнергией около 1000 домов. Оцените количество турбин на вершине хребта, которые потребуются для снабжения электроэнергией 70 000 домов, приблизительное количество владений в округе Гумбольдт, Калифорния. John Driscoll Times-Standard 24.12.09 Проект ветроэнергетики находится на анализе.

51. Самосвалы. На шоссе 199 США произошел оползень, в результате которого на дорогу упало до 3000 кубических ярдов материала, для вывоза которого, как сообщается, потребовалось около 200 больших самосвалов. Всего за неделю до этого на шоссе 96 упало 40 000 кубических ярдов материала. Оцените количество самосвалов, необходимых для этого спуска, округлив до ближайшего целого числа. Ассошиэйтед Пресс-Таймс-Стандарт 03/09/10 Еще одно шоссе закрыто оползнем.

52. Продажа пиломатериалов. План национального леса Тонгасс площадью 26 000 квадратных миль на Аляске позволяет продавать древесину до 267 миллионов досочных футов в год — этого достаточно для почти 27 000 домов с двумя спальнями, но спрос на древесину намного меньше этого. В 2009 году в лесу было вырублено менее 25 миллионов досок-футов.. Чиновники Лесной службы заявили, что надеются увеличить лесозаготовку в Тонгассе примерно до 100 миллионов доск-футов в год. Associated Press-Times-Standard 18.02.10 Промышленность проигрывает судебный процесс по вырубке леса на Аляске.

i) Оцените количество домов с 2 спальнями, которые можно построить из 25 миллионов деревянных досок.

ii) Сколько домов с 2 спальнями можно построить из 100 миллионов деревянных досок?

53. Дорогостоящий разлив. В Австралии штрафы для судов, виновных в разливе нефти, составляют примерно 1,75 млн австралийских долларов, что эквивалентно примерно 1,64 млн долларов США. После того, как нефтяной танкер наскочил на коралловый риф, австралийские власти рассматривают возможность увеличения штрафа до 10 миллионов австралийских долларов. Каким будет новый штраф в долларах США? Округлите ответ до ближайшей сотой доли миллиона долларов. Associated Press-Times-Standard 13.04.10 Корабль, выливший нефть на Большой Барьерный риф, удален.

Ответы

1. $\frac{9}{7} = \frac{27}{21}$ пропорция

3. $\frac{7}{6} = \frac {28}{24}$ — пропорция

5. $\frac{6}{5} = \frac{24}{20}$ — пропорция

7. $\frac{3} {7} = \frac{6}{14}$ — пропорция

9. $\frac{5}{4} = \frac{25}{20}$ — пропорция

11. \ (\frac{3}{5} = \frac{6}{10}\) пропорция

13. 102

15. 2

17. 34

19. 44

21. 5

23. 55

900 02 25. 0

27. 180

29. 32

31. 88

33. 9

35. 6

37. 1,06 $

39. 5,10 $

41. 3,05 $

43. 5,33 $ 9 0003

45.