Прогиб свободно опертой балки — Энциклопедия по машиностроению XXL
В 12-м примере Максвелл вычисляет прогиб свободно опертой балки и дает формулу, в которой учитывается влияние поперечной силы на величину прогиба. Это делается в том предположении, что названные напряжения равномерно распределены по поперечному сечению. [c.325]Теперь используем дифференциальное уравнение линии прогибов для получения прогибов свободно опертой балки. Если балка нагружена равномерно распределенной нагрузкой интенсивностью [c.213]
Пример /. В качестве иллюстрации к методу конечных разностей рассмотрим задачу об определении прогибов свободно опертой балки, нагруженной равномерно распределенной нагрузкой д (рис. 6.19, а). Предполагается, что балка имеет постоянную жесткость при изгибе Е1 и длину 1. В данном примере балка раз- [c.
Линия прогибов свободно опертой балки прямоугольного поперечного сечения с равномерно распределенной нагрузкой была определена методами теории упругости в работе [6.14]. Было обнаружено, что для коэффициента Пуассона г=0,25 прогиб в середине пролета составляет [c.250]
Найти уравнение линии прогибов свободно опертой балки, нагруженной сосредоточенным изгибающим моментом Мо, приложенным на конце (см. рисунок). Чему равен максимальный прогиб балки [c.259]
Прогиб свободно опертой баЛки, нагруженной сосредоточенным грузом [c.128]
Определение прогиба свободно опертой балки графоаналитическим методом [c.137]
Представим себе свободно опертую балку, нагруженную несколькими сосредоточенными грузами. Масса последних т,- различна (фиг. 28). Пусть требуется приближенно определить низшую собственную частоту колебаний 03i. Предположим, что при первой форме колебаний кривая прогибов будет такой же, как и кривая прогибов при статическом действии сосредоточенного груза массы т,.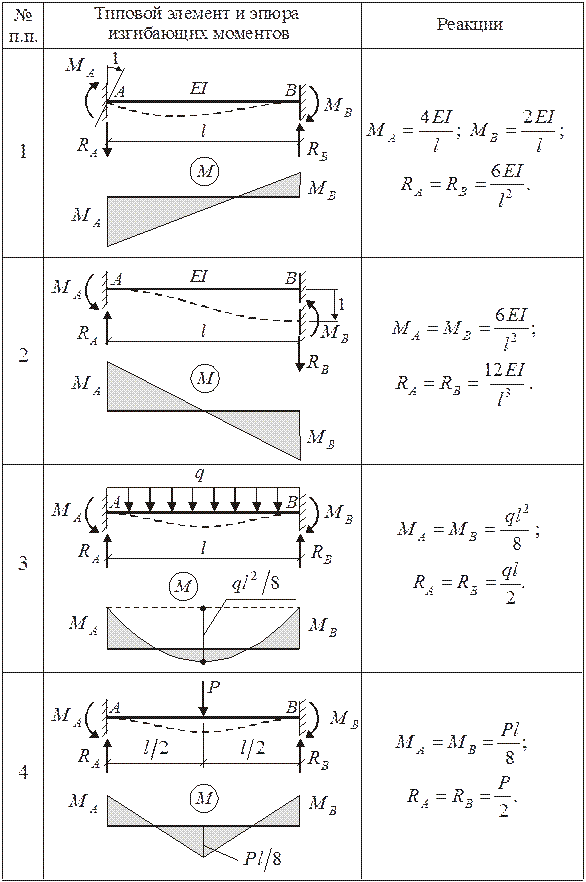
Для определения прогиба балки можно пользоваться обычными формулами, выведенными для изотропного материала. Для балок, нагруженных длительное время, необходимо вместо кратковременного модуля упругости подставлять в формулы значение долговременного модуля упругости. Ввиду очень низкого модуля упругости при сдвиге G по сравнению с Е необходимо в ответственных случаях учитывать также влияния напряжения сдвига на величину прогиба. Например, для свободно опертой балки при сплошной равномерной нагрузке имеем
Пример 1. Найти прогиб призматической свободно опертой балки жесткостью на изгиб EJ, загруженной равномерно распределенной нагрузкой интенсивностью q.
[c.48]Метод наложения. Решения для случая малых прогибов свободно опертых по концам балок, подобные обсужденным выше, можно распространить и аа другие виды условий на концах, наложив на них решения для показанной на рис. 2.12 балки с нулевой поперечной нагрузкой вдоль длины и нагруженной на концах X = 0 и X — I изгибающими моментами Mt и Мг ж поперечными силами Fai — F = Шг —Для этого случая прогиб w и углы поворотов концевых сечений 6i и 02, как известно, равны [c.90]
Консольная балка длиной I, нагруженная на свободном конце сосредоточенной силой Р, а на другом конце жестко заделанная с отсутствием сдвигов по шву (рис. 64, а), эквивалентна половине шарнирно опертой балки, имеющей пролет 21 и загруженной в середине пролета силой — 2Р (рис. 64, б). При этом прогибы консольной балки 4/ связаны с прогибами шарнирно опертой балки зависимостью [c.129]
На рис. 3.23 показаны графики зависимости между нагрузкой и прогибом посередине пролета, полученные для свободно опертой балки длиной 14 дюймов, шириной 0,95 дюйма и высотой 0,375 дюйма, с расстоянием между опорами 13 дюймов.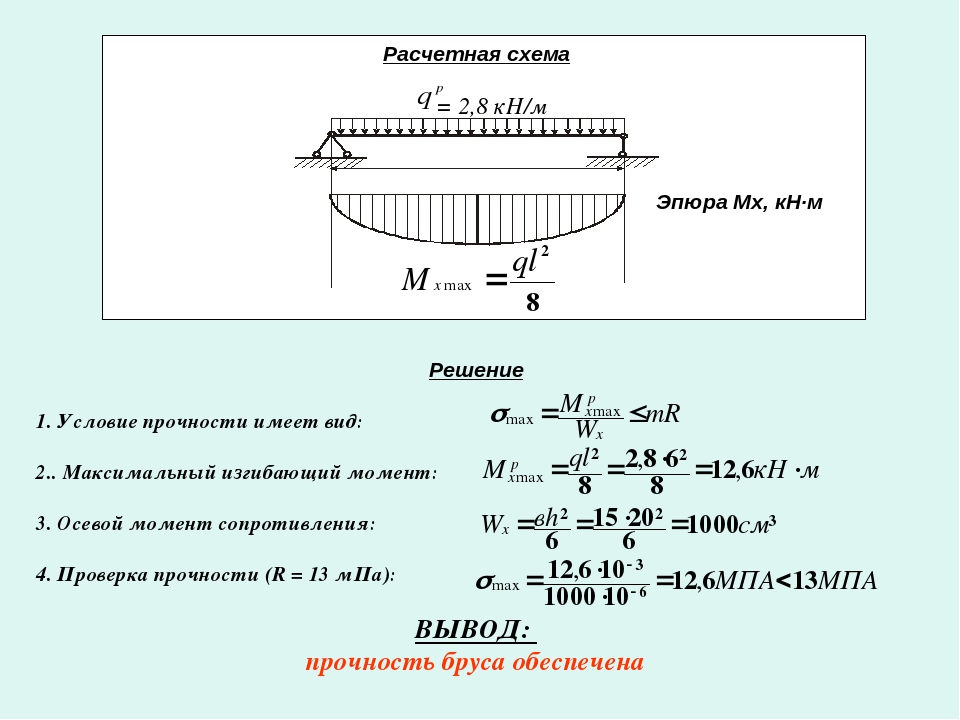
[c.285]
Чтобы перейти к формуле для прогиба балки с заделанными концами, он рассматривает бесконечно длинный брус, загруженный, как показано на рис. 50, а. Выделив участок получающейся при этом волнообразной изогнутой оси (рис. 50,6) длиной I, он заключает, что заделка концов уменьшает прогиб в середине пролета до /4 той величины, которая получается в свободно опертой балке того же пролета.
Если оболочка длинная, то а неопределенно возрастает и второй член в скобках в выражении (т) становится малым, вследствие чего и прогиб приближается к значению (d), вычисленному для случая свободных торцов. Это указывает на то, что в случае длинной оболочки влиянием концевых опор на прогиб в середине можно пренебречь. Взяв другой крайний случай, а именно случай, когда величина а весьма мала, мы можем, разлагая тригонометрическую и гиперболическую функции в степенные ряды, показать, что заключенное в скобки выражение из уравнения (т) приближается к значению 5а /6 и что прогиб (1) приближается к значению, соответствующему равномерно нагруженной и свободно опертой балке длиной I, обладающей жесткостью при изгибе, равной D.
[c.526]
Начнем обсуждение задачи о прогибах балок с рассмотрения изображенной на рис. 6. 1, а свободно опертой балки АВ. [c.209]
Для того чтобы иным путем вывести уравнение линии прогибов равномерно нагруженной свободно опертой балки, можно в качестве исходного взять днф( ренциальное уравнение четвертого порядка (6.9с) [c.214]
На рис. 6.4 изображена консольная балка, защемленная на левом конце и несущая равномерно распределенную нагрузку интенсивностью д. Для того чтобы получить уравнение линии прогибов этой балки, можно воспользоваться тем же способом, что и в случае свободно опертой балки, т. е. решить любое из трех дифференциальных уравнений (6.9). Если начать с уравнения (6.9а) второго поряд- [c.217]
Пример 3. На свободно опертую балку А В действует сосредоточенная сила Р (рис. 6.8). Найдем угол поворота 6д линии прогибов в точке Л, прогиб о в точке приложения силы Р и максимальный прогиб балки.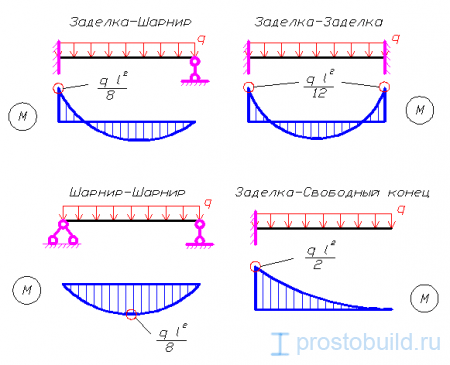
Способом наложения можно воспользоваться также и в случае распределенной нагрузки, рассматривая малый элемент распределенной нагрузки как сосредоточенную нагрузку и затем интегрируя полученное выражение по всей области нагружения. Эту процедуру можно легко попять из примера, подобного представленному на рис, 6.10, На левую половину свободно опертой балки А В действует распределенная по закону треугольника нагрузка требуется найти прогиб 6 Б середине пролета. Элемент распределенной нагрузки можно представить себе как сосредоточенную нагрузку. Прогиб в середине пролета, вызываемый сосредоточенной нагрузкой Р, приложенной на расстоянии л от левого края, равен (см, п. 5 табл. 2 в приложении С) [c.226]
Пример 1. Свободно опертая балка нагружается приложенными на концах моментами (рис. 6.11). Найдем выражения для углов поворотов 6ц и 0 , на концах балкн и для прогиба б в середине пролета. [c.227]
Пример 2.
Используя уравнение линии прогибов для свободно опертой балки с равномерно распределенной нагрузкой (см. рис. 6.2), получим выражение для энергии деформации V, накопленной в этой балке.
[c.239]
Для того чтобы показать, как вычисляются обусловленные сдвигом прогибы, возьмем в качестве первого примера свободно опертую балку с равномерно распределенной нагрузкой q (см. рис. 6.2). Выражение для кривизны этой балки будет (см. уравнение (6.44 ) [c.249]
Дифференциальное уравнение, использованное выше для определения прогибов, обусловленных сдвигом, было выведено в предположении, что каждое поперечное сечение балки может свободно искривляться, как это показано на рис. 6.25, а. Равномерно нагруженная свободно опертая балка является тем случаем, где это предположение почти удовлетворяется. В середине пролета балки может не возникнуть искажения поперечного сечения (вследствие симметрии).
Прогиб на конце консольной балки, найденный методами теории упругости, можно получить по приведенной выше формуле для свободно опертой балки с приложенной в середине пролета сосредоточенной силой (см. выражение (6.52)), заме- [c.252]
Полное решение задачи о консольной балке с вертикальной нагрузкой на конце (рис. 6.26) приводится в работах [6.28], [6.35] и [6.36], а прогиб консольной балки с равномерно распределенной нагрузкой рассматривается в статье [6.
37]. Решения для консольных балок могут быть применены и к симметрично нагруженным свободно опертым балкам, поскольку половина свободно опертой балки аналогична консольной балке. Многочисленные примеры поведения балок при больших прогибах приведены в книге [6.28],
[c.258]
Свободно опертая балка прямоугольного поперечного сечения, на которую действует равномерно распределенная нагрузка, имеет в середине пролета прогиб 5 см. Эта балка заменяется другой балкой из того же самого материала и также прямоугольного поперечного сечения, но с шириной поперечного сечения вдвое меньшей, чем у исходной балки. Какова должна быть высота новой балки по сравнению с высотой исходной балки, если новая балка при действии той же самой нагрузки прогибается только на 1,25 см
Найти угол поворота 0 и прогиб 6 в середине пролета свободно опертой балки с равномерно распределенной нагрузкой (см. рис. 6.2). [c.262]
Найти максимальный прогиб бща свободно опертой балки, нагруженной на одном конце сосредоточенным изгибающим моментом Мл (см, рисунок к задаче 6.
2.7).
[c.262]
На свободно опертую балку действует распределенная по закону треугольника нагрузка (см. рисунок к задаче 6.2.9). Найти угол поворота 0д на левой опоре и максимальный прогиб б,,,ах- [c.262]
Б росс включает в свой курс рассмотрение задач о продольных и поперечных колебаниях призматического бруса. Изучая опросы поперечных колебаний, он первый пользуется при этом аонятием инерции вращения для отдельных элементов бруса. Рассматривает он также и динамический прогиб свободно опертой балки под подвижной нагрузкой. К этой теме мы вернемся ниже (см. стр. 209). [c.183]
Чтобы определить положение нейтральной линии , как он ее называл ), при малых деформациях, И. Ходкинсон прикладывал к свободно опертым балкам, пролетом 9 футов с поперечным сечением в виде квадрата со стороной 1 дюйм, изготовленным из сосны, данцигской пихты и квебекского дуба, сосредоточенные нагрузки посередине пролета.
С помощью градуированной масштабной полосы из белой жести длиной 9 футов, достаточно гибкой, чтобы следовать кривизне выпуклой или вогнутой частей поверхности изгибаемой балки, он измерил изменение длины крайних волокон и установил, что отношение высоты зоны сжатия к высоте зоны растяжения составляло 169/190 для сосны, 17/20 для данцигской пихты и 3/4 для квебекского дуба, что в среднем дает примерно 4/5. Ходкинсон противопоставил эти результаты широко известным результатам П. Барлоу, у которого такое отношение получилось равным 3/5, критически заметив, что в опытах Барлоу измерения проводились при очень больших прогибах, перед самым разрушением балки.
[c.55]
Многие из 105 экспериментов Дюло послужили предметами отдельных дискуссий на протяжении последующего полувека не только о предполагаемом и действительном национальном превосходстве версии о железе в одной стране над версией в другой, но также относительно деталей частных испытаний (см.
, например, Ходкинсон (Hodg-kinson [1831, 1]) или Барлоу (Barlow [1837, 1])). Так, эксперимент Дюло по изгибу свободно опертой балки с поперечным сечением в форме равностороннего треугольника, нагруженной посередине пролета, в котором он не обнаружил различия в зависимости между прогибом и нагрузкой при опирании балки на вершину или на сторону треугольника, вызвал оживленную дискуссию в 20-х и 30-х гг.
[c.271]
Примечания Сен-Венана к книге Клебша также представляют большую ценность, в особенности в части, касающейся колебаний стержней и теории удара. Говоря о поперечном ударе балок, мы уже отметили важный вклад Сен-Венана в этот вопрос (стр. 217). Предполагая, что тело после удара по свободно опертой балке продолжает оставаться в соприкосновевии с ней, он трактует проблему удара как задачу колебаний балки с присоединенной к ней массой. Он исследует первые семь форм колебаний системы, вычисляет соответствующие частоты и находит формы соответ-.
твующих кривых для различных значений отношения между несом балки и весом ударяющего тела. Полагая, что балка в начальный момент находится в покое, между тем как присоединенная к ней масса обладает некоторой скоростью, Сен-Венан вычисляет амплитуду для каждой формы колебаний. Суммируя прогибы,, соответствующие этим элементарным колебаниям, он получает кривую прогибов балки для различных моментов времени t, а также находит наибольший прогиб и наибольшую кривизну )
[c.289]Рибьер ) использовал для исследования изгиба прямоугольных балок ряды Фурье. Эта работа была продолжена Л. Файлоном ), применившим общее решение к частным случаям, имеющим практическое значение. Г. Лэмб ) изучал работу бесконечной прямоугольной полосы, загруженной через равные интервалы равными сосредоточенными силами, направленными попеременно вверх и вниз. Исходя из этой схемы, он определял прогибы под сосредоточенной нагрузкой. Той же задачей занимался и Т. Карман ), получивший точную формулу для прогиба, вызываемого сосредоточенной силой в свободно опертой балке.
[c.485]
Чтобы уяснить характер подобной нагрузки, представим себе, что свободно опертая балка пролетом L, жесткостью Е1 загружена двумя моментами М, приложенными на расстоянии Дл один от другого таким образом, что эпюра моментов изображается прямоугольником со сторонами х и М, расположенным симметрично относительно середины балки. Поступая, как и прежде, т. е. полагая Дл ->0 с сохранением постоянного значения Н = М х, мы приходим к эпюре/ /, сосредоточенной в середине балки. Вводя фиктивную нагрузку в середине HIEI и применив метод Мора, мы получили бы треугольную эпюру прогибов балки с максимальной ординатой HLj EI. Подобная же эпюра прогибов получается и для нагрузки, приложенной в середине идеально гибкой струны. [c.364]
Определить кривизну к и максимальный прогиб o для свободно опертой балки (длина пролета L) прямоугольного поперечного сечения, подвергающе ся неоднородному по высоте h поперечного сечения нагреву. Предполагается, что температура на верхней поверхнсх ти балки равна Т , а на нижней Тц (T2>Ti), причем по высоте поперечного сечения балки она изменяется по линейному закону.
(Коэффициент линейного температурного расширения материала балки равен а, Е — модуль упругости.)
[c.197]
Пример 3. Свободно опертая балка с выступающей частью нагружена, как показано на рнс. 6.13, а. Найдем прогиб 6 , на конце выступающей части балки. Прогиб в точке С складывается из двух частей 1) прогиба й , вызванного поворотом оси балки вокруг опоры В, и 2) прогиба бд, обусловленного изгибогд участка ВС, работающего как консольная балка. Чтобы получить первую часть про- [c.228]
Приведем еще один пример задачи о заполняемой емкости, а именно яредпо-.ножим, что на первоначально прямую свободно опертую балку действует равномерно распределенная нагрузка интенсивностью до- Вследствие изгиба при заполнении емкости появляется дополнительная нагрузка дх зую, где зу— полный прогиб балки. Следовательно, полная нагрузка будет и дифференциальное уравнение линии прогибов примет вид [c.244]
Коэффициент ф1 является безразмерным коэффициентом усиления, который равен единице при а1=0 и неогранйченно возрастает, когда величина аЬ стремится к я. Итак, вновь находим, что существует критическая величина ниже которой балка является устойчивой и достигается состояние равновесия. Эта критическая величина задается соотношением а/.=л, или Ь=, а условие устойчивости совпадает с приведенным выше условием (6.39). В общем случае можно показать, что это условие устойчивости сохраняется для свободно опертой балки независимо от типа нагрузки, создающей начальный прогиб. [c.245]
Расчет нагрузки фальшпола — семинар
Главная — Семинары — Допустимая сосредоточенная нагрузка и распределенная нагрузка
Допустимая сосредоточенная нагрузка и допустимая распределенная нагрузка – что более важно?
Многие технические условия характеризуют прочность фальшполов, исходя из значения допустимой распределенной нагрузки (UDL). Например, она составляет 30 кН/м2. Это означает, что ящик с весом 3000 кг, равномерно распределенным по всему объему, имеющий полностью ровную поверхность, может быть установлен на такой пол, – и пол не обрушится.
Однако в действительности нагрузки не является настолько идеальными. Обычно мебель или техническое оборудование (стойки или корпуса) располагаются на металлических опорах, снабженных снизу резиновыми прокладками. Размер такой опоры, к примеру, 25х25 мм, или отпечаток круга диаметром 30 мм.
В таком случае вес тяжелого корпуса (допустим, 1500 кг), занимающего площадь один квадратный метр, будет распределяться по четырем точкам сосредоточения нагрузки. Каждая такая точка будет нести нагрузку 1500/4=375 кг. Сосредоточенная нагрузка в этом случае равна 3,75 кН на площади 625 мм2. Эта площадь точно соответствует действующему в Европе стандарту, относящемуся к сосредоточенной нагрузке. Панель ДСП толщиной 38 мм с подложкой из алюминиевой фольги не выдержит такую точечную нагрузку. Хотя в технических характеристиках указано, что пол может выдержать распределенную нагрузку в 30 кН, фальшпол не сможет выдержать достаточно тяжелый корпус на 4 ножках.
При определении параметров фальшпола необходимо принимать во внимание и распределенную, и сосредоточенную нагрузку. Кроме того, заданная сосредоточенная нагрузка связана с прогибом панели пола в миллиметрах. Величина прогиба в некоторых случаях может иметь значение в помещениях, в которых станки или оборудования располагаются на поверхности пола. Работающее оборудование, производящее детали с заданными допусками, может требовать наличия совершенно стабильного, не прогибающегося пола. Таким образом, проектирование конструкции фальшпола не является простой задачей.
В помещениях распределительных устройств нередко существуют области, в которых величина распределенной нагрузки UDL может достигать 20-30 кН/м2, в то время как в других участках помещения установлено менее тяжелое оборудование. Стандартный пол может теоретически выдержать нагрузку около 25-30 кН/м2. Эта цифра может ввести в заблуждение неопытного специалиста при выборе такого пола для помещений с тяжелым оборудованием. Ошибка заключается в том, что способность выдерживать нагрузку применима только тогда, когда все панели расположены на своих местах. Когда одна или несколько панелей сняты, существует опасность возникновения горизонтально направленной силы, действующей на установленное на поверхности пола тяжелое оборудование, в результате которой пол начнет разрушаться, начиная с участков на которых сняты панели, но затем разрушение затронет все участки помещения (как кости домино).
Существует лишь один способ избежать такой ситуации – использовать фальшполы промышленного типа в помещениях, в которых предполагается установка тяжелого оборудования. При использовании такого фальшпола все панели могут быть сняты без влияния на поперечную устойчивость пола.
Расчет балки на прогиб — онлайн калькулятор
Онлайн калькулятор по определению прогиба балки.
Для расчета вам необходимо:
1. Выбрать форму поперечного сечения
2. Выбрать материал (при использовании металлических балок — можно использовать сортамент)
3. Выбрать необходимую расчетную схему
4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)
5. Указать геометрические размеры, указанные на картинках
6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)
Из возможных поперечных сечений в данном онлайн калькуляторе выбраны само часто встречающиеся сечения: круг, труба, двутавр, швеллер, уголок, прямоугольник, квадрат и профильная труба.
В расчет входят такие материалы как дерево, сталь, железобетон, алюминий, медь и стекло.
Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка и заделка-свободный конец.
После того, как прогиб балки рассчитается – появится кнопка Подробнее, нажав на которую, можно узнать площадь сечения рассчитываемого элемента, его массу, распределенную нагрузку от собственного веса и момент инерции заданного сечения).
Зная значение длины пролета балки по СП 20.13330.2016 «Нагрузки и воздействия» для таких конструкций как балка, ферма, ригель, прогон, плита, настил покрытий и перекрытий, рассчитывается предельный прогиб, который можно сравнить с получившимся прогибом и принять решение о сечении вашей конструкции (для уменьшения прогиба в 1-ую очередь надо увеличивать высоту сечения).
При расчете балки программа уже учитывает собственный вес.
Помимо того, что Вы рассчитаете балку на прогиб, нужно ее проверить и на прочность здесь .
Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.
Последние изменения:
— Добавлен расчет предельного прогиба балки
— Добавлена возможность загружения балки сосредоточенной силой
— Исправлены графические замечания с расположением швеллера
— Добавлен расчет таврого сечения
— Исправлено положение прямоугольного сечения
— Добавлена возможность поворота швеллера
— Добавлена возможность ввода своих значений модуля упругости и плотности материала
— Исправлено отображение толщины стенки и полки швеллера
Механическая прочность
Временные нагрузки, как статические, так и динамические, которым может подвергаться потолок, ограничиваются вероятностью разрушения или деформации потолка. Деформация может быть в виде прогиба или искривления.
Вид деформации: искривление профиля.
Разрушение
Непременным требованием является исключение вероятности разрушения или обвала потолка вследствие перегрузки. Следовательно, предельно допустимая нагрузка для каждого типа потолка (см. монтажные схемы) рассчитывается и определяется с многократным запасом прочности по каждому виду поломки.
Предельно допустимая нагрузка может быть приложена только в том случае, когда потолок собран в соответствии с монтажной схемой. Другими словами, к потолку со всеми установленными панелями должны крепиться только аксессуары Ecophon.
В то время как профили и подвесы подвесной системы определяют несущую способность и прочность потолка, потолочные панели играют важную роль в обеспечении горизонтальной стабилизации профилей. Это особенно важно в тех случаях, когда профиль нагружен эксцентрично, что является причиной его искривления. В связи с этим центрическая нагрузка профиля предпочтительна во всех случаях. Например, очень важно устанавливать светильники и другие дополнительные устройства таким образом, чтобы временная нагрузка центрически передавалась на T-образные профили.
Прогиб профилей подвесной системы
Когда предельно допустимая нагрузка на потолочную систему производства компании Ecophon рассчитана правильно, потолок может только прогнуться, но ни в коем случае не разрушиться.
Подвешенный T-образный профиль подвергнут нагрузке (F), обусловившей его прогиб (f).
Нагрузка на профиль всегда вызывает его прогиб (f). Прогиб пропорционален нагрузке и в значительной мере зависит от длины пролета (L) между несущими элементами. Если удвоить нагрузку (F), прогиб увеличится вдвое. Однако прогиб станет еще больше, если пролет между двумя несущими элементами увеличить в два раза. Прогиб от сосредоточенной нагрузки, например, станет в восемь раз больше.
В представленной ниже таблице излагаются наши рекомендации относительно выбора системы подвеса в зависимости от предельно допустимой величины прилагаемой временной нагрузки. При составлении этой таблицы мы руководствовались наиболее важными стандартами, в частности, стандартами ASTM C635, BS 8290 Часть 2, DIN 18 168 и SS 81 51 13. Чрезвычайно важно, чтобы деформация потолка была ограничена пределом L/500. Когда прогиб составляет примерно L/400, деформация видна невооруженным глазом. При деформации L/500 потолок безопасен и имеет ровную поверхность.
Пример: Для пролета L=1200 мм допустимый прогиб составляет 2,4 мм.
Рекомендуемая временная нагрузка
Данные рекомендации применимы к временной нагрузке, составляющей дополнение к собственной массе потолка. Временная нагрузка может быть сосредоточенной нагрузкой (светильник, вывески и тому подобное), приложенной к подвесной системе произвольно, но с интервалом не менее 1 м. Если подвесы расположены ближе друг к другу, то допустимая временная нагрузка может быть больше той, которая указана в таблице. Вместе с тем, большие нагрузки должны быть переданы непосредственно на перекрытие.
Если фактическая временная нагрузка распределяется по площади в 0,36 м2 (600×600, 1200×300) или по большей площади, то подвесная система способна выдержать нагрузку, которая на 65% больше рекомендованной предельной временной нагрузки, указанной в таблице, но при условии, что эта нагрузка крепится непосредственно к подвесной системе. Фактическая временная нагрузка определяется, конечно же, с учетом несущей способности подвесов и креплений.
Пример: Светильник размером 600×600 мм и весом 7 кг может быть смонтирован на потолке типа «Focus», поскольку согласно таблице такой потолок способен нести нагрузку в 83 N (8,3 кг), если площадь распределения нагрузки составляет 0,36 м2 и более.
Рекомендуемая нагрузка
The above applies provided that the distance from the joint between two main runners to the nearest support point does not exceed ¼ of the allowable distance between suspensions.
Изложенное выше верно при условии, что расстояние от стыка двух профилей до ближайшей опорной точки не превышает ¼ допустимого расстояния между подвесами.
Это значит, что когда расстояние между подвесами составляет 1200 мм, точка соединения двух профилей должна находиться в пределах 300 мм от опорной точки. Изложенное выше верно при условии, что нагрузка центрически передается на T-образный профиль.
Нагрузки — словарь основных терминов
Статические нагрузки
Вес самого потолка и вес предметов, прикрепленных к потолку, например, светильников, громкоговорителей, вентиляционных решеток, вывесок и тому подобное.
Динамические нагрузки
Механическое воздействие на потолок, оказываемое, например, мячами в гимнастических залах или струей воды, при мойке под высоким давлением.
Собственная масса (г)
Вес самого потолка вместе с панелями, подвесной системой и аксессуарами. Это всегда статическая нагрузка.
Подвешенный T-образный профиль с различными грузами.
Временные нагрузки
Все нагрузки, прилагаемые к потолку. Временные нагрузки могут быть статическими или динамическими, и включают в себя:
Равномерно распределенную нагрузку (q) от осветительной арматуры, вывесок, от разности давлений, от воздействия в процессе мойки и т. п.
Сосредоточенную нагрузку (F) от осветительной арматуры, вывесок, от ударных воздействий, от воздействия в процессе мойки и т. п.
Нормальное усилие (N) усилие, которое вызывается каким-либо воздействием, трением, мойкой или в процессе монтажных работ — динамическая нагрузка.
Проектная нагрузка
Собственная масса подвесного потолка и фактические временные нагрузки, на которые рассчитан потолок.
Выбранная подвесная система (подвесы, прямые крепежные кронштейны, шурупы и тому подобное) должны нести проектную нагрузку (собственная масса подвесного потолка и фактическая временная нагрузка) с трехкратным запасом прочности. Это значит, что подвесы и крепления, используемые для поддержки потолка, должны выдерживать нагрузку, которая в три раза больше той, которая может быть приложена к ним. Этому требованию удовлетворяют все регулируемые подвесы и соединительные кронштейны системы Connect при том условии, что монтаж потолка выполняется в соответствии с монтажными схемами компании Ecophon, а максимальная временная нагрузка на потолок соответствует рекомендованной.
Несущая способность (предельно допустимая нагрузка) подвесов и креплений системы Connect указана в разделе «Несущая подвесная система Connect и аксессуары». Значения предельно допустимой временной нагрузки и минимальной несущей способности подвесов и креплений для каждого типа потолка приводятся в соответствующей монтажной схеме.
Пример: Для потолка Ecophon Master A предельно допустимая временная нагрузка составляет 40 N (4 кг). Минимальная несущая способность подвесов и креплений должна быть не меньше 160 N (16 кг).
Основное правило заключается в том, что нагрузка не должна прилагаться к звукопоглощающим материалам. Светильники, вентиляционные устройства и тому подобное должны крепиться к подвесной системе или непосредственно к перекрытию.
Нагрузка на панель должна равномерно распределяться по ее краям.
Вместе с тем звукопоглощающие панели Ecophon размером 600×600 мм и 1200×600 мм способны нести небольшую нагрузку, например, галогенные светильники. Звукопоглощающие панели толщиной 20 мм и больше, например, панели серии Focus или Master, способны нести нагрузку максимум 500 г, если диаметр отверстия не превышает 100 мм. Допустимая нагрузка для панелей толщиной 15 мм, например, для панели Gedina составляет 300 г.
Панели шириной больше 600 мм и длиной больше 1200 мм не должны подвергаться нагрузке.
Ограничения по несущей способности панелей Master Solo S учитывают возможное наличие отверстий для светильников, прикрепленных грузов. В таблице ниже указаны данные по ограничению нагрузки; для получения наглядного представления см. монтажную схему IG 222.
Master Solo S | 1200 x 1200 | 2400 x 1200 | ||||
Тип монтажа | С нагрузкой | Без нагрузки
| С нагрузкой | Без нагрузки | ||
Макс. длина окружности (мм) | 600 x 600 | 600 x 600 | 600 x 600 | 1700 x 600 | ||
Миним. длина окружности (мм): | ||||||
Диаметр отверстия или короткая сторона ≤ 10 мм | 50 | — | ||||
Диаметр отверстия или короткая сторона 11-300 mm | 150 | 150 | ||||
Диаметр отверстия или короткая сторона 301-600 mm |
| 400 | 150 | |||
Макс. нагрузка на отверстие*(кг) Master Solo S: | ||||||
Размер отверстия ≤ 100 x 100 мм | 0,5 (0,25) | — | ||||
Размер отверстия > 100 x 100 мм |
| 2,0 (-) | — | |||
Макс. общая нагрузка*(кг) Master Solo S |
| 4,5(1,0) | — | |||
*Цифры в скобках — при отклонении угла установки ≤ 30°.
Величина динамической нагрузки является показателем способности материала или изделия выдерживать переменное во времени воздействие, например, трение или ударное воздействие.
Динамическая временная нагрузка может проявляться в виде разового удара мячом или палкой. Она может быть также периодической, например, в случае, когда какой-нибудь предмет ударяется о поверхность объекта в течение некоторого времени. Другим примером динамической нагрузки является воздействие разности давлений, которое может возникнуть в помещении при открывании-закрывании дверей или окон, или, при включении-выключении системы вентиляции.
The test method and evaluation scheme for ball impact resistance used by Ecophon is described in Annex D of the European standard EN 13964:2004 Suspended ceilings – requirements and test methods.
Метод тестирования и способ оценки ударостойкости, используемый компанией Ecophon, описан в Приложении D Европейского стандарта EN 13964:2004 Suspended ceilings – requirements and test methods. Этот метод базируется на старом немецком стандарте DIN 18 032 часть 3. Однако, EN 13964 допускает классификацию по трем классам (1A, 2A и 3A). Классификация зависит от выбора скорости мяча.Испытанию подвергается полностью собранная система подвесного потолка (включая подвесы, профили, фиксаторы, а также панели). Она обстреливается мячом из специального аппарата. При таком испытании система должна быть подвергнута 36 ударам под тремя различными углами. Метод также подходит для тестирования систем стеновых панелей.
Поперечный изгиб | Все о ремонте и строительстве
Поперечный изгиб получается, когда сила действует на брус по направлению, поперечному к его длине.
Рассмотрим два варианта поперечного изгиба: первый, балка лежит на двух опорах, причем груз расположен на балке в пределах между опорами и второй, балка прочно заделана одним концом в стену, а груз находится на свободном конце балки.
Прежде всего выясним, какое влияние на изгиб оказывает место приложения силы. Если мы положим доску на две опоры и будем по ней двигаться от опоры к середине, то прогиб доски будет непрерывно возрастать по мере нашего приближения к середине. Из этого опыта можно сделать заключение, что чем ближе к середине будет приложена сила, тем больше будет прогиб балки. То же самое явление мы будем наблюдать при опыте с балкой, заделанной одним концом в стену, при перемещении груза от стены к концу балки.
В зданиях и сооружениях на балку могут действовать одновременно несколько сил, и притом они могут перемещаться, как, например, автомобили на мосту. Определить влияние этих сил на балку не так просто, как это мы делаем при растяжении или сжатии. Зависимость получается не простая, и человеку без высшего технического образования заниматься этим вопросом сложно.
Как уже было сказано, сила может быть приложена в любом месте балки. Такая сила, имеющая одну точку приложения, называется сосредоточенной.
Если сила равномерно распределена по всей длине балки, то такая сила называется равномерно-распределенной.
Например, на балке в одном месте находится мешок с песком весом 100 кг, это будет сосредоточенная нагрузка (сила), а если тот же груз равномерно рассыпать по всей длине балки, то это будет равномерно-распределенная нагрузка. И в том и в другом случае величина силы одинакова 100 кг, но способ распределения различен. В зависимости от этого и напряжение в балке будет различное, а именно, при сосредоточенной по середине балки нагрузке напряжение будет в 2 раза больше, чем при нагрузке, равномерно-распределенной.
Нам уже известно, что, чем больше сосредоточенный груз будет приближаться к опоре, тем меньше будет прогиб балки, и тем меньше напряжение в материале. Следовательно, если балка будет иметь достаточную прочность при расположении какого-либо груза по середине, то она, безусловно, выдержит этот груз, если он будет находиться в каком угодно месте балки.
Далее, очень интересно выяснить, какие получаются напряжения в нагруженной балке, и как они распределены. Произведем такой опыт: возьмем брус и сделаем на нем пропил в верхней стороне, а затем его нагрузим. Мы увидим, что обе стороны пропила сблизятся вплотную друг к другу. Из этого опыта мы заключаем, что в верхней части бруса, под влиянием нагрузки, происходит сжатие.
Если мы теперь сделаем пропил в нижней стороне бруса и опять его нагрузим, то увидим, что края пропила разошлись и пропил в нижней части сделался очень широким. Из этого мы заключаем, что в нижней части бруса, под влиянием нагрузки, происходит растяжение. Итак, следовательно, в верхней части бруса или балки под влиянием нагрузки происходит сжатие, а в нижней — растяжение. Но так как это происходит в одной и той же балке одновременно, то очевидно, что где-то есть место, в котором растяжение переходит в сжатие, и наоборот. Такое место, действительно, имеется в каждой балке. Эту линию, или вернее плоскость раздела сжатия от растяжения, называют нейтральной осью. В деревянной балке прямоугольного сечения она находится приблизительно посредине высоты.
Так как мы теперь знаем распределение усилий в брусе, находящемся под грузом, то нам будет вполне понятно, как иногда выпрямляют сильно погнувшуюся балку. Для этого ее подпирают и в верхней части балки делают пропил с забиванием в него клина с одновременным поддомкрачиванием снизу. Так как в целой балке, находящейся под грузом, сила растяжения в нижней части равна силе сжатия в верхней, то при забивке клиньев, очевидно, сила сжатия в верхней части балки увеличится, и балка искривится в обратную сторону, т. е. выпрямится.
Далее, не трудно убедиться, что при изгибе балки в ней появляются скалывающие усилия. Для этого опыта возьмем два одинаковой длины бруса и положим один брус на другой. В ненагруженном состоянии торцы их будут совпадать, как показано на рис. 4а. Если теперь мы их нагрузим, то произойдет прогиб брусьев, и торцы их будут расположены так, как показано на рис. 4б. Мы видим, что торцы брусьев не совпадают и нижняя кромка торца верхнего бруса выступает за линию верхней кромки торца нижнего бруса. Очевидно, что по плоскости соприкосновения брусьев произошел сдвиг, в результате которого и появилось выдвижение концов одного бруса над другим. Если бы брус был из одного куска дерева, то очевидно, что никаких изменений на концах бруса мы не заметили бы, но несомненно, что в этом брусе в нейтральной плоскости были бы скалывающие усилия, и если бы прочность дерева была недостаточна, то по концам бруса обнаружилось бы расслоение.
Рис. 4. Изгиб составной балкиПосле этого опыта становится вполне понятным устройство составных балок на шпонках. На рис. 5 показана такая балка, состоящая из трех брусков, между которыми врублены шпонки. Очевидно, что конец одной балки не может сдвинуться относительно другой, так как этому перемещению препятствуют шпонки. Чем прочнее связь между шпонками и балками, тем жестче балка.
Продолжим предыдущий опыт. Если мы через оба бруса проведем на равном расстоянии черты карандашом, как показано на рис. 4а, и затем нагрузим брусья, то увидим, что средняя черта на обоих брусьях останется без изменения, а все остальные сместятся, как показано на рис. 4б. При этом расхождение черточек будет тем больше, чем дальше они отстоят от середины. Из этого опыта мы заключаем, что наибольшая скалывающая сила находится у концов балок. Вот почему в балках на шпонках следует шпонки ставить чаще к концам и реже к середине.
Рис. 5. Составная балка с врубленными шпонкамиИтак, все проделанные опыты убеждают нас в том, что в нагруженной балке возникают различные напряжения.
Будем опять учиться на опыте. Все знают, что если положить доску плашмя и нагрузить ее, то она заметно прогнется, а если ту же доску поставить на ребро и нагрузить ее той же нагрузкой, то прогиб почти не будет заметен. Этот опыт убеждает нас в том, что величина изгиба зависит, главным образом, от высоты балки, а не от ширины. Если взять два квадратных бруса и сплотить их шпонками и болтами, так чтобы получилась одна балка высотою в два квадрата, то такая балка сможет выдержать груз в два раза больше, чем обе эти балки, положенные рядом. При трех балках груз может быть в 4,5 раза больше и т. д.
Из этих опытов нам ясно, что гораздо выгоднее увеличивать высоту балки, чем ее ширину, но, конечно, до известного предела, так как при очень высокой и тонкой балке она сможет изогнуться в сторону.
Так как балки вытесываются или выпиливаются из бревен, то является вопрос, какое же отношение должно быть между высотой и шириной балки, чтобы получить балку наибольшей прочности. Строительная механика дает точный ответ на этот вопрос, а именно, в высоте должно быть 7 каких-либо мер, а в ширине таких же точно мер только 5. Практически это делается, следующим образом. На торце круглого бревна (рис.6) проводят, через центр линию и делят ее на три равные части. Затем из этих точек по наугольнику проводят в противоположные стороны линии до края торца. Наконец, эти крайние точки соединяют с концами линии, проведенной через центр торца, и у нас получится прямоугольник, у которого длинная сторона будет иметь 7 мер, а короткая таких же 5. По этим линиям производится опиловка или обтеска бревна и получается самая прочная балка прямоугольного сечения, какую только можно сделать из данного бревна.
Рис. 6. Балка наибольшей прочности, которую можно вырубить из бревнаИнтересно отметить, что, круглое бревно менее прочно в отношении изгиба, чем тоже бревно со слегка стесанными горбылями с верхней и нижней стороны.
На основании всего вышеизложенного можно сделать заключение, что точное определение размеров балок зависит от многих обстоятельств: от числа и местоположения грузов, от рода нагрузки, от способа ее распределения (сплошная или сосредоточенная), от формы балки, ее длины и т. д. Учет всех этих обстоятельств довольно сложен и плотнику-практику он недоступен.
При определении размеров балок, необходимо, кроме прочности, иметь в виду также и прогиб балок. Иногда на постройке плотники высказывают недоумение, почему ставится такая толстая балка, можно было бы взять и потоньше. Совершенно верно, и более тонкая балка выдержит тот груз, который на ней будет расположен, но когда впоследствии по полу на тонких балках будут ходить или танцевать, то такой пол будет гнуться, как качели. Для избегания очень неприятной зыбкости пола, балки кладут толще, чем это требуется по условиям прочности. В жилых домах прогиб балок допускается не свыше 1/250 пролета. Если, например, пролет 9 м, то есть 900 см, то наибольший прогиб должен быть не больше 900 : 250, что составит З,6 см.
В заключение следует упомянуть об одном практическом правиле для определения высоты балок в жилых зданиях, а именно: высота балки должна быть не менее 1/24 длины балки. Например, если длина балки 8 м (800 см), то высота должна быть 800 : 24 = 33 см.
Для практических целей, помимо всего вышеизложенного, следует ознакомиться с прилагаемыми таблицами, которые дадут возможность, без всяких затруднений легко и быстро определять нужный размер балки для случая равномерно-распределенной нагрузки. В этих таблицах указаны допускаемые нагрузки на балки прямоугольного и круглого сечения, для различных размеров балок и для разных пролетов.
Пример1. В помещении с пролетом 8 м имеется нагрузка весом 2,5 т (2500 кг). Нужно подобрать балки для этой нагрузки.В таблице прямоугольных балок рассматриваем столбец с пролетом 8 м. Нагрузку в 2500 кг может выдержать балка сечением 31×22 см или две балки 26×18,5, или три балки 24,5×17,5 см и т.д. Балки нужно распределить с соответствующим шагом учитывая, что крайние балки несут половину нагрузки от балок, расположенных посредине.Для груза, расположенного сосредоточенно по середине пролета, величина его должна быть в два раза меньше, чем указано в таблице.
Пример 2. Для прямоугольной балки 7 к 5 из 32-сантиметрового бревна при пролете в 6 м можно допустить равномерно-распределенную нагрузку в 2632 кг (см. таблицу). Если груз будет сосредоточен посредине балки, то можно допустить нагрузку лишь вдвое меньшую, а именно 2632 : 2 = 1316 кг.Пример 3. Какого размера балка из бревна, отесанного или опиленного на два канта, выдержит сосредоточенную посредине нагрузку в 1,6 тонны (1600 кг), при пролете в 8 м?В задании дана сосредоточенная сила, мы знаем, что эта балка должна выдерживать в два раза большую равномерно-распределенную нагрузку, то есть 1600×2=3200 кг. Смотрим в таблице для лафета столбец для пролета в 8 м. Ближайшая к 3200 цифра в таблице 3411 каковой цифре соответствует бревно диаметром в 34 см.
Если балка заделана прочно одним концом в стену, то она может выдержать груз, сосредоточенный на ее свободном конце, в 8 раз меньший, чем та же балка, лежащая на двух опорах и несущая равномерно-распределенную нагрузку.
Пример 4. Какого диаметра бревно, отесанное или опиленное на четыре канта, прочно заделанное одним концом в стену и имеющее свободный конец в 3 м, может выдержать сосредоточенный груз в 800 кг, прикрепленный к ее свободному концу?Если бы эта балка лежала, на двух опорах, то она могла бы выдержать груз в 8 раз больший, то есть 800 × 8 = 6400 кг. Смотрим в таблице для обзольного бруса столбец для пролета в 3 м и находим две ближайшие цифры 5644 кг и 6948 кг. Этим цифрам соответствуют бревна в 30 и 32 см. Можно взять бревно в 31 см.Если на балке, заделанной одним концом в стену, нагрузка распределена равномерно, то такая балка может выдержать нагрузку в 4 раза меньшую, чем та же балка, лежащая на двух опорах.
Пример 5. Какой груз может выдержать балка прямоугольного сечения, заделанная одним концом в стену, со свободным концом длиною в 4 м, нагруженная равномерно-распределенной нагрузкой общим весом в 600 кг?Если бы эта балка лежала на двух опорах, то она могла бы выдержать груз в 4 раза больший, то есть 600×4=2400 кг. Смотрим в таблице для балки 7 к 5 столбец для пролета в 4 м. Ближайшая цифра 2746, каковой цифре соответствует бревно в 28 см, или брус в 23×16 см.При расчетах балок может встретиться такой вопрос какое давление испытывают опоры (стены или колонны) от лежащей на них балки с грузом?
Если груз распределен равномерно по всей балке или сосредоточен посредине, то обе опоры несут одинаковую нагрузку.
Если груз расположен ближе к одной опоре, то эта опора несет больший груз, чем другая. Чтобы узнать какой именно, — нужно величину груза умножить на расстояние до другой опоры и разделить на пролет.
Пример 6. На балке, длиною в 4 м, расположен груз в 100 кг, в расстоянии 1 м от левой опоры и, следовательно, в расстоянии 3 м от правой. Требуется найти нагрузку на левую опору.Умножаем 100 на 3 и полученное число делим на 4, получим 75. Следовательно, левая опора испытывает давление в 75, а правая оставшуюся часть нагрузки, то есть 100-75=25 кг.Если на балке находятся несколько грузов, то расчет нужно сделать для каждого груза отдельно, и затем полученные нагрузки на одну опору сложить.
Таблица нагрузок сварного настила SPПояснения к таблице нагрузок сварного настила SP
Таблица нагрузок сварного настила SP
ЦВЕТОМ выделен настил, прогиб которого не превышает 1/200 от пролета, при указанных величинах нагрузок.
Таблица нагрузок сварного настила SP
ЦВЕТОМ выделен настил, прогиб которого не превышает 1/200 от пролета, при указанных величинах нагрузок.
ВНИМАНИЕ: нагрузочные характеристики остальных типов настила, указанных в ПРОИЗВОДСТВЕННОЙ ПРОГРАМME, могут быть представлены по запросу Заказчика. |
||||||||||||||||||||||
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Простая балка — сосредоточенная нагрузка в любой точке
Статьи, связанные со структурой
Простая балка — сосредоточенная нагрузка в любой точке формулы
Где:
\ (\ large {\ Delta} \) = прогиб или деформация
\ (\ large {a, b} \) = расстояние до точечной нагрузки
\ (\ large {x} \) = горизонтальное расстояние от точки реакции до точки на балке
\ (\ large {M} \) = максимальный изгибающий момент
\ (\ large {V} \) = максимальная сила сдвига
\ (\ large {I} \) = момент инерции
\ (\ large {\ lambda} \) (греческий символ лямбда) = модуль упругости
\ (\ large {R} \) = реактивная нагрузка в точке опоры
\ (\ large {L} \) = длина пролета гибочного элемента
\ (\ large {P} \) = общая сосредоточенная нагрузка
% PDF-1.3 % 790 0 obj> эндобдж xref 790 87 0000000016 00000 н. 0000003638 00000 н. 0000002077 00000 н. 0000003742 00000 н. 0000003768 00000 н. 0000003814 00000 н. 0000004206 00000 н. 0000004286 00000 п. 0000004366 00000 н. 0000004446 00000 н. 0000004526 00000 н. 0000004606 00000 н. 0000004686 00000 н. 0000004766 00000 н. 0000004846 00000 н. 0000004926 00000 н. 0000005006 00000 н. 0000005086 00000 н. 0000005166 00000 н. 0000005246 00000 н. 0000005326 00000 н. 0000005405 00000 н. 0000005484 00000 н. 0000005563 00000 н. 0000005642 00000 н. 0000005721 00000 н. 0000005800 00000 н. 0000005879 00000 п. 0000005958 00000 н. 0000006037 00000 н. 0000006116 00000 п. 0000006195 00000 н. 0000006274 00000 н. 0000006353 00000 п. 0000006432 00000 н. 0000006511 00000 н. 0000006590 00000 н. 0000006669 00000 н. 0000006748 00000 н. 0000006827 00000 н. 0000006906 00000 н. 0000006985 00000 н. 0000007064 00000 н. 0000007143 00000 н. 0000007222 00000 п. 0000007301 00000 н. 0000007380 00000 н. 0000007459 00000 н. 0000007538 00000 п. 0000007616 00000 н. 0000007694 00000 н. 0000007772 00000 н. 0000008144 00000 н. 0000012271 00000 п. 0000012850 00000 п. 0000013048 00000 п. 0000013549 00000 п. 0000019289 00000 п. 0000019998 00000 п. 0000020324 00000 п. 0000020906 00000 н. 0000027647 00000 н. 0000028472 00000 п. 0000028889 00000 п. 0000028957 00000 п. 0000029405 00000 п. 0000030554 00000 п. 0000030916 00000 п. 0000031438 00000 п. 0000032252 00000 п. 0000032281 00000 п. 0000032366 00000 п. 0000032798 00000 п. 0000033385 00000 п. 0000034526 00000 п. 0000034622 00000 п. 0000034714 00000 п. 0000035389 00000 п. 0000036044 00000 п. 0000036678 00000 п. 0000036774 00000 п. 0000037386 00000 п. 0000038153 00000 п. 0000038785 00000 п. 0000039357 00000 п. 0000039385 00000 п. 0000003444 00000 н. трейлер ] >> startxref 0 %% EOF 792 0 obj> поток xb«b`tg`
точек по сравнению с равномерно распределенными нагрузками: понять разницу
При размещении грузов одинакового веса на стеллаже для хранения важно помнить, что не все поддоны или грузы созданы одинаковыми.Некоторые поддоны имеют несколько досок или стрингеров, охватывающих нижнюю поверхность; у других по ноге в каждом углу. Грузы необычной формы, такие как рулоны стали или рулоны бумаги, также могут создавать проблемы. Конструкция днища поддона в значительной степени определяет, равномерно ли распределяется нагрузка или лежит на определенных точках. Это означает, что распределение веса груза может быть разным, в зависимости от типа поддона под ним или конкретного типа продукта, хранящегося на стеллажной системе.
При размещении в стальных стеллажах для хранения равномерно распределенная нагрузка — это нагрузка, вес которой равномерно распределяется по всей поверхности балок или настила стеллажа. Точечная нагрузка — это нагрузка, вес которой значительно сконцентрирован в одном (или нескольких) местах балок или настилов стеллажа. Например, стальной рулон, хранящийся непосредственно на балке стеллажа, может создавать очень концентрированную точечную нагрузку; даже если стальной рулон весит столько же, сколько груз на поддоне, грузовая балка, вероятно, будет более тяжелой.(Существует также третий тип распределения нагрузки: линейная нагрузка, у которой есть только две или три доски на дне, что создает более равномерное распределение веса, чем точечная нагрузка, но менее равномерное, чем равномерно распределенная нагрузка).
Итак, что это означает для безопасности стойки? Размещение точечной нагрузки в стальном стеллаже для хранения, который был разработан исключительно для поддержки равномерно распределенных нагрузок, может вызвать одну из двух ситуаций: чрезмерный прогиб и / или отказ балки или настила.
Прогиб балки: Когда инженер-проектировщик стеллажей определяет спецификации для опорной балки поддонов, максимальная величина допустимого прогиба — или изгиба — включается в расчеты, как указано в Разделе 5.3 ANSI Mh26.1-2012 RMI: Спецификация по проектированию, испытанию и использованию промышленных стальных стеллажей для хранения. Предел отклонения равен длине балки по горизонтали, деленной на 180 (т. Е. L / 180). Риск безопасности возникает, если точечная нагрузка помещается на балку, которая рассчитана только на то, чтобы выдерживать вес равномерно распределенных нагрузок.Это связано с тем, что концентрация может привести к отклонению луча за пределы максимально допустимой величины, что приведет к возможному отказу и потенциально может привести к падению груза.
Отказ настила: Обычно настил изготавливается из сварной проволоки с армирующими швеллерами или гофрированной стали. Настил часто помещается на балки стеллажа для поддонов, чтобы перекрыть расстояние между ними. Хотя это обеспечивает дополнительную поддержку груза поддона, если настил не был должным образом спроектирован для восприятия точечных нагрузок, как указано в стандарте ANSI Mh36 RMI.2-2017: Проектирование, изготовление, испытание и использование сварного настила стеллажа из проволоки — сосредоточенная точечная нагрузка может привести к его выходу из строя и падению нагрузки.
Следовательно, чтобы обеспечить наиболее безопасную конструкцию стеллажа для поддонов, квалифицированный инженер-конструктор должен быть проинформирован о типах грузов и поддонах, на которые они будут помещены для хранения. В приложениях, где несколько типов поддонов могут храниться в одной стеллажной конструкции, система должна быть спроектирована так, чтобы выдерживать точечные нагрузки, что является наиболее консервативным и самым безопасным подходом.
Есть еще вопросы о стальных стеллажах? Получите ответы из списка часто задаваемых вопросов RMI.
Прогибы балки с простой опорой: артикул
Изгибы и уклоны балки с простой опорой
На главную> Ресурсы> Прогибы и уклоны балки с простой опоройСодержание
Введение
Балка с простой опорой — одна из самых простых конструкций.У него всего две опоры, по одной с каждой стороны. Штифтовая опора и роликовая опора. В этой конфигурации балке разрешено вращаться на двух концах, но любое вертикальное движение в ней запрещено. Благодаря роликовой опоре, она также может расширяться или сжиматься в осевом направлении, хотя свободному горизонтальному перемещению препятствует другая опора. {3/2}} {27 EIL} &, \ textrm {if:} a> L / 2 \ end {выровнено} \ право.4} {3375 EI}
где, C = \ sqrt {15- \ sqrt {120}} \ left (\ sqrt {15} + \ sqrt {50} \ right) \ приблизительно 22.01237
Classical теория балок
Пытаясь оценить деформации балки при поперечной нагрузке, существует несколько теорий балок. Наиболее широко используется теория пучка Эйлера-Бернулли , также называемая классической теорией пучка . Два основных предположения теории:
- деформации остаются небольшими
- поперечные сечения балки при деформации остаются перпендикулярными отклоненной оси (так называемая упругая кривая).
Второе предположение практически справедливо для балок из однородного и изотропного материала, с симметричным поперечным сечением и длиной, значительно превышающей размеры их поперечного сечения (10 и более раз — это общее практическое правило). Фактически, если балка значительно деформируется в любой другой форме, кроме симметричного изгиба, то предположение о нормальном и плоском поперечном сечении не выполняется. Примеры таких случаев включают короткие балки, балки с поперечным сечением многослойного типа или узкие поперечные сечения или открытые несимметричные поперечные сечения.2} = {M (x) \ over EI}
где E — модуль упругости, I — момент инерции поперечного сечения.
Обнаружение прогибов и уклонов
В зависимости от материала балка может иметь большие прогибы без разрушения, даже оставаясь упругой. Таким образом, он может быть защищен от поломки, но есть и другие причины, по которым чрезмерные прогибы нежелательны. К ним относятся комфорт пользователей, безопасность движения (для моста), повреждение неструктурных элементов и т. Д. Таким образом, определение прогибов является важным шагом в статическом анализе конструкции.2} = {M (x) \ over EI}, может использоваться как средство для определения прогибов и уклонов поперек балки. Если мы проинтегрируем один раз, мы найдем первую производную прогиба, которая представляет наклон балки:
\ varphi (x) = \ frac {dy} {dx} = {1 \ over EI} \ int M (x) \ dx
Еще раз интегрировав прогибы:
y (x) = \ int \ varphi (x) \ dx
Метод прямого интегрирования эффективен только для простых случаев. Другие методики расчета прогибов включают:
- Метод площади моментов
- Метод сопряженных балок
- Метод Кастильяно
- Принцип виртуальной работы
Примеры
В этом разделе будут приведены некоторые примеры для оценки прогибов балок с простой опорой. и уклоны, используя метод прямого интегрирования.Этот метод требует предварительного расчета диаграммы изгибающего момента. В контексте примеров это будет дано, однако, если вам нужно заняться и этой темой, пожалуйста, ознакомьтесь с нашей соответствующей статьей здесь.
Шаги методологии повторяются здесь, как они были описаны ранее в тексте.
Пример 1: прогибы свободно опертой балки с равномерно распределенной нагрузкой (udf), используя прямое интегрирование
- Найдите прогибы свободно опертой балки с равномерно распределенной нагрузкой как функцию расстояния x от конца A.4 \ over12} + c x + k \ right)
Необходимо определить две константы. 3 \ вправо )
2.4 \ over 384EI}
Физический смысл отрицательного знака заключается в том, что максимальное отклонение происходит в направлении вниз.
Пример 2
Найдите предельное отклонение свободно опертой балки при равномерно распределенной нагрузке, которое показано на схеме. Его поперечное сечение может быть A или B, как показано на рисунке ниже. Оба сечения имеют одинаковые размеры, но различаются ориентацией оси изгиба (нейтральная ось показана красной пунктирной линией).4}} = 0,035 \ \ mathrm {m}
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
Балка с простой опорой и точечной нагрузкой
Балка с простой опорой и точечной нагрузкой Калькулятор для определения сил, моментов, напряжений, прогибов и уклонов балки с простой опорой.
Примечание. Используйте точку «.» как десятичный разделитель.
Примечание *: P имеет положительное значение в направлении вниз, как показано на рисунке, и отрицательное значение. в восходящем направлении.
Примечание **: Второй момент расчета площади несущих балок см. На странице » Калькуляторы сечений ».
РЕЗУЛЬТАТЫ Параметр Стоимость Сила реакции 1 [R 1 ] — NkNlbf Сила реакции 2 [R 2 ] — Поперечное поперечное усилие на расстоянии x [V x ] — Максимальное поперечное усилие сдвига [V max ] — Момент на расстоянии x [M x ] — Н * мкН * млбс * дюйм фунт-сила * фут Максимальный момент [M max ] — Наклон 1 [θ 1 ] — радианград. arcminarcsec Наклон 2 [θ 2 ] — Наклон на расстоянии x [θ x ] — Максимальный наклон [θ макс. ] — Прогиб на расстоянии x [y x ] — ммминчфт Максимальный прогиб [y max ] — Напряжение изгиба на расстоянии x [σ x ] — МПапсикси Максимальное напряжение изгиба [σ макс ] — Примечание *: R 1 и R 2 являются вертикальными концевыми реакциями слева и справа, соответственно, и положительны вверх.Сдвиговые силы и прогибы положительны в направлении вверх и отрицательны. в нисходящем направлении. Все моменты положительны при создании сжатия на верхней части поперечины балки. раздел. Все наклоны положительные, когда вверх и вправо.
Примечание. Напряжения — это положительные числа, и это величины напряжений в луч. Он не делает различий между растяжением и сжатием конструкции. луч.Это различие зависит от того, с какой стороны нейтральной плоскости луча вход соответствует.
Наклон
Прогиб
Момент
Усилие сдвига
Центральная сосредоточенная нагрузка — обзор
Линия влияния изгибающего момента в точке F находится путем вставки шарнира в точке F и применения относительного вращения единиц, как показано на рис.20.20 (г). Снова часть ABF балки будет изогнутой, как и часть FC, поскольку эта часть балки должна вращаться так, чтобы сумма поворотов двух частей балки в точке F была равна единице.
Пример 20.9Постройте линии влияния для реакции в точке B и для поперечной силы и изгибающего момента в точке D в двухпролетной неразрезной балке, показанной на рис. 20.21 (a).
Рисунок 20.21. Линии влияния для непрерывной балки Ex. 20.9.
Форму каждой линии влияния можно нарисовать с использованием принципа Мюллера – Бреслау, как показано на рис.20.21 (b), (c) и (d). Однако, прежде чем они могут быть непосредственно использованы при определении максимальных значений, например, различных функций, связанных с прохождением систем нагружения, необходимо вычислить ординаты; для этого, поскольку линии влияния состоят из криволинейных сегментов, нам необходимо вывести их уравнения.
Однако, как только линия влияния для опорной реакции, в данном случае R B , была установлена, оставшиеся линии влияния вытекают из статического равновесия.
R
B Линия влиянияПредположим изначально, что единичная нагрузка — это расстояние x 1 от A, между A и B. Чтобы определить R B , мы можем использовать гибкость метод, описанный в Разделе 16.4. Таким образом, мы удаляем опору в точке B (точка 2) и вычисляем смещение, a 21 , в точке B из-за удельной нагрузки при x 1 (точка 1). Затем мы вычисляем смещение, a 22 , в точке B из-за вертикально направленной единичной нагрузки в точке B.Общее смещение в точке B из-за удельной нагрузки при x 1 и реакции R B будет тогда
(i) a21 – a22RB = 0
, поскольку опора в точке B не смещается. В формуле. (i) член a 22 R B отрицателен, поскольку R B находится в направлении, противоположном приложенной единичной нагрузке в B.Оба коэффициента гибкости в уравнении. (i) может быть получено из приложения единичной единичной нагрузки, поскольку из теоремы взаимности (Раздел 15.4), смещение в точке B из-за единичной нагрузки при x 1 равно смещению при x 1 из-за удельной нагрузки в B. Поэтому мы применяем вертикально направленную единичную нагрузку в B.
Уравнение смещенной формы балки — это уравнение для балки с простой опорой, несущей центральную сосредоточенную нагрузку. Следовательно, из уравнения. (iv) Исх. 13,5
(ii) υ = 148EI (4×3−3L2x)
или для балки на рис. 20.21 (a)(iii) υ = x12EI (x2−48)
В точке B, когда x = 4 м
(iv) υB = −323EI = a22
Кроме того, смещение в точке B из-за удельной нагрузки при x 1 (= смещение при x 1 из-за удельной нагрузки в точке B) из уравнения.(iii)
(v) υx1 = x112EI (x12−48) = a21
Замена на 22 и на 21 в уравнении. (i) имеем
x112EI (x12−48) + 323EIRB = 0
, откуда(vi) RB = −x1128 (x12−48) (0≤x1≤4.0m)
Уравнение (vi) дает влияние линия для R B с удельной нагрузкой между A и B; остальная часть линии влияния следует из симметрии. Уравнение (vi) можно проверить, поскольку нам известно значение R B с удельной нагрузкой в A и B.Таким образом, из уравнения. (vi), когда x 1 = 0, R B = 0 и когда x 1 = 4,0 м, R B = 1, как и ожидалось.
Если опора в точке B не была расположена симметрично, описанная выше процедура была бы повторена для единичной нагрузки на пролет BC. В этом случае уравнения для отклоненной формы AB и BC будут уравнениями (xiv) и (xv) в Ex. 13.6 Уравнение (xiv) Уравнение (xv).
В этом примере нам требуется линия влияния S D , так что нам фактически необходимо учитывать значение R B с удельной нагрузкой на пролет BC.Поэтому из уравнения. (xv) в Исх. 13,6
(vii) υx1 = −112EI (x13−24×12 + 144×1−128) (4.0m≤x1≤8.0m)
Следовательно, из уравнения. (i)
(viii) RB = 1128 (x13−24×12 + 144×1−128) (4.0m≤x1≤8.0m)
Проверка по формуле. (viii) показывает, что когда x 1 = 4,0 м, R B = 1, а когда x 1 = 8,0 м, R B = 0,
S
D линия влиянияПри единичной нагрузке слева от D поперечная сила S D , в точке D проще всего определяется как
(ix) SD = −RA + 1
, где , взяв моменты около C, мы имеем(x) RA × 8−1 (8 − x1) + RB × 4 = 0
Подставляя в уравнение.(x) для R B из уравнения. (vi) и перестановка дает
(xi) RA = 1256 (x13−80×1 + 256)
, откуда из уравнения. (ix)(xii) SD = −1256 (x13−80×1) (0≤x1≤2,0 м)
Следовательно, когда x 1 = 0, S D = 0 и когда x 1 = 2,0 м, S D = 0,59, ордината d 1 г на линии влияния S D на рис. 20.21 (c).
При удельной нагрузке между D и B
SD = −RA
, так что, заменяя R A из уравнения.(xi)(xiii) SD = −1256 (x13−80×1 + 256) (2.0m≤x1≤4.0m)
Таким образом, когда x 1 = 2.0 м, S D = — 0,41, ордината d 1 f на рис. 20.21 (c), и когда x 1 = 4,0 м, S D = 0.
Теперь рассмотрим удельную нагрузку между B и C.
SD = −RA
, но в этом случае R B в уравнении. (x) задается формулой. (viii). Замена R B из уравнения.(viii) в формуле. (x) получаем(xiv) RA = −SD = −1256 (x13−24×12 + 176×1−384) (4.0m≤x1≤8.0m)
Следовательно, линия влияния S D состоит из трех сегментов , a 1 g, fb 1 и b 1 c 1 .
M
D Линия влиянияС удельной нагрузкой между A и D
(xv) MD = RA × 2 + 1 (2 − x1)
Замена на R A от Уравнение (xi) в формуле. (xv) и упрощая, получаем
(xvi) MD = 1128 (x13−48×1) (0≤x1≤2.0 м)
При x 1 = 0, M D = 0 и при x 1 = 2,0 м, M D = 0,81, ордината d 2 h в линии влияния M D на Рис. 20.21 (d).
Теперь с удельной нагрузкой между D и B
(xvii) MD = RA × 2
Таким образом, замена на R A из уравнения. (xi) имеем
(xviii) MD = 1128 (x13−80×1 + 256) (2.0m≤x1≤4.0m)
Из уравнения. (xviii) мы видим, что когда x 1 = 2,0 м, M D = 0,81, снова ордината d 2 h на рис. 20.21 (d). Кроме того, когда x 1 = 4,0 м, M D = 0.
Наконец, с удельной нагрузкой между B и C, M D снова определяется уравнением. (xvii), но в котором R A определяется формулой. (xiv). Следовательно,
(xix) MD = −1128 (x13−24×12 + 176×1−384) (4.0m≤x1≤8,0 м)
Максимальные ординаты в линиях влияния S D и M D для пролета BC могут быть найдены путем дифференцирования уравнений (xiv) и (xix) относительно x 1 , приравняв к нулю и затем подставив полученные значения x 1 обратно в уравнения. Таким образом, например, из уравнения. (xiv)
dSDdx1 = 1256 (3×12−48×1 + 176) = 0
, откуда x 1 = 5,7 м.Следовательно,SD (макс.) = 0,1
Аналогично M D (макс.) = -0,2 при x 1 = 5,7 м.
Сравнение кривой прогиб балок для сосредоточенной нагрузки …
Контекст 1
… изменено между 0,1 и × — 10 10 10 для достижения сходимости на каждом приращении. Для решения уравнений использовался метод Ньютона. Наблюдение за анализами продолжалось после отказа балок. Был использован метод автоматической стабилизации, чтобы избежать локальной нестабильности, такой как морщинистость поверхности, нестабильность материала или локальное коробление.На рис. 6 показаны графики сдвига и отклонения, которые сравнивают экспериментальные испытания и моделирование методом конечных элементов. Рис. 7 подтверждает, что рисунки трещин, полученные в результате моделирования методом конечных элементов, были аналогичны рисункам, полученным в результате экспериментальных испытаний, проведенных Веккио и Шимом [16]. Как и ожидалось, благодаря [16]. сосредоточенная нагрузка в середине пролета, трещины сдвига сходились …
Контекст 2
… предложенный каркас был применен к обозначенным балкам OA1, OA2 и OA3 [16] для оценки их прочности при равномерном распределении нагрузки, как показано на рис.8. Кривые полного сдвига и прогиба были построены для получения предельной прочности каждой балки, как показано на рис. 6. На этом рисунке также показано сравнение прочности балок при точечной нагрузке в середине пролета и при равномерной нагрузке. распределенная нагрузка. Как и ожидалось, наклонные к сдвигу трещины равномерной нагрузки возникли на расстоянии эффективной глубины (d) от опор, в то время как трещины сосредоточенной нагрузки возникли под нагрузкой. …
Контекст 3
… метод. Модель FEM была разработана для имитации сдвига трех балок, испытанных Веккио и Шимом [16]. Подтвержденный анализ методом конечных элементов был использован для получения значений деформации и прочности бетона на сдвиг (фактор β) для 24 железобетонных балок, проанализированных при сосредоточенной нагрузке в середине пролета и эквивалентной равномерно распределенной нагрузке. На рис. 6a-c сравниваются кривые отклонения от общего усилия сдвига экспериментального испытания с результатами МКЭ и показано соответствие между ними: 9,4%, 2,4% и 19.Разница в предельной нагрузке на 9% для балок OA1, OA2 и OA3 соответственно. На рис. 7a-c показаны аналогичные структуры трещин, полученные по результатам экспериментальных испытаний и конечных элементов …
Контекст 4
… в этом исследовании арматурный стержень был встроен в бетон, чтобы гарантировать, что бетон и сталь будут иметь одинаковую деформацию в каждой секции. Была принята общая контрольная нагрузка статического смещения. Нагрузка прикладывалась с очень низкой скоростью в течение определенного времени, при этом пандус располагался линейно над ступенькой.Скорость загрузки автоматически изменялась от 0,1 до × — 10 10 10 для достижения сходимости при каждом приращении. Для решения уравнений использовался метод Ньютона. Наблюдение за анализами продолжалось после отказа балок. Был использован метод автоматической стабилизации, чтобы избежать локальной нестабильности, такой как морщинистость поверхности, нестабильность материала или локальное коробление. На рис. 6 показаны графики сдвига и отклонения, которые сравнивают экспериментальные испытания и моделирование методом конечных элементов. Рис. 7 подтверждает, что рисунки трещин, полученные в результате моделирования методом конечных элементов, были аналогичны рисункам, полученным в результате экспериментальных испытаний, проведенных Веккио и Шимом [16].Как и ожидалось, благодаря [16]. сосредоточенная нагрузка в середине пролета, трещины сдвига сходились при точечной нагрузке …
Контекст 5
… предложенный каркас был применен к обозначенным балкам OA1, OA2 и OA3 [16] для оценки их прочности при равномерно распределенная нагрузка, как показано на рис. 8. Кривые полного сдвига и отклонения были построены для получения предельной прочности каждой балки, как показано на рис. 6. На этом рисунке также показано сравнение прочности балок. при точечной нагрузке в середине пролета и при равномерно распределенной нагрузке.Как и ожидалось, наклонные к сдвигу трещины равномерной нагрузки возникли на расстоянии эффективной глубины (d) от опор, в то время как трещины сосредоточенной нагрузки возникли под нагрузкой. На рис. 7 сравниваются рисунки трещин в балках как для сосредоточенных, так и для равномерно распределенных …
Context 6
… Каркас был разработан для выполнения анализа с управляемым смещением равномерно распределенных нагрузок на балки. Эта структура служила механизмом нагрузки для оценки предельной прочности балок на сдвиг при равномерно распределенной нагрузке с использованием метода связанных нелинейных конечных элементов.Модель FEM была разработана для имитации сдвига трех балок, испытанных Веккио и Шимом [16]. Подтвержденный анализ методом конечных элементов был использован для получения значений деформации и прочности бетона на сдвиг (фактор β) для 24 железобетонных балок, проанализированных при сосредоточенной нагрузке в середине пролета и эквивалентной равномерно распределенной нагрузке. На рис. 6a-c сравниваются экспериментальные кривые общего усилия сдвига-прогиба при испытании с результатами МКЭ и показано соответствие между ними с различиями в предельной нагрузке на 9,4%, 2,4% и 19,9% для балок OA1, OA2 и OA3, соответственно.На рис. 7a-c показаны аналогичные структуры трещин, полученные по результатам экспериментальных испытаний и моделирования методом конечных элементов балок OA1, OA2 и OA3, которые возникли из-за сосредоточенной нагрузки в середине пролета. Следует отметить, что предложенная каркасная система использовалась для преобразования одиночной управляющей нагрузки смещения в равномерно распределенную нагрузку на .