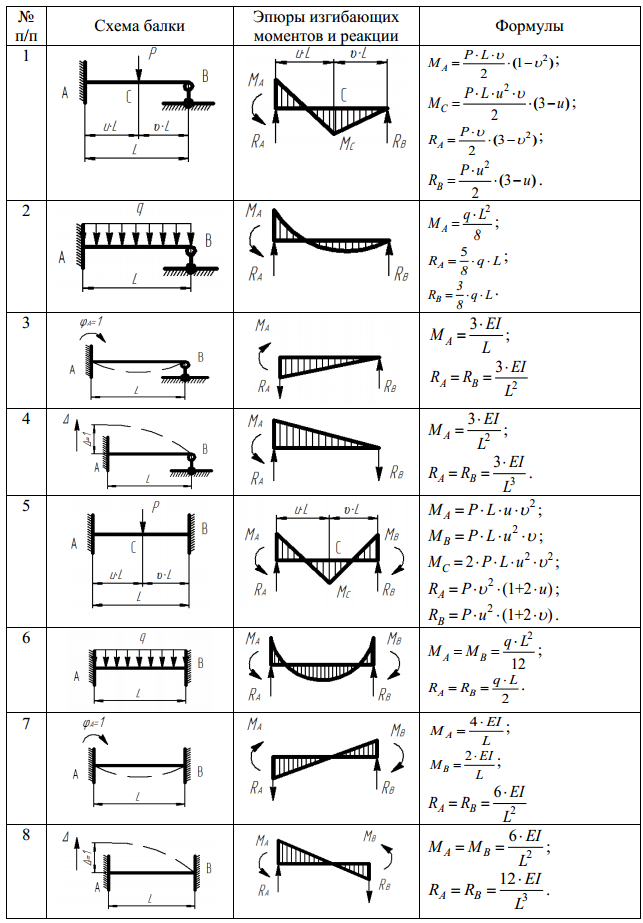
Построение эпюр статически неопределимых балок онлайн: СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр

Посстроение эпюр балки бесплатно. Примеры построения эпюр.

Определение опорных реакций

Построение эпюры поперечных сил (Q)

Построение эпюры продольных сил (Q)

Построение эпюры моментов (M)

Перейти к подробному решению

Определение опорных реакций

Построение эпюры поперечных сил (Q)

Построение эпюры продольных сил (Q)

Построение эпюры моментов (M)

Перейти к подробному решению

Определение опорных реакций

Построение эпюры поперечных сил (Q)

Построение эпюры продольных сил (Q)

Построение эпюры моментов (M)

Перейти к подробному решению

Треугольная нагрзука

Определение опорных реакций

Построение эпюры поперечных сил (Q)

Построение эпюры моментов (M)

Перейти к подробному решению

Трапециевидная нагрузка

Определение опорных реакций

Построение эпюры поперечных сил (Q)

Построение эпюры моментов (M)

Перейти к подробному решению

Треугольная нагрузка

Определение опорных реакций

Построение эпюры поперечных сил (Q)

Построение эпюры моментов (M)

Перейти к подробному решению

Знакопеременная нагрузка

Определение опорных реакций

Построение эпюры поперечных сил (Q)

Построение эпюры моментов (M)

Перейти к подробному решению


решение задач.

Лекции. Изгиб. Изгиб. определение перемещений. Расчет статически неопределимых балок.
Меню сайта

Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.

Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!

Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.

Лекции — теория, практика, задачи…

Примеры решения задач

Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.

Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).

Форум сопромата и механики

Книги — разная литература по теме.

Заказать задачу

Друзья сайта (ссылки)

WIKIbetta

Разработчикам (сотрудничество)

Веб-мастерам (партнёрка)

О проекте, контакты

Подпроекты

Базовый курс лекций по сопромату, теория, практика, задачи.

::Оглавление::


4. Изгиб. определение перемещений.

4.6. Расчет статически неопределимых балок.

Общие понятия и метод расчета.

   До сих пор мы рассматривали только статически определимые балки, у которых три опорные реакции определялись из условий равновесия. Очень часто, по условиям работы конструкции, оказывается необходимым увеличить число опорных закреплений; тогда мы получаем так называемую статически неопределимую балку.

Рис.1. Схемы статически неопределимых балок

 

   Например, для уменьшения пролета балки АВ на двух опорах (Рис.1, а) можно поставить опору еще посредине, а для уменьшения деформаций балки, защемленной одним концом (Рис.1, б), можно подпереть ее свободный конец.

   Для подбора сечения таких балок, так же как и в рассмотренных ранее задачах, необходимо построить обычным порядком эпюры изгибающих моментов и поперечных сил, а стало быть, определить опорные реакции.

   Во всех подобных случаях число опорных реакций, которые могут возникнуть, превышает число уравнений статики, например, для балок рис.2. Соответственно: четыре, четыре и пять опорных реакций.

Рис.2. Механизм появления дополнительных связей

 

   Поэтому необходимо составить дополнительные уравнения, выражающие условия совместности деформаций, которые вместе с обычными уравнениями равновесия и дадут возможность определить все опорные реакции.

   Определим опорные реакции и построим эпюру моментов для балки, находящейся под действием равномерно распределенной нагрузки q рис.3. Сначала изобразим все реакции, которые по устройству опор могут возникнуть в этой балке. Таких реакций может быть на опоре А три: вертикальная А, горизонтальная и опорный момент , на опоре В возможно появление лишь одной реакции В. Таким образом, число опорных реакций на одну больше, чем уравнений статики.

   Одна из реакций является добавочной, как говорят, «лишней» неизвестной. Этот термин прочно укоренился в технической литературе; между тем, принять его можно лишь условно.


Рис.3. Исходная расчетная схема статически неопределимой балки.

 

   Действительно, добавочная реакция и соответствующее ей добавочное опорное закрепление являются «лишними» только с точки зрения необходимости этих закреплений для равновесия балки как жесткого целого.

С точки же зрения инженера добавленное закрепление во многих случаях не только не является лишним, а наоборот, позволяет осуществить такую конструкцию, которая без него была бы невозможна. Поэтому мы будем пользоваться термином «лишняя опорная реакция», «лишняя неизвестная» лишь условно.

   Составим все уравнения статики для нашей балки, приравнивая нулю сумму проекций всех сил на направление оси балки, на перпендикуляр к ней, и сумму моментов относительно точки А. Получим систему:

,

   Из первого уравнения сразу определяется опорная реакция Для определения трех других остаются лишь два уравнения.

   За лишнюю реакцию можно взять любую из этих трех: попробуем взять реакцию опоры В. В таком случае мы должны считать, что рассматриваемая балка получилась из статически определимой балки

АВ, защемленной концом А, у которой потом поставили добавочную опору в точке В. Эта статически определимая балка, которая получается из статически неопределимой при удалении добавочного, лишнего опорного закрепления, называется основной системой. Выбрав какую-либо из реакций за лишнюю неизвестную, мы тем самым выбираем основную систему.

   Попробуем теперь превратить основную систему без опоры В в систему, полностью совпадающую с заданной статически неопределимой балкой (Рис.3).



Рис.4. Эквивалентная система

 

Для этого загрузим ее сплошной нагрузкой q и в точке В приложим лишнюю реакцию В (Рис.4).

   Однако этого мало: в балке, представленной на рис.4, точка

В может перемещаться по вертикали под действием нагрузок q и В; между тем, в нашей статически неопределимой балке точка В не имеет этой возможности, она должна совпадать с опорным шарниром. Поэтому, чтобы привести к окончательному совпадению, надо к последней добавить условие, что прогиб точки В основной системы под действием нагрузок q и В должен быть равен нулю:

   Это и будет добавочное уравнение, определяющее реакцию В; оно является условием совместности деформаций в рассматриваемом случае: конец В балки не отрывается от опоры.

Решение этого добавочного уравнения возможно несколькими способами.

 

Способ сравнения деформаций.

   Выполняя решение уравнения , названного уравнением совместности деформаций, можно рассуждать следующим образом.

   Прогиб точки В основной системы под действием нагрузок q и В складывается из двух прогибов: одного , вызванного лишь нагрузкой q, и другого , вызванного реакцией В. Таким образом,

(1)

Остается вычислить эти прогибы. Для этого загрузим основную систему одной нагрузкой q (рис.4, а).

Рис.4. Расчет прогиба от исходной нагрузки — а) и реакции — б)

 

Тогда прогиб точки В будет равен:

При нагружении основной системы реакцией В (Рис. 4,б) имеем:

Подставляя эти значения прогибов в уравнение (1), получаем:

Отсюда

   В этом способе мы сначала даем возможность основной системе деформироваться под действием внешней нагрузки q, а затем подбираем такую силу В, которая бы вернула точку В обратно. Таким образом, мы подбираем величину неизвестной дополнительной реакции В с тем расчетом, чтобы уравнять прогибы от нагрузки q и силы В. Этот способ и называют способом сравнения деформаций.


Рис.5. Эпюры поперечных сил и внутренних изгибающих моментов.

 

Подставляя значение лишней реакции В в уравнения статики, получаем

Выражение изгибающего момента получаем, рассматривая правую часть балки (Рис.4) и подставляя значение В:

Поперечная сила Q выражается формулой

   Эпюры моментов и поперечных сил изображены на рис. 5. Сечение с наибольшим положительным моментом соответствует абсциссе , определяемой равенством

т.е.

Отсюда соответствующая ордината эпюры моментов, равна:

::Оглавление::
Сообщество

Поиск людей


Вход

Решение задач

Заказать задачу
Профессиональное решение задач в короткие сроки.


Расчет редукторов

Расчет редуктора он-лайн
Расчет любого редуктора он-лайн.
Записка + чертежи


Для Android (рекомендую)

NEWMobile Beam 2.0
Программа для расчета балок на прочность на Вашем Android устройстве…


Java 2 ME
Симбим

· PyPI

Педагогический пакет для гибки балки.

SymBeam — это педагогический программный пакет, написанный на языке Python и предназначенный для студентов, изучающих машиностроение, гражданское строительство и промышленное строительство, изучающих основы гибки балок, а именно схемы изгиба и прогибов.

Модульный объектно-ориентированный дизайн SymBeam в сочетании с превосходным символьным движком SymPy, на который SymBeam в значительной степени опирается, обеспечивает уникальную вычислительную среду обучения для студентов, впервые постигающих эти концепции. SymBeam можно использовать для быстрой оценки решений упражнений для широкого спектра изгибающих нагрузок и опор, позволяя легко изменять параметры задачи, развивая физическую интуицию и улучшая понимание явлений учащимися.

И наоборот, SymBeam также может использоваться учителями для создания и проверки новых задач для занятий и экзаменов, облегчая эту иногда громоздкую задачу.

В следующих параграфах приводится подробное описание того, как использовать SymBeam для решения проблемы равновесия балки, а также его возможности и ограничения. Просмотрите полный список примеров приложений SymBeam, чтобы получить более наглядный обзор.

Попробуйте

Вам не нужно быть Python Pro или вообще знать Python, чтобы использовать SymBeam в своем исследовании. Изучите этот интерактивный блокнот и наслаждайтесь функциями SymBeam в своем кабинете!

По состоянию на февраль 2021 года SymBeam теперь является частью онлайн-платформы Centric Engineers. Здесь вы можете найти очень удобный графический пользовательский интерфейс для нескольких проектов с открытым исходным кодом по проектированию конструкций. Проверьте их утилиту для построения диаграмм гибки на базе SymBeam!

Установка

Установка из исходного кода

Клонировать этот репозиторий в вашу систему

 клон git [email protected]:amcc1996/symbeam.git

и установите пакет Python с pip3 , выполнив следующую команду в корневом каталоге SymBeam, где находится setup.py 

 pip3 install .

Кроме того, вы можете установить его непосредственно из PyPI с помощью

 pip3 install symbeam

На этом этапе SymBeam можно импортировать в ваши скрипты и модули Python обычным способом Python

 import symbeam

Теория

SymBeam основан на классических результатах механики твердого тела и сопротивления материалов для решения проблемы равновесия балки. В настоящем разделе следует простой план, без каких-либо математических выводов.

  • Расчет реакции — В настоящее время SymBeam не учитывает осевые нагрузки. Следовательно, в зависимости от типа опоры необходимо рассчитывать либо поперечную силу реакции, либо момент реакции. Они вычисляются путем решения алгебраической системы линейных уравнений, возникающих из равновесия сил и моментов конструкции, с одновременным учетом точечных нагрузок и моментов и распределенных сил.

  • Диаграммы изгиба — диаграммы поперечной силы и изгибающего момента рассчитываются путем интегрирования дифференциальных уравнений равновесия балки и последовательного наложения граничных условий, начиная с начальной точки x0 . Выражения, полученные на предыдущем отрезке, используются для задания граничных условий для следующего.

  • Прогиб — наклон и прогиб балки получаются интегрированием уравнения упругой кривой в каждом сегменте один и два раза соответственно. Геометрические граничные условия используются для построения системы алгебраических уравнений относительно постоянных интегрирования (удвоенного числа отрезков).

Usage

Все полезные функции SymBeam доступны через класс beam . Объекты луча , то есть конкретные экземпляры класса луча , изначально определяются начальной координатой x и длиной луча (неявно предполагается, что она находится в положительном направлении x). Опоры балки, свойства материала и сечения, а также нагрузки задаются путем вызова определенного набора методов для объекта балки.

В следующих разделах дается подробное описание примера приложения SymBeam.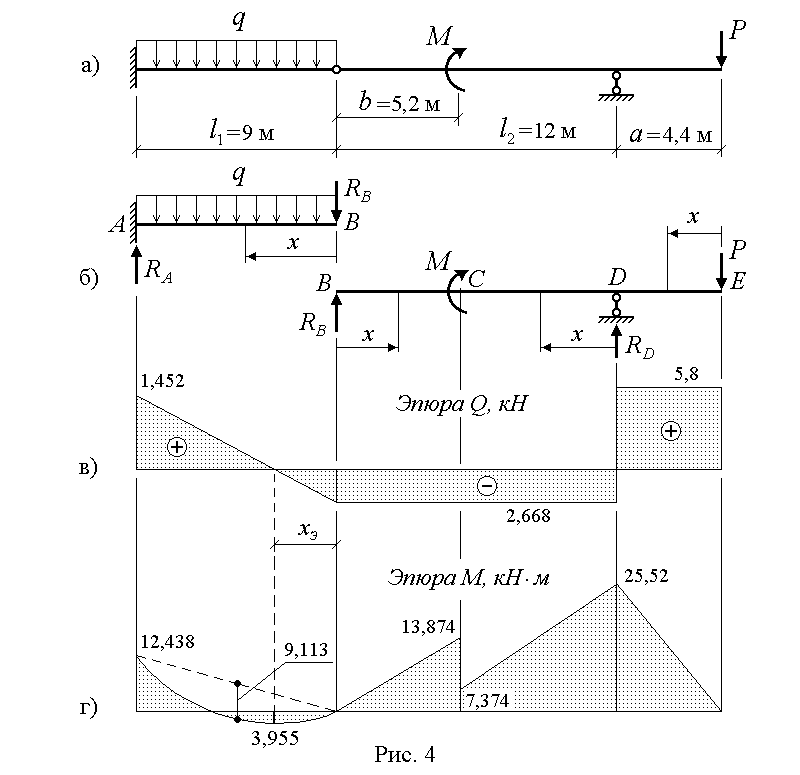 Следует заранее отметить, что большинство (если не все) значений, характеризующих проблему, могут быть заданы либо с помощью числового ввода (например, 100), либо с помощью буквального выражения (‘100 * x + 100’). В любом случае этот вход равен упростил , используя средства SymPy , что позволяет обрабатывать ввод различных типов «из коробки». Анализируемый пример показан на следующем рисунке (распределенные нагрузки на верхней стороне балки обозначают направленные вниз силы).

:warning: Символ x используется SymBeam как независимая переменная для положения вдоль луча. Эта переменная должна использоваться для указания любого изменения длины балки и ни для чего другого.

Создание балки

Основным инструментом для анализа изгиба с помощью SymBeam является объект балка , как подчеркивалось выше. Чтобы создать новый луч, импортируйте класс луча из пакета SymBeam. Затем просто вызовите конструктор beam , передав длину луча и, при необходимости, начальную точку (0 по умолчанию). Например, луч с длиной, равной 1 и начинающейся с 0, может быть создан с помощью

 из symbeam import beam.
новый_луч = луч (1, x0 = 0)

Как было сказано ранее, луч можно создать как с числовым, так и с символьным вводом. Далее следует список различных альтернатив для создания экземпляра луча (необязательная начальная позиция x0 здесь опущена для простоты). Обратите внимание, что эти альтернативы также применяются к любым входным данным, которые могут быть заданы для методов балки , например, для определения опор, нагрузок и свойств.

  1. Цифровой ввод
 из импортного луча symbeam
новый_луч = луч (1)
  1. Числовой ввод из строки
 из импортного луча symbeam
новый_луч = луч ("1")
  1. Символьный ввод из строки
 из импортного луча symbeam
новый_луч = луч ("L")
  1. Символьный ввод из символьной переменной, созданной с помощью SymPy
 из импортного луча symbeam
импорт симпи
L = символ. символы("L")
новый_луч = луч (L)
  1. Символьный ввод из символьной переменной, предоставленной SymPy
 из импортного луча symbeam
из sympy.abc импорт L
новый_луч = луч (L)

Настройка свойств балки: модуль Юнга и второй момент площади

Балка должна быть связана с некоторым распределением свойств материала и геометрией сечения по ее длине, а именно, модулем Юнга материала и вторым моментом площади сечения . Хотя они не требуются для нахождения диаграмм изгиба, поскольку они вытекают просто из соображений равновесия, они обязательны для расчета прогибов балки.

В SymBeam эти свойства можно задать для отдельных сегментов вдоль балки, так что набор сегментов для каждого свойства должен охватывать весь пролет балки и не перекрываться ни в одной области. Например, рассмотрим балку длиной L , модуль Юнга и второй момент площади задаются путем передачи начальной и конечной координаты и значения методам set_young() и set_inertia() следующим образом

 из луча импорта symbeam
из sympy. abc импортировать L, E, I
новый_луч = луч (L)
# new_beam.set_young(x_start, x_end, значение)
new_beam.set_young(0, L/2, E)
new_beam.set_young(L/2, L, E/10)
# new_beam.set_inertia(x_start, x_end, значение)
new_beam.set_inertia(0, L/2, I)
new_beam.set_inertia (L/2, L, I/2)

По умолчанию, если свойства явно не заданы пользователем, SymBeam считает постоянными значения E и I вдоль пролета балки, то есть методы задания свойств вызывать не нужно. Если какой-либо сегмент задан явно, пользователь должен последовательно указать все сегменты.

:warning: Наши любимые символы E и I : Будьте осторожны при указании символического модуля Юнга и второго момента площади через строки, например, с «E» и «I». SymPy анализирует строку в выражении и интерпретирует «E» как число Эйлера, а «I» — как мнимую единицу. Расставьте приоритеты, используя переменные, напрямую импортированные из sympy.abc или создайте переменные напрямую с помощью sympy. symbols() .

Добавление опор

Балка должна быть соединена с внешним видом через заданное количество опор, которые материализуют геометрические граничные условия задачи. В настоящее время SymBeam может решать только статически определяемые балки, поэтому избыточные опоры не могут быть обработаны. К балке можно добавить опоры, указав координату и тип опоры. Например, это достигается вызовом метода add_support() 

 # new_beam.add_support(x_coord, тип)
new_beam.add_support (0, «исправлено»)
new_beam.add_support(L, 'ролик')
new_beam.add_support(3*L/4, 'шарнир')

В SymBeam доступны следующие типы опор:

  • ролик : ролик, закрепленный в поперечном направлении и допускающий вращение в плоскости изгиба
  • штифт : шарнирная опора, фиксируемая в осевом и поперечном направлениях и обеспечивающая возможность вращения в плоскости изгиба
  • фиксированный : фиксированная/зажатая опора, все степени свободы ограничены (без перемещений и без вращения)
  • петля : допускает различное вращение слева и справа от острия, но не фиксирует балку в любом направлении

Добавление нагрузок

Приложенные внешние нагрузки — недостающий элемент для полного определения задачи изгиба балки. Это могут быть точечные, а именно поперечные точечные нагрузки/силы и моменты, и нагрузки сегментного типа, то есть поперечные силы, распределенные по пролету балки.

Точечные нагрузки и моменты включаются путем вызова методов add_point_load() и add_point_moment() , которые получают координату точки и значение нагрузки. Распределенные нагрузки применяются путем вызова метода add_distributed_load() , который получает начальную и конечную точки распределенной нагрузки и соответствующее выражение.

 new_beam.add_point_load(3*L/4, -P)
new_beam.add_point_moment (L, M)
new_beam.add_distributed_load(0, L/2, -q * x)

Решение задачи

После задания свойств балки, опор и нагрузок можно решить задачу, вызвав метод solve() . Программа будет действовать следующим образом:

  1. проверить согласованность входных данных
  2. определяют отдельные сегменты балки таким образом, чтобы каждый из них был связан с непрерывной функцией модуля Юнга, вторым моментом площади и распределенной нагрузкой: в целом, это подразделение должно гарантировать, что диаграммы поперечной силы и изгибающего момента непрерывны в каждом сегменте. и кусочно-непрерывным по пролету балки
  3. решить для сил реакции и моментов опор (уравнения равновесия)
  4. решить внутренние нагрузки (интегрировать дифференциальные уравнения для равновесия балки)
  5. найти прогибы (интегрировать уравнение упругой кривой)
  6. вывод результатов (может быть скрыт, если необязательный аргумент output=False ): идентифицированные сегменты, внешние реакции, поперечная сила, изгибающий момент, наклон и прогиб для каждого сегмента балки. Для текущего примера вывод должен быть следующим.
 Балочные точки
================================================== ==================================
     Тип координаты Момент нагрузки
-------------------------------------------------- ----------------------------------
         0 Фиксированный 0 0
        L/2 Точка непрерывности 0 0
       3*L/4 Петля -P 0
         L Ролик 0 M
================================================== ==================================
                                   Сегменты балки
================================================== ==================================
        Пролет Модуль Юнга Инерция Распределенная нагрузка
-------------------------------------------------- ----------------------------------
 [ 0 - L/2 ] E I -q*x
 [ Л/2 - 3*Л/4 ] Е/10 I/2 0
 [ 3*L/4 - L ] E/10 I/2 0
================================================== ==================================
                                Внешние реакции
================================================== ==================================
           Тип точки Значение
-------------------------------------------------- ----------------------------------
             0 Сила L**2*q/8 + P + 4*M/L
             0 Момент L**3*q/24 + 3*L*P/4 + 3*M
             L Сила -4*M/L
================================================== ==================================
                                  Внутренние нагрузки
================================================== ==================================
        Выражение диаграммы охвата
-------------------------------------------------- ----------------------------------
 [ 0 - L/2 ] V(x) -L**2*q/8 - P + q*x**2/2 - 4*M/L
 [ 0 - L/2 ] M(x) -L**3*q/24 - 3*L*P/4 - 3*M - q*x**3/6 + x*(L**3* д + 8*Д*П + 32*М)/(8*Д)
-------------------------------------------------- ----------------------------------
 [ Л/2 - 3*Л/4 ] V(x) -P - 4*М/Л
 [ L/2 - 3*L/4 ] M(x) -3*L*P/4 - 3*M + x*(P + 4*M/L)
-------------------------------------------------- ----------------------------------
 [ 3*L/4 - L ] V(x) -4*M/L
 [ 3*L/4 - L ] M(x) -3*M + 4*M*x/L
================================================== ==================================
                              Вращение и отклонение
================================================== ==================================
        Выражение переменной диапазона
-------------------------------------------------- ----------------------------------
 [ 0 - L/2 ] v(x) -q*x**5/(120*E*I) + x**2*(-L**3*q - 18*L*P - 72*M )/(48*E*I) + x**3*(L**3*q + 8*L*P + 32*M)/(48*E*I*L)
 [ 0 - L/2 ] dv/dx(x) -q*x**4/(24*E*I) + x*(-L**3*q - 18*L*P - 72*M) /(24*E*I) + x**2*(L**3*q + 8*L*P + 32*M)/(16*E*I*L)
-------------------------------------------------- ----------------------------------
 [ L/2 - 3*L/4 ] v(x) L**2*(L**3*q - 950*L*P - 3800*M)/(960*E*I) + L*x*(-L**3*q + 608*L*P + 2432*M)/(128*E*I) + x**2*(-15*L*P - 60*M)/(2*E*I) + x**3*(10*L*P + 40*M)/(3*E*I *Л)
 [ L/2 - 3*L/4 ] dv/dx(x) L*(-L**3*q + 608*L*P + 2432*M)/(128*E*I) + x*( -15*L*P - 60*M)/(E*I) + x**2*(10*L*P + 40*M)/(E*I*L)
-------------------------------------------------- ----------------------------------
 [ 3*L/4 - L ] v(x) -L**2*(37*L**3*q + 1840*L*P + 16960*M)/(1920*E*I) + L* x*(37*L**3*q + 1840*L*P + 48960*M)/(1920*E*I) - 30*M*x**2/(E*I) + 40*M* х**3/(3*Э*И*Л)
 [ 3*L/4 - L ] dv/dx(x) L*(37*L**3*q + 1840*L*P + 48960*M)/(1920*E*I) - 60*M*x/(E*I) + 40*M*x**2/(E*I*L)
================================================== ==================================

:warning: Не пугайтесь результата: Выбранный пример охватывает несколько функций SymBeam, поэтому аналитические выражения имеют тенденцию очень быстро увеличиваться в размерах, особенно отклонение.

Построение графика результатов

Результаты можно построить с помощью matplotlib, вызвав метод plot на лучевой объект. Произведенный рисунок содержит

  1. схематическое изображение проблемы
  2. диаграмма поперечной силы
  3. диаграмма изгибающего момента
  4. деформированная форма балки.

На этом этапе, чтобы иметь возможность построить выражения, все параметры задачи должны быть заменены числовыми значениями, за естественным исключением переменной x , так как это независимая переменная. Этого можно добиться, передав необязательный аргумент subs к методу участка . Это должен быть словарь, ключи которого являются строковыми представлениями переменных, а значения — эффективными числовыми значениями.

Принимая замены L=2 , P=1000 , q=5000 и M=1000 , SymBeam выводит рисунок ниже.

:warning: Не забудьте сохранить цифры с помощью метода savefig() из matplotlib. pyplot.figure . На самом деле вы также можете просто вывести рисунок на экран с помощью show() from matplotlib.pyplot , но имейте в виду, что это может немного изменить формат макета, в зависимости от характеристик вашей системы.

Окончательный сценарий

Здесь вы можете найти полный сценарий, обсуждавшийся в предыдущих разделах.

 из импортного луча symbeam
из sympy.abc импортировать L, E, I, P, M, q, x
импортировать matplotlib.pyplot как plt
новый_луч = луч (L)
# new_beam.set_young(x_start, x_end, значение)
new_beam.set_young(0, L/2, E)
new_beam.set_young(L/2, L, E/10)
# new_beam.set_inertia(x_start, x_end, значение)
new_beam.set_inertia(0, L/2, I)
new_beam.set_inertia (L/2, L, I/2)
# new_beam.add_support(x_coord, тип)
new_beam.add_support (0, «исправлено»)
new_beam.add_support(L, 'ролик')
new_beam.add_support(3*L/4, 'шарнир')
new_beam.add_point_load(3*L/4, -P)
new_beam.add_point_moment (L, M)
new_beam.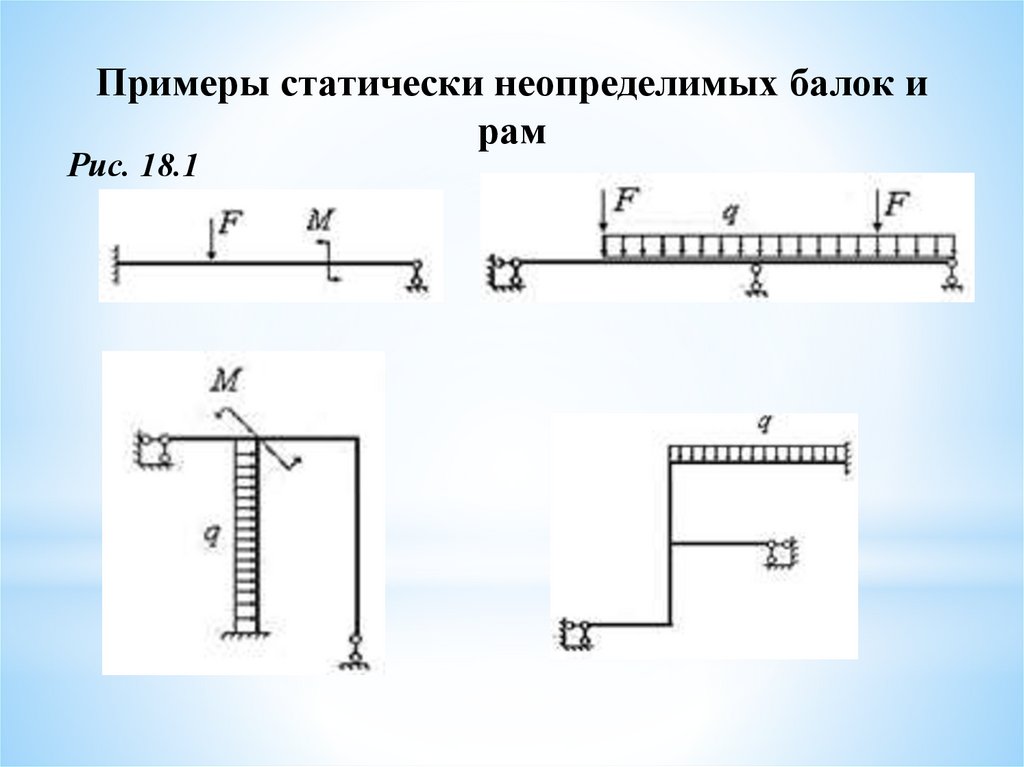 add_distributed_load(0, L/2, -q * x)
new_beam.решить()
new_beam.plot(subs={'P':1000, 'q':5000, 'L':2, 'M':1000})
plt.savefig("beam.pdf")

Запуск тестов

Тесты SymBeam можно запустить с помощью pytest и плагина сравнения изображений pytest-mpl, поэтому начните с установки фреймворка

 pip3 install pytest pytest-mpl
pip3 install pytest-cov # необязательно, для создания отчетов о покрытии

и запустите утилиту тестирования из корневого каталога SymBeam

 сделайте тесты

SymBeam использует pytest-mpl для сравнения графиков изгиба между версиями. При вызове maketests pytest будет вызываться с соответствующим инструментом командной строки и настройками каталога. Эталонные изображения хранятся в тестах/базовом уровне. Если сравнение изображений не удается, базовое изображение записывается в тесты/результаты вместе с (неудачным) изображением, созданным моей текущей версией и соответствующей разницей.

Отчеты о покрытии могут быть созданы с помощью

 сделать покрытие

, который запустит тест и создаст информацию о покрытии в htmlcov .

Лицензия

Copyright 2020, António Carneiro

SymBeam — это бесплатное программное обеспечение с открытым исходным кодом, которое распространяется под лицензией MIT.

Код Python для рисования BMD и SFD (изгибающий момент и сила сдвига) для SSB с точечной нагрузкой

Python, HTML, CSS Programming / By Санджай Кумар Шарма / 25 сентября 2020 г. 25 декабря 2022 г.

 Здравствуйте,

Я создал две программы для построения диаграмм поперечной силы и изгибающего момента. Я предоставляю один из них, здесь, бесплатно!

Это простой код, который решает только проблемы с точечными нагрузками и только для SSB (просто поддерживаемых балок). Другой, который не является бесплатным, может создавать BMD и SFD для любых типов нагрузок, таких как точечные нагрузки, чистые пары, UDL (равномерно распределенные нагрузки) и UVL (равномерно изменяющиеся нагрузки).

Он не только рисует SFD и BMD, но также дает уравнения для поперечной силы и изгибающего момента в различных сечениях балки. Если вы хотите узнать больше о том, на что способна вторая программа, посмотрите видео. Если все звучит хорошо, вы можете купить код в интернет-магазине.

Перечислим преимущества и недостатки каждой версии кода.

Бесплатная версия:
  1. Работает только с SSB
  2. Только для точечных нагрузок.
  3. SFD и BMD не аннотированы.

Версия Elite:
  1. Работает с SSB, консолями, выступами и балками с внутренними петлями.
  2. Работает с точечными нагрузками, чистыми парами, UDL, UVL и комбинацией этих нагрузок одновременно.
  3. SFD и BMD правильно аннотированы, показывая максимальное, минимальное и все узловые значения поперечной силы и изгибающего момента на балке.

Купить элитную версию сейчас: Код Python для SFD и BMD статически детерминированных балок ниже создан с использованием Python и библиотек Numpy и Matplotlib. Он может нарисовать диаграмму изгибающего момента (BMD) и диаграмму поперечной силы (SFD) для просто поддерживаемой балки (SSB) с точечной нагрузкой в ​​любом месте этой балки.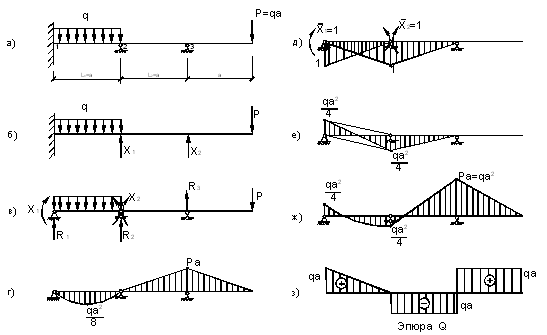

Код при запуске запросит следующие входные данные :

  1. Загрузка,
  2. Нагрузочное устройство,
  3. Длина балки,
  4. ед. длины,
  5. и расположение точечной нагрузки на балку.

Выход элементов:

  1. Реакции,
  2. Уравнение сдвига и момента в любом месте балки,
  3. Максимальное усилие сдвига и максимальный изгибающий момент
  4. Расположение максимального БМ,
  5. и Участок ЮФО и БМД.

 

Вот код:

 импортировать numpy как np
импортировать matplotlib.pyplot как plt
P = с плавающей запятой (ввод ('загрузка ='))
u1 = ввод ('блок загрузки =')
L = float(input('Длина балки ='))
u2 = ввод ('единица длины =')
a = float(input('Расстояние точечной нагрузки от левого конца = '))
б = л - а
R1 = P*b/L
Р2 = Р - Р1
R1 = круглый (R1, 3)
R2 = круглый (R2, 3)
печать (ф'''
В соответствии со статическим равновесием чистая сумма моментов на обоих концах равна нулю,
следовательно, реакция R1 = P*b/L = {R1} {u1},
Также чистая сумма вертикальных сил равна нулю,
следовательно, R1+R2 = P, R2 = P - R1 = {R2} {u1}. ''')
л = np.linspace (0, L, 1000)
Х = []
СФ = []
М = []
maxBM= с плавающей запятой()
для х в л:
 если х <= а:
 м = R1*х
 сф = R1
 элиф х > а:
 m = R1*x - P*(x-a)
 сф = -R2
 М. добавить (м)
 X.добавить(х)
 SF.append(sf)
печать (ф'''
Сила сдвига в точке x (x<{a}), Vx = R1 = {R1} {u1}
 в точке x (x>{a}), SF = R1 - P = {R1} - {P} = -{R1-P} {u1}
Изгибающий момент в точке x (x<{a}), Mx = R1*x = {R1}*x
 при x (x>={a}), Mx = R1*x - P*(x-{a})
 = {R1}x - {P}(x-{a}) = -{R2}x + {P*a}
''')
макс_СФ = 0
для k в SF:
 если max_SF < k:
 макс_СФ = к
print(f'Максимальная сила сдвига Vmax = {max_SF} {u1}')
для к в М:
 если maxBM < k:
 максВМ = к
print(f'максимальное BM, Mmax = {round(maxBM, 3)} {u1}{u2}')
Мх = с плавающей запятой ()
для х в л:
 если х<а:
 Мх = R1*х
 если maxBM == Mx:
 print(f'максимальное BM в точке x = {round(x,3)} {u2}')
 Элиф х>=а:
 Мх = R1*x - P*(x- а)
 если maxBM == Mx:
 print(f'максимальное BM в точке x = {round(x,3)} {u2}')
plt.