Построение эпюры внутренних продольных сил при растяжении-сжатии
Задача
Для прямого стержня нагруженного системой внешних сил требуется построить эпюру внутренних продольных сил N.
Решение
В предыдущем пункте решения задачи была определена опорная реакция R в заделке стержня.
Для расчета величины внутренних сил обозначим характерные сечения стержня (B, C, D, K и M).
Заданный стержень имеет 3 силовых участка: BC, CK и KM. Обозначим эти участки римскими цифрами, например, справа налево.
Сечение D, где меняется поперечный размер стержня, границей силового участка не является.
На каждом из этих участков определим величину и знак внутренней продольной силы.
Для этого воспользуемся методом сечений.
Начнем с I силового участка (KM):
Проведем мысленно сечение в пределах рассматриваемого участка.
Это сечение делит стержень на две части: левую и правую.
Для упрощения расчетов рекомендуется выбирать ту часть стержня, к которой приложено меньше сил. Очевидно, это будет правая часть стержня (т.к. слева от сечения 4 силы, а справа всего одна).
Внутренняя сила в данном сечении будет равна сумме внешних сил рассматриваемой правой части стержня. С учетом правила знаков при растяжении-сжатии эта сумма будет иметь следующий вид:
Здесь сила F3 записана отрицательной, так как сжимает рассматриваемую часть стержня (направлена в сторону проведенного сечения).
Переходим на второй силовой участок (CK).
Рассекаем стержень в произвольном месте участка и рассматриваем, например левую его часть.
Здесь силы R и F1 положительны, т.к. стремятся растянуть II участок стержня (направлены от сечения).
Аналогично для третьего силового участка (BC)
По полученным данным строим эпюру продольных сил N.
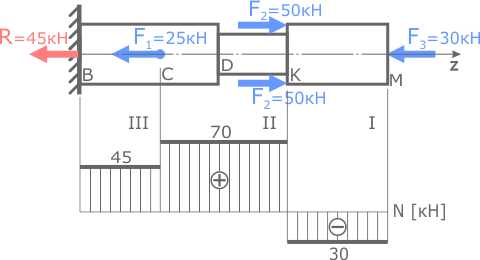
Правильность построения эпюры можно проверить по «скачкам».
Расчет размеров стержня постоянного сечения >
Подбор размеров стержня заданной формы >
Другие примеры решения задач >
isopromat.ru
Технология построения эпюры внутренней продольной силы — КиберПедия
Что такое внутренняя продольная сила?
Это внутренний силовой фактор, возникающий в поперечных сечениях элемента конструкции, нагруженного внешними силами, производящими деформацию растяжения или сжатия.
Зачем нужно уметь строить эпюры внутренней продольной силы?
Это необходимо для определения положения опасного сечения элемента конструкции, т.е. для определения величины максимального напряжения и получения условия прочности, выполнение которого позволит обеспечить прочностную надежность конструкции при ее эксплуатации.
Чтобы научиться строить эпюры внутренней продольной силы надо знать!
1. Метод сечений и вытекающие из него закономерности для построения эпюры N:
· Внешняя сосредоточенная сила на эпюре N дает скачок на величину силы в сторону знака ее воздействия.
· Если участок ничем не загружен (отсутствует распределенная по длине нагрузка), то на соответствующем участке эпюры должна быть прямая, параллельная базе.
· Если участок загружен равномерно распределенной нагрузкой интенсивностью q, то на соответствующем участке эпюры должна быть наклонная прямая с угловым коэффициентом, равным q.
2. Правило знаков для продольной силы N.
· Продольная сила считается положительной, если вызывающая её внешняя сила относительно рассматриваемого сечения растягивает стержень:
· Продольная сила считается отрицательной, если вызывающая её внешняя сила относительно рассматриваемого сечения сжимает стержень:
· Знак продольной силы имеет физическое значение в связи с тем, что некоторые материалы по-разному сопротивляются деформации растяжения и деформации сжатия.
Алгоритм построения эпюры продольной силы
1. Для построения эпюры провести базу – линию, параллельную продольной оси стержня, равную длине стержня.
2. Разделить базу эпюры на участки, соответственно участкам стержня.
Для этого надо знать: Участком является часть длины стержня между точками приложения сосредоточенных сил или началом и концом действия распределенной нагрузки.
3. Для консольного типа стержней (один конец свободный, другой в жесткой заделке) выбрать направление построения эпюры от свободного конца к заделке.
4. Определить состояние в начале участка: если есть сосредоточенная сила, производящая деформацию растяжения, отложить на эпюре ординату, равную величине силы, со знаком «+». Со знаком «–», если сила производит деформацию сжатия. При отсутствии силы построение эпюры начинаем с нуля.
5. Определить состояние внутри участка:
· если участок пустой, провести прямую, параллельную базе, высотой, равной отложенной ординате в начале участка;
· если участок загружен равномерно распределенной нагрузкой интенсивностью q, проводим наклонную прямую с угловым коэффициентом =q. Для определения величины продольной силы в конце участка, прибавляем к значению ординаты в начале участка с учетом ее знака произведение q·ℓ в случае растягивающей распределенной нагрузки. И наоборот, вычитаем от значения ординаты в начале участка произведение q·ℓ в случае сжимающей распределенной нагрузки. Здесь ℓ – длина участка.
6. И т.д. по каждому участку.
1.2.2. Пример решения задачи
Задача
Для данного стержня построить эпюру продольной силы N.

РЕШЕНИЕ
Стержень имеет пять участков: BC, CD, DL, LS, SK.
Проведем параллельно продольной оси стержня базу эпюры (ось, относительно которой будем откладывать ординаты (значения) внутренней продольной силы). Разделим базу на участки, соответственно участкам стержня, проводя из граничных точек участков стержня прямые ┴ базе до пересечения с базой. Направление построения эпюры примем от свободного конца к заделке, не определяя реактивных сил в заделке.
Ый участок (BC)
Правая граница участка в т. «В»: Отсутствует сосредоточенная сила, поэтому начинаем эпюру N c нуля.
Состояние по длине участка: участок загружен равномерно распределенной нагрузкой интенсивностью q=20кН/м, поэтому должна быть наклонная прямая с угловым коэффициентом = +q, т.к. нагрузка производит деформацию растяжения, и наклонная прямая пойдет в положительную область. Для построения наклонной прямой определим значение на левой границе участка.
Левая граница участка т. «С». Значение продольной силы определим, умножив интенсивность нагрузки на длину участка: 20×0,8=16 (кН). Откладываем в точке «С» 16кН вверх от базы и соединяем с нулем в т. «В» наклонной прямой.
Ой участок (CD)
Правая граница участка т. «С»: здесь находится сосредоточенная сила F1=20кН, производящая деформацию сжатия, что на эпюре вызывает скачок в отрицательную сторону от ординаты 16кН. Получим -4кН.
Состояние по длине участка: участок загружен равномерно распределенной нагрузкой интенсивностью q=20кН/м, поэтому должна быть наклонная прямая с угловым коэффициентом = +q, т.к. нагрузка производит деформацию растяжения, и наклонная прямая пойдет в положительную область. Для построения наклонной прямой определим значение на левой границе участка.
Левая граница участка т. «D». Значение продольной силы в этой точке определяем следующим образом: к значению ординаты в начале участка -4 кН прибавляем произведение q=20 кН/м на длину участка 0,4м. Получаем следующее значение продольной силы: N=-4+20×0,4=4кН, которое откладываем выше базы в конце второго участка, и наклонной прямой соединяем ординаты: в точке «С» -4кН и в точке «D»+4кН.
Ий участок (DL)
Правая граница участка т. «D»: сосредоточенная сила отсутствует, поэтому значение N=4кН, полученное в данной точке на предыдущем участке, не изменяется.
Состояние по длине участка: участок ничем не загружен, поэтому на эпюре должна быть прямая, параллельная базе.
Левая граница участка т. «L»: Значение продольной силы будет таким же, как в начале участка. Проводим прямую линию, параллельную базе, ординатой 4кН.
Ый участок (LS)
Правая граница участка т. «L»: приложена сосредоточенная сила F1=15кН, которая производит деформацию растяжения и дает на эпюре скачок на величину 15 кН вверх от ординаты 4кН. Получим 19кН.
Состояние по длине участка: участок ничем не загружен. Поэтому на эпюре должна быть прямая, параллельная базе.
Левая граница участка т. «S»: значение продольной силы будет таким же, как в начале участка, т.е. 19кН. Проводим прямую линию, параллельную базе, ординатой 19кН.
Ый участок (SK)
Правая граница участка т. «S»: здесь находится сосредоточенная сила F3=30 кН, производящая деформацию сжатия. На эпюре это вызывает скачок на величину -30кН от ординаты 19кН. Получим величину -11кН.
Состояние по длине участка: участок ничем не загружен. Поэтому на эпюре должна быть прямая, параллельная базе.
Левая граница участка т. «К»: значение продольной силы будет таким же, как в начале участка, т.е. равным -11кН. Проводим прямую линию, параллельную базе, ординатой -11кН.
Внутри эпюры ставим знаки и делаем штриховку перпендикулярно базе эпюры. Почему перпендикулярно базе ? Потому, что каждая штриховая линия определяет значение внутренней силы в соответствующем сечении.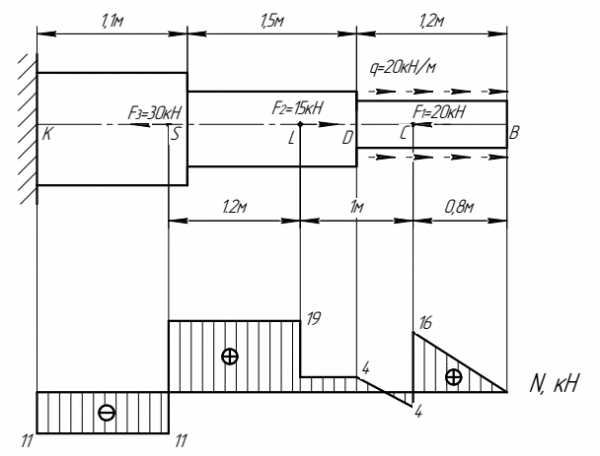
Эпюра построена
1.2.3. Технология построения эпюры внутреннего крутящего момента Mz
Что такое внутренний крутящий момент?
Это внутренний силовой фактор, возникающий в поперечных сечениях элемента конструкции, нагруженного внешними парами сил, воздействующими относительно продольной оси и производящими деформацию кручения.
Зачем нужно уметь строить эпюры внутреннего крутящего момента?
Это необходимо для определения положения опасного сечения элемента конструкции, т.е. для определения величины максимального напряжения и получения условия прочности, выполнение которого позволит обеспечить прочностную надежность конструкции при ее эксплуатации.
Чтобы научиться строить эпюры внутреннего крутящего момента
надо знать!
1. Метод сечений и вытекающие из него закономерности для построения эпюры Mz:
· Внешняя сосредоточенная пара сил на эпюре Mz дает скачок на величину пары сил в сторону знака ее воздействия.
· Если участок ничем не загружен (отсутствует распределенный по длине момент), то на соответствующем участке эпюры Mz должна быть прямая, параллельная базе.
· Если участок загружен равномерно распределенным моментом интенсивностью m, то на соответствующем участке эпюры должна быть наклонная прямая с угловым коэффициентом, равным m.
2. Правило знаков для внутреннего крутящего момента:

Что мы видим на графической иллюстрации правила знаков?
· Прежде, чем определять направление вращения внешнего момента, от которого назначается знак внутреннего, Вы должны мысленно сделать сечение в пределах участка, на котором хотите определить Mz, оставить любую из полученных частей вала и посмотреть в торец сделанному сечению.
· Поворачивая внешний момент, определите его направление и назначьте знак внутреннему моменту. Например, как это сделано на иллюстрации. Если внешний момент поворачивается против часовой стрелки, то внутренний момент принимается положительным. И наоборот.
Т.к. знак внутреннего момента не имеет физического смысла, Вы имеете возможность правило знаков назначать произвольно. Т.е. не будет ошибки, если Вы назначите знак плюс внутреннему моменту, возникающему от внешнего момента, вращающегося по часовой стрелке. Важным в правиле знаков является лишь то, что при определении направления вращения внешнего момента, Вы обязательно должны смотреть со стороны сделанного сечения ! Знак внутри эпюры крутящего момента не ставится.
Алгоритм построения эпюры Mz
1. Для построения эпюры провести базу – линию, параллельную продольной оси стержня, равную длине вала.
2. Разделить базу на участки соответственно участкам вала.
Для этого нужно знать: Участок – часть длины вала между точками приложения сосредоточенных пар сил или между началом и концом действия распределенного момента.
3. Для консольного типа валов (один конец свободный, другой в жесткой заделке) выбрать направление построения эпюры от свободного конца к заделке.
4. Определить состояние в начале участка: если есть сосредоточенная пара сил, отложить ординату на эпюре, равную величине пары сил, выше или ниже базы эпюры, согласно правилу знаков. При отсутствии пары сил построение эпюры начинаем с нуля.
5. Определить состояние внутри участка:
· если участок пустой, провести прямую линию, параллельную базе, высотой, равной отложенной ординате в начале участка;
· если участок загружен равномерно распределенным моментом интенсивностью m, проводим наклонную прямую с угловым коэффициентом =m. Для определения величины внутреннего крутящего момента в конце участка, увеличиваем ординату в начале участка с учетом ее знака на величину произведения m·ℓ в случае, если направление распределенного момента совпадает с направлением сосредоточенного. И наоборот, уменьшаем значение ординаты в начале участка на величину произведения m·ℓ в случае несовпадения направления распределенного момента с направлением сосредоточенного в начале участка.
6. И т.д. по каждому участку.
1.2.4. Пример решения задачи
Задача
Для данного вала построить эпюру внутреннего крутящего момента.
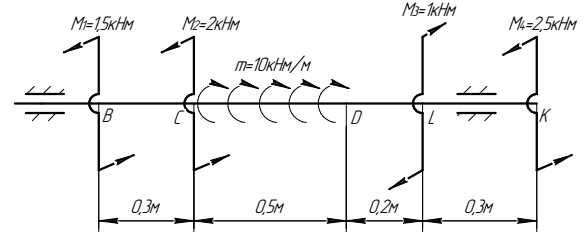
РЕШЕНИЕ
Сначала проведем краткий анализ данной расчетной схемы и определим количество участков, на которые надо разделить вал:
1. Вал нагружен системой самоуравновешенных моментов. В этом можно убедиться, если алгебраически сложить все моменты, учитывая их разные направления. Одного направления на схеме моменты М1, М2 и М4. Их сумма составляет 6кНм. Противоположно им направлен равномерно распределенный момент и момент М3. Их сумма составляет: . Таким образом, сумма всех моментов будет равна нулю. Это означает, что реактивные моменты в опорах будут отсутствовать и крайний левый участок от опоры до момента М1 не будет испытывать внешнего воздействия, а значит в его поперечных сечениях не будет возникать внутреннего крутящего момента.
2. В результате вал можно разделить на четыре участка: BC, CD, DL, LK.
3. Под расчетной схемой параллельно продольной оси проведем базу эпюры в границах длины BK.
4. Базу эпюры поделим на участки, соответствующие участкам расчетной схемы.
Ый участок (BC)
Выберем направление построения эпюры слева направо.
Левая граница участка т. «В»: здесь находится сосредоточенный момент М1 =1,5кНм, который на эпюре должен вызывать скачок на величину 1,5кНм. Примем знак скачка положительным.
Состояние по длине участка: участок ничем не загружен, т.е. на эпюре должна быть прямая, параллельная базе.
Правая граница участка т. «C»: значение крутящего момента будет таким же, как в начале участка. Проведем прямую линию, параллельную базе, с ординатой 1,5кНм.
Ой участок (CD)
Левая граница участка т. «С»: здесь находится сосредоточенный момент М2=2кНм того же направления, что и М1. Это вызывает на эпюре скачок на 2кНм вверх. Получим 3,5кНм.
Состояние по длине участка: участок загружен равномерно распределенным моментом, поэтому на эпюре должна быть наклонная прямая с угловым коэффициентом, равным m=10кНм/м. Поскольку направление равномерно распределенного момента противоположно М1 и М2, то наклонная прямая пойдет в отрицательную сторону, т.е. знак углового коэффициента примем «–». Для построения наклонной прямой определим значение внутреннего крутящего момента в конце участка.
Правая граница участка т. «D». Величину Mz вычислим как: , т.е. из значения в начале участка вычитаем величину равнодействующей равномерно распределенного момента. Соединяем ординату в начале участка =3,5кНм с ординатой в конце участка = ‑1,5кНм наклонной прямой.
Ий участок (DL)
Левая граница участка т. «D»: сосредоточенный внешний момент отсутствует, поэтому ордината -1,5кНм не изменится.
Состояние по длине участка: участок ничем не загружен, поэтому на эпюре будет прямая, параллельная базе.
Правая граница участка т. «L»: значение Mz будет таким же, как в начале участка в т. «D».
Ый участок (LK)
Левая граница участка т. «L»: здесь находится сосредоточенный момент М3=1кНм того же направления, что и равномерно распределенный момент. Поэтому он вызовет скачок на эпюре крутящего момента в отрицательную сторону, и мы получим ординату величиной -2,5кНм.
Состояние по длине участка: участок ничем не загружен, поэтому на эпюре будет прямая, параллельная базе.
Правая граница участка т. «К»: значение Mz будет таким же, как в начале участка в т. «L».
Знак внутри эпюры крутящего момента не ставится, а штриховка используется спиралью.
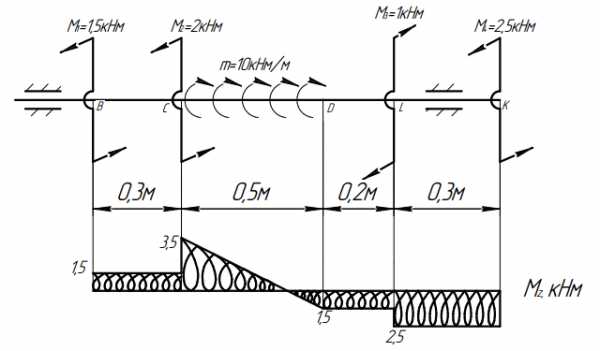
Эпюра построена
1.2.5. Задачи для самостоятельного решения на занятии
Задача 1
Для данной расчетной схемы построить эпюру продольной силы N, используя метод построения по характерным сечениям.

Задача 2
Для данной расчетной схемы построить эпюру крутящего момента Mz, используя метод построения по характерным сечениям.

1.2.6. Потренируемся?
· Пройти тестовый тренинг (Приложение 2, тесты к ПЗ №1, стр. 191)
· Решить задачу 1.1 и 1.2 из РПР№1 (Приложение 4, стр. 255, 258)
1.3. Практическое занятие №2
Построение эпюры внутренней поперечной силы и изгибающего момента при прямом изгибе балок.
Часть 1 и часть 2
cyberpedia.su
Задача 9 Построение эпюр поперечных сил, продольных и изгибающих моментов в плоских рамах
Последовательность решения аналогична задачам 1, 2, 3, 5, 6. В плоской раме внутренними силовыми факторами являются продольная сила N, поперечная силаQи изгибающий моментМ. Для контроля правильности построения эпюр внутренних силовых факторов в плоской раме проверяются выполнение рассмотренных ранее дифференциальных зависимостей и равновесие узлов рамы. На эпюреМдолжно выполняться «правило циркуля» — если в ненагруженном узле сходятся только два стержня (под любым углом), ординатыЭМна стержнях этого узла должны быть равны и отложены либо обе внутрь, либо обе наружу.
Задача 14 Построение эпюр поперечных сил, продольных и изгибающих моментов в плоско-пространственных рамах
В плоско- пространственной раме
внутренними силовыми факторами являются
поперечная сила 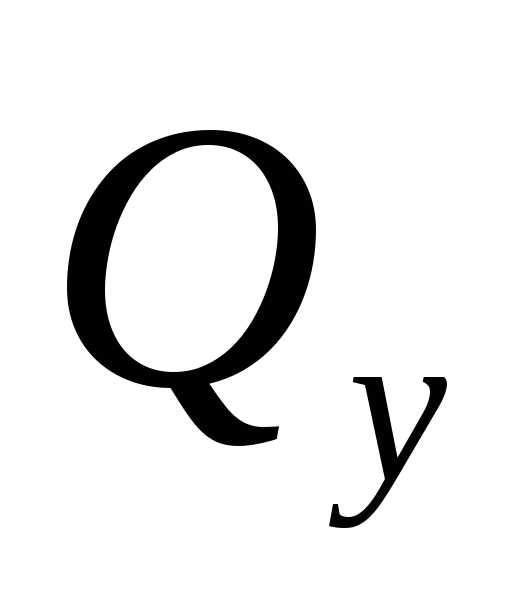 ,
изгибающий
,
изгибающий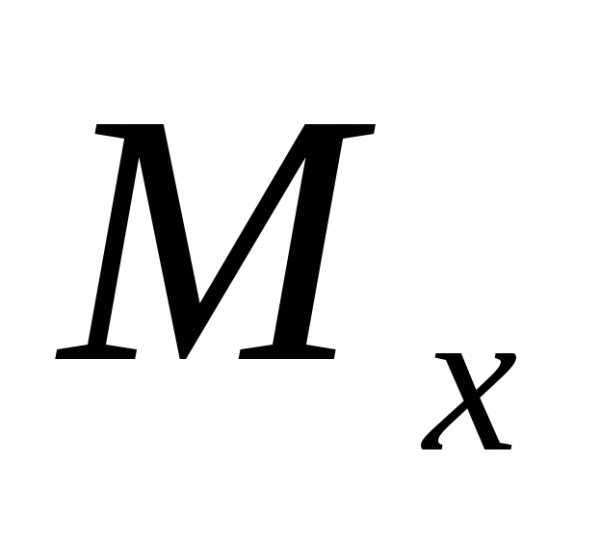 и крутящий
и крутящий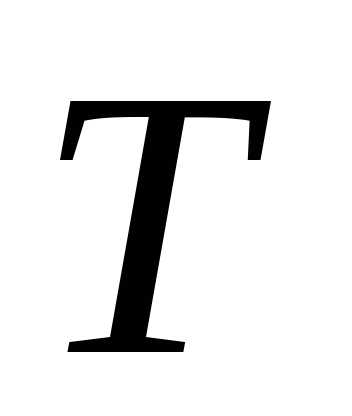 моменты, действующие в плоскостях,
перпендикулярных плоскости рамы (силовые
факторы
моменты, действующие в плоскостях,
перпендикулярных плоскости рамы (силовые
факторы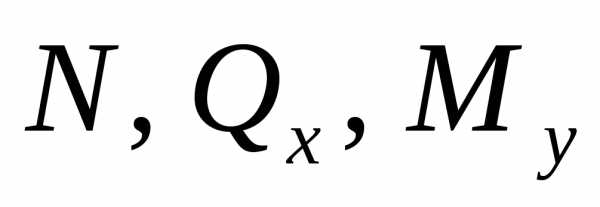 ,
расположенные в плоскости рамы, заведомо
равны нулю).
,
расположенные в плоскости рамы, заведомо
равны нулю).
Эпюры внутренних силовых факторов изображаются в изометрических проекциях. При построении эпюр удобно применять скользящую систему осей координат, обычно правовинтовую: ось zвсегда направлена по оси стержня в сторону свободного конца, осиxиy– перпендикулярно осиz.
Задача 18 Расчеты на прочность при растяжении (сжатии)
Изобразить расчетную схему стержня, приложить заданные силы, выраженные в долях параметра
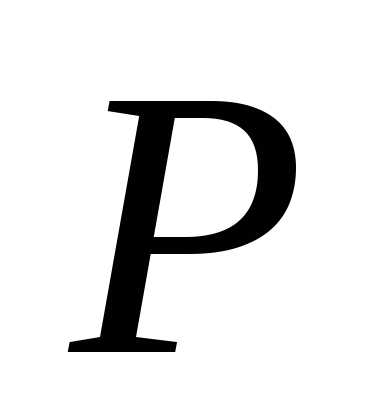 и разбить стержень на участки (границами
участков являются точки приложения
внешних сил и места изменения площади
поперечного сечения).
и разбить стержень на участки (границами
участков являются точки приложения
внешних сил и места изменения площади
поперечного сечения).Построить эпюру продольных сил
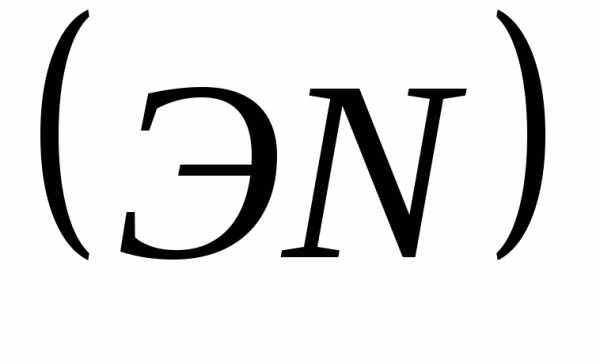 .
.В соответствии с
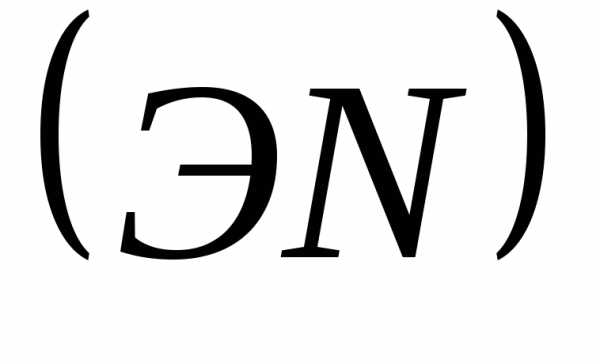 построить (в долях
построить (в долях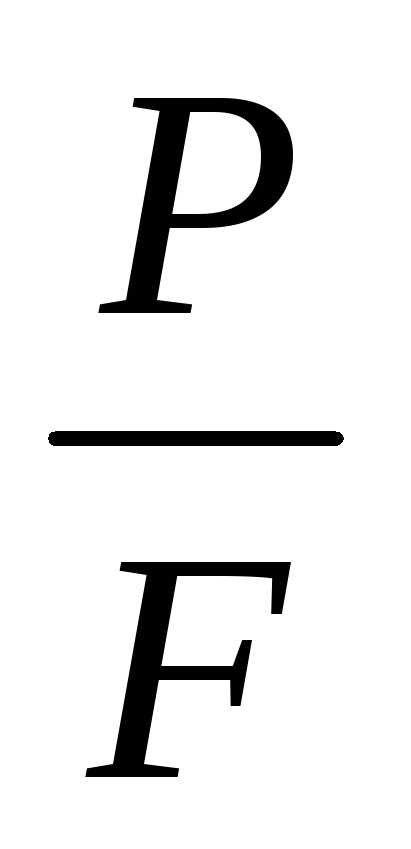 )
эпюру нормальных напряжений в поперечных
сечениях стержня
)
эпюру нормальных напряжений в поперечных
сечениях стержня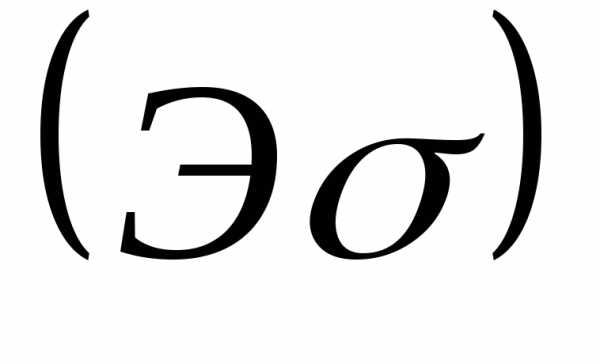 .
.Начиная от сечения, соответствующего заделке, перемещение которого известно (равно нулю), последовательно вычислить перемещения характерных сечений – в начале и в конце каждого участка. В соответствии с условием неразрывности деформаций перемещения смежных сечений на границе участков одинаковы.
Найденные величины перемещений (в долях
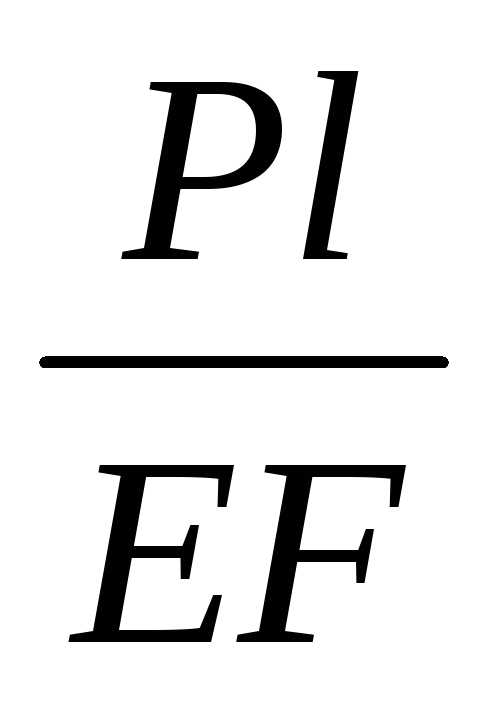 )
отложит в масштабе в виде ординат,
перпендикулярных оси стержня. Эпюра
перемещений
)
отложит в масштабе в виде ординат,
перпендикулярных оси стержня. Эпюра
перемещений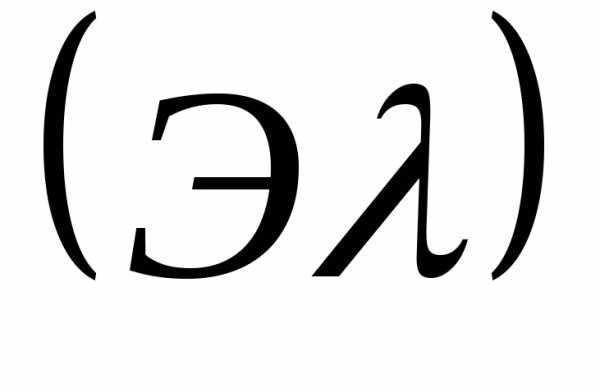 не имеет скачков; штриховка осуществляется
линиями, перпендикулярными оси стержня.
не имеет скачков; штриховка осуществляется
линиями, перпендикулярными оси стержня.По
 найти наибольшее по модулю напряжение
и из условия прочности:
найти наибольшее по модулю напряжение
и из условия прочности: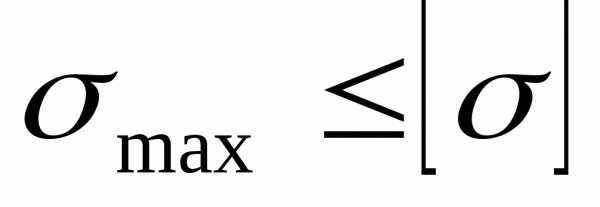 найти параметр нагрузки
найти параметр нагрузки .
Полученное число в
.
Полученное число в округлить до ближайшего кратного двум
или пяти целого числа (допускается
перенапряжение до 5%).
округлить до ближайшего кратного двум
или пяти целого числа (допускается
перенапряжение до 5%).По
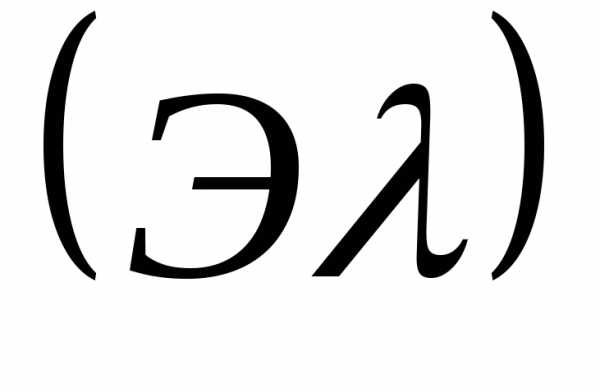 найти удлинение или укорочение отрезка
и наибольшее (по модулю) перемещение
найти удлинение или укорочение отрезка
и наибольшее (по модулю) перемещение .
Вычислить
.
Вычислить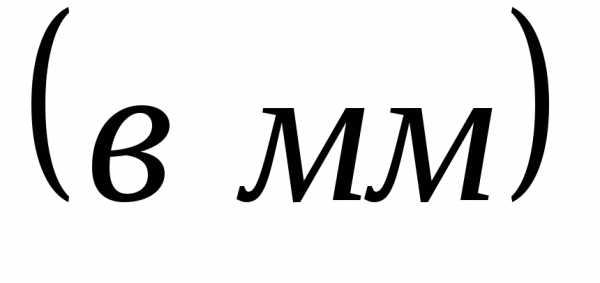 удлинение или укорочение отрезка и
удлинение или укорочение отрезка и при принятом параметре нагрузки
при принятом параметре нагрузки .
.
Задача 22 Расчеты на прочность и жесткость при кручении
Изобразить расчетную схему стержня, разбить стержень на участки и поперечные силы каждого участка выразить в долях параметра поперечных размеров (в качестве такого параметра удобно принять размер d).
Построить эпюру крутящих моментов (ЭТ).
Вычислить геометрические факторы прочности
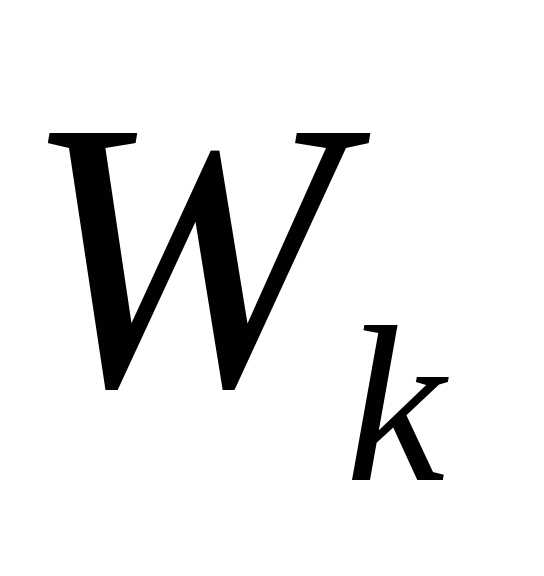 и жесткости
и жесткости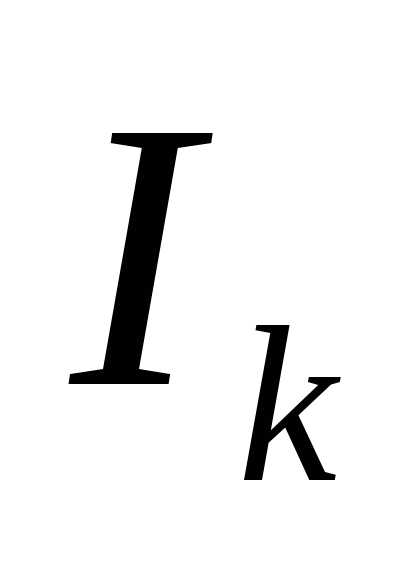 участков в долях параметра поперечных
размеровd.
участков в долях параметра поперечных
размеровd.Вычислить на каждом участке наибольшие касательные напряжения
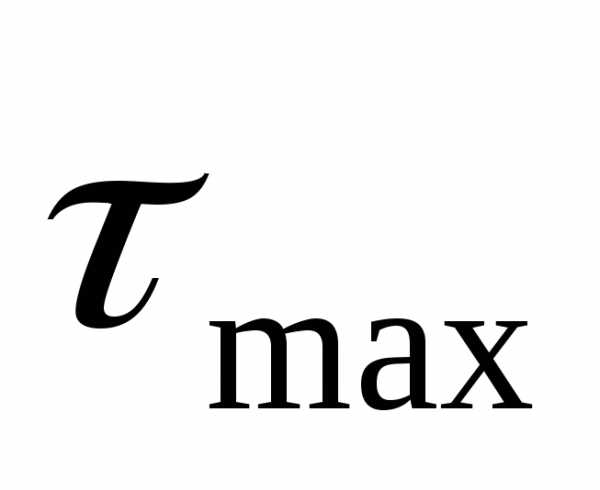
(в долях 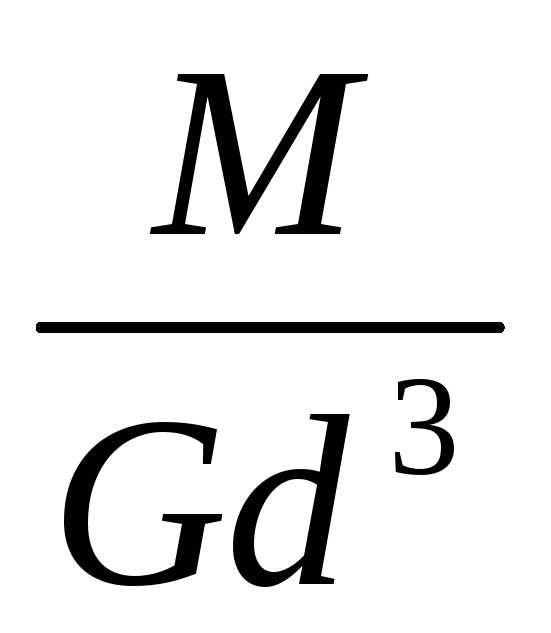 )
и построить (
)
и построить (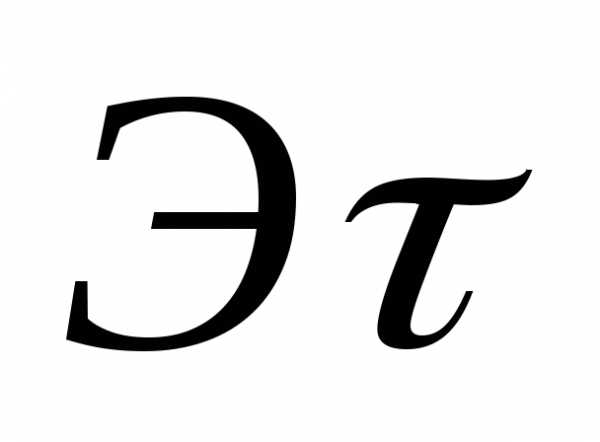 ).
).
5. Из условия прочности: 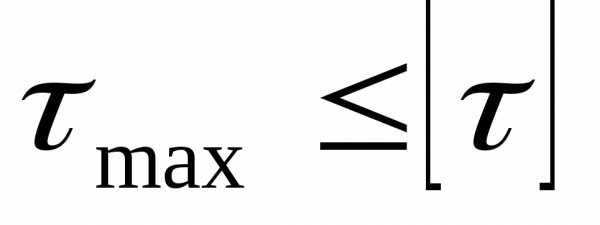 для опасного сечения участка стержня
вычислить допустимые размеры поперечных
сечений.
для опасного сечения участка стержня
вычислить допустимые размеры поперечных
сечений.
6. Вычислить на каждом участке
относительные углы закручивания  (в долях
(в долях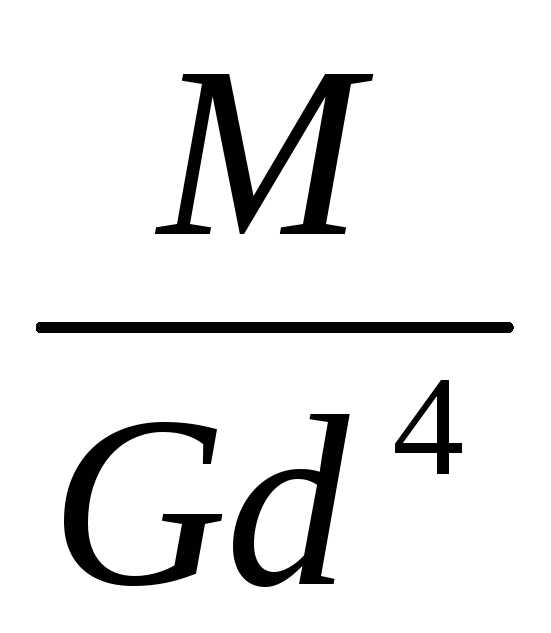 )
и построить для стержня эпюру относительных
углов закручивания (Э
)
и построить для стержня эпюру относительных
углов закручивания (Э ).
).
7. Построить эпюру относительных углов
поворота сечения 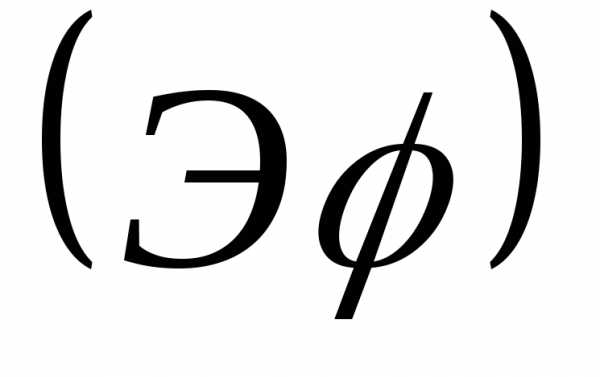 в
относительных величинах (в долях
в
относительных величинах (в долях ).
).
8. Из условия жесткости:  определить числовое значение параметра
поперечных размеровd (мм) и округлить полученное значение
до кратного двум или пяти целого числа.
При выполнении расчета на жесткость
необходимо учесть, что на (ЭQ)
относительные углы закручивания,
представленные в относительных величинах,
имеют размерностьрад/м, а относительный
угол закручивания
определить числовое значение параметра
поперечных размеровd (мм) и округлить полученное значение
до кратного двум или пяти целого числа.
При выполнении расчета на жесткость
необходимо учесть, что на (ЭQ)
относительные углы закручивания,
представленные в относительных величинах,
имеют размерностьрад/м, а относительный
угол закручивания задан по условию задачиград/м.
задан по условию задачиград/м.
9. Выбрать размеры поперечных сечений, удовлетворяющих условиям прочности и жесткости.
10. Вычислить (в град) наибольший угол
поворота поперечного сечения 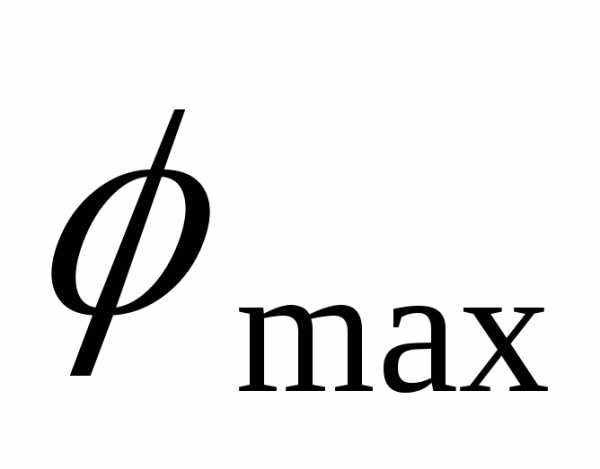 .
.
studfiles.net