Глава 2. Построение эпюр внутренних усилий

Эпюрой называется графическое изображение закона изменения внутренних усилий по длине стержня.

Эпюры внутренних усилий строят для того, что бы определить опасные сечения стержня, т.е. сечения, в которых внутренние усилия достигают наибольших значений, поскольку существует большая вероятность наступления разрушения в этих сечениях.

2.1 Построение эпюры продольной силы

Под действием внешних нагрузок, направленных вдоль оси стержня, или нагрузок, равнодействующая которых направлена также вдоль продольной оси, в поперечных сечениях возникает только один внутренний силовой фактор – продольная сила (N). Такая деформация стержня называется осевое растяжение (сжатие).

Эпюрой продольной силы N называется графическое изображение закона её изменения по длине бруса.

Правило знаков:

Растягивающая продольная сила, т.

е. направленная от сечения, считается положительной, а сжимающая, т.е. направленная к сечению — отрицательной.

Рис.2.1 Правило знаков

Величина и направление продольной силы в сечениях стержня определяются с помощь метода сечений (см. п. 1.3) .

Продольная сила в поперечных сечениях стержня численно равна алгебраической сумме проекций внешних сил на ось стержня, приложенных к рассматриваемой отсеченной части.

. (2.1)

Порядок построения эпюры продольной силы (n)

1. Изображается расчетная схема бруса с указанием численных значений приложенных нагрузок и геометрических размеров бруса.

2. Брус разбивается на участки, границами которых являются точки приложения сосредоточенных сил, а так же начало и конец распределенной нагрузки.

3. Для каждого участка из уравнения равновесия записывается аналитическое выражение продольной силы согласно (2.

1) и вычисляются все её значения, необходимые для построения эпюры, обычно в начале и конце участка.

4. Проводится ось (база) эпюры, параллельно оси бруса. Значения продольной силы для каждого участка откладываются перпендикулярно оси в масштабе. Положительные значения выше оси, отрицательные – ниже.

5. На эпюре ставятся её знаки: «+» или «­», она штрихуется прямыми параллельными линиями, перпендикулярными оси.

6. Проводится проверка правильности построения эпюры.

Для исключения ошибки при составлении уравнения равновесия следует неизвестное внутреннее усилие принимать всегда положительным, так как знак усилия, полученный из решения, позволяет установить, правилен ли был сделан выбор направления силы N, и какой вид деформации при этом возникает – растяжение, если значение

N положительно, или сжатие, если отрицательно.

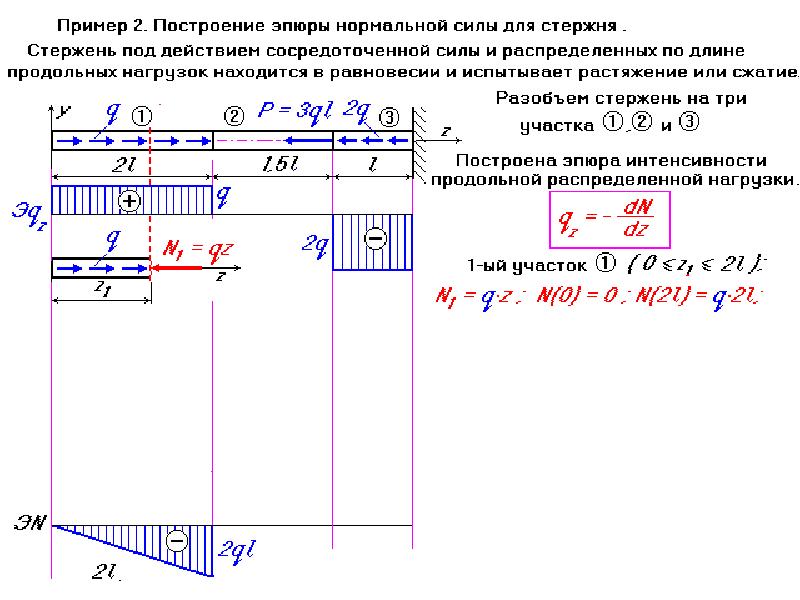
Пример №2.1: Построить эпюру продольной силы для бруса жестко закрепленного левым концом, на который действуют осевые силы F₁ , F₂ , F₃(рис 2. 2)_.

Рис. 2.2 Расчетная схема бруса

Внешние осевые нагрузки делят брус на три участка. Пронумеруем участки со свободного конца. Определим величину продольной силы с помощью метода сечений, а направление в соответствии с правилом знаков.

Эпюра строится под расчетной схемой. Проводится проверка правильности построения эпюры.

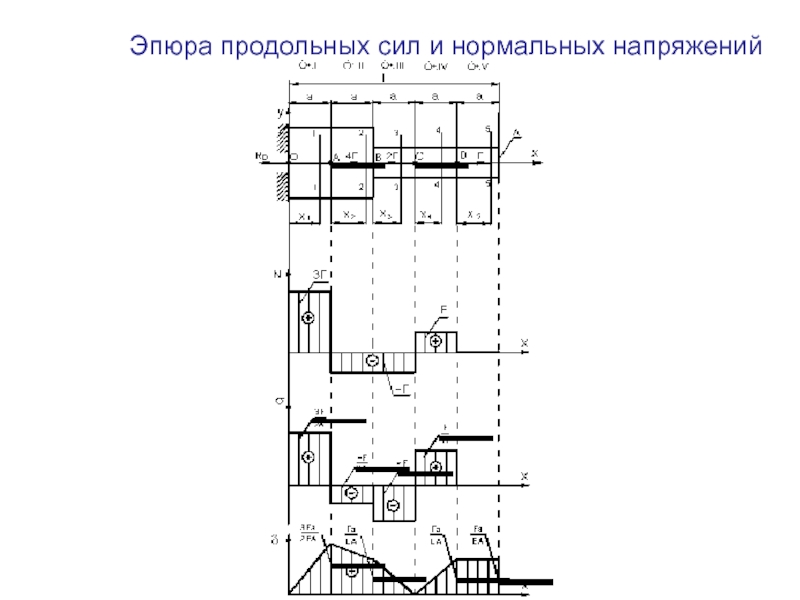
Рис. 2.3 К примеру №2.1. Эпюра продольной силы.

Пример №2.2. Построить эпюру продольной силы для бруса жестко закрепленного левым концом, на который действуют сосредоточенные силы F₁ и F₂, а так же равномернораспределенная нагрузка интенсивностью q₁ и q₂.

Рис. 2.4 К примеру №2.2

Внешние нагрузки делят брус на три участка.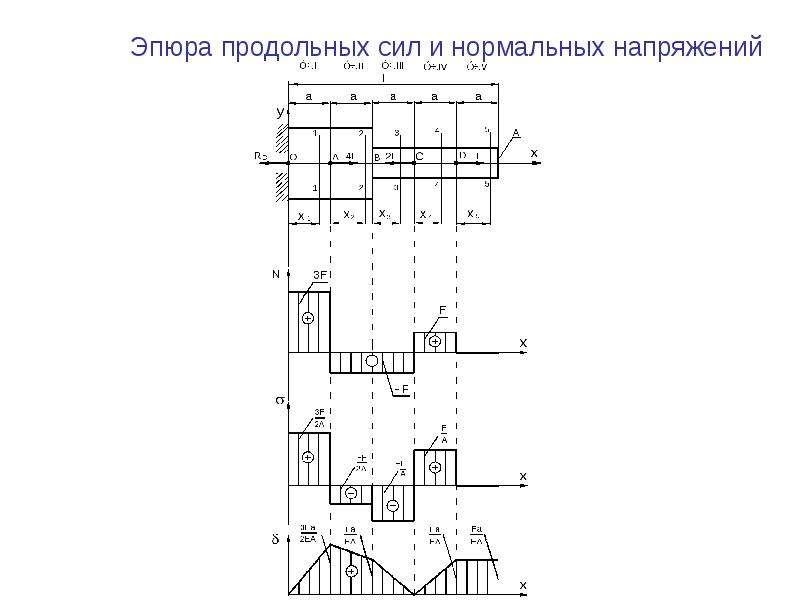 Начнем рассматривать участки со свободного конца. Применяем метод сечений и для каждого участка составляем уравнение равновесия отсеченной части бруса (в данном случае правой), находим значение продольной силы в крайних точках : начало и конец участка.

По полученным значениям строим эпюру продольной силы (рис. 2.4). Проводим проверку правильности построения эпюры.

Эпюры внутренних усилий при растяжении-сжатии и кручении (Лекция №3)

ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ ПРИ РАСТЯЖЕНИИ-СЖАТИИ

Растяжением или сжатием называется такой простой вид сопротивления, при котором внешние силы приложены вдоль продольной оси бруса, а в поперечном сечении его возникает только нормальная сила.

Рассмотрим расчетную схему бруса постоянного поперечного сечения с заданной внешней сосредоточенной нагрузкой Р и распределенной q, (рис.1).

а) расчетная схема, б) первый участок, левая отсеченная часть, в) второй участок, левая отсеченная часть, г) второй участок, правая отсеченная часть, д) эпюра нормальных сил

Рис. 1. Построение эпюры нормальных сил:

 

Пусть . Прежде всего определим опорную реакцию R, задавшись ее направлением вдоль оси х.

Брус имеет 2 участка 1 и 2.

В пределах первого участка мысленно рассечем брус на 2 части нормальным сечением и рассмотрим равновесие, допустим левой части, введя следующую координату х₁, рис.1 б:

Следовательно, в пределах первого участка брус претерпевает сжатие постоянной нормальной силой.

Аналогично поступим со вторым участком. Мысленно рассечем его сечением 2—2, и рассмотрим равновесие левой части (рис.1 в).Установим предварительно границы изменения х₂:

Подставляя граничные значения параметра х₂, получим:

Таким образом, в пределах второго участка брус растянут и нормальная сила изменяется по линейному закону.

Аналогичный результат получается и при рассмотрении правой отсеченной части (рис.1 г):

На основе полученных данных строится эпюра нормальных сил в виде графика распределения нормальной силы по длине бруса (рис. 1 д). Характерно, что скачки на эпюре обусловлены наличием в соответствующих сечениях сосредоточенных сил R и Р, что в свою очередь может служить правилом правильности выполненных построений.

 

ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ ПРИ КРУЧЕНИИ

Кручением называется простой вид сопротивления, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.

Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: m, рис.2.

Методика построения эпюры аналогична только что рассмотренной методике при растяжении-сжатии.

а) расчетная схема, б) первый участок, левая часть в) второй участок, левая часть г) третий участок, правая часть, д) эпюра внутренних крутящих моментов

Рис. 2. Построение эпюры внутренних крутящих моментов:

 

В исходных сечениях No 1,2 и 3 задаются положительными значениями внутренних крутящих моментов М₁, М₂, М₃. Пусть М=ml.

Для первого участка (рис.2 б):

Для второго участка (рис.2 в):

Для третьего участка (рис.2 г):

Границы измерения параметра х₃ в следующей системе координат:

Тогда:

Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис.2 д).

Дальше…

Быстрый и простой способ анализа автомобиля и поведения водителя

Если вы увлекаетесь автоспортом, вы, вероятно, слышали от своего приятеля в пабе, что сегодня он проехал на своей машине разворот со скоростью 1 g и не перестанет хвастаться тем, как великий водитель он. Хотя цифра Фреда в 1 г может выглядеть впечатляюще, это не обязательно означает, что он следующий Айртон Сенна. Лучший способ определить это — посмотреть на диаграмму G-G его машины.

В этой статье будет рассказано, что такое диаграмма G-G и как ее интерпретировать. Как вы увидите, диаграмма G-G двояка. Во-первых, его можно использовать для сравнения или анализа характеристик автомобиля. Во-вторых, мы можем использовать диаграмму G-G, чтобы убедиться, что водитель транспортного средства использует автомобиль в полной мере.

Что такое диаграмма G-G?

Диаграмма G-G — это графический способ представления характеристик автомобиля. По сути, это означает нанесение на график зоны, которая определяет, где автомобиль стабилен и сохраняет сцепление с дорогой.

Рисунок 1: Диаграмма G-G

Ключ к диаграмме G-G кроется в названии. По одной оси у вас есть поперечная сила G, а по другой оси отложена продольная сила G. G — это, по сути, безразмерный способ измерения ускорения. 1 G примерно равен 9 долларам2$   (Гравитация). Так зачем использовать ускорение? Ускорение представляет собой скорость изменения скорости и может быть легко связано с силой уравнением $F = ma$. Таким образом, диаграмма G-G — отличный способ связать воедино скорость и силу, действующую на транспортное средство, в графическом и удобном для чтения формате.

Зона торможения

Важно отметить, что шины обладают ограниченным сцеплением или усилием, которое они могут создать для прилипания автомобиля к поверхности дороги.

Другими словами, они могут выдержать только определенное количество перегрузки, прежде чем они прервут сцепление и начнут скользить. Эта сила может быть продольной (торможение/ускорение), поперечной (поворот) или их комбинацией (например, ускорение вне поворота).

Рисунок 2: Зона торможения

Рассмотрим зону, выделенную на рисунке 2, которая показывает, когда автомобиль тормозит и поворачивает. Здесь единственным ограничивающим фактором является сцепление шин. Тормоза могут приложить более чем достаточное усилие, чтобы заставить шины заблокироваться и потерять сцепление с дорогой, и нет ограничения мощности, когда водитель тормозит перед поворотом.

При торможении автомобиль может снизить ускорение максимум на 1 g. Важно отметить, что это замедление в 1 g происходит, когда автомобиль только тормозит, а не поворачивает. Аналогичным образом, в поворотах автомобиль может достигать максимум 0,8 g, если автомобиль только поворачивает, не нажимая педаль акселератора или тормоз.

Это немного меньше, чем максимальное тормозное усилие из-за таких факторов, как крен кузова и перенос веса в автомобиле.

Однако во время гонки гонщик также окажется в ситуации, когда он тормозит и поворачивает одновременно. Вот тут-то и проявляется магия диаграммы G-G. Диаграмма определяет точку, в которой сцепление будет потеряно для всех различных сценариев, в которых может оказаться водитель.

Рис. 3. Вождение в пределах рабочих характеристик

. Рассмотрим рис. 3. В точке А водитель находится на пределе возможностей автомобиля, достигнуты максимально возможные пределы сцепления с дорогой, и любой дальнейший поворот или торможение могут привести к нестабильности автомобиля. В точке B водитель его немного переварил. Ему нужно либо нажать на тормоза и уйти глубоко в поворот, либо уменьшить угол поворота руля и разбежаться, чтобы машина не скользила. В точке C водитель слишком осторожен. Он может либо поворачивать более агрессивно, либо сильнее тормозить в зависимости от того, где он находится на трассе.

Позже в статье мы увидим, как это можно использовать для анализа производительности водителей по сравнению с производительностью транспортных средств.

Зона ускорения

На рисунке 1 вы, возможно, заметили, что верхняя половина круга не показывает круглую кривую, как нижняя половина круга.

Рисунок 4: Зона ускорения

Причина этого в том, что автомобиль больше не ограничен в сцеплении с дорогой в этих зонах. Вместо этого был достигнут предел мощности двигателя. Например, на первой передаче автомобиль может легко тронуться с места с более чем достаточной мощностью, чтобы колеса потеряли сцепление с дорогой и начали пробуксовывать. Однако в 5

-й -й или 6-й ^-й -й передачи это уже невозможно.

Достижимое ускорение также зависит от скорости. Рассмотрим автомобиль, разгоняющийся от 50 до 100 км/ч. При такой относительно небольшой скорости при минимальном аэродинамическом сопротивлении, действующем на автомобиль, разгон будет намного быстрее, чем, скажем, от 200–250 км/ч, хотя разность скоростей все равно составляет всего 50 км/ч. Диаграмма обычно рисуется для максимального ускорения, которое может развить автомобиль на обычном круге трассы.

Некоторые практические примеры

Надеюсь, теперь концепция диаграммы G-G ясна, и вы понимаете, почему это такой замечательный инструмент для просмотра производительности автомобиля. Теперь мы кратко рассмотрим некоторые практические примеры, чтобы превратить теорию в реальность.

Сравнение двух диапазонов производительности транспортных средств

Как мы уже упоминали, диаграмма G-G определяет диапазон производительности транспортного средства. Следовательно, более спортивный автомобиль будет иметь большую диаграмму GG в качестве максимального предела сцепления, и, следовательно, силы будут больше.

Рисунок 5: Сравнение диапазонов производительности

Рассмотрим рисунок 5, на котором сравниваются два диапазона производительности Toyota Celica и Porsche 928S. Как вы можете видеть, общая форма диаграммы G-G соответствует тому, что мы ожидаем, но конверт Porsche намного больше, чем у Toyota.

Большой круг можно отнести к нескольким вещам. Первое и, пожалуй, самое важное отличие — это шины на двух автомобилях. Porsche оснащен гораздо более мягкими и спортивными шинами, чем Toyota, что сразу же создает огромную разницу в производительности. Кроме того, Porsche спроектирован так, чтобы быть намного более быстрым автомобилем, чем Toyota, с гораздо более жесткой подвеской, более качественными тормозами и в целом более жесткой, хорошо сбалансированной конструкцией для гоночной трассы.

Все это приводит к гораздо большему диапазону производительности Porsche.

Анализ производительности водителя

Как мы кратко коснулись рис. 3, GG-диаграмму можно использовать для проверки того, максимально ли использует водитель возможности своего автомобиля.

Рис. 6: Анализ производительности водителей

Рассмотрим рис. 6. Здесь огибающая характеристик транспортных средств наложена на фактические данные о перегрузке от водителя в течение нескольких кругов. Отсюда можно сделать несколько интересных выводов.

Во-первых, это схема с вращением против часовой стрелки, так как большая часть данных о перегрузке находится в левой части схемы, поскольку схема в основном состоит из левых поворотов.

Вторая и более важная информация заключается в том, что у водителя есть некоторое время, которое можно выиграть в зонах торможения. В зоне разгона видно, что по большей части водитель использует доступные характеристики автомобиля. Это видно по данным, заполняющим большую часть диаграммы G-G в зоне ускорения.

Тем не менее, в зоне торможения есть две четкие зоны, где нет данных о перегрузке, но на диаграмме G-G имеется значительный объем производительности (отмечено стрелками A). Это показывает нам, что водитель мог либо сильнее тормозить, либо более резко поворачивать в этих зонах, не выходя за пределы возможностей своего автомобиля. Как вы можете видеть, диаграмма предлагает почти мгновенное представление о производительности водителя, что является одним из основных преимуществ диаграммы G-G.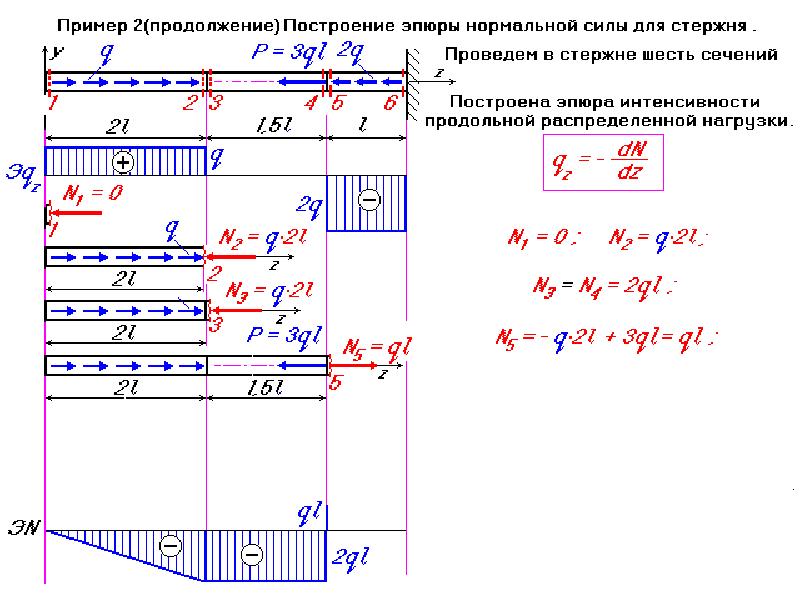 С этого момента команда могла глубже погрузиться в настройку автомобиля или стиль вождения водителя, чтобы улучшить использование общих характеристик автомобилей.

Вот оно!

Надеюсь, что концепция диаграммы G-G была передана понятно и всем понятно, как ее можно использовать для анализа работы автомобиля или водителя. Если у вас есть какие-либо вопросы по этой теме, дайте мне знать, оставив комментарий ниже, и я свяжусь с вами.

Как обычно, я оставлю несколько ссылок ниже, если вы захотите еще немного почитать сами.

Спасибо за чтение и не забывайте мыть руки и берегите себя во время Коронавируса!

Полезные ссылки

http://hpwizard.com/gg-diagram.html

https://www.trailbrake.us/featured-articles/the-g-g-diagram

Шины. .net

[su_list icon=»icon: angle-double-right» icon_color=»#3498db»]

• Часть 1 — Шина как вертикальная пружина
• Часть 2. Взаимодействие с дорогой и контактная накладка

[/su_list]

Наконец-то мы подошли к самому интересному в нашем кратком обзоре шин – анализу того, как шина развивает продольные и поперечные силы в пятне контакта и какие ключевые параметры определяют ее поведение.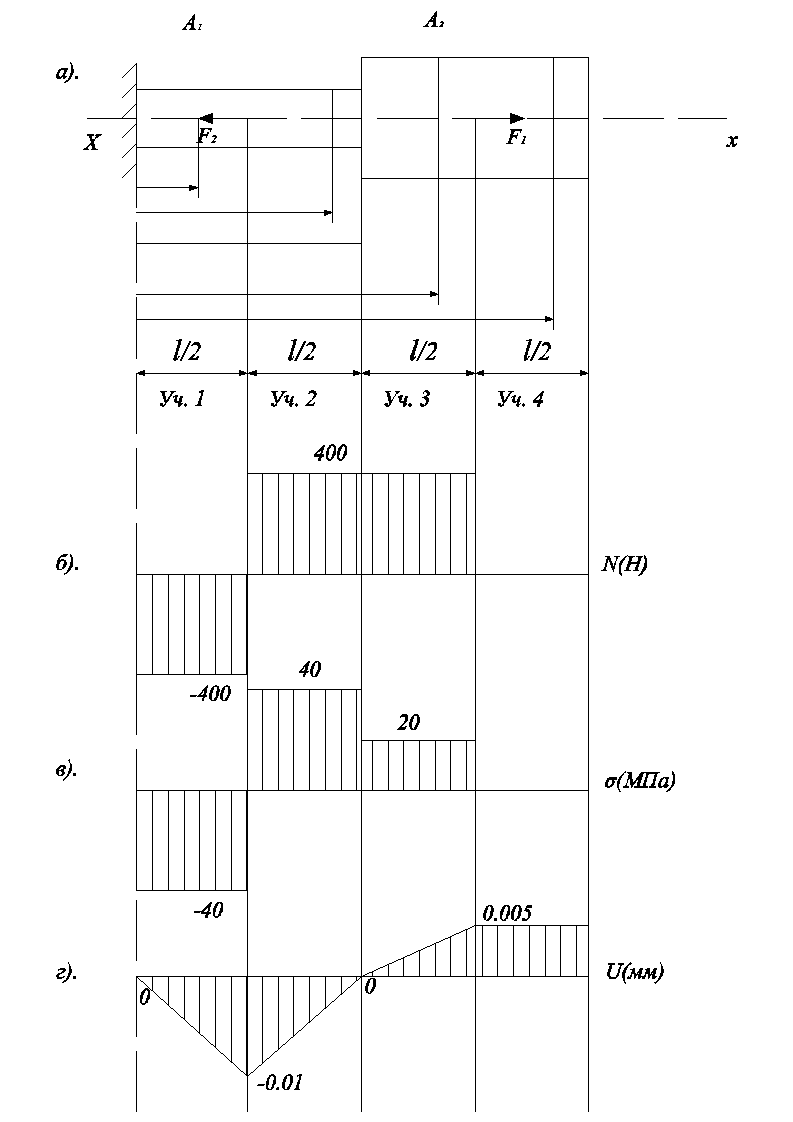

Начнем с продольной силы F _x .

Продольная сила

Прежде всего, мы кратко проанализируем, по каким причинам автомобилям с четырьмя шинами необходимо обмениваться (продольными) силами с дорогой, например, при торможении.

Если мы рассмотрим автомобиль, движущийся по прямой, и водитель хочет замедлить его, задействовав тормоза. Мы понимаем, что четырем шинам необходимо обмениваться продольными силами с дорогой, чтобы вызвать замедление и уравновесить связанную с ним инерционную силу.

Если автомобиль замедляется с продольным ускорением A _x , то для достижения равновесия (в устойчивом состоянии) дорога должна будет применить к автомобилю F _x , заданное уравнением:

F _х = -м * А _х

Где м — масса автомобиля. Сумма сил, которыми каждая шина обменивается с дорогой, должна быть равна F _x . На нашей картинке ниже это указано:

F _x = F _xf + F _xr

Где F _xf и F _xr соответственно тормозные силы передней и задней осей.

Силы, воздействующие на шины и транспортное средство

Чтобы понять, как шина может обмениваться продольными силами с дорогой, нам сначала нужно определить ключевое понятие: коэффициент скольжения .

Коэффициент скольжения и кривая скольжения

Представьте себе автомобиль, который движется по прямой с определенной скоростью, а водитель начинает тормозить. Тормозной момент, действующий на колеса, вызовет замедление, и скорость вращения колеса станет меньше, чем скорость, которую имело бы колесо, если бы оно двигалось с той же скоростью, но без торможения.

Коэффициент скольжения — это измерение разницы между скоростью движения автомобиля и скоростью качения колес.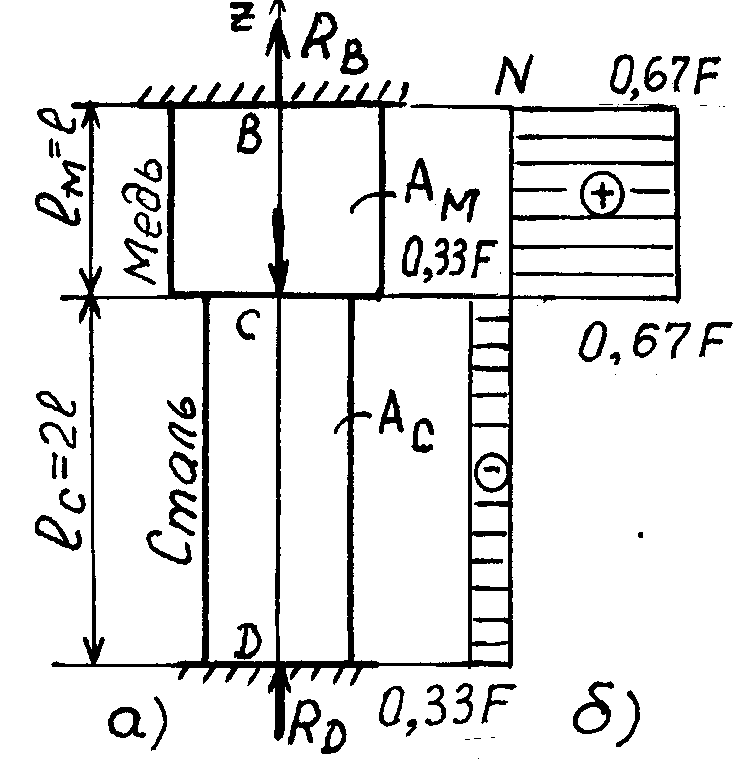 Его значение определяется следующим уравнением:

, где ω — угловая скорость колеса, R — его радиус качения и V — поступательная скорость автомобиля. Из-за проскальзывания шины (соотношение) происходит молекулярное сцепление и вдавливание, вызывая продольную силу в пятне контакта.

SR отрицательна при торможении, положительна при ускорении вперед и примерно равна нулю при свободном качении колеса.

Как мы упоминали в самом начале, когда мы анализировали обмен силами сцепления в пятне контакта, наличие проскальзывания необходимо для того, чтобы шина создавала плоские силы. Как мы увидим позже более подробно, величина продольной силы зависит также от вертикальной нагрузки, действующей на шину. Аналогично тому, что мы видели для нашей простой резиновой накладки, мы можем определить коэффициент продольного трения шины как отношение между F _x и вертикальной силой F _z действующая на шину:

Для заданной вертикальной нагрузки соотношение между коэффициентом скольжения и продольной силой F _x может быть описано с помощью графика, часто называемого кривой скольжения :

График кривой скольжения

Гоночные шины обычно достигают максимального значения, когда SR принимает значения от 0,05 до 0,15.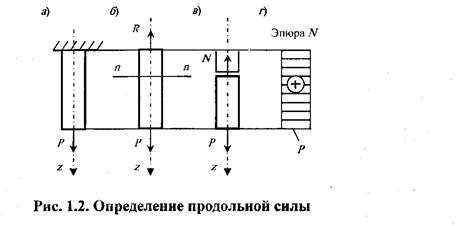 Как мы уже упоминали, максимальное доступное F _x для определенного SR зависит также от вертикальной нагрузки, действующей на шину: если вертикальная нагрузка увеличивается, то же самое F _х . Как мы увидим позже, скорость, с которой F _x растет с F _z , не является линейной.

Если мы проанализируем форму кривой F _x vs SR, мы можем выделить три основных области.

Первую область, A на графике кривой скольжения, часто называют линейной областью , потому что связь между F _x и SR является более или менее линейной. Вторая область, B , часто называется переходной и характеризуется изгибом кривой скольжения до достижения пикового значения силы. Наконец, третья область, C , обычно идентифицируется как фрикционная область , потому что при столь высоких значениях проскальзывания проскальзывает все пятно контакта шины.

Форма кривой очень сильно связана с тем, что физически происходит в пятне контакта, когда, например, к колесу прикладывается тормозной момент. Поскольку скорость вращения колеса меньше скорости автомобиля, дорога будет тянуть протектор шины, как только он соприкоснется с землей во время вращения колеса. Каждая резиновая часть, входящая в зону контакта, первоначально находится в условиях сдвига. Когда он скользит по дорожному полотну, покидая пятно контакта, он попадает в ситуацию проскальзывания.

Протектор шины может деформироваться, а ее брекер намного жестче. Следовательно, когда к колесу прикладывается тормозной момент, поверхность дороги оттягивает пятно контакта назад, но искривление испытывает только протектор, а брекер сохраняет более или менее свою первоначальную форму. Это приводит к относительному движению между нижней частью протектора и брекером. Это приводит к сдвигу на передней кромке пятна контакта. Когда шина катится, а резина движется к задней кромке пятна контакта, напряжение протектора увеличивается, и, оставаясь сдвинутой, резина переходит в состояние скольжения.

Из F1 Technical .net

Важным моментом в кривых продольного скольжения является влияние температуры шин. В условиях очень высокого напряжения/высокой деформации/высокого проскальзывания температура резины имеет тенденцию к очень быстрому повышению; Коэффициент трения шин сильно зависит от их температуры.

Чем больше проскальзывание, тем больше выделяется теплоты и тем выше температура.

В области A приведенной выше кривой проскальзывания протектор в основном подвергается сдвигу, что приводит к умеренному количеству высвобождаемой энергии. По мере продвижения в регион B и C коэффициент скольжения увеличивается, и шина входит в состояние истинного скольжения, высвобождая, таким образом, гораздо большее количество энергии. Это происходит в виде тепла, которое повышает температуру протектора и каркаса.

В экстремальной ситуации, когда шина заблокирована и коэффициент скольжения равен единице, это явление проявляется еще сильнее. Нередко заблокированные шины дымятся из-за того, что резина нагревается до очень высоких температур.

При высоких температурах гистерезис резины падает, и то же самое происходит с доступным сцеплением, что еще больше способствует наклону кривой скольжения после пика.

Последний интересный момент о кривых скольжения заключается в том, что при заданном значении F _x мы можем найти два различных значения коэффициента скольжения, создающие его.

Slip Curve Plot 2

Мы еще вернемся к этому при описании боковых кривых. Поскольку более высокие коэффициенты скольжения соответствуют большему количеству энергии, высвобождаемой в виде тепла, работа в режиме SR1 вызовет меньшее повышение температуры в шине, чем работа в режиме SR2, при одном и том же F _x . Шина, способная заменить дорогу той же F _x также для более высоких коэффициентов скольжения является причиной того, что можно увидеть, как автомобили пробуксовывают свои шины на выходе из поворота и все еще очень быстро ускоряются.