| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Основные законы Динамики. Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||
3. Динамика материальной точки и поступательного движения твердого тела Основные формулы
,
где -масса материальной точки, — скорость движения.,
где – тангенциальное (касательное) ускорение,
– нормальное (центростремительное) ускорение.
где – коэффициент трения скольжения; – сила нормального давления.
,
где — величина деформации; — коэффициент жесткости.
,
где – гравитационная постоянная, и – массы взаимодействующих точек, – расстояние между точками.
где — число материальных точек (или тел), входящих в систему.
,
где — проекция силы на направление перемещения; — угол между направлениями силы и перемещения.
,
, или .
.
,
где – ускорение свободного падения.
.
.
.
Примеры решения задач
Задача 1. На шнуре, перекинутом через неподвижный блок, подвешены грузы массами и (). Считаем нить и блок невесомыми и пренебрегаем трением в блоке. С каким ускорением движутся грузы? Какова сила натяжения шнура во время движения?
Дано: Решение:
Записываем второй закон Ньютона для каждого тела в векторной форме:
Поскольку ,
считаем, что тело массой движется вниз, а тело массой
—
вверх. Ось совпадает с направлением ускорения.
Записываем второй закон Ньютона для
каждого тела в проекции на направление
оси :
Ось совпадает с направлением ускорения.
Записываем второй закон Ньютона для
каждого тела в проекции на направление
оси :
Складывая почленно эти уравнения, получаем:
.
Подставляя это выражение в одно из уравнений системы, получаем выражение для силы натяжения:
.
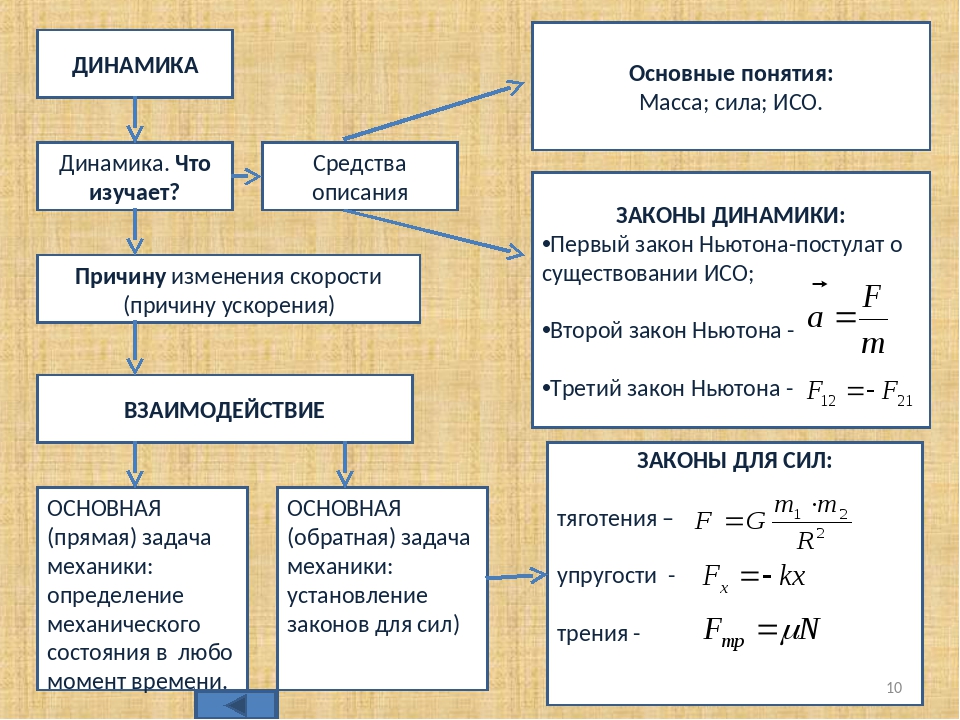
Задача 2. В установке (см. рис.2.2) угол наклонной плоскости с горизонтом , массы тели. Считая нить и блок невесомыми, определите ускорение, с которым движутся тела, и силу натяжения нити, если телоопускается. Коэффициент трения телао плоскость равен 0,1.
Дано: Решение:
; ; ; . | Делаем рисунок, расставляем силы, действующие на каждое тело:Рис.2.2 |
Записываем второй закон Ньютона для каждого тела в векторной форме: | |
Для каждого тела устанавливаем оси координат и записываем второй закон Ньютона для каждого тела в проекциях на направления и :
.
Учитывая, что , получаем систему:
Складываем почленно эти уравнения:
.
Отсюда получаем выражение для ускорения:
.
Подставляем числа:
.
Из уравнения 2) выражаем силу натяжения: .
Подставляем числа: .
Ответ: ;.
Задача 3. Движущееся тело массой ударяется о неподвижное тело массой . Считая удар упругим и центральным, определите, какую часть своей первоначальной кинетической энергии первое тело передает второму при ударе. Задачу решите сначала в общем виде, а затем рассмотрите случаи: 1) ; 2) .
. (1)
Для
определения скорости второго тела после
удара запишем закон сохранения импульса
в проекции на направление движения и
закон сохранения механической энергии,
полагая, что система тел замкнута и в
ней действуют только консервативные
силы.
(2)
Преобразуем систему (2) к виду
(3)
Разделив одно на другое выражения системы (3), получим , а после подстановки скорости в первую формулу системы (3) получим
. (4)
Отношение энергий (1) приобретает вид
.
1) Если , то =1. При равенстве масс первое тело полностью отдает энергию второму, т.е. первое тело остановится, а второе начнет двигаться со скоростью первого тела.
2) Если , то .
Ответ: 1) =1; 2) .
Основы динамики для чайников в физике. Решение задач, законы
Динамика изучает причины, по которым движение происходит именно так, а не иначе. Ее интересуют силы, которые действуют на тела. У динамики есть прямая и обратная задачи. Прямая — по известному характеру движения определить равнодействующую всех сил, действующих на тело. Обратная — по заданным силам определить характер движения тела. Конечно, мы должны познакомиться с понятием силы, инерциальной системы отсчета, законами Ньютона. Но обо всех основах динамики по порядку. В данной статье рассмотрим основные законы динамики и приведем пример решения задачи по основам динамики.
У динамики есть прямая и обратная задачи. Прямая — по известному характеру движения определить равнодействующую всех сил, действующих на тело. Обратная — по заданным силам определить характер движения тела. Конечно, мы должны познакомиться с понятием силы, инерциальной системы отсчета, законами Ньютона. Но обо всех основах динамики по порядку. В данной статье рассмотрим основные законы динамики и приведем пример решения задачи по основам динамики.
В чем сила, брат?
Красота – страшная сила! А еще, конечно, сила в правде, а у кого-то в деньгах. Но мы-то знаем, что все это заблуждения и домыслы. Сила – в Ньютонах!
Сила. Измеряется в Ньютонах
Сила – векторная физическая величина, количественная мера интенсивности взаимодействия тел.
Единицей измерения силы в системе СИ является Ньютон. Один Ньютон – это такая сила, которую мы можем приложить к телу массой один килограмм. При этом она изменит скорость тела на 1 м/с за одну секунду.
Бывает , что на тело действует сразу несколько сил. В принципе, в мире нет тел и предметов, на которые не действуют вообще никакие силы. Вот с утра едем мы на экзамен, и так бы нам хотелось, чтоб никакие силы нас не трогали и оставили в покое… Но нет. Притяжение давит вниз, ветер сдувает вбок, кто-то еще нагло толкает в метро. В таком случае можно все эти силы представить как одну, но оказывающую то же действие, что и все. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.
Например, на рисунке ниже равнодействующая сил равна нулю, потому как лебедь рак и щука так никуда и не сдвинули воз.
Равнодействующая сила
Масса и Вес
Масса – скалярная аддитивная физическая величина, являющаяся количественной мерой инертности тела, то есть его способности сохранять постоянную скорость.
В системе СИ измеряется в килограммах. Если не ищете легких путей и хотите быть особенно экстравагантным, можете измерять в фунтах, пудах и унциях.
Важно! Не стоит путать массу тела и вес. Ведь масса – скалярная величина, а вес – это сила, с которой тело действует на опору или подвес. Другими словами, масса всегда остается постоянной, это собственная характеристика тела. А вот вес может меняться. Например, Ваш лунный вес будет отличаться от земного, т.к. ускорение свободного падения на планетах различно.
Вы все еще читаете? Поздравляем, Вы просто молодцы! Давайте переходить к законам Ньютона, ведь рассматривая основы динамики невозможно обойти их стороной. Законы Ньютона — основные законы динамики.
Первый закон Ньютона
Как мы уже знаем, движение осуществляется в системе отсчета. Так вот, существуют такие системы отсчета, которые называются инерциальными (ИСО). Что это значит? Это тоже идеализация, наподобие материальной точки. Существование ИСО постулируется первым законом Ньютона, который собственно гласит вот что:
Существуют системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно или покоятся, если на них не действуют никакие силы, или действие других сил скомпенсировано (равнодействующая равна нулю).
Если в инерциальной системе отсчета мы разгоним автомобиль до скорости 60 км/ч, пренебрежем силой трения колес об асфальт и сопротивлением воздуха, а потом выключим двигатель, авто продолжит катиться по прямой со скоростью 60 км/ч бесконечно долго, пока не закончится дорога.
Второй закон Ньютона
Второй закон Ньютона еще называют основным законом динамики. Самая простая его формулировка такова:
В ИСО ускорение, приобретаемое телом, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе тела.
Еще одна формулировка второго закона Ньютона: производная импульса материальной точки по времени равна действующей на материальную точку силе. Импульс – мера количества движения, равняется произведению массы на скорость.
Действительно, вспомним кинематику (производная от скорости равна ускорению) и запишем:
Третий закон Ньютона
В ИСО тела действуют друг на друга с силами, лежащими на одной прямой, противоположными по направлению и равными по модулю.
Напоследок, как всегда, приведем пример решения задачи на основы динамики.
Брусок массой 5кг тянут по горизонтальной поверхности за веревку, составляющую угол 30 градусов с горизонтом. Сила натяжения веревки – 30 Ньютонов. За 10 секунд, двигаясь равноускоренно, брусок изменил скорость с 2 м/с до 12 м/с. Найти коэффициент трения бруска о плоскость.
Решение:
Нарисуем брусок. На него действуют сила тяжести, сила нормальной реакции опоры, сила трения и сила натяжения веревки. Веревку будем считать нерастяжимой. Первым делом найдем ускорение бруска, а затем вычислим проекцию сил на горизонтальную ось и запишем второй закон Ньютона.
Основы динамики в физике очень важны для понимания процесса движения. Помните, друзья, в экстремальных условиях сессии наши авторы всегда готовы поддержать Вас и облегчить учебную нагрузку. Удачи Вам!
+50 формул по физике за 7-11 класс с пояснением
Мы собрали основные формулы по физике с пояснениями в картинках.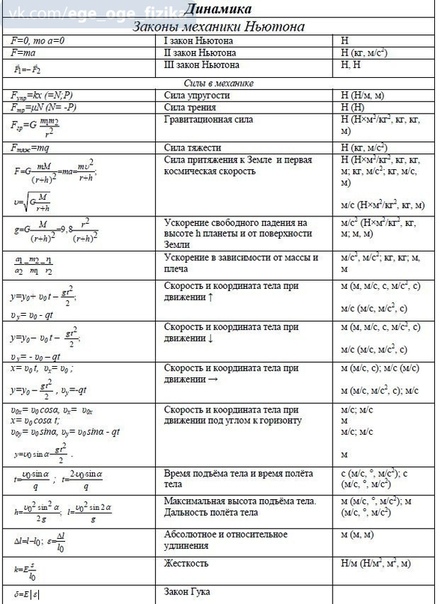 Более пятидесяти формул, разделенные по категориям физики: кинетика, динамика, статика, молекулярка, термодинамика, электричество, магнетизм, оптика, кинетика. Это не статья, а огромная шпаргалка по физике!
Более пятидесяти формул, разделенные по категориям физики: кинетика, динамика, статика, молекулярка, термодинамика, электричество, магнетизм, оптика, кинетика. Это не статья, а огромная шпаргалка по физике!
Основные формулы по физике: кинематика, динамика, статика
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:
Это термодинамика:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Основные формулы оптической физики
Переходим к следующему разделу по физике – оптика. Здесь даны 8 основных формул, которые необходимо знать. Будьте уверены, задачи по оптике – частое явление:
Основные формулы элементов теории относительности
И последнее, что нужно знать перед экзаменом. Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Основные формулы световых квантов
Этими формулами приходится часто пользоваться в силу того, что на тему “Световые кванты” попадается немало задач. Итак, рассмотрим их:
Итак, рассмотрим их:
На этом можно заканчивать. Конечно, по физике есть ещё огромное количество формул, но они вам не столь не нужны.
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
P.S. Хватило ли вам 50 формул по физике, или статью нужно дополнить? Пишите в комментариях.
Более 50 основных формул по физике с пояснением обновлено: 22 ноября, 2019 автором: Научные Статьи.Ру
формулы, определение, задачи / Блог / Справочник :: Бингоскул
Кратко о 2 законе Ньютона: формулы, определение, задачи
Ньютон установил связь между ускорением и силой, где F – сила, действующая на тело массой m, вызывает ускорение тела равное – a.
Помни!!!
- 2 закон Ньютона называют еще основным законом динамики.
- Под телом подразумевают материальную точку, движение которой рассматривают в инерциальной системе отсчета.
1. Формулировка
«В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки»
2. Определение
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение, причем направления силы и ускорения совпадают.
Если на тело действует сила, то оно приобретает ускорение.
3. Формула
Математически второй закон Ньютона записать в виде:
m\overrightarrow { a } =\overrightarrow { F }
- m — масса материальной точки
- \overrightarrow { F } — сила действующая на тело/ускорение материальной точки
- \overrightarrow { a } — ускорение тела
Второй закон Ньютона в импульсной форме:
\frac { d \overrightarrow { p } } { dt } =\overrightarrow { F }
- \overrightarrow { p } — импульс точки,
\overrightarrow { p } = m\overrightarrow { v }
- \overrightarrow { v } — скорость точки.
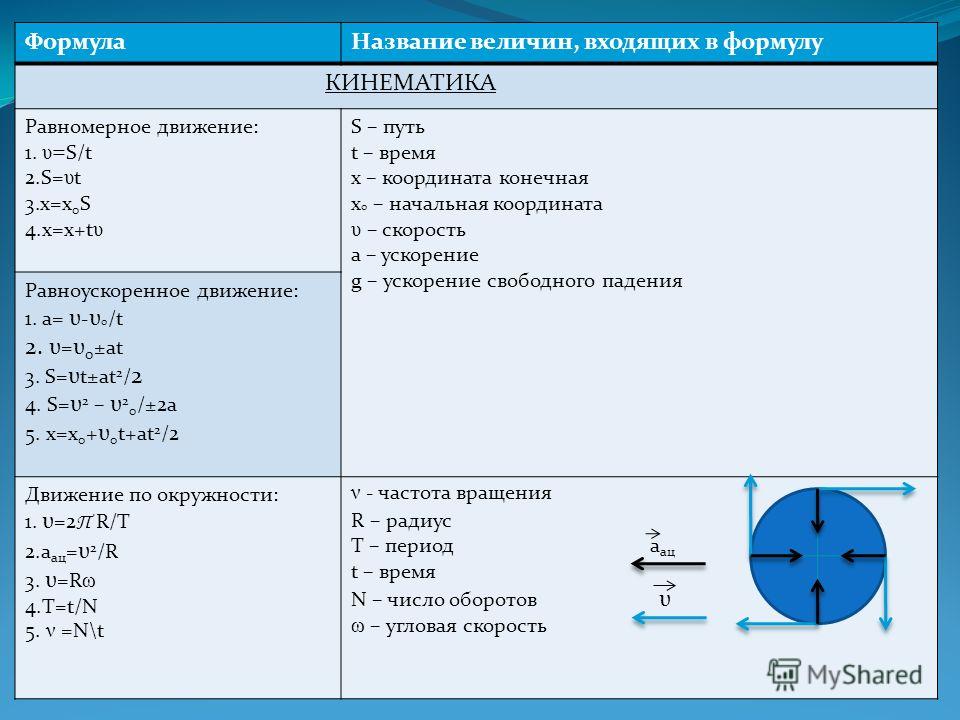
- \frac { d \overrightarrow { p } } { dt } — производная импульса по времени.
Единица измерения — единица силы — 1 Н (1 ньютон) — сила, которая телу массой 1 кг сообщает ускорение 1 м/с2.
1 Н = 1 кг · 1 м/с2 = 1 кг · м/с2.
Ускорение, приобретаемое материальной точкой в ИСО:
- Прямо пропорционально действующей на точку силе;
- Обратно пропорционально массе точки;
- Направлено в сторону действия силы.
Если на тело одновременно действуют несколько сил — F1,F2 и F3, то под силой в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил:
F=F1+F2+F3
Задачи с ответами смотри в задании 2 по физике.
Смотри также:
Глава 7. Вращательное движение. Кинематика и динамика
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
(7. |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2. 1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7. |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7. 1.2) используем связь угловой и линейной скоростей (7.5). Имеем
1.2) используем связь угловой и линейной скоростей (7.5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7.5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7. 2.5), центростремительное ускорение сообщается силой трения
2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7.2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7. 2.10 – ответ 2).
2.10 – ответ 2).
Инфляция с поправкой на вирус
С началом коронакризиса аналитики столкнулись с неопределенностью изменения многих экономических показателей – и, соответственно, с недоверием обывателей, да и некоторых специалистов. Точность измерения вообще снижается во время кризисов – т. е. именно тогда, когда потребность в надежных оценках наиболее велика. Но текущий кризис выделяется даже на этом фоне: он аномально скоротечен и во многом вызван неэкономическими причинами.
Бросающиеся в глаза проблемы измерения связаны с построением индексов потребительских цен (ИПЦ). Во-первых, с началом карантина резко изменилась структура потребительских расходов. Особенно сильно снизилось потребление услуг, а также приобретение ряда непродовольственных товаров. Структура потребительских расходов определяет веса, с которыми при построении ИПЦ учитывается динамика цен и тарифов на отдельные товары и услуги. Если во время кризиса использовать докризисные веса, получим искаженные оценки динамики стоимости жизни. Чтобы учесть изменения структуры потребительских расходов, необходимы результаты обследований бюджетов домашних хозяйств. Но эти обследования проводятся в квартальном режиме, а для построения новой системы весов на их основе требуется дополнительное время. В результате обновление весов с целью учета кризисных реалий возможно, лишь когда скоротечный коронакризис уже закончится.
Чтобы учесть изменения структуры потребительских расходов, необходимы результаты обследований бюджетов домашних хозяйств. Но эти обследования проводятся в квартальном режиме, а для построения новой системы весов на их основе требуется дополнительное время. В результате обновление весов с целью учета кризисных реалий возможно, лишь когда скоротечный коронакризис уже закончится.
В соответствии с действующей методологией уточнения весов вслед за изменением структуры потребительских расходов производятся в России ежегодно с началом календарного года. Более частые уточнения весов в мире не практикуются, поскольку это чревато возникновением искажений по причинам, связанным с нюансами методов. Ситуация усугубляется тем, что во всем мире однажды опубликованные оценки ИПЦ впоследствии не уточняются. Другими словами, статистика потребительских цен сразу пишется набело, без черновиков. Это означает, что оценки динамики потребительских цен, доступные нам в ходе кризиса, неизбежно искажены. Чтобы понять направление и масштаб искажений, необходимо проведение специального исследования.
Чтобы понять направление и масштаб искажений, необходимо проведение специального исследования.
Во-вторых, некоторые товары и услуги, цены и тарифы которых учитываются при построении ИПЦ, перестают быть доступными потребителям. С точки зрения измерения инфляции карантин в первые месяцы коронакризиса напоминает плановую экономику с ее вечным дефицитом, когда свободно приобрести многие товары и услуги было невозможно. Как в такой ситуации строить индексы цен? Как их интерпретировать? Казалось бы, можно строить индексы лишь на основе цен и тарифов тех товаров и услуг, которые доступны потребителям, используя веса, основанные на фактической (кризисной) структуре потребительских расходов. Но выше было показано, что в режиме реального времени это невозможно.
Это значит, что в процессе кризиса можно использовать лишь докризисную корзину с докризисными весами. Но где взять ценовые котировки на товары и услуги, ставшие недоступными потребителям? Единственный выход – в их доопределении (импутации) в соответствии с некоторым алгоритмом. Каким бы ни был этот алгоритм, он порождает неопределенность оценок динамики потребительских цен. Это, в принципе, можно сделать по окончании кризиса, но проведение такого анализа не является задачей статистической службы.
Каким бы ни был этот алгоритм, он порождает неопределенность оценок динамики потребительских цен. Это, в принципе, можно сделать по окончании кризиса, но проведение такого анализа не является задачей статистической службы.
В-третьих, даже в периоды стабильного (некризисного) развития, цены и тарифы на потребительские товары и услуги меняются по-разному. Но во время кризисов (а нынешний – самый резкий в богатой негативными событиями истории современной России) такие расхождения кардинально увеличиваются. Что-то начинает резко дорожать, а что-то – дешеветь. В такой ситуации динамика сводного ИПЦ, учитывающего все потребительские товары и услуги, сильнее зависит от нюансов методики его построения – таких, как выбор индексной формулы, степень охвата корзиной всего множества товаров и услуг, алгоритмы импутации данных и многие другие. Так, при построении ИПЦ на протяжении 2020 г. используются веса, основанные на информации о структуре потребительских расходов за два года – с IV квартала 2017 г. по III квартал 2019 г. Для построения ИПЦ в 2021 г. этот двухлетний интервал будет сдвинут на год вперед и т. д. Это значит, что докризисные и кризисные реалии будут существенно влиять на веса, с которыми российские ИПЦ будут строиться вплоть до конца 2022 г., что будет искажать динамику текущих оценок российской инфляции.
по III квартал 2019 г. Для построения ИПЦ в 2021 г. этот двухлетний интервал будет сдвинут на год вперед и т. д. Это значит, что докризисные и кризисные реалии будут существенно влиять на веса, с которыми российские ИПЦ будут строиться вплоть до конца 2022 г., что будет искажать динамику текущих оценок российской инфляции.
В-четвертых, начало коронакризиса в нашей стране сопровождалось ожиданиями резкого всплеска инфляции, в частности из-за снижения курса рубля вследствие падения мировых цен на нефть. При этом чем выше темпы инфляции, тем ниже точность их измерения. Хорошая новость в том, что серьезного всплеска инфляции не произошло, иначе масштаб неопределенности динамики ИПЦ мог бы быть значительно большим.
Таким образом, в динамике российского ИПЦ во время коронакризиса имеется неустранимая неопределенность. Масштаб ее невелик, поскольку не было всплеска инфляции. Но изменение потребительских цен за весь период коронакризиса, т. е. от момента, предшествовавшего введению ограничений, до времени, когда ситуация на потребительском рынке в целом восстановится, можно будет измерить достаточно точно. Это обусловлено тем, что по окончании коронакризиса можно ожидать устранения основных перекосов структуры потребительских расходов и возвращения на рынок товаров и услуг, недоступных во время кризиса.
Это обусловлено тем, что по окончании коронакризиса можно ожидать устранения основных перекосов структуры потребительских расходов и возвращения на рынок товаров и услуг, недоступных во время кризиса.
Dynamics — The Physics Hypertextbook
Обсуждение
Почему существует эта страница?
Это не страница о каком-то фундаментальном принципе физики. Это страница о решении конкретной (и распространенной) проблемы механики.
Неформально динамика — это исследование сил и движения. Говоря более формально, динамика — это раздел механики, изучающий влияние сил на движение объектов. Напротив, statics — это исследование сил без движения; или, более формально, раздел механики, который имеет дело с силами при отсутствии изменений в движении.Динамика предполагает изменение. Статика предполагает неизменность. Важное изменение — это ускорение.
Цель этого раздела этой книги — служить хранилищем проблем в динамике. Ускорение в каждой задаче будет отличным от нуля в одном направлении. Это верно только для этого раздела. Идея состоит в том, чтобы увидеть, каково решать такие проблемы, чтобы вы могли распознать их, когда они появятся позже.
Это верно только для этого раздела. Идея состоит в том, чтобы увидеть, каково решать такие проблемы, чтобы вы могли распознать их, когда они появятся позже.
Аккуратная сила
Возьмите первый закон движения Ньютона и разделите его на две части.«Покоящийся объект имеет тенденцию оставаться в покое, а объект в движении имеет тенденцию продолжать движение с постоянной скоростью…». В этом длинном главном предложении живет статика. «Если только на это не действует чистая внешняя сила». В этом коротком придаточном предложении мы находим динамику.
Слово чистая во фразе чистая сила означает общую, комбинированную или общую. Это то, что вы получаете, когда все обдумываете. Слово net связано со словом аккуратный. Поиск чистой стоимости — это что-то вроде уборки математического беспорядка (или, по крайней мере, уменьшения беспорядка).Это может быть записано как ∑ F (с использованием греческой буквы сигма для обозначения суммы и жирным шрифтом, чтобы указать, что силы являются векторами) или как F net (с использованием нижнего индекса net, чтобы символ читался больше как произносимый язык и курсив, чтобы указать, что знание величины силы часто имеет значение) или другие подобные варианты.
Сила — это векторная величина, что означает, что направление имеет значение. Используйте положительные значения для сил, которые указывают в предпочтительном направлении, и отрицательные значения для сил, которые направлены в противоположном направлении.Если проблема двумерная, выберите два предпочтительных направления под прямым углом — что-то вроде вверх и вправо. Выберите предпочтительные направления, которые сделают вашу жизнь проще. Законы физики не заботятся о том, называете ли вы правое положительное или левое положительным. Пространство в математическом смысле изотропно . Он измеряет одинаково во всех направлениях.
Второй закон движения Ньютона описывает, как связаны чистая сила, масса и ускорение. По сути, чистая сила вызывает ускорение, а масса ему сопротивляется.Лучше всего писать не словами, а символами. Примерно так…
| ∑ F = м a | или | F нетто = ма |
Теперь вы готовы начать следующий этап обучения.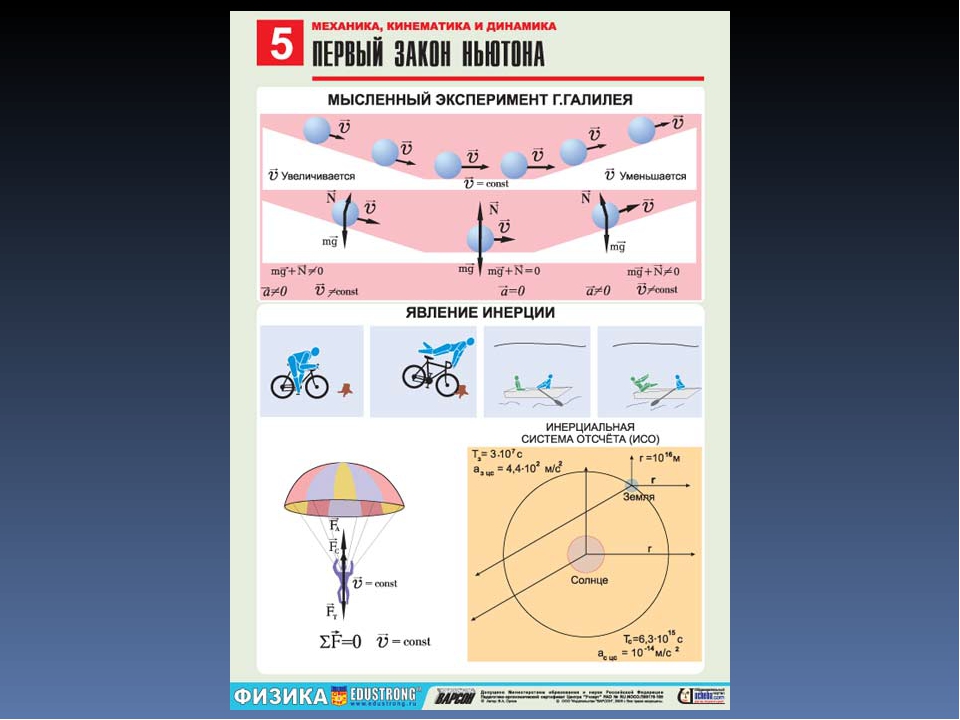
Например,
Возьмем беспрецедентный пример обычного велосипеда, который безупречно крутил педали по обычной ровной дороге безупречным образом.Какие силы действуют на велосипед и гонщика (вместе в целом)?
Начните с очевидного. У всего вес и вес вниз. Велосипед стоит на твердой поверхности, поэтому нормальная сила и направлена перпендикулярно этой поверхности. Поверхность ровная, нормальное направление — вверх. Всадник крутит педали. Это означает, что есть какая-то сила, толкающая велосипед вперед. Я не хочу чрезмерно анализировать ситуацию, поэтому давайте просто назовем эту силу push .Даже должным образом накачанные шины сопротивляются качению, ось может нуждаться в смазке, а может и не нуждаться в смазке, и воздух определенно затягивает движущееся тело. Давайте упростим жизнь и назовем все эти силы вместе трением . Гонщик толкает велосипед вперед, а трение толкает назад.
Готовы сделать свободную схему тела. Нарисуйте рамку, изображающую велосипед и всадника. Нарисуйте четыре стрелки, выходящие из центра прямоугольника, чтобы обозначить четыре силы, действующие на велосипед и гонщика. Хотя это не всегда необходимо, следует попытаться нарисовать стрелки, длина которых соответствует относительным величинам сил.Длинные стрелки для сильных сил. Короткие для слабых.
Нарисуйте рамку, изображающую велосипед и всадника. Нарисуйте четыре стрелки, выходящие из центра прямоугольника, чтобы обозначить четыре силы, действующие на велосипед и гонщика. Хотя это не всегда необходимо, следует попытаться нарисовать стрелки, длина которых соответствует относительным величинам сил.Длинные стрелки для сильных сил. Короткие для слабых.
Начните с легкой пары — весовой и нормальной. В этом сценарии ничего не происходит в вертикальном направлении. Дорога ровная, и гонщик не выполняет трюков. Вес и нормальный вес уравновешивают друг друга. Нарисуйте одну стрелку вниз, а другую вверх и придайте им одинаковую длину.
Завершите несколько менее легкой парой — толчок и трение. Что-то — это происходит в горизонтальном направлении. Движение происходит в горизонтальном направлении.Велосипед куда-то едет. Это должно быть хорошо для чего-то. Разве не должно?
Извините, но нет. Движение не имеет значения. Изменение движения — вот что важно. Велосипед ускоряется или движется с постоянной скоростью? Ускорение делает ситуацию динамичной. Отсутствие ускорения делает его статичным. Направление чистой силы определяет ускорение. Сила, направленная в направлении чистой силы, будет более сильной из двух.
Велосипед ускоряется или движется с постоянной скоростью? Ускорение делает ситуацию динамичной. Отсутствие ускорения делает его статичным. Направление чистой силы определяет ускорение. Сила, направленная в направлении чистой силы, будет более сильной из двух.
Если велосипед ускоряется, значит, гонщик толкает велосипед вперед больше, чем трение толкает его назад.Если велосипед движется с постоянной скоростью, толчок и трение равны. Если велосипед замедляется, сила трения побеждает силу, толкающую велосипед вперед.
Вот несколько рисунков, которые показывают то, что я только что сказал.
Вот набор уравнений, которые показывают то, что я только что сказал. Мне нравится использовать «вверх» и «вправо» в качестве положительных направлений, но это не закон физики. Это просто предпочтение.
| ||||||||||||||
| ||||||||||||||
| ↙ | ↓ | ↘ | ||||||||||||
|
|
|
Идите и решайте проблемы.
Перевернутые (деформированные) координаты
два тела, соединенные струной
Dynamics
Движение — скорость и ускорение, силы и моменты
Ускорение
Изменение скорости и времени
Уравнения ускорения и скорости
Полезные уравнения, связанные с ускорением, средней скоростью, конечной скоростью и пройденным расстоянием
Ускорение Гравитация и второй закон Ньютона
Ускорение силы тяжести и второй закон Ньютона — единицы СИ и имперские единицы
Конвертер единиц ускорения
Преобразование единиц ускорения
Угловое движение — мощность и крутящий момент
Угловая скорость и ускорение — мощность и крутящий момент
Средняя скорость
Пройденное расстояние по сравнению сиспользованное время
Поворот с наклоном
Поворот с наклоном — это поворот или изменение направления, в котором транспортное средство кренится или наклоняется, обычно в сторону внутренней части поворота.
Усилие на болларде
Трение каната вокруг столба — нагрузка и усилие в канате вокруг болларда
Автомобиль — Требуемая мощность и крутящий момент
Мощность, крутящий момент, КПД и усилие на колесах
Автомобиль — Сила тяги
Сцепление и сцепление усилие
Ускорение автомобиля
Рассчитать ускорение автомобиля
Центростремительная и центробежная сила — ускорение
Центростремительное и центробежное ускорение — силы, обусловленные круговым движением
Пройденное расстояние vs.Таблица калькулятора скорости и времени
График скорости на временной диаграмме
Высота подъемного моста — силы и моменты
Расчет момента подъема подъемного моста или балки
Лифт — сила и мощность
Требуемая сила и мощность для подъема лифта
Кинетическая энергия маховика
Кинетическая энергия, запасенная в маховике — момент инерции
Сила
Третий закон Ньютона — масса и ускорение
Силы, действующие на тело, движущееся по наклонной плоскости
Сила, необходимая для перемещения тела по наклонной плоскости
Формулы движения — линейное и круговое
Линейное и угловое (вращательное) ускорение, скорость, скорость и расстояние
Ударная сила
Ударная сила действует на падающие объекты, ударяющиеся о землю, разбивающиеся автомобили и т. п.
п.
Импульсная и импульсная сила
Силы, действующие очень короткое время называются импульсными силами
Кинетическая энергия
Кинетическая энергия твердого тела — это энергия, которой обладает его движение
Подъемные колеса
Подъемные колеса — сила нагрузки и усилия
Массовый момент инерции
Массовый момент Инерция (момент инерции) зависит от массы объекта, его формы и его относительной точки вращения — Radius of Gyration
Movement Ratio
Machines and move ratio (speed ratio)
Pendulum
Простой маятник колеблется в вертикальная плоскость из-за силы тяжести
Потенциальная энергия
Гидроэнергетика — высота и потенциальная энергия
Дальность полета снаряда
Движение в двух измерениях — вычисление дальности полета снаряда
Шкивы
Шкивы, блоки и захваты
Тяга самолета
Сил, необходимых для о.у. ll air plane
Сопротивление качению
Трение качения и сопротивление качению
Вращающиеся тела — напряжение
Напряжение во вращающихся дисковых и кольцевых телах
Универсальный закон гравитации
Гравитационное притяжение между двумя объектами зависит от массы объектов и расстояние между ними
Сложение векторов
Онлайн-калькулятор векторов — добавление векторов с разной величиной и направлением, например силы, скорости и т. д.
д.
Транспортное средство — пройденное расстояние vs.Скорость и время (км / ч)
Скорость (км в час), время (часы) и пройденное расстояние (км)
Лебедки
Усилие для подъема груза
Работа, выполненная силами
Работа, выполненная сила, действующая на объект
Кинематические уравнения
Целью этого первого раздела «Класса физики» было исследование разнообразных средств, с помощью которых можно описать движение объектов. Разнообразие представлений, которые мы исследовали, включает словесные представления, графические представления, числовые представления и графические представления (графики положения-времени и графики скорости-времени).В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов. Эти уравнения известны как кинематические уравнения.
Есть множество величин, связанных с движением объектов — смещение (и расстояние), скорость (и скорость), ускорение и время. Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22.0 м / с, север в течение 12,0 секунд для смещения на север на 264 метра, затем движение автомобиля полностью описывается. И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины. Эти два утверждения дают полное описание движения объекта. Однако не всегда такая полнота известна.Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны. Например, приближаясь к светофору, вы можете узнать, что ваша машина развивает скорость 22 м / с, восток и способна к заносу 8,0 м / с 2 , запад. Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться.
Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22.0 м / с, север в течение 12,0 секунд для смещения на север на 264 метра, затем движение автомобиля полностью описывается. И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины. Эти два утверждения дают полное описание движения объекта. Однако не всегда такая полнота известна.Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны. Например, приближаясь к светофору, вы можете узнать, что ваша машина развивает скорость 22 м / с, восток и способна к заносу 8,0 м / с 2 , запад. Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием физических принципов и математических уравнений (кинематических уравнений).
В таком случае неизвестные параметры могут быть определены с использованием физических принципов и математических уравнений (кинематических уравнений).
БОЛЬШОЙ 4
Кинематические уравнения — это набор из четырех уравнений, которые можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение 0 м / с / с) или движение с постоянным ускорением. Их нельзя использовать в течение какого-либо периода времени, в течение которого изменяется ускорение.Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно рассчитать значение четвертой переменной. Таким образом, кинематические уравнения предоставляют полезные средства прогнозирования информации о движении объекта, если известна другая информация. Например, если известно значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля, то смещение автомобиля и время можно предсказать с помощью кинематических уравнений.Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Например, если известно значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля, то смещение автомобиля и время можно предсказать с помощью кинематических уравнений.Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Четыре кинематических уравнения, описывающие движение объекта:
В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался.Символ a обозначает ускорение объекта. А символ v обозначает скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. Таким образом, они могут использоваться для прогнозирования неизвестной информации о движении объекта, если известна другая информация.В следующей части Урока 6 мы исследуем процесс этого.
Таким образом, они могут использоваться для прогнозирования неизвестной информации о движении объекта, если известна другая информация.В следующей части Урока 6 мы исследуем процесс этого.
Решение проблем базовой кинематики | Безграничная физика
Приложения
Есть четыре кинематических уравнения, которые описывают движение объектов без учета его причин.
Цели обучения
Выберите, какое уравнение кинематики использовать в задачах, в которых начальное начальное положение равно нулю
Ключевые выводы
Ключевые моменты
- Четыре кинематических уравнения включают пять кинематических переменных: [latex] \ text {d} [/ latex], [latex] \ text {v} [/ latex], [latex] \ text {v} _0 [/ latex] , [латекс] \ text {a} [/ latex] и [латекс] \ text {t} [/ latex].
- Каждое уравнение содержит только четыре из пяти переменных, а другая отсутствует.
- Важно выбрать уравнение, которое содержит три известные переменные и одну неизвестную переменную для каждой конкретной ситуации.

Ключевые термины
- кинематика : Раздел физики, связанный с движущимися объектами.
Кинематика — это раздел классической механики, который описывает движение точек, тел (объектов) и систем тел (групп объектов) без учета причин движения.2 + 2 \ text {ad} [/ latex]
Обратите внимание, что четыре кинематических уравнения включают пять кинематических переменных: [latex] \ text {d} [/ latex] , [latex] \ text {v} [/ latex] , [latex] \ text {v } _0 [/ latex] , [латекс] \ text {a} [/ latex] и [латекс] \ text {t} [/ latex]. Каждое из этих уравнений содержит только четыре из пяти переменных, а другая отсутствует. Это говорит нам, что нам нужны значения трех переменных, чтобы получить значение четвертой, и нам нужно выбрать уравнение, которое содержит три известные переменные и одну неизвестную переменную для каждой конкретной ситуации.
Вот основные этапы решения проблем с использованием этих уравнений:
Шаг первый — Определите, что именно необходимо определить в проблеме (определите неизвестные).
Шаг второй. Найдите уравнение или систему уравнений, которые помогут вам решить проблему.
Шаг третий — Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения вместе с единицами измерения.
Шаг четвертый. Проверьте ответ, чтобы узнать, разумен ли он: имеет ли он смысл?
Навыки решения проблем, безусловно, необходимы для успешного прохождения количественного курса физики.Что еще более важно, способность применять общие физические принципы, обычно представленные уравнениями, к конкретным ситуациям — очень мощная форма знания. Это намного эффективнее, чем запоминание списка фактов. Аналитические навыки и способности решать проблемы могут быть применены к новым ситуациям, тогда как список фактов не может быть достаточно длинным, чтобы содержать все возможные обстоятельства. Такие аналитические навыки полезны как для решения задач на уроках физики, так и для применения физики в повседневной и профессиональной жизни.
Диаграммы движения
Диаграмма движения — это графическое описание движения объекта, которое представляет положение объекта через равные промежутки времени.
Цели обучения
Построить диаграмму движения
Ключевые выводы
Ключевые моменты
- Диаграммы движения представляют движение объекта, отображая его местоположение в разное время с равным интервалом на одной диаграмме.
- Диаграммы движения показывают начальное положение и скорость объекта, а также несколько точек в центре диаграммы.Эти пятна показывают состояние движения объекта.
- Диаграммы движения содержат информацию о положении объекта в определенные моменты времени и поэтому более информативны, чем диаграмма путей.
Ключевые термины
- стробоскопический : Относится к инструменту, который заставляет циклически движущийся объект казаться медленно движущимся или неподвижным.
- диаграмма : график или диаграмма.

- движение : изменение положения относительно времени.
Диаграмма движения — это графическое описание движения объекта. Он отображает местоположение объекта в разное время с равным интервалом на одной диаграмме; показывает начальное положение и скорость объекта; и представляет собой несколько точек в центре диаграммы. Эти пятна показывают, ускорился или замедлился объект. Для простоты объект представлен простой формой, например закрашенным кружком, который содержит информацию о положении объекта в определенные моменты времени.По этой причине диаграмма движения дает больше информации, чем диаграмма пути. Он также может отображать силы, действующие на объект в каждый момент времени.
— диаграмма движения по простой траектории. Представьте себе объект в виде хоккейной шайбы, скользящей по льду. Обратите внимание, что шайба преодолевает одинаковое расстояние за единицу пути по траектории. Можно сделать вывод, что шайба движется с постоянной скоростью и, следовательно, во время движения нет ускорения или замедления.
Шайба, скользящая по льду : Диаграмма движения шайбы, скользящей по льду.Шайба движется с постоянной скоростью.
Одно из основных применений диаграмм движения — это представление фильма через серию кадров, снятых камерой; это иногда называют стробоскопической техникой (как показано на рисунке). Просмотр объекта на диаграмме движения позволяет определить, ускоряется или замедляется объект или находится в постоянном покое. Когда кадры сделаны, мы можем предположить, что объект находится в постоянном покое, если он занимает одно и то же положение с течением времени. Мы можем предположить, что объект ускоряется, если есть видимое увеличение пространства между объектами с течением времени, и что он замедляется, если есть видимое уменьшение пространства между объектами с течением времени.Объекты на кадре очень близко подходят друг к другу.
прыгающий мяч : прыгающий мяч, снятый с помощью стробоскопической вспышки со скоростью 25 изображений в секунду.
2.5 Уравнения движения для постоянного ускорения в одном измерении — College Physics
Расчет смещения: как далеко уходит автомобиль при остановке?
На сухом бетоне автомобиль может замедляться со скоростью 7,00 м / с 27,00 м / с2 размер 12 {7 «.» «00 м / с» rSup {размер 8 {2}}} {}, тогда как на мокром бетоне он может замедляться всего на 5.00 м / с 25,00 м / с2 размер 12 {5 «.» «00 м / с» rSup {размер 8 {2}}} {}. Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) (а) по сухому бетону и (б) по мокрому бетону. (c) Повторите оба вычисления, определив смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.
Стратегия
Нарисуйте эскиз.
Рисунок 2.34
Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить. Мы сделаем это явно в следующих нескольких примерах, используя таблицы для их выделения.
Решение для (a)
1. Определите, что мы знаем и что мы хотим решить. Мы знаем, что v0 = 30,0 м / sv0 = 30,0 м / с размер 12 {v rSub {size 8 {0}} = «30» «.» «0 м / с»} {}; v = 0 v = 0 размер 12 {v = «0»} {}; a = −7,00 м / с2a = −7,00 м / с2 (aa отрицательно, потому что оно находится в направлении, противоположном скорости).Возьмем x0x0 равным 0. Мы ищем смещение ΔxΔx или x − x0x − x0 размером 12 {x — x rSub {size 8 {0}}} {}.
2. Найдите уравнение, которое поможет решить проблему. Лучшее уравнение для использования —
. v2 = v02 + 2ax − x0. v2 = v02 + 2ax − x0. размер 12 {v rSup {размер 8 {2}} = v rSub {размер 8 {0}} rSup {размер 8 {2}} + 2a слева (x — x rSub {размер 8 {0}} справа)} {}2,55
Это уравнение лучше всего, потому что оно включает только одно неизвестное, размер xx 12 {x} {}. Нам известны значения всех других переменных в этом уравнении.(Существуют и другие уравнения, которые позволят нам решить для xx размера 12 {x} {}, но они требуют, чтобы мы знали время остановки, tt size 12 {t} {}, которое мы не знаем. Мы могли бы их использовать но это потребовало бы дополнительных вычислений.)
3. Измените уравнение, чтобы найти размер xx 12 {x} {}.
x − x0 = v2 − v022ax − x0 = v2 − v022a2,56
4. Введите известные значения.
x − 0 = 02−30,0 м / с22−7,00 м / с2x − 0 = 02−30,0 м / с22−7,00 м / с2 размер 12 {x — 0 = {{0 rSup {размер 8 {2}} — левый ( «30» ».»» 0 м / с «справа) rSup {размер 8 {2}}} больше {2 слева (- 7 дюймов.» «00 м / с» rSup {размер 8 {2}} справа)}}} {}2,57
Таким образом,
x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне. размер 12 {x = «64» «.» «3 м по сухому бетону» «. } {}2,58
Решение для (b)
Эта часть может быть решена точно так же, как часть A. Единственное отличие состоит в том, что замедление составляет –5,00 м / с2–5,00 м / с2 размер 12 {+ — 5 «». «00 м / с» rSup {размер 8 {2}}} {}.Результат
xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону. размер 12 {x rSub {размер 8 {«мокрый»}} = «90» «.» «0 м по мокрому бетону» «. } {}2,59
Решение для (c)
После реакции водителя тормозной путь будет таким же, как в частях A и B для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно рассчитать, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
1. Определите, что мы знаем и что мы хотим решить. Мы знаем, что v- = 30,0 м / св- = 30,0 м / с; treaction = 0.500streaction = 0.500s; область действия = 0 область действия = 0. Мы принимаем x0-реакция x0-реакция равна 0. Ищем xreactionxreaction.
2. Определите лучшее уравнение для использования.
x = x0 + v-tx = x0 + vt size 12 {x = x rSub {size 8 {0}} + {bar {v}} t} {} работает хорошо, потому что единственное неизвестное значение — xx размер 12 {x } {}, и это то, что мы хотим решить.
3.Подключите известные знания, чтобы решить уравнение.
x = 0 + 30,0 м / с 0,500 с = 15,0 м. x = 0 + 30,0 м / с 0,500 с = 15,0 м. размер 12 {x = 0 + слева («30» «.» «0 м / с» справа) слева (0 «.» «500 с» справа) = «15» «.» «0 м»} {}2,60
Это означает, что автомобиль едет 15,0 м, пока водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем при мгновенной реакции.
4. Добавьте смещение во время реакции к смещению при торможении.
xbraking + xreaction = xtotalxbraking + xreaction = xtotal size 12 {x rSub {size 8 {«braking»}} + x rSub {size 8 {«response»}} = x rSub {size 8 {«total»}}} {}2,61
- 64,3 м + 15,0 м = 79,3 м в сухом состоянии
- 90,0 м + 15,0 м = 105 м во влажном состоянии
Рис. 2.35 Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого асфальта, рассчитанные в этом примере для автомобиля, изначально движущегося со скоростью 30.0 м / с. Также показаны общие расстояния, пройденные от точки, где водитель впервые видит красный свет, при условии, что время реакции составляет 0,500 с.
Обсуждение
Смещения, найденные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля. Остановка автомобиля на мокром, а не на сухом асфальте займет больше времени. Интересно, что время реакции значительно увеличивает смещения. Но важнее общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение.Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но решения, представленные выше, являются самыми короткими.
Законы динамики — Энциклопедия окружающей среды
Закон Ньютона, связывающий силу и ускорение, лежит в основе современной физики. Применительно к каждому графику жидкости он лежит в основе моделей прогнозирования погоды и климата. Интуитивное понятие силы использовалось с древних времен для понимания статического равновесия.Это позволяет спроектировать своды в архитектуре, использовать рычаг, чтобы описать баланс жидкости под действием тяги Архимеда. Именно принцип инерции, открытый Галилеем, проложил путь к законам ньютоновской динамики, чей большой успех заключался в объяснении движения планет и спутников, а также приливов и отливов. Это потребовало большого математического опыта, который имеет свои пределы для более сложных систем, таких как атмосфера или океан. Решение уравнений динамики стало возможным только с момента появления компьютерных вычислений.Однако законы сохранения, количества движения, энергии, кинетического момента накладывают глобальные ограничения, позволяющие более непосредственно понять определенные явления.
1. Уравновешивающие силы
Понятие силы выражает механическое воздействие на объект. Силы имеют четко определенное физическое происхождение, например, гравитационная сила (вес ), электрическая сила на заряженной частице , контакт или натяжение сила на кабеле или сила упругости пружина.Как и многие фундаментальные понятия физики, силу трудно определить сама по себе, но к ней можно подойти с помощью экспериментальных примеров, а также с помощью математических соотношений, которые она имеет с другими величинами.
Рис. 1. Равновесие противоположных сил, а) в пружинном динамометре, б) в воздушном шаре. [Источник: Traité de Physique Elemententaire — DRION et FERNET — 1885] Таким образом, сила характеризуется интенсивностью (или модулем ) и направлением , а также точкой приложения, и математически представляется в виде вектор .Сумма сил, действующих на покоящийся объект, должна нейтрализовать друг друга. Сила может быть измерена по удлинению пружины из ее положения покоя (рис. 1). Экспериментально подтверждается, что это удлинение пропорционально силе путем последовательного добавления нескольких одинаковых грузов. После калибровки этот датчик силы пружины можно использовать для измерения различных сил. Для теплового шара, неподвижного в воздухе, общий вес уравновешивается тягой Архимеда , равной и противоположной массе вытесненного объема воздуха.Это не что иное, как результат сил атмосферного давления , действующих по всей оболочке: из-за уменьшения давления с высотой давление в нижней части оболочки выше, чем в верхней части, что переводится в чистую восходящую силу . Этот баланс между давлением и силой тяжести фактически применяется к любому объему жидкости в равновесии, известном как гидростатическое равновесие (см. «Давление, температура, тепло»). Именно благодаря этому балансу воздушные участки или водные участки в бассейне не падают на землю под действием силы тяжести.Когда воздух нагревается, его плотность и, следовательно, масса данного объема уменьшается, в то время как давление остается неизменным, поскольку оно контролируется весом окружающего воздуха. Затем равновесие нарушается, что приводит к вертикальному ускорению воздушного шара. В атмосфере воздушная масса, локально нагретая солнечным излучением, также будет иметь тенденцию подниматься: это принцип конвекции .
Рис. 2. Перевернутая модель Собора Святого Семейства Гауди. Форма равновесия такова, что на каждом пересечении проводов векторная сумма сил равна нулю.Каждый элемент балки представлен проволокой, а его масса моделируется грузом. Сила натяжения пряжи обязательно совпадает с пряжей. В реальной перевернутой конфигурации соответствующая сила будет тогда силой сжатия, направленной вдоль балки, что гарантирует ее механическую прочность. [Источник: http://olive-art.weebly.com/uploads/2/6/0/5/26053332/6555663_orig.jpg]. В общем, баланс сил должен быть выражен как вектора , что является Основа для расчета конструкций в архитектуре, см. рисунок 2.Для каждой материальной точки, например, узла пересечения проводов, векторная сумма сил должна уравновешивать друг друга в состоянии равновесия, как показано на рисунке 3a. Это позволяет, например, найти интенсивности сил F1 и F2 , зная силу F3 и углы θ1 и θ2 , либо геометрическим построением, либо численно. путем проецирования векторов по вертикальной и горизонтальной осям.Протяженный объект, например твердое тело , описывается в физике как набор из материальных точек , удерживаемых вместе внутренними силами. Эти силы следует отличать от внешних сил, таких как вес или силы контакта с другими объектами. Сумма внутренних сил компенсируется принципом действия и противодействия , так что равновесие требует отмены суммы внешних сил.
Рисунок 3. Баланс сил на материальной точке а) и баланс моментов на протяженном объекте — рычаге.Но состояние равновесия протяженного объекта также требует отмены полного момента сил, чтобы избежать его вращения. Момент силы относительно оси определяется как произведение силы, проецируемой перпендикулярно оси, на расстояние до оси. Классическим примером является рычаг, показанный на рисунке 3b. В состоянии равновесия или квазиравновесия для медленного движения для компенсации моментов требуется, чтобы F1d1 = F2d2 (силы здесь перпендикулярны оси), что позволяет увеличить силу, действующую в обратном отношении расстояния до оси (согласно обычному соглашению мы отмечаем здесь F1 интенсивность силы, а F1 представляет вектор силы).Обычно моменты рассматривают относительно оси рычага, потому что момент силы реакции R земли компенсируется сам собой. Однако тот же результат можно получить, вычислив момент относительно любой математической оси, добавив момент реакции R , который является равным вектором и противоположен сумме двух сил F1 и F2 .
2. Силы и ускорение
Теперь, покидая область статики, ускорение объекта связано с общей силой F , которая действует на него по знаменитому закону ньютоновской динамики , F = мг где м — это масса объекта, а г, — его вектор ускорения.Это позволяет определить единицу силы, Ньютон (Н), как силу, создающую ускорение в 1 (м / с) / с над массой 1 кг, что записывается как 1 Н = 1 кг · м · с-2. .
В отсутствие силы объект движется с постоянной скоростью, это принцип инерции , впервые сформулированный Галилеем (1564-1642). В то время этот принцип был не очень интуитивно понятным, потому что в повседневной жизни любое движение имеет тенденцию останавливаться без усилия. Это замедление (отрицательное ускорение) теперь приписывается трению силам, которые противоположны скорости.Но трение становится незначительным в межпланетной пустоте, и большой успех Ньютона (1643-1727) заключался в математическом описании движения планет и спутников на основе простого закона универсальной гравитационной силы , убывающей как величина, обратная квадрату расстояния r. .
Применение закона Ньютона потребовало изобретения математической концепции производной , определяющей понятия скорости и ускорения. Отметим скорость v = dz / dt, где dz — небольшое смещение во временном интервале dt.Фактически, мы считаем предел равным очень коротким временным интервалом. Точно так же ускорение обозначается как g = dv / dt. Для постоянного ускорения g скорость пропорциональна времени, v = gt , и легко продемонстрировать, что расстояние падения (разница между начальной высотой z0 и высотой z ) будет тогда z0- z = (1/2) gt2 . Таким образом, на Земле под действием силы тяжести, г, = 9,8 м / с, объект достигает скорости 9.8 м / с (35 км / ч) за 1 секунду, падает с высоты 4,9 м.
Закон Ньютона применяется в более общем смысле в векторной форме : объект может упасть вертикально, как было указано ранее, сохраняя при этом свою горизонтальную составляющую скорости по инерции. При достаточно высокой горизонтальной скорости необходимо учесть кривизну Земли и получить круговое движение спутника , см. Рис. 4. В этом случае скорость постоянна по модулю, но вектор скорости вращается на такая же угловая скорость [1], что и у спутника.Ускорение тогда перпендикулярно скорости и направлено к центру Земли, со значением g = v2 / r , как показано на рисунке 4. Таким образом, для спутника, близкого [2] к Земле, g. = 9,8 мс-2, r = 6500 км, что приводит к: скорости v = (gr ) 1/2 = 8 км / с, времени обращения (длина 40 000 км) T = 5000 с (1 ч 23 мин).
Рисунок 4. a) Движение запущенного тела с увеличивающейся горизонтальной скоростью до спутника на круговой орбите (8000 м / с) и выброс Земли (11000 м / с) [Источник: иллюстрация теории Ньютона, опубликованная в «Popular Astronomy» ].(б) Закон динамики применяется к круговому движению спутника: за короткий промежуток времени dt спутник поворачивается на угол dq = (v / r) dt, а вектор скорости поворачивается на тот же угол dq = (g / v) dt, откуда выводится g = (v2 / r), что позволяет рассчитать скорость спутника v = 8000 м / с у поверхности Земли (r = 6500 км, g = 9,81 м / с-2). ). Если теперь сила тяжести g уменьшается на 1 / r2, скорость v = (gr ) 1/2 от кругового движения уменьшается на 1 / r1 / 2, а период вращения равен 2πr / v , увеличивается в r3 / 2 .Таким образом, Луна удалена от Земли r = 384 000 км, т.е. е. В 60 раз больше радиуса Земли, он должен вращаться за время в 465 раз дольше, чем ближайший спутник, т.е. е. 27 дн. Это согласуется с наблюдениями [3]. Закон роста времени обращения в r3 / 2 был открыт Кеплером (1571-1630) для планет, вращающихся вокруг Солнца. Помимо частного случая круговой орбиты, Ньютон смог продемонстрировать, что общее движение следует за эллипсом (или гиперболой за пределами скорости истечения), и он смог найти три закона, ранее установленные Кеплером, на основе точных измерений положения планет.
Бывает, что сила тяжести сама по себе пропорциональна массе, поэтому возникающее ускорение не зависит от нее: все тела падают с одинаковым ускорением в одном и том же месте. Это равенство между тяжелой массой и инертной массой было заявлено Галилеем и проиллюстрировано его знаменитыми экспериментами (возможно, только воображаемыми) с падающими объектами с Пизанской башни. Это было сделано снова с большой точностью в вакууме, избегая трения воздуха. В качестве демонстрации для публики был снят фильм, сравнивающий падение молотка и пера на Луне во время полета Аполлона XV [4], и аналогичный эксперимент был снят на Земле в огромной вакуумной камере [5].Именно из-за этого принципа эквивалентности все объекты плавают в невесомости на спутнике, каждый движется по одной и той же орбите вокруг Земли. Эта эквивалентность сейчас проверяется с относительной точностью 10-13 (1/10 триллиона), а точность 10-15 ожидается от недавно запущенного спутника «Микроскоп». Эти сверхточные измерения предназначены для проверки отклонений от принципа эквивалентности, предсказываемого новыми теориями гравитации.
3. Кинетическая и потенциальная энергия
В приведенном выше примере свободного падения можно отметить, что мг (z0-z ) = м (1/2 ) g2t2 = (1/2 ) mv2 .Это соответствует более общему свойству сохранения полной энергии, состоящему из кинетической энергии (1/2 ) mv2 и потенциальной энергии mgz . Когда объект падает, его кинетическая энергия увеличивается, но его потенциальная энергия также уменьшается, так что полная механическая энергия сохраняется (при отсутствии трения). В общем случае кинетическая энергия (1/2 ) mv2 выражается как функция модуля скорости. Сохранение механической энергии становится все более распространенным в случае спутника, но выражение потенциальной энергии должно быть изменено, чтобы учесть уменьшение силы тяжести.Эта потенциальная энергия зависит только от положения объекта, так что он принимает то же значение после вращения, и кинетическая энергия также имеет такое же значение в соответствии с тем фактом, что движение планеты сохраняется бесконечно. Гравитационный потенциал определяется делением этой потенциальной энергии на массу объекта. Этот потенциал характеризует гравитационное поле независимо от объекта, вращающегося вокруг него (до тех пор, пока объект мал и не приводит планету в движение посредством реакции).
Сохранение механической энергии требует особой формы законов силы. Силы трения, в отличие от силы тяжести, уменьшают механическую энергию, так что спутник в конечном итоге входит в контакт с остаточной атмосферой. Однако потерянная механическая энергия преобразуется в тепло, так что общая энергия сохраняется (см. «Энергия»). Тепло по существу соответствует неупорядоченной кинетической энергии молекул газа. Для однородной сферической планеты потенциал изменяется в пределах -1 / r, так что эквипотенциалы представляют собой концентрические сферы.Однако эти сферы слегка деформированы из-за вращения Земли и неоднородностей. Равновесная форма поверхности океана является таким эквипотенциалом (см. «Морская среда»). Действительно, объект, движущийся по эквипотенциалу, сохраняет ту же потенциальную энергию, и, поскольку его полная энергия сохраняется, он не может приобретать (или терять) скорость под действием только силы тяжести. И наоборот, если форма океана отклоняется от эквипотенциальной, поверхностная вода имеет тенденцию течь в области с более низким потенциалом, пока она не заполнит их и не достигнет состояния равновесия, при котором поверхность является эквипотенциальной.Поверхность твердой Земли также приближается к эквипотенциальности из-за эрозии и пластичности мантии Земли.
4. Количество движения
Количество движения, равное элементарной массе (рассматриваемой как точечная), определяется как произведение массы и скорости, определение, которое может быть распространено на любую физическую систему, добавляя (векторно) количества движения каждой из ее элементарные массы. Легко продемонстрировать, что величина движения равна величине движения центра инерции (центр тяжести ) системы, на которую воздействует ее общая масса.Затем закон динамики Ньютона указывает, что производная от количества движения по времени равна сумме сил, действующих на систему.
Согласно фундаментальному принципу физики, количество перемещений изолированной системы сохраняется. Другими словами, его центр инерции движется поступательно с постоянной скоростью, и только внешние силы могут изменить эту скорость. Другой эквивалентной формулировкой является принцип действия и противодействия , который гласит, что любое тело A, оказывающее силу на тело B, испытывает силу равной интенсивности, но в противоположном направлении, действующую со стороны тела B.Затем закон динамики указывает, что эти внутренние силы не изменяют величину движения глобальной системы A + B. Это обобщает рассмотренное выше условие статического равновесия.
Зная начальные массы m1 и m2 и начальные скорости u1 и u2 каждой массы, вычисляется величина движения до удара m1u1 + m2u2 , которая должна сохраниться после удара , таким образом, обеспечивая ограничение на конечные скорости.Если дополнительно предположить, что амортизатор упругий , т.е. е. что кинетическая энергия (1/2 ) m1u12 + (1/2 ) m2u22 сохраняется, мы можем вывести две конечные скорости. Для двух равных масс мы имеем обмен скоростями (рис. 5а). В случае полностью неупругого удара массы остаются связанными после удара с конечной скоростью, равной средневзвешенному значению начальных скоростей m1u1 + m2u2 / (m1 + m2 ) при сохранении количества движение.Применительно к молекулам газа эти ударные свойства позволяют интерпретировать явление вязкости, которое уравнивает количество движений быстрой и медленной зон внутри жидкости, сохраняя при этом общее количество движения.
Привод ракет или самолетов — еще один классический пример: величина движения, передаваемого транспортному средству, прямо противоположна движению выбрасываемого газа, независимо от задействованных сложных механизмов. Это также относится к силам гравитации: Луна притягивает Землю с силой, равной силе тяжести Земли, действующей на Луну, и противоположной ей.Таким образом, Земля вращается вокруг центра инерции системы Земля-Луна так же, как и молотковая установка, которая должна вращаться, чтобы компенсировать реакцию вращающегося шара (см. «Приливы»). Именно этот центр инерции описывает эллиптическую орбиту вокруг Солнца, а не саму Землю.
Рисунок 5-а. Choc élastique entre deux masses égales [Источник: Саймон Штайнманн (собственная работа) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5)]] Рис. 5-b.Choc élastique entre deux masses inégales [Источник: Саймон Штайнманн (собственная работа) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5) через Wikimedia Commons] Рисунок 5-c. Отличное неэластичное блюдо из двух масс [Источник: Par Raul Roque (персонал Travail) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5)], через Wikimedia Commons]
5. Угловой момент
Угловой момент относительно оси определяется для точечной массы как произведение расстояния до оси на величину ее движения, проецируемого перпендикулярно этой оси.Это определение обобщается на протяженное тело, например твердое тело, путем деления его мыслью на элементарные массы и сложения их угловых моментов. Мы демонстрируем из закона динамики, что производная кинетического момента по времени равна суммарному моменту сил (также называемых «крутящий момент , »), действующих на систему. Это обобщает закон статики, который требует, чтобы полный момент сил был равен нулю.
Закон сохранения кинетического момента гласит, что полный момент внутренних сил уравновешивается, и поэтому только момент внешних сил может изменить кинетический момент.Таким образом, в твердом состоянии внутренние силы сцепления не вмешиваются в баланс кинетического момента, так же как они не вмешиваются в величину движения. Это фундаментальный закон физики, отличный от принципа действия и противодействия и дополняющий его.
Другими словами, система не может начать самопроизвольно вращаться или потерять свое начальное вращение без действия внешних сил. Однако скорость его вращения может измениться в случае сжатия или растяжения.Действительно, для точечной массы это произведение , скорости и на расстояние r до оси, которая сохраняется, поэтому скорость и увеличивается обратно пропорционально расстоянию r , и его угловая скорость u / r обратно пропорциональна квадрату этого расстояния.
Классический пример — фигурист, а в естественной среде — образование торнадо и циклонов (см. «Торнадо: мощные разрушительные водовороты»).Само вращение Земли является результатом увеличения угловой скорости при аккреции вещества, которое привело к ее образованию. Самый яркий пример — пульсары, чрезвычайно плотные звезды, вращающиеся с периодом от нескольких секунд до нескольких миллисекунд. Эти объекты возникают в результате коллапса массивной звезды, обычно в радиусе от 1 миллиона км до 10 км. Такое сжатие увеличивает угловую скорость вращения в 10 миллиардов раз (часть углового момента выбрасывается вместе с газом, испускаемым взрывом).
Момент импульса на самом деле является вектором, выровненным с осью вращения [6], и поэтому он сохраняется как по направлению, так и по модулю. Это принцип работы гироскопа . Точно так же ось вращения Земли остается выровненной по отношению к звездам, а Северный полюс по-прежнему указывает на область, близкую к Полярной звезде.
Рисунок 6. Прецессия фрезера: вес создает разрез, ориентированный перпендикулярно рисунку и горизонтальный. Таким образом, результирующее изменение вектора кинетического момента перпендикулярно этому вектору, что приводит к прецессионному движению, показанному на рисунке.Аналогичное явление происходит с вращением Земли под действием крутящего момента из-за лунного притяжения (однако, прецессия происходит в противоположном направлении, потому что крутящий момент имеет противоположный знак по отношению к вершине). Источник: http://hyperphysics.phy astr.gsu.edu/hbase/mechanics/imgmechs/imgmech/topp.gif]Это верно только для изолированной системы, а точнее при отсутствии крутящего момента (или момента) от внешние силы. Крутящий момент, перпендикулярный оси вращения, вызывает вращение оси вращения без какого-либо изменения угловой скорости: это явление прецессии , наблюдаемое на маршрутизаторе, см. Рисунок 6 (точно так же, как ускорение, перпендикулярное скорости, производит вращение скорости без изменения ее модуля).Аналогичный эффект происходит с Землей из-за ее уплощенной формы на полюсе: крутящий момент возникает из-за более сильного притяжения Луны на части около бусинки, чем на ее противоположной части. Это приводит к медленному прецессионному движению вращения Земли в течение 26 000 лет (см. Рисунок 6). Таким образом, направление полюса медленно перемещается по небесной сфере на протяжении веков. Это приводит к смещению орбиты Земли относительно положения равноденствий, когда ось вращения Земли ориентирована перпендикулярно направлению Солнца.Вот почему это явление получило название « прецессии равноденствий ». Связанные с этим изменения солнечного света происходят при изменении климата между ледниковым и умеренным периодами.
Ссылки и примечания
Фотография на обложке. Автор http://creativecommons.org/licenses/by-sa/2.0 (загружен на Flickr как обычный jfpds) [CC BY-SA 2.0 (极 博 双 板 滑雪 俱乐部)] через Wikimedia Commons.
[1] Угловая скорость Ω — это угол, пройденный за единицу времени, обычно выражаемый в радианах / с, так что Ω = v / r.Радиан определяется как угол, пересекающий дугу окружности, равную радиусу, так что полный оборот (окружность 2πr ) представляет 2π радиан, а период вращения равен T = 2π / Ω = 2πr / v .
[2] Высота должна составлять несколько сотен километров, чтобы избежать атмосферного трения, но ускорение свободного падения остается близким к ускорению земной поверхности, а радиус орбиты мало отличается от радиуса Земли.
[3] Это сидеральная революция, i.е. относительно звезд, в то время как время между двумя полными лунами, равное 29,5 дня, является синодическим оборотом, i. е . по отношению к Солнцу.
[4] Молот и перо Аполлона 15 — Youtube
[5] Брайан Кокс посещает самую большую в мире вакуумную камеру — Вселенная человека: превью 4 серии — BBC Two — Youtube
[6] Момент импульса более точно определяется относительно исходной точки O. Для точки массой м в точке M это векторное произведение вектора на вектор OM на величину движения м и массы в точке М.Для осесимметричного твердого тела, такого как маршрутизатор или Земля, кинетический момент выровнен по оси вращения со значением, пропорциональным угловой скорости и моменту инерции .
Экологическая энциклопедия окружающей среды Ассоциации энциклопедий окружающей среды и энергии (www.a3e.fr), по контракту связана с Университетом Гренобль-Альп и ИЯФ Гренобля и спонсируется Французской академией наук .
Для цитирования: SOMMERIA Joël (2021), Законы динамики, Энциклопедия окружающей среды, [онлайн ISSN 2555-0950] URL: https://www.encyclopedie-environnement.org/en/physics/laws-of -динамика /.
Статьи в Энциклопедии окружающей среды доступны в соответствии с условиями лицензии Creative Commons BY-NC-SA, которая разрешает воспроизведение при следующих условиях: ссылка на источник, не коммерческое использование их, использование идентичных исходных условий, воспроизведение в при каждом повторном использовании или распространении эта лицензия Creative Commons BY-NC-SA упоминается.
Уравнения кинематики и постоянное ускорение
В своих «Диалогах двух новых наук» Галилей вывел взаимосвязь между пройденным расстоянием и временем, когда шары катились по наклонной плоскости. Это часто называют законом падающих тел. Интересно, что в доказательстве Галилея использовалась классическая евклидова геометрия (которая была бы незнакома современному изучающему геометрию из учебников) вместо алгебры, которую мы здесь и представим. Учащиеся продвинутого уровня могут получить те же уравнения, используя математический анализ.
Основа Закона падающих тел заключается в том, что по мере того, как мяч катится по рампе, он ускоряется. По мере увеличения его скорости увеличивается расстояние, которое он проходит за каждую единицу времени. Галилей определил это с помощью колокольчиков на спусковом крючке катящегося шарика.
Процитируем Галилея в переводе:
По сути, Галилей представил, что не только ускорение вниз по рампе из-за постоянной силы тяжести, но и что скорость увеличивается линейно с временем .Он представил, что положение увеличивается с квадратом времени, что часто называют Законом падающих тел. Последний пункт в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.
Основываясь на том, что вы уже узнали и что представил Галилей, у нас есть то, что мой учитель физики Гленн Глейзер любил называть пятью священными уравнениями кинематики для постоянного ускорения. В этих уравнениях v — скорость, x — положение, t — время и a — ускорение.Помните, что Δ означает изменение.
1. или Δx = v ср. Δt
2. или v f = v o + aΔt или Δv = aΔt
3.
4. Δx = v o Δt + ½ a Δt 2
5. v f 2 = v o 2 + 2aΔx
Первые два уравнения, которые мы видели раньше. Важно отметить, что первое уравнение использует средней скорости , тогда как второе уравнение использует изменение между исходной скоростью и конечной скоростью .Связь между ними представлена в третьем уравнении, которое представляет собой просто закон средних чисел. Средняя скорость — это среднее значение исходной и конечной скорости.
Из этих трех основных определений мы можем вывести следующие два уравнения, используя либо геометрию, либо алгебру (или исчисление).
Используя алгебру, мы можем вывести уравнение №4.
Исходя из уравнения № 1
Δx = v ср. Δt
Затем мы подставляем определение средней скорости из уравнения №3.
Отсюда мы подставляем окончательную скорость, полученную в уравнении № 2
Затем мы распределяем член Δt и упрощаем, комбинируя члены v o .
Мы упрощаем оставшиеся два члена, чтобы получить
.Стоит отметить, что происходит, когда исходная скорость v o, равна нулю. Это уравнение еще больше упрощается и становится
.Если мы предположим, что исходная позиция и время равны нулю, мы можем дополнительно уменьшить это до
.Используя геометрию, мы можем исследовать область под кривой графика зависимости скорости от времени для движения с постоянным ускорением.
Если мы посмотрим на область под кривой, мы можем разбить ее на прямоугольник и треугольник. Красный прямоугольник — это вклад исходной скорости объекта. Смещение из-за ускорения представлено зеленым треугольником. Треугольник имеет ширину Δt и высоту aΔt, которые мы знаем из уравнения №2. Член ½ происходит от формулы площади треугольника.
Мы также можем использовать исчисление для вывода этого уравнения путем интегрирования удвоенного ускорения по времени.
Пятое священное уравнение может быть получено аналогичными заменами, и его оставят как домашнее задание.
Теперь давайте рассмотрим несколько примеров задач: Численное решение задач.
Пример 1
По легенде, Галилей уронил мяч из Пизанской башни. Если высота башни составляет 55,9 м , и если пренебречь сопротивлением воздуха, сколько времени потребуется свинцовому мячу, чтобы достичь земли?
Гивенс: a = g ≈ 10 м / с 2
Δx = 55.9 м
Неизвестно: t = ???
Уравнение, связывающее эти переменные, — это священное уравнение 4 th .
Δx = v o Δt + ½ a Δt 2
Как упоминалось ранее, поскольку начальная скорость равна нулю, уравнение упрощается.
Δx = v o Δt + ½ a Δt 2 = ½ a Δt 2
Поскольку мы хотим изолировать переменную для времени, мы пересекаем умножение, чтобы переместить ½ и член ускорения на другую сторону.
Затем извлекаем квадратный корень из обеих частей.
Это дает выражение для времени. Обратите внимание, что я вставил несколько дополнительных скобок, которые могут вам не понадобиться.
При подключении номеров это довольно просто то, что мы называем «включил и нажал». Однако с агрегатами нужно быть осторожным. Вы, наверное, догадались, что время будет измеряться в секундах. Однако у вас должна быть возможность отменить фактические единицы, чтобы получить время в секундах.
Пример 2
Койот падает со скалы высотой 25 метров. Как быстро койот падает, когда ударяется о землю? Если проблема койота
Дано x = 25 м
a = g ≈ 10 м / с 2
Неизвестно: v = ???
Эту проблему можно решить несколькими способами. Можно использовать комбинацию или Священные уравнения №2 и №4. Или вы можете напрямую использовать уравнение №5.
Использование v f 2 = v o 2 + 2aΔx
Это упрощается, поскольку исходная скорость v o, равна нулю.
Если извлечь квадратный корень из обеих частей уравнения
Обратите внимание, как вы извлекаете квадратный корень из единиц, чтобы получить м / с .
Мы оставим решение этой задачи с двумя уравнениями для домашней задачи.
Резюме по построению графиков и задачам наклона и площади под кривыми
Изучая графики положения, скорости и ускорения, вы сможете рисовать их как взаимозаменяемые.
 Законы Ньютона — первый, второй, третий. Принцип относительности
Законы Ньютона — первый, второй, третий. Принцип относительности

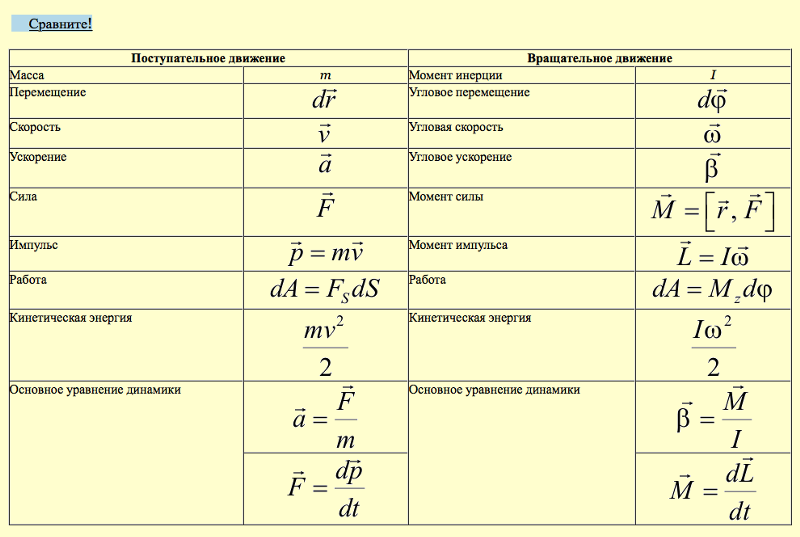 Трение покоя = силе, приложенной к телу
Трение покоя = силе, приложенной к телу
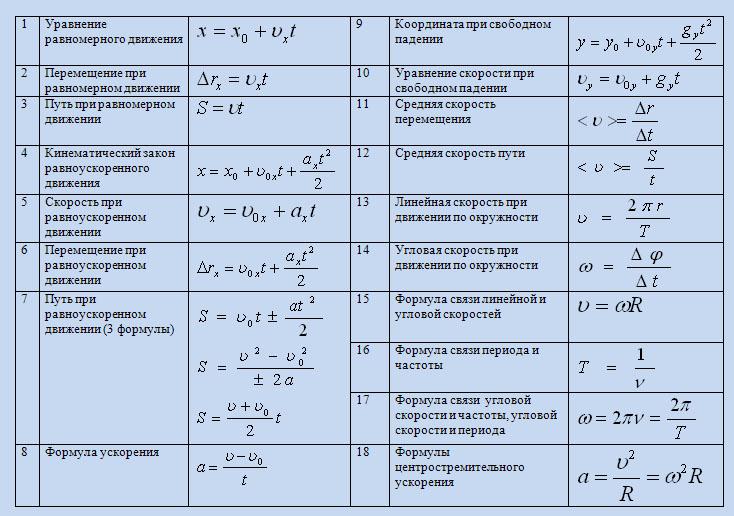
 2)
2)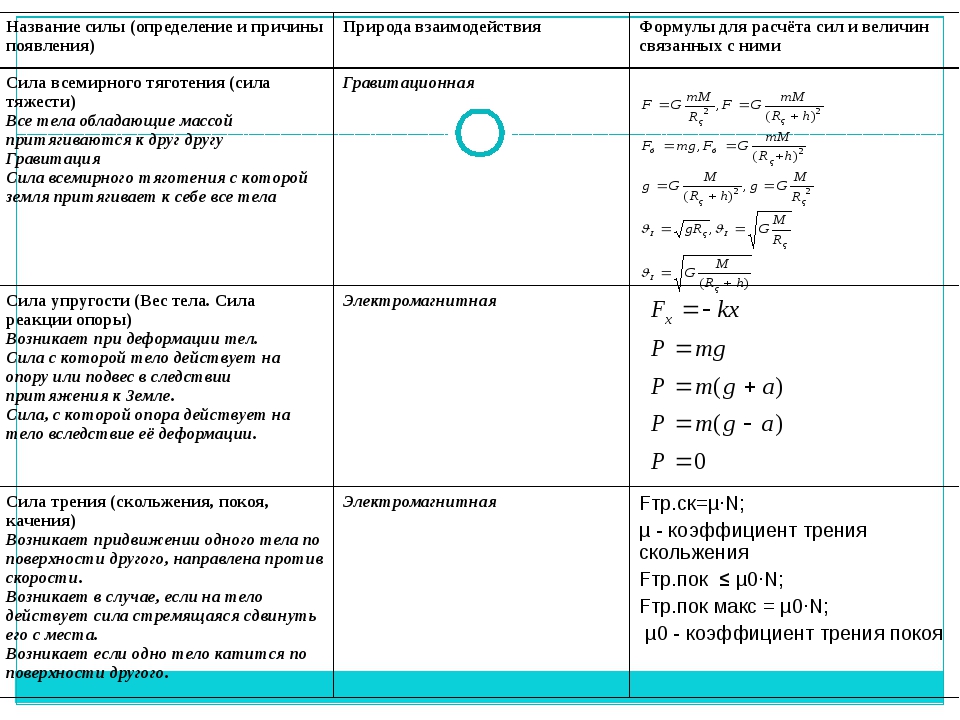 6)
6)