термех
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНЖЕНЕРНЫХ ТЕХНОЛОГИЙ»
КАФЕДРА ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА»
Выполнил студент: 1 курса дистанционного обучения
Направление: 150302с
“Технологические машины и оборудование”
Шифр: 14-012
Ф.И.О
Проверил: Давыдов Олег Юрьевич
Воронеж2015
Вариант 12
ЗАДАНИЕ 1
Определение реакций опор криволинейного бруса
Способ
закрепления криволинейного жесткого
бруса показан в таблице 1.
1 на рисунках
1.0 – 1.9 . К брусу приложена пара сил с
крутящим моментом и две силы, численные значения которых,
направления и точки приложения указаны
в таблице 1.2. Определить реакции,
возникающие в местах крепления бруса.
В ходе расчетов подсчетах принять
.
Дано: M=100 Нм, а=0,5 м, F2=20 Н, 2=45, F3=30 Н, 3=30.
Определить: XA YA RB
Решение
Для полученной плоской системы сил составим три уравнения равновесия
(1)
(2)
(3)Решаем полученную систему уравнений .
кН,
кН.
Ответ: XA=40.1
кН, YA=75.5
кН, RB=76.
6
кН. Знаки указывают, что направление
сил XA и YA противоположно показанному на рисунке.
ЗАДАНИЕ 3
Преобразование поступательного и вращательного движения системы твердых тел.
Определение скоростей и ускорений точек твердого тела.
Механизм состоит из ступенчатых колес 1-3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес.
Определить в момент времени t1=2 c: скорости , , ускорения , , , если тело 5 движется со скоростью .
Решение
Угловые
скорости всех колес.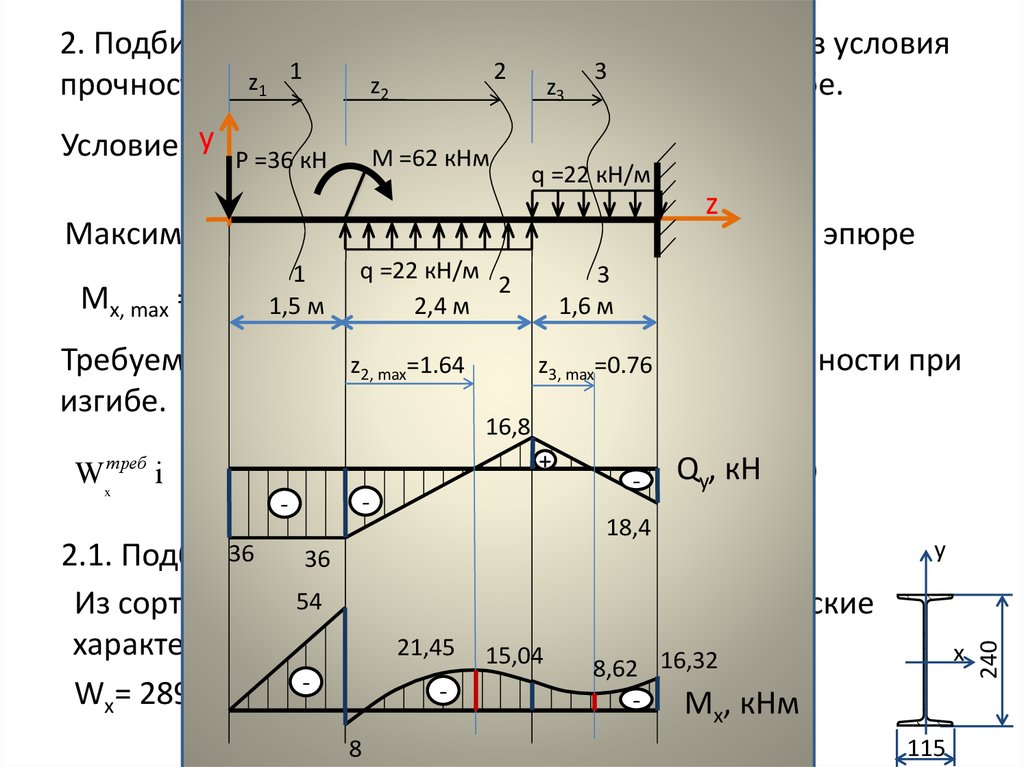
при t=2c
Т.к. колеса 1 и 2 связаны ременной передачей то
Колеса 1 и 3 находятся в зацеплении
Скорость
при t=2c
Угловое ускорение
Ускорение и
где и
Угловое ускорение
При t=2c
касательная составляющая
нормальная составляющая
Ответ:
ЗАДАНИЕ 4
Определение закона движения материальной точки.
Дано: m=8 кг, V0=10 м/с, Q=16 Н, R=0,5V2 H, , Fx=
Определить: x=x(t) – закон движения груза на участке BC.
Решение.
Рассмотрим движение груза на участке AB, считая его материальной точкой. Изображаем груз в произвольном положении и действующие на него силы: P – сила тяжести, N – реакция поверхности, R, Q. Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось:
или
Далее находим , , ,
Получим
Решебник Яблонский 1985 года — Задание С1_Тема: Определение реакций опор твердого тела
|
Физика Волькенштейн Практический курс физики Малекулярная и термодинамика Теоретическая механика Мещерский Математика Филиппов |
| Наши группы: |
|
На схемах (рис. Определить реакции опор для того способа закрепления бруса, при котором реакция, указанная в табл. 1, имеет наименьший модуль.
|
|||||||||||||||||||||||||||||||||
1 — 4) показаны три способа закрепления бруса, ось которого — ломаная линия. Задаваемая нагрузка (см. табл. 1) и размеры (м) во всех трех случаях одинаковы.Анализ и проектирование криволинейных круглых балок в резервуаре
Изогнутые в плане балки часто встречаются в зданиях, круглых резервуарах, мостах и других конструкциях с криволинейной формой.
Криволинейные балки всегда развивают кручение (закручивание) помимо изгибающего момента и поперечных сил, так как центр тяжести нагрузок, действующих нормально к плоскости конструкции, лежит вне линий, соединяющих ее опоры. Поэтому для поддержания равновесия в конструкции опоры криволинейной балки должны быть фиксированными или непрерывными.
В этом посте мы максимально упрощенно покажем, как анализировать непрерывные круглые (кольцевые) балки.
Круглая балка, поддерживающая верхний водяной бак Для кольцевых балок;
Максимальный отрицательный момент на любой опоре = K 1 wr 2
Максимальный положительный момент на любом пролете = K 2 wr 2
Максимальный крутящий момент = K 3 3 2 0 3 2 wr 29001 на каждой нагрузке столбец (опорная реакция) R = wr(2θ)
Поперечная сила на любой опоре = R/2 = wrθ
Коэффициенты приведены в таблице ниже;
Источник: Таблица 21.
1, Hassoun and Al-Manaseer (2008) Решенный пример
Цилиндрический резервуар диаметром 6 м поддерживается кольцевой балкой, которая опирается на 8 равноудаленных колонн. Желательно проанализировать и спроектировать кольцевую балку для поддержки нагрузки от надстройки.
Структурное расположение резервуара в плане показано ниже;
Анализ нагрузки
(a) Геометрия срезов
Размер балок = 450 мм x 300 мм
Размер колонны = ϕ300 мм. (b) Плотность материалов
Плотность складируемого материала = 10 кН/м 3
Плотность бетона = 25 кН/м 3
(c) Статическая нагрузка
5 Вес стен кН/м 3 × 0,25 м × 4,75 м × 18,849 м) = 559,579 кН
Вес плиты днища = (25 кН/м 3 × 0,25 м × 28,274 м 2 ) = 176,7120 кН накопленной воды 10 кН/м 3 × 4,5 м × 23,758 м 2 ) = 1069,11 кН
Итого = 1805,4015 кН
Перенесем эту нагрузку на кольцевую балку по периметру.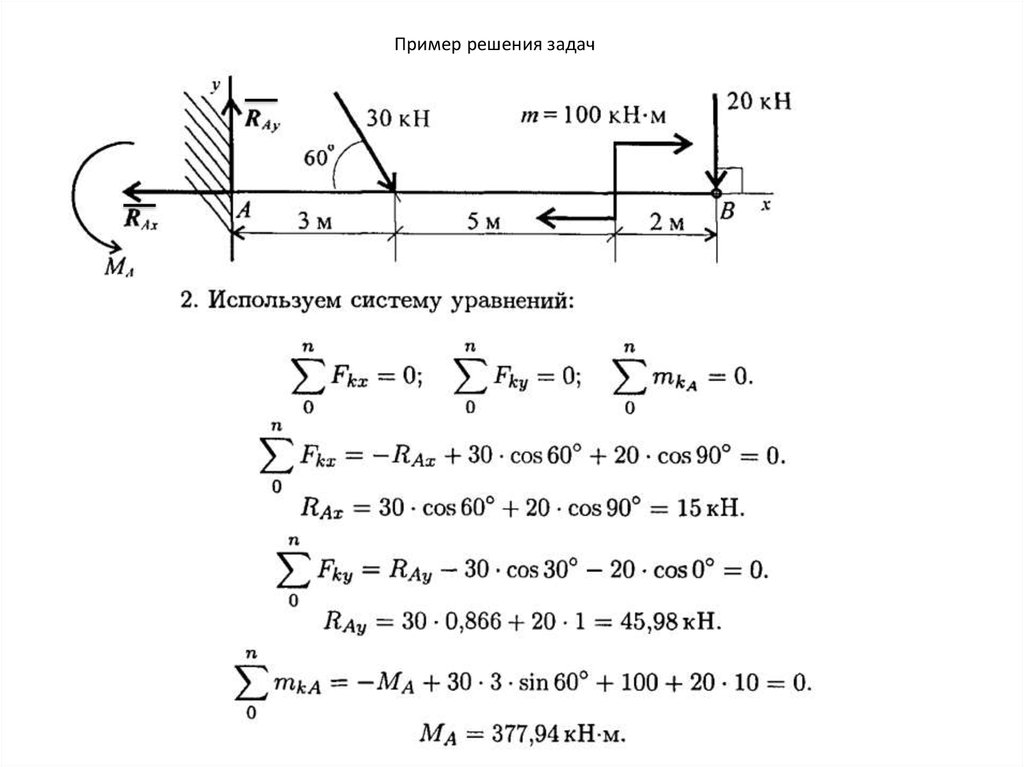
Периметр кольцевой балки = πd = π × 6 = 18,849 м
w = 1805,4015 кН / Периметр кольцевой балки = 1805,4015 кН / 18,849m = 95,782 кН/м
Собственный вес балки = 25 кН/м 3 × 0,3 м × 0,45 м = 3,375 кН/м
Общая статическая нагрузка на балку = 95,782 кН/м + 3,375 кН/м = 99,157 кН/м
Фактор нагрузки на балки в предельном состоянии по несущей способности = 1,35 × 99,157 кН/м = 133,862 кН/м
Из таблицы выше;
Количество опор (n) = 8
θ = π/n = 45°
K 1 = 0,052
K 2 = 0,026
K 3 = 5 90 r 3 м (
)0002 Максимальный отрицательный момент на опорах = K 1 wr 2 = -0,052 × 133,862 × 3 2 = -62,647 кН·м
Максимальный положительный момент в пролетах = 1 90 90 wr 3 2 90 1 2 90 0,026 × 133,862 × 3 2 = 31,323 кН.M
Максимальный момент кручения = K 3 WR 2 = 0,0040 × 133,862 × 3 2 = 4,819 КН
SHAR.
/2 = wrθ = 133,862 × 3 × (π/8) = 157,7 кН
Структурная конструкция
Прочность на конструкцию бетона F CK = 35 Н/мм 2
Прочность на армию F YK = 500 Н/мм 2
Номинальная крышка для усиления = 30 мм
M Ed = 31,323 кН·м
Эффективная глубина (d) = h – C nom – ϕ/2 – ϕlinks
Предполагается, что стержни ϕ12 мм будут использоваться для основных стержней, а стержни ϕ8 мм для хомутов (звенья)
d = 450 – 30 – 6 – 8 = 406 мм
k = M Ed /(f ck bd 2 ) = (31,323 × 10 6 )/(35 × 300 × 406 2 ) = 0,0003 требуется
z = d[0,5+ √(0,25 – 0,882K) ] = z = d[0,5+ √(0,25 – 0,882(0,0181))] = 0,95d
A с1 = M Ed7 /(0,95d
yk z) = (31,323×10 6 )/(0,87×500×0,95×406) = 186,69 мм 2
Обеспечить 3х22 мм СЭП (АС пров = 330911мм 2 )
Опоры
M Ed = 62,647 кН·м
Эффективная глубина (d) = h – C nom – ϕ/2 – ϕ3 для стержней ϕ3 при условии, что 6 мм стержней 9000 основные стержни и стержни ϕ8 мм для хомутов (звеньев)
d = 450 – 30 – 8 – 8 = 404 мм
k = M Ed /(f ck bd 2 ) = (62,647 × 12 9000 6 )/(35 × 300 × 404 2 ) = 0,0365
Поскольку k < 0,167, усиление сжатия не требуется
z = d[0,5+ √(0,25 – 0,882K)] = z = d[0,5+ √(0,25 – 0,882(0,0365))] = 0,95d
A s1 = M Ed /(0,87f yk z) = (62.
647 × 10 6 )/(0.87 × 500 × 0.95 × 404) = 375.23 mm 2
Provide 2h26 mm TOP (AS prov = 402 mm 2 )
Взаимодействие сдвига и кручения
В соответствии с пунктом 6.3.2(2) Еврокода 2 эффекты кручения и сдвига как для полых, так и для сплошных элементов могут накладываться друг на друга при одинаковом значении наклона стойки θ. Пределы для θ, указанные в 6.2.3 (2) EC2, также полностью применимы для случая комбинированного сдвига и кручения.
В соответствии с пунктом 6.3.2(4) EC2 максимальное сопротивление элемента, подвергаемого кручению и сдвигу, ограничено мощностью бетонных стоек. Чтобы не превысить это сопротивление, должно выполняться следующее условие:
T Ed /T Rd,max + V Ed /V Rd,max ≤ 1 ———- Уравнение (6.29 EC2 )
V Ed = 157,7 кН
T Ed = 4,819 кН·м
T Rd,max = расчетный момент сопротивления кручению
V Rd,max = максимальное сопротивление сдвигу поперечного сечения
Геометрические свойства для расчета на кручение
Площадь (A) = 300 мм × 450 мм = 135000 мм 2
Периметр (30) = 2(0) ) + 2(450) = 1500 мм
Эквивалентная толщина = t ef,i = A/U = 135000/1500 = 90 мм
Эквивалентное тонкостенное сечение для прямоугольного сечения приведено ниже;
A k = площадь, ограниченная осевыми линиями соединительных стен, включая внутренние полости = (450 – 90) × (300 – 90) = 75600 мм 2
U k = периметр площади A k = 2(450 – 90) + 2(300 – 90) = 1140 мм
T RD, MAX = 2 V α CW F CD A K T EF, I SINθ COSθ
Предполагая θ = 21,8 ° (COT θ = 2,5)
V = 0,6 (1 — F ck /250) = 0,6(1 – 35/250) = 0,516
f cd = (α cc × f ck )/γ c = (1 × 35)/1,3 = / 23,3 N мм 2
T Rd,max = 2 × 0.
516 × 1.0 × 23.33 × 75600 × 90 × cos 21.8° × sin 21.8° × 10 -6 = 56.485 KNm
V Rd,c = [ C Rd,c .k.(100ρ 1 f ck ) (1/3) + k 1 .σ cp ]b w 92 .d;
C Rd,c = 0,18/γ c = 0,18/1,5 = 0,12
k = 1 + √(200/d) = 1 + √(200/404) = 1,704 > 2,0, следовательно, k = 1,702
р 1 = As/bd = 402/(300 × 404) = 0,003317 < 0,02; K 1 = 0,15
V RD, C = [0,12 × 1,704 (100 × 0,003317 × 35) (1/3) ] 300 × 404 = 65469.358 n = 65,469 КН
С RD, V RD, V . c (65,469 кН) < V Ed (157,7 кН), требуется поперечная арматура.
Грузоподъемность сжимающей стойки (V Rd,max ) при θ = 21,8° (cot θ = 2,5)
V Rd,max = (b w .z.v 1 .f cd )/(cotθ + tanθ)
V 1 = 0,6(1 – f ck /250) = 0,6(1 – 903 f0011/250) = 0,6(1 – 903 f006) = 0,6 CD = (α CC ) F CK )/γ C = (1 × 35) /1,5 = 23,33 Н/мм 2
LET Z = 0,9D
В RD, MAX
= [(300 × 0,9 × 404 × 0,516 × 23,333)/(2,5 + 0,4)] × 10 -3 = 452,863 кН
Поскольку V Rd,c < V Ed 0 1 0 V
Следовательно, А sw /S = V Ed /(0,87F yk zcot θ) = 157700/(0,87 × 500 × 0,9 × 404 × 2,5) = 0,3988
Минимальная поперечная арматура;
A sw /S = ρ w,min × b w × sinα (α = 90° для вертикальных звеньев)
ρ w,min = (0,08 × √(f
1 ck )) /f
yk = (0,08 × √35)/500 = 0,0009465A sw /S (мин) = 0,0009465 × 300 × 1 = 0,2839
Поскольку 0,2839 < 0,39 09 0,398
Максимальное расстояние между поперечными звеньями = 0,75d = 0,75 × 404 = 303 мм
Обеспечьте H8 мм при 250 мм c/c (A sw /S = 0,402) Хорошо
Обратите внимание, что это звено должно быть правильно закрыто с достаточной длиной анкеровки, потому что это поможет противостоять скручиванию.
Конструктивные соображения для кручения
T ED /T RD, MAX + V ED /V RD, MAX ≤ 1
(4,891/56,485) + (157,7/453,863) = 0,434 <434 <434. 1.0 Следовательно, все в порядке
Однако обратите внимание, что фактическая сила сдвига в точке, где кручение максимально, на самом деле меньше, чем сила сдвига на опоре. Соотношение выше является ошибкой, но на безопасной стороне.
Максимальное кручение происходит под углом 9,5° от опоры (см. Таблицу выше). Следовательно, фактическая сила сдвига в этом сечении ( V Ed ) = Сила сдвига на опоре – wrα
V Ed = 157,7 – (133,862 × 3 × (9,5/180) × π) = 91,114 кН
Следовательно в учебных целях это сила сдвига, которую следует использовать для проверки взаимодействия сдвига и кручения. Небольшое рассмотрение покажет, что V Rd,max постоянна по всему сечению, но V Rd,c может варьироваться в зависимости от продольной арматуры, предусмотренной в сечении.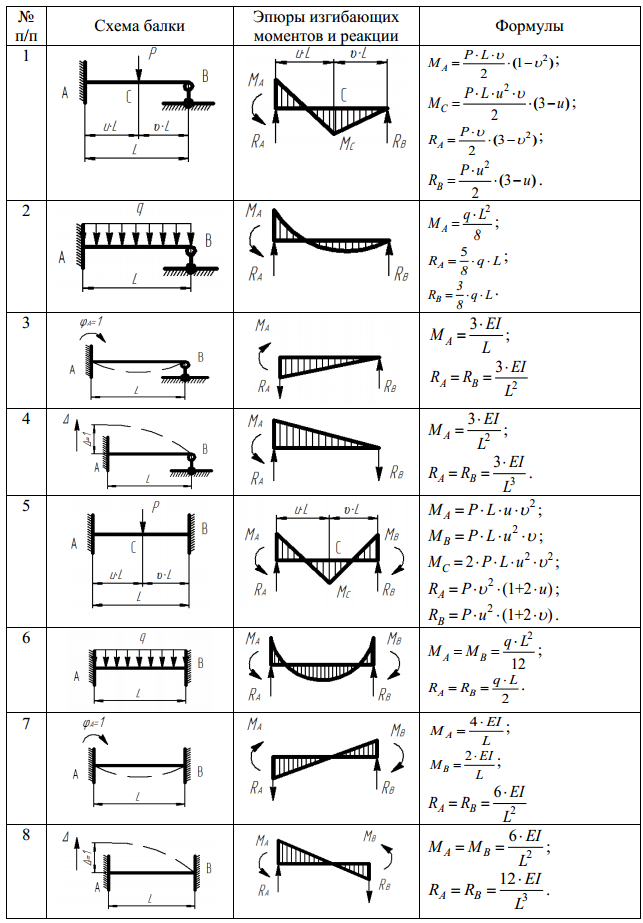
Повторная проверка описанного выше взаимодействия;
(4,891 /56,485) + (91,114 /453,863) = 0,287 <1,0 Следовательно, это нормально
Область поперечного усиления для сопротивления отрывкам
A SW /S = T ED /2A K F /S = T ED /2A K F F F F F F F = T ED /2A 1111111111111111111111111111111111110 гг. yw,d cotθ
A sw /s = (4,819 × 10 6 ) / (2 × 135000 × 0,87 × 500 × 2,5) = 0,0164 < A sw /S (мин)
Следовательно, звенья, рассчитанные на сдвиг, будут достаточными для сопротивления кручению.
Площадь продольного армирования, чтобы противостоять кручению
A S1 = T ED U K COT / 2A K F YD
A S1 = (4.819 × 1119
A S1111 = (4.819 × 6 a S1111 = (4.
819 × 6 a S1111111 = (4.819 × 9 110. 1140 × 2,5) / (2 × 75600 × 0,87 × 500) = 208 мм 2
В соответствии с пунктом 6.3.2(4) в сжимающих поясах продольная арматура может быть уменьшена пропорционально имеющейся сжимающей силе. В растянутых поясах продольная арматура на кручение должна быть добавлена к другой арматуре. Продольная арматура, как правило, должна быть распределена по длине стороны, но для меньших сечений она может быть сосредоточена на концах этой длины.
Тем не менее, во избежание сомнений, поскольку не было дано определение того, что можно рассматривать как «меньшую секцию», предусмотрите стержень 1х22 мм в середине секции с обеих сторон. Растяжимая и продольная арматура, предусмотренная в верхней и нижней части секции, должна быть в состоянии позаботиться обо всем остальном.
Дополнительная информация
Арматура на сдвиг требуется в прямоугольных сечениях, когда;
T Ed /T Rd,c + V Ed /V Rd,c ≤ 1 ————– Уравнение (6.
31 EC2)
Где;
T Rd,c является значением момента разрушения при кручении:
V Rd,c определено выше.
T RD, C = F CTD ⋅T⋅2A K
τ = F CTD = F CTK /γ C = 2,2/1,5 = 1,466 MPA (F CTK DED DED. из таблицы [3.1 – EC2]).
Отсюда получается:
T Rd,c = f ctd ⋅t⋅2A k = 1,466 × 90 × 2 × 75600 × 10 -6 = 19,949 кНм
Из приведенных выше расчетов;
V RD, C = [0,12 × 1,704 (100 × 0,003317 × 35) (1/3) ] 300 × 404 = 65469.358 N = 65,469 КН
(4,819/19,949)+ 91,114/65,469) = 4693333333333333 гг. > 1,0 (Использовалась поперечная сила в точке максимального кручения)
Таким образом, очевидно, что это показало необходимость расчетов поперечной арматуры.
Ссылки
Хассун М.Н., Аль-Манасир А. (2008 г.): Теория и проектирование конструкционного бетона (4-е издание).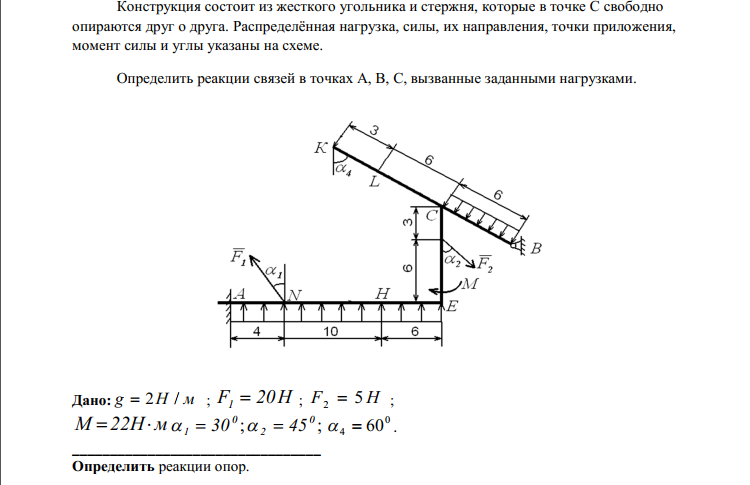
John Wile and Son Inc ., Нью-Джерси
Балки — фиксированные на обоих концах
- Балки — поддерживаемые на обоих концах — сплошные и точечные нагрузки
- Балки — фиксированные на одном конце и поддерживаемые на другом — сплошные и точечные нагрузки
- Балки — фиксированные с обоих концов — сплошные и точечные нагрузки
Балки фиксированные с обоих концов — одноточечная нагрузка
Изгибающий момент
M A = — F a b 2 / L 2 (1A)
, где
M A = момент на фиксированном конце A (NM, LB F FT)
F = LB F FT)
9000 2 F = нагрузка = нагрузка F FT) LB F )M B = — F A 2 B / L 2 (1B)
, где
, где
.
B (Нм, фунт F FT)
M F = 2 F A 2 B 2 / L 3 (1C)
, где
011111111111111111111111111111111111111111111111111111111111111111111111
гг. load (Nm, lb f ft)
Deflection
δ F = F a 3 b 3 / (3 L 3 E I) (1d)
where
δ F = прогиб при точечной нагрузке (м, фут)
E = Модуль упругости (Па (Н/м 2 2 901 мм) 0 ), Н/кв. дюйм
I = Area Moment of Inertia (m 4 , mm 4 , in 4 )
Support Reactions
R A = F (3 a + b) b 2 / L 3 (1f)
, где
R A = Сила поддержки на фиксированном конце A (N, LB F )
R B = F (A + 3 B) A 2 / L.
3 (1G)
, где
R B = Сила поддержки на фиксированном конце B (N, LB F )
BEAM с фиксированным на обоих концах — универсальная. Момент
M A = M B
= — Q L 2 /12 (2A)
, где
M = MOMPT ft)
q = uniform load (N/m, lb f /ft)
M 1 = q L 2 / 24 (2b)
where
М 1 = moment at the center (Nm, lb f ft)
Deflection
δ max = q L 4 / (384 E I) (2c)
where
δ max = максимальное отклонение в центре (м, фут)
E = Модуль упругости (Па (Н/м 2 7 3 ), Н/мм 2 9001
I = МОМЕНТ Инерции площади (M 4 , MM 4 , в 4 )
Реакция поддержки
R 1101010101010101010101010101010101010101010101010101010101010 2101010101010101010101010101010101010101010101010101011 .
Q L / 2 (2d)
, где
R = силы поддержки на фиксированных концах (n, LB F )
БАЙК ПЕРЕКРЫТА ДЛЯ ОБ ОБ ОБ ОБСОЯХ КОНЦИИ0621
Bending Moment
M A = — q L 2 / 20 (3a)
where
M A = moments at the fixed end A (Nm, lb f FT)
Q = равномерная снижающаяся нагрузка (N /M, LB F /FT)
M B = — Q L 2 /30 (3B)
/304504504040450450445045. 905 905. 905. 905.905 4 49504904. 905. 905. 04. M B = moments at the fixed end B (Nm, lb f ft) M 1 = q L 2 / 46.6 (3c) where M 1 = moment at x = 0.475 L (Nm, lb f ft) δ max = q L 4 / (764 E I) (3d) где δ max = max deflection at x = 0. E = Modulus of Elasticity (Pa (N/m 2 ), N/mm 2 , psi) I = Area Moment of Inertia (m 4 , mm 4 , in 4 ) δ 1/2 = q L 4 / (768 E I) (3e) , где Δ 1/2 = отклонение при x = 0,5 л (м, фут) R A , где R A = Сила поддержки на фиксированном конце A (N, LB F ) R B = 3 К.0603, где R B = Сила поддержки на фиксированном конце B (N, LB F ) Deflection
475 L (m, ft)
Реакция поддержки
.
BEAM зафиксировано на обоих концах — частично равномерная непрерывная распределенная нагрузка
МОМОН
= — (Q A 2 /6) (3 — 4 A / L + 1,5 (A / L) 2 ) (4A)
, где
M A = момент в фиксированном виде.