Строительная механика
Строительная механика
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ Глава 1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ СООРУЖЕНИЙ § 1.  § 1.3. УСЛОВИЯ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ГЕОМЕТРИЧЕСКИ НЕИЗМЕНЯЕМЫХ СТЕРЖНЕВЫХ СИСТЕМ Глава 2. БАЛКИ § 2.2. ЛИНИИ ВЛИЯНИЯ ОПОРНЫХ РЕАКЦИЙ ДЛЯ ОДНОПРОЛЕТНЫХ И КОНСОЛЬНЫХ БАЛОК § 2.3. ЛИНИИ ВЛИЯНИЯ ИЗГИБАЮЩИХ МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ ДЛЯ ОДНОПРОЛЕТНЫХ И КОНСОЛЬНЫХ БАЛОК § 2.4. ЛИНИИ ВЛИЯНИЯ ПРИ УЗЛОВОЙ ПЕРЕДАЧЕ НАГРУЗКИ § 2.5. ОПРЕДЕЛЕНИЕ УСИЛИЙ С ПОМОЩЬЮ ЛИНИЙ ВЛИЯНИЯ § 2.6. ОПРЕДЕЛЕНИЕ НЕВЫГОДНЕЙШЕГО ПОЛОЖЕНИЯ НАГРУЗКИ НА СООРУЖЕНИИ. ЭКВИВАЛЕНТНАЯ НАГРУЗКА § 2.7. МНОГОПРОЛЕТНЫЕ СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ БАЛКИ § 2.8. ОПРЕДЕЛЕНИЕ УСИЛИЙ В МНОГОПРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ ОТ НЕПОДВИЖНОЙ НАГРУЗКИ § 2.9. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ ДЛЯ МНОГОПРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК § 2.10. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ С ЛОМАНЫМИ ОСЯМИ ОТ НЕПОДВИЖНОЙ НАГРУЗКИ § 2.11. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ В БАЛКАХ КИНЕМАТИЧЕСКИМ МЕТОДОМ Глава 3. ТРЕХШАРНИРНЫЕ АРКИ И РАМЫ § 3.  1. ПОНЯТИЕ ОБ АРКЕ И СРАВНЕНИЕ ЕЕ С БАЛКОЙ 1. ПОНЯТИЕ ОБ АРКЕ И СРАВНЕНИЕ ЕЕ С БАЛКОЙ§ 3.2. АНАЛИТИЧЕСКИЙ РАСЧЕТ ТРЕХШАРНИРНОЙ АРКИ § 3.3. ГРАФИЧЕСКИЙ РАСЧЕТ ТРЕХШАРНИРНОЙ АРКИ. МНОГОУГОЛЬНИК ДАВЛЕНИЯ § 3.4. УРАВНЕНИЕ РАЦИОНАЛЬНОЙ ОСИ ТРЕХШАРНИРНОЙ АРКИ § 3.5. РАСЧЕТ ТРЕХШАРНИРНЫХ АРОК НА ПОДВИЖНУЮ НАГРУЗКУ § 3.6. ЯДРОВЫЕ МОМЕНТЫ И НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ Глава 4. ПЛОСКИЕ ФЕРМЫ § 4.1. ПОНЯТИЕ О ФЕРМЕ. КЛАССИФИКАЦИЯ ФЕРМ § 4.2. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ПРОСТЕЙШИХ ФЕРМ § 4.3. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ СЛОЖНЫХ ФЕРМ § 4.4. РАСПРЕДЕЛЕНИЕ УСИЛИЙ В ЭЛЕМЕНТАХ ФЕРМ РАЗЛИЧНОГО ОЧЕРТАНИЯ § 4.5. ИССЛЕДОВАНИЕ НЕИЗМЕНЯЕМОСТИ ФЕРМ § 4.6. ЛИНИИ ВЛИЯНИЯ УСИЛИИ В СТЕРЖНЯХ ПРОСТЕЙШИХ ФЕРМ § 4.7. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ В СТЕРЖНЯХ СЛОЖНЫХ ФЕРМ § 4.8. ШПРЕНГЕЛЬНЫЕ СИСТЕМЫ § 4,9. ТРЕХШАРНИРНЫЕ АРОЧНЫЕ ФЕРМЫ И КОМБИНИРОВАННЫЕ СИСТЕМЫ Глава 5. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В УПРУГИХ СИСТЕМАХ § 5.3. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЙ § 5.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ.  ИНТЕГРАЛ МОРА ИНТЕГРАЛ МОРА§ 5.5. ПРАВИЛО ВЕРЕЩАГИНА § 5.6. ПРИМЕРЫ РАСЧЕТА § 5.7. ТЕМПЕРАТУРНЫЕ ПЕРЕМЕЩЕНИЯ § 5.8. ЭНЕРГЕТИЧЕСКИЙ ПРИЕМ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ § 5.9. ПЕРЕМЕЩЕНИЯ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ, ВЫЗЫВАЕМЫЕ ПЕРЕМЕЩЕНИЯМИ ОПОР Глава 6. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ СИЛ § 6.2. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 6.3. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ НА ДЕЙСТВИЕ ЗАДАННОЙ НАГРУЗКИ § 6.4. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ § 6.5. СОСТАВЛЕНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ПРИ РАСЧЕТЕ СИСТЕМ НА ПЕРЕМЕЩЕНИЯ ОПОР § 6.6. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМАХ § 6.7. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ. ПРОВЕРКА ЭПЮР § 6.8. СПОСОБ УПРУГОГО ЦЕНТРА § 6.9. ЛИНИИ ВЛИЯНИЯ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 6.10. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 6.11. ГРУППИРОВКА НЕИЗВЕСТНЫХ § 6.12. СИММЕТРИЧНЫЕ И ОБРАТНОСИММЕТРИЧНЫЕ НАГРУЗКИ § 6.13. СПОСОБ ПРЕОБРАЗОВАНИЯ НАГРУЗКИ § 6.  14. ПРОВЕРКА КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ 14. ПРОВЕРКА КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ§ 6.15. ПРИМЕРЫ РАСЧЕТА РАМ § 6.16. «МОДЕЛИ» ЛИНИЙ ВЛИЯНИЯ УСИЛИИ ДЛЯ НЕРАЗРЕЗНЫХ БАЛОК Глава 7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДАМИ ПЕРЕМЕЩЕНИЙ И СМЕШАННЫМ § 7.2. ОПРЕДЕЛЕНИЕ ЧИСЛА НЕИЗВЕСТНЫХ § 7.3. ОСНОВНАЯ СИСТЕМА § 7.4. КАНОНИЧЕСКИЕ УРАВНЕНИЯ § 7.5. СТАТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ § 7.6. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ ПЕРЕМНОЖЕНИЕМ ЭПЮР § 7.8. ПОСТРОЕНИЕ ЭПЮР M, Q И N В ЗАДАННОЙ СИСТЕМЕ § 7.9. РАСЧЕТ МЕТОДОМ ПЕРЕМЕЩЕНИЙ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ § 7.10. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ ПРИ РАСЧЕТЕ РАМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ § 7.11. ПРИМЕР РАСЧЕТА РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ § 7.12. СМЕШАННЫЙ МЕТОД РАСЧЕТА § 7.13. КОМБИНИРОВАННОЕ РЕШЕНИЕ ЗАДАЧ МЕТОДАМИ СИЛ И ПЕРЕМЕЩЕНИЙ § 7.  14. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ МЕТОДОМ ПЕРЕМЕЩЕНИЙ 14. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ МЕТОДОМ ПЕРЕМЕЩЕНИЙГлава 8. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ СТЕРЖНЕВЫХ СИСТЕМ И МЕТОДЫ ЕЕ РЕШЕНИЯ § 8.2. СОСТАВЛЕНИЕ УРАВНЕНИЙ РАВНОВЕСИЯ, СТАТИЧЕСКИЕ УРАВНЕНИЯ. ИССЛЕДОВАНИЕ ОБРАЗОВАНИЯ СИСТЕМ § 8.3. СОСТАВЛЕНИЕ УРАВНЕНИЙ СОВМЕСТНОСТИ, ГЕОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. ПРИНЦИП ДВОЙСТВЕННОСТИ § 8.4. ЗАКОН ГУКА. ФИЗИЧЕСКИЕ УРАВНЕНИЯ § 8.5. СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ. СМЕШАННЫЙ МЕТОД § 8.6. МЕТОД ПЕРЕМЕЩЕНИЙ § 8.7. МЕТОД СИЛ § 8.8. УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ И ИХ СВЯЗЬ С УРАВНЕНИЯМИ СТРОИТЕЛЬНОЙ МЕХАНИКИ Глава 9. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ЭВМ § 9.2. ПОЛУАВТОМАТИЗИРОВАННЫЙ РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ КАЛЬКУЛЯТОРОВ § 9.3. АВТОМАТИЗАЦИЯ РАСЧЕТА СТЕРЖНЕВЫХ СИСТЕМ. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ ДЛЯ СТЕРЖНЯ § 9.4. МАТРИЦЫ РЕАКЦИЙ (ЖЕСТКОСТИ) ДЛЯ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ СТЕРЖНЕЙ И ИХ ИСПОЛЬЗОВАНИЕ § 9.5. ОПИСАНИЕ УЧЕБНОГО КОМПЛЕКСА ПО РАСЧЕТУ СТЕРЖНЕВЫХ СИСТЕМ.  ВНУТРЕННЕЕ И ВНЕШНЕЕ ПРЕДСТАВЛЕНИЕ ИСХОДНЫХ ДАННЫХ. БЛОК-СХЕМА КОМПЛЕКСА ПО РАСЧЕТУ СТЕРЖНЕВЫХ СИСТЕМ ВНУТРЕННЕЕ И ВНЕШНЕЕ ПРЕДСТАВЛЕНИЕ ИСХОДНЫХ ДАННЫХ. БЛОК-СХЕМА КОМПЛЕКСА ПО РАСЧЕТУ СТЕРЖНЕВЫХ СИСТЕМГлава 10. УЧЕТ ГЕОМЕТРИЧЕСКОЙ И ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ ПРИ РАСЧЕТЕ СТЕРЖНЕВЫХ СИСТЕМ § 10.2. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С УЧЕТОМ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ § 10.4. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С УЧЕТОМ ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ Глава 11. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ (МКЭ) § 11.2. СВЯЗЬ МКЭ С УРАВНЕНИЯМИ СТРОИТЕЛЬНОЙ МЕХАНИКИ § 11.3. ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ РЕШЕНИЯ ПЛОСКОЙ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ § 11.4. ПРЕДЕЛЬНЫЙ ПЕРЕХОД ДЛЯ ПЛОСКОЙ ЗАДАЧИ § 11.5. ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ РЕШЕНИЯ ОБЪЕМНОЙ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ § 11.6. СЛОЖНЫЕ ЭЛЕМЕНТЫ, ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ ЭЛЕМЕНТОВ С ИСКРИВЛЕННОЙ ГРАНИЦЕЙ § 11.7. ПОСТРОЕНИЕ МАТРИЦ РЕАКЦИЙ ДЛЯ РАСЧЕТА ПЛАСТИНОК И ОБОЛОЧЕК § 11.8. ОСОБЕННОСТИ КОМПЛЕКСОВ ДЛЯ РАСЧЕТА КОНСТРУКЦИЙ ПО МКЭ. СУПЕРЭЛЕМЕНТНЫЙ ПОДХОД Глава 12. ОСНОВЫ ДИНАМИКИ СООРУЖЕНИЙ § 12.  2. СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 2. СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ§ 12.3. РАСЧЕТ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ ДЕЙСТВИИ ПЕРИОДИЧЕСКОЙ НАГРУЗКИ § 12.4. РАСЧЕТ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ ДЕЙСТВИИ ПРОИЗВОЛЬНОЙ НАГРУЗКИ. ИНТЕГРАЛ ДЮАМЕЛЯ § 12.5. ДВИЖЕНИЕ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ. ПРИВЕДЕНИЕ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ К ДВУМ СИСТЕМАМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 12.6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ. УРАВНЕНИЕ ЛАГРАНЖА § 12.7. ПРИВЕДЕНИЕ КИНЕМАТИЧЕСКОГО ВОЗДЕЙСТВИЯ К СИЛОВОМУ § 12.8. СВЕДЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДИНАМИКИ К РАЗДЕЛЯЮЩИМСЯ УРАВНЕНИЯМ С ПОМОЩЬЮ РЕШЕНИЯ ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ § 12.9. МЕТОД ПОСТОЯННОГО УСКОРЕНИЯ И ЕГО ИСПОЛЬЗОВАНИЕ ДЛЯ РЕШЕНИЯ ДИНАМИЧЕСКИХ ЗАДАЧ Глава 13. СВЕДЕНИЯ ИЗ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ, ИСПОЛЬЗУЕМЫЕ В СТРОИТЕЛЬНОЙ МЕХАНИКЕ § 13.2. МАТРИЦЫ, ИХ ВИДЫ, ПРОСТЕЙШИЕ ОПЕРАЦИИ НАД МАТРИЦАМИ § 13.3. ПЕРЕМНОЖЕНИЕ МАТРИЦ. ОБРАТНАЯ МАТРИЦА § 13.4. МЕТОД ГАУССА ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.  РАЗЛОЖЕНИЕ МАТРИЦЫ В ПРОИЗВЕДЕНИЕ ТРЕХ МАТРИЦ РАЗЛОЖЕНИЕ МАТРИЦЫ В ПРОИЗВЕДЕНИЕ ТРЕХ МАТРИЦ§ 13.6. КВАДРАТИЧНАЯ ФОРМА. МАТРИЦА КВАДРАТИЧНОЙ ФОРМЫ. ПРОИЗВОДНАЯ ОТ КВАДРАТИЧНОЙ ФОРМЫ § 13.7. СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ВЕКТОРЫ ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННОЙ МАТРИЦЫ § 13.8. ОДНОРОДНЫЕ КООРДИНАТЫ И ИНТЕГРИРОВАНИЕ ПО ТРЕУГОЛЬНОЙ ОБЛАСТИ § 13.9. СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ, ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ И ЭКСПОНЕНЦИАЛЬНОЙ ФУНКЦИЕЙ ЗАКЛЮЧЕНИЕ ЛИТЕРАТУРА |
404 Cтраница не найдена
Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь.
Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
1.
 3: Равновесные конструкции, опорные реакции, детерминированность и устойчивость балок и рам
3: Равновесные конструкции, опорные реакции, детерминированность и устойчивость балок и рам- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 17609
- Felix Udoeyo
- Университет Темпл
Глава 3
Равновесные конструкции, опорные реакции, детерминированность и устойчивость балок и рам
3.1 Равновесие структур
Инженерные конструкции должны оставаться в равновесии как внешне, так и внутренне при воздействии системы сил. Требования к равновесию для конструкций в двух и трех измерениях изложены ниже.
3.1.1 Равновесие в двух измерениях
Для конструкции, находящейся под действием системы сил и пар, лежащих в xy плоскость, чтобы оставаться в покое, должна удовлетворять следующим трем условиям равновесия:
Вышеуказанные три условия обычно называют уравнениями равновесия для плоских конструкций. ∑ F x и ∑ F y являются суммой x и y составляющих всех сил, действующих на конструкцию, и ∑ M 90 049 z является суммой пары моментов и моментов всех сил относительно оси z , перпендикулярно плоскости xy действия сил.
∑ F x и ∑ F y являются суммой x и y составляющих всех сил, действующих на конструкцию, и ∑ M 90 049 z является суммой пары моментов и моментов всех сил относительно оси z , перпендикулярно плоскости xy действия сил.
3.1.2 Равновесие в трех измерениях
Структура в трех измерениях, то есть в пространстве, должна удовлетворять следующим шести требованиям, чтобы оставаться в равновесии под действием внешних сил:
3.2 Типы опор и их характеристики
Тип опоры, предусмотренной для конструкции, важен для обеспечения ее устойчивости. Опоры соединяют элемент с землей или с некоторыми другими частями конструкции. Предполагается, что учащийся уже знаком с несколькими типами опор для твердых тел, так как это было введено в курсе статики. Однако характеристики некоторых опор описаны ниже и показаны в таблице 3.1.
3.2.1 Штифтовая или шарнирная опора
Штифтовая опора допускает вращение вокруг любой оси, но предотвращает перемещение в горизонтальном и вертикальном направлениях. Его идеализированное представление и реакции показаны в таблице 3.1.
Его идеализированное представление и реакции показаны в таблице 3.1.
3.2.2 Роликовая опора
Роликовая опора допускает вращение вокруг любой оси и перемещение (горизонтальное перемещение) в любом направлении параллельно поверхности, на которую она опирается. Он сдерживает конструкцию от перемещения в вертикальном направлении. Идеализированное представление ролика и его реакции также показаны в таблице 3.1.
3.2.3 Подставка коромысла
Характеристики качающейся опоры аналогичны характеристикам роликовой опоры. Его идеализированная форма изображена в таблице 3.1.
3.2.4 Ссылка
Звено имеет два шарнира, по одному на каждом конце. Он допускает движение во всех направлениях, кроме направления, параллельного его продольной оси, которая проходит через два шарнира. Другими словами, сила реакции звена направлена в направлении звена вдоль его продольной оси.
3.2.5 Фиксированная опора
Фиксированная опора ограничивает вращение в любом направлении и предотвращает движение как в горизонтальном, так и в вертикальном направлениях.
3.3 Определенность и устойчивость балок и рам
Перед выбором аналитического метода важно установить определенность и устойчивость структуры. Детерминированная структура — это структура, неизвестная внешняя реакция или внутренние элементы которой могут быть определены только с помощью условий равновесия. Неопределенной конструкцией является та, неизвестные силы которой не могут быть определены только условиями статического равновесия и потребуют, кроме того, рассмотрения условий совместимости различных частей конструкции для ее полного анализа. Кроме того, структуры должны быть стабильными, чтобы иметь возможность выполнять свои желаемые функции. Конструкция считается устойчивой, если она сохраняет свою геометрическую форму при воздействии внешних сил.
3.3.1 Формулы устойчивости и определенности балок и рам
Условия определенности, неопределенности и неустойчивости балок и шпангоутов можно сформулировать следующим образом:
где
r = количество реакций поддержки.
C = уравнения состояния (два уравнения для одного внутреннего ролика и одно уравнение для каждого внутреннего штифта).
м = количество элементов.
j = количество соединений.
Таблица 3.1. Виды опор.
3.3.2 Альтернативная формулировка определенности и устойчивости балок и рам
где
r = количество реакций поддержки.
F i = количество сил реакции, передаваемых внутренним шарниром или внутренним роликом.
м = количество элементов.
Пример 3.1
Классифицируйте лучи, показанные на рис. 3.1 — рис. 3.5, как стабильные, детерминированные или недетерминированные, и при необходимости укажите степень неопределенности.
Рис. 3.1. Луч.Решение
Сначала нарисуйте диаграмму свободного тела каждой балки. Чтобы определить классификацию, примените уравнение 3.3 или уравнение 3.4.
Используя уравнение 3. 3, r = 7, м = 2, c = 0, j = 3. Применение уравнения приводит к 3(2) + 7 > 3(3) + 0, или 13 > 9. Следовательно, луч статически неопределим с точностью до 4°.
3, r = 7, м = 2, c = 0, j = 3. Применение уравнения приводит к 3(2) + 7 > 3(3) + 0, или 13 > 9. Следовательно, луч статически неопределим с точностью до 4°.
Используя уравнение 3.4, r = 7, m = 1, F i = 0. Применение уравнения приводит к 7 + 0 > (3)(1) или 7 > 3. Следовательно, луч статически неопределим с точностью до 4°.
Примечание. При использовании уравнения 3.3 части по обе стороны от внутренней опоры считаются отдельными элементами.
Рис. 3.2. Луч.Решение
Использование уравнения 3.3, r = 6, m = 3, c = 0, j = 4. Применение уравнения приводит к 3(3) + 6 > 3(4) + 0 или 15 > 12. Следовательно, луч статически неопределим с точностью до 3°.
Используя уравнение 3.4, r = 6, m = 1, F i = 0. Применение уравнения приводит к 6 + 0 > (3)(1) или 6 > 3. Следовательно, луч статически неопределим с точностью до 3°.
Раствор
Используя уравнение 3.3, r = 5, м = 3, c = 1, j = 4. Применение уравнения приводит к 3(3) + 5 > 3(4) + 1 или 14 > 13. Следовательно, луч статически неопределим с точностью до 1°.
Использование уравнения 3.4, R = 5, M = 2, F I = 2. Применение уравнения. луч статически неопределим с точностью до 1°.
Рис. 3.4. Луч.Решение
Используя уравнение 3.3, r = 5, m = 4, c = 1, j = 5. Применение уравнения приводит к 3(4) + 5 > 3(5) + 1 , или 17 > 16. Следовательно, уравнение статически неопределимо с точностью до 1°.
Использование уравнения 3.4, R = 5, M = 2, F I = 2. Применение уравнения. луч статически неопределим с точностью до 1°.
Рис. 3.5. Луч.Решение
Используя уравнение 3.3, r = 5, м = 5, c = 2, j = 6. Применение уравнения приводит к 3(5) + 5 = 3(6) + 2 , или 20 = 20. Следовательно, балка статически определима.
Применение уравнения приводит к 3(5) + 5 = 3(6) + 2 , или 20 = 20. Следовательно, балка статически определима.
Использование уравнения 3.4, R = 5, M = 3, F I = 4. Применение уравнения ведет к 5 + 4> 3 (3), или 9 = 9. Следовательно,. пучок статически определим.
Пример 3.2
Классифицируйте кадры, показанные на рис. 3.6–рис. 3.8, как стабильные или нестабильные, а также определенные или неопределенные. Если неопределенно, укажите степень неопределенности.
Рис. 3.6. Рамка.Решение
Используя уравнение 3.3, r = 3, м = 3, c = 0, j = 4. Применение уравнения приводит к 3(3) + 3 = 3(4) + 0 , или 12 = 12. Следовательно, репер статически определим.
Используя уравнение 3.4, r = 3, м = 1, F i = 0. Применение уравнения приводит к 3 + 0 = (3)(1), или 3 = 3. определить.
Примечание. При использовании уравнения 3.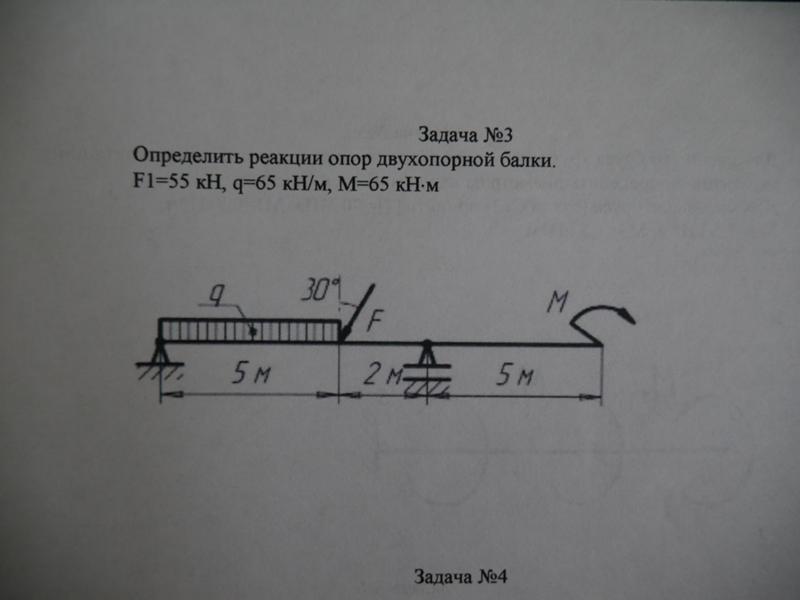 3 для классификации рамы рама должна быть разобрана в местах соединений, чтобы правильно определить количество элементов.
3 для классификации рамы рама должна быть разобрана в местах соединений, чтобы правильно определить количество элементов.
Решение
Используя уравнение 3.3, r = 6, м = 3, c = 1, j = 4. Применение уравнения приводит к 3(3) + 6 > 3(4) + 1 , или 15 > 13. Следовательно, репер статически неопределим с точностью до 2°.
Используя уравнение 3.4, r = 6, m = 2, F i = 2. Применение уравнения приводит к 6 + 2 > 3(2), или 8 > 6. Следовательно, система статически неопределима с точностью до 2°.
Рис. 3.8. Рамка.Решение
Используя уравнение 3.3, r = 4, м = 9, c = 0, j = 8. Применение уравнения приводит к 3(9) + 4 > 3(8) + 0 , или 31 > 24. Следовательно, репер статически неопределим с точностью до 7°.
Используя уравнение 3.4, r = 4, m = 1, F i = 9. Применение уравнения приводит к 4 + 9 > (3)(2) или 13 > 6. Следовательно, система статически неопределима с точностью до 7°.
Следовательно, система статически неопределима с точностью до 7°.
Примечание. При использовании уравнения 3.4 для классификации рамы с замкнутой петлей, как указано здесь, петля должна быть разрезана методом разреза, и при анализе следует учитывать внутренние реакции в разрезе.
3.4 Расчет опорных реакций для плоских конструкций
Опорные реакции для статически определимых и устойчивых конструкций на плоскости определяются с помощью уравнений равновесия. Процедура расчета описана ниже.
Процедура расчета опорных реакций
• Нарисуйте диаграмму конструкции в свободном теле, указав все неизвестные реакции с помощью стрелочной диаграммы.
• Проверьте устойчивость и определенность конструкции, используя уравнение 3.3 или 3.4. Если структура классифицируется как детерминированная, приступайте к анализу.
•Определите неизвестные реакции, применяя три уравнения равновесия. Если расчетная реакция приводит к отрицательному ответу, первоначально предполагаемое направление неизвестной реакции, как показано стрелкой на диаграмме свободного тела, неверно и должно быть исправлено, чтобы показать противоположное направление.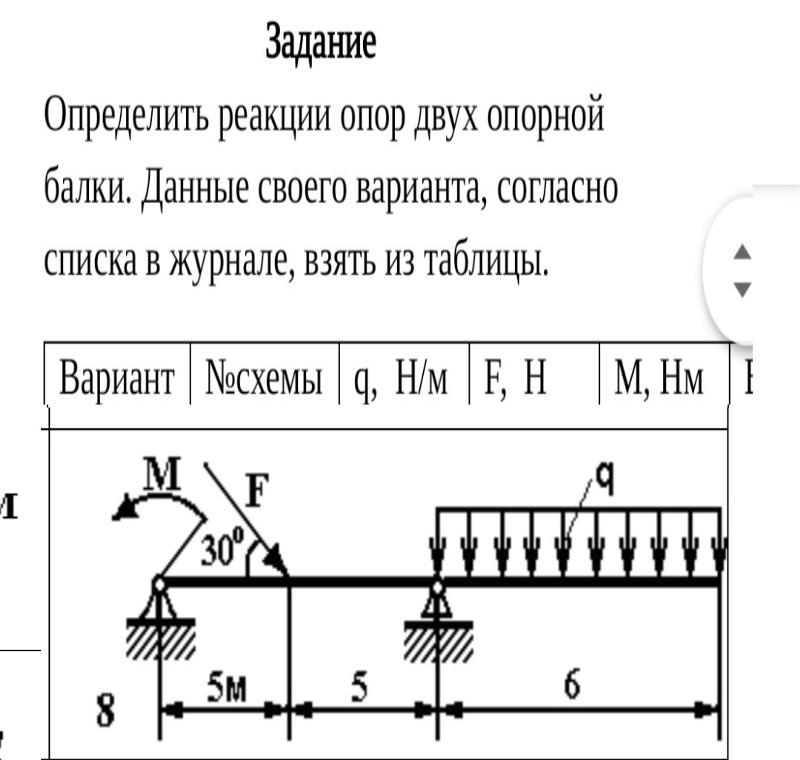 После внесения поправки величина силы должна быть указана в виде положительного числа в скорректированном наконечнике стрелки на диаграмме свободного тела
После внесения поправки величина силы должна быть указана в виде положительного числа в скорректированном наконечнике стрелки на диаграмме свободного тела
Пример 3.3
На консольную балку действует равномерно распределенная нагрузка и наклонная сосредоточенная нагрузка, как показано на рис. 3.9а. Определить реакции на опоре A .
Рис. 3.9. ЛучРешение
Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.9b. Опорные реакции, как показано на диаграмме свободного тела, таковы: A y , A x и M .
Расчет реакций. Перед расчетом опорных реакций распределенную нагрузку следует заменить единой равнодействующей силой, а наклонную нагрузку разложить на вертикальную и горизонтальную составляющие. Величина равнодействующей силы равна площади под прямоугольной нагрузкой и действует через центр тяжести прямоугольника. Как видно на рисунке 3.9c, P = [(4 кН/м)(2 м)], и его расположение находится в центре тяжести прямоугольной нагрузки. Применение уравнений статического равновесия дает следующее:
Применение уравнений статического равновесия дает следующее:
Пример 3.4
Простая балка длиной 12 футов несет равномерно распределенную нагрузку в 2 тысячи фунтов на фут по всему пролету и сосредоточенную нагрузку в 8 тысяч фунтов в середине пролета, как показано на рис. 3.10a. Определить реакции у опор А и В балки.
Рис. 3.10. Простой луч.Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.10b.
Расчет реакций. Распределенная нагрузка сначала заменяется единой равнодействующей силой, как показано на рис. 3.10c. Величина равнодействующей силы равна площади прямоугольного нагружения (распределенная сила). Таким образом, P = [(2 k/ft)(12 ft)], и его положение находится в центре тяжести прямоугольной нагрузки. Поскольку в этом примере нагрузка симметрична, реакции на обоих концах балки равны равны, и их можно было бы определить с помощью уравнений статического равновесия и принципа суперпозиции следующим образом:
Пример 3. 5
5
Балка с выступом подвергается воздействию переменной нагрузки, как показано на рис. 3.11а. Определить реакции опор A и B .
Рис. 3.11. Балка с навесом.Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.11b.
Расчет реакций. Обратите внимание, что распределенная нагрузка в балке треугольная. Распределенная нагрузка сначала заменяется единой равнодействующей силой, как показано на рис. 3.11c. Величина единой равнодействующей силы равна площади под треугольным нагружением. Таким образом, P = ()(6 м)(10 кН/м), а его центр тяжести находится в центре нагрузки (6 м). Применение уравнений равновесия дает следующее:
Пример 3.6
Балка с выступающими концами выдерживает три сосредоточенные нагрузки в 12 тысяч фунтов, 14 тысяч фунтов и 16 тысяч фунтов и момент 100 тысяч фунтов на фут, как показано на рисунке 3.12a. Определить реакции опор A и B .
Рис. 3.12. Брус с выступающими концами.
3.12. Брус с выступающими концами.Решение
Схема свободного тела. Диаграмма свободного тела балки показана на рисунке 3.12b.
Расчет реакций. Применение уравнений равновесия дает следующее:
Пример 3.7
Составная балка подвергается нагрузкам, показанным на рис. 3.13а. Найти опорные реакции в точках А и В балки.
Рис. 3.13. Составной луч.Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.13b.
Идентификация основных и дополнительных структур. Для правильного анализа составной структуры необходимо идентифицировать основные и дополнительные части структуры для правильного понимания их взаимодействия. Взаимодействие этих частей показано на рис. 3.13c. Первичная конструкция — это часть составной конструкции, которая может выдерживать приложенную внешнюю нагрузку без помощи дополнительной конструкции. С другой стороны, дополнительная конструкция является частью составной конструкции, которая зависит от основной конструкции для поддержки приложенной внешней нагрузки.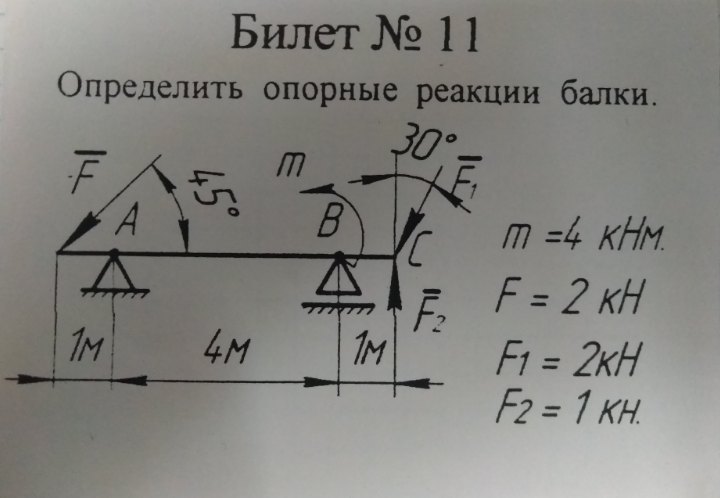 Для данной структуры часть AC является основной структурой, а часть CB — дополнительной структурой.
Для данной структуры часть AC является основной структурой, а часть CB — дополнительной структурой.
Расчет реакций. Анализ сложной структуры всегда должен начинаться с анализа дополнительной структуры, поскольку дополнительная структура поддерживается первичной структурой. Используя уравнения равновесия, опорные реакции балки определяются следующим образом:
Расчет комплементарной конструкции CB.
Рисунок 3.13e. Применяя уравнения равновесия и учитывая, что из-за симметрии нагрузки опорные реакции в точке C и B равны по величине, обеспечивает следующее:Анализ первичной конструкции AC.
Расчет опорной реакции. Обратите внимание, что до расчета реакций реакция в точке C в комплементарной структуре прикладывается к основной структуре в качестве нагрузки. Величина приложенной нагрузки такая же, как и у комплементарной конструкции, но противоположна по направлению. Применение уравнений равновесия позволяет сделать следующее:
Пример 3. 8
8
Найдите реакции опор A , C и E составной балки, несущей равномерно распределенную нагрузку 10 тысяч фунтов/фут по всей длине, как показано на рис. 3.14a.
Рис. 3.14. Составной луч.Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.14b.
Идентификация основных и дополнительных структур. Диаграмма взаимодействия для данной структуры показана на рис. 3.14в. AB является основной структурой, а BD и DE являются дополнительными структурами.
Расчет реакций.
Анализ комплементарной структуры DE.
Рисунок 3.14d. Применяя уравнения равновесия и отмечая, что из-за симметрии в нагружении опорные реакции в точках D и E равны по величине, можно сделать следующее:Анализ дополнительной конструкции БД.
Рисунок 3.14f. Нагрузка от комплементарной конструкции приложена в точке D . Применение уравнений равновесия предполагает следующее: Анализ первичной структуры AB.
Расчет опорной реакции. Обратите внимание, что до расчета реакций равномерная нагрузка заменяется единой равнодействующей силой, а реакция в точке B в комплементарной конструкции прикладывается к основной конструкции в качестве нагрузки. Применение требования равновесия дает следующее:
Пример 3.9
Найдите реакции опор A , B , E и F нагруженной составной балки, как показано на рис. 3.15a.
Рис. 3.15. Составной луч.Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.15b.
Идентификация основной и дополнительной структуры. Диаграмма взаимодействия для данной структуры показана на рис. 3.15в. CD является дополнительной структурой, а AC и DF являются основными структурами.
Расчет реакций.
Анализ комплементарной структуры CD.
Рисунок 3.15d. Применяя уравнения равновесия и отмечая, что из-за симметрии нагрузки опорные реакции в точках C и D равны по величине, можно сделать следующее: Анализ первичной конструкции AC.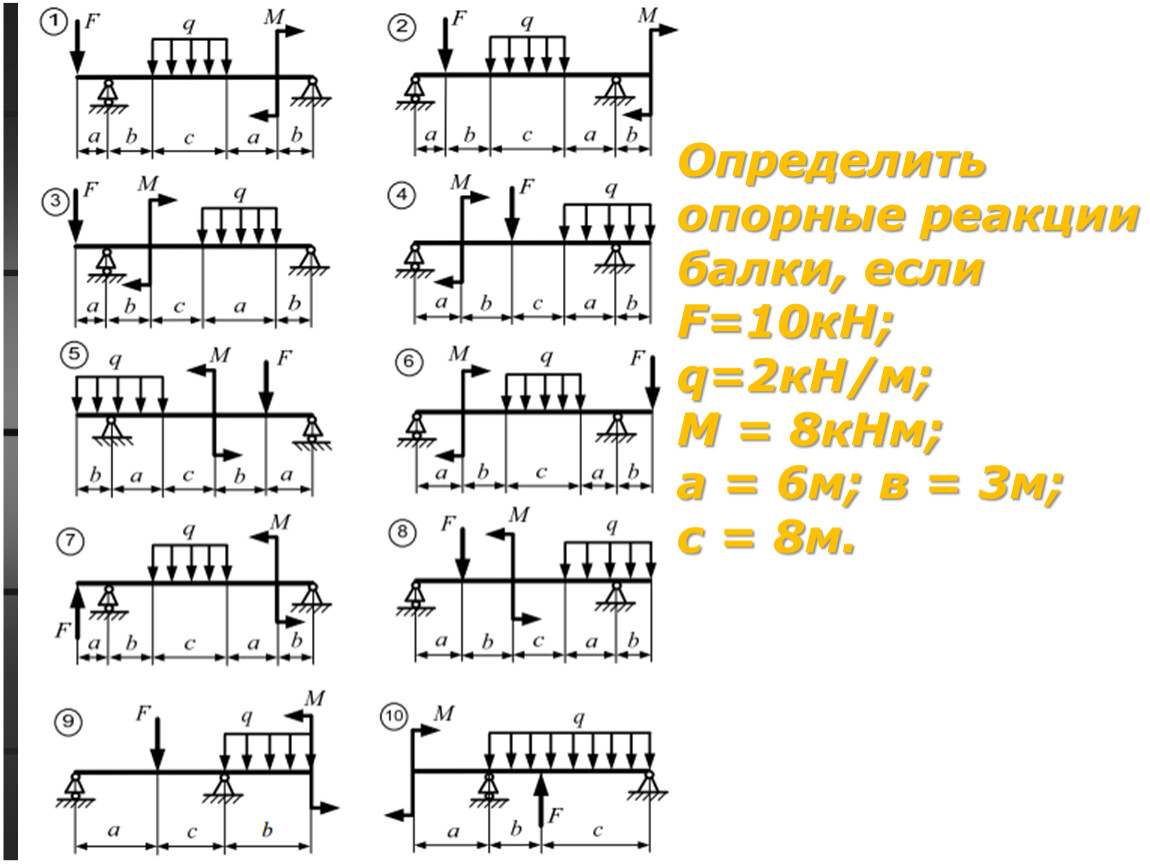
Расчет опорной реакции. Обратите внимание, что реакция комплементарной структуры при C действует как направленная вниз сила той же величины в той же точке первичной структуры. Применение уравнения равновесия предполагает следующее:
Анализ первичной структуры DF.
Рисунок 3.15ж. Применяя уравнения равновесия и учитывая, что опорная реакция в точке D дополняющей конструкции прикладывается в качестве нагрузки к основной конструкции, предполагает следующее:Пример 3.10
Определите реакции опор A и D рамы, показанной на рис. 3.16а.
Рис. 3.16. Рамка.Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.16b.
Расчет реакций. Распределенные нагрузки в колонне AB и балке BC сначала заменяются единичными равнодействующими силами, определяемыми как площадь их соответствующего оттенка нагрузки, как показано на рис. 3.16c. Применение условий равновесия предполагает следующее:
3.16c. Применение условий равновесия предполагает следующее:
Пример 3.11
Жесткая рама нагружена, как показано на рис. 3.17а. Определить реакции на опоре D .
Рис. 3.17. Жесткая рама.Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.17b.
Расчет реакций. Распределенная нагрузка в части AB рамы сначала заменяется единой равнодействующей силой, как показано на рис. 3.17c. Применение уравнений равновесия позволяет сделать следующее:
Пример 3.12
Найдите реакции на опорах E и F рамы, показанной на рис. 3.18а.
Рис. 3.18. Рамка.Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.18b.
Расчет реакций. Распределенные нагрузки сначала заменяются единичными равнодействующими силами, как показано на рис. 3.18c. Применение уравнений статического равновесия позволяет сделать следующее:
Пример 3. 13
13
Определите реакции опоры A жесткой рамы, показанной на рис. 3.19а.
Рис. 3.19. Жесткая рама.Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.19b.
Расчет реакций. Распределенная нагрузка в столбце AB сначала заменяется одной равнодействующей силой, как показано на рис. 3.19c. Применение уравнений статического равновесия позволяет сделать следующее:
Пример 3.14
Определите реакции опор A и E рамы, шарнирно закрепленной в точке C , как показано на рис. 3.20a.
Рис. 3.20. Рамка.Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.20b.
Расчет реакций. Реакции в составной раме рассчитываются с учетом диаграмм свободного тела как всей рамы, так и ее части. Перед расчетом реакций распределенную нагрузку в колонне заменяют единой равнодействующей силой. Вертикальные реакции в точках E и A , а также горизонтальные реакции в точках A находятся путем применения уравнений статического равновесия и рассмотрения диаграммы свободного тела всего каркаса. Горизонтальная реакция в E находится при рассмотрении части CDE диаграммы свободного тела.
Горизонтальная реакция в E находится при рассмотрении части CDE диаграммы свободного тела.
Знак минус означает, что первоначально предполагаемое направление A y было неверным. Следовательно, A y действует вниз, а не вверх, как предполагалось изначально. Это должно быть исправлено при последующем анализе.
Для определения E x рассмотрим момент сил в элементе CDE относительно шарнира.
Пример 3.15
Найдите реакции на опорах A и B нагруженной рамы на рис. 3.21а. Рама шарнирно закреплена на D .
Рис. 3.21. Загруженный кадр.Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.21b.
Расчет реакций. Распределенная нагрузка в столбце AC сначала заменяется единой равнодействующей силой путем нахождения области нагрузки, как показано на рис. 3.21. Реакция в 9. 0042 B рассчитывается путем принятия момента сил в части DB рамы относительно штифта в точке D , а другие реакции определяются путем применения других условий равновесия.
0042 B рассчитывается путем принятия момента сил в части DB рамы относительно штифта в точке D , а другие реакции определяются путем применения других условий равновесия.
Знак минус означает, что первоначально предполагаемое направление A y было неверным. Следовательно, A y действует вниз, а не вверх, как предполагалось изначально. Это должно быть исправлено при последующем анализе.
Резюме главы
Условия статического равновесия: Конструкция находится в состоянии статического равновесия, если равнодействующая всех сил и моментов, действующих на нее, равна нулю. Математически это выражается следующим образом:
∑ Ж = 0∑ М = 0
Для тела на плоскости существуют следующие три уравнения равновесия:
∑ F x = 0∑ F y = 0∑ М 0 = 0
Типы опор: Различные символические представления используются для моделирования различных типов опор для конструкций. Ролик используется для моделирования опоры, которая препятствует вертикальному движению конструкции, но допускает горизонтальное перемещение и вращение. Штифт используется для моделирования опоры, которая предотвращает горизонтальные и вертикальные перемещения, но допускает вращение. Неподвижная опора моделирует опору, предотвращающую горизонтальные и вертикальные перемещения и повороты.
Ролик используется для моделирования опоры, которая препятствует вертикальному движению конструкции, но допускает горизонтальное перемещение и вращение. Штифт используется для моделирования опоры, которая предотвращает горизонтальные и вертикальные перемещения, но допускает вращение. Неподвижная опора моделирует опору, предотвращающую горизонтальные и вертикальные перемещения и повороты.
Детерминированность, неопределенность и устойчивость структур: Структура является детерминированной, если число неизвестных реакций равно числу статических равновесий. Таким образом, для определения опор такой конструкции достаточно уравнений статического равновесия. С другой стороны, статически неопределимая структура — это структура, в которой количество неизвестных реакций превышает уравнения равновесия. Для анализа неопределенной конструкции нужны дополнительные уравнения, и эти уравнения можно получить, рассматривая совместность конструкции. Неопределенные конструкции иногда необходимы, когда необходимо уменьшить размеры элементов или увеличить жесткость элементов. Стабильная структура — это структура, в которой опорные реакции не параллельны и не параллельны друг другу. Формулировки устойчивости и определенности балок и шпангоутов следующие:
Стабильная структура — это структура, в которой опорные реакции не параллельны и не параллельны друг другу. Формулировки устойчивости и определенности балок и шпангоутов следующие:
Балки и рамы: | 3 m + r < 3 j + C Конструкция неустойчивая |
3 m + r = 3 j + C Структура определенная | |
3 м + r > 3 j + C Структура не определена |
Практические задачи
3.1 Классифицируйте конструкции, показанные на рисунках P3.1a–P3.1p, как статически определимые или неопределимые, а также статически устойчивые или неустойчивые. Если неопределенно, укажите степень неопределенности.
Рис. П3.1. Структурная классификация. 3.2. Определите опорные реакции для балок, показанных на рис. P3.2–рис. P3.12.
P3.2–рис. P3.12.
3.3. Определите опорные реакции для рам, показанных на рис. P3.13–рис. P3.20.
Рис. P3.13. Рамка.Рис. P3.14. Рамка.Рис. P3.15. Рамка.Рис. P3.16. Рамка.Рис. 3.17. Рамка.Рис. 3.18. Рамка.Рис. 3.19. Рамка.Рис. 3.20. Рамка.3.4 Определите опорные реакции для ферм, показанных на рис. P3.21–рис. P3.27.
Рис. P3.21. Ферма.Рис. P3.22. Ферма.Рис. P3.23. Ферма.Рис. P3.24. Ферма.Рис. P3.25. Ферма.Рис. P3.26. Ферма.Рис. P3.27. Ферма.- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Феликс Удоэйо
- Лицензия
- CC BY-NC-ND
- Версия лицензии
- 4,0
- Теги
- источник@https://temple.
 manifoldapp.org/projects/structural-analysis
manifoldapp.org/projects/structural-analysis
- источник@https://temple.
Электронная таблица анализа однопролетных и неразрезных балок
CESDb > > BEAMANAL
ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ :BEAMANAL
РАЗРАБОТЧИК :Алекс Томанович
ВЕРСИЯ: 2.5
ПЛАТФОРМА: Электронная таблица
РАЗМЕР ФАЙЛА: 1,1 МБ
ЛИЦЕНЗИЯ: Бесплатное ПО
Описание программы
BEAMANAL — это программа для работы с электронными таблицами, написанная в MS-Excel для анализа однопролетных или неразрезных балок, подверженных практически любому типу нагрузки. Рассмотрены четыре (4) типа однопролетных балок и два (2) — (5) пролетных, неразрезных балки. В частности, рассчитываются реакции концов балки, а также максимальные моменты и прогибы. Создаются графики всех диаграмм, а также таблицы сдвига, момента, наклона и прогиба для балки или каждого отдельного пролета. Кроме того, для однопролетных балок из конструкционной стали AISC 9th Edition (ASD) Проверка кода может выполняться для изгиба и сдвига по оси X.
Допущения и ограничения программы:
1. При разработке этой программы использовалась следующая ссылка (см. ниже):
«Современные формулы статики и динамики, подход с учетом напряжений и деформаций» Уолтера Д. Pilkey and Pin Yu Chang, McGraw-Hill Book Company (1978), страницы с 11 по 21.
2. Эта программа использует три (3) следующих предположения в качестве основы для анализа:
- Балки должны быть постоянного сечения (E и I постоянны по всей длине пролета).
- Отклонения не должны существенно изменять геометрию задачи.
- Напряжение должно оставаться в «упругой» области.
3. На балке или каждом отдельном пролете эта программа обрабатывает равномерную нагрузку по всей длине и до восьми (8) частичных равномерных, треугольных или трапециевидных нагрузок, до пятнадцати (15) точечных нагрузок и до четыре (4) приложенных момента.
4. Для однопролетных балок эта программа всегда предполагает определенную ориентацию для двух (2) из четырех (4) различных типов. В частности, всегда предполагается, что фиксированный конец «подпорной» или «консольной» балки находится на правом конце балки.
В частности, всегда предполагается, что фиксированный конец «подпорной» или «консольной» балки находится на правом конце балки.
5. Эта программа рассчитает вертикальные реакции концов балки и моментные реакции (если применимо), максимальный положительный момент и отрицательный момент (если применимо), а также максимальный отрицательный и положительный прогиб (если применимо). Расчетные значения концевых реакций и максимальных моментов и прогибов определяются путем деления балки на пятьдесят (50) равных сегментов с пятьдесят одной (51) точкой, а также с учетом всех точечных нагрузок и местоположений приложенных моментов. (Примечание: фактическая точка максимального момента возникает там, где сдвиг = 0 или проходит через ноль, а фактическая точка максимального прогиба находится там, где наклон = 0.)
6. Пользователю предоставляется возможность ввести два (2) конкретных местоположения от левого конца балки для расчета сдвига, момента, наклона и прогиба.
7. Пользователю также предоставляется возможность выбрать форму AISC W, S, C, MC или HSS (прямоугольная труба), чтобы облегчить получение момента инерции по оси X для ввода в чисто аналитические рабочие листы.
 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав