Расчёт вала на прочность

Конструктивные размеры вала принимаем в зависимости от диаметра выходного конца. Этот размер определяем приближенно из расчёта на прочность при кручении по заниженным допускаемым напряжениям . Принимаем для изготовления быстроходного вала сталь 40Х (предполагая, что шестерню изготовляем вместе с валом), и назначаем .

Из уравнения прочности определяем диаметр выходного конца вала:

получаем:

В соответствии с рядом принимаем

Поскольку диаметр вала двигателя и превышает более чем на 25%, то рассчитывать на стандартную упругую муфту не приходится. Назначаем:

Диаметр вала под уплотнение — .

Диаметр резьбы —

Диаметр под дистанционную шайбу —

Диаметр под подшипники —

(роликовые радиально-упорные лёгкой серии)

Диаметр опорного бурта —

Длинна выходного конца вала — , принимаем .

Ширина маслоудерживающего кольца — , принимаем

Точки приложения (активных сил) реакции опор вала ориентировочно находятся на уровне торцов радиально-упорных подшипников.

где =18.5 для подшипников 7207.

принимаем — расстояние от делительного диаметра до первой опоры со стороны шестерни.

Расстояние между опорами (точками приложения реакций).

, принимаем .

. Вычерчиваем схему нагружения вала, определяем силы действующие на шестерне и реакции опор.

Окружная сила на окружности среднего делительного диаметра:

, принимаем для удобства вычислений:

Рис.1 Эпюра напряжений вала

 

Осевая сила для шестерни (радиальная для колеса).

,

где .

Радиальная сила для шестерни (осевая для колеса).

Определяем реакции опор:

а) в вертикальной плоскости zoy от сил и

; .

б) в горизонтальной плоскости xOz от силы

Определяем момент изгибающих моментов в характерных сечениях (А, В,С)

и строим опоры.

а) В плоскости xOz

следовательно:

Строим эпюру — (см. рис.1)

б) В плоскости xOz:

Строим эпюру (см. рис.1)

Крутящий момент ,

Вычисляем суммарный изгибающий момент и определяем нормальные напряжения изгиба в опасном сечении А при .

Напряжение от силы крайне малы их можно не учитывать.

Определяем напряжение кручения в опасных сечениях.

Определяем допускаемое напряжение изгиба при симметричном цикле

для материала вала (сталь 40) по табл. 4.1 при d<120мм.,

, принимаем коэф. запаса , ()

эфф. коэф. концентр. напр.

— коэф. режима нагрузки (стр. 195 ).

По гипотезе наибольших касательных напряжений находим эквивалентное напряжение и сравниваем его с допустимым.

Так как расчётное напряжение значительно меньше допустимого, а коэф. запаса прочности значителен, то проверку на жесткость вала можно не проводить.

Расчет валов на статическую, усталостную жесткость и прочность (вариант 7)

• формат doc
• размер 2. 31 МБ
• добавлен 22 марта 2009 г.

Проектировочный расчет вала на статическую прочность.
Расчет вала на жесткость.
Расчет вала на усталостную прочность.
Статически неопределимая рама.
Статически не определимая балка.
Расчет стержней на устойчивость.

Читать онлайн

Похожие разделы

1. Академическая и специальная литература
2. Металлургия
3. Металловедение
4. Механические и физические свойства металлов
5. Дефекты металлов
6. Усталость металлов

Смотрите также

• формат djvu
• размер 8. 72 МБ
• добавлен 23 августа 2009 г.

Справочник. 4-е изд, перераб. и доп. — М.: Машиностроение, 1993. -640 с. Расчет на прочность деталей поршневых двигателей, турбомашин, компрессоров, методы расчета контактных напряжений, расчет на усталость, термопрочность, устойчивость. Расчет лопаток, дисков, валов. Критические частоты вращения валов. Оценка прочности и надежности.

• формат pdf
• размер 520.92 КБ
• добавлен 16 апреля 2010 г.

Метод. указания. — Хабаровск: ДВГУПС, 2001. — 40 с: ил. Содержат теоретический материал и примеры расчета стержней на прочность и жесткость при простых деформациях. Приведены варианты расчетно-проектных работ. Методические указания предназначены для студентов всех форм обучения, изучающих курс сопротивления материалов.

Практикум

• формат doc
• размер 452.44 КБ
• добавлен 02 февраля 2012 г.

Методические указания к выполнению расчетно-графических работ для студентов механических специальностей. – Омск: Изд-во СибАДИ, 2008. – 28 с. Содержатся основные теоретические положения по расчету на прочность и жесткость при растяжении, сжатии, кручении и изгибе. В приведенных числовых примерах на предложенных схемах показывается последовательность выполнения задания, приводятся результаты расчетов и их графическая интерпретация. Примеры соотве…

• формат pdf
• размер 13.42 МБ
• добавлен 25 июля 2010 г.

Учебное пособие для вузов. 3-е издание. СПб.: БХВ-Петербург, 2004, 544 с. Учебное пособие включает в себя все основные разделы общепрофессиональной дисциплины «Сопротивление материалов»: геометрические характеристики сечений, виды деформаций и напряжений, прочность и жесткость, испытание материалов и расчет конструкций. В соответствии с современными государственными образовательными стандартами рассматриваются также разделы о малоцикловой усталос…

• формат doc
• размер 1.65 МБ
• добавлен 04 апреля 2009 г.

Северодонецк, ТИ СНУ им. В. Даля. Расчет статически неопределимых стержней при растяжении. Расчет круглого вала на прочность и жесткость при кручении. Полный расчет балок на прочность. Расчет плоских рам. Статически неопределимые рамы. Сложный изгиб. Расчет на устойчивость сжатого стержня. Расчет на прочность при ударных нагрузках. Заархивированная папка с файлами .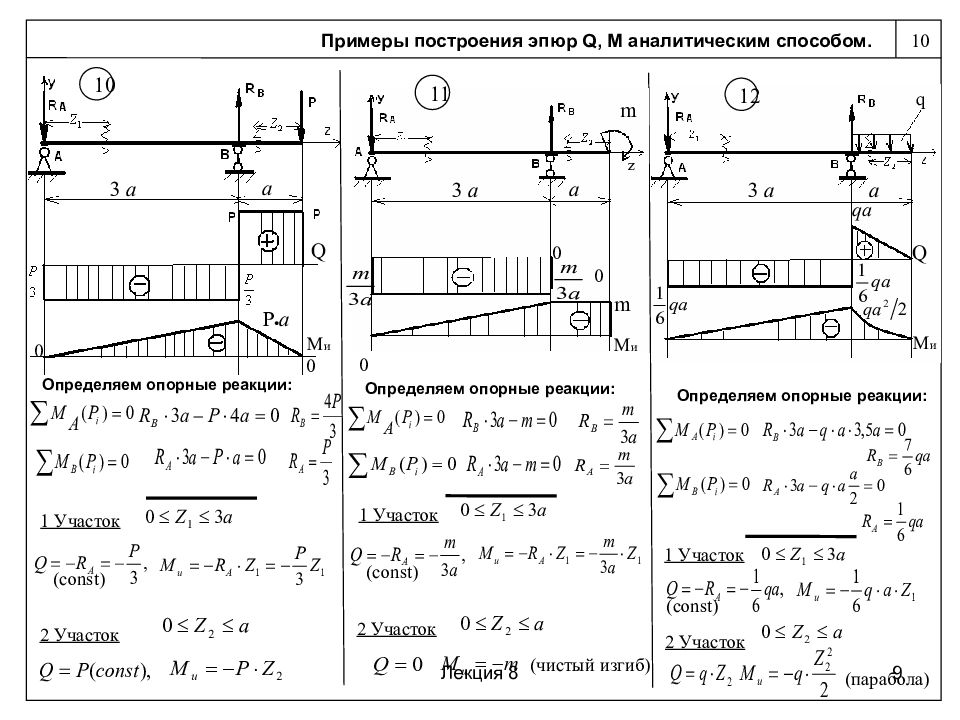

DOC.

• формат doc
• размер 1004.73 КБ
• добавлен 15 апреля 2010 г.

Расчет стержневых статически неопределимых систем при растяжении (сжатии). Расчет валов и пружин на жесткость и прочность при кручении. Построение эпюр внутренних силовых факторов для балок и рам. Задачи на прочность и жесткость при изгибе статически определимых систем. Расчет статически неопределимых систем по методу сил. Расчеты на прочность при сложном напряженном состоянии. Задачи на прочность при циклических напряжениях. Расчеты элементов ко…

Практикум

• формат jpg
• размер 5.62 МБ
• добавлен 26 января 2011 г.

УГАТУ. 2003. Требования к выполнению курсовых и ргр. Проектировочный расчет вала на статическую прочность. Расчет вала на жесткость. Проверочный расчет вала на усталостную прочность. Методичка для выполнения курсовой работы по сопротивлению материалов, по теме сложное сопротивление. 2003.rn

Практикум

• формат djvu
• размер 738.52 КБ
• добавлен 10 октября 2011 г.

Методические указания к расчетно- проектировочной работе по сопротивлению материалов. — Гомель: БелИЖТ, 1987. — 68с. Излагаются основы расчета на прочность и жесткость балок при плоском изгибе. Рассмотрены численные методы определения нормальных, касательных, главных и эквивалентных напряжений, перемещений сечений, а также примеры проектировочного и проверочного расчетов балок при изгибе.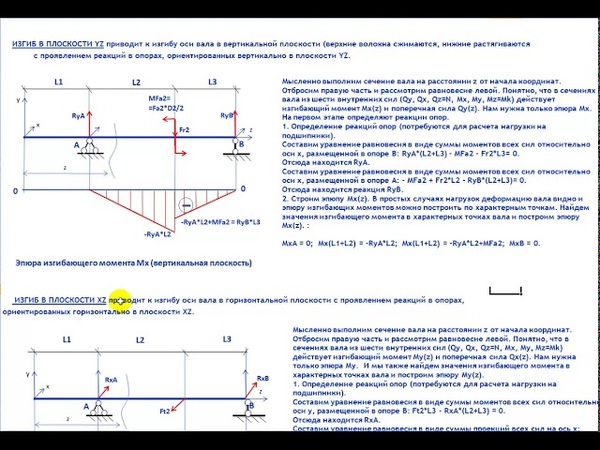 В отдельной главе приведены краткие сведения о геометричес…

• формат djv
• размер 2.07 МБ
• добавлен 09 марта 2011 г.

Справочное пособие. Л., Машиностроение, 1977. -184 с. с ил. В пособии приведены расчеты на прочность, жесткость, устойчивость и колебания нагруженных круговых и кольцевых пластин.

• формат djvu
• размер 1.01 МБ
• добавлен 30 ноября 2008 г.

Сп-б. : 2004, 43 стр. Целью настоящих методических указаний является развитие навыков самостоятельного расчета элементов конструкции на прочность, жесткость и устойчивость. Методические указания содержат краткие сведения по теории курса «Сопротивление материалов» и примеры решения задач по расчету стержней на прочность, жесткость и устойчивость. Методическое указания предназначены для студентов-заочников специальностей 100700, 250100, 263000, вы…

Изгибающий момент круглого вала Калькулятор

9 0011

✖Напряжение при изгибе — это нормальное напряжение, возникающее в точке тела, подвергаемого нагрузкам, вызывающим его изгиб.ⓘ Напряжение изгиба [σ b ]		Дина на квадратный сантиметрГигапаскальКилограмм-сила на квадратный сантиметрКилограмм-сила на квадратный дюймКилограмм-сила на квадратный метрКилограмм-сила на квадратный миллиметрКилоньютон на квадратный сантиметрКилоньютон на квадратный метрКилоньютон на квадратный миллиметрКилопаскальМегапаскальНьютон на квадратный сантиметрНьютон на квадрат МетрНьютон на квадратный миллиметрПаскаль-Фунт-сила на квадратный фут-фунт — Сила на квадратный дюйм	+10% -10%
✖Диаметр круглого вала обозначается через d.ⓘ Диаметр круглого вала [Φ]	AlnAngstromArpentАстрономическая единица Аттометр AU длиныЯчменное зерноМиллиард световых лет Радиус БораКабель (Международный )Кабель (Великобритания)Кабель (США)КалибрСантиметрЦепьКубит (Греческий)Кубит (длинный)Кубит (Великобритания)ДекаметрДециметрРасстояние от Земли до ЛуныРасстояние от Земли до СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиЭлектронный радиус (классический)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US) Обзор)ФурлонгГигаметрРукаШирина ладониГектометрДюйм КенКилометрКилопарсекКилоярдЛигаЛига (Статут)Свет YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (ткань)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman Act usRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter	+10% -10%

✖Максимальный изгибающий момент возникает там, где поперечная сила равна нулю. ⓘ Изгибающий момент круглого вала [M max ]

Грамм-сила-сантиметрКилограмм-сила-метрКилоньютон-метрМикроньютон-метрМиллиньютон-метрНьютон-метрНьютон-миллиметрФунт-футПаунд-дюймФунт-сила-футТонна-сила (длинная) Метр-тонна-сила (метрическая) Метр-тонна-сила (короткая) Метр

⎘ Копировать

👎

Формула

Перезагрузить

👍

Изгибающий момент круглого вала Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1: Преобразование входных данных в базовые единицы

Напряжение изгиба: 0,72 МПа —> 720000 Па (проверьте преобразование здесь)
Диаметр круглого вала: 0,75 метра —> 0,75 метра Преобразование не требуется

ШАГ 2: Вычисление формулы

ШАГ 3: Преобразование результата в единицу измерения

29820,5865164969 Ньютон-метр —> 29,8205865164969 Килоньютон-метр (Проверьте конвертацию здесь)

< 12 основных калькуляторов напряжения

Расположение основных плоскостей

Идти Theta = ((0,5*atan((2*Напряжение сдвига xy)/(Напряжение в направлении x-Напряжение в направлении y))))

Диаметр круглого вала при эквивалентном изгибающем моменте и максимальном главном напряжении 93))

Угол наклонной плоскости с использованием касательного напряжения на ней и осевой нагрузки

Идти Theta = (arsin((Напряжение сдвига в наклонной плоскости*2/Аксиальное напряжение)))/2

Изгибающий момент круглого вала Формула 93)))

Что такое комбинированный изгиб и кручение?

Комбинированные изгибающие, прямые и крутильные напряжения в валах возникают, например, в гребных валах судов, где на вал помимо изгибающего момента и кручения действует прямая тяга. В таких случаях прямые напряжения из-за изгибающего момента и осевой нагрузки должны быть объединены в единую равнодействующую.

Как рассчитать изгибающий момент круглого вала? 93)))

для расчета Максимальный изгибающий момент. Изгибающий момент круглого вала представляет собой реакцию, возникающую в элементе конструкции, когда к элементу прилагается внешняя сила или момент, вызывающий изгиб элемента. Максимальный изгибающий момент обозначается символом M _max .

Как рассчитать изгибающий момент круглого вала с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для изгибающего момента круглого вала, введите напряжение изгиба (σ 93))) . Напряжение изгиба — это нормальное напряжение, возникающее в точке тела, подвергаемого нагрузкам, вызывающим его изгиб. Диаметр круглого вала обозначается буквой d.

Как рассчитать изгибающий момент круглого вала?

Изгибающий момент круглого вала — это реакция, возникающая в элементе конструкции, когда к элементу прилагается внешняя сила или момент, вызывающий изгиб элемента, рассчитывается с использованием Максимальный изгибающий момент = Напряжение изгиба/(32/(pi* (Диаметр круглого вала^3))) . Чтобы рассчитать изгибающий момент круглого вала, вам необходимо напряжение изгиба (σ _b ) и диаметр круглого вала (Φ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для напряжения изгиба и диаметра круглого вала и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.

Доля

Скопировано!

Расчет вала WL1+

Расчет вала WL1+ | немецкий

---

(C) Copyright 1991-2022 by HEXAGON Software, Берлин

---

WL1+ рассчитывает нагрузки, напряжения и критические скорости валов, безопасность в соответствии с DIN743, а также ожидаемый срок службы роликовых подшипников в соответствии с DIN.

Быстрый ввод

Быстрый ввод обеспечивает ввод всех размеров, оснований, материалов, усилий, траекторных нагрузок, изгибающих моментов и крутящего момента в одном диалоговом окне.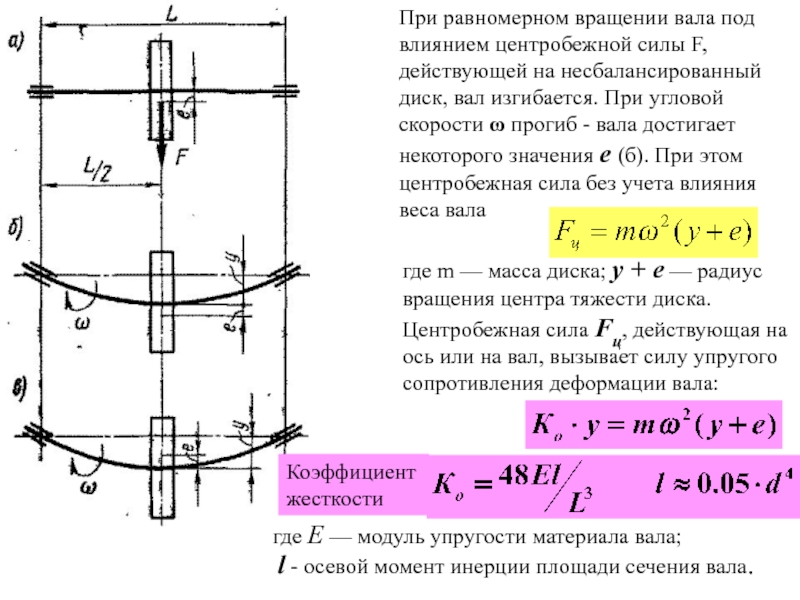 Нажмите кнопку «Рассчитать» для расчета вала и выберите в «Показать» результат в виде графика, таблицы, чертежа, диаграммы.

Вал и нагрузки

Вал может иметь до 100 цилиндрических или конических сегментов вала. Можно задать до 50 отдельных сил, траекторных нагрузок, изгибающих моментов, крутящих моментов и осевых усилий. WL1+ преобразует напряжение от зубчатых колес в траекторные нагрузки, осевые силы, крутящие моменты и изгибающие моменты. Однако самый простой способ ввода — это импорт сил зубчатого колеса, рассчитанных нашей программой Gear Program. ZAR1+.

Эффект концентрации стресса

Повышенное напряжение на переходах вала автоматически учитывается при вводе значений поверхности, коэффициентов чувствительности и радиуса перехода. Зоны с повышенным эффектом концентрации напряжений (например, от канавок скользящих шпонок) можно учитывать, вводя beta k, beta kb и beta kt при расчете напряжения кручения и изгиба.

Подшипники

WL1+ предназначен для расчета статически определимых поддерживаемых валов с фиксированными и незакрепленными подшипниками, фиксированными зажимными и радиально-упорными подшипниками, каждый подшипник воспринимает осевые усилия только в одном направлении. Кроме того, можно рассчитать статически неопределимые опорные валы с 3, 4 или 5 подшипниками.

База данных материалов

Наиболее важные стали включены в предоставленную базу данных. Другие стали и цветные металлы доступны при доступе к базе данных материалов WST1.

Критическая скорость

Критические скорости для изгибных и крутильных колебаний рассчитываются исходя из собственной массы вала и других установленных масс (например, корпуса ротора, зубчатого венца, ременного шкива) по методу Кулла и Дункерли.

Эталонное напряжение

Можно рассчитать эталонное напряжение из напряжений изгиба, растяжения и сдвига в соответствии с теорией максимального напряжения, теорией максимального сдвига или теорией максимальной энергии деформации.

База данных подшипников качения

Пакет WL1+ включает файлы базы данных в формате XBase с 600 радиальными шарикоподшипниками, 100 самоустанавливающимися шарикоподшипниками, 70 игольчатыми втулками, 170 игольчатыми подшипниками, 500 цилиндрическими роликоподшипниками, 300 коническими роликоподшипниками, 360 самоустанавливающимися роликоподшипниками, 100 радиально-упорных шарикоподшипников и 180 игольчатых роликовых сепараторов в соответствии с документацией SKF и INA. База данных может быть дополнена и изменена по мере необходимости.

Карты

Крутящий момент, изгибающий момент, угол изгиба, линия прогиба, напряжение изгиба, напряжение сдвига и эталонные кривые напряжения предоставляют важную информацию. Вы можете распечатать диаграммы, сохранить их в файлы DXF или включить в свою документацию через буфер обмена.

Расчет подшипников качения

На основании рассчитанных значений силы реакции и расчетных значений грузоподъемности можно выбрать подходящий роликоподшипник из базы данных WL1+. WL1+ рассчитывает ожидаемый срок службы в соответствии со стандартом ISO 281.

Распечатка

В распечатке показаны экстремальные значения изгибающего момента, линии прогиба, напряжения изгиба, напряжения сдвига и эталонного напряжения, а также веса вала, момента инерции массы, центра тяжести, опорных сил, угла изгиба на опорной поверхности, ожидаемого срока службы подшипника, критические скорости, материальные ценности и все входные данные.