Метод сечений. Внутренние силовые факторы
1. Метод сечений. Внутренние силовые факторы
Внешние силы стремятся разрушить конструкции или узлы, а внутренние силы противодействуют этому.
Рассмотрим произвольный брус, нагруженный самоуравновешенной системой сил (рис. 1.1):
Рис. 1.1 Приведение внешних нагрузок
Чтобы найти внутренние силы воспользуемся методом сечений РОЗУ (рис. 1.2).
Р – разрезаем произвольной плоскостью на А и В.
О – отбрасываем одну из этих частей, например, В (рис. 1.2а). Рассмотрим оставшуюся часть(рис. 1.2б).
З – заменяем. Внутренние силы мы заменяем главным вектором и главным моментом.
Рис. 1.2 Метод сечений РОЗУ
Раскладываем главный вектор и главный момент в плоскости на оси (рис. 1.2в).
Внутренние силовые факторы:
Qx, Qy – вызывают сдвиг – перерезывающие поперечные силы;
N – нормальная продольная шина, растяжение, сжатие бруса;
Мz – крутящий момент;
Мx, Мy – изгибающий момент (рис.
1.2в).
В общем случае нагружения в сечении действуют 6 внутренних факторов. График изменения внутреннего фактора при передвижении вдоль оси стержня называется – эпюрой.
У – уравновешиваем.
1.1 Построение эпюр внутренних факторов для стержней
Построение эпюр нормальных сил N
Правило знаков для N имеет физический смысл: нормальная сила является положительной, если вызывает растяжение бруса, отрицательной – если сжатие.
Пример 1 (рис. 1.3).
Если на стержень действуют силы, приложенные вдоль его оси, то он находится в условиях растяжения и остается только один внутренний фактор N.
Рис. 1.3 Стержень
Порядок построения эпюр:
1. Определяем реакции опор.
2. Разбиваем стержень на участки.
Участок – часть стержня между точками приложения сосредоточенных сил, включая опорные реакции.
3. Записываем аналитические выражения для внутренних силовых факторов.
4.
Строим график (эпюру) (рис. 1.4).
Рис. 1.4 Построение эпюры нормальных сил
Эпюра – график, заштрихованный линиями, перпендикулярными оси.
Используя метод РОЗУ, отбрасывают ту часть, где больше нагрузки.
Внутренний фактор – равнодействующая внутренних сил.
Nz2 = P-3P = -2P
Nz2 = P-3P = -2P
Пример 2 (рис. 1.5).
Построить эпюру нормальных сил N.
q – интенсивность равномерно – распределенной нагрузки.
Опасное сечение в заделке, т.к. там самое большое значение N.
Рис. 1.5 Построение эпюры нормальных сил
Построим эпюру нормальных сил
1.2 Построение эпюр крутящих моментов
Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент, а прочие силовые факторы равны нулю. Для крутящего момента, независимо от формы сечения, принято следующее правило знаков.
Рис.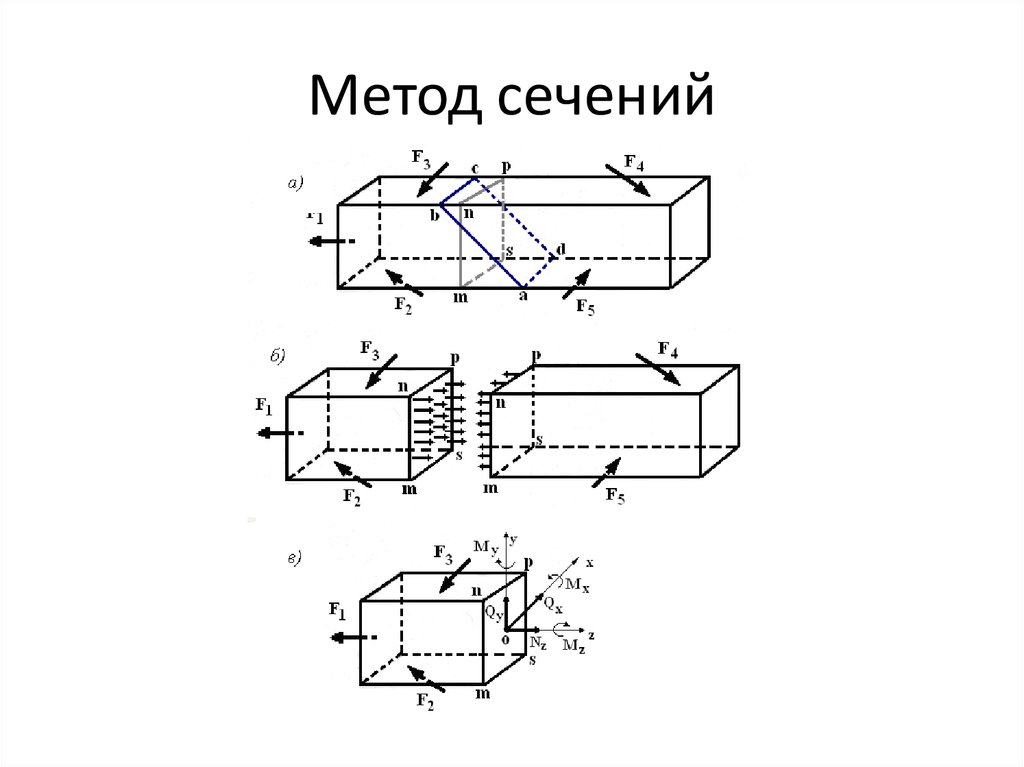
1.6 Правило знаков для крутящего момента
Если со стороны внешней нормали к сечению вращение осуществляется против часовой стрелки, то крутящий момент положительный (рис.1.6).
Правило знаков носит формальный характер (можно установить произвольно).
Стержень, в основном работающий на кручение, называется валом.
Рис.1.7 Схематичное изображение крутящего момента (против часовой стрелки).
Пример (К — 1)
Построить эпюру крутящих моментов (рис 1.9).
Рис.1.9 Построение эпюры крутящих моментов
Пример на построение эпюры крутящих моментов (рис 1.10).
Рис.1.10 Построение эпюры крутящих моментов
1.3 Построение эпюр поперечных сил Q и изгибающих моментов M для балок
Балка – стержень, в основном работающий на изгиб. При расчете балку принято заменять ее осью, все нагрузки приводятся к этой оси, а силовая плоскость будет совпадать с плоскостью чертежа.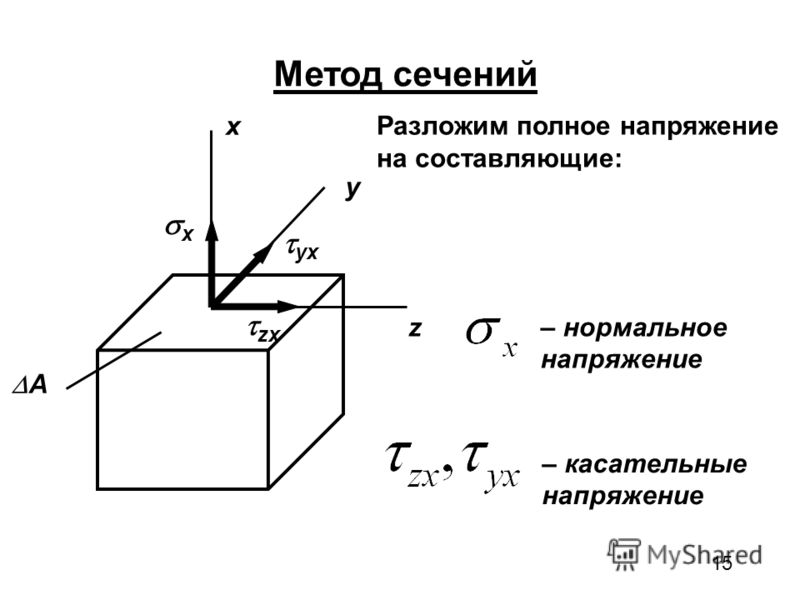
Вал – стержень в основном работающий на кручение.
Виды опор:
Шарнирно-подвижная опора – опора, в которой может возникать только одна составляющая реакции, направленная вдоль опорного стержня (рис.1.11).
Рис.1.11 Шарнирно-подвижная опора
Шарнирно-неподвижная опора – опора, в которой могут возникать две составляющие реакции: вертикальная и горизонтальная (рис.1.12).
Рис.1.12 Шарнирно-неподвижная опора
Заделка (жесткое защемление) – опора, в которой могут быть: вертикальная и горизонтальная реакции и опорный момент (рис.1.13).
Рис.1.13 Заделка
1.3.1 Правило знаков для Q
1.3.2 Правило знаков для М
Эпюру для М строят на сжатых волокнах.
Пример (Э-3)
Построить эпюры внутренних усилий Q и M для однопролетной балки (рис. 1.14).
Рис. 1.14 Расчетная схема
Дано:
Р=0,5qa
M=0,5qa2
Решение:
Вычислим реакции опор.
Освободим балку от связей и заменим их действие реакциями.
Y: RA-P-q·2a+RB=0
Составим уравнения равновесия:
Сумма моментов всех сил относительно точки А равна
откуда
Сумма моментов всех сил относительно точки В равна
Разделим балку на четыре участка. Применим метод сечений на каждом из участков и запишем выражения для внутренних усилий
Внутренние усилия на втором участке равны
На третьем участке
Внутренние усилия на четвертом участке равны
Строим эпюры для M и Q (рис 1.15). Для проверки правильности полученных эпюр могут быть использованы следствия из дифференциальных зависимостей между Q и M.
Ещё посмотрите лекцию «Содержание и литература» по этой теме.
Рис. 1.15 Построение эпюр Q и M
МЕТОД СЕЧЕНИЙ (РОЗУ) Содержаниие и основные понятия
Привет, мой друг, тебе интересно узнать все про метод сечений розу , тогда с вдохновением прочти до конца.
Для того чтобы лучше понимать что такое
метод сечений розу , настоятельно рекомендую прочитать все из категории Содержаниие и основные понятия.
| Так как внутренние силы взаимно уравновешены и стоит задача выразить их через внешние, то необходимо выполнить такую операцию, чтобы внутренние силы стали явными. |
| Например для стержня можно применить прием мысленного рассечения на две части плоскостью, перпендикулярной продольной оси. Затем отбросить одну из полученных частей, что позволяет превратить внутренние силы, для целого стержня, во внешние для оставленной части стержня (рис.1.5). |
| Рис. 1.5 |
| Силы взаимодействия будут в каждой точке проведенного сечения (рис. 1.6). |
| Рис. 1.6 |
Эту систему большого числа сил по правилам теоретической механики можно привести к одной точке (центру тяжести поперечного сечения), в результате чего получим главный вектор R и главный момент М (рис. 1.7). |
| 2. Отбрасываем одну часть |
| Рис . Об этом говорит сайт https://intellect.icu . 1.7 |
| Теперь спроектируем на три оси (продольную z и две взаимно-перпендикулярные поперечные х и у). В результате получим шесть внутренних силовых факторов: три силы N, Qx Qyи три момента Мx, My и Мz |
| Сила N называется продольной силой, силы Qx и Qy — поперечные силы. Момент относительно оси z — Мz — крутящий момент; и моменты Мx, My относительно поперечных осей — изгибающие. |
| Каждому из внутренних усилий соответствует определенный вид деформации (изменение формы), бруса. Например, продопьной силе N соответствует растяжение (или сжатие) бруса. |
| 3. Заменяем |
| Рис. 1.8 |
Таким образом, рассматривается одна из полученных при рассечении частей стержня, которая нагружена приложенными к этой части внешними силами и шестью внутренними усилиями (рис. 1.8). |
| 4. Уравновешиваем |
| Для установления связи внутренних и внешних сил можно к этой части применить уравнения равновесия, (уравновешиваем), так как известно, что если тело находится в целом в равновесии, то в равновесии и любая его часть. |
| Рассмотрим, например, уравнение . Из внутренних усилий на ось z проектируется только продольная сила N. |
| Тогда |
| где — проекция всех внешних сил, действующих на оставленную часть стержня, на ось z. |
| Отсюда вытекает следующее определение: продольная сила N численно равна алгебраической сумме проекций на ось стержня всех внешних сил, расположенных по одну сторону (рассматриваемую) от проведенного сечения. |
Аналогичные определения для Qx, Qy , Мx, My и Mz. По первым буквам выполняемых операций (рассекаем, отбрасываем, заменяем и уравновешиваем) метод сечений иногда называют методом РОЗУ. |