Как варить овсянку — рецепт овсяной каши на воде и молоке, пропорции — УНИАН

Как варить овсянку / фото ua.depositphotos.com

Овсяная каша — полезное и питательное блюдо на завтрак. Чтобы получить идеальную кашу, нужно знать несколько принципов ее приготовления. Как варить овсянку, из крупы или хлопьев, на воде или на молоке — читайте в материале УНИАН.

• Как варить овсянку — из крупы или хлопьев
• Овсянка на воде — самый простой рецепт 
• Овсянка на молоке — рецепт сладкой каши 

Ранее мы рассказывали, как правильно варить перловую кашу в кастрюле, мультиварке и микроволновке. 

Читайте такжеВкусные воздушные пирожные: как приготовить профитроли с заварным кремом

Видео дня

Как варить овсянку — из крупы или хлопьев

Кашу можно приготовить из овсяной крупы или хлопьев. Считается, что чем больше помол, тем овсяная каша полезнее, но варится она довольно долго. К тому же перед приготовлением крупу следует замочить на несколько часов и варить затем около 30-40 минут.

Между тем, из овсяных хлопьев каша готовится значительно быстрее. Сами овсяные хлопья отличаются помолом и, соответственно, временем приготовления — более мелкие варятся быстрее. Кроме того, некоторые овсяные хлопья не нуждаются в варке, их просто заливают кипятком, соком, кефиром или другими кисломолочными продуктами. Информация об этом обычно указана на коробке.

Хлопья бывают, в частности, таких видов:

• экстра №1 — тонкие, крупные и полезные из овсяных хлопьев; варятся 15 минут;
• экстра №2 — тонкие хлопья меньшего размера, варятся 5-10 минут;
• экстра №3 — тонкие и маленькие, варятся всего 2-5 минут;
• геркулес — толстые крупные хлопья, обработанные паром и потому менее полезные; варятся около 20 минут;
• лепестковые — толстые хлопья, на вкус нежнее, чем геркулес; варятся около 10 минут.

Овсяную говорю можно варить на воде или на молоке. Также возможен вариант, когда ее готовят на воде и молоке в соотношении 50 на 50 (или в другой желаемой пропорции).

Рецепт приготовления овсянки — пропорции / фото ua.depositphotos.com

Относительно того, в каких пропорциях брать овсянку и жидкость, то это зависит от желаемой консистенции каши:

• для вязкой овсянки — 1:2, то есть, на 1 часть хлопьев (или крупы) следует брать 2 части жидкости;
• для полувязкой каши — пропорция 1:2,5;
• для жидкой — пропорция 3-3,5.

Овсянка на воде — самый простой рецепт 

• Хлопья — 100 г
• Вода — 200 мл

Доведите воду до кипения, добавьте хлопья и аккуратно помешивайте венчиком. Таким образом масса получится однородной консистенции. В процессе приготовления добавьте соль или сахар по вкусу. 

Подавайте готовую овсяную кашу можно со сливочным маслом, сливками, свежими ягодами, медом, орехами. 

Овсянка на молоке — рецепт сладкой каши 

• Хлопья — 1 стакан
• Молоко — 2,5 стакана
• Соль — щепотка
• Сахар — 1 ст. л.

Молоко поставьте на огонь, добавьте соль и сахар. Когда молоко прогреется, всыпьте овсяные хлопья. Варите, постоянно помешивая, на небольшом огне, в соответствии с указанным на упаковке временем. В готовую кашу добавьте сливочное масло. Хорошо перемешайте.

Совет: чтобы овсяная каша была воздушной, пышной и мягкой, постоянно перемешивайте ее, пока она не станет теплой.

Подавайте кашу со свежими фруктами и ягодами, медом, любимым сиропом, корицей.

Вас также могут заинтересовать новости:

• Что приготовить из остатков рисовой каши: 3 вкусные идеи
• Овсяное печенье с корицей, изюмом и орехами: 4 простых рецепта
• Рецепт идеальных блинов на молоке, которые получатся у всех

Масштабирование и размер изображений на современных страницах SharePoint

Современные страницы и веб-части полностью реагируют на различные устройства, поэтому масштаб изображений, используемых в веб-частях, зависит от того, где они показаны, какой макет используется и какое устройство их просматривает.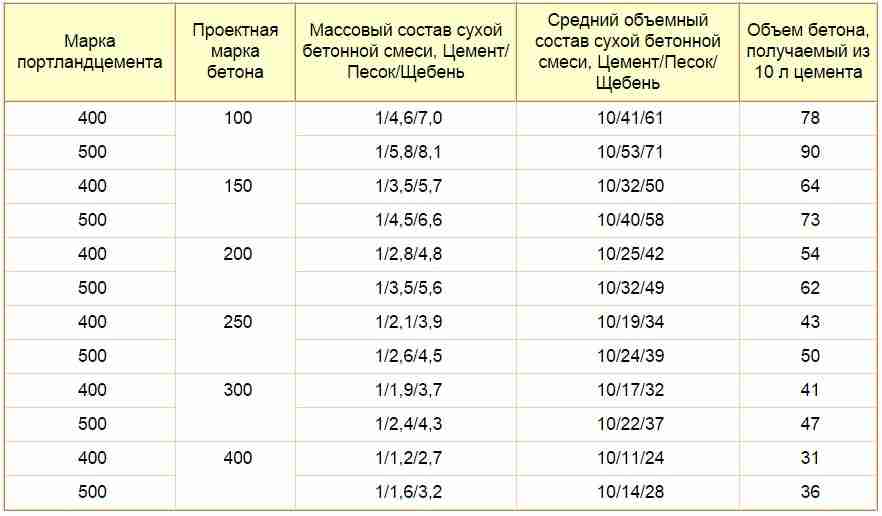 Например, современные страницы прекрасно смотрятся на мобильных устройствах, а автоматическое масштабирование изображений помогает создать привлекательный вид.

Какие размеры изображений лучше всего работают?

Из-за быстрой компоновки страницы не существует определенной высоты или ширины в пикселях, что гарантирует сохранение определенной фигуры на разных устройствах и макетах. Изображения автоматически меняются и обрезаются, чтобы демонстрировать наилучший результат на различных устройствах и макетах. Однако существуют некоторые рекомендации, которые помогут вам убедиться, что изображения хорошо смотрятся на страницах.

Поиск изображений наилучшего размера зависит от указанных здесь факторов.

• Пропорции:отношение между высотой и шириной изображений

• org/ListItem»>

  Макет столбца:тип и количество столбцов на странице

• Макет веб-части:макет веб-части, в которой используется изображение

Пропорции

Пропорции — это отношение между шириной и высотой изображений. Обычно оно выражается в двух числах, таких как 3:2, 4:3 или 16:9. Ширина всегда является первым числом. Например, соотношение 16:9 может иметь ширину 1600 пикселей на 900 пикселей в высоту. Это может быть 1920 x 1080, 1280 x 720 или любые другие комбинации ширины и высоты, которые можно вычислить, равные 16:9. Калькуляторы пропорций можно найти в Интернете и некоторых средствах редактирования фотографий, чтобы определить пропорции изображений. 

В большинстве случаев изображения в современных веб-частях лучше всего работают на разных макетах и устройствах с соотношением сторон 16:9 или 4:3 в зависимости от макета.

Макеты столбцов

На странице можно найти разделы с различными типами столбцов и макетами, такими как полно ширинные столбцы, один столбец, два столбца, три столбца, один третий левый и один третий правый столбец. Обычно изображения, которые должны заполнять ширину столбца, должны быть по крайней мере такой же ширины, как и в столбце, в котором они размещены. Например, изображение веб-части изображения в одном столбце должно иметь ширину не менее 1204 пикселей. Ниже указаны правила ширины для каждого макета столбца.

Макет	Ширина в пикселях
Столбец «Ширина»	1920
Одна колонка	1204
Два столбца	586 в столбец
Три столбца	380 в столбец
Третий левый столбец	380 для левого столбца; 792 для правого столбца
Один-третий правый столбец	792 для левого столбца; 380 для правого столбца

Из-за скорости реагирования страниц изображения в полношириных столбцах всегда будут отображаться на полноширивной странице с автоматической высотой в зависимости от размера экрана.

Высота изображений в других макетах столбцов будет зависеть от пропорций. Ниже указаны рекомендации по высоте и ширине для пропорций 16:9 и 4:3 (округлка вверх/вниз до ближайшего пикселя). Это помогает, например, сохранить ширину и высоту изображений с соответствующим масштабом для мобильных устройств.

ПРОПОРЦИИ МАКЕТ	16 x 9 Ширина x высота в пикселях	4 x 3 Ширина x высота в пикселях
Одна колонка	1204 x 677	1204 x 903
Два столбца	586 x 330	586 x 439
Три столбца	380 x 214	380 x 285
Третий левый столбец	380 x 446 для левого столбца; 792 x 446 для правого столбца	380 x 594 для левого столбца; 792 x 594 для правого столбца
Один-третий правый столбец	792 x 446 для левого столбца; 380 x 446 для правого столбца	792 x 594 для левого столбца; 380 x 594 для правого столбца

Макеты веб-части

Макеты в веб-частях, которые вы используете, также влияют на масштаб изображений.

В следующих примерах различные веб-части и их макеты в одном столбце, а также пропорции, используемые в каждой из них.

Рассмотрим это изображение с исходными пропорциами 16:9:

Ниже показаны примеры рисунка, показанного в макете страницы с одной колонкой в разных веб-частях и макетах.

Веб-часть «Главного сайта»	Для макетов плиток и слоев имеются следующие пропорции: Плитки: высота веб-части масштабется до пропорций 8:3, а изображения в масштабе веб-части — с соотношением сторон 4:3. Слои: индивидуальные шкалы слоев до пропорций 8:3, а изображения внутри каждой шкалы слоев — с соотношением сторон 16:9. На мобильных устройствах макет карусели используется в 16:9. Ниже показан пример изображения, показанного в макетах «Слои» (сверху) и «Плитки» (внизу).
Веб-часть «Выделенное содержимое»	16:9 — пропорции для макетов «Карусель», «Пленка» и «Карточки». Ниже показан пример изображения, показанного в макетах «Пленка» (сверху) и «Карточки» (внизу).
Веб-часть «Изображение»	Изображения будут расширяться по ширине раздела, содержащего веб-часть. Вы можете изменить пропорции или обрезать рисунок вручную с помощью панели инструментов «Изображение», а также увеличить или увеличить изображение с помощью хи24-часового режима. Ниже показан пример обрезных меток изображения (синие линии) в 4:3
Веб-часть «Галерея изображений»	В разных макетах используются следующие пропорции: org/ListItem»> В макете «Блок-блоки» пропорции всех показанных изображений: 16:9, 1:1, 4:3 и так далее.  Плитки, карточки: 4:3 Ниже показан пример изображения, показанного в макетах «Плитки» (сверху) и «Мозаика» (внизу).
Веб-часть «Новости»:	В зависимости от макета, изображения в веб-части «Новости» могут быть 4:3, 16:9 или 21:9. Вот пример изображений в верхней истории и макете карусель.
Область заголовка страницы	Изображения лучше всего выглядят, когда они имеют альбомную или соотношение сторон 16:9 или больше и имеют размер не менее 1 МБ. Кроме того, не забудьте установить фокальной точкой, чтобы сохранить наиболее важную часть рисунка в представлении, особенно если рисунок используется в эскизах, макетах новостей и результатах поиска. Пример (исходное изображение 16:9) с фокальной точкой на динамике.
Эскиз страницы	Эскизы страниц можно вывести в таких местах, как результаты поиска, выделенное содержимое, новости и другие. По умолчанию эскизы выводится из области заголовка страницы или веб-части, которая находится в первом порядке на странице (например, слева вверху). Вы можете переопременить заданный по умолчанию и изменить эскиз страницы. При этом лучше использовать изображение с пропорцией 16:9. Пример (исходное изображение 16:9)
Веб-часть «Быстрые ссылки»	Веб-часть «Быстрые ссылки» имеет шесть разных макетов. Ниже советуем использовать пропорции. Пленка, сетка, кнопка: 16:9 Сжатие, список, плитки: 1:1, 4:3 Ниже показан пример изображения, показанного в макетах «Сжатая» (сверху) и «Пленка» (внизу).

Советы: 

• При добавлении изображения в область заголовка страницы или веб-части главного имиджегового рисунка также лучше всего установить его фокальной точкой. Дополнительные информацию о настройке фокальной точки для этих двух сценариев см. в веб-части «Изменение фокальной точки рисунка в веб-части «Главного имиджевного рисунка» и настройке области заголовка на странице.

Рекомендации по изображению в заглавной области сайта

Кроме страниц, может потребоваться добавить дополнительные логотипы или изображения. Ниже рекомендации по размеру этих элементов.

Элемент	Описание	Рекомендации Ширина x высота в пикселях
Логотип сайта	Логотип большего размера, который может быть не квадратным и прозрачным в зависимости от добавленного оформления	192 x 64  Формат: PNG, JPEG, SVG (SVG не разрешено на сайтах, подключенных к группе)
Эскиз логотипа сайта	Эскиз квадратного логотипа, который используется при отправке логотипа сайта или в местах, где требуется использовать квадратный формат Это необходимый элемент.	64 x 64  Формат: PNG, JPEG, SVG (SVG не разрешено на сайтах, подключенных к группе)
Логотип сайта с расширенным макетом	В расширенном макете загона имеется расширенная ширина логотипа сайта.	300 x 64p Формат: JPEG, PNG, SVG
Фоновое изображение расширенного макета	Новое фоновое изображение, которое можно использовать с расширенным header.	2560 x 164 Формат: JPEG, PNG

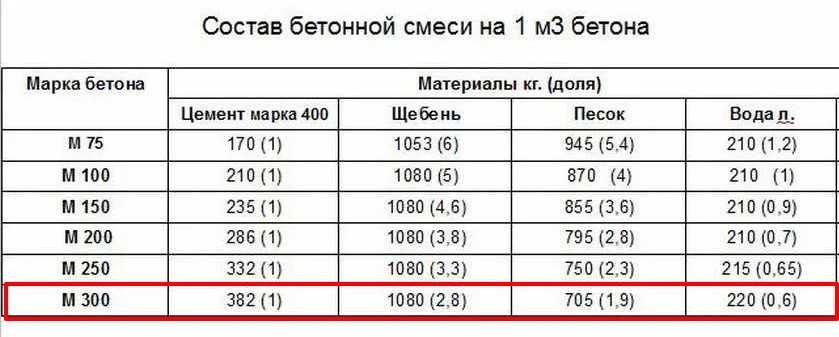
Обратная пропорция — формула, примеры, определение, график

Когда две величины связаны друг с другом обратно пропорционально, т. е. когда увеличение одной величины приводит к уменьшению другой и наоборот, говорят, что они находятся в обратной пропорции. В обратной пропорции произведение данных двух величин равно постоянной величине. Давайте узнаем об этом подробнее в этой статье.

1.	Что такое обратная пропорция?
2.	Формула обратной пропорции
3.	График обратной пропорциональности
4.	Прямая и обратная пропорция
5.	Часто задаваемые вопросы об обратной пропорции

Что такое обратная пропорция?

Определение обратной пропорциональности гласит: «Две величины называются обратно пропорциональными, если увеличение одной ведет к уменьшению другой величины, а уменьшение одной ведет к увеличению другой величины». Другими словами, если произведение обеих величин, независимо от изменения их значений, равно постоянной величине, то говорят, что они находятся в обратной пропорции. Например, возьмем количество рабочих и количество дней, необходимых им для выполнения данного объема работы, как x и y соответственно.

Количество рабочих (x)	Требуемое количество дней (г)
16	3
12	4
8	6
4	12

Количество рабочих и количество дней находятся в обратно пропорциональной зависимости? Давай выясним.

Внимательно соблюдайте значения, указанные в таблице. Вы обнаружите, что для каждой строки произведение x и y одинаково. Это означает, что если есть 16 рабочих, они выполнят работу за 3 дня. Итак, здесь x × y = 16 × 3 = 48. Теперь, уменьшая количество рабочих, очевидно, что меньшее количество рабочих будет выполнять ту же работу за большее время. Но мы видим произведение x и y здесь, это 12 × 4 = 48. Опять же, для 8 рабочих за 6 дней произведение равно 48. И то же самое для 4 рабочих за 12 дней. Итак, произведение двух величин в обратной пропорции всегда равно.

Формула обратной пропорции

Формула обратной пропорции помогает установить связь между двумя обратно пропорциональными величинами. Пусть x и y — две величины, и предположим, что x уменьшается, когда y увеличивается, и наоборот. Пример: Скорость обратно пропорциональна времени. С увеличением скорости время, затрачиваемое нами на преодоление того же расстояния, уменьшается. Приняв скорость за y, а время за x, мы можем сказать, что y обратно пропорционально x и математически записывается как формула обратной пропорции.

Формула обратной пропорциональности записывается как

y = k/x

, где

• k — константа пропорциональности.
• y увеличивается по мере уменьшения x.
• y уменьшается с увеличением x.

Здесь символ ∝ обозначает пропорциональное соотношение между двумя величинами.

График обратной пропорциональности

График обратной пропорциональности обычно представляет собой кривую, которая изгибается к началу координат, образуя форму гиперболы. Если есть любые две случайные точки на оси x и оси y на графике обратной пропорции (x) ₁ , (x) ₂ , (y) ₁ и (y) ₂ , такие, что (x) ₁ < (x) ₂ и (y) ₁ < ( y) ₂ , график будет выглядеть следующим образом:

Это означает, что если мы увеличим значение x от \(x_{1}\) до \(x_{2}\), значение y уменьшается от \(y_{2}\) до \(y_{1}\).

Прямая и обратная пропорция

Существует два основных вида пропорциональности — прямая пропорция и обратная пропорция. Говорят, что две переменные x и y прямо пропорциональны, когда y ∝ x (или x ∝ y). Отсюда следует, что y = kx для константы k. В то время как две переменные x и y называются обратно пропорциональными, если y ∝ 1/x (или x ∝ 1/y).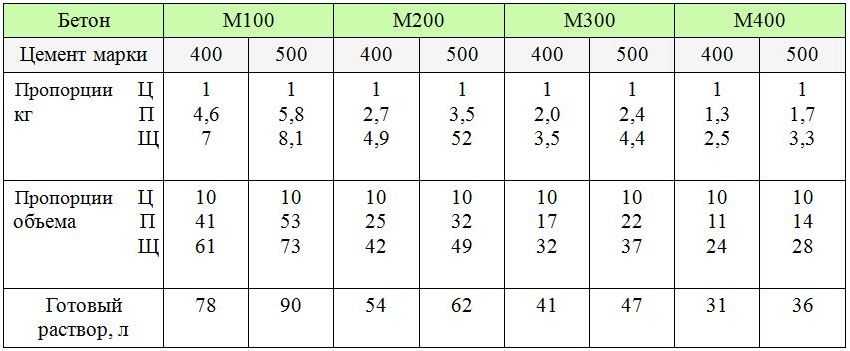 Отсюда следует, что y = k/x для константы k. В прямом вариационном отношении отношение двух переменных одинаково при любых значениях, а в обратной пропорциональности произведение двух переменных равно при любых значениях. Посмотрите на изображение, приведенное ниже, чтобы наглядно понять разницу между прямой и обратной пропорцией.

Похожие темы

Проверьте эти интересные статьи, связанные с концепцией обратной пропорции.

• Доля
• Константа пропорциональности
• Прямая пропорция
• Процентная доля

Часто задаваемые вопросы об обратной пропорции

Что такое косвенная пропорция?

Косвенная или обратная пропорция – это соотношение между двумя величинами, при котором увеличение одной ведет к уменьшению другой, и наоборот. Это прямо противоположно прямой пропорциональности.

Что обозначает символ ∝ в формуле обратной пропорции?

В формуле обратной пропорции символ пропорциональности ∝ обозначает соотношение между двумя величинами. Он выражается как x ∝ 1/y. Отсюда следует, что x = k/y, где k — константа пропорциональности.

Как найти K в обратной пропорции?

K в обратной пропорции представляет собой константу пропорциональности, которая одинакова независимо от значений данных переменных. Чтобы найти k в обратной пропорции, найдите произведение x и y. Формула y = k/x, что дает нам k=xy.

Как представить формулу обратной пропорциональности?

Формула обратной пропорциональности описывает соотношение между двумя величинами, которое можно понять по приведенной ниже формуле:

• Определите две величины, которые различаются в данной задаче.
• Определите, что существует обратная вариация. х ∝ 1/год
• Примените формулу обратной пропорции x = k/y.

В чем разница между прямой и обратной пропорцией?

Разница между прямой и обратной пропорцией заключается в том, что прямая пропорция показывает прямую зависимость между двумя величинами, при которой увеличение одной ведет к увеличению другой величины и наоборот. С другой стороны, обратная пропорция представляет собой косвенную связь между двумя величинами или переменными, когда увеличение одной ведет к уменьшению другой переменной, и наоборот.

Что такое формула обратной пропорции?

Формула обратной пропорциональности: y = k/x, где x и y — две обратно пропорциональные величины, а k — константа пропорциональности.

Как показать отношение между двумя величинами, используя формулу обратной пропорции?

Обратно пропорциональную зависимость между двумя величинами можно показать, если произведение двух величин (x × y) постоянно, то они изображают обратно пропорциональную зависимость. Он выражается как x ∝ 1/y или x = k/y, где k — константа пропорциональности.

Константа пропорциональности с примером

 

Когда две переменные прямо или косвенно пропорциональны друг другу, то их отношение может быть описано как y = kx или y = k/x, где k определяет, как две переменные связаны с друг друга. Это k известно как константа пропорциональности.

1.	Что такое константа пропорциональности?
2.	Почему мы используем константу пропорциональности?
3.	Как решить константу пропорциональности?
4.	Определение константы пропорциональности
5.	Решенные примеры
6.	Практические вопросы
7.	Часто задаваемые вопросы о константе пропорциональности

Что такое константа пропорциональности?

Константа пропорциональности – это постоянное значение отношения между двумя пропорциональными величинами. Говорят, что две изменяющиеся величины находятся в отношении пропорциональности, если либо их отношение, либо их произведение дают постоянную величину. Значение константы пропорциональности зависит от типа пропорции между двумя заданными величинами: Прямая вариация и Обратная вариация.

• Прямая вариация: Уравнение прямой пропорциональности: y = kx, которое показывает, что по мере увеличения x y также увеличивается с той же скоростью. Пример. Стоимость товара (y) прямо пропорциональна количеству приобретенных товаров (x), выраженному как y ∝ x 90 101.
• Обратная вариация: Уравнение косвенной пропорциональности y = k/x, которое показывает, что при увеличении y x уменьшается, и наоборот. Пример: скорость движущегося транспортного средства (y) обратно пропорциональна времени (x), затрачиваемому на преодоление определенного расстояния, выраженному как y ∝ 1/x

В обоих случаях k является постоянным. Значение этой константы называется коэффициентом пропорциональности. Константа пропорциональности также известна как удельная ставка.

Почему мы используем константу пропорциональности?

Мы используем константу пропорциональности в математике, чтобы рассчитать скорость изменения и в то же время определить, с чем мы имеем дело – прямой или обратной вариацией.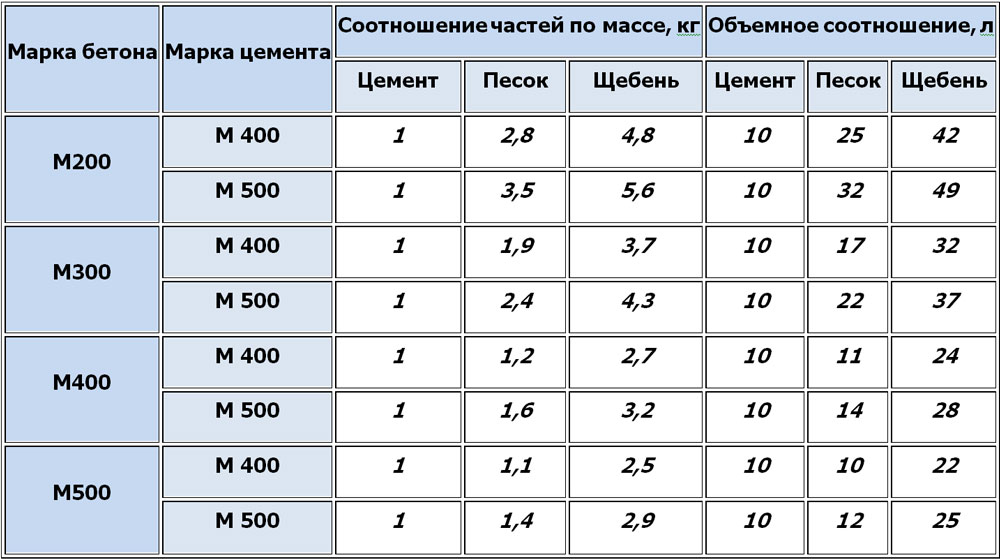 Предположим, что стоимость 2 яблок = 20 долларов. Определяем, что стоимость 1 яблока = 10 долларов. Мы нашли константу пропорциональности для стоимости яблока, равной 2,9.0003

Если мы хотим нарисовать изображение Тадж-Махала, сидя перед ним на листе бумаги и глядя на реальное изображение перед нами, мы должны поддерживать пропорциональное соотношение между мерами длины, высоты и ширина здания. Нам нужно определить константу пропорциональности, чтобы получить желаемый результат. Исходя из этого, мы можем нарисовать памятник с пропорциональными размерами. Например, если высота купола 2 метра, то на нашем рисунке мы можем изобразить тот же купол высотой 2 дюйма. Точно так же мы можем нарисовать и другие части. В таких сценариях мы используем константу пропорциональности.

Работа с пропорциональными отношениями позволяет решать многие реальные проблемы, такие как:

1. Регулировка соотношения ингредиентов в рецепте
2. Количественная оценка шансов, например определение шансов и вероятности событий
3. Масштабирование схемы для черчения и использования в архитектуре
4. Нахождение процентного увеличения или процентного уменьшения наценок
5. Скидки на товары на основе цены за единицу

Как решить константу пропорциональности?

Мы применяем наши знания о прямых и обратных вариациях, идентифицируем их, затем определяем константу пропорциональности и тем самым получаем решения наших задач.

Пример 1: Найдите константу пропорциональности, если y=24 и x=3 и y ∝ x.

Решение. Мы знаем, что у меняется пропорционально х. Мы можем записать уравнение пропорциональной зависимости как y = kx. Подставьте данные значения x и y и найдите k.

24 = к (3)

k = 24 ÷ 3 = 8

Следовательно, константа пропорциональности равна 8.

Пример 2: 4 рабочих выполняют требуемую работу за 3 часа. Если нанять еще 2 рабочих, за сколько времени они выполнят работу?

Решение: Пусть x1 = количество рабочих в случае 1 = 4

x2 = количество рабочих в случае 2 = 6

y1 = количество часов в случае 1 = 3

y2 = количество часов в случае 2 = Будет найдено

 Если количество рабочих увеличить, время, необходимое для завершения, сократится. Мы находим, что количество рабочих обратно пропорционально затраченному времени, (y1 = k/x1) ⇒ 3 = k / 4 ⇒ k = 12

Опять же, чтобы найти количество часов, (y2 = k/x2) ⇒ y2 = 12/6 = 2 часа.

Определение константы пропорциональности

Теперь мы научимся определять константу пропорциональности (единицу измерения) в таблицах или графиках. Изучите приведенную ниже таблицу и определите, является ли отношение пропорциональным, и найдите константу пропорциональности.

Количество дней = х	1	3	5	6
Количество написанных статей = y	3	9	15	18

Мы делаем вывод, что по мере увеличения количества дней количество написанных статей также увеличивается. Здесь мы определяем, что она прямо пропорциональна. Применим уравнение y=kx. Для нахождения константы пропорциональности определяем соотношение между количеством статей и количеством дней. Нам нужно оценить для k = y/x

y/x = 3/1 = 9/3 = 15/5 = 18/6 = 3

Из результата соотношений y и x для заданных значений можно заметить, что такое же значение получается для все экземпляры. Константа пропорциональности равна 3.

Если мы нанесем значения из приведенной выше таблицы на график, мы увидим, что прямая линия, проходящая через начало координат, показывает пропорциональную зависимость. Константа пропорциональности при условии прямой зависимости представляет собой наклон линии при построении двух пропорциональных констант x и y на графике.

 

Темы, связанные с Константа пропорциональности

• Формула обратной пропорции
• Формула прямой пропорции
• Константа пропорциональности Калькулятор

Важные примечания

• Чтобы проверить, пропорциональны две величины или нет, мы должны найти отношение двух величин для всех заданных величин. Если их отношения равны, то они демонстрируют пропорциональную связь. Если все отношения не равны, то отношение между ними не является пропорциональным.
• Если две величины пропорциональны друг другу, отношение между ними может быть определено как y = kx, где k – постоянное отношение значений y к соответствующим значениям x.
90 100 То же отношение можно определить по формуле x=(1/k)y, где 1/k – это постоянное отношение значений x к значениям y.

 

 

1. Пример 1: Посмотрите на таблицу ниже. Имеют ли переменные какую-либо пропорцию? Если да, то какова константа пропорциональности?

   Х	Д
   5	1
   25	5
   16	3
   35	7

   Решение: 

   Для проверки константы пропорциональности используем: y = kx

   k = y/x

   y/x = 1/5 = 5/25 =7/3 ≠ 3/16

   Мы можем заметить, что все отношения в приведенной выше таблице не равны. Следовательно, эти значения НЕ находятся в пропорциональном соотношении.

2. Пример 2. Предположим, что y напрямую зависит от x, и y=30, когда x=6. Используйте константу пропорциональности и найдите значение y, когда x=100.

   Решение: Во-первых, мы должны написать уравнение константы пропорциональности, y = kx. Подставьте данные значения x и y и найдите k. 30 = k × 6 ⇒ k=5 

   Уравнение: y = 5x. Теперь подставьте x=100 и найдите y

   y= 5 × 100 = 500 
   . Следовательно, значение y равно 500, когда x=100.

3. Пример 3: Энтони требуется 15 дней, чтобы похудеть на 30 кг, выполняя упражнения по 30 минут в день. Если он будет тренироваться по 1 часу 30 минут каждый день, за сколько дней он похудеет на тот же вес?

   Решение:

   В зависимости от ситуации вес и упражнения обратно пропорциональны. По мере увеличения количества минут тренировки вес Энтони уменьшается. Пусть m — минуты, а d — дни.
   м = к/д. Пусть m1 = 30, m2 = 90, d1 = 15. Требуется найти d2.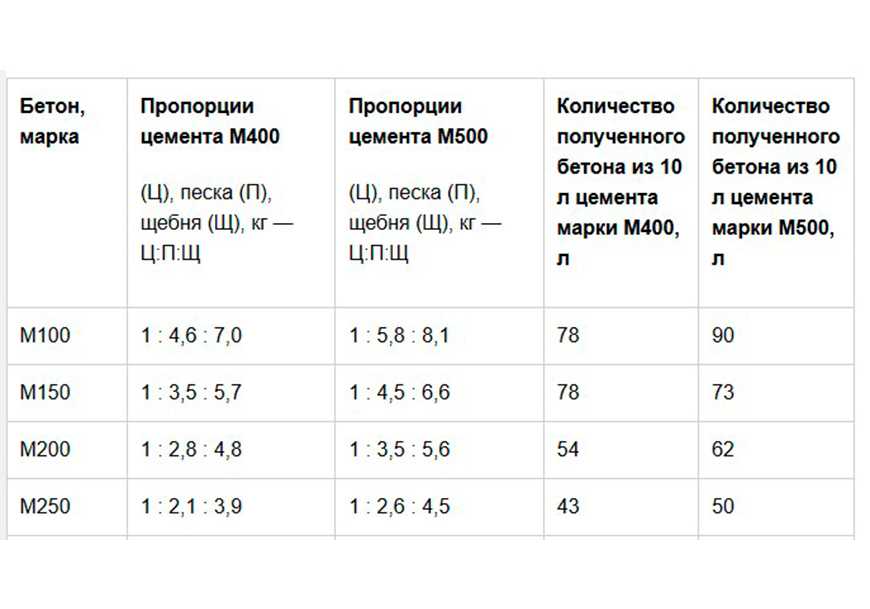

   м1 = к/д1
   k = 30 × 15 = 450 (Подставляя известные значения, определите k)

   m2 = k/d2

   90 = 450/d2

   d2 = 450/90 = 5 (Подставив известные значения, определите d2)

   Следовательно, если Энтони будет заниматься по 1 часу 30 минут в день, то для снижения веса на 30 килограммов потребуется всего 5 дней.

перейти к слайдуперейти к слайдуперейти к слайду

 

Как ваш ребенок может освоить математические понятия?

Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.

 

Забронировать бесплатный пробный урок

 

 

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о константе пропорциональности

Какое другое название константы пропорциональности?

Другим названием константы пропорциональности в математике является единичная скорость.