Как правильно рассчитать кубатуру бруса

Технология рассчета будет отличаться в зависимости от количества бруса в партии. Для небольшого количества она очень проста: если весь материал имеет одинаковые размеры, необходимо сначала площадь сечения (она будет равна ширине умноженной на высоту сечения) одного бруса умножить на его длину. Таким образом, вы находите количество кубических метров одной единицы пиломатериала, после чего полученное число умножаете на общее количество единиц – это и будет точная кубатура купленных вами единиц бруса.

Неспециалисту в области деревообработки очень сложно разобраться, как рассчитать кубатуру бруса или других деревянных погонажных изделий. А это важно, так как продажа бруса, досок, брусков на лесопилках и магазинах-складах осуществляется именно в кубических метрах, чем и пользуются многие торговцы, зарабатывая себе в карман.

Существует как минимум два достаточно простых способа расчета, которые любой неспециалист может освоить и чувствовать себя уверенно при покупке пиломатериалов для дома.

Содержание

• 1 Расчеты для небольшого количества
• 2 Потолочные и напольные балки перекрытия
• 3 Стропильная система
• 4 Расчет кубатуры бруса на стропильную систему
• 5 Наружные стены, фронтоны и внутренние перегородки
• 6 Каков вес бруса?
• 7 Что такое кубатура?
• 8 Расчёт кубатуры круглого леса
• 9 Расчёт кубатуры досок и их количества
• 10 Самостоятельный расчёт
• 11 Расчёт кубатуры бруса и его количества
• 12 Онлайн-расчёт количества досок и бруса на 1 м3

Расчеты для небольшого количества

Как уже было сказано выше, тут нужно просто площадь сечения одного буса умножить на его длину. Например, куплено 15 единиц бруса сечением 150 х 150 мм и длиной 6 метров. Находим площадь сечения бруса – 0,15 х 0,15 = 0,0225 квадратных метра, после чего умножаем эту площадь на 6 и получаем 0,135 куб.

м. – именно столько имеет один брус. После этого полученное число умножаем на 15 (количество единиц бруса) и получаем 2,025 – общая кубатура купленного бруса.

Вот таким, очень простым и доступным всем способом можно посчитать небольшое количество бруса и других пиломатериалов.

Также необходимо помнить, что существуют специальные таблицы – кубатурники, которые сведут к минимуму использование с калькулятора и значительно упростят расчеты:

— брус 0,10 х 0,10 х 6м – 0,060 куб.

м. – 16,67 штук в куб. м.— брус 0,10 х 0,15 х 6м – 0,090 куб.

м. – 11,11 штук в куб. м.— брус 0,15 х 0,15 х 6м – 0,135 куб.

м. – 07,41 штук в куб. м.— брус 0,10 х 0,20 х 6м – 0,120 куб.

м. – 08,33 штук в куб. м.— брус 0,15 х 0,20 х 6м – 0,180 куб.

м. – 05,56 штук в куб. м.

— брус 0,20 х 0,20 х 6м – 0,240 куб.

м. – 04,17 штук в куб. м.

При сооружении любого здания главным вопросом является подбор необходимого материала и определение его потребного количества. Еще до начала строительства хороший хозяин составляет план предстоящих работ и смету. Наиболее популярным материалом, используемым при возведении индивидуальных построек, является брус.

Но жилой дом имеет довольно сложную архитектуру. Поэтому даже однотипные материалы используются разных размеров, в зависимости от того, для какой части постройки они применяются.

От «габаритов» зависит и объем закупки. Тем более что и цена пиломатериалов выражается, как правило, в рублях за кубический метр. Ведь покупается он в основном также в «кубах», а не поштучно.

Прежде всего, требуется максимально точно произвести все замеры. После этого, чтобы определить потребное количество конкретной продукции, все результаты суммировать и перевести в «м3». Так легче считать.

Разберемся, как рассчитать кубатуру бруса на отдельных примерах

Для начала следует составить перечень необходимых для строительства заготовок, «рассортировав» их по размерам. Как уже говорилось, для различных элементов конструкции дома и брус нужен разный: и по длине, и по сечению. После этого определяется объем заготовки (длина, ширина сечения, его высота), только не забывать о единицах измерения.

В строительстве часто используются данные, выраженные в «мм». В том числе, и размеры бруса.

К примеру, 100 х 100 означает, что это заготовка с квадратным сечением. Сторона такого квадрата равна 100 мм (или 10 см, или 0,1 м). Умножив полученное значение на необходимое количество изделий, получаем «кубатуру» потребного материала определенных габаритов.

Допустим, нам нужно купить 20 брусов с сечением 150 х 150 мм, имеющих длину 6 м.

Переводим «мм» в «м»: 150 мм = 0,15 м.

Умножаем: 0,15 м х 0,15 м х 6 м = 0,135 м3. Это – объем одного бруса. Теперь полученное значение перемножить на их количество: 0,135 м3х 20 = 2,7 м3.

Другой пример

Надо закупить 30 заготовок с размерами: 120 мм х100 мм х 3 м. Аналогично осуществляем перевод всех единиц измерение в метры.

Получаем: 0,12 м х 0,1 м х 3 м. Перемножив эти данные, получим объем 1 изделия – 0,036 м3. Общая «кубатура» составит 0,036 м3х 30 = 1,08 м3.

Иногда нужно определить, сколько штук бруса будет в 1 м3. Производим обратное действие – деление. Для этого 1 м3 разделить на объем одной заготовки.

Наиболее часто в индивидуальном строительстве применяется продукция нескольких основных размеров. Приведем данные для таких изделий из расчета на 1 м3, причем длину возьмем равной 6 м.

100 х 100 – в кубе 16,6 штук; объем одной заготовки равен 0,06 м3100 х 150 – 11,1 шт.

при объеме 0,09 м3150 х 150 – 7,4 шт. при объеме 0,135 м3200 х 200 – соответственно 4,1 шт. и 0,24 м3

При определении количества учесть такие моменты:

Практически никогда в 1 м3продукции не будет «ровного» количества бруса.При монтаже элементов конструкции дома обязательно где-то чего-то не хватит.Даже в самой качественной поставке может быть от одной до нескольких «единиц» брака.Если докупать то, скорее всего, это будет уже другая партия.

А применять заготовки из разных нежелательно. Могут быть некоторые отклонения в технологии обработки. И, как результат, возникнут сложности при стыковке элементов.

Большинство поставщиков пиломатериалов указывают стоимость продукции в кубометрах. Расчет количества бруса или обрезных досок, содержащихся в кубометре пиломатериалов производится довольно просто. Для того чтобы определить данную величину, нужно знать размеры пиломатериала.

К примеру, ширина – 150 мм, длина равна 6 метрам, а толщина  – 100 мм. Как рассчитать кубатуру бруса? Для того чтобы найти количество бревен в одном кубометре надо 1 м3разделить на объем единицы материала:

1/0,15/0,1/6=11,11.

Это означает, что количество бруса в  кубе  равняется 11 штукам.

Как произвести расчет бруса на дом? Для того чтобы определить количество пиломатериалов для возведения объекта, следует выполнить несколько подсчетов:

Потолочные и напольные балки перекрытия

Если дом из брусабудет возводиться на нестабильных грунтах лучше вместо пола по балкам выбрать монолитное основание.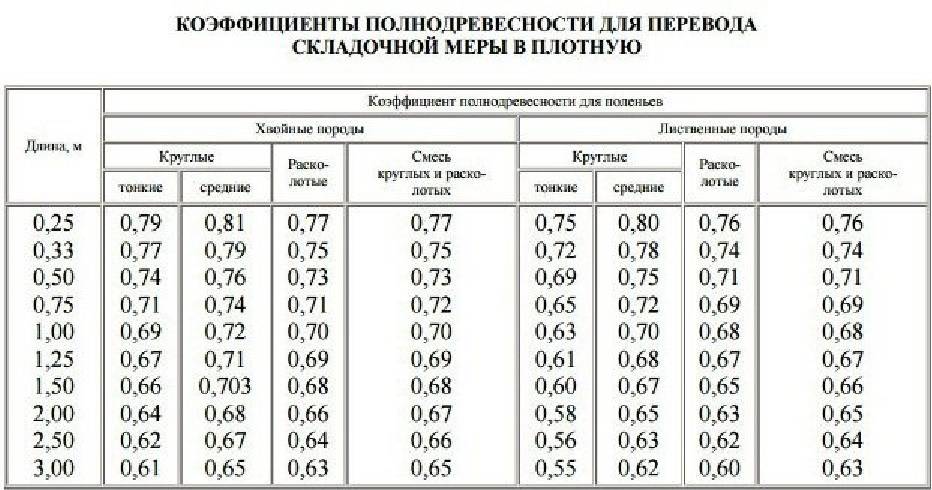 Во всех других случаях можно использовать дерево.

Потолочные и половые балки чаще всего имеют размеры 100*150 мм, при этом шаг составляет 0,8-1 метр. Максимальная жесткость конструкции обеспечивается в случае, если балки врезаются вертикально в венцы. Суммарная длина и количество балок рассчитываем следующим образом:

делим длину дома на длину шага между баками и отнимаем единицу. Для дома, имеющего размеры 6-10 метров, при условии, что шаг составляет 0,9 м, понадобится 10 балок (1/0,9-1).

Стандартная длина балок 6 метров, на 60 метров (6*10) понадобиться 60 погонных метров. Учитывая тот факт, что пиломатериалы продаются в м3, рассмотрим, как рассчитать куб бруса. В нашем случае, зная сечение и длину бруса, а также погонную длину получаем  – 0,1*60*0,15=0,9 м3.

Стропильная система

Рассмотрим вариант с двускатной прямой крышей. Шаг стропил равен 60 см, угол кровли – 45°, сечение материала 100-150 мм. Помните, что чем больше угол наклона, тем ниже максимальная масса снега, способная скапливаться на крыше, однако при этом  растет парусность кровли.

В ветреных регионах лучше создавать стропильную систему с меньшим уклоном, в снежных – с большим. Чем меньше шаг стропил, тем меньше можно выбирать их сечение. Объясняется это равномерностью распределения нагрузки.

Устройство стропильной системы предельно просто – над серединой дома находятся 2 стропильные ноги. Их фиксируют продольным прогоном с помощью бруса того же сечения. С его помощью соединяются вершины треугольников.

Расчет кубатуры бруса на стропильную систему

Прогон дома –  10 м, уклон кровли – 45°, рассчитаем длину стропильной ноги (сумма квадратов катетов) – 4,24 м. На каждый треугольник потребуется 8,5 метров пиломатериалов.

Количество треугольников, из которых состоит хребет кровли – 10/0,6-1 равно 16 (после округления).

Длина стропил в таком случае составляет 16*8,5=136 м. К полученной цифре добавляем прогон 10 м и получаем 145 погонных метра материала. При сечении 50*150 мм переводим погонные метры в кубические 146*0,15*0,5=10,95 м3.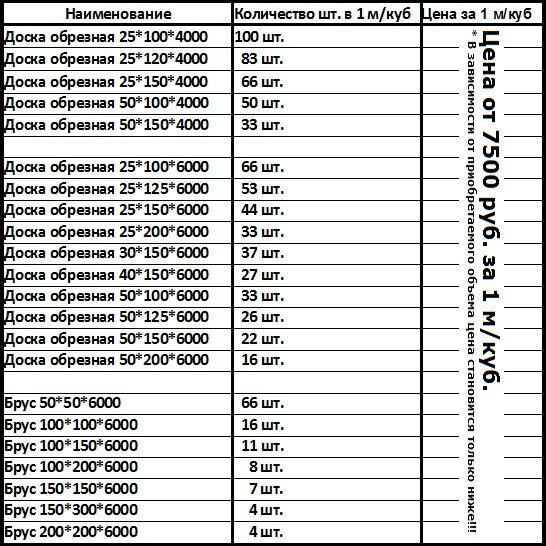

Специалисты рекомендуют умножить полученное количество на 1,3 (запас на обрезки и свесы).

Наружные стены, фронтоны и внутренние перегородки

Производим расчет бурса на дом с учетом того, что для определения несущих перегородок и внешних стен используется один и тот же подход. Представив перегородки, стены и фронтоны в виде геометрических фигур, найдем их площадь.

Далее определяем площадь проема и отнимаем ее от цифры, полученной ранее. Толщину стен умножаем на площадь и получаем общий объем бруса, требуемый для возведения данных элементов конструкции. Если необходимо вычислить кубатуру материала, воспользуйтесь алгоритмом подсчета приведенным выше.

Каков вес бруса?

Данный параметр зависит от породы и влажности древесины. Влажность – процентное отношение массы воды к весу сухой древесины. Показатель влажности зависит от продолжительности сушки, а также условий дальнейшего хранения пиломатериалов.

Сухая древесина  – та, которая прошла технологическую сушку либо долгое время находившаяся в теплом сухом помещении.

Сырая древесина – материал на стадии высыхания от свежесрубленного состояния вплоть до равновесного.

Воздушно-сухая древесина – пиломатериал с равновесной влажностью. При хранении в естественных условиях брус обретает влажность, уравновешенную с уровнем влажности воздуха.

Мокрая и свежесрубленная древесина – материал, который долгое время находился в воде либо был недавно срублен.

Вопрос о том, как рассчитать кубатуру строительных материалов из дерева, волнует многих застройщиков. Чтобы не переплачивать за излишнюю продукцию или не попасть в трудное положение, когда приходится останавливать строительство из-за нехватки пиломатериалов, требуется правильная методика подсчёта лесоматериалов.

Что такое кубатура?

Кубатура — это объём тела, занимаемого им в пространстве.

Данная величина определяется произведением длины, ширины и высоты однородного массива. Что касается древесины, то это может быть лес-кругляк, доски и брус. Параметр этих видов строительной древесины исчисляют в кубических метрах.

К этому вопросу можно подойти с нескольких сторон. Каждая методика расчёта объёма древесины во многом зависит от вида самого пиломатериала.

Расчёт кубатуры круглого леса

Для подсчёта объёма небольших партий кругляка существуют таблицы, которые учитывают средний диаметр ствола каждого дерева, длину бревна. Подробные таблицы легко можно найти в интернете.

Примерная таблица кубатуры круглого леса м3

Диаметр ствола, ммДлина ствола1 м2 м3 м4 м5 м6 м8 м1400,0160,03490,0520,0730,0970,1230,1792000,0320,0690,0870,1470,1920,2290,3293000,0770,1650,250,330,4190,5190,563400,10,2090,3190,4290,5390,6590,924000,140,2780,4280,5770,740,91,254800,1890,4080,6180,841,061,291,78

Пользоваться такой таблицей удобно при оценке нескольких брёвен. При подсчёте объёмов большого количества леса идут другим путём. Кругляк складируют в наиболее плотные массивы.

Поступают следующим образом:

Лес сортируют по длине. Двухметровые лесины складывают в отдельный гурт.

Более длинные брёвна группируют в другом штабеле.Стволы укладывают, ориентируя поочерёдно основания и вершины кругляка в разные стороны. Это позволяет получить наиболее плотный штабель из брёвен.Отдельные чурки выкладывают в одну линию по длине штабеля.Массив древесины нужно складировать по форме максимально приближенному к правильному параллелепипеду.Произведение ширины, длины и высоты штабеля будет определять складочную кубатуру кругляка.Полученный результат умножают на поправочный коэффициент. Так, для лесин до 2-х метров k = 0,56, а для более длинных брёвен k = 0,5.

Такая методика определения объёма кругляка наиболее приближена к реальному объёму древесины. Всеми тонкостями подсчёта этого параметра в совершенстве владеют работники лесных складов. Без опыта работы в этой сфере самостоятельный расчёт может оказаться далеко не в пользу покупателя.

Расчёт кубатуры досок и их количества

Основной единицей расчёта за пиломатериалы является 1 м3. Определение кубатуры штабелированной обрезной доски производится довольно просто.

Пиломатериал одного вида и размеров плотно складывают в штабели. Достаточно измерить длину, ширину и высоту параллелепипеда в метрах, а затем перемножить их. Полученный результат и будет реальной величиной объёма обрезного материала.

Застройщику важно знать, сколько единиц продукции определённых размеров помещается в 1 м3. В некоторых случаях поставщик пиломатериалов на каждой упаковке досок крепит торговую карту с указанием в ней характеристик древесины, величины объёма, цены за 1 м3 продукции, а также числа досок в штабеле.

Самостоятельный расчёт

Можно самостоятельно определить число штук досок.

Для этого нужно измерить штабель и высчитать объём упаковки. Зная размеры пиломатериала, определяют объём единицы продукции. Частное от деления этих двух параметров даст реальное число штук досок.

Например, доска имеет размеры 200 х 30 х 6000 мм. Следовательно, объём пиломатериала будет равен 0,036 м3. В 1 м3 поместится – 1 / 0,036 = 28 шт.

Чтобы не возиться с измерениями и расчётами, можно воспользоваться таблицами. Для обрезного материала длиной 6 метров таблица будет выглядеть примерно так:

Сечение, смОбъём 1 шт, м3Количество в 1 м3, шт2,5 х 100,01566,52,5 х 150,02644,34 х 100,023941,74 х 150,035627,84 х 200,047820,95 х 100,03233,25 х 150,04622,15 х 200,0616,65 х 250,074813,2

Для необрезной доски применяют ориентировочные таблицы — с учётом непостоянной ширины по всей длине единицы продукции. Расчёт объёма древесины производят по той же методике, что и расчёт объёмов обрезного материала, с вводом поправочного коэффициента k в пределах от 0,6 до 0,8. Величина коэффициента зависит от степени кривизны и толщины коры.

Таблица объёмов необрезной древесины длиной 6 м с условным k = 0,7 будет такой:

Сечение, смОбъём 1 шт, м3Количество в 1 м3, шт2,5 х 100,01546,62,5 х 150,025531,24 х 100,02429,24 х 150,03619,34 х 200,04814,55 х 100,0323,25 х 150,04515,55 х 200,0611,75 х 250,0759,2

Расчёт кубатуры бруса и его количества

Ручной способ

Брус представляет собой параллелепипед с практически ровными гранями. Ручной метод определения кубатуры бруса и количества единиц древесины в 1 м3 приемлем для небольших партий товара. Выполняется он точно так же, как и расчёт обрезной доски.

Табличный метод

Во избежание временных затрат при поставках большого количества деревянных изделий, для определения объёмных показателей пользуются таблицами. При стандартной длине бруса 6 м табличные данные будут такими:

Сечение, смОбъём 1 шт, м3Количество в 1 м3, шт4 х 40,00961045 х 50,01566,710 х 100,0616,715 х 150,1357,4110 х 200,128,3315 х 200,185,5620 х 200,244,17

Онлайн-расчёт количества досок и бруса на 1 м3

Широкая доступность интернета позволяет воспользоваться различными калькуляторами для различных видов древесины. Можно найти онлайн-калькуляторы отдельно для круглого леса, бруса, необрезной и обрезной доски.

Интерфейсы калькуляторов созданы таким образом, что достаточно ввести исходные данные (длина, ширина, высота штабеля, вид пиломатериала), и на выходе получить общий объём древесины, вес и количество единиц товара.

Некоторые сервисы учитывают влажность леса, условия складирования. Можно узнать общую площадь пиломатериала, что удобно для расчёта опалубки, настилов, возведения заборов и других строительных объектов. Тут же можно ознакомиться с ценами на нужные пиломатериалы.

Пользуясь онлайн-калькуляторами, можно не покидая своего рабочего места составить смету будущих расходов на строительство или ремонт объектов.

Источники:

• silastroy.com
• elbruso.ru
• aquagroup.ru
• remboo.ru

Как рассчитать объем снега для уборки: формулы и расчеты

Для точного определения стоимости услуг по уборке территории на вашем объекте необходимо правильно рассчитать объем снега. Почему это важно? Дело в том, что такие услуги обычно оплачиваются заранее. При этом, подрядчик может предложить вам разные варианты оплаты. Например, это может быть почасовка или расчет за количество рейсов, которые потребуются самосвалам для вывоза снега с вашего объекта. Некоторые фирмы предлагают оплату за объем – то есть, за количество кубов снега, которые нужно почистить и/или вывезти.

• Как рассчитать объем снега
• Расчет объема снега в куче
• Усеченный конус
• Сферический сегмент
• Полусфера
• Расчет объема свободно лежащего снега
• Расчет с помощью калькулятора
• Расчет по норме осадков
• Расчет по замерам
• Как рассчитать стоимость услуг, зная объем снега
• Расчет при почасовой оплате
• Расчет при порейсовой оплате

Если вы не знаете точного количества времени, рейсов или кубов, то вам просто выставят счет, включающий минимальный тариф.

Обычно это 4 или 8 часов работы погрузчика, плюс 1 или 2 рейса самосвала. Если по факту потребуется больше, то вы внесете доплату, когда услуга будет полностью оказана.

Но, согласитесь, хочется знать заранее конечную сумму. И спрогнозировать ее можно; для этого как раз и потребуется знать объем снега на вашей территории.

В этой статье мы расскажем о том, как произвести расчеты, какие способы при этом можно использовать. Кроме того, вы узнаете, как применить данные по объему снега для определения стоимости услуг по его уборке и вывозу.

Итак, прежде всего нужно понять, в каком виде находится снег.

Он может быть:

1. Собран в кучи
2. Распределен по всей территории

Начнем с первого пункта.

Расчет объема снега в куче

Самая простая формула расчета объема – это перемножение длины, ширины и высоты.

Таким образом можно точно рассчитать объем только в том случае, когда снег на вашем объекте собран в кубовидные кучи.

Для более сложных форм (например, пирамидальных, конусовидных и т.д.) тоже есть формулы вычисления объема. Чтобы не заставлять вас изучать их все, мы сделали удобный калькулятор, с помощью которого можно быстро рассчитать объем.

Все, что вам нужно сделать, — это выбрать в калькуляторе фигуру, наиболее похожую на кучу снега у вас на объекте, а затем ввести в поля размеры этой кучи (в метрах).

Далее мы покажем, как использовать калькулятор на примере нескольких фигур.

Усеченный конус

Чаще всего кучи снега напоминают именно такую форму.

Предположим, что куча будет иметь следующие размеры:

• Радиус 1 (R) у основания – 3,8 метра
• Радиус 2 (r) у вершины – 0,8 метра
• Высота (h) – 2,5 метра

Чтобы рассчитать объем:

1. Выберите в калькуляторе вкладку «Усеченный конус»
2. Введите значения Радиуса 1 (R), Радиуса 2 (r) и Высоты (h). Высоту следует указать в поле «Глубина (h)»
3. Нажмите кнопку «Рассчитать»
4. В нижней правой части калькулятора появится результат расчета

Таким образом, куча, изображенная на фото, имеет объем 47,44 м3

Сферический сегмент

Это более грубый расчет, он не учитывает верхний радиус кучи.

Здесь будет достаточно указать лишь радиус основания (r) и высоту (h):

Как видите, разница в расчетах серьезная – более 10 кубов.

Полусфера

Этот вариант подойдет только тогда, когда радиус и высота кучи одинаковы.

Для вычисления достаточно указать лишь радиус (r):

Как вы могли заметить, фигуры в калькуляторе перевернуты. Это сделано не случайно. Данный калькулятор позволяет рассчитывать объем не только в случае со снегом. Он также поможет узнать необходимое количество материала для засыпки ям и канав. Принцип тот же самый – достаточно указать параметры фигуры.

Расчет объема свободно лежащего снега

Теперь давайте разберем более сложную ситуацию. Снег не собран в кучи, а просто лежит на территории. Притом высота покрова в разных участках может различаться.

Здесь есть три способа расчета:

1. С помощью калькулятора
2. По норме осадков
3. По замерам на территории

Они различаются трудоемкостью и степенью точности.

Далее мы разберем каждый способ.

Расчет с помощью калькулятора

Это – наименее точный способ. Здесь достаточно знать длину и ширину объекта, а также примерную высоту снежного покрова.

Допустим, у нас будут такие значения:

• Длина – 20 метров
• Ширина – 10 метров
• Высота – 0,2 метра

Чтобы рассчитать объем:

1. Выберите в калькуляторе вкладку «Куб»
2. Введите значения Высоты (a), Длины (b) и Ширины (c)
3. Нажмите кнопку «Рассчитать»
4. В нижней правой части калькулятора появится результат расчета

У нас получилось 40 кубов. Учтите, что цифра эта – примерная. Она не учитывает возможные перепады по высоте. То есть, посчитано все так, будто у вас на площади 200 м2 снег лежит ровным слоем в 20 сантиметров. На практике такого не бывает. Всегда есть участки, на которых снега больше или меньше.

Расчет по норме осадков

Этот способ подойдет для прогнозирования – например, для составления сметы. Но он не дает точного понимания того, сколько снега лежит на вашей территории прямо сейчас.

На сайтах метеослужб (например, https://rp5.ru/) вы можете найти данные о количестве осадков, выпавших в вашем регионе за определенный период (например, за прошлый год). Эти данные можно использовать, чтобы понять, сколько снега выпадет предстоящей зимой.

Затем количество осадков умножается на площадь вашей территории – и вы получаете примерный объем снега, который нужно будет убрать.

К примеру, мы взяли для анализа данные по осадкам, выпавшим в прошлом феврале. Получилось 45 миллиметров. Умножаем эту сумму на площадь нашего объекта (200 м2) – и получаем объем: 90 м3.

Однако повторим: этот способ дает лишь приблизительное представление. Он не учитывает, например, то, что часть выпавшего снега растает или будет убрана вручную дворниками. Кроме того, погода непредсказуема, и в новом году количество осадков может сильно отличаться от прошлогодних показателей.

Такой способ вы можете использовать, чтобы рассчитать примерный бюджет на уборку и вывоз снега в будущем году. Но для определения объема снега на вашей территории прямо сейчас этот вариант не подойдет.

Расчет по замерам

Этот способ сложнее, но гораздо точнее.

Расчеты ведутся по следующей формуле:

V = S * h

Где S – площадь территории, с которой нужно убрать снег

h – высота снежного покрова

Для замеров высоты можно использовать линейку или рулетку. Для быстрого расчета вы можете взять усредненный показатель высоты снежного покрова, замерив самый низкий и самый высокий уровень снега на вашем объекте.

Затем сложите эти показатели и разделите на 2. Так вы получите среднее арифметическое.

hсред = (hmin + hmax) : 2

Например:

• hmin = 10 миллиметров
• hmax = 100 миллиметров

 (10+100) : 2 = 55

Средняя высота получится 55 миллиметров.

Если вы хотите получить как можно более точный расчет, вам нужно сделать несколько замеров высоты снежного слоя. Производить их нужно в тех местах, где высота покрова меняется.

Затем все показатели суммируются и делятся на их количество.

Продемонстрируем это на примере.

Допустим, на вашем объекте замеры дали следующие результаты:

• h2 = 10 мм
• h3 = 13 мм
• h4 = 15 мм
• h5 = 20 мм
• h5 = 30 мм
• h6 = 100 мм

 (10+13+15+20+30+100) : 6 = 31,33 мм

Как видите, диапазон высот остался прежним – от 10 до 100 мм. Однако средняя высота снежного покрова изменилась в меньшую сторону и теперь составляет 31,33 миллиметра.

Казалось бы, разница не очень большая. Но давайте попробуем посчитать объем снега на территории, воспользовавшись каждым из этих показателей.

Предположим, нам нужно рассчитать объем снега на площади 200 м2:

V = 200*0,55

Получается 110 кубов снега

V = 200*0,31

А теперь уже 62 куба

Разница – почти в 2 раза. При расчете стоимости это будет ощутимо. Тем не менее, даже если вы сделаете замеры снежного покрова в 20 или 30 разных точках, вам все равно не удастся рассчитать объем с точностью до куба.

Но чем больше замеров вы произведете, тем более точный результат получится.

Как рассчитать стоимость услуг, зная объем снега

А теперь давайте поговорим о том, как можно использовать полученные расчеты. Самое простое – это при заказе сообщить, какой объем снега вам нужно почистить и/или вывезти.

Но если вы хотите оплачивать услугу не за объем, а почасово или порейсово, то тут тоже можно узнать примерную стоимость.

Расчет при почасовой оплате

Сразу скажем: он очень условный.

Есть специальная формула, по которой можно рассчитать скорость работы погрузчика, а по ней уже количество кубов, которое погрузчик уберет за час.

Выглядит эта формула так:

V*Кс*(60/Т) *Кв

V – это объем ковша погрузчика (в кубах)

Кс – коэффициент заполнения ковша

T – время цикла погрузчика (в минутах)

Кв – коэффициент использования погрузчика по времени

Результат получается в м3/ч. Для расчетов принимается во внимание большое количество факторов: тип погрузчика (колесный или гусеничный), скорость его движения (с учетом груза и без), расстояние движения и так далее.

По этой формуле обычно рассчитывают производительность работы карьерных погрузчиков. Для расчета скорости уборки снега такие сложные вычисления не требуются – они все равно не дадут объективной картины. Ведь важно еще и мастерство оператора. Если он неопытный, то никакая формула не поможет оценить скорость его работы.

В среднем, можно ориентироваться на следующие данные:

Объём ковша погрузчика	Скорость уборки*
0,5м3	до 25м3/час
1м3	до 50м3/час
2м3	до 100 м3/час

*Под скоростью уборки подразумевается скорость погрузки снега из кучи в кузов самосвала – без учета времени движения погрузчика до самосвала.

А более крупная техника на уборке снега обычно не работает.

Расчет при порейсовой оплате

Здесь суть в том, что вы заплатите за каждый рейс, который сделает самосвал, чтобы вывезти снег с вашего объекта. А самосвалы бывают разные: у некоторых объем кузова не превышает 6 кубов, другие могут вместить до 20 кубов и более.

Исходя из того, сколько снега у вас на территории, вы можете рассчитать количество рейсов и даже подобрать оптимальную технику.

Предположим, что у вас 90 м3 снега. Они поместятся либо в 15 шестикубовых самосвалов, либо в 5 двадцатикубовых. Выгоднее будет заказать большегрузы. Только учтите, что крупногабаритная техника сможет проехать не везде. Если на вашем объекте есть узкие участки или какие-либо помехи, лучше всего сообщить об этом подрядчику. В противном случае может оказаться так, что самосвалы просто не смогут попасть на территорию.

Итак, теперь вы знаете, как рассчитать объем снега. Это поможет вам заранее понять итоговую стоимость услуг по его уборке и вывозу. Для удобства расчетов вы можете использовать Калькулятор на нашем сайте.

Хотите узнать больше?

• На странице Уборка и вывоз снега вы найдете подробное описание наших услуг и базовые цены на них.
• Скачать общий прайс-лист  на услуги по аренде спецтехники в PDF (0.3мб)
• Скачать прайс-лист на услуги по уборке и вывозу снега в PDF (0.3мб)

Хотите регулярно получать информацию по данной теме? Тогда рекомендуем подписаться на наши группы в социальных сетях:

• ВКонтакте: https://vk.com/uborka_vyvoz_snega_ekaterinburg
• Facebook: https://www.facebook.com/uborkasnegaekb/
• Одноклассники: https://ok.ru/group/56486898958351

Рекомендуем также ознакомиться с другими статьями этого раздела:

• Как организовать уборку и вывоз снега
• Меры безопасности при уборке снега
• Меры безопасности при уборке снега во дворах
• Уборка снега в городе
• Что делать, если управляющая компания не убирает снег во дворе
• Как правильно уведомить жителей дома для плановой уборки снега
• Кто должен убирать снег во дворе
• Кто должен убирать снег с улиц
• Кто должен убирать снег у магазинов
• Нормативы уборки снега в городе
• Примеры расчёта стоимости уборки и вывоза снега
• Советы по организации уборки и вывоза снега
• Уборка и вывоз снега (расценки на готовые пакеты услуг)
• Уборка снега в гаражах (ГСК)
• Что делать, если машины мешают уборке и вывозу снега во дворе

c — быстрое вычисление двойных интегралов в R

Задавать вопрос

спросил 11 лет, 6 месяцев назад

Изменено 11 лет, 6 месяцев назад

Просмотрено 20 тысяч раз

Часть R Language Collective

Я ищу решение для двойного интеграла быстрее, чем

 интегрировать(функция(у) {
   sapply (у, функция (у) {
     интегрировать (функция (x) myfun (x, y), llim, ulim) $ значение
   })
 }, ллим, улим)
 

, например,

 myfun <- function(x,y) cos(x+y)
llim <- -0,5
улим <- 0,5
 

Я нашел старую статью, в которой упоминалась программа FORTRAN под названием quad2d , но я не смог найти ничего, кроме нескольких справочных страниц для Matlab для остальных. Поэтому я ищу библиотеку C или FORTRAN, которая может быстро вычислять двойные интегралы (т. е. без цикла sapply) и которую можно вызывать из R. Все идеи очень ценятся, если они все совместимы с GPL.

Если решение включает в себя вызов других функций из библиотек, которые уже поставляются с R, я также хотел бы получить от них известие.

• c
• r
• фортран
• интегральный
1

Кубический пакет выполняет интеграцию 2D (и N-D) с использованием адаптивного алгоритма. Он должен превзойти более простые подходы для большинства подынтегральных выражений.

3

Пакет pracma , на который указал Джошуа, содержит версию quad2d .

 quad2d(myfun, llim, ulim, llim, ulim)
 

Это дает тот же ответ с числовым допуском, что и ваш цикл, используя пример функции.

По умолчанию в вашем примере функция quad2d работает медленнее, чем цикл. Если вы отбросите n вниз, вы можете сделать это быстрее, но я думаю, это зависит от того, насколько плавной будет ваша функция и какой точностью вы готовы пожертвовать ради скорости.

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.

Новый кубатурный фильтр Калмана пятой степени для определения орбиты в реальном времени с помощью радара

На этой странице радар. Вводится полностью симметричное кубатурное правило, приближающееся к взвешенному интегралу Гаусса от нелинейной функции в общем виде, а конкретные точки и веса вычисляются путем сопоставления мономов степени не выше пятой с точными значениями. На основе вышеуказанного правила новый кубатурный фильтр Калмана пятой степени, который может достигать более высокой точности, чем UKF и CKF, получен в рамках байесовской фильтрации. Затем для более точного описания нелинейной системы в качестве уравнения состояния используется уравнение орбитальной динамики с возмущением J2, а в качестве уравнения измерения строится нелинейная связь между элементами радиолокационных измерений и орбитальными состояниями. Результаты моделирования показывают, что по сравнению с традиционным алгоритмом третьей степени предложенный алгоритм пятой степени имеет более высокую точность определения орбиты.

1. Введение

С увеличением количества спутников, выводимых на орбиту с каждым годом, мониторинг и каталогизация спутников играют важную роль в повышении степени использования космических ресурсов и снижении нагрузки на орбитальные ресурсы. Как вид датчиков в системах наблюдения за космическим пространством, наземная РЛС оборудуется без учета влияния погоды и других особых обстоятельств, а использование данных ее измерений для определения орбиты в режиме реального времени является ключевой технологией сопровождения космических целей [1, 2]. Из-за нелинейности модели спутниковой орбитальной динамики с влиянием возмущения орбиты, суть определения орбиты в режиме реального времени заключается в достижении оптимальной оценки состояния орбиты с помощью технологии нелинейной фильтрации в рамках байесовской схемы с использованием измеренных данных дальности, скорости и угла с шумом измерений, что имеет важное исследовательское значение.

Основной проблемой нелинейной фильтрации Калмана является вычисление трудноразрешимого многомерного векторного интеграла, такого как «нелинейная функция плотности вероятности Гаусса (PDF)», для которой трудно получить аналитическое решение [3, 4].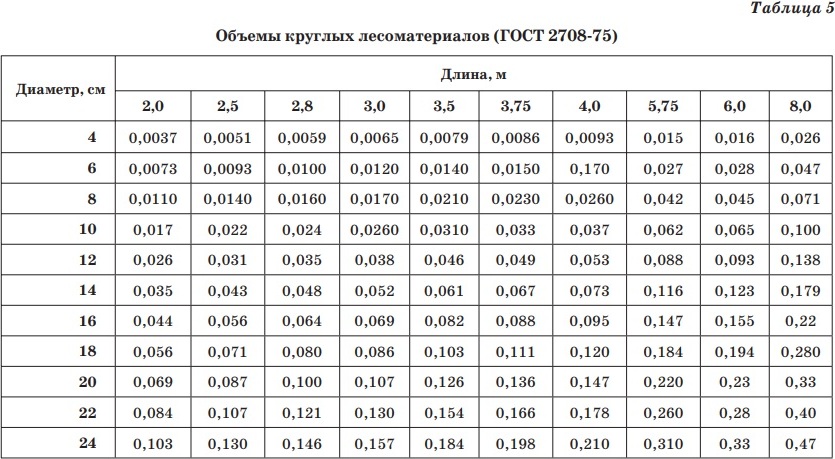 В настоящее время в основном используются два метода, в том числе аппроксимация нелинейной функцией и аппроксимация гауссовской PDF. В первом методе нелинейная функция аппроксимируется полиномом и приводит к расширенному фильтру Калмана (EKF) [5, 6], фильтру с разделенной разностью (DDKF) [7] и полиномиальному фильтру Калмана (PKF) [8, 9].], где разложение Тейлора первого порядка, многомерная интерполяция Стирлинга и многочлены, включая Чебышева и Фурье-Эрмита, используются для аппроксимации нелинейной функции, соответственно, в EKF, DDKF и PKF. Однако вышеупомянутые методы, как правило, ограничены, когда система имеет сильную нелинейность с высокой размерностью. Для последнего гауссовский PDF аппроксимируется с использованием детерминистического подхода к выборке, который в основном включает преобразование без запаха (UT) и правило сферически-радиального излучения (SRR). Затем путем встраивания UT и SRR в структуру байесовской фильтрации получают соответственно неароматизированный фильтр Калмана (UKF) [10, 11] и кубатурный фильтр Калмана (CKF) [12–14], которые имеют широкий спектр приложений в технике [15–20], но эти два типа алгоритмов имеют только третью степень точности фильтрации, которая требует дальнейшего улучшения. В этой статье предлагается новый кубатурный фильтр Калмана пятой степени без дифференциальной операции для повышения точности фильтрации с третьей до пятой степени. Целочисленные точки с соответствующими весами в общем кубатурном правиле вычисляются путем сопоставления мономов степени не выше пятой с их точными значениями в полностью симметричной области. Затем предложенный метод фильтрации, который может обеспечить более высокую точность по сравнению с UKF и CKF, выводится путем внедрения нового кубатурного правила пятой степени в структуру байесовской фильтрации. Предложенный алгоритм фильтрации применяется для определения орбиты в реальном времени, и достигается более точная оценка орбиты.

Остальная часть статьи организована следующим образом: традиционный кубатурный фильтр Калмана описан в разделе 2, новое кубатурное правило пятой степени и связанный с ним фильтр Калмана выводятся в разделе 3, математические модели, используемые для определения орбиты, описаны в разделе 4, численный эксперимент и результаты представлены в разделе 5, а выводы сделаны в разделе 6.

2. Традиционный кубатурный фильтр Калмана

Основной проблемой любого нелинейного фильтра Калмана является вычисление интеграла , для которого, вообще говоря, трудно найти аналитическое решение, где обозначает произвольную функцию, обозначает гауссову плотность вероятности. В частности, рассматривается интеграл вида в декартовой системе координат. Пусть с , где обозначает вектор направления и обозначает радиус, так что и тогда интеграл можно переписать в сферически-радиальной системе координат следующим образом: где – поверхность сферы, определяемая и – элемент площади на . Таким образом, интеграл разлагается на сферический интеграл и радиальный интеграл соответственно и приближенно представляется с помощью численного интегрирования следующим образом: где обозначают интегральные точки и веса сферического интеграла и обозначают число целых точек. Точно так же обозначаются интегральные точки и веса радиального интеграла, а также обозначается количество точек. Из сферически-радиального кубатурного правила третьей степени, использованного в [12], мы получаем, что где – площадь поверхности единичной сферы, – гамма-функция и обозначает единичный вектор с th-м элементом, равным 1. подставляется в , чтобы получить

Из тождественного уравнения

видно, что

Процесс вычисления, используемый в традиционной CKF, приведен ниже.

Обновление времени . Оцените кубатурные точки.

Оценить распространенные кубатурные точки.

Оценить прогнозируемое состояние.

Оценить прогнозируемую ковариацию ошибок.

Обновление измерений . Оцените кубатурные точки.

Оценить распространенные кубатурные точки.

Оценка предсказанного измерения.

Оценить ковариационную матрицу измерений.

Оценить матрицу взаимной ковариации .

Оценка усиления Калмана.

Оценить обновленное состояние.

Оцените соответствующую ковариацию ошибки.

Из алгоритма видно, что 2 n точек принимается при аппроксимации гауссовой PDF. Для повышения точности фильтрации необходимо больше точек с соответствующими весами.

3. Кубатурное правило пятой степени и алгоритм кубатурной фильтрации

3.

1. Кубатурное правило пятой степени

Интеграл , для которого трудно найти аналитическое решение, может быть аппроксимирован с помощью кубатурного правила путем выбора соответствующих кубатурных точек и соответствующих весов, где обозначает кубатурные точки, обозначает веса, не зависящие от подынтегрального выражения, а L обозначает количество кубатурных точек. Мы будем писать для обозначения произвольной точки в вещественном н -мерное пространство. Одночленом степени d назовем функцию вида , где индексы - целые неотрицательные числа такие, что . Вводятся следующие определения и лемма.

Определение 1 (см. [21]). — область в -мерном пространстве; учитывая , полностью симметричный набор , является набором всех точек , где любая перестановка .

Определение 2 (см. [21]). Область называется полностью симметричной тогда и только тогда, когда следует .

Определение 3 (см. [21]). Правило интегрирования R называется полностью симметричным тогда и только тогда, когда всякий раз, когда является абсциссой правила R , каждый элемент является абсциссой R и один и тот же вес соответствует всем абсциссам, принадлежащим данному полностью симметричному множеству.

Лемма 4 (см. [21]). Правило полной симметрии, примененное к полностью симметричной -мерной области, имеет степень тогда и только тогда, когда оно точно для всех мономов степени

Учитывается следующее кубатурное правило:

Приведенное выше правило полностью симметрично; поэтому она будет пятой степени, если она точна для мономов 1, , , и ; таким образом получаются следующие уравнения:

Для случая имеем , где Гамма-функция удовлетворяет и ; таким образом, мы получаем

Формула (21) объединяется с формулой (22) для решения следующих параметров как

Таким образом, конкретная форма правила достигается заменой формулы (23) в формулу (20), и общее количество кубатурных точек, необходимых для правила, составляет . Кроме того, интеграл записывается по правилу в следующем виде:

Определены следующие векторы:где обозначает й столбец матрицы. Из формулы (5) кубатурное правило пятой степени, аппроксимирующее взвешенный интеграл Гаусса от нелинейной функции, получается путем объединения формулы (24) с векторами, определенными в формулах (25) следующим образом:

3.

2. Кубатурный фильтр Калмана пятой степени

Рассматривается следующая дискретная нелинейная динамическая система: где – вектор состояния, – вектор измерения, – известные нелинейные функции, а шум процесса и шум измерения – некоррелированные гауссовский белый шум с нулевым средним с ковариационными матрицами и , соответственно.

Кубатурные точки и соответствующие веса получаются из кубатурного правила пятой степени, показанного в формуле (26), следующим образом:

Предлагаемый кубатурный фильтр Калмана пятой степени выводится с использованием точек и весов, показанных, соответственно, в формулах (28) в рамках байесовской фильтрации со ссылкой на алгоритм третьей степени в [12], а конкретные этапы расчета перечислены ниже.

Шаг 1 (инициализация фильтра). Цикл и выполните следующие шаги.

Шаг 2 (обновление времени). Вычислите точки, используя апостериорную оценку состояния и апостериорную ковариационную матрицу ошибок.

Шаг 3 (обновление измерения). Вычислить точки, используя априорную оценку состояния и априорная матрица ковариации ошибок . Вычислить нелинейное распространение с помощью. Вычислить прогнозируемое значение измерения путем взвешенного слияния. Вычислить прогнозируемую ковариационную матрицу измерения. Вычислить матрицу взаимной ковариации. матрица ковариации ошибок. Псевдокод, представляющий предлагаемый алгоритм, приведен в Алгоритме 1.

() Вычислить , и ; () Ввод : , , () для до до () ; ()  для до до ()  Вычислить с использованием , , и ; ()  ; ()  конец () ; () ; () ; ()  для по до ()  Вычислите с помощью , , , и ; ()  ; ()  конец () ; () ; () ; () ; () ; () ; () end () Выход : ,

Примечание 5. 9 0114 Предлагаемый метод является бездифференциальным; то есть нет необходимости вычислять матрицу Якоби.

Замечание 6. По сравнению с CKF третьей степени точность фильтрации предлагаемого метода повышена до пятой степени.

Замечание 7. Общий способ вычисления кубатурного правила приведен в предлагаемом методе фильтрации без разделения неразрешимого интеграла на сферический интеграл и радиальный интеграл.

4. Математическая модель для определения орбиты

4.1. Модель орбитальной динамики

Спутники на орбите подвергаются различным возмущениям, в основном включая несферическое гравитационное возмущение, гравитационное возмущение третьего тела, возмущение атмосферного сопротивления и возмущение давления солнечного излучения, среди которых несферическое гравитационное возмущение J2 является наиболее влиятельным возмущением. Для более точного описания движения спутника на орбите модель орбитальной динамики с возмущением J2 в центральной фиксированной системе координат Земли (ECF) используется для описания орбиты спутника следующим образом [22]: где – положение и скорость спутника в ECF, – постоянная гравитации Земли, – коэффициент гармоник, – радиус Земли, – угловая скорость Земли, – сумма других возмущений, которую можно аппроксимировать нулевым средним гауссовским белым шумом. в исследовании. Формула (42) может быть записана в форме дискретного уравнения состояния следующим образом: где обозначает орбитальное состояние в момент времени, а обозначает шум процесса.

4.2. Модель радиолокационных измерений

Модель радиолокационных измерений описывается в местной горизонтальной (LH) системе координат, а матрица преобразования из ECF в LH выглядит следующим образом: где и обозначают геоцентрическую долготу и геоцентрическую широту радиолокатора соответственно, которые также могут быть представлены геоцентрическими координатами. Мы определяем состояния орбит спутников в LH, и получаем следующие уравнения:

Геометрическая взаимосвязь между состояниями орбит и значениями измерений радара получается следующим образом: где обозначает значение дальности, обозначает значение скорости, обозначает азимутальный угол и обозначает угол места. Формула (46) записывается в следующей форме уравнения измерения: где обозначает значения измерения во времени, а обозначает шум измерения.

5. Численный эксперимент

Платформа моделирования построена с использованием Satellite Tool Kit (STK) и MATLAB, спутник работает на низкой околоземной солнечно-синхронной орбите, а данные опорной орбиты генерируются с помощью алгоритма High-Precision Orbit Prediction (HPOP). В HPOP учитывается гравитационная модель Земли 21-го порядка, коэффициент атмосферного сопротивления, в качестве модели плотности атмосферы принята модель Джаккиа-Робертса, коэффициент давления солнечного излучения, отношение площади к массе равно 0,02 м ² /кг, учитываются гравитационные возмущения Солнца и Луны третьего тела, а также учитывается приливное возмущение. Точность значений дальности, скорости и угла принимается равной 20 м, 0,1 м/с и 0,015° соответственно. Шесть элементов орбиты, включая большую полуось (), эксцентриситет (), наклонение (), прямое восхождение восходящего узла (RAAN), аргумент перигея (), истинную аномалию (), а также широту и долготу радиолокационной станции, перечислены в таблице 1.

Исходное состояние фильтра = .

Исходная ковариационная матрица = .

Время доступа от радиолокационной станции к спутнику с 1 июля 2015 г., 16:14:00 до 1 июля 2015 г., 16:21:00, и для оценки результатов определения орбиты в реальном времени используется среднеквадратическая ошибка (RMSE). Цикл фильтрации составляет 1 с, и мы провели 200 симуляций методом Монте-Карло. UKF и CKF сравниваются в этом эксперименте, чтобы проверить производительность предложенного алгоритма. СКО трех алгоритмов показаны на рисунке 1, а среднестатистические СКО приведены в таблице 2. Из результатов видно, что точность определения орбиты, полученная с помощью UKF, почти соответствует точности CKF из-за того, что два алгоритма были созданы для принятия метода детерминированной выборки третьей степени. В отличие от CKF, предложенный кубатурный фильтр Калмана пятой степени способен достигать более высокой точности, а точность положения увеличивается на 3,204 м при увеличении точности скорости на 0,04 м/с. Для низкоорбитального спутника возмущение атмосферного сопротивления оказывает влияние на орбиту, а это означает, что уравнение состояния (формула (42)) не может точно описать орбиту, и если используется высокоточная модель возмущения орбиты, чрезмерная потребность в вычислениях ухудшит производительность алгоритма фильтрации в реальном времени; однако ошибки, вызванные орбитальной моделью, в целом допустимы из-за короткого времени доступа спутника LEO.

6. Заключение

В этой статье предлагается новый кубатурный фильтр Калмана пятой степени для повышения точности определения орбиты в реальном времени с помощью наземного радара. Целочисленные точки и веса в общем кубатурном правиле решаются путем сопоставления мономов степени не выше пятой с их точными значениями, а затем выводится кубатурное правило пятой степени. Предлагаемый новый кубатурный фильтр Калмана пятой степени, который может обеспечить более высокую точность фильтрации, чем UKF и CKF, получен с использованием вышеупомянутого правила, основанного на структуре байесовской фильтрации. Результаты моделирования показывают, что точность позиционирования, достигаемая CKF и предложенным алгоритмом, составляет 27,148 м и 23,9 м.44  м соответственно, при точности скорости 0,347  м/с и 0,307  м/с соответственно. По сравнению с результатами CKF точность позиционирования и точность скорости улучшены на 3,204 м и 0,04 м/с соответственно, что подтверждает правильность предложенного алгоритма.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Благодарности

Эта работа частично поддерживается Национальной программой исследований и разработок в области высоких технологий Китая (2015AA7026085).

Ссылки

1. M. Sciotti, P. Besso, T. Flohrer, and H. Krag, «Отслеживание объектов на низкой околоземной орбите и определение орбиты с помощью наземных радиолокационных систем с фазированной антенной решеткой», в Proceedings of the International Radar Symposium, IRS 2011 , стр. 591–596, Leipzig, Germany, 2011.

   Просмотр по адресу:
   Google Scholar

2. X. Ning, C. M. Ye, J. Yang, and B. Shen, «Кубатурная калмановская фильтрация для определения орбиты космических целей», Китайский журнал радионауки , том. 29, нет. 1, стр. 27–32, 2014.

   Посмотреть по адресу:
   Google Scholar

3. «Кубатурный квадратурный фильтр Калмана», IET Signal Processing , vol. 7, нет. 7, стр. 533–541, 2013 г.

   Посмотреть по адресу:
   Сайт издателя | ученый Google | MathSciNet

4. Дж. Зарей и Э. Шокри, «Анализ сходимости нелинейной фильтрации на основе кубатурного фильтра Калмана», IET Science, Measurement and Technology , том. 9, нет. 3, стр. 294–305, 2015.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

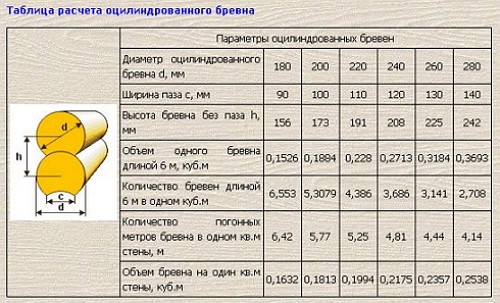5. K. Reif, S. Gunther, E. Yaz, and R. Unbehauen, «Стохастическая устойчивость расширенного фильтра Калмана с дискретным временем», IEEE Transactions on Automatic and Control , vol. 44, нет. 4, стр. 714–728, 1999.

   Посмотреть по адресу:
   Сайт издателя | ученый Google | MathSciNet

6. Т. Эйнскоу, Р. Занетти, Дж. Кристиан и П. Д. Спанос, «Расширенный фильтр Калмана Q-метода», Journal of Guidance, Control and Dynamics , vol. 38, нет. 4, стр. 752–760, 2015.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

7. К. Д. Карлгаард и Х. Шен, «Надежная оценка состояния с использованием десенсибилизированного фильтра разделенных разностей», ISA Transactions , vol. 52, нет. 5, стр. 629–637, 2013 г.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

8. М. Ф. Хубер, «Полиномиальный фильтр Калмана Чебышева», Цифровая обработка сигналов , том. 23, нет. 5, стр. 1620–1629, 2013.

   Посмотреть по адресу:
   Сайт издателя | ученый Google | MathSciNet

9. Дж. Сармавуори и С. Саркка, «Фильтр Калмана Фурье-Эрмита», IEEE Transactions on Automatic and Control , vol. 57, нет. 6, стр. 1511–1515, 2012.

   Посмотреть по адресу:
   Сайт издателя | ученый Google | MathSciNet

10. С. Джулиер, Дж. Ульманн и Х. Ф. Даррант-Уайт, «Новый метод нелинейного преобразования средних и ковариаций в фильтрах и оценках», Институт инженеров по электротехнике и электронике. Труды по автоматическому управлению , вып. 45, нет. 3, стр. 477–482, 2000.

    Посмотреть по адресу:
    Сайт издателя | ученый Google | MathSciNet

11. Х. М. Менегаз, Дж. Ю. Исихара, Г. А. Борхес и А. Н. Варгас, «Систематизация теории фильтра Калмана без запаха», Институт инженеров по электротехнике и электронике. Труды по автоматическому управлению , вып. 60, нет. 2015. Т. 10. С. 2583–2598.

    Посмотреть по адресу:
    Сайт издателя | ученый Google | MathSciNet

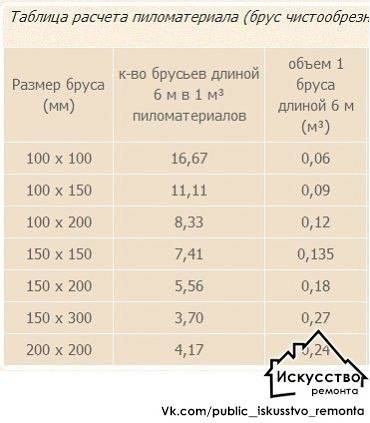12. И. Арасаратнам и С. Хайкин, «Кубатурные фильтры Калмана», Институт инженеров по электротехнике и электронике. Труды по автоматическому управлению , вып. 54, нет. 6, стр. 1254–1269, 2009.

    Посмотреть по адресу:
    Сайт издателя | ученый Google | MathSciNet

13. И. Арасаратнам, С. Хайкин и Т. Р. Херд, «Кубатурная фильтрация Калмана для непрерывно-дискретных систем: теория и моделирование», IEEE Transactions on Signal Processing , vol. 58, нет. 10, стр. 4977–4993, 2010.

    Посмотреть по адресу:
    Сайт издателя | ученый Google | MathSciNet

14. Дж. Чен, Н. Ван, Л. Ма и Б. Сюй, «Расширенный фильтр плотности гипотезы целевой вероятности на основе кубатурного фильтра Калмана», IET Radar, Sonar and Navigation , vol. 9, нет. 3, стр. 324–332, 2015 г.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

15. Д. Потнуру, К.П.Б. Чандра, И. Арасаратнам, Д.-В. Гу, К. А. Мэри и С. Б. Ч, «Кубатурный фильтр Калмана с квадратным корнем без производных для нелинейных бесщеточных двигателей постоянного тока», Электроэнергетические приложения ИЭТ , том. 10, нет. 5, стр. 419–429, 2016.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

16. Л. Чжан, Х. Ян, Х. Лу, С. Чжан, Х. Кай и С. Цянь, «Кубатурная фильтрация Калмана для оценки относительного положения и положения космического корабля», Acta Astronautica , vol. 105, нет. 1, стр. 254–264, 2014.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

17. П. Х. Леонг, С. Арулампалам, Т. А. Ламахева и Т. Д. Абхаяпала, «Кубатурный фильтр Калмана на основе суммы Гаусса для отслеживания только пеленгов», IEEE Transactions on Aerospace and Electronic Systems , vol. 49, нет. 2, стр. 1161–1176, 2013 г.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

18. A. Noor, E. Serpedin, M. Nounou и H. Nounou, «Обратное проектирование разреженных сетей регуляции генов с использованием кубатурного фильтра Калмана и сжатого зондирования», Advances in Bioinformatics , vol. 2013 г., идентификатор статьи 205763, 2013 г.

    Посмотреть по адресу:
    Сайт издателя | Академия Google

19. Б. Сюй, Ю. П. Сяо, В. Гао, Ю. Г. Чжан, Ю. Л. Лю и Ю. Лю, «Алгоритм обратного CKF с двойной моделью в совместной навигации для USV», Mathematical Problems in Engineering , vol. 2014 г., идентификатор статьи 186785, 2014 г.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

20. Л. Ван, М. Чен, Г. Ли и Ю. Фан, «Управление роботами-гуманоидами на основе данных с использованием регрессии опорных векторов, нечеткой логики и кубатурного фильтра Калмана», Математические проблемы в инженерии , Артикул ID 1984634, Ст. ID 1984634, 19 страниц, 2016 г.

    Посмотреть по адресу:
    Сайт издателя | ученый Google | MathSciNet

21. Г. Филлипс, «Обзор одномерного и многомерного численного интегрирования», Computer Physics Communications , vol. 20, нет. 1, стр. 17–27, 1980.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

22. С.