калькулятор, расход на м3, маркировка

Любая строительная конструкция, даже небольшая хозяйственная постройка, требует надежного основания. Бетон для заливки такового заказывается или готовится самостоятельно. Независимо от принятого решения, застройщик должен уметь провести расчет фундамента, чтобы получить оптимальное количество рабочей смеси. Сделать это можно вручную, используя справочную литературу, или же загрузить исходные данные в онлайн калькулятор на любом серьезном сайте строительной тематики. В индивидуальном строительстве популярны: ленточный, плитный и столбчатый фундаменты, расчет каждого из которых имеет свои особенности.

Оглавление:

1. Монолитная конструкция
2. Столбчатое основание
3. Ленточный фундамент
4. Как приготовить бетонный раствор?

Монолит

Он представляет собой плоскую цельную конструкцию, расположенную под всем сооружением. Объем необходимого бетона узнать проще всего: достаточно перемножить ее площадь и высоту. Например, Sпл под хозяйственной постройкой размером 5х5 м — 25 м2. В соответствии с требованиями нормативных актов, минимальная толщина плиты — 0,1 м, а оптимальная — 0,2 м. При этом расчет бетонной смеси для ее заливки выглядит так: Vпл = 25×0,2 = 5 м3.

Иногда для придания такому фундаменту дополнительной прочности применяют ребра жесткости, которые располагают в нижней его части, обращенной к грунту. Они выполняются в виде перпендикулярных продольных и поперечных бетонных полос. Чтобы рассчитать их общий объем, надо знать длину и площадь сечения каждой. Для основания со сторонами 5х5 (при шаге 2,5 м), понадобится 6 5-метровых ребер: 4 по краям и 2 в центре. Их протяженность — 30 м.

Чаще всего полосы бывают прямоугольными или трапециевидными. Их высота должна быть равна толщине плиты, а ширина – соотноситься с ней в пропорции 1:0,8. Для заданных условий Sр = 0,08×0,2 = 0,016 м2, а Vр = 0,016×30 = 0,48 м3. При вычислении трапециевидной формы надо учесть, что ее нижнее основание в полтора раза шире обычного. Потому площадь сечения будет Sтр = 0,2×(0,12+0,08)× ½ = 0,012 м2, а Vтр = 0,012х30= 0,36 м3. Так же производится расчет ребер усиления для основания другой толщины.

В справочной литературе имеются готовые значения объема бетона, необходимого для заливки плиточных фундаментов различных размеров, с учетом ребер. Например, для дома 6х6 м они будут выглядеть так:

Толщина, мм	Ребра жесткости	Расход бетона, м3
100	нет	3,6
	прямоугольные	3,89
	трапециевидные	3,96
200	нет	7,2
	прямоугольные	8,35
	трапециевидные	9
300	нет	10,8
	прямоугольные	13,4
	трапециевидные	14,85

Столбчатый фундамент

Фактически, это монолитный ростверк, опирающийся на опоры, установленные под всеми углами сооружения, точками пересечения несущих стен и местами, испытывающими повышенные нагрузки. Чтобы правильно произвести расчет количества бетона на фундамент такого типа, потребуется измерить длину всех поддерживающих элементов, а также определить площадь Sст (поперечного среза). Для круглых столбов Sст = π×R², где π — константа, а R — радиус (в метрах). Таким образом, при ø30 см она будет 3,14×(0,15)² = 0,07065 м². Объем (Vст) такого столба, высотой 2 м, равен 2х0,07065 = 0,1413 м³. По такой же схеме производится расчет бетона для опор с другими параметрами, после чего полученные данные умножаются на их общее количество в фундаменте.

Тип столба	Сечение, см	Расход бетона, м3
Круглый	ø 15	0,0353
	ø 20	0,0628
	ø 30	0,1413
Квадратный	20×20	0,08
	30×30	0,18
	40×40	0,32

Ленточный

Это наиболее популярный тип оснований зданий и сооружений ввиду его универсальности и доступности. Чтобы узнать, сколько бетонной смеси нужно на ленточный фундамент, потребуется провести расчет его общей протяженности, высоты и ширины. Первый параметр — сумма длин всех внешних сторон (периметра) и внутренних стен. Второй получается сложением размеров его надземной и заглубленной части. Ширина фундамента зависит от грунта, веса здания и чаще всего выбирается равной 0,2–0,4 м.

Таким образом, для хозяйственного сооружения со сторонами 5х5 м и одной внутренней стеной исходные данные для вычислений объема бетона будут такими: протяженность ленты — 25 м (20 м — периметр и 5 м — внутренняя стена). При заглублении в грунт на 1,5 м и возвышении над землей — 0,4 м ее высота равна 1,9 м. Учитывая классическую ширину в 40 см, расчет ленточного основания выглядит так: V = 0,4×25×1,9 = 19 м3. Быстрее и проще проводить автоматические вычисления, используя онлайн калькулятор. Его формы позволяют не только вводить числовые значения, но и предлагают выбрать тип фундамента, марку цемента, рассчитать параметры армирующих элементов, опалубки и примерную стоимость материалов. Причем вычисления происходят практически мгновенно, а отчеты распечатываются в графическом виде как схема или таблица.

Состав смеси

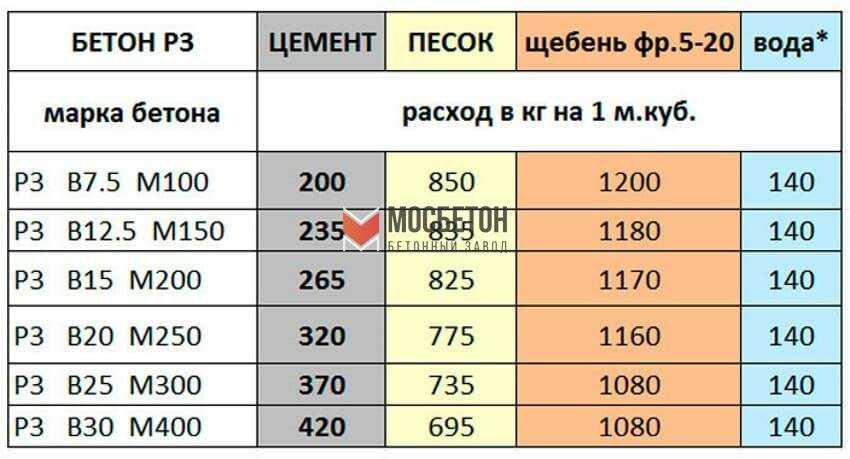
Чтобы приготовить бетон для заливки фундамента, понадобится песок без примесей с размером фракций не более 3,5 мм. Его чистоту можно проверить, поместив в прозрачную бутыль с водой. Если наблюдается лишь легкое помутнение жидкости — заполнитель хорошего качества. Допустимые фракции гравия — 10–80 мм. Вместо него допускается использование щебенки аналогичной величины. В качестве вяжущего материала для возведения основания покупают портландцемент.

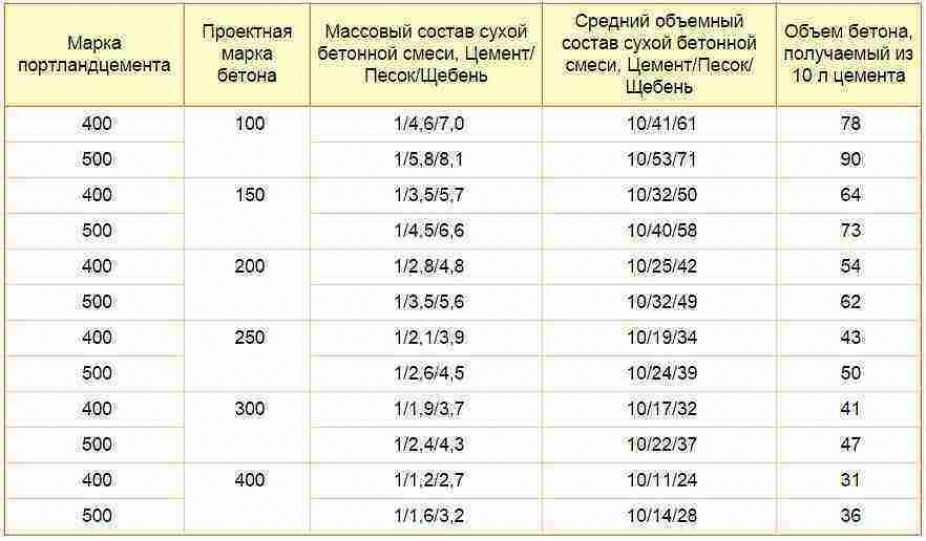
Традиционно выбирается марка цемента, в 2 раза превышающая требуемый класс бетона. Количество составных компонентов рабочей смеси измеряют в долях по отношению к вяжущему элементу. Обычно пропорция такая: 1 часть цемента, 3 — песка и 5 — щебня (гравия). Водоцементное соотношение при расчете выбирается в зависимости от прочности бетона. Его значение находится в справочных таблицах по строительству.

Марка цемента	Класс бетона
	М400 (В30)	М300 (В22,5)	М200 (В15)	М100 (В7,5)
М300	–	0,4	0,55	0,75
М400	0,4	0,5	0,63	0,85
М500	0,46	0,6	0,71	–
М600	0,5	0,63	0,75

Произвести расчет состава бетонной смеси для фундамента вполне можно и своими руками, используя значения, рекомендованные СНиП 52-01-2003 и ГОСТ 7473-2010. Например, чтобы замесить раствор класса В22,5 (М300), потребуется одно 10-литровое ведро портландцемента марки М500, 2 песка, 4 щебня (гравия) и 5 литров воды.

Нахождение объема цилиндров: определение, формула

Сталкиваетесь ли вы с трудностями при нахождении объема цилиндров, если его форма искажена? Задумывались ли вы над тем, как найти объем таких цилиндров? Это то, что вы узнаете через мгновение.

Объем цилиндра означает пространство внутри цилиндра, которое может вместить определенное количество материала. Проще говоря, способность цилиндра удерживать предмет — это его объем. Внутри пространства цилиндра вы можете удерживать любой из трех типов материи — твердое, жидкое или газообразное. Эту емкость можно наблюдать только в трехмерном цилиндре, т. е. вы не можете удержать ни жидкость, ни твердое тело, ни газ в двумерном цилиндре.

Совершенный трехмерный цилиндр имеет два конгруэнтных и параллельных одинаковых основания. Это известно как правильный круговой цилиндр. В прямом круговом цилиндре основания круглые, а каждый отрезок является частью боковой криволинейной поверхности, перпендикулярной основаниям. Вы могли видеть правильные круглые цилиндры в своей повседневной жизни. Формы банок, формы рулонов бумаги, прямое стекло и многое другое.

Однако, если форма стакана совершенно прямая, он будет называться правильным круглым цилиндром. Если форма нелинейна, то какой она будет?

Если две конгруэнтные и идентичные параллельные стороны каким-то образом станут непараллельными или деформируются, вы получите любой из следующих цилиндров:

1. Наклонный цилиндр — это цилиндр, стороны которого наклонены к основанию под углом, не равен прямому углу. Это будет форма искаженного стекла, о которой говорилось выше.
2. Эллиптический цилиндр – Это цилиндр, основания которого представляют собой эллипсы.
3. Правый круглый полый цилиндр
   — Имеет форму правильного круглого цилиндра. Однако в конце нет замкнутых кругов.

Как найти объем цилиндра – традиционный метод 

Найти объем цилиндра проще, чем вы думали. Если вам все еще интересно, как найти объем цилиндра, все, что вам нужно, это ведро с водой, весы и пустая плоская поверхность, на которую можно поставить ведро.

Поставьте ванну на ровную пустую поверхность и начните наполнять ее водой. Вы должны убедиться, что вода заполнена до краев. Как только ванна наполнится водой, поместите цилиндр, объем которого вам нужно найти, внутрь ванны. Вы увидите, как вода начнет выходить из ванны.

Соберите выпавшую воду в стакан. Убедитесь, что вода не падает, пока вы делаете преобразование. Поставьте стакан на весы и запишите вес воды. Не забудьте вычесть вес стакана. Вы должны иметь только вес воды.

Согласно закону Архимеда, вес воды, падающей из ванны, будет равен весу цилиндра. Следовательно, вес полученной воды будет равен весу цилиндра. Вам может быть интересно, как найти объем цилиндра?

Согласно физике, если вы находитесь в помещении с комнатной температурой, вес будет равен объему. Это означает, что 1 кг будет эквивалентен 1 литру и так далее. Следовательно, вы получите объем цилиндра из объема воды.

Но что, если вы живете в холодном или жарком регионе? Тогда вам придется использовать другой метод.

Формула для нахождения объема цилиндра s

Вы можете найти объем цилиндра, используя формулу. Это универсально и может применяться независимо от вашего региона. Единицами объема являются кубические сантиметры, кубические дюймы или любые стандартные единицы с префиксом «кубический».

Существует два метода определения объема цилиндра.

Это:

1. Использование площади и высоты
2. Использование размеров

• Нахождение объема цилиндров по площади и высоте есть не что иное, как произведение площади и высоты любой формы. Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем.

В цилиндрах V = площадь x высота 

• Нахождение площади при известных размерах – Универсальная формула для нахождения объема цилиндра: π r ² ч, где значение π (пи) равно 3,14 или 22/7, r — радиус верха или низа цилиндра, h — высота. Используя формулу, можно найти объемы прямых круговых цилиндров и косых цилиндров.

Однако для эллиптических цилиндров формула другая. Поскольку эллиптические цилиндры имеют разные радиусы, формула для нахождения их объемов имеет вид: V = π abh, где π = 22/7 или 3,14, a и b — радиусы основания эллиптического цилиндра, а h — высота .

Кроме того, формула также отличается для полых прямоугольных цилиндров. Объем полого прямоугольного цилиндра определяется формулой: V = π (R ² – r ² ) h , где R — внешний радиус круглого основания, r — внутренний радиус, а h — высота цилиндра.

Если вы ищете формулу площади поверхности цилиндра, то вот она: A = 2πr ²  + 2πrh , где r и h — радиус и высота цилиндра соответственно. Единицами площади поверхности будут квадратные единицы.

Шаги для расчета объема цилиндра

Следуя приведенным ниже методам, вы можете найти объем цилиндра.

Шаг 1: Определите тип цилиндра, данный вам в вопросе или в реальной жизни.

Шаг 2: Когда у вас есть тип цилиндра, вам нужно выяснить формулу, по которой можно найти объем цилиндра.

Шаг 3: Теперь у вас есть и формула. Проверьте, какие размеры вам нужны, чтобы найти объем. Убедитесь, что все размеры имеют одинаковые единицы измерения.

Шаг 4: Поместите их на соответствующие места и рассчитайте объем.

Шаг 5: Сохраните единицы измерения после расчетного значения как «кубические единицы». Используйте соответствующую единицу измерения, такую ​​как метр, сантиметр или любую другую, вместо слова единица измерения.

Примеры для нахождения объема цилиндра

Пример 1: Цилиндр имеет радиус 50 см и высоту 100 см. Как найти объем цилиндра?  

Решение: Мы знаем, что объем цилиндра находится по формуле – π r ² h, где r — радиус цилиндра, а h — высота.

Следовательно, размещение значений, мы получаем,

V = π r ² H

= 3,14 x 50 ² x 100 = 785 000,000 см ³ .

Пример 2: Как найти объем цилиндра, у которого один из радиусов равен 40 см, а другой — 60 см? Цилиндр имеет высоту 200 см.

Решение: Из приведенных данных видно, что цилиндр эллиптический, так как радиусы разные. Чтобы найти объем эллиптического цилиндра, используется формула V = π abh, где a и b — радиусы, а h — высота.

Следовательно, объем цилиндра = V = π abh

= π x 40 x 60 x 200 = 1507200 см ³ .

Пример 3: Как найти объем полого цилиндра изнутри и имеет внешний и внутренний радиусы единиц 6 и 8 соответственно? Высота этого полого цилиндра составляет 15 единиц.  

Решение. Мы знаем, что формула объема полого цилиндра имеет вид V = π (R ² – r ² ) h .

Таким образом, подставив значения, получим ) 15 = 1318,8 единиц ² .

Пример 4. Однажды Алекс задался вопросом: «Как мне найти объем цилиндра, высота которого равна 6 дюймам, а радиус — 3 дюймам». Можете ли вы помочь ей найти объем этого цилиндра?

Ответ: Да, можно! Вы знаете формулу для нахождения объема цилиндра: V = π r ² ч.

Таким образом, подставив значения, вы получите V = π r ² ч

= π x 3 ² x 6 = 169,56 в ³ .

Вы можете сказать Алексу, что объем цилиндра равен 169,56 в ³ .

Часто задаваемые вопросы – Часто задаваемые вопросы

1. Какова площадь криволинейной поверхности цилиндра?

Площадь криволинейной поверхности цилиндра = 2πrh

2. Каков объем цилиндра?

Объем цилиндра – это количество свободного места в нем. Его можно получить, умножив площадь основания на высоту. Объем цилиндра с радиусом основания «r» и высотой «h» равен V = πr2h.

3. Каков объем полого цилиндра?

Мы измеряем два радиуса объема полого цилиндра, один для внутренней окружности, а другой для внешней окружности, образованной основанием полого цилиндра, и если «R» — внешний радиус, а «r» — внутренний радиус и « h” – высота, то объем полого цилиндра равен V = πh (R2 – r2).

4. Какая единица измерения объема цилиндра?

Объем цилиндра измеряется в кубических единицах, таких как кубические сантиметры (см3), кубические метры (м3), кубические футы (фут3) и так далее.

Практический вопрос

1. Вычислите объем заданного цилиндра высотой 30 см и радиусом основания 15 см. (Возьмите пи = 22/7)?

Ответ) Дано:

Высота = 30 см

Радиус = 15 см

мы это знаем;

Объем, V = πr2h кубических единиц

V=(22/7) × 15 × 15 × 30

V= 212142,85 см3

Следовательно, объем цилиндра = 212142,85 см3 90 003

2. Цилиндр имеет высота 15см и объем 500см3 ! Каков радиус цилиндра?

Ответ) 3.257

Как рассчитать объем прямоугольной призмы?

В геометрии призма представляет собой объект трехмерной формы, который состоит из двух одинаковых многоугольников, обращенных друг к другу и соединенных по бокам прямоугольными или параллелограммными гранями. Эти одинаковые многоугольники называются основаниями призмы и могут иметь любую форму, например треугольники, квадраты, прямоугольники или любой n-сторонний многоугольник. Призма является важным членом семейства многогранников. В зависимости от типа многоугольного основания призмы делятся на два типа: правильные и неправильные призмы. И в зависимости от выравнивания оснований существует два типа призм: прямые призмы и наклонные призмы. Кроме того, в зависимости от формы многоугольного основания призмы подразделяются на различные типы: треугольные призмы, прямоугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д.

Прямоугольная призма

Прямоугольная призма представляет собой трехмерную фигуру, состоящую из шести прямоугольных плоских граней. Это призма с двумя прямоугольными основаниями и четырьмя боковыми прямоугольными гранями, двенадцатью сторонами и восемью вершинами. Согласно математическим исследованиям, прямоугольным параллелепипедом называется любой многогранник, напоминающий прямоугольную призму. В прямоугольной призме каждый угол прямой. Он также известен как прямоугольный шестигранник, правильная прямоугольная призма и прямоугольный параллелепипед.

Объем прямоугольной призмы

Объем прямоугольной призмы — это полное пространство, заключенное внутри прямоугольной призмы. Она обычно обозначается буквой «V» и измеряется в см ³ , м ³ , в ³ и т. д. Объем прямоугольной призмы определяется путем умножения площади ее основания на ее высоту.

 

Формула объема прямоугольной призмы дается следующим образом:

Объем прямоугольной призмы = площадь основания × высота призмы

Поскольку основание призмы представляет собой прямоугольник, его площадь равна произведению длины и ширины. Пусть «h» — высота призмы, «l» — длина основания, а «b» — ширина основания.

Теперь формула для объема прямоугольной призмы дается следующим образом:

Объем прямоугольной призмы = l × w × h кубических единиц

Решаемые примеры на основе

Объем прямоугольной призмы

Задача 1. Найдите высоту прямоугольной призмы, если ее объем равен 90 кубических дюймов, а его базовая площадь равна 15 квадратных дюймов.

Решение:

Приведены данные,

Объем прямоугольной призмы = 90 куб. в

Площадь основания = 15 кв. в

Мы знаем, что,

Объем прямоугольной призмы формула = Площадь основания × Высота призмы

⇒ 90 = 15 × h

⇒ h = 90/15 = 6 дюймы.

Следовательно, высота данной призмы равна 6 дюймам.

Задача 2: Определить объем прямоугольной призмы, если длина ее основания 10 см, ширина основания 6 см, а высота призмы 15 см.

Решение:

Приведенные данные,

Высота прямоугольной призмы (h) = 15 см

Длина основания (l) = 10 см

Ширина основания (w) = 6 см

Мы знать, что,

Объем прямоугольной призмы формула (V) = площадь основания × высота призмы

площадь основания = l × w

= 10 × 6 = 60 кв. см.

В = 60 × 15 = 900 куб. см

Отсюда объем прямоугольной призмы 900 куб. см.

Задача 3: Какова ширина основания прямоугольной призмы, если ее объем 2100 куб. см, а его высота и длина основания равны 25 см и 12 см соответственно?

Решение:

Приведены данные,

Объем прямоугольной призмы = 2100 куб. см

Высота прямоугольной призмы (h) = 25 см

Длина основания (l) = 12 см

Мы знаем, что,

Объем прямоугольной призмы формула (V) = площадь основания × высота призмы

Площадь основания = l × w

⇒ V = l × w × h

⇒ 2100= 12 × w × 25

⇒ 300w = 2100

⇒ w = 2100/ 300 = 7 см

Отсюда ширина основания прямоугольной призмы 7 см.

Задача 4. Каков объем прямоугольной призмы высотой 20 единиц и площадью основания 120 квадратных единиц?

Решение:

Приведены данные,

Высота прямоугольной призмы (h) = 20 единиц

Площадь основания = 120 квадратных единиц

Мы знаем, что

Объем прямоугольной призмы по формуле (V) = Площадь основания × Высота призмы

V = 120 × 20 = 2400 кубических единиц.

Следовательно, объем прямоугольной призмы равен 2400 кубических единиц.

Задача 5. Какова длина основания прямоугольной призмы, если ее объем 150 куб. см, а его высота и ширина основания равны 10 см и 3 см соответственно?

Решение:

Приведенные данные,

Объем прямоугольной призмы = 150 куб. см

Высота прямоугольной призмы (h) = 10 см

Ширина основания (w) = 3 см

Мы знаем, что,

Формула объема прямоугольной призмы (V) = площадь основания × высота призмы

Площадь основания = l × w 

⇒ V = l × w × h

⇒ 150 = l × 3 × 10

⇒ 30l = 150 5 см

Отсюда длина основания прямоугольной призмы равна 5 см.

Задача 6. Каков объем прямоугольной призмы, высота которой равна 20 единицам, а длина и ширина основания равны 15 единицам и 12 единицам соответственно?

Решение:

Данные,

Высота прямоугольной призмы (h) = 20 единиц

Длина основания (l) = 15 единиц

Ширина основания (w) = 12 шт.

Мы знать, что,

Объем прямоугольной призмы = l × w × h кубических единиц

V = 15 × 12 × 20 = 3600 кубических единиц.

Следовательно, объем прямоугольной призмы равен 3600 кубических единиц.

Задача 7. Определить объем прямоугольной призмы, если ее высота равна 10 см, а длина и ширина основания равны 8 см и 6 см соответственно.

Решение:

Приведенные данные,

Высота прямоугольной призмы (h) = 10 см см

Мы знаем, что,

Объем прямоугольной призмы = l × w × h кубических единиц

V = 8 × 6 × 10 = 480 куб. см

Значит, объем прямоугольной призмы равен 480 куб. см.

Часто задаваемые вопросы на основе прямоугольной призмы

Вопрос 1: Каков объем прямоугольной призмы?

Ответ:

Объем прямоугольной призмы — это количество вещества, которое она может удержать, или это пространство, занимаемое ею в трехмерном пространстве. Итак, объем прямоугольной призмы рассчитывается путем умножения площади ее основания на ее высоту. Формула для нахождения объема прямоугольной призмы:

 Объем (V) = высота призмы × площадь основания.

 Рассчитывается в кубических единицах, таких как см ³ , м ³ , ин ³ и т. д.

Вопрос 2: Какие изменения происходят с объемом прямоугольного см, если его высота удвоится ?

Ответ:

Объем прямоугольной призмы является произведением ее трех измерений, т. е.

объем = длина × ширина × высота.

Если высоту прямоугольной призмы увеличить вдвое, то ее объем будет V ₂ = l × w × (2h) = 2 × lwh = 2 × V ₁ . Таким образом, можно с уверенностью сказать, что объем прямоугольной призмы удваивается, когда ее высота увеличивается вдвое.

Вопрос 3: Что произойдет с объемом прямоугольной призмы, если ее высоту уменьшить вдвое?

Ответ:

Объем прямоугольной призмы равен произведению ее трех измерений, т.