Расчет и нанесение уклона на обмерных чертежах » Лазерное сканирование и архитектурные обмеры в Санкт-Петербурге | Архитектурная Фотограмметрия
С необходимостью посчитать уклон постоянно сталкиваются проектировщики, строители, архитекторы, а также люди ряда других профессий, в силу того, что на земной поверхности очень трудно найти идеально ровный участок. Уклон выражается в градусах или в процентах. Обозначение в градусах показывает угол кривизны поверхности. Но уклон может быть представлен и в виде тангенса этого угла, умноженного на 100%.
Как рассчитать уклон поверхности?
Уклон – это отношение превышения (ВС) к заложению (АС) и обозначается в текстовых документах буквой i.
Например, i=1:6
Разделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам нужно получить уклон в процентах, умножьте полученное число на 100%. Чтобы получить уклон в промилле, умножьте результат деления на 1000‰.
Если вам необходимо получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов результат – тангенс угла наклона.
На видах (фасадах), разрезах, сечениях и схемах перед размерным числом, определяющим величину уклона, наносят знак , острый угол которого должен быть направлен в сторону уклона.
Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
На планах направление уклона плоскостей указывают стрелкой, на которой, при необходимости, проставляют величину уклона (см.рис.).
Построение и обозначение уклона. Пример изображения уклона на планах.
Величину уклона (тангенс угла наклона) указывают в виде простой или десятичной дроби с точностью до третьего знака.
Уклон (в строительстве) — показатель крутизны склона (а также ската кровли).
Укло́н (в геодезии) — показатель крутизны склона; отношение превышения местности к горизонтальному проложению, на котором оно наблюдается.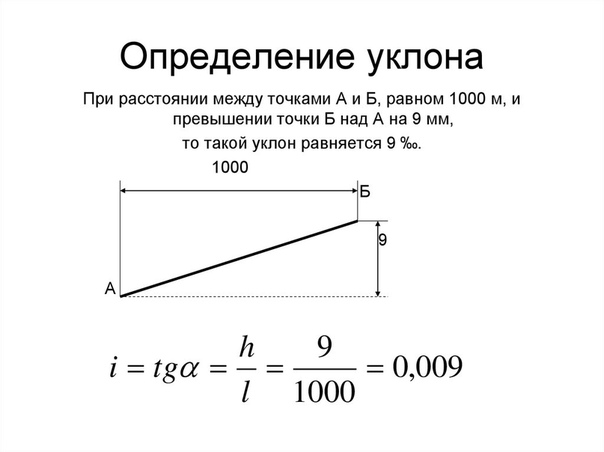
Уклон поверхности равен тангенсу угла α, tgα = h/l — отношение перпендикуляра, опущенного из точки поверхности на прямую поверхность, к длине прямой поверхности от начала склона (при вершине угла α) до перпендикуляра.
Например, подъёму 12 м на 100 м перемещения по горизонтали соответствует уклон, равный 0,12 (12 % или 120 ‰).
При чтении нотации знак «%» произносится «сотых», а «‰» — «тысячных».
Источник:
книга: Единые требования по выполнению строительных чертежей.
М.: Изд-во «Архитектура-С», 2004.
Справочное пособие.
Автор: Георгиевский О.В.
Аннотация:
Справочное пособие по строительному черчению для студентов средних и высших учебных заведений. Пособие выполнено в соответствии с требованиями ГОСТов.
Пособие может быть использовано при выполнении заданий по архитектурно-строительному черчению, а также при выполнении курсовых и дипломных проектов студентами всех строительных специальностей средних и высших учебных заведений.
Распечатать
как посчитать, методы, как перевести градусы в промилле
Существуют нормативы на уклоны при проектировании различных коммуникаций и сооружений, которыми руководствуются в своей работе архитекторы и строители. Пользоваться можно любыми размерностями, в том числе и градусами. На практике принято крутые склоны обозначать в градусах, а пологие — в процентах и промилле.
- Способы вычисления склона в процентах
- Определение угла наклона через тангенс
- Соотношение величин с уклоном крыши
Способы вычисления склона в процентах
Единицей измерения крена, в зависимости от его величины, бывают градус, процент, промилле — тысячная доля целого числа: 1‰ = 1/10% = 1/1000 от 1.
Физический смысл уклона — отношение перепада высот к длине участка, на котором это наблюдается. По сути — тангенс угла: превышение 12 метров на отрезке дороги в сто метров выражается величиной 0,12 (тангенс) = 12% = 120 ‰. То есть чтобы сделать расчёт уклона в промилле, надо умножить процентный показатель на десять.
При выполнении планировочных работ на земельном участке приходится прибегать к измерениям крутизны косогоров. Сделать это можно несколькими методами:
- С помощью нивелира выполняются все необходимые измерения, а потом несложными вычислениями формируется уклон в процентах. Как считать: перепад высот делится на расстояние между точками замеров, и результат умножается на сто процентов.
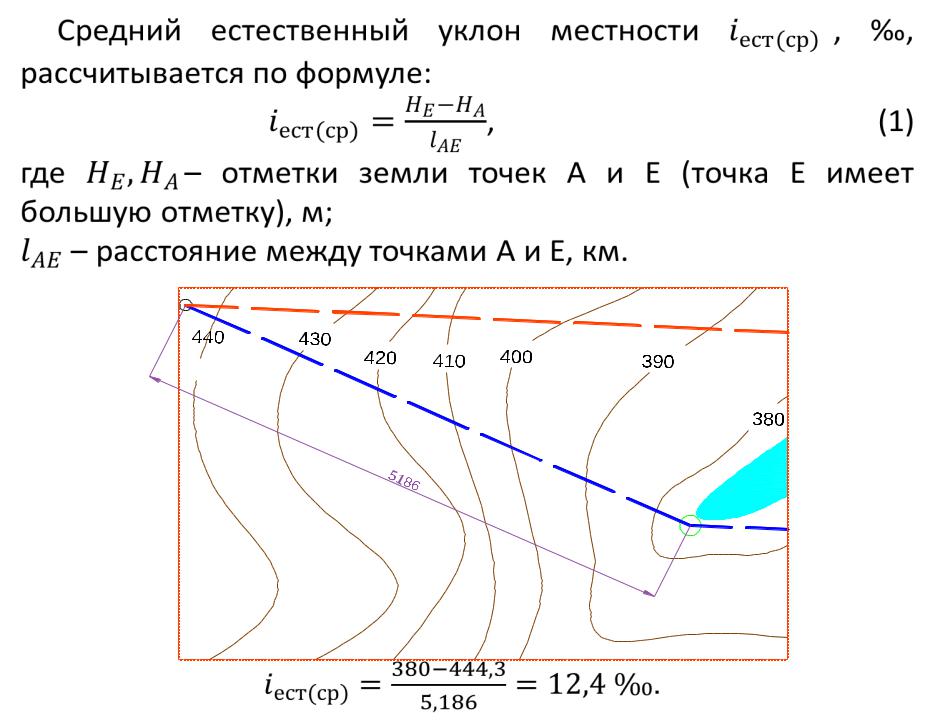
- По плану земельного участка, если на нём вынесены отметки рельефа местности. Разница высот между необходимыми точками считывается с рисунка, а расстояние замеряется масштабной линейкой. Дальнейшие вычисления аналогичны предыдущему способу.
Кровельщики часто сталкиваются с необходимостью определить фактический скат крыши, и знают, как рассчитать уклон с помощью специального инструмента, называемого уклономер. Конструкция приспособления несложная: на рейке закреплена рамка с закреплённым внутри транспортиром и маятником, имеющим груз и указатель. Основу прибора ставят на нижнюю поверхность измеряемого участка кровли, и стрелка обозначит угол.
Определение угла наклона через тангенс
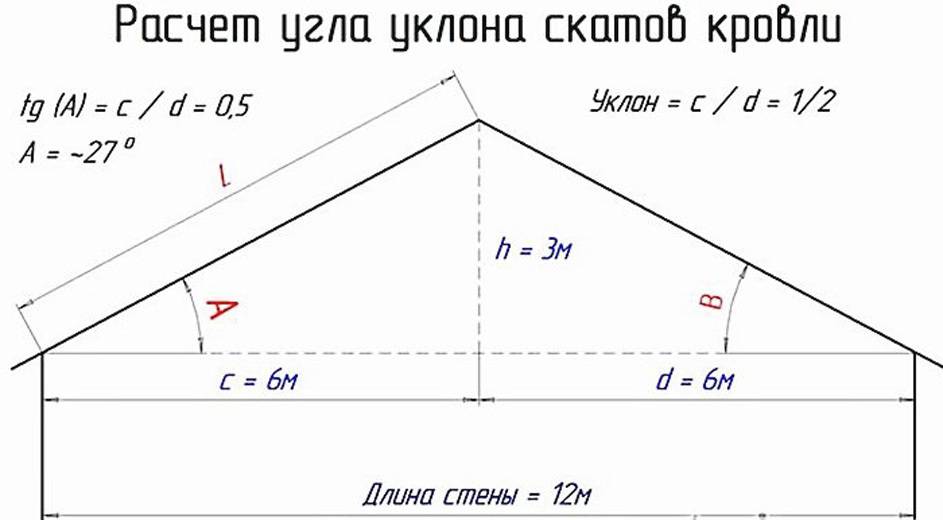
Из тригонометрии известно, что тангенс — дробь, в основании которой прилежащий к углу катет, а поверх — противолежащий (перепад высот). Чтобы определить уклон кровли в процентах и градусах через тангенс, понадобится выполнить замеры:
- высоты от потолочного перекрытия до конька кровли;
- расстояния от края ската до проекции верхней линии смыкания двух плоскостей.
Сделав несложные расчёты, получают некоторое значение и по таблице Брадиса или с помощью инженерного калькулятора находят соответствующее число градусов для искомого угла.
Как посчитать уклон в процентах — определено выше: высоту конька делят на половину ширины чердачного перекрытия, если скаты равной величины. Или на проекцию каждой из поверхностей кровли, когда размеры сторон различаются. Можно заметить, что это и есть тангенс уже определённого в градусах угла. Чтобы перейти к процентному выражению уклона, надо выполнить действие: значение tg *100, и результат получится в процентах.
Соотношение величин с уклоном крыши
Для каждого кровельного материала установлены допуски по наименьшему уклону. Другие факторы, влияющие на выбор угла скатов крыши:
- способность комплексно защищать строение от внешних воздействий — техногенных и природных;
- стойкость к ветровой нагрузке — крутые поверхности увеличивают парусность сооружения, это делает конструкцию уязвимой;
- преобладание определённых решений архитекторов в отдельных регионах;
- количество атмосферных осадков и загрязнений — на кровле с большим уклоном груз накапливаться не будет.
Строительные нормы и правила — СНиП II -26−76 регламентируют пологость скатов в процентах. Соотношение процентов и градусов для некоторых углов приведено в таблице.
| Градус º | Тангенс | Процент, % | Промилле, ‰ | Градус º | Тангенс | Процент, % | Промилле, ‰ |
| 1 | 0,0175 | 1,75 | 17,5 | 22 | 0,4040 | 40,40 | — |
| 5 | 0,0875 | 8,75 | 87,5 | 24 | 0,4452 | 44,52 | — |
| 10 | 0,1740 | 17,40 | 174 | 26 | 0,4878 | 48,78 | — |
| 0,2125 | 21,25 | — | 28 | 0,5318 | 53,18 | — | |
| 14 | 0,2494 | 24,94 | — | 30 | 0,5773 | 57,73 | — |
| 16 | 0,2868 | 28,68 | — | 35 | 0,7001 | 70,01 | — |
| 18 | 0,3250 | 32,50 | — | 40 | 0,8390 | 83,90 | — |
| 20 | 0,3828 | 38,28 | — | 45 | 1,0000 | 100,0 | — |
Математические способы расчёта уклона применяются, когда особая точность не нужна, и измерения делают приблизительные.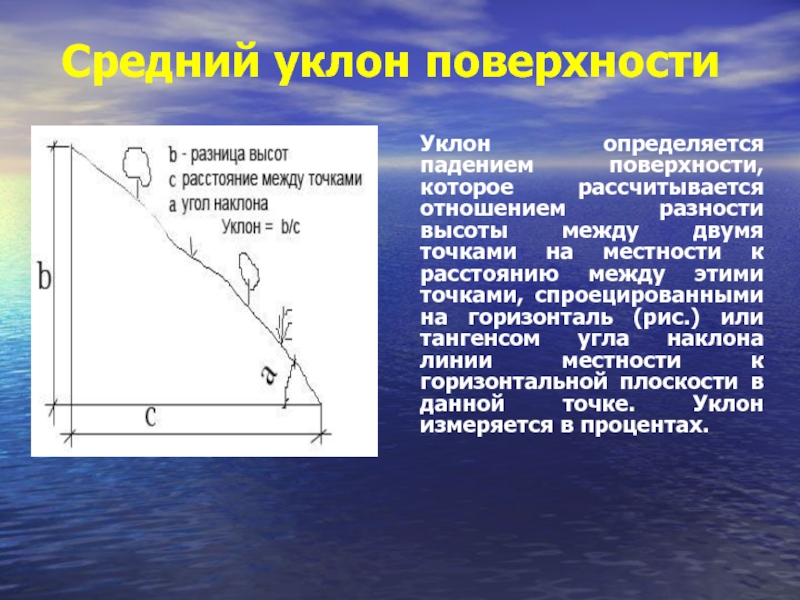
При необходимости вычислить точные показатели, пользуются современными измерительными приборами.
Пример вычисления: расстояние от края ската кровли до проекции линии сопряжения сторон — длина заложения, 5,2 м. Высота от чердачного перекрытия до верхней отметки кровли 2 метра. Уклон (тангенс угла) определяется действием: 2/5,2 = 0,3846. Ближайшее значение из таблицы — 20 градусов, что соответствует примерно 38%.
Другой вариант — с помощью угломера определили угол наклона кровли, его значение 5º. По соответствующей строке уклон поверхности составит 8,75 процента или 87,5 промилле.
Algebra 1 Help
Студенты, нуждающиеся в помощи по алгебре 1, получат большую пользу от нашей интерактивной программы.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по Алгебре 1.
Имея под рукой обязательные концепции обучения и соответствующие практические вопросы, вы мгновенно получите много помощи по Алгебре 1.
Алгебра 1
Распределительная собственность
Как использовать FOIL в дистрибутивной собственности
Как использовать метод сетки для FOIL
Уравнения / Неравенства
Системы уравнений
Уравнения/наборы решений
Как разложить уравнение на множители
Как найти решение set
Как найти решение системы уравнений
Линейные/рациональные уравнения/уравнения с переменными
Как узнать, когда уравнение не имеет решения
Как найти решение рационального уравнения с LCD
Как найти решение уравнения
Квадратные уравнения
Как разложить на множители квадратное уравнение
Как найти решение квадратного уравнения
Системы неравенств
Как найти решение неравенства со сложением
Как найти решение неравенства с делением
Как найти решение неравенства с умножением
Как найти решение неравенства с вычитанием
Функции и линии
Алгебраические функции
Как найти прямой вариант
Как найти f(x)
Как найти обратную вариацию
Как найти домен функции
Как использовать квадратичную функцию
Уравнения прямых
Формула средней точки
Как найти концы отрезка
Как найти середину отрезка
Параллельные линии
Как узнать, параллельны ли прямые
Как найти уравнение параллельной прямой
Как найти наклон параллельных прямых
Перпендикулярные линии
Как узнать, перпендикулярны ли прямые
Как найти уравнение перпендикулярной прямой
Как найти наклон перпендикулярных линий
Точки и формула расстояния
Как узнать, находится ли точка на прямой с уравнением
Как найти длину линии по формуле расстояния
Уравнения наклона и линии
Как найти наклон линии
Как найти уравнение прямой
Графика
Как построить график функции
Как построить линию
Как нарисовать точку
Как построить график квадратичной функции
Как построить график двухшагового неравенства
Как построить график функции абсолютного значения
Как построить график экспоненциальной функции
Как построить график упорядоченной пары
последовательности
Как найти последовательные целые числа
Как найти ответ на арифметическую прогрессию
Как найти общее различие в последовательностях
Как найти следующий член арифметической прогрессии
Как найти n-й член арифметической прогрессии
Линейные уравнения
Преобразование измерений
Как решать уравнения абсолютного значения
Как решить одношаговые уравнения
Как решать двухшаговые уравнения
Как писать выражения и уравнения
Проценты
Пропорции
Линейные неравенства
Неравенства абсолютного значения
Графические неравенства
Запись неравенств
Проценты
Десятичные числа и проценты
Как найти десятичный эквивалент процента
Как найти процент эквивалентный десятичной дроби
Дроби и проценты
Как найти дробь от процента
Как найти дробные проценты
Как найти процент от дроби
Денежный процент
Как найти размер прибыли
Как найти простые проценты
Как найти сумму налога с продаж
Как узнать цену продажи
Процент изменения
Как найти процент уменьшения
Как найти процент увеличения
Целое и часть
Как найти часть от целого в процентах
Как найти целое из части с процентами
Реальные числа
Подсчет/наборы
Как найти недостающее число в наборе
Как найти количество целых чисел между двумя другими целыми числами
Целочисленные операции
Как складывать целые числа
Как делить целые числа
Как умножать целые числа
Как вычитать целые числа
Количество линий и абсолютное значение
Как найти абсолютное значение
Как найти значение с числовой строкой
Как построить график неравенства с числовой прямой
Как построить дроби на числовой прямой
Статистика и вероятность
Как найти межквартильный размах
Как найти среднее
Как найти медиану
Как найти режим
Как найти диапазон
Как найти стандартное отклонение
Переменные
мономы
Как делить одночленные частные
Как умножить одночлен на многочлен
Как умножать одночленные частные
Многочлены
Биномы
Как найти решение рационального уравнения с биномиальным знаменателем
Как найти решение биномиальной задачи
Как найти значение коэффициента
Как умножать биномы с распределительным свойством
Как упростить биномы
Факторные полиномы
Как разложить многочлен на множители
Как факторизовать переменную
Полиномиальные операции
Как складывать многочлены
Как делить многочлены
Как найти степень многочлена
Как умножать многочлены
Как вычитать многочлены
Трехчлены
Как складывать трехчлены
Как делить трехчлены
Как разложить трехчлен на множители
Как умножать трехчлены
Как вычитать трехчлены
Алгебра I часто впервые знакомит учащихся с процессами вычисления переменных, понимания неравенств и использования порядка операций для упрощения выражений.
Некоторым учащимся часто бывает трудно освоить эти новые навыки; однако усердная практика основных алгебраических принципов жизненно важна для успеха в дальнейших курсах математики. Понимание геометрии, предварительного исчисления, исчисления и высшей математики, физики и химии требует фундаментального понимания того, как упростить выражения и манипулировать переменными. Нужны ли вам лучшие репетиторы по алгебре 1 в Бостоне, репетиторы по алгебре 1 в Детройте или лучшие репетиторы по алгебре 1 в Далласе, Форт-Уэрт, работа с профессионалом может вывести ваше обучение на новый уровень.
В общем, Алгебра I фокусируется на основах понимания и упрощения задач. Учащиеся работают над тем, чтобы логически продумать этапы решения проблемы, не делая немедленных выводов или решений. Кроме того, учащихся учат объяснять отношения между уравнениями, давать словесные описания графиков, таблиц и диаграмм и предсказывать форму фигур на основе математических соотношений. Репетиторы Varsity Tutors предлагают такие ресурсы, как бесплатные практические тесты по алгебре 1, которые помогут вам в самостоятельном обучении.
Общие темы по алгебре I включают:
Арифметика с полиномиальными и рациональными выражениями: учащимся предлагается упростить числовые выражения с помощью порядка операций, разложить переменные в числовые уравнения и упростить сложные выражения с помощью различных комбинаций чисел и переменных.
Создание выражений: используя графики и таблицы в качестве руководства, учащимся предлагается определить взаимосвязь между двумя или более переменными. Например, учащимся может быть предоставлена таблица пройденного расстояния и времени, необходимого для преодоления этого расстояния. Ожидается, что учащиеся определят, как пройденное расстояние влияет на затраченное время (удвоение пройденного расстояния требует удвоения времени при той же скорости).
Рассуждения с помощью уравнений и неравенств: учащиеся, изучающие алгебру I, должны найти значение переменных, упрощая числовые выражения.
Кроме того, студентов учат, как графически отображать эти решения в системах координатной плоскости. Также рассматриваются неравенства и определение того, как будет затеняться график системы координат на основе численного решения.Видение структуры в выражении: используя в качестве основы рассуждения с помощью уравнений и неравенств, учащихся учат писать алгебраические выражения и неравенства на основе графиков, а иногда и таблиц данных.
Кроме того, студентов учат, как графически отображать эти решения в системах координатной плоскости. Также рассматриваются неравенства и определение того, как будет затеняться график системы координат на основе численного решения. Ключом к успеху в алгебре I является постоянная практика. В то время как некоторые учащиеся будут иметь опыт упрощения выражений, добавление графиков, диаграмм, неравенств и факторизации будет новым для других. Общие стратегии достижения успеха включают просмотр кратких резюме в учебниках перед выполнением домашних заданий и отработку дополнительных 10–15 заданий после выполнения назначенных отрывков домашнего задания. Часто учащиеся изучают шаблоны, необходимые для решения задач, путем постоянного повторения вместо того, чтобы читать разделы книги.
Наличие другого метода материального подкрепления в дополнение к обучению в классе и домашнему заданию обычно полезно для большинства учащихся. В дополнение к справочному разделу по алгебре 1 и урокам по алгебре 1 вы также можете рассмотреть некоторые из наших карточек по алгебре 1.
Если вы хотите укрепить свои знания по алгебре I, решая практические задачи, ознакомьтесь с бесплатными ресурсами по алгебре I от Varsity Tutors. Каждая практическая задача сопровождается подробным пошаговым ответом, поэтому, если вы пропустите какой-либо из них, вы сможете точно определить, где в своих расчетах или рассуждениях вы ошиблись, и избежать повторения этой ошибки позже. Практические задачи также организованы по понятиям, поэтому, если у вас возникают трудности с графическим отображением линейных функций или порядком операций, вы можете отвечать на вопросы только по этим темам, не перебирая материал, который будет полезен для ваших конкретных учебных потребностей. Бесплатные практические задачи по алгебре I от Varsity Tutors помогут вам получить дополнительную практику, которая вам нужна при сдаче или повторении алгебры I!
Как использовать формулу наклона и найти наклон линии, независимо от того, является ли наклон положительным, отрицательным или неопределенным.
Рабочий лист по наклону линии
Апплет наклона (html5)
Калькулятор формулы уклона (бесплатный онлайн-инструмент вычисляет уклон с учетом 2 баллов)
Наклон линии характеризует направление линии. Чтобы найти наклон, вы делите разницу координат y двух точек на прямой на разницу координат x тех же двух точек.
Разные слова, та же формула
Учителя используют разные слова для координат y и координат x.
- Некоторые называют координаты у подъемом, а координатами х — бег.
- Другие предпочитают использовать нотацию $$\Delta$$ и называть y-координаты $$\Delta y$$ , а x-координаты $$\Delta x$$ .
Все эти слова означают одно и то же , то есть значения y находятся вверху формулы (числитель), а значения x внизу формулы (знаменатель)!
Пример 1
Наклон прямой , проходящей через точки (1, 2) и точки (4, 3), равен $$ \frac{1}{3}$$.
Помните: разница в значениях y идет в числителе формулы, а разница в значениях x идет в знаменателе формулы.
Может ли любая точка быть $$( x_1 , y_1 ) $$ ?
Есть только один способ узнать!
Во-первых, мы будем использовать точку (1, 2) как $$x_1, y_1$$, и, как вы можете видеть: наклон: $ \boxed {\frac{1}{3} }$ .
Теперь давайте используем точку (4, 3) как $$x_1, y_1$$, и, как вы можете видеть, наклон упрощается до того же значения: $ \boxed {\frac{1}{3} }$ .
Работа рядом
точка (4, 3) как $$ (x_1, y_1 )$$
Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{3-2}{4-1} = \frac{1}{3} $$
точек (1, 2) как $$ (x_1, y_1 )$$
Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{2-3}{1-4} = \frac{-1}{- 3} = \frac{1}{3} $$
Ответ: , а не не имеет значения, какую точку поставить первой.
Вы можете начать с (4, 3) или с (1, 2), и в любом случае вы закончите точно таким же числом!
$$ \фракция{1}{3} $$
Пример 2 наклона линии А
Наклон линии , проходящей через точки (3, 4) и (5, 1), равен $$- \frac{3}{2}$$, потому что каждый раз, когда линия опускается на 3 (изменение y или подъем) линия смещается вправо (разбег) на 2.
Эта страница:
- Формула
- Пример
- Видео
- Заказать?
- Любые две точки определяют наклон линии?
- Наклон вертикальной линии
- Наклон горизонтальной линии
- Практические задачи
youtube.com/embed/JYZU1B5zOjg?hl=en&fs=1″ frameborder=»0″ allowfullscreen=»»> Наклон вертикальных и горизонтальных линий
Наклон вертикальной линии не определен
Это связано с тем, что любая вертикальная линия имеет $$\Delta x$$ или «пробег» нуля. Всякий раз, когда ноль является знаменателем дроби в этом случае дроби, представляющей наклон линии, дробь не определена. На рисунке ниже показана вертикальная линия (x = 1).
Наклон горизонтальной линии равен нулю
Это потому, что любая горизонтальная линия имеет $$\Delta y$$ или «подъем» нуля. Следовательно, независимо от того, каков пробег (при условии, что он не равен нулю!), дробь, представляющая уклон, имеет в числителе ноль.
Следовательно, наклон должен оцениваться как нулевой. Ниже приведено изображение горизонтальной линии — вы можете видеть, что у нее нет «подъема».
Любые две точки на прямой имеют одинаковый наклон?
Ответ: Да, и это фундаментальный момент, который следует помнить при расчете уклона.
Каждая линия имеет постоянный наклон. Другими словами, наклон линии никогда не меняется. Эта фундаментальная идея означает, что вы можете выбрать любых 2 точек на линии.
Подумайте об идее прямой линии. Если бы наклон линии изменился, то это была бы зигзагообразная линия, а не прямая линия, как вы можете видеть на рисунке выше.
Как вы можете видеть ниже, наклон одинаков независимо от того, какие 2 точки вы выбрали.
Наклон линии
Никогда не меняетсяЭта страница:
- Формула
- Пример
- Видео
- Заказать?
- Любые две точки определяют наклон линии?
- Наклон вертикальной линии
- Наклон горизонтальной линии
- Практические задачи
Рабочий лист по наклону линии
Апплет наклона (html5)
Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)
Практика ПроблемыПроблема 1
Каков наклон прямой, проходящей через точки (10,3) и (7, 9)?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ (10,3)}$$ как $$x_1, y_1$$
$ \frac{9- \red 3}{7- \red{10}} \\ = \frac{6}{-3} \\ = \ в коробке {-2 } $
Используя $$ \red{ (7,9)} $$ как $$x_1, y_1$$
$ \frac{3- \red 9{10- \красное 7} \\ =\ гидроразрыв{-6}{3} \\ = \в коробке{-2} $
Проблема 2
Прямая проходит через (4, -2) и (4, 3).
Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 4,3 )}$$ как $$x_1, y_1$$
$ = \frac{-2 — \red 3}{4- \red 4} «=» \frac{-5}{\color{red}{0}} \\ = \text{неопределенный} $
Используя $$ \red{ ( 4, -2 )}$$ как $$x_1, y_1$$
$ = \frac{3- \red{-2}}{4- \red 4} «=» \frac{5}{\color{red}{0}} \\ = \текст{неопределенный} $
Всякий раз, когда длина линии равна нулю, наклон не определен. Это потому, что в знаменателе наклона стоит ноль! Любой наклон любой вертикальной линии не определен.
Проблема 3
Прямая проходит через (2, 10) и (8, 7).
Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 8, 7 )}$$ как $$x_1, y_1$$
$ \frac{10 — \red 7}{2 — \red 8} \\ = \ гидроразрыва {3}{-6} \\ = -\фракция{1}{2} $
Используя $$ \red{ ( 2,10 )}$$ как $$x_1, y_1$$
$ \frac{7 — \red {10}}{8- \red 2} \\ = \ гидроразрыв {-3} {6} \\ = -\фракция{1}{2} $
Проблема 4
Прямая проходит через (7, 3) и (8, 5). Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ (7,3 )}$$ как $$x_1, y_1$$
$$ \frac{ 5- \red 3}{8- \red 7} \\ = \ гидроразрыва {2} {1} \\ = 2 $$
Используя $$ \red{ ( 8,5 )}$$ как $$x_1, y_1$$
$$ \frac{ 3- \red 5}{7- \red 8} \\= \фракция{-2}{-1} \\ = 2 $$
Проблема 5
Прямая проходит через (12, 11) и (9, 5) .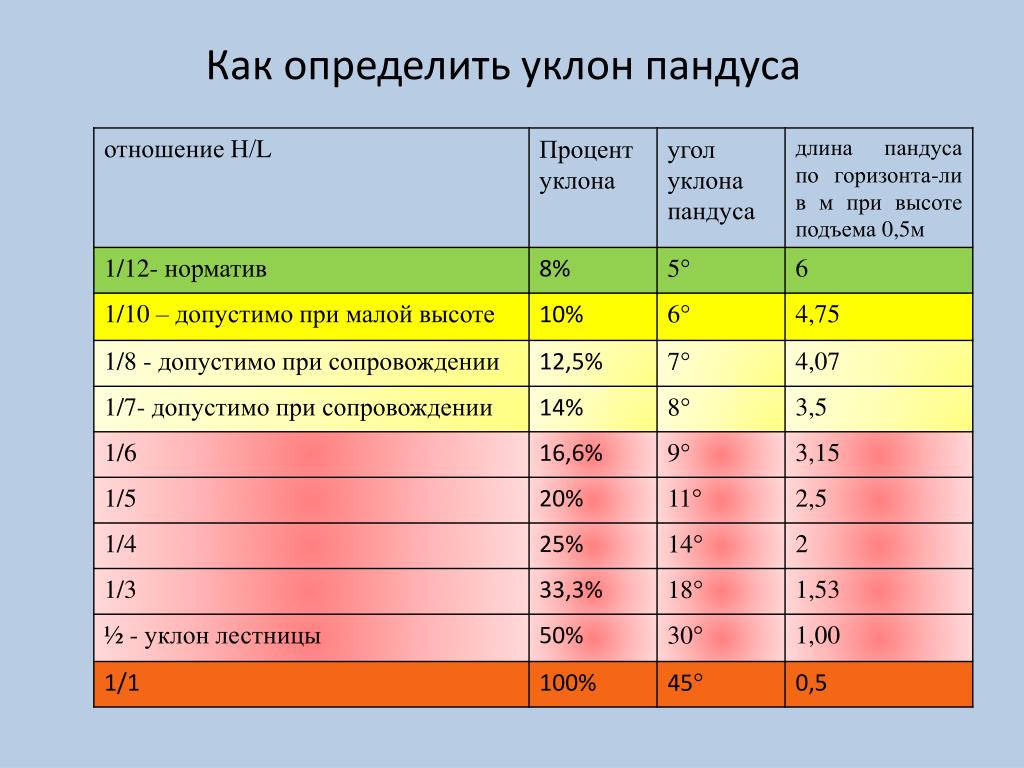
Каков его наклон?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 5, 9)}$$ как $$x_1, y_1$$
$$ \frac{ 11 — \red 5}{12- \red 9} \\ = \ гидроразрыва {6} {3} \\ =2 $$
Используя $$ \red{ (12, 11 )}$$ как $$x_1, y_1$$
$$ \frac{ 5- \red{ 11} }{9- \red { 12}} \\ = \фракция{-6}{-3} \\ = 2$$
Проблема 6
Каков наклон линии, проходящей через (4, 2) и (4, 5)?
$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $
Используя $$ \red{ ( 4,5 )}$$ как $$x_1, y_1$$
$$ \frac{ 2 — \red 5}{4- \red 4} \\ = \frac{-3}{\color{red}{0}} \\ = не определено $$
Используя $$ \red{ ( 4,2 )}$$ как $$x_1, y_1$$
$$ \frac{ 5 — \red 2}{4- \red 4} \\ = \frac{ 3}{\color{red}{0}} \\ = не определено $$
ПРЕДУПРЕЖДЕНИЕ! Уловите ошибку в следующей задаче: Дженнифер пыталась найти наклон, проходящий через точки $$(\color{blue}{1},\color{red}{3})$$ и $$ (\color {синий}{2}, \цвет{красный}{6})$$ .
У нее были небольшие проблемы с применением формулы наклона, она пыталась вычислить наклон 3 раза и дала 3 разных ответа. Сможете ли вы определить правильный ответ?
Задача-вызов
Найдите наклон прямой через две точки.
Попытка №1
$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} «=» \ гидроразрыв {6-3} {1-2} \\= \фракция{3}{-1} =\в коробке{-3} $
Попытка #2
$$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} «=» \фракция{6-3}{2-1} \\= \фракция{3}{1} \\ = \в коробке{3} $$
Попытка №3
$$ уклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} \\ =\ гидроразрыва {2-1} {6-3} \\ =\в коробке{ \frac{1}{3}} $$
Правильный ответ — попытка №2.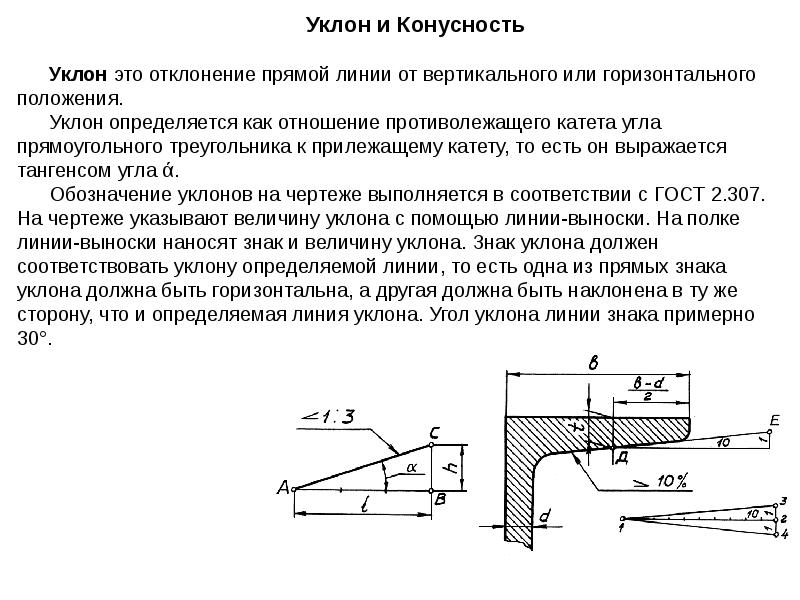
В попытке №1 она не всегда использовала очки. В первой попытке она сделала следующее:
$$ \frac{\color{red}{y{\boxed{_2}}-y_{1}}}{\color{blue}{x\boxed{_{1}}-x_{2}}} $$
Проблема с попыткой №3 заключалась в обратном подъеме и беге. Она поместила значения x в числитель (сверху), а значения y в знаменатель, что, конечно же, противоположно!
$$ \ отмена {\ frac {\ color {синий} {x_ {2} -x_ {1}}} {\ color {red} {y_ {2} -y_ {1}}}} $$
Тренировка склонов Генератор проблем Вы можете сколько угодно практиковаться в решении подобных задач с помощью приведенного ниже генератора задач на уклон.