Построение эпюры изгибающих моментов

Рассмотрим порядок построения эпюры изгибающих моментов M_x для консольной балки с жесткой заделкой.

Ранее для данной балки уже были рассмотрены примеры определения опорных реакций и построения эпюры поперечных сил Q_y.

Покажем найденные опорные реакции и выбранную систему координат.

Для построения эпюры изгибающих моментов M_x запишем их выражение по каждому силовому участку и рассчитаем их значения на границах участков. При этом воспользуемся методом сечений.

Нумерацию силовых участков балки, сечения и другие вспомогательные обозначения примем из расчета эпюры Q_y.

Рассмотрим I силовой участок:

Выбрав левую часть балки, отбросим ненадолго правую, и запишем имеющиеся данные.

I с.у. (AB) 0 ≤ z₁≤ 0,5м

Внутренний изгибающий момент в указанном сечении равен сумме всех внешних моментов, воздействующих на рассматриваемую часть балки.

Здесь на момент в рассматриваемом сечении влияют только опорные реакции M и R, то есть сумма моментов состоит из двух слагаемых.

По правилу знаков момент, который стремится сжать верхние слои балки, принимается положительным, следовательно:

M_xI=Σm_i=M+R∙z₁=30+60z₁

В выражении переменная z₁ в первой степени, поэтому эпюра M_x на первом участке будет иметь вид прямой линии.

Рассчитаем значения M_xI на границах участка, т.е. при z₁=0 и при z₁=0,5м

M_xI (z₁=0)=30кНм
M_xI (z₁=0,5м)=60кНм

Переходим на второй силовой участок:

Рассекаем балку в произвольном месте участка и рассматриваем её правую часть.

Эта часть балки изгибается силой F и распределенной нагрузкой q.

II с.у. (BC) 0 ≤ z₂ ≤ 1м
M_xII=Σm_i=-q∙z₂(z₂/2)+F∙z₂= -50∙z₂²+40∙z₂

Получено выражение с переменной z₂ во второй степени, значит, эпюра M_x на втором участке будет иметь вид параболы.

Для построения параболы требуется как минимум три точки. Этими точками будут значения M_x на границах и в середине II силового участка, то есть при z₂=0, z₂=1м и z₂=0,5м.

M_xII(z₂=0)=0
M_xII(z₂=0,5м)=7,5кНм
M_xII(z₂=1м)= -10кНм

По полученным данным строим эпюру изгибающих моментов M_x (готовую эпюру Q_y перенесем из ранее рассмотренной задачи)

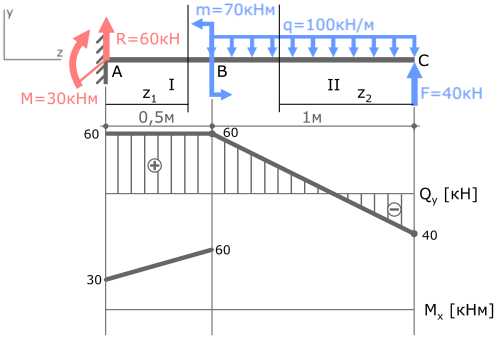
I с.у. (AB) 0 ≤ z₁ ≤ 0,5м.
M_xI=30+60z₁ (прямая)
M_xI(z₁=0)=30кНм
M_xI(z₁=0,5м)=60кНм

II с.у. (BC) 0 ≤ z₂ ≤ 1м
M_xII= -50z₂²+40z₂ (парабола)
M_xII(z₂=0)=0
M_xII(z₂=0,5м)=7,5кНм
M_xII(z₂=1м)= -10кНм

Прежде чем соединять отмеченные точки эпюры параболой, обратите внимание на эпюру поперечных сил Q_y.

Q_y — первая производная от M_x. Поэтому в том месте, где Q_y пересекает базовую линию (т.е. Q_y=0) на эпюре M_x будет экстремум.

Рассчитаем значение экстремума эпюры M_x на II участке балки.

Для этого:

1. Выражение Q_yII приравняем к нулю
   Q_yII=100z₂-40=0
2. Выразим из него z₂
   z₂=40/100=0,4м
3. Подставим z₂ в выражение для M_{xII
   MxIIэкстр(z2=0,4м)= -50∙0,4²+40∙0,4=8кНм}

Отметив эту точку в области эпюры где Q_y=0 соединим ее с тремя другими параболой.

Эпюра изгибающих моментов построена. Проверка эпюры M_x.

Расчеты на прочность >
Другие примеры решения задач >

isopromat.ru

Построение эпюр Q и M для двухопорной балки

Задача

Для заданной двухопорной балки, нагруженной силой F, моментом M и равномерно распределенной нагрузкой q построить эпюры внутренних поперечных сил Q

y и изгибающих моментов M_x.

Решение задачи

Опорные реакции для данной расчетной схемы были определены здесь.

Балка имеет 3 силовых участка. Обозначим их римскими цифрами, например, справа налево.

Для расчета внутренних силовых факторов по участкам балки воспользуемся методом сечений.

Расчет значений

Начнем с первого силового участка (CD).

Проведем поперечное сечение в пределах участка, в любом месте между точками C и D.

Данное сечение делит балку на две части (левую и правую). Для определения внутренних факторов можно выбрать любую из них, но лучше выбирать менее нагруженную часть балки. Очевидно это будет ее правая часть.

Расстояние от правой границы участка до рассматриваемого сечения обозначим переменной z₁, которая может принимать значения от 0 до 1,5 метров (т.е. 0 ≤ z₁ ≤ 1,5м).

Мысленно отбросим на время всю левую часть балки.

Поперечная сила Q в данном сечении первого участка будет равна сумме всех внешних сил приложенных к рассматриваемой части балки с учетом их знака, т.е.

Здесь сила F записана положительной, т.к. стремится повернуть правую часть балки по ходу часовой стрелки относительно рассматриваемого сечения.

В данном выражении отсутствует переменная z₁, что говорит о том, что внутренняя поперечная сила будет одинакова для всех сечений этого участка.

Изгибающий момент M в рассматриваемом сечении определяется как сумма изгибающих моментов от всех внешних нагрузок выбранной части балки.

С учетом правила знаков при изгибе получаем

Здесь сила F по правилу знаков записана отрицательной, т.к. стремиться сжать нижний слой балки.

В полученном выражении переменная z₁ является плечом момента силы F для данного сечения балки.

Как видно из полученного выражения изгибающий момент по длине участка меняется линейно (т.к. z₁ в первой степени), поэтому для построения эпюры на данном участке нам достаточно двух точек.

Этими точками будут значения изгибающего момента на границах I участка, т.е. при z₁=0 и при z₁=1,5м

На первом участке внутренние усилия определены.

Переходим на второй силовой участок (BC).

Так же начинаем с того, что проводим сечение в любом месте участка и выбираем рассматриваемую часть балки. Здесь также удобнее рассмотреть правую часть балки.

Расстояние до рассматриваемого сечения от правой границы участка обозначим переменной z₂. При этом 0 ≤ z

2 ≤ 1м.

Запишем выражения и рассчитаем граничные значения внутренней поперечной силы Q

И изгибающего момента M

Здесь опорная реакция R_C положительна, потому что сжимает верхний слой, а сила F и распределенная нагрузка q отрицательны, т.к. сжимают нижний слой балки.
Как записывается момент распределенной нагрузки показано здесь.

В выражении для M_xII переменная во второй степени, поэтому эпюра моментов на втором участке будет иметь вид параболы.

Как известно, для построения параболы необходимо знать положение минимум трех ее точек. Но как будет показано дальше, в некоторых случаях при построении эпюр, параболы можно вычерчивать всего лишь по двум точкам. Рассчитаем их значения:

Осталось найти внутренние усилия на III силовом участке (AB).

Рассекаем балку между точками A и B. Выбираем менее нагруженную левую часть. 0 ≤ z₃ ≤ 2м – интервал возможных положений сечения относительно левой границы участка.

Записываем выражения для Q и M и вычисляем значения в крайних точках

Здесь видно что выражение для Q_yIII — линейное, а на эпюре M_x на данном участке будет парабола.

По полученным данным строим эпюры.

Построение эпюр

Для построения эпюр рассчитанные значения откладываем от базовой линии на соответствующих участках.

Начинаем с эпюры поперечных сил Q.

На первом участке выражение для Q не зависело от z₁ поэтому его значение будет постоянным (Q_yI=const) по длине участка, т.е. линия эпюры будет параллельна базовой.

На втором участке были получены два значения Q: -58,3 кН при z₂=0 и -18,3кН при z₂=1м. Переменная z₂ откладывалась от правой границы участка, поэтому z₂=0 в точке C, соответственно в т. B переменная z

2=1м.

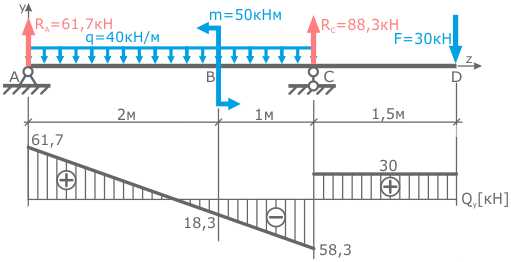
Аналогично откладываются значения Q на третьем участке и значения M на эпюре изгибающих моментов.

Точки на II и III участках эпюры Q и на I участке эпюры M соединяются отрезками, так как распределение внутренних сил и моментов там линейное (переменная z в первой степени).

А при соединении точек эпюры M параболами, надо смотреть на эпюру Q.

Дело в том, что эпюра поперечных сил это первая производная эпюры изгибающих моментов. Поэтому в сечениях балки, где Q=0 на эпюре M будет экстремум.

Как видно эпюра Q пересекает нулевую линию только на третьем силовом участке балки. Поэтому, ввиду того что нас интересуют только пиковые значения изгибающих моментов, на втором участке две крайние точки достаточно соединить параболой, не имеющей экстремума, выпуклость которой направлена навстречу распределенной нагрузке.

Для более точного построения линии параболы на данном участке можно найти значения момента для промежуточных положений сечения, например при z₂=0,5м.

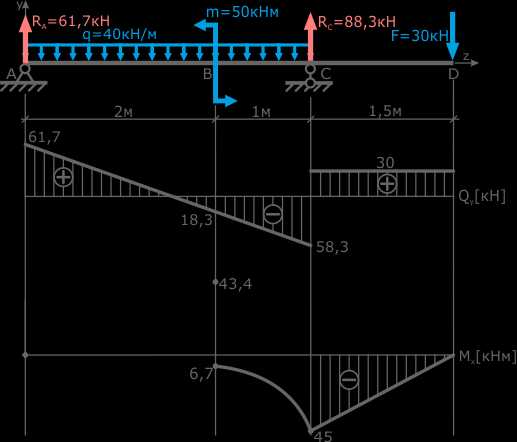
На третьем участке, в сечении, где Q пересекает базовую линию необходимо рассчитать точку экстремума.

Для этого выражение для Q_yIII приравнивается к нулю и рассчитывается значение z₃, при котором изгибающий момент на участке принимает экстремальное значение. Его подставляют в выражение для M_xIII

Это значение откладывается на эпюре M под точкой пересечения эпюры Q с базовой линией

после чего три точки соединяются плавной линией.

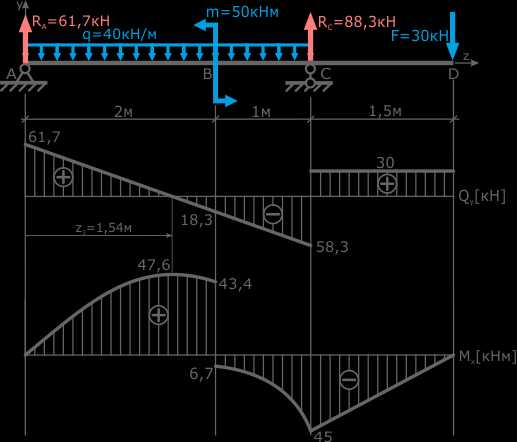
Эпюры внутренних поперечных сил и изгибающих моментов построены.

Проверка эпюр поперечных сил >
и изгибающих моментов >
Расчеты для подбора сечений балки >
Другие примеры решения задач >

isopromat.ru

Эпюры поперечных сил и изгибающих моментов

Эпюрами поперечных сил и изгибающих моментов называют графические изображения функций Q и M по длине балки при изгибе.

Посмотреть подробные примеры построения эпюр >>

Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.

Рассмотрим некоторые примеры на построение эпюр в балках:

Эпюры при чистом изгибе

Для консольной балки:

Рис. 1

имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.

Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
I силовой участок (BC): 0 ≥ z₁ ≥ 2a (рис. 2 а,г)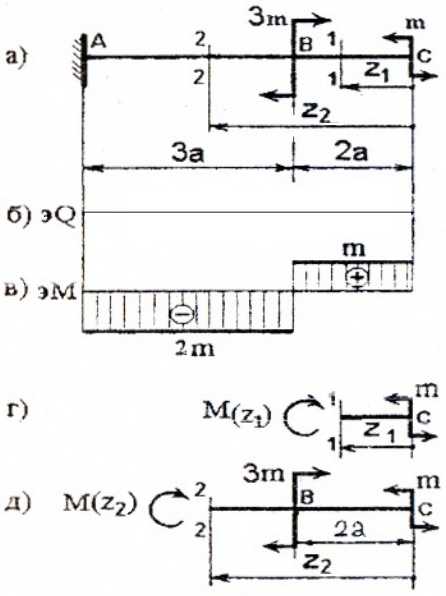

Рис. 2

т.е. Q(z₁)=0 на всем участке, а M(z₁)=m=const.
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.

II силовой участок (AB): 2a ≥ z₂ ≥ 5a (рис. 2 а,д)

Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).

Более нагруженным оказался участок AB, он и является опасным: M_max=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.

Эпюры при поперечном изгибе

Построение эпюр Q и M для балки, изображенной на рис. 3

Рис. 3

проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.

I силовой участок (AB): 0 ≥ z₁ ≥ l₁ (рис. 4, а, г)
Q(z₁)= F=const, на всем участке постоянная величина,
M(z₁)=F×z₁, уравнение прямой, график строим по двум граничным точкам:
M(z₁=0)=F×0=0 – в сечении A;
M(z₁=l₁)=F× l₁ — в сечении B.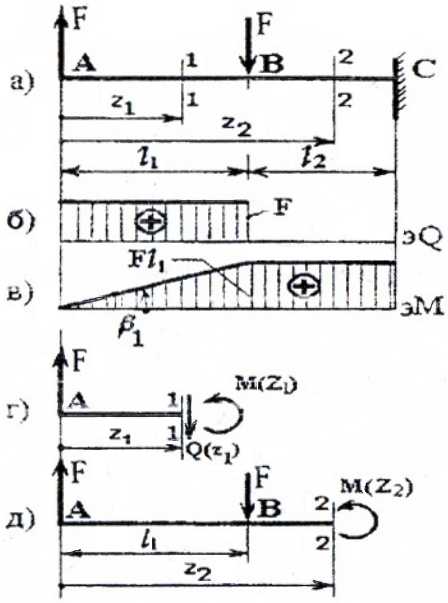

Рис. 4

II силовой участок (BC): l₁ ≥ z₂ ≥ (l₁+ l₂) (рис. 4, а, д)
Q(z₂)= F-F=0;
M(z₂)=F×z₂— F×(z₂— l₁)=F ×l₁=const.
Построив эпюры Q и M по всей длине балки (рис. 4 а, б, в), видим, что на первом участке — деформация прямого поперечного изгиба, т.к. Q≠0, M≠0; а на втором – прямого чистого изгиба.

Опасным является сечение B, в котором действуют Q_max=F, M_max=Fl₁.

Геометрическая проверка эпюр

Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем:
Для всех силовых участков находим:

где α, β – углы наклона касательных к эпюрам Q и M относительно оси абсцисс (базовой линии).
На участке “AB” α₁=0 (линия эпюры Q горизонтальна), следовательно,

распределенная нагрузка отсутствует;

функция M (z₁) – возрастающая.

На участке “BC”:

Так как все дифференциальные проверки выполняются, эпюры построены верно.

Эпюры для двухопорных балок

Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),

Рис. 5

необходимо вначале найти опорные реакции и только потом строить эпюры.

Определим реакции в обеих опорах, для этого используем два независимых уравнения статики, т.к. у нас плоская система параллельных сил.

Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑M_A=0 и ∑M_B=0.

Записываем уравнения и находим значения реакций:

Чтобы убедиться в правильности полученных значений необходимо провести «арифметическую проверку» тождества по оставшемуся из зависимых уравнений: ∑F_Y=0 или ∑M_С=0.

Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).

Для построения эпюр рассмотрим два силовых участка:

Рис. 6

I участок (AC): 0 ≥ z₁ ≥2a (рис. 6, а, г)
Q(z₁)=R_A-qz₁ — прямая, которую строим по двум граничным точкам:

M(z₁)=R_Az₁-qz₁(z₁/2)= R_Az₁-qz₁²/2 – парабола.

Строим эту кривую по трем точкам: по двум граничным (0 и 2a) и z*, которая соответствует M_max(z*), и дифференциальной зависимости: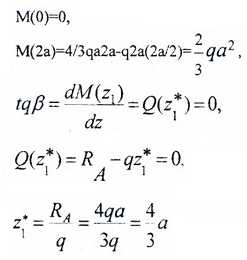

Определяем экстремум эпюры M на участке:

II участок (BC): 0 ≥ z₂ ≥ a (рис. 6, а, д)
Q(z₂)= -R_B= -2/3qa;
M(z₂)=R_Bz₂,
M(z₂=0)=0,
M(z₂=a)=2/3qa².
Выполним проверку дифференциальных зависимостей.
I силовой участок: 0 ≥ z₁ ≥ 2a

— направлена вниз, функция Q(z₁) – убывающая.

— проверка визуально: чем больше угол наклона β₁, тем больше значение Q(z₁).

II силовой участок: 0 ≥ z₂ ≥ a.

следовательно, q=0.

функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z₁*=4/3a

По силе в сечении «A»

После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.

Подробные примеры построения эпюр >
Лекции по сопромату >
Примеры решения задач >

isopromat.ru

Контроль правильности построения эпюр q и м

Контроль правильности построения эпюр Q и M

1. Если поперечная сила положительная Q>0, то эпюра M имеет вниз сходящую линию (см. пример 1)

2. Если Q – отрицательная (Q<0), то эпюра М на этом участке имеет восходящую линию.

3. Если Q меняет знак с «+» на «-», то эпюра М меняет также направление (М имеет М_max в этой точке)

4. Если Q меняет знак с «-» на «+», то M имеет значение M_min ( см. пример 2).

5. Под сосредоточенными силами на эпюре Q имеем скачок равный величине силы, а на эпюре М – перелом.

6. Под моментом на эпюре М имеем скачок на величину момента.

7. На участках нагруженных равномерно распределенной нагрузкой на эпюре Q имеем прямую наклонную линию, а на эпюре М – параболическую кривую ( см. пример 2) выгнутую в сторону действия нагрузки q.

8. На участках нагруженных неравномерно распределенной нагрузкой эпюры Q и М очерчены кривыми линиями.

Эпюры внутренних усилий для стержней ломаного и искривленного очертаний

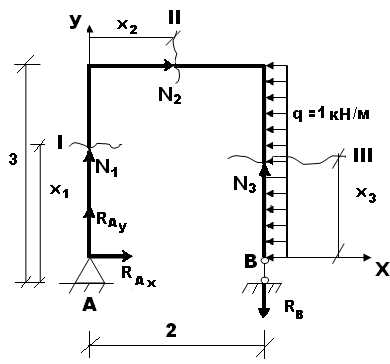
Пример №1: Построить эпюрыQ,N,Mдля плоской рамы.

Находим опорные реакции

2. Построение эпюр Q,N,M.

В ломанных стержнях кроме Qи М возникают продольные силыN. Изгибающие моменты будем откладывать в сторону растянутых волокон (без указания знака)

Участок I:

Участок II:

Участок III:

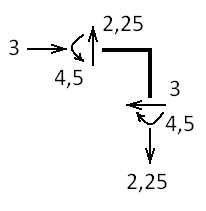
Проверка узла №1:

1. Прикладываем к узлу усилия, показанные на эпюрах.

2. Внешние моменты тоже прикладываем к узлу(если имеются).

3. Составляем уравнения равновесия узла. Если уравнения равны нулю, то узлы находятся в равновесии.

Проверка узла №2:

∑Х=3-3=0 ∑У=2,25-2,25=0 ∑М=4,5-4,5=0

Пример №2. Построить эпюрыQ,N,Mдля арки.

Определение нормальных напряжений при изгибе балки. Формула Новье.

Рассмотрим участок балки, работающей на чистый изгиб.

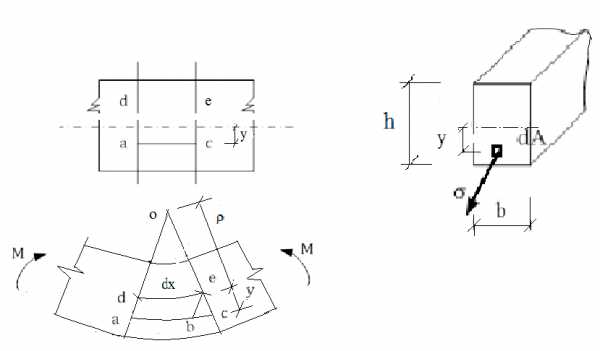
dx – начальная длина волокна, bc – удлиннение. волокна (а с)

– радиус кривизны,1/ρ – кривизна балки

– относительное удлинение

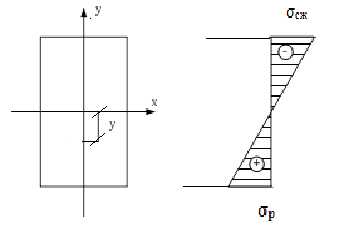
	— Формула Новье. По ней определяются нормальные напряжения в сечении балки. y – расстояние от нейтрального волокна до точки, где определяется напряжение. I – момент инерции, относительно нейтральной оси.
		при y = 0; σ= 0 при y = max; σ = max

Понятие о моменте сопротивления.

Момент сопротивления.

где y_max – расстояние от нейтральной оси до наиболее удаленного волокна.

Моменты сопротивления некоторых простых фигур:

1. Прямоугольное сечение.

2. Круглое сечение.

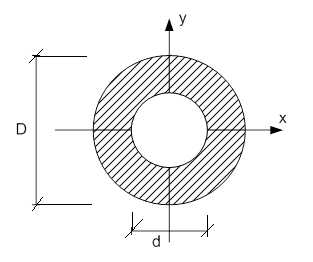
3. Кольцевое сечение.

studfiles.net

1.2.5. Построение эпюры суммарных изгибающих моментов

Поскольку вал имеет круглое поперечное сечение, определим в сечениях величину суммарного изгибающего момента . В сечениях А, В, С иD их значения будут соответственно равны

По полученным данным построим эпюру суммарных изгибающих моментов ЭМ_И.

1.3. Расчёт диаметра вала

Для определения опасного сечения находим величины эквивалентных моментов по третьей теории прочности . Тогда в сечениях А, В, С иD вала:

Анализ результатов показывает, что опасным является сечение С, в котором эквивалентный момент достигает максимального значения и равен М_ЭКВмах = 517,7Н·м.

Найдём допускаемое напряжение Так как сталь 12XH3A пластична, то за σ_пред принимаем σ_Т. Согласно [3, стр. 648 ] σ_Т = [390-420]МПа, коэффициент запаса для пластичных материалов n = 1,5÷2.

Примем n = 2, σ_Т = 400 МПа ,

тогда .

Из условия прочности

, где

–осевой момент сопротивления круглого поперечного сечения диаметром d, определим расчётный диаметр вала

В соответствии с ГОСТ округляем d_РАСЧ до ближайшего большего значения и принимаем d = 30 мм. Вычислим геометрические характеристики этого сечения:

• площадь поперечного сечения

• осевой момент инерции

• осевой момент сопротивления

• полярный момент инерции

• полярный момент сопротивления

Рассмотрим опасное сечение вала С, в котором действует суммарный изгибающий момент М_И = 1440 Н·м, крутящий момент Т = 480 Н·м и продольная сила N = 760 Н.

Нормальные напряжения от изгиба . На внешних волокнах, в точках А и В, они наибольшие и равны

Нормальные напряжения от сжатия определим как

Касательные напряжения τ по сечению меняются по линейному закону (ρ – расстояние от центра сечения до точки, в которой определяется напряжение). Максимальные напряжения возникают на контуре сечения

Построим эпюры этих напряжений Эσ_И, Эσ_С и Эτ.

В этой точке действуют максимальные эквивалентные напряжения σ_ЭКВmax. Определим их по III теории прочности:

Видно, что условие прочности σ_ЭКВmax ≤ [σ] выполняется, так как 197,9 МПа < 200 МПа.

Определим недогрузку вала Δ_σ, учитывая, что диаметр вала выбран больше расчётного:

Недогрузка Δ_σ близка к рекомендуемому значению 15%. Таким образом, диаметр вала d = 30 мм из условия статической прочности подобран правильно.

2. Расчёт вала на жёсткость

В расчётах примем модуль упругости Е = 210 ГПа, жёсткость сечения ЕJ_ОС = 210·10⁹·1,63·10^-8 = 3423 Н·м².

2.1 Расчёт прогибов вала в местах установки колёс

Для определения перемещений воспользуемся способом Верещагина.

-формула, выражающая способ Верещагина

где — это площадь эпюры изгибающего момента под действием внешней нагрузки (грузовой эпюры).

-это ордината эпюры эMz, называемой единичной под центром тяжести, (т.е. при ) грузовой эпюры.

Рассчитаем прогиб балки в месте установки левого колеса.

Для определения прогиба балки в месте соответствующего сечения приложим еденичную силу F=1,0 (а) и построим единичную эпюру (б) M1=M2. Построим грузовые эпюры (в) и (г) эMx и эMy.

Найдем прогибы балки по формулам:

z= M1эMx -вертикальная плоскость

y= M2эMy -горизонтальная плоскость

Балка имеет несколько участков в этом случае производится суммирование по участкам .

Вертикальная плоскость

Горизонтальная плоскость

Полные линейные перемещения

Полное линейное перемещение в данном сечении вычислим по формуле:

studfiles.net

Построение эпюры внутренних поперечных сил

Построим эпюру внутренних поперечных сил Q для консольной балки с заданной системой изгибающих нагрузок.

Покажем опорные реакции, которые были рассчитаны ранее и установим систему координат y-z так, чтобы ось z совпадала с продольной осью балки.

Для построения эпюр внутренних поперечных сил Q_y рассчитаем их значения на границах силовых участков.

Балка имеет 2 силовых участка (с.у.) — AB и BC.
Обозначим их на расчетной схеме римскими цифрами I и II соответственно.

Для расчета значений поперечных сил на каждом участке используем метод сечений.

Начнем с первого силового участка.
Проведем сечение в произвольном месте участка между точками A и B.
Это сечение условно делит балку на две части: левую и правую.
Можно рассмотреть любую из них, но лучше выбрать ту часть, к которой приложено меньше нагрузок.

Очевидно, это будет левая часть балки.

Расстояние от левой границы участка до сечения обозначим переменной z₁.
Возможные значения переменной z₁ находятся в пределах от 0 до 0,5м,
z₁=0 — если сечение переместить в точку A
z₁=0,5м — в точке B.

Отбросим на время правую часть балки.

Запишем имеющиеся данные:

I с.у. (AB) 0≤z₁≤0,5м

Поперечная сила в указанном сечении равна сумме всех вертикальных внешних сил, приложенных к рассматриваемой части балки.

К рассматриваемой левой части балки приложена только одна сила — опорная реакция R.

Поэтому сумма сил для первого участка будет состоять только из одного слагаемого R.

По правилу знаков, если сила стремится повернуть рассматриваемую часть балки относительно сечения по ходу часовой стрелки, она записывается положительной.

Q_yI=ΣF_i=R=60кН

В выражении отсутствует переменная z₁. Это указывает на то, что поперечная сила Q_yI одинакова для всех сечений I силового участка.

Переходим на второй силовой участок.

Так же начинаем с того, что проводим сечение в любом месте между точками B и C.
Здесь для рассмотрения лучше выбрать правую часть балки.

Обозначим переменной z₂ положение сечения относительно правой границы участка и мысленно отбросим левую часть балки.

II с.у. (BC) 0≤z₂≤1м

Q_yII=ΣF_i=q∙z₂-F=100z₂-40

Получено выражение, где имеется переменная Z₂.
Переменная имеет первую степень, поэтому ее графиком будет прямая.
Для её построения достаточно двух точек.

Этими точками будут значения Q_y на границах II силового участка, то есть при z₂=0 и при z₂=1м.

Рассчитаем их:

Q_yII(z₂=0)=100∙0-40=-40кН

Q_yII(z₂=1м)=100∙1-40=60кН

Теперь у нас есть все данные для построения эпюры Q_y.

Удлиним линии границ силовых участков, начертим базовую линию и укажем обозначение и размерность эпюры.
Обозначим полученные значения соответствующими точками на эпюре и соединим их.

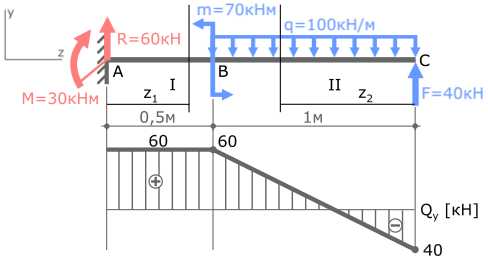
Эпюра Q_y для консольной балки построена. Ее желательно проверить.

Построение эпюры изгибающих моментов >
Другие примеры решения задач >

isopromat.ru

2.6. Построение эпюр q и m для балок

Рассмотрим порядок построения эпюр Q u M для наиболее ха­рактерных случаев нагружения балок.

Сосредоточенная сила на свободном конце консоли (рис. 10). Балка имеет лишь один участок. На­чало координат выбираем в крайней левой точкеА балки, ось х направляем вдоль оси балки направо

Вычисляем Q и М в произвольном сечении с абсциссой х.

Справа от рассматриваемого се­чения действует только одна сила P, поэтому

Поперечная сила одинакова во всех сечениях балки, по этому эпюра Q имеет вид прямоугольника. Функция М (х) линейна.

Рис 10 Для построения ее графика достаточно получить две точки — в начале и в конце участка:приX = 0 (сечение А) 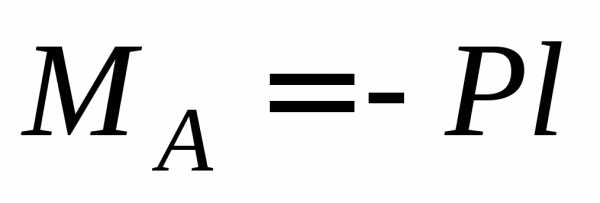, при х = l (сечение В) .

Положительные ординаты эпюр Q и М откладываем вверх от базы.

На рис. 10 штриховой линией показана балка в деформиро­ванном состоянии. Как Сжаты нижние волокна балки. Если совместить базисную линию эпюры изгибающих мо­ментов с осью балки, то эпюра М окажется как бы построенной на сжатых волокнах.

Равномерно распределенная нагрузка ин­тенсивностью q кгс/м на консоли (рис. 11). Попе­речную силу и изгибающий момент в произвольном сечении X бу­дем вычислять как результат действия распределенной нагрузки, расположенной слева от сечения:

Поперечная сила Q (х) изменяется по закону пря­мой линии, а изгибающий момент М (х) — по параболическому закону. Для построения эпюры Q вычисляем ординаты в двух точ­ках:

при х = 0 Q_A = 0; при х = l Qb= — gl и проводим прямую.

Эпюра М криволинейна, для ее построения вычисляем ординаты в трех сечениях:

и проводим через полученные три точки кривую.

Нагрузка интенсивностью q н/м, равно­мерно распределенная по всей длине про­лета двухопорной балки (рис. 12).

В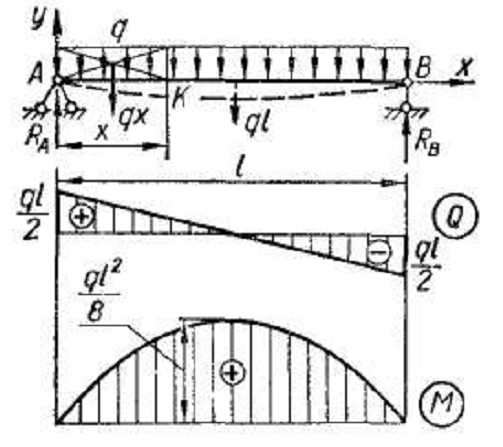данном случае необходимо сначала определить опорные реакции. Равнодействующая всей распределенной нагрузки равнаgl, и линия действия ее проходит через середину балки. Поэтому

|

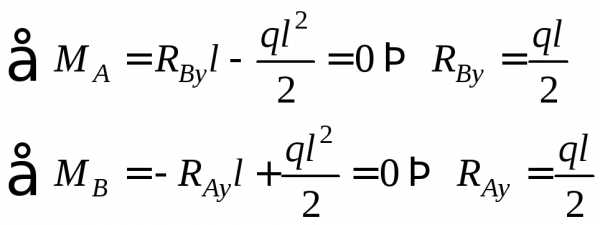Вычисляя поперечную силу и изгибающий момент в произволь­ном сечении x как результат действия сил, расположенных слева от сечения x, (левую часть мысленно отбрасываем) получим

Эпюра Q будет прямоли­нейной, а эпюра М — параболической. Для построения эпюр вычисляем:

Чтобы определить экстремальное значение изгибающего момента, приравниваем нулю производную от изгибающего момента М(х) по абсциссе х сечения:

Т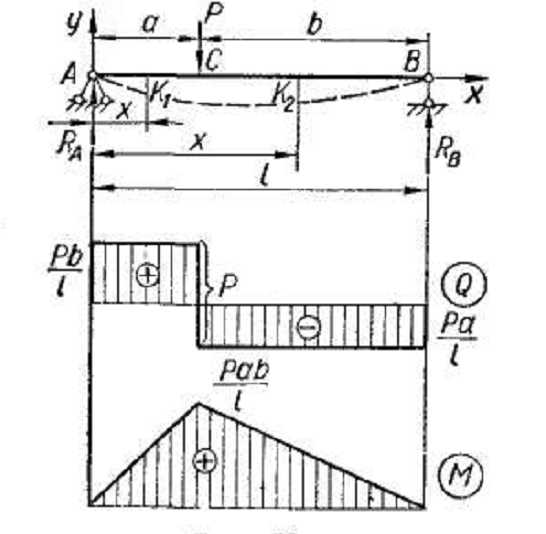ак как вторая производная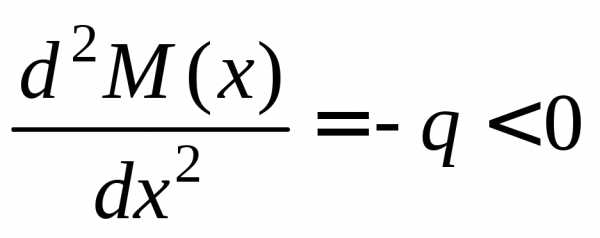, то в сечении при 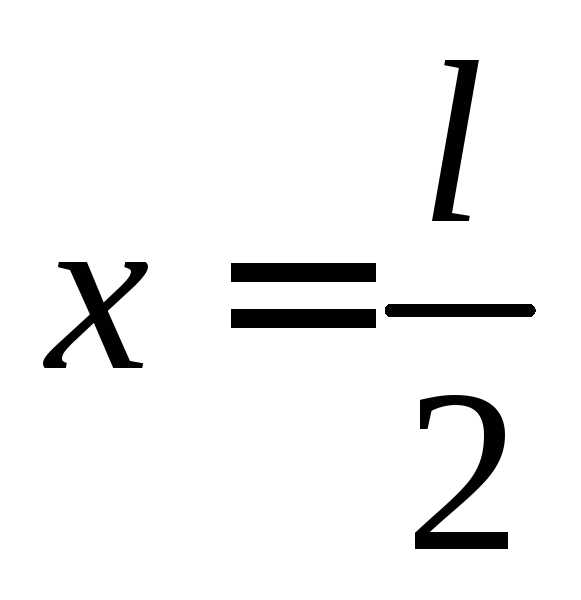имеем максимальное значение момента:

Сосредоточенная сила Р, приложенная к двухопорной балке (рис. 13).

Прежде всего найдем опорные реакции:

В данном случае имеем на балке два участка. Вычисляем Q и М в произвольном сечении К₁ на участке АС (0 х а):

Следовательно, во всех сечениях участка поперечные силы одинако­вы и эпюра Q имеет вид прямоугольника.

Изгибающий момент М (х) изменяется по линейному закону:

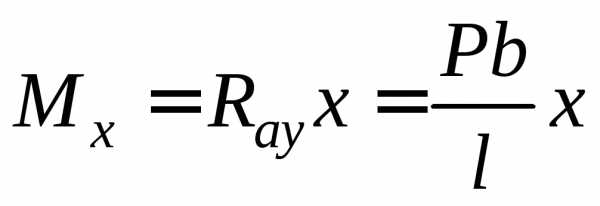
Для построения эпюры вычисляем ординаты на границах участка:

при х = 0 Ма = 0;

при х = а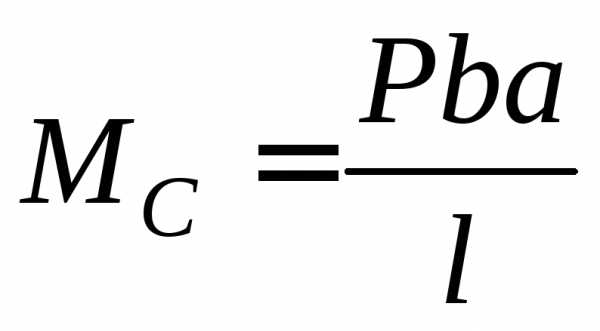

В произвольном сечении К₂ на участке СВ (а х l), рас­сматривая действие сил, расположенных справа от него, получим

;

Как и на участке АС, эпюра Q на участке СВ также имеет вид прямоугольника. Для построения эпюры М находим значения ординат в точках С и В

при х; = а M_C =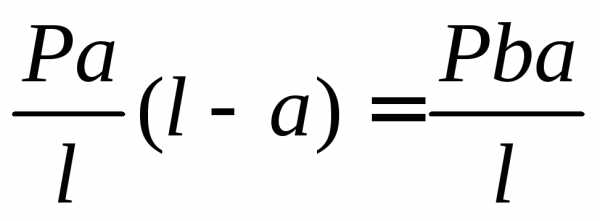

при х: = / M_B = 0.

Эпюры пред­ставлены на рис. 13. Они показывают, что при х ~ а функция Q (х) терпит раз­рыв и на эпюре Q получается скачок, равный по абсолютной величине внеш­ней силе Р в этом сечении,на эпюре М в этом сечении имеет место излом (угловая точка).

Сосредоточенный момент в пролете двухопорной балки (рис. 14).

Находим опорные реакции, на­правив их вверх:

— отсюда

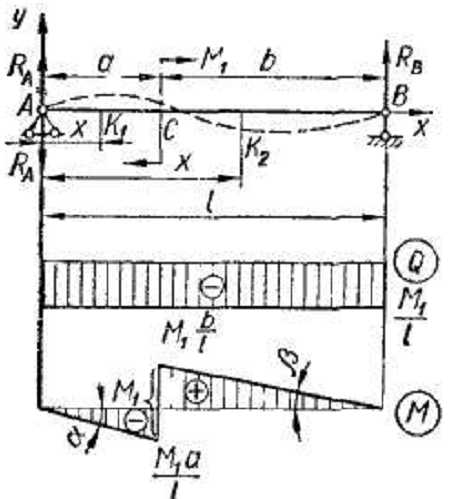
Меняем направление R_A на обратное. Отметив на участках АС и СВ произвольные сечения х1 и х₂, записываем уравнения для функций О (х) и М (х):

для участка АС (0 х а)

;

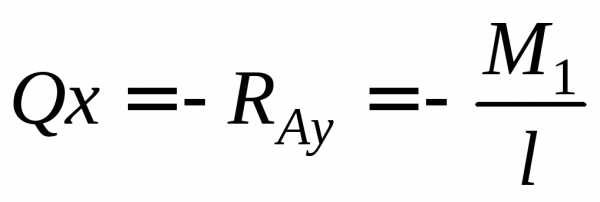для участка СВ (а; х /)

;

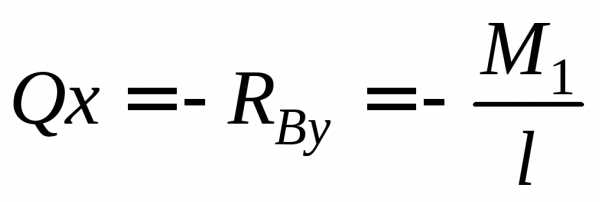На основании этих уравнений строим эпюры Q и М. Эпюра М расположена частично под осью, частично над осью. Поскольку она построена на сжатых волокнах, видим, что на участке АС сжаты нижние волокна балки, а на участке С В — верхние. Этому соответ­ствует изображенная штриховой деформированная ось балки. В том сечении, где изгибающий момент меняет знак, на ней будет точка перегиба.

Там, где приложен внешний момент (сечение С), на эпюре Q изменений нет, а функция М (х) претерпе­вает разрыв и на эпюре М получается скачок, равный по величине внешнему моменту.

Сосредоточенные моменты на опорах однопролетной балки (рис. 15).

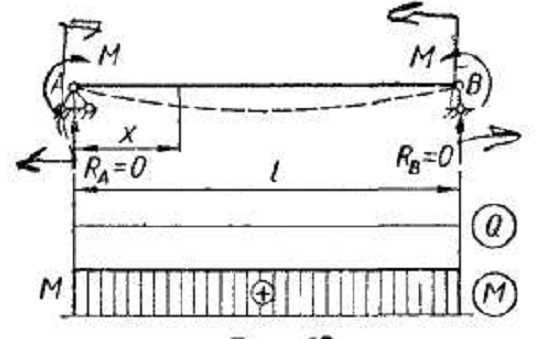
Рис 15

Находим опорные реакции:

Тогда для произвольного сечения, находящегося на расстоянии х от левой опоры,

Q(x) =R_A = 0; М(х) = М = const.

Итак, в любом сечении Q = 0, а изгибающий момент постоянен вдоль балки. Такой случай изгиба носит название чистого изгиба.

studfiles.net