Определение перемещения методом Мора. Правило Верещагина

УО «БГУИР»

кафедра инженерной графики

РЕФЕРАТ

на тему:

«ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ МЕТОДОМ МОРА. ПРАВИЛО ВЕРЕЩАГИНА»

МИНСК, 2008

Рассмотрим теперь общий метод определения перемещений, пригодный для любой, линейно деформируемой системы при любой нагрузке. Этот метод предложен выдающимся немецким ученым О. Мором.

Пусть, например, требуется определить вертикальное перемещение точки А балки, представленной на рис. 7.13, а. Заданное (грузовое) состояние обозначим буквой к. Выберем вспомогательное состояние той же балки с единичной

силой, действующей в точке A и в направлении искомого перемещения. Вспомогательное состояние обозначим буквой i(рис. 7.13,6).

Вычислим работу внешних и внутренних сил вспомогательного состояния на перемещениях, вызванных действием сил грузового состояния.

Работа внешних сил будет равна произведению единичной силы на искомое перемещение ya

а работа внутренних сил по абсолютной величине равна интегралу

Имеем

или

(1)

Формула (7.33) и есть формула Мора (интеграл Мора), которая дает возможность определить перемещение в любой точке линейно-деформируемой системы.

В этой формуле подынтегральное произведение MiMkположительно, если оба изгибающих момента имеют одинаковый знак, и отрицательно, если Miи Мк имеют разные знаки.

Если бы мы определяли угловое перемещение в точке А, то в состоянии iследовало бы приложить в точке А момент, равный единице (без размерности).

Обозначая буквой Δ любое перемещение (линейное или угловое), формулу (интеграл) Мора напишем в виде

(2)

В общем случае аналитическое выражение Miи Мк может быть различным на разных участках балки или вообще упругой системы. Поэтому вместо формулы (2) следует пользоваться более общей формулой

(3)

Если стержни системы работают не на изгиб, а на растяжение (сжатие), как, например, в фермах, то формула Мора имеет вид

(4)

В этой формуле произведение NiNKположительно, если оба усилия растягивающие или оба сжимающие. Если стержни одновременно работают и на изгиб и на растяжение (сжатие), то в обычных случаях, как показывают сравнительные расчеты, перемещения можно определять, учитывая лишь изгибающие моменты, так как влияние продольных сил весьма мало.

По тем же соображениям, как отмечалось ранее, в обычных случаях можно не учитывать влияния поперечных сил.

Вместо непосредственного вычисления интеграла Мора можно пользоваться графо-аналитическим приемом «способом перемножения эпюр», или правилом Верещагина.

Рассмотрим две эпюры изгибающих моментов, из которых одна Мк имеет произвольное очертание, а другая Мi прямолинейна (Рис 7.14, а и б).

Сечение стержня на участке AВ будем считать постоянным. В этом случае

(5)

Величина MKdzпредставляет собой элементарную площадь dωk эпюры Мк (заштрихована на рисунке). Таким образом,

(6)

Но

(7)

следовательно,

(8)

Но

представляет собой статический момент площади эпюры Мк относительно некоторой оси у, проходящей через точку О, равный ωkzc, где ωk — площадь эпюры моментов; zс — расстояние от оси у до центра тяжести эпюры Мк. Из чертежа видно,

mirznanii.com

7.4. Определение перемещений способом Верещагина

Для конструкций, состоящих из прямолинейных стержней с постоянным поперечным участком на i—м участке, интегралы Мора удобно вычислять по формуле Верещагина:

. (7.14)

Рассматриваемый подход представляет собою графоаналитический способ. В формуле (7.14)

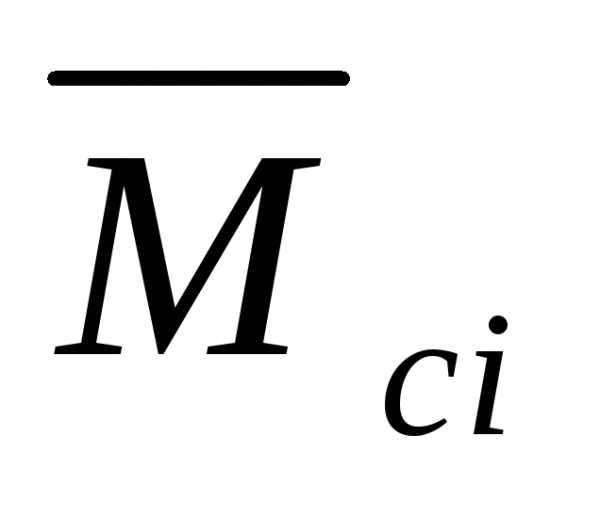– площадь эпюры грузового силового фактора;– значение ординаты единичного силового фактора под центром тяжести площади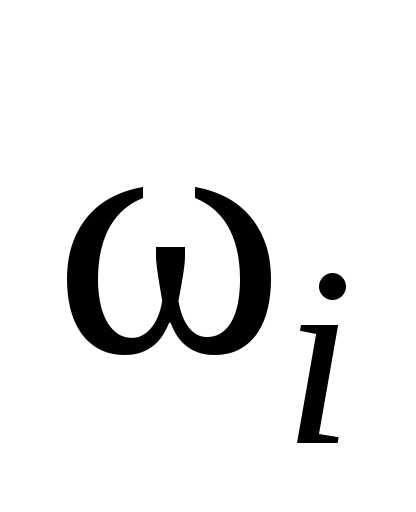;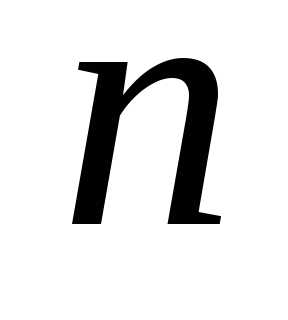– число площадей. Перемещения по способу Верещагина определяют следующим образом.

1. Строят эпюру изгибающих моментов 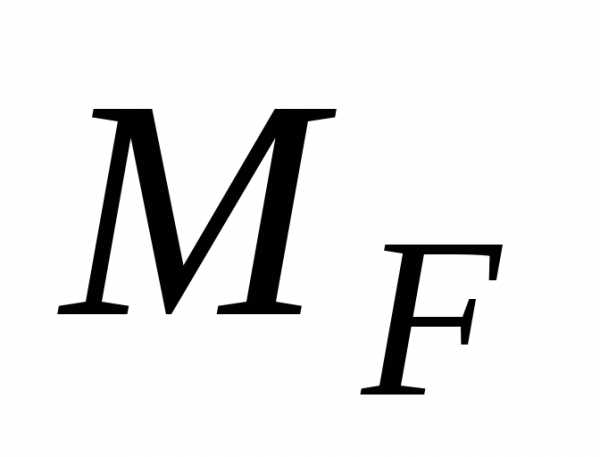для заданной системы от внешней нагрузки.

2. Составляют схему единичного загружения и строят эпюру изгибающих моментов от единичной нагрузки .

3. Разбивают эпюры 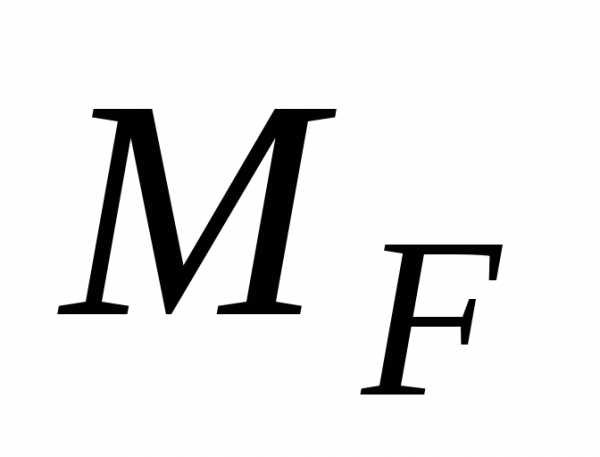и наn одинаковых участков так, чтобы выполнялись следующие условия:

a) под каждым участком эпюры лежал линейный (без изломов и скачков) участок эпюры ;

б) можно было применить известные формулы для вычисления площадей _i участков эпюры 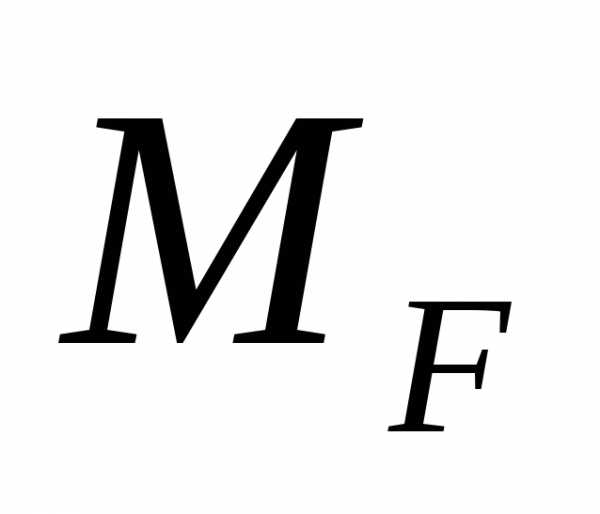и положение центров тяжести этих площадей;

в) изгибная жесткость EJ_х на каждом участке была постоянной.

4. Вычисляют площади _i и ординат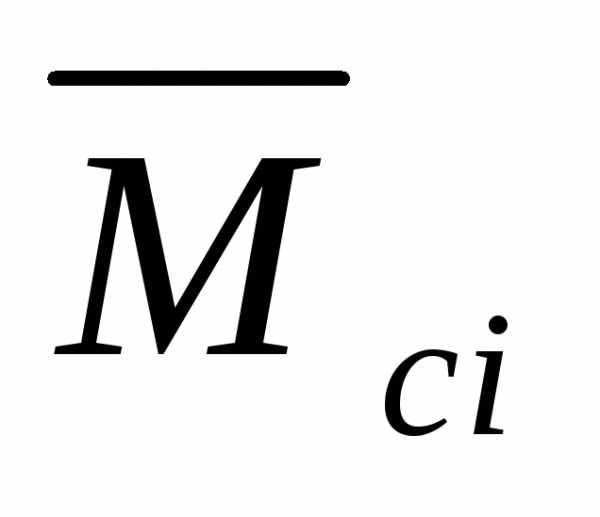ы эпюры, расположенных под центрами тяжести площадей_i.

5. Применяют формулу Верещагина, суммируя произведения

. Эту операцию называют перемножением эпюр и . Действительное направление искомого перемещения определяется так же, как в методе Мора.

а б

Рис. 7.5

Для того чтобы пользоваться формулой Верещагина, надо знать площадь  и положение центра тяжести для характерных фигур. На рис. 7.5 приводятся необходимые справочные данные.

7.5. Примеры определения перемещений методом Мора и способом Верещагина Пример

Для заданной стальной балки (рис.7.6, а) подобрать стандартный двутавр из условия прочности. Определить прогиб и угол поворота сечения С, [] = 160 МПа, Е = 210⁵ МПа.

Решение

Рис. 7.6

1. Составить уравнения поперечных сил Q_y и изгибающих моментов М_F от внешней нагрузки и построить их эпюры.

Для консольных балок эпюры Q и М можно строить без определения реакций в заделке, если анализ на участках проводить со стороны свободного конца балки в направлении защемления. Выделим балки и участки балки (см. рис. 7.6, а), запишем выражения внутренних усилий и найдем их значения на границах участков.

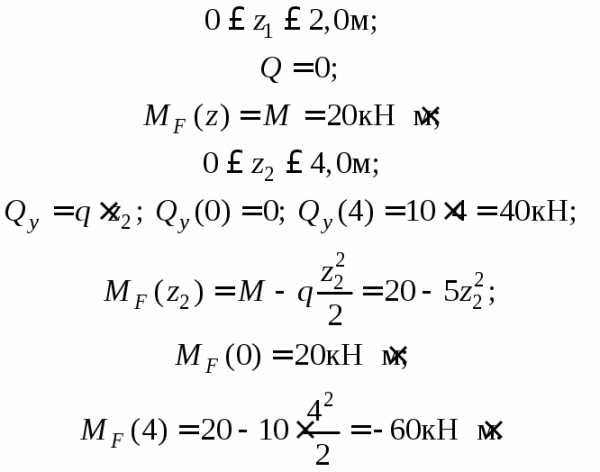
Строим эпюру Q_y (рис. 7.6, б) и М_F (рис. 7.6, в).

2. Подобрать двутавровое сечение из условия прочности по _max.

Определяем требуемый момент сопротивления изгибу:

.

Подбираем по ГОСТ 8239–72 двутавр № 27а, у которого W_х = 407,0 см³, момент инерции J_х = 5500 см⁴.

3. Определить прогиб сечения С методом Мора.

Составляем схему единичного нагружения, прикладывая к заданной балке безразмерную силу, равную единице в точке С (рис.7.6, г). Разбиваем схему единичного нагружения на такие же участки, что и на схеме грузового нагружения (см. рис. 7.6, а). Записываем для каждого участка выражения изгибающих моментов 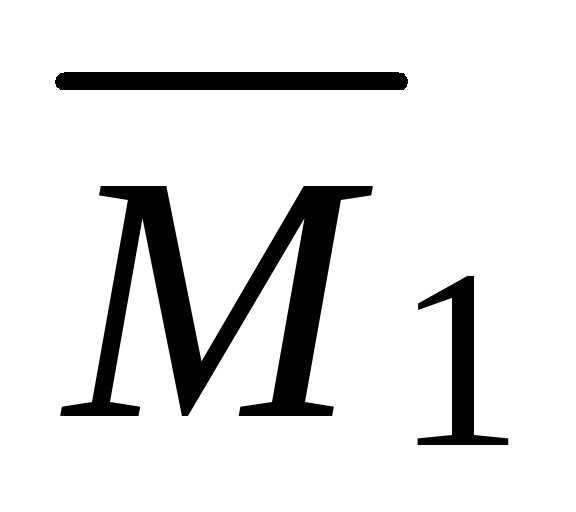от единичной нагрузки .

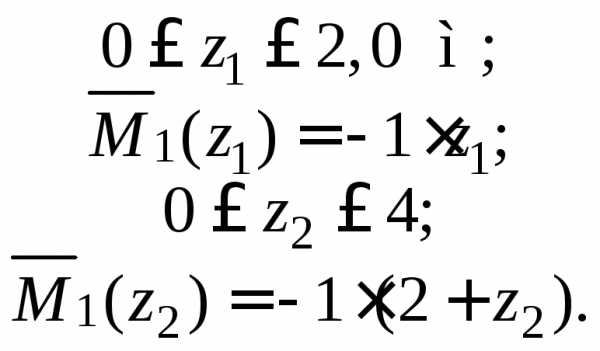
Записываем интегралы Мора на каждом участке и, суммируя результаты, вычисляем прогиб сечения

С.

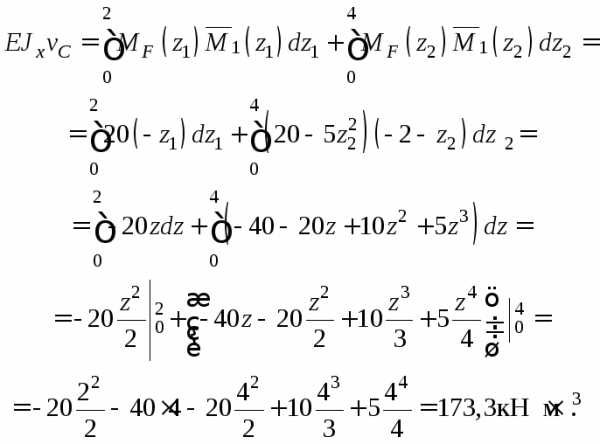
studfiles.net

метод Верещагина — Стр 2

Вычислим опорные реакции, составив три уравнения равновесия.

Проверка Реакции найдены верно

Эпюра показана на рис. ж.

Далее по формуле Мора

Сечение 1 поворачивается по часовой стрелке.

 

Пример 15.

Найдем перемещения – прогиб сечения С и угол поворота сечения В в балке, показанной на рис. 1,

 а, методом Максвелла – Мора и сравним их с теми же перемещениями, найденными ранее аналитическим способом.

Решение.

В соответствии с методом Максвелла – Мора перемещения находим по формуле . Рассмотрим два варианта использования этой формулы:

— аналитическое интегрирование формулы;

— интегрирование с помощью правила Верещагина.

Вариант 1. Аналитическое интегрирование формулы Максвелла – Мора

Для определения перемещений по формуле выпишем выражения для изгибающих моментов в балке от заданной нагрузки на каждом участке балки. Начало координатх можно выбирать произвольным образом, например, так, как показано на рис. 1, а.

                                                                                      

Рис.1

 

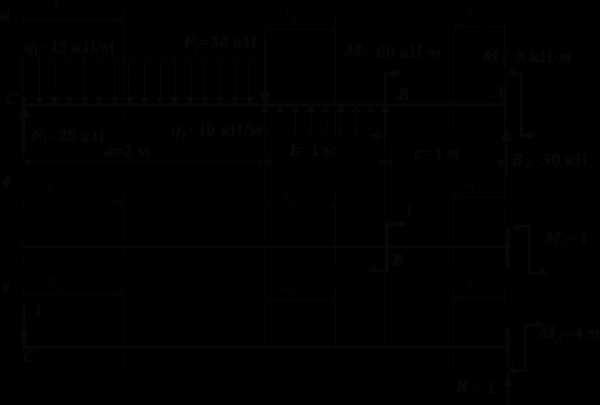
Тогда выражения для изгибающих моментов на трех участках будут такими:

участок 1:   ;

;

участок 2:  ;

;

участок 3:  ;

.

Найдем сначала угол поворота сечения В балки. Загрузим балку в сечении В единичной обобщенной силой, соответствующей искомому перемещению, то есть парой сил, равной единице (рис. 1, б). Запишем выражения для изгибающих моментов на каждом участке от единичной пары сил. Начало отсчета координатых должно быть таким же, как при записи выражений для изгибающих моментов от заданной нагрузки (см. рис. 1, б). Тогда:

участок 1:    ;;

участок 2:  ;;

участок 3:  ;.

Подставим записанные выражения в интеграл Максвелла – Мора и проинтегрируем (на первых двух участках интегралы в рассматриваемом примере равны нулю):

.

Чтобы найти прогиб сечения С , приложим в точке С новую единичную обобщенную силу – сосредоточенную силу, положив ее равной единице (рис. 1, в). Выражения для изгибающих моментов на каждом участке от единичной сосредоточенной силы будут такими:

участок 1:   ;;

участок 2: ;;

участок 3: ;.

После подстановки функций ив интеграли интегрирования на каждом участке получим

Величины найденных перемещений совпадают с результатами, полученными ранее аналитическим способом, а знак у угла поворота другой. Это следствие разных правил знаков в аналитическом методе и методе Максвелла – Мора. Обсудим полученные знаки перемещений. Положительный знак угла поворота показывает, что поворот происходит по направлению обобщенной силы. Поскольку единичная пара принята направленной по часовой стрелке, то и сечение В поворачивается по часовой стрелке. Отрицательный знак прогиба означает, что сечение С перемещается в сторону, противоположную принятому направлению единичной силы, то есть вверх. Таким образом, результаты решения полностью совпадают с полученными ранее аналитическим методом.

Вариант 2. Интегрирование формулы Максвелла – Мора с помощью правила Верещагина

Как отмечалось раньше, процесс интегрирования формулы Максвелла – Мора с помощью правила Верещагина (или Симпсона) называется «перемножением эпюр». Чтобы «перемножить эпюры», построим их. Сначала построим эпюру изгибающих моментов от заданной нагрузки (рис. 2, а). Разобьем эпюру М на 6 простых фигур: три треугольника ,и, два сегмента, ограниченных квадратной параболой,ии трапецию. Порядок разбивки эпюры моментов на составляющие фигуры на втором участке поясняет рис. 3 (эпюру М на втором участке можно разбить и на две фигуры: трапецию, у которой основания имеют разные знаки (10 и –25) и сегмент. В этом случае удобно воспользоваться правилом перемножения трапеций).

Найдем площади этих фигур:

кНм²,                    кНм²,

 кНм²,                      кНм²,

 кНм²,           кНм².

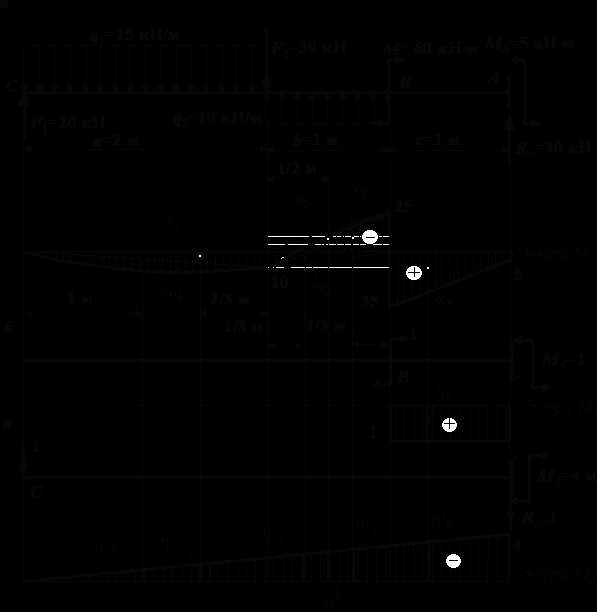
                                                                                        Рис.2

 

                                                                                         Рис.3

 

Для определения площадей ииспользована формула. Затем строим эпюры моментов от единичных обобщенных сил, соответствующих искомым перемещениям. Чтобы определитьугол поворота сечения В, приложим в точке В балки пару сил, равную единице, и построим эпюру изгибающих моментов М₁ от этой пары сил (рис. 2, б). Найдем ординату под центром тяжести площади . Независимо от положения центра тяжести трапеции (а оно не определено) ордината под центром тяжести равна единице, так как изгибающий моментМ₁ на участке перемножения является постоянной величиной, всюду равной единице. То есть . Поскольку на всех остальных участках изгибающий моментМ₁ = 0 и , то по формулеискомое перемещение

.

Полученная величина угла поворота совпадает с найденной ранее аналитическим методом. Положительный знак говорит о том, что поворот сечения В происходит по направлению обобщенной силы, то есть в соответствии с принятым на рис. 3, б направлением единичной пары по часовой стрелке. Теперь будем искать прогиб сечения С. Загрузим балку новой обобщенной силой, соответствующей прогибу в точке С. Такой обобщенной силой будет сосредоточенная сила, равная единице и приложенная в точке С. Эпюра изгибающих моментов М₂ от этой единичной силы показана на рис. 3, в. Согласно формуле искомый прогиб

.

Найдем ординаты на эпюре М₂, расположенные под центрами тяжести шести фигур, на которые разбита эпюра М. Положение центров тяжестей всех фигур, кроме , показано на рис. 3, а. Ординату на эпюре М₂, расположенную под центром тяжести какой-то фигуры, можно найти либо из подобия треугольников, либо как изгибающий момент от единичной силы под центром тяжести рассматриваемой фигуры. Используем второй вариант вычисления ординат. Изгибающий момент под центром тяжести треугольника равен значению силы (1), расположенной слева от сечения, умноженной на плечо (4/3 м), со знаком минус. То есть

м.

Аналогично ордината под центром тяжести треугольника равна силе (1), умноженной на плечо (2 +2/3 = 8/3 м), со знаком минус. И так же для остальных фигур, положение центров тяжести которых известно:

м,       м,м,м.

Поскольку положение центра тяжести трапеции не определено и невозможно в этом случае найти ординату под центром тяжести, воспользуемся на этом участке формулой перемножения трапеций:

 кНм³.

Искомое перемещение – прогиб в точке С

.

Результат совпадает с найденным ранее прогибом в точке С аналитическим способом. Отрицательный знак перемещения показывает, что точка С перемещается в сторону, противоположную выбранному направлению единичной силы (см. рис. 3, в), то есть вверх.

 

Пример 16.

Определим угол поворота сечения А и прогиб сечения D в балке, показанной на рис. 1, а, методом Максвелла – Мора с использованием правила Верещагина (перемножением эпюр). Ранее эти перемещения были найдены аналитическим методом, сравним результаты, полученные двумя способами.

                                                      Рис.1

 

Решение.

Построим эпюры изгибающих моментов от заданной нагрузки (рис. 2, а) и от единичных обобщенных сил, соответствующих искомым перемещениям (рис. 2, б, в).

                                                              Рис.2

 

Разобьем эпюру моментов от заданной нагрузки на три треугольника и найдем их площади:

кНм²;       кНм²;     кНм².

Для определения угла поворота сечения А перемножим эпюры М и М₁. Для этого найдем ординаты на эпюре М₁, расположенные под центрами тяжести треугольников:

;     ;.

Тогда угол поворота сечения А согласно формуле 

.

Положительный знак угла поворота показывает, что поворот сечения А происходит по направлению обобщенной силы, то есть в соответствии с показанной на рис. 2, б единичной парой сил по ходу часовой стрелки. Результат совпадает с полученным ранее аналитическим способом.

Чтобы найти прогиб сечения D, используем при перемножении эпюру М₂. Ординаты на эпюре М₂ под центрами тяжести треугольников будут такими:

 м;      м;м.

Найдем прогиб сечения D по формуле :

.

Прогиб сечения D получился положительным. Это означает, что точка D перемещается по направлению единичной силы. Поскольку единичная сила показана на рис. 2, в направленной вниз, то и перемещение точки D происходит вниз. Полученный результат совпадает с тем, который был получен ранее аналитическим способом.

 

Пример 17.

Для двутавровой балки  № 12  определить допускаемое значение моментаиз условия жесткости, еслимм (рис.1).

                                                       Рис.1

 

Решение.

Строим эпюру грузовых моментов (рис.2) и эпюруот единичной силы, приложенной в произвольном сечении (рис.3). Тогда прогиб в этом сечении

 

                                                 Рис.2

 

                                                  Рис.3

 

где 

 Проверим выполнение граничных условий. При и. Далее определяем величину максимального прогиба. Для этого необходимо решить задачу  определения экстремума функции. Вычисляя производную функциии  приравнивая  ее нулю, получаем следующее уравнение

,

корни которого равны . Первый корень соответствует точке, лежащей вне балки, а второй

 или . Условие жесткости балки при этом запишется:

Решая это неравенство относительно m, получаем

Таким образом, допускаемый момент равен

 

Пример 18.

Исходные данные.

, ,,, жесткость балкиEI_x — постоянная.

Требуется:

Определить по правилу Верещагина вертикальное перемещение точки «В»

    

Решение.

Определение вертикального перемещения сечения «В» выполняется в следующей последовательности:

— Строим эпюру изгибающих моментов от заданной нагрузки, то есть грузовую эпюру (рис.1, б).

— Рассматриваем единичное состояние  системы: к заданной конструкции в требуемом направлении прикладываем единичную безразмерную силу в том сечении, линейное перемещение которого требуется определить (рис.1, в).

— Строим единичную эпюру, то есть эпюру изгибающих моментов от единичной нагрузки (рис.1, г).

— Приводим в соответствие участки грузовой и единичной эпюр: каждому участку грузовой эпюры должен соответствовать участок единичной эпюры, ограниченный прямой (не ломаной) линией.

В примере вдоль всей длины балки единичная эпюра ограничена прямой, однако её следует разбить на два участка, так как грузовая эпюра состоит из двух участков, площади которых и(см. рис.1,б).

— Определяем площади отдельных участков грузовой эпюры и соответствующие им абсциссы центров тяжести.

Так как участки грузовой эпюры представляют собой фигуры, площади и центры тяжести которых определить затруднительно, разобьём их на более простые составляющие с площадями ,,,.

;   ;

;   ;

;

;

; .

— Определяем ординаты на единичной эпюре под центрами тяжести простых составляющих отдельных участков грузовой эпюры. Для определения ординат используем подобие треугольников, у которых отношения катетов равны.

;

.

Аналогично:

,     .

— Записываем формулу Верещагина для рассматриваемой задачи. При этом учитываем: если грузовая и единичная эпюры на участке имеют одинаковый знак, то произведение положительно, если разный знак – отрицательно.

Если общий вид формулы Верещагина: , то для рассматриваемой задачи она принимает вид:

, .

Положительное значение указывает, что перемещение конца консоли направлено в сторону действия единичной нагрузки.

— Можно воспользоваться иным подходом для решения поставленной задачи. Ввиду того, что грузовая эпюра изгибающих моментов имеет сложные очертания, её можно «расслоить», то есть построить эпюру моментов от каждой нагрузки в отдельности (рис.1, д).

Тогда

;          ;;

;        ;;

;   ;;

;                 ;.

Полученный результат отличается от предыдущего на 0,8%, что лежит в пределах допустимой погрешности. При решении можно воспользоваться любым удобным для студента подходом.

 

Пример 19.

Для заданной  стальной балки (рис.1) требуется в сечении К  определить  прогиб Y и угол поворота :

а) методом начальных параметров;

б) по интегралу Мора;

с) способом Верещагина.

Исходные  данные:   q₁ = q₂ = 2 кН/м;   F = 1 кН;   М = 4 кНм;   a = 4 м;  b = 2 м;  EJ_x = const.

 

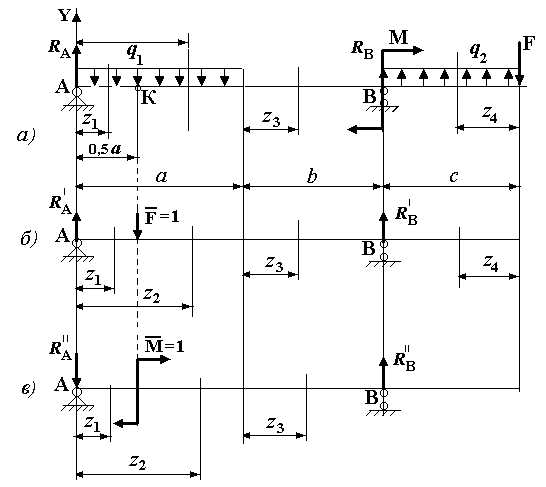
                                                                                  Рис.1

 

Решение.

1. Для определения перемещений  методом начальных  параметров необходимо знать все силы, приложенные к балке, в том числе и силы реакции опор.

Определяем опорные реакции:

;

= ;

;

= 

Проверка:

Расположим начало координат на левом конце балки, на опоре А (рис. 1)   

Прогиб на опоре А не существует, т.е. Y₀ = 0, чтобы определить ₀ запишем прогиб на опоре В, который также равен 0, при

studfiles.net

3.6. Формула Верещагина

Интеграл (3.17) можно вычислить аналитически, однако если жесткости стержней постоянны, удобнее воспользоваться другим способом, который обычно и применяют на практике.

Учитывая, что эпюра`M<sub>i</sub> от единичного силового фактора является кусочно-линейной, можно выбрать промежутки a,b, где она будет просто линейной. Тогда выбирая начало локальной системы отсчета так, как показано на рис. 3.12, б, ее уравнение можно записать в виде: `M_i(x) = tgx. При этом интеграл в (3.17) примет вид:

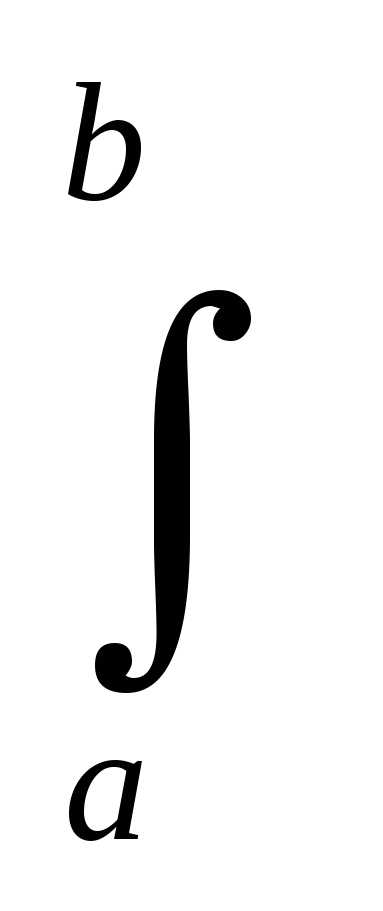( M_pM_i /EJ)dx = (tg/EJ) x M_p dx. (3.19)

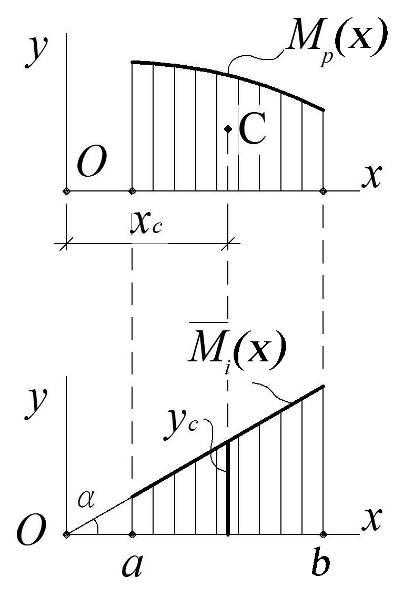
Рис.3.12

Обозначая через  площадь эпюры M_p:

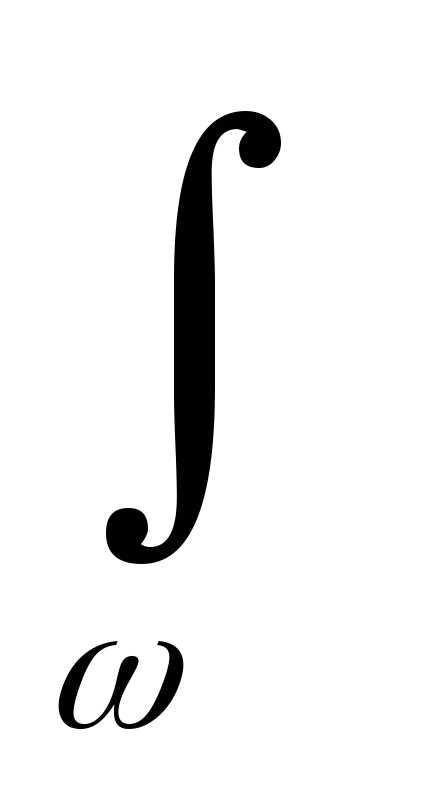 = d = M_p dx ,

и учитывая, что ее статический момент относительно оси Oy равен:

S_y=xd = x_c,

представим (3.19) в виде:

(tg/EJ) 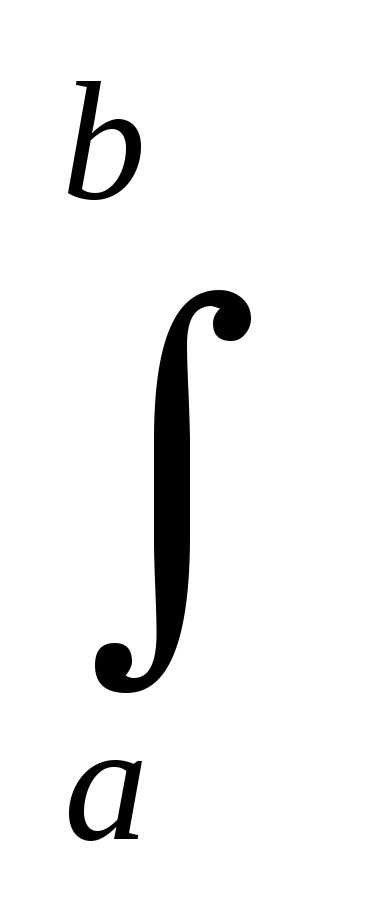x M_p dx = (tg/EJ) 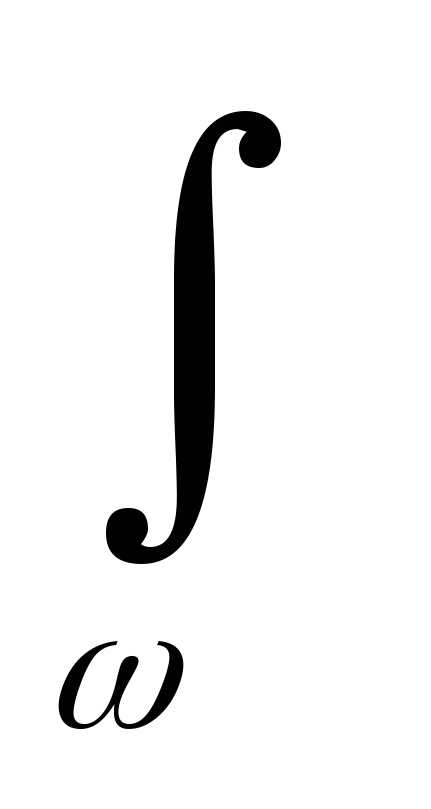xd= (tg/EJ) x_c = (y_c)/EJ,

где y_c = tgx_c.

Возвращаясь к формуле (3.17), получим:

_ip =  (_ky_ck)/(EJ_k). (3.20)

Таким образом, чтобы перемножить две эпюры, из которых хотя бы одна является линейной, нужно вычислить площадь криволинейной эпюры –  и умножить ее на ординату y_c в линейной эпюре, вычисленную под центром тяжести криволинейной.

Для реализации формулы (3.20) остается рассмотреть геометрические характеристики стандартных эпюр (рис. 3.13), где две последние – соответствуют эпюрам от равномерно распределенной нагрузки. Поскольку любую нестандартную эпюру можно представить комбинацией стандартных, с помощью последних можно перемножить произвольные эпюры.

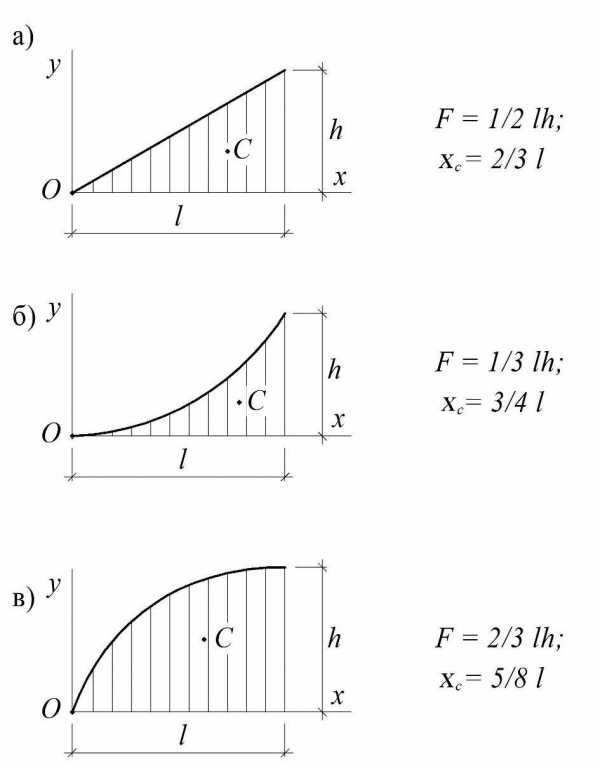
Рис.3.13

Примечания:

1. При выводе формулы (3.20) криволинейная эпюра M_p с площадью w предполагается однозначной. Если это условие не выполнено, ее представляют комбинацией двух или большего числа стандартных эпюр.

2. Для вычисления интеграла (3.17) можно применять формулы численного интегрирования, в том числе – формулу Симпсона:

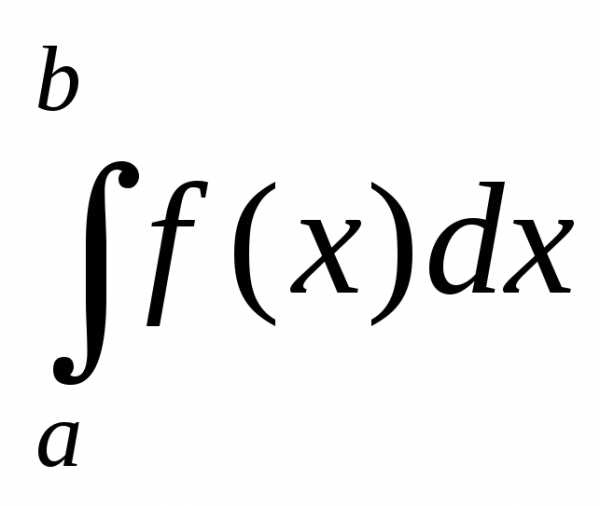=  (b – a)/6 f(a) + 4f  (a + b)/2 + f(b),

которая позволяет получить точный результат, если функция f (x) является многочленом до третьей степени включительно.

Таким образом, если на всем промежутке a,b эпюра `M_i линейна, а эпюра M_p является квадратичной параболой, интеграл (3.17) можно вычислить по формуле:

D_ip=(l_k/6EJ_k) M_p(a_k) `M<sub>i</sub>(a<sub>k</sub>) +4 M<sub>p</sub> (a<sub>k</sub> +b<sub>k</sub>)/2 `M_i (a_k+b_k)/2+M_p(b_k)  `M_i(b_k) . (3.21)

При этом однозначности эпюры M_p на промежутке a,b не требуется, а формулу можно, конечно, применять и для линейной функции M_p(x).

3.7. Примеры определения перемещений

Рассмотрим примеры определения перемещений в СОС от действующей нагрузки. Во всех случаях изгибная жесткость элементов системы – EJ и их продольная жесткость – EF предполагаются известными.

Пример 3.1. Определить максимальные прогибы балки (рис. 3.14, а).

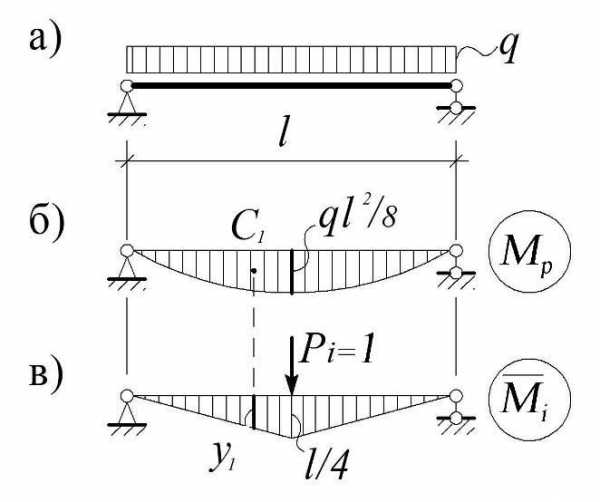
Рис.3.14

Решение. В соответствии с формулой (3.17) строим эпюру M_p от заданной нагрузки (рис. 3.14, б) и эпюру M_i от единичной силы, приложенной в середине балки (рис. 3.14, в).

Вычислим интеграл (3.17) по формуле Верещагина. На всем промежутке 0,l эпюра M_p является однозначной, то есть отвечает предъявляемым к ней требованиям, а эпюраM_i на всем промежутке 0,l будет нелинейной. Поэтому область интегрирования делим на два участка: 0, l/2 и l/2, l, на каждом из которых M_i(x) будет линейной. С учетом симметрии получим:

v_max = _ip = 2 (w₁ y_c1)/EJ = 2 (2/3)( l/2)(ql²/8)(5/8)(l/4) = 5ql⁴/384EJ.

Для того чтобы получить тот же результат с помощью интегрирования дифференциального уравнения изогнутой оси балки, нужно затратить примерно втрое больше усилий – хотя бы потому, что придется находить угол поворота балки в ее начальном сечении – ₀.

Формально воспользовавшись для всего промежутка 0,l формулой Симпсона (3.21), и учитывая, что значения M_p иM_i на его концах равны нулю, получим:

v_max = (l/6EJ)4(ql²/8)(l/4) = ql⁴/48EJ.

Найденный результат оказался неверным, поскольку на всем промежутке 0,l подынтегральная функция f(x) = M_p(x)  M_i (x) не отвечает требованиям, предъявляемым к ней этой формулой. 

Пример 3.2. Найти линейное и угловое перемещения точки A на конце Г-образной консольной рамы, у которой жесткость стойки вдвое больше жесткости ригеля (рис. 3.15, а).

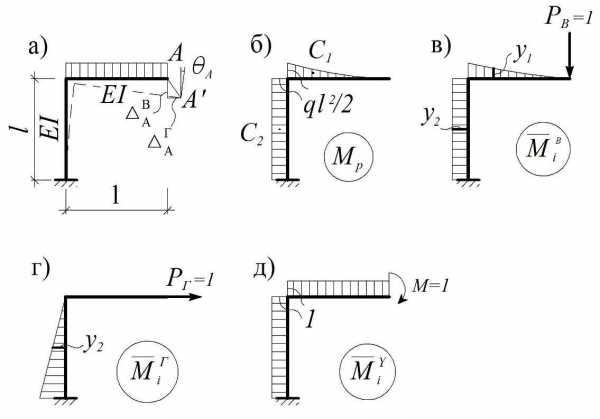
Рис.3.15

Решение. Строим эпюру M_p от заданной нагрузки и эпюрыM_i от единичных сил и моментов, приложенных в точке A (рис. 3.15, б-д).

Определяем вертикальное перемещение точки А, перемножая эпюры M_p иM ^в:

^в = (M_p M ^в) = (1/EJ) w₁ y₁ + (1/2EJ) w₂ y₂ = (1/EJ)(1/3)l (ql²/2)(3/4)l +

+ (1/2EJ) l(ql²/2)l = (3/8)(ql⁴/EJ).

Находим горизонтальное перемещение точки А:

^г = (M_p M ^г) = (1/2EJ) l(ql²/2)(l/2) = (1/8)(ql⁴/EJ).

Полное перемещение точки А составит:

___________ __

_А =  (^в)² + (^г)² = (10 ql⁴)/8EJ.

Угол поворота сечения в точке А будет равен:

_А = (M_p M ^у) = (1/EJ) w₁×1 + + (1/2EJ) w₂×1 = (1/EJ)(1/3)l (ql²/2)1 +

+ (1/2EJ) l(ql²/2)1 = (5ql³/12EJ ). 

Рассмотренный пример наглядно показывает, почему при определении перемещений в рамах мы пренебрегаем продольными деформациями. Вертикальное перемещение точки А от заданной нагрузки в основном определяется изгибом ригеля, изгибом стойки и только в очень незначительной степени – ее сжатием.

Пример 3.3. Найти угол поворота сечения на правой опоре рамы, рассмотренной в примере 2.5, полагая EJ = const (рис. 2.9, а).

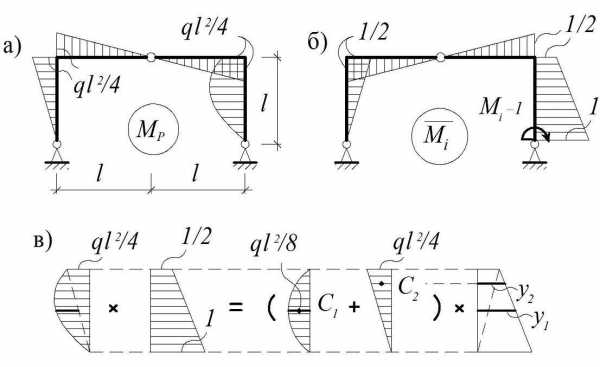
Рис.3.16

Решение. Воспользуемся уже построенной ранее эпюрой M_p от заданной нагрузки (рис. 2.9, б) и (рис. 3.16, а), и умножим ее на эпюру`M<sub>i</sub> от единичного момента (рис. 3.16, б). На левой стойке и ригеле эпюра M<sub>p</sub> представлена тремя треугольниками с равной площадью w<sub>тр</sub> = (1/2)l (ql<sup>2</sup>/4), которые умножаются на три одинаковых треугольника в эпюре `M_i.

Нестандартную эпюру M_p на правой стойке с площадью w_пар представим суммой стандартных эпюр: параболы с площадью w₁ и треугольника с площадью w₂ (рис. 3.16, в).

Поскольку перемножаемые эпюры расположены на разных волокнах, результат получится со знаком минус. Как и при определении опорных реакций, это означает, что действительное направление угла поворота будет противоположно направлению, указанному на рисунке:

_В = (M_p  M_i) = (1/EJ) (–3) w_тр y_тр — w_пар y_пар = – (1/EJ) 3w_тр y_тр+w₁ y₁+

+w₂ y₂ = – (1/EJ) 3 (1/2) l (ql²/4) (2/3)(1/2) + (2/3)  l (ql²/8) [(1/2)(1/2+1) + (1/2) l (ql²/4) [(2/3)(1/2) + (1/3)×1] = – (11ql³) / (48EJ). 

studfiles.net

2)Вывод формулы способа Верещагина для вычисления интеграла Мора.

Если стержень состоит из прямых участков с постоянной в пределах каждого участка жесткостью, эпюры от единич­ных силовых факторов на прямолинейных участках оказыва­ются линейными.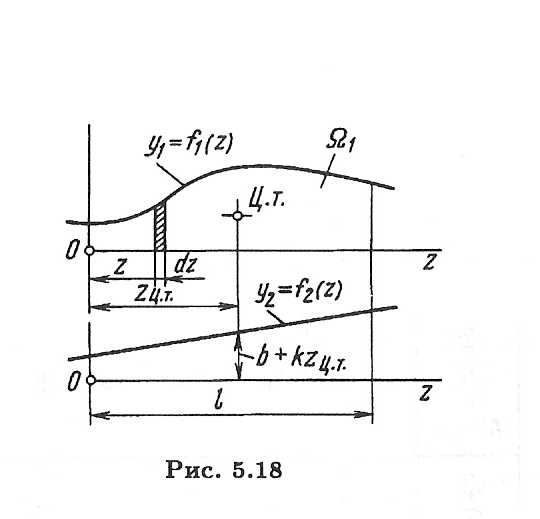

Положим, на участке длиной 1 нужно взять интеграл от произведения двух функцийf₁(z)*f₂(z):J =f₁ (z) f₂(z) dz (1)

при условии, что хотя бы одна из этих функций — ли­нейная. Пусть f₂(Z) =b +kz. Тогда выражение (1) примет видJ =f₁ (z) dz+ kzf₁ (z) dz

Первый из написанных интегралов представляет собой пло­щадь, ограниченную кривой f₁ (z) (рис. 5.18), или, короче го­воря, площадь эпюрыf₁(z):

Второй интеграл характеризует статический момент этой пло­щади относительно оси ординат, т.е.

где Zц.т — координата центра тяжести первой эпюры. Теперь получаем

Но =f₂(z_ц.т.) Следовательно,

Таким образом, по способу Верещагина операция интегри­рования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой.

Билет 20

1)Главные осевые моменты инерции. Определение их величин и направлений главных осей.

Оси, относительно которых центробежный момент J_XcYc=0, наз-ся главными. Осевые моменты инерции относительно главных осей наз-ся главными моментами инерции.

«+» соответсвует максимальному моменту инерции, « — » — минимальному. После того как сечение вычерчено в масштабе и показано положение главных осей на глаз устанавливается направление осей (которой из двух соответствует максимальный, а которой – минимальный момент инерции).

2) Кручение стержня прямоугольного поперечного сечения (определение напряжений и перемещений).

На рисунке показана полученная методом теории упругости эпюра касательных напряжений для бруса прямоугольного сечения. В углах, как мы видим, напряжения равны нулю. Наибольшие напряжения возникают по серединам больших сторон, в точках А:

τ_А= τ_max=

В точках В:

_в=τ_max, где а — большая, b — малая сторона прямоугольника. Коэффициентыизависят от отношения сторонКоэффициент β также зависит от этого отношения. Эти данные приводятся в таблицах.

Угловое перемещение:

Обобщённые ф-лы:

Ф-ла для расчёта касательных напряжений: , где

для расчёта углового перемещения:

Для прямоугольника: ,–геометрические параметры, зависящие от формы сечения.

Потенциальная энергия, накопленная закрученным брусом:

Билет 21

1)Определение перемещений при растяжении-сжатии.

, где W – перемещение, – удлинение, N – внутренняя сила на участке, E – модуль упругости первого рода, А – площадь поперечного сечения на участке.

Для однородного стержня длины , при Е= const, N = const:

2) Расчёт на прочность при изгибе. Понятие о расчётном и нормативном коэффициенте запаса.

По принципу независимости действия сил нормаль­ное напряжение в произвольной точке, принадлежащей попереч­ному сечению бруса и имеющей координаты x, y, опр-ся суммой напр-й, обусловленных моментами M_x и M_y , т.е. (5.26)

Mx = Msin; My = Mcos, где- угол между плоскостью главного мемента М и осью Ох или Оу. (5.25)

Правило знаков для моментов: момент считается положительным, если в первой четверти координатной плоскости (там, где координаты x и y обе положительны) он вызывает сжимающие напряжения.

Если изгиб чистый, то один из моментов M_x или M_y равен 0 и выражение (5.26) принимает вид

, где — осевой момент сопротивления,– осевой момент инерции,- расстояние по модулю до наиболее удалённой точки сечения от Ох.

При косом изгибе М_Х , М_{У .}

Уравнение нейтральной линии, т.е. геометрического места точек, где нормальное напряжение принимает нулевые значения, находят, полагая в (5.26)  = 0:

Откуда определяется: (5.27)

Эпюра напряжений в поперечных сечениях бруса линейна, следовательно, максимальные напряжения в сечении возникают в точках наиболее удаленных от нейтральной линии.

Расчёт на прочность при изгибе проводится при условиях:

1. материал работает одинаково на растяжение и сжатие, т.е.

Условие прочности: , где,, где– допускаемое значение предела текучести,- коэф. запаса.

2. если неодинаково, то работают два условия:

, где,

Если расчёт проектировочный, то из двух коэффициентов выбирется наибольший. В поверочном – наоборот.

В целях безопасной работы напряжения должны быть ниже предельных значений для данного материала. Таким образом при поверочном расчёте (нахожд. Нормативного коэф. запаса):

, где — предельное кас. напряжение материала,n_Т – коэф. запаса,

за расчётный коэффициент принимают [n] > n_Т, где [n] – нормативный (предписываемый нормами проектирования конструкций) коэф. запаса.

привести пример

studfiles.net

Формула Верещагина — Энциклопедия по машиностроению XXL

Эти коэффициенты могут быть вычислены также при помощи формулы Верещагина  [c.561]

Окончательно имеем следующую формулу Верещагина для определения перемещений  [c.187]

Теперь определим искомое перемещение в каждом из пяти вариантов единичного состояния, пользуясь формулой Верещагина (рис. 15.28, а)  [c.514]

Во многих случаях удобна формула Верещагина, являющаяся графоаналитической интерпретацией формулы Мора  [c.102]

При пользовании формулой Верещагина необходимо разделить длину стержня на такие участки, чтобы в пределах каждого из них эпюра Ми была ограничена прямой линией.  [c.102]

Строим эпюры изгибающих моментов от силы Р1 = I и момента Р2 = I (рис. 11.42, б—д) и вычисляем по формуле Верещагина  [c.105]

Учитывая это для определения перемещений в системе, имеющей п таких участков, можно воспользоваться формулой Верещагина для определения перемещений в балках и рамах  [c.203]

В рассматриваемом примере формулу Верещагина применяем отдельно к стойке и ригелю. Применяя размерность кГ, см], получим вертикальное и горизонтальное перемещения, а также угол поворота  [c.222]

Формуле Верещагина часто придают следующий вид  [c.280]

Дадим другой более наглядный вывод формулы Верещагина.  [c.214]

Применяя формулу Верещагина (327), углы 6д и бдо найдем -путем на М и эпюры М на М о-  [c.246]

По формуле Верещагина (37) находим единичные перемещения  [c.40]

Для возможности пользоваться формулой Верещагина надо знать площадь П и положение центра тяжести для характерных кривых. На рис. П.1.3 приводятся необходимые справочные данные.  [c.551]

Для вычисления прогибов методом Максвелла—Мора используем формулу Верещагина. Площадь эпюры Мр равна  [c.92]

Применяя к формуле (13.64) способ Верещагина, находим, что  [c.385]

Перемещения определяем по способу Мора—Верещагина, при этом перемещение бп определяем по формуле (VI 1.45)  [c.211]

Решение. Принимаем, что стержень при потере устойчивости деформируется примерно таи же, как и при действии горизонтальной силы Р. Строим эпюру М от действии силы Р (рис. Х.7, б) и вычисляем потенциальную энергию изгиба по формуле (УТ.22) или по правилу Верещагина, перемножая эпюру М саму на себя  [c.286]

Наибольшее распространение в инженерной практике получили правило Верещагина и формула Симпсона.  [c.72]

Для определения единичного 6л и грузового А,р перемещений строим эпюры моментов в основной системе от единичного неизвестного = 1 и от заданной нагрузки (рис. в и г). По формуле Мора, используя способ Верещагина, найдем перемещения  [c.178]

Практически это правило Верещагина применяется для определения линейных и угловых перемещений в балочно-рамных системах от действия изгибающих моментов. Формула, определяющая перемещение, записывается следующим образом  [c.308]

Описанный графоаналитический способ вычисления интеграла Мора был предложен А. Н. Верещагиным и носит название способа Верещагина. Вычисления по этой формуле проводят по участкам, на каждом из которых эпюра от единичной нагрузки должна быть прямолинейной (рис. 382). В тех случаях, когда обе эпюры прямолинейны, можно умножать площадь любой из них на ординату другой под центром тяжести первой.  [c.404]

В этих случаях рекомендуется пользоваться энергетическим методом определения перемещений — частными формулами (интегралом) Мора или способом Верещагина.  [c.45]

Применение метода единичной нагрузки (Максвелла—Мора) с использованием правила Верещагина или формулы Симпсона.  [c.309]

Перемножая эпюры Мр а М способом Верещагина по формуле (11.22), определяем искомое перемещение Д, при этом учитываем, что моменты инерции поперечных сечений различных элементов рамы различны  [c.445]

Перемещения определяем по формуле (11.23), учитывая лишь первые три ее члена. Урожая по способу Верещагина эпюру Л/р (рис. 11.24,6) на эпюру Л/» (рис. 11.24,6) и эпюру Л/ (рис. 11.24, в) на эпюру М (рис. 11.24, с), получаем  [c.450]

Правило Верещагина — графо-аналитический прием вычисления интегралов, входящих в формулы Мора. Правило применимо, если ось участка прямолинейна, и удобно применимо, если жесткость поперечных сечений по длине участка постоянна.  [c.223]

Формула (У1.49) есть аналитическая запись правила Верещагина.  [c.224]

Прежде всего определим першещения уточек приложения грузов под действием единичных сил Pi = l, Р2=1 и Рз=1- С этой целью построим эпюры изгибающих моментов от указанных единичных сил (рис. 562). Пользуясь формулой Верещагина, найдем перемещения от единичных нагрузок  [c.625]

На практике очень часто встречаются многопролётные коленчатые валы (у двигателей внутреннего сгорания). Они представляют собой своеобразную неразрезную балку, для которой можно составить в два раза больше дополнительных уравнений, аналогичных обычным уравнениям трёх моментов, чем мы имеем дополнительных опор (в пространстве каждая опора даёт две реакции). Вывод этих уравнений требует умения вычислять углы поворота сечений коленчатого вала, расположенных над центрами подшипников. Эти вычисления не представляют собой ничего принципиально трудного их можно произвести, применяя теорему Кастильяно или формулу Верещагина.  [c.527]

Формула Верещагина. В большинстве случаев одна из эпюр, например /(х), является на рассматриваемом участке а -А линейной (рис. П.1.2). В этом сл) чае, обозначив Р[c.550]

Вычисление интеграла Мора по формуле (7-3) может быть ныпо нено по правилу Верещагина (указания об области применимости этого правила, данные выше, остаются в силе). Соответствующая формула может быть записана в виде  [c.140]

Графоаналитический прием вычиеления интеграла Мора называется способом Верещагина и сводится к перемножению эпюр изгибак1щих моментов Мд (от заданной нагрузки) и /Я (от единичной нагрузки) по формуле  [c.46]

Определение перемещений по правилу Верещагина иногда на-зьшают перемножением эпюр. Чтобы воспользоваться правилом Верещагина на участках с криволинейным очертанием эпюра надо иметь готовые формулы для определения площадей эпюр изгибающих моментов и абсцисс их центров тяжести для некоторых нагружений консольной балки. Эти формулы даны в табл. 9.  [c.225]

---

mash-xxl.info

Формула Мора Правило Верещагина Доцент кафедры самолетостроения к

Формула Мора Правило Верещагина Доцент кафедры самолетостроения к. т. н. Мухин Д. В.

1. Интеграл Мора Используется в тех случаях, когда требуется найти перемещение в направлении не совпадающем с направлением действия сил. Сущность интеграла Мора в следующем идеальном построении: 1. Прикладываем в интересующем направлении внешнюю силу Ф. 2. Составляем для системы выражение для потенциальной энергии деформации U. 3. Дифференцируем выражение для U по Ф и получаем выражение для перемещения в направлении действия Ф (то есть в интересующем направлении) 4. В полученном выражении приравниваем Ф=0, получаем окончательное выражение.

Фиктивную силу Ф представляем в виде произведения скалярной величины Ф на единичный силовой фактор в соответствующем направлении. Таким образом фиктивная сила в зависимости от интересующего нас направления будет выражена: — в случае продольной силы. Определяем продольное перемещение. N 1 – единичная продольная сила приложенная в интересующей нас точке. — в случае горизонтальной перерезывающей силы. Определяем прогиб в горизонтальной плоскости. Qz 1 – единичная горизонтальная перерезывающая сила приложенная в интересующей нас точке. — в случае вертикальной перерезывающей силы. Определяем прогиб в вертикальной плоскости. Qy 1 – единичная горизонтальная перерезывающая сила приложенная в интересующей нас точке.

— в случае крутящего момента. Определяем угол закручивания. MK 1 – единичный крутящий момент приложенный в интересующей нас точке. — в случае момента изгибающего в горизонтальной плоскости. Определяем угол поворота сечения в горизонтальной плоскости. My 1 – единичный изгибающий момент в горизонтальной плоскости приложенный в интересующей нас точке. — в случае момента изгибающего в вертикальной плоскости. Определяем угол поворота сечения в вертикальной плоскости. Mz 1 – единичный изгибающий момент в вертикальной плоскости приложенный в интересующей нас точке.

После приложения фиктивной силы Ф значения силовых факторов в интересующем сечении будут равны сумме значений силовых факторов от исходной системы сил и от силы Ф. — значения силовых факторов до приложения силы Ф. (То есть в реально существующей системе) Подставляем в формулу для внутренней энергии:

Дифференцируя по Ф, и принимая после этого Ф=0, находим перемещение. (формулы громоздкие, поэтому на примере одного слагаемого)

Суммируя все интегралы находим перемещение Формула носит название формула Мора, а входящие в формулу интегралы – интегралы Мора

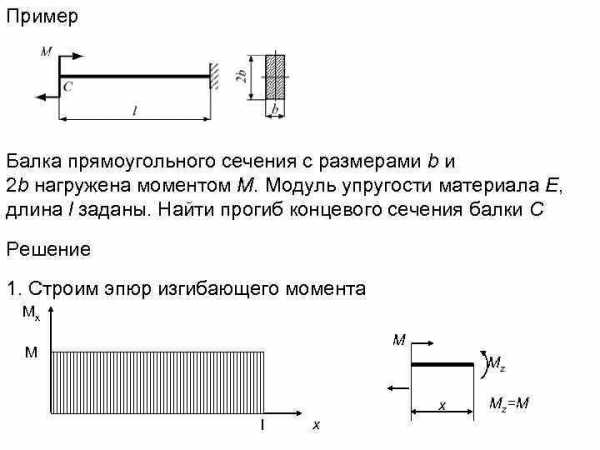Пример Балка прямоугольного сечения с размерами b и 2 b нагружена моментом М. Модуль упругости материала Е, длина l заданы. Найти прогиб концевого сечения балки С Решение 1. Строим эпюр изгибающего момента Мx M М Mz x l x Mz=M

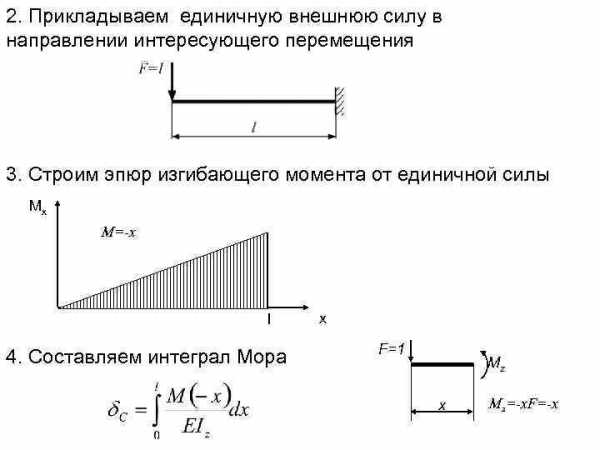2. Прикладываем единичную внешнюю силу в направлении интересующего перемещения 3. Строим эпюр изгибающего момента от единичной силы Мx М=-x l 4. Составляем интеграл Мора x F=1 Mz x Mz=-x. F=-x

5. Вычисляем интеграл

Интеграл Мора можно использовать для определения перемещений как прямолинейных, так и криволинейных стержневых систем. Поскольку интеграл Мора вычисляется по длине, для криволинейных стержней вместо dx в подынтегральном выражении используется элемент длины дуги ds=ρdφ где ρ — радиус кривизны стержня, который может быть постоянным, а может быть функцией от угловой координаты φ. ρ dφ φ1 φ φ2 ds

Пример: Для кривого бруса в форме четверти круга найти горизонтальное перемещение точки А. Нарисуем вспомогательную единичную систему и нагрузим ее горизонтальной единичной силой в точке А. В полярной системе координат положение произвольного сечения характеризуется радиусом-вектором ρ (в нашей задаче ρ = Const — радиус круга) и углом φ от произвольно выбранной начальной точки дуги.

Изгибающий момент от внешних сил Изгибающий момент от единичной силы Горизонтальное перемещение точки А

Правило Верещагина – графо-аналитический метод, позволяющий упростить вычисления интегралов, входящих в формулу Мора. Упрощение основано на том, что эпюры от единичных силовых факторов на прямолинейных участках оказываются линейными. Предположим, что необходимо взять интеграл от произведения двух функций Пусть вторая из этих функций — линейная Тогда Первый интеграл – площадь эпюры f 1(z) Второй интеграл – статический момент этой эпюры относительно оси ординат

По свойству статического момента z. ЦТ – координата центра тяжести первого эпюра В сумме получаем Выражение в скобках – значение функции f 2 под центром тяжести первой фигуры h ЦТ

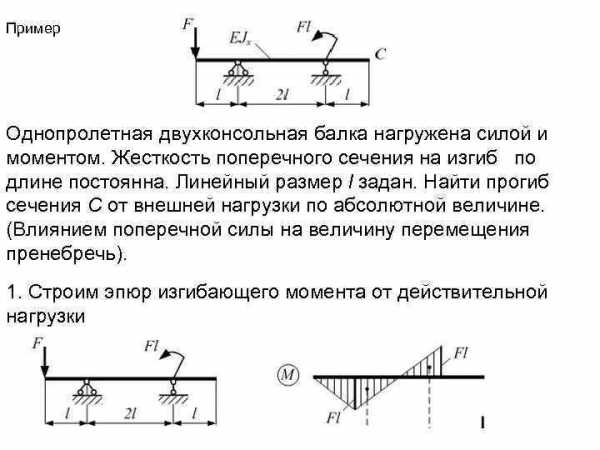Пример Однопролетная двухконсольная балка нагружена силой и моментом. Жесткость поперечного сечения на изгиб по длине постоянна. Линейный размер l задан. Найти прогиб сечения С от внешней нагрузки по абсолютной величине. (Влиянием поперечной силы на величину перемещения пренебречь). 1. Строим эпюр изгибающего момента от действительной нагрузки

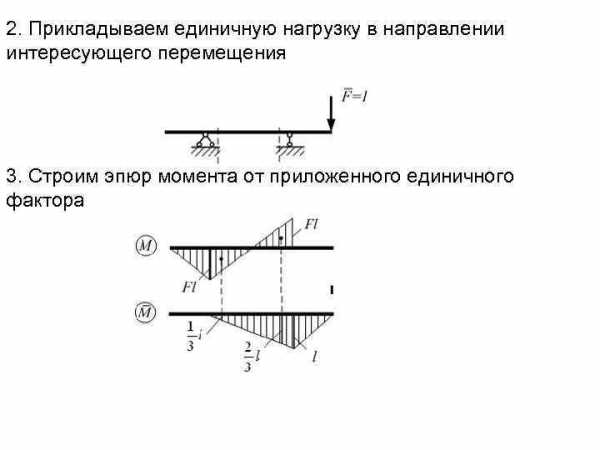2. Прикладываем единичную нагрузку в направлении интересующего перемещения 3. Строим эпюр момента от приложенного единичного фактора

4. Находим интеграл Мора по правилу Верещагина

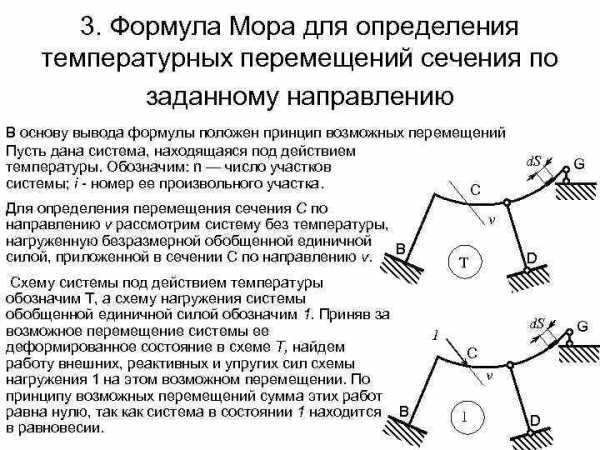3. Формула Мора для определения температурных перемещений сечения по заданному направлению В основу вывода формулы положен принцип возможных перемещений Пусть дана система, находящаяся под действием температуры. Обозначим: n — число участков системы; i — номер ее произвольного участка. C Для определения перемещения сечения С по направлению v рассмотрим систему без температуры, нагруженную безразмерной обобщенной единичной B силой, приложенной в сечении С по направлению v. Схему системы под действием температуры обозначим Т, а схему нагружения системы обобщенной единичной силой обозначим 1. Приняв за возможное перемещение системы ее деформированное состояние в схеме Т, найдем работу внешних, реактивных и упругих сил схемы нагружения 1 на этом возможном перемещении. По принципу возможных перемещений сумма этих работ равна нулю, так как система в состоянии 1 находится B в равновесии. d. S G v D T d. S 1 C v 1 D G

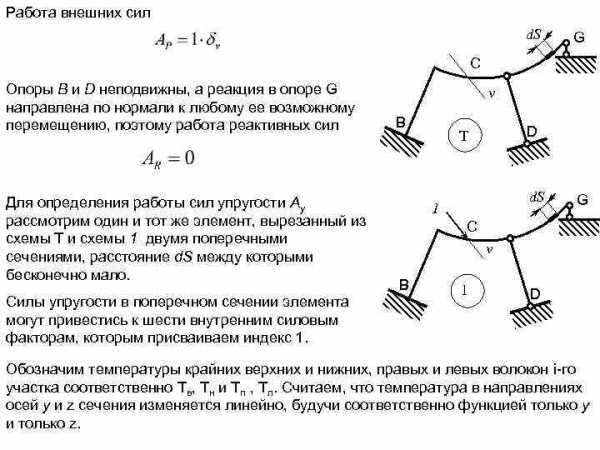Работа внешних сил d. S G C Опоры В и D неподвижны, а реакция в опоре G направлена по нормали к любому ее возможному перемещению, поэтому работа реактивных сил Для определения работы сил упругости Ау рассмотрим один и тот же элемент, вырезанный из схемы Т и схемы 1 двумя поперечными сечениями, расcтояние d. S между которыми бесконечно мало. Силы упругости в поперечном сечении элемента могут привестись к шести внутренним силовым факторам, которым присваиваем индекс 1. v B D T d. S 1 G C v B 1 D Обозначим температуры крайних верхних и нижних, правых и левых волокон i-го участка соответственно Тв, Tн и Тп , Tл. Считаем, что температура в направлениях осей у и z сечения изменяется линейно, будучи соответственно функцией только у и только z.

Законы изменения температуры по поперечному сечению показаны на рис. TB y z Очевидно, что A A T(y) a A’ x b M 21 TH d. S B c d h 2 TП dδT x z B B’ d. S C N 1 y C’ TЛ или hy Температура на оси элемента C T(z) Пусть dδT — возможное перемещение центра тяжести поперечного сечения в схеме от изменения температуры элемента. где α — коэффициент линейного расширения материала элемента. Пусть dθTz — возможный относительный поворот концевых сечений элемента около оси z в схеме от изменения температуры где — наибольший размер поперечного сечения в направлении оси у.

По аналогии, возможный относительный поворот концевых сечений элемента вокруг оси y где — наибольший размер поперечного сечения в направлении оси z. 1. d. Ay — работа сил упругости в элементе d. S по абсолютной величине равна работе внутренних силовых факторов состояния на возможных перемещениях состояния и противоположна ей по знаку, так как силы упругости всегда направлены в сторону, противоположную направлению изменения расстояния между точками тела. 2. Работа МК 1, Qy 1 и Qz 1 равна нулю, так концевые сечения элемента при нагреве относительно оси х не поворачиваются, a Qy 1 и Qz 1 перпендикулярны направлению dδT, поэтому Подставляя сюда полученные ранее выражения и интегрируя полученное выражение по si —длине i-гo участка найдем работу сил упругости на i-м участке.

Суммируя эти интегралы по всем участкам системы, найдем Aу. Складывая Ар с Ау и приравнивая сумму нулю, получим формулу Мора для определения температурных перемещений сечений стержневой системы по заданному направлению:

present5.com