Формула стрела прогиба: Расчет радиуса кривой по хорде и стреле прогиба

Как показывает теория упругости, величина стрелы прогиба может быть вычислена по формуле:

,

где — величина силы, производящей деформацию;

— длина стержня между опорами; как видно стрела прогиба прямо

пропорциональна величине деформирующей силы;

— некоторое постоянное число, зависящее от способа закрепления

стержня, а именно: стержень лежит свободно на двух подставках

(рис.6), то ;

если стержень закреплен с обоих концов, то ;

если стержень закреплен с одного конца, то ;

— величина, зависящая от формы и размеров поперечного сечения

исследуемого образца. Так, например, для стержня с прямоуголь-

ным сечением со сторонами величиной и, если сторона раз-

мером параллельна направлению действующей силы, то

;

для стержня скруглым сечением радиуса .

В итоге для модуля Юнга можно записать формулу:

(2)

Описание прибора.

Прибор для определения модуля Юнга состоит из двух стоек с опорами, на которые помещается испытываемяй образец. Стойки находятся на общем основании, причем одна из них может перемещаться. Это позволяет регулировать длину испытываемого образца. Нагружение испытуемого образца осуществляется с помощью гиревого подвеса и набора грузов.

Измерение прогиба образца производится с помощью индикатора часового типа с ценой деления 0.01 мм. Фиксация стойки к направляющей осуществляется с помощью стопора.

Порядок выполнения работы.

  1. Испытуемый образец поместить на опоры, с серединой его совместить индикатор и вращением стекла установить стрелку индикатора на “0”.

  2. Нагрузить образец начальной нагрузкой “Р” и произвести отсчет стрелы прогиба по шкале индикатора.

  3. Прибавляя грузы “Р1”, затем “Р2”, и т. д. Определяют стрелы прогиба и и т. д., соответствующие нагрузкам Р1+Р2, Р1+Р2+Р3, и т. д. Затем идут в обратном порядке, уменьшая нагрузку и снова определяя стрелу прогиба для каждой нагрузки. Когда все грузы сняты, проверяют соответствие показания индикатора нулевому делению.

Запись результатов измерений и расчетов.

  1. Материал стержня и его форма.

  2. Заносят в таблицу размеры стержня.

№измерений

l, мм

l, мм

r, мм

r, мм

1. Латунь

1000

1

5

0. 1

2. Сталь

1000

1

5

0.1

3. Определяют стрелу прогиба при различных нагрузках и данные заносят в таблицу:

4. Вычисляют среднее значение .

При увеличении нагрузки таблица заполняется сверху вниз, а при уменьшении-снизу вверх.

Расчет модуля Юнга производится по формуле (2) после подстановки в нее К и с учетом формы сечения образца. Для подсчета погрешности проанализировать, какой тип ошибок является определяющим и составить формулу для расчета погрешности исходя из выражения (2).

Сравнить полученный результат с табличным с учетом системы единиц.

нагрузка

, мм

, мм

при

данной

нагрузке

H/мм

H/мм

№

, кг

, Н

при увеличении

нагрузки

при уменьшении

нагрузки

1

2

3

4

1.

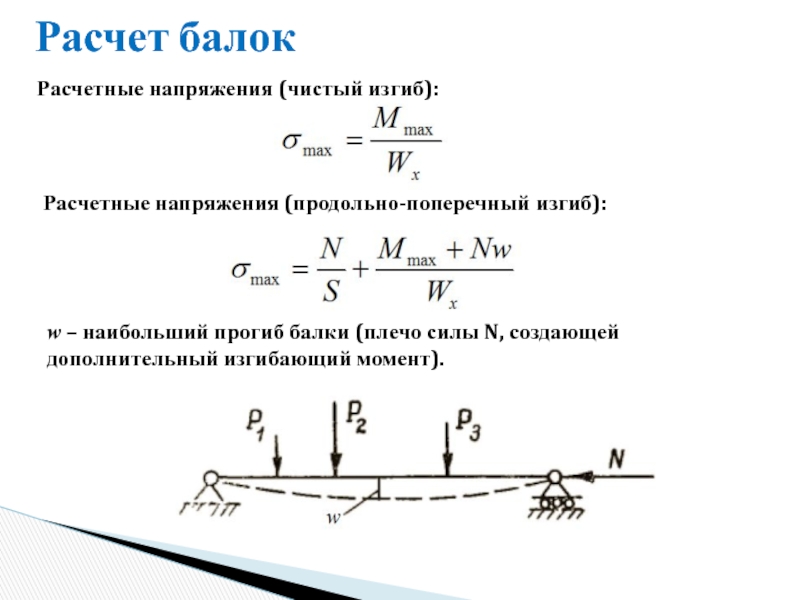2. Вывод расчетной формулы

В задачу данной лабораторной работы входит определение модуля упругости (модуля Юнга) по деформации изгиба. Деформация изгиба в наиболее простой форме возникает в стержне прямоугольного или квадратного сечения, причем в зависимости от положения точек опоры стержня и способа его закрепления возможны три основных случая (рис.2а, 2б, 2в).

Во всех случаях изгиба деформация определяется «стрелкой прогиба» , т.е. тем расстоянием, на которое опускается точка приложения силы, действующей на стержень. Стрелка прогиба зависит от величины нагрузки размеров стержня и формы поперечного стержня, а так же от модуля упругости материала стержня.

Рассмотрим первый случай изгиба (рис.3), т.е., допустим что прямой горизонтальный стержень длиной l с прямоугольным сечением закреплен одним концом неподвижно, а на втором конце имеет нагрузку Р, действующую вертикально. Боковые стороны поперечного сечения стержня расположены вертикально.

Следовательно, нагрузка действует параллельно боковым сторонам сечения (высоте сечения) и перпендикулярно двум другим сторонам (ширине сечения). Размеры этих сторон обозначим «b» и «a».

Весом самого стержня мы пренебрегаем и допускаем, кроме того, что при изгибе верхняя и нижняя грани стержня принимают форму цилиндрических поверхностей.

Рис. 2. Деформации изгиба длинного стержня

Известно, что при изгибе стержня слои, лежащие выше некоторого «нейтрального» уровня ОО, удлиняются а слои, лежащие ниже его, укорачиваются; таким образом, при деформации изгиба слои, лежащие ближе к вогнутой стороне, сжимаются. Следовательно, напряжения, возникающие в стержне при изгибе, определяются деформациями растяжения и сжатия. Между зонами растяжения и сжатия, очевидно, должен лежать бесконечно тонкий слой

ОО, длина которого при изгибе не меняется. Этот слой и называется нейтральным.

Так по закону Гука растяжения и сжатия по абсолютной величине должны быть одинаковы, то нейтральный слой проходит по середине высоты стержня, образуя цилиндрическую поверхность концентрически расположенную с его выпуклой и вогнутой стороной.

Напряжение в стержне, величина которого во всех точках нейтрального слоя равна нулю, постепенно возрастают по мере удаления от него в ту другую сторону, достигая наибольшего значения на его внешних поверхностях.

Для определения стрелы прогиба (рис.3) рассмотрим какое-нибудь поперечное сечение нашего прямоугольного стержня. Далее в нашем участке стержня dx выделим некоторый бесконечно малой величины слой , расположенный на расстоянии

у от нейтрального слоя (рис.3). Этот слой лежит в верхней половине стержня и при деформации удлиняется. Удлинение его dl выразится так:

(3)

Рис.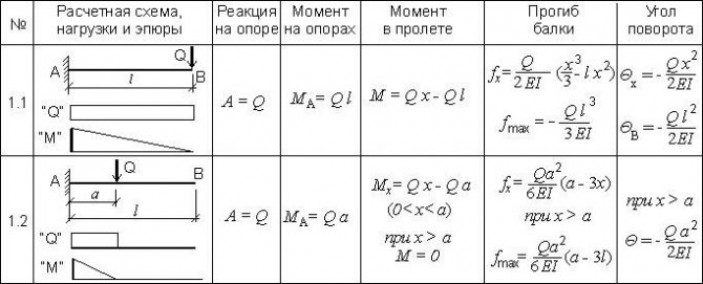 3. Деформация изгиба

Это удлинение создается действием силы dF, которая может быть определена из формулы (2):

(4)

где S= – площадь поперечного сечения деформируемого слоя. Подставляя в формулу (4) значения S и dl получим:

(5)

Момент этой силы относительно нейтрального слоя равен

т.е. (6)

Для вычисления момента силы , вызывающего растяжения стержня по всей верхней половине его поперечного сечения, следует взять сумму элементарных моментов сил для всей верхней части стержня в пределах от

y = 0 (нейтральный слой) до y = b/2

(7)

Нижняя половина стержня подвергается деформации сжатия. Одностороннее сжатие можно рассматривать как деформацию, противоположную продольному растяжению, и применять знака деформации. В результате при вычислении момента силы, вызывающего сжатие нижней половины стержня, для него получается совершенно такое же выражение (7).

Отсюда следует, что момент силы, вызывающий деформацию по всему сечению стержня, равен удвоенному моменту силы , т.е.

(8)

При равновесии стержня вращающий момент, вызываемый напряжениями в сечении S, должен быть равен моменту внешней силы, т.е. , где

Р – нагрузка, вызывающая деформацию стержня.

Следовательно:

(9)

Принимая во внимание, что элемент стрелы прогиба d = xdy , исключим из уравнения (9) величину dy и получим: , откуда

(10)

Для определения полной стрелы прогиба следует проинтегрировать выражение (10) по х в пределах от 0 до l. Вынося величины, не зависящие от переменной х за знак интеграла, получим:

(11)

Формула (11) определяет стрелу прогиба для случая, изображенного на рис. 2а.

Для случая изгиба, изображенного на рис.2б, действие нагрузки Р передается на две неподвижные опоры, каждая из которых оказывает на концы стержня противодействие, равное половине нагрузки Р, т.к. нагрузка приложена посередине между опорами. Таким образом, каждый из концов стержня находится под действием изгибающей силы Р/2, точка приложения которой отстоит от середины стержня на расстоянии , — расстояние между опорами. Можно считать, что стержень в этом случае (рис.2б) находится в таких условиях, что его середина как бы закреплена, а на каждый из концов действует в направлении вверх сила Р/2, которая отстоит от точки закрепления стержня на расстоянии .

Если применить форму (10) для стержня, который обоими концами свободно положен на твердые опоры, пределы интегрирования следует брать от 0 до и вместо Р подставить Р/2, то для стрелы прогиба получим: .

Отсюда:

(12)

Если ввести величину — стрела прогиба, соответствующая единичной нагрузке, тогда

(13)

где l – расстояние между опорами,

a – ширина образца,

b – высота образца (размер, параллельный действию нагрузки),

 — стрела прогиба, соответствующая нагрузка в (СИ).

Выражение (13) является расчетной формулой работы.

Электрическая революция

 

расчет провеса ЛЭП производится с учетом

( 1 ) опор находятся на одном уровне

( 2 ) Опоры находятся на неравном уровне

Мы рассчитает провисание для опор, находящихся на одном уровне.

Предположения

  • Когда проводник установлен между двумя опорами ЛЭП, кривая образованная им форма контактной сети.
  • На самом деле провисание меньше по сравнению пролету, поэтому его можно принять за параболу.
  • Напряжение на проводник в любой точке считается расположенным в горизонтальном направлении.
  • Напряжение у опор одинакова и находится в горизонтальном направлении.

Расчет провеса

Пусть

л = длина пролета (метры)

Ш С = Вес проводника на метр (кг/метр)

T = Напряжение на проводнике (кг)

  • форма прогиба — парабола, поэтому расчет провиса выполняется по формуле учитывая только небольшую часть проводника.
  • Максимальный прогиб в нижней точке (посередине) проводника.
  • Предположим, что самая нижняя точка на проводнике равно O. 
  • Возьмем точку P на проводнике с координатами ( x , y ).
  • Как кривизна мала, длина кривизны OP считается расстоянием по горизонтали Икс.

Сила на проводнике

  • груз W C действует вертикально вниз. Он действует на расстояние x/2 от точки O или точки P. 
  • Горизонтальное натяжение Т в любой точке на проводника (показан на рисунке в точке О.)

момент относительно точки P

Горизонтальная сила × Вертикальное расстояние = Вертикальная сила × Горизонтальное расстояние

T × у = Вт С х ( х / 2 )

у = W C x 2 / 2T  ….. ( 1 )

значение провиса становится максимальным в центральной точке проводника

Прокладка x = L / 2 и y = s ( провисание ) в уравнении ( 1 )

Провисание s = W C ( L / 2 ) 2 / 2T

Прогиб s = W C L 2 / 8T

Следование следует отметить

  • стрела прямо пропорциональна квадрату длины проводника. Если длина проводника удваивается, стрела увеличивается в четыре раза.

       С α (Д) 2

  • провес прямо пропорционален массе проводника на метр.

        С α W C

  • провисание обратно пропорционально обратно пропорционально натяжению на проводник.

        С α ( 1 / T )

( 1 ) Эффект ветра на провесе

  • давление ветра действует в горизонтальном направлении проводника.
  • Действующий сила, действующая на проводник за счет давления ветра и веса проводника, находится в поперечном направлении, как показано на рисунке.
  • Пусть интенсивность ветрового давления p кг/метр 2 и D диаметр проводника.

Площадь расчет на метр длины проводника = D × 1 метр 2

Итого давление ветра на проводник = pD кг

Эффект сила на проводнике из-за веса проводника и давления ветра

Вт e = √ ( W W 2 + W C 2 )

Прогиб s = Ш e Д 2 / 8T

Где W e = Действующая сила на проводнике

действующая сила на проводник имеет две составляющие

( 1 ) W e Cos θ – действует по вертикали вниз и

( 2 ) W e Sin θ – действует на положительное направление оси x.

Вертикальный прогиб = s Cos θ

                    = s ( W C / W e )

( 2 ) Эффект ледового покрытия на провесе

Пусть мы рассмотрим

T = Толщина ледяного покрытия на проводнике

D = Диаметр проводника

вес льда действует вертикально вниз.

Вт и = Вес (масса) льда на метр длины

     = Объем льда на метр длины × плотность льда

     = π / 4 { ( D + 2t ) 2 – D 2 }× плотность

     = π / 4 { ( D 2 + 4Dt + 4t 2 – Д 2 }× плотность льда

     = π / 4 { ( 4Dt + 4t 2 ) } × плотность льда

     = π { ( Dt + t 2 ) } × плотность лед

     = πt { ( D + t ) }× плотность льда …..( 2 )

плотность льда принимается в кг на кубический метр, если дана длина проводника в метре.

Прогиб s = ( W C + W i ) L 2 / 8T

Где W i = πt { ( D + t ) } × плотность льда

( 3 ) Комбинированный влияние ветра и льда на провисание

показана сила воздействия на проводник за счет совместного воздействия ветра и льда на рисунке.

Вес льда на метр длины из уравнения ( 2 )

Вт i = πt { ( D + t ) } × плотность льда

Давление на проводник из-за ветра W w = p × (D + 2t) × 1

= p × (D + 2t)… (3)

Действует усилие на проводнике

Вт e = √ ( W C + W i ) 2 + W w 2

Прогиб s = W e L 2 / 8T

Где W e = √ ( W C + W i ) 2 + W w 2

Вертикально Sag = s Cos θ

                    = s {( W C + W i ) / W e }

Прогиб

Формула прогиба

Проводник только вес

Прогиб s = Ш С Д 2 / 8Т

 

Эффект ветра на стреле

Прогиб s = W e L 2 / 8T

Где W e = √ ( W В 2 + В С 2 )

Вертикальный прогиб = с Cos θ

                   = s ( W C / W e )

Эффект ледового покрытия на провесе

 

Прогиб s = (W C + W i ) L 2 / 8T

Где W i = πt { ( D + t ) } × плотность льда

 

Комбинированный влияние ветра и льда на провисание

 

Прогиб s = W e L 2 / 8T

Где W e = √ ( W C + W i ) 2 + W w 2

Вертикальный Провисание = с Cos θ

                    = s {( W C + W i ) / Вт е }

 

Вы может также понравиться :

Что Вы имеете в виду гармоники напряжения и гармоники тока?

Эффект гармоник коэффициента мощности

Типы сглаживающего реактора

Функция шунтирующего реактора

Одиночный фаза TCR 


Что такое провисание и напряжение в линиях электропередачи и формула расчета

        Провисание является интересной темой для обсуждения. Обычно мы встречаем много воздушных линий на нашем пути. Провис в общих словах можно сказать, что расстояние между самой высокой точкой электрических столбов или опор и самой низкой точкой проводника, соединенного между собой два столба или башни. Вы будете знать , как рассчитать провисание и формулу провисания .

                                                                     

                           что проводники находятся под сейфом напряжение . Если проводники слишком сильно натянуты между опорами в целях экономии материала проводника, напряжение в проводнике может достичь небезопасного значения, а в некоторых случаях проводник может разорваться из-за чрезмерного натяжения. Чтобы обеспечить безопасное натяжение проводов, они не полностью натянуты, но могут иметь провал или провисание .

Разность уровней между точками опор и самой нижней точкой проводника называется прогиб .

Этот учебник «Основы энергосистемы В.К.Мехты» является лучшим в отрасли. Возьмите его сейчас по очень низкой цене.


Обязательно прочитать:

  • Основные элементы воздушных линий электропередачи

              На рисунке (i) ниже показан проводник, подвешенный между двумя равноуровневыми опорами A и B. Проводник не полностью растянут, но может иметь провисание. Самая нижняя точка проводника — O, а провисание — S. Можно отметить следующие точки:

                                 

(i) Когда проводник подвешен между двумя опорами на одном уровне, он принимает форму контактной сети. Однако, если провис очень мал по сравнению с пролетом, то пролет провисания кривая похожа на параболу.

(ii) Напряжение в любой точке проводника действует по касательной. Таким образом, напряжение ТО в самой нижней точке О действует горизонтально, как показано на рисунке (ii).

(iii) Горизонтальная составляющая натяжения постоянна по всей длине проволоки.

(iv) Натяжение на опорах приблизительно равно горизонтальному натяжению, действующему в любой точке провода. Таким образом, если Т — напряжение на опоре В, то Т = ТО.

Провисание и натяжение проводника:  

        Это важное соображение в механической конструкции воздушных линий . Провисание проводника должно быть сведено к минимуму, чтобы уменьшить требуемый материал проводника и избежать дополнительной высоты столба для достаточного зазора над уровнем земли. Также желательно, чтобы натяжение проводника было низким, чтобы избежать механического разрушения проводника и позволить использовать менее прочные опоры. Тем не менее, низкая натяжение проводника и минимальный провес не возможен. Это связано с тем, что низкое провисание означает натяжение проволоки и высокое натяжение, тогда как низкое натяжение означает ослабление проволоки и повышенное провисание. Поэтому на практике между ними достигается компромисс.

Расчет провисания в воздушных линиях электропередачи:

         В воздушной линии провисание должно быть отрегулировано таким образом, чтобы натяжение проводов находилось в безопасных пределах. Натяжение зависит от веса проводника, воздействия ветра, нагрузка на лед и перепады температуры. Стандартной практикой является поддержание натяжения проводника на уровне менее 50% от его предела прочности на растяжение, т. е. минимальный коэффициент безопасности в отношении натяжение проводника должно быть равно 2. Теперь мы вычислим провисание и натяжение проводника, когда

 (i) опоры находятся на одном уровне                      

 (ii) опоры находятся на разных уровнях

(i) Когда поддерживает находятся на одном уровне:  Рассмотрите проводник между двумя равноуровневыми опорами A и B, где O является самой нижней точкой, как показано на рисунке ниже. Можно доказать, что самая нижняя точка будет в середине пролета. Пусть

                  l = Длина пролета

                 w = вес на единицу длины проводника

                 T = Напряжение в проводнике.

           Рассмотрим точку P на проводнике. Взяв самую нижнюю точку O за начало координат, пусть координаты точки P равны x и y. Предположим, что кривизна настолько мала, что длина кривой равна ее горизонтальной проекции (т. е. OP = x), две силы, действующие на часть OP проводника, равны:

(a) Вес wx проводника, действующий на расстоянии x/2 от O.

(b) Напряжение T, действующее в точке O.                 

Максимальное падение ( прогиб ) представлено значение y на любой из опор A и B. На опоре A x = l/2 и y = S. ) Когда опоры находятся на неравных уровнях: В холмистой местности мы обычно встречаем проводники, подвешенные между опорами на разных уровнях. На рисунке ниже показан проводник, подвешенный между двумя опорами A и B, которые находятся на разных уровнях. Самая нижняя точка проводника — O.

Пусть l    =  Длина пролета

     h   =  Разность уровней между двумя опорами

     x1 =  Расстояние опоры на нижнем уровне (т. е. A) от O

    x2 = расстояние поддержки на более высоком уровне (т.е. B) от O

      T  = Натяжение в проводнике на единицу длины проводника, то

= l

                

Найдя x1 и x2 значения S1 и S2 можно легко рассчитать.

Учебник «Основы энергосистемы В.К.Мехты» является лучшим в отрасли. Возьмите его сейчас по очень низкой цене.


Влияние ветровой и ледовой нагрузки на линии электропередачи :

             Вышеприведенная формула для провеса верна только в неподвижном воздухе и при нормальной температуре, когда на провод действует только его вес. Однако на практике проводник может иметь ледяное покрытие и одновременно подвергаться ветровому давлению. Вес льда действует вертикально вниз, т. е. в том же направлении, что и вес проводника. Предполагается, что сила ветра действует горизонтально, т. е. под прямым углом к ​​проецируемой поверхности проводника. Следовательно, общая сила, действующая на проводник, представляет собой векторную сумму горизонтальных и вертикальных сил, как показано на рисунке (iii) ниже.

                                               

Общий вес проводника на единицу длины                                            

Если на кондуктор воздействуют также ветровая и ледовая нагрузки, можно отметить следующие моменты:

(i) Кондуктор устанавливается в плоскости под углом θ к вертикали

0483 определяется как:

                                     

Следовательно, S представляет собой наклон провисания в направлении, составляющем угол θ к вертикальный. Если в задаче не указано конкретное упоминание, то наклонный шлак рассчитывается по приведенной выше формуле.