Пластичность грунта – описание, формула

Пластичность грунта – это физическое свойство связных дисперсных грунтов менять свою форму без разрыва под воздействием внешних нагрузок. После снятия давления форма сохраняется. Характеристика в большинстве своем зависит от влажности.

• Пластичность грунта
• Что такое пластичность грунта
• Определение пластичности грунта
• Определение верхнего предела пластичности
• Определение нижнего предела пластичности
• Метод раскатывания шнура
• Метод прессования
• Расчет числа пластичности
• Практическое значение показателя пластичности грунтов
• Другие свойства грунтов, связанные с пластичностью
• Показатель текучести
• Консистенция
• Активность грунта

Пластичность свойственна глинистым и лёссовидным грунтам с мелкими частицами. Определяется свойство по верхнему и нижнему пределу пластичности. Цифровым выражением показателя является число пластичности.

Что такое пластичность грунта

В любом грунте присутствует влага.

Она бывает:

• Связанной
  Молекулы воды связываются с глинистыми минералами, гумусом и другими веществами. Чаще всего такой тип встречается в глинистых и пылеватых грунтах, плодородных почвах, торфе. Связанная влага с трудом удаляется при высушивании.
• Капиллярной
  Эта вода находится в мелких порах с размерами 0,001-1 мм. Она способна подниматься из нижних горизонтов в верхние под влиянием силы поверхностного натяжения. Жидкость может отжиматься и удаляться из открытых капилляров, из закрытых – только после их разрушения.
• Осмотической
  Вода проникает в микроагрегаты и глинистые зерна под влиянием осмотических сил. Она связывается с минералами, отвечает за набухание грунта и его пластические свойства.
• Свободной
  Вода находится в крупных порах с размерами больше 1 мм. Она не связана с химическими элементами грунта, свободно удаляется под давлением или при высушивании.

Пластические свойства проявляются, когда в материале преобладает капиллярная и осмотическая влаги. Такая вода накапливается в микропорах глинистого грунта и внутри его зерен.

Существует две основные теории, объясняющие механизм возникновения пластичности:

• Коллоидная
  В глинистых грунтах всегда присутствуют коллоиды – мелкие твердые частицы, распределенные в жидкости. Они связывают между собой глинистые зерна грунта, при этом не препятствуют их перемещению относительно друг друга. Коллоиды выступают своеобразной смазкой, позволяющей грунту деформироваться без потери связности.
• Гидратная
  Согласно этой теории, пластичность обеспечивает тонкая прослойка воды между глинистыми частицами. Она связывает между собой элементы грунта, но при этом они могут перемещаться относительно друг друга.

Обе теории дополняют друг друга. Скорее всего пластичность обеспечивается как коллоидами, так и водными прослойками.

При снижении влажности связь между частицами ослабевает, грунт твердеет или начинает распадаться на куски. Повышение влажности ведет к появлению большого количества свободной воды. Глинистый грунт в таком случае переходит в текучее состояние (превращается в эмульсию).

По показателю влажности определяют основные параметры пластичности:

• Нижний предел пластичности (Wp) – влажность, при которой грунт становится твердым или теряет связность
• Верхний предел пластичности (Wl) – влажность, при которой грунт становится текучим (превращается в жидкую эмульсию)
• Число пластичности (Ip) – разница между верхним и нижним пределом (Ip=Wl-Wp)

Именно на числе пластичности основывается классификация глинистых грунтов (ГОСТ 25100-2011 и новый ГОСТ 25100-2020). Она дана в таблице.

Тип грунта	Число пластичности, lp
Супесь	1-7
Лёгкий суглинок	7-12
Тяжёлый суглинок	12-17
Лёгкая глина	17-27
Тяжёлая глина	Больше 27

Пластичность, даже при определенной влажности, есть не у всех грунтов.

Она зависит от ряда характеристик:

• Гранулометрического состава
  Площадь поверхности мелких глинистых частиц очень большая, что позволяет конденсироваться на их поверхности большему количеству воды.
• Минерального состава
  Глины на основе монтмориллонита (слоистого глинистого минерала, обладающего способностью впитывать большое количество воды и набухать) обладают большей пластичностью, чем на основе каолинита (глинистого минерала класса водных силикатов алюминия с меньшей склонностью к набуханию).
• Молекулярного состава
  Пластичность падает при возрастании в грунте трехвалентных ионов (алюминия, трехвалентного железа) и увеличивается при появлении одно- и двухвалентных (лития, калия, натрия, двухвалентного железа).
• Состава воды
  В естественных условиях вода представляет собой раствор солей разной концентрации. Чем больше в ней соли, тем меньше пластичность грунта при определенных параметрах влажности.

Дальше мы опишем, как определяются все показатели пластичности.

Определение пластичности грунта

Верхний и нижний предел пластичности определяют экспериментально по влажности на границе раскатывания и текучести. Затем по полученным данным вычисляют число пластичности.  Методики описаны в ГОСТ 5180-2015. Подробно о каждой читайте в соответствующей части статьи.

Определение верхнего предела пластичности

Чтобы определить верхний предел пластичности (или влажность на границе текучести), понадобятся:

• Сушильный шкаф
• Аналитические весы
• Балансирный конус Васильева массой 76±2 г и с углом уклона возле вершины 30°
• Цилиндрическая чаша (идет в наборе с конусом)
• Металлическая или фарфоровая чаша для размельчения грунта диаметром 7-8 см
• Шпатель
• Фарфоровая миска с пестиком
• Терка
• Вазелин
• Сито с ячейками 1 мм

Образец для испытания может иметь нарушенное сложение.

Минеральные грунты берут как с природной влажностью, так и в воздушно-сухом состоянии. Ил и почва должны иметь естественную влажность.

Пробу подготавливают следующим образом:

1. Грунт растирают в миске или натирают на терке
2. Органические останки с размерами больше 1 мм обязательно вынимают
3. Материал просеивают через сито с ячейками 1 мм
4. Отбирают пробу массой около 100 г, к ней добавляют дистиллированную воду и выдерживают массу в чаше 2 часа (тяжелые суглинки – 6 часов)
5. Лишнюю влагу из ила удаляют фильтровальной бумагой или отжимают образец в хлопчатобумажной ткани

Проведение испытания:

1. Подготовленную пасту из грунта выкладывают в цилиндрическую чашу. Она должна полностью заполнить емкость. Поверхность выравнивают на уровне краев чаши.
2. Поверхность балансирного конуса смазывают вазелином и подводят его острие к поверхности грунтовой пасты.
3. Затем конус плавно опускают, чтобы он погружался в грунт под давлением собственного веса.
4. Влажность на границе текучести фиксируется в том случае, когда конус опускается за 5 секунд на глубину 10 мм.
5. После этого из образца отбирают пробу 15-30 г и определяют ее влажность по стандартной методике. О ней вы можете прочитать в статье Влажность грунта.

Если за 5 секунд конус погружается на меньшую глубину, чем 10 мм, пасту вынимают из цилиндра, доливают к ней дистиллированную воду, тщательно перемешивают и повторяют опыт.

Если за такой же промежуток времени конус опускается в грунт больше, чем на 10 мм, образец следует просушить. Для этого пасту перекладывают в фарфоровую чашу и слегка просушивают ее на воздухе, постоянно помешивая шпателем.

В США для определения границы текучести используется метод Казагранде (Casagrande). В этом случае в специальную чашу накладывают грунтовую пасту. По центру делают борозду шириной 1,25 см. Затем на приборе с электрическим приводом чашу приподнимают и бросают на резиновое покрытие. На границе текучести после 25 ударов бороздка должна закрыться. Метод довольно субъективный, поэтому показатели американских, европейских и российских стандартов могут не совпадать.

В Западной Европе, Канаде, Японии, Австралии используется 2 типа цилиндров – весом 80 г и 60 г. В первом случаев угол скоса у вершины 30°, во втором – 60°. В остальном методика не отличается от предложенной российским ГОСТ 5180-2015.

Определение нижнего предела пластичности

Нижний предел пластичности – это влажность, при которой грунт начинает твердеть и распадаться на куски.

Ее определяют двумя методами:

• Раскатыванием шнура
• Прессованием

Их описание вы найдете в продолжении текста.

Метод раскатывания шнура

Для проведения опыта понадобятся:

• Сушильный шкаф
• Аналитические весы
• Стеклянные или металлические бюксы (небольшие баночки с крышками)
• Шпатель
• Ступка с пестиком
• Фарфоровая чаша
• Мелкая терка
• Сито с ячейками 1 мм
• Пластиковая или стеклянная пластина

Проба готовится так же, как и при определении влажности на границе текучести. Чаще всего из предыдущего образца берут пробу 40-50 г.

Порядок проведения исследования следующий:

1. Берут небольшую часть грунта, разминают его и раскатывают на пластине шнур. Его диаметр – 3 мм, длина – около ширины ладони.
2. После раскатывания грунт сминают в комок и опять раскатывают. Процедуру повторяют до тех пор, пока шнур не начнет распадаться на куски по 3-10 мм.
3. Куски собирают в бюксы и закрывают крышками.
4. Когда масса кусочков грунта достигнет 10-15 г, определяют их влажность по стандартной методике.

Метод прессования

Для определения нижнего предела пластичности в этой методике используется прессование грунта в контакте с целлюлозой (фильтровальной бумагой). Суть опыта в том, что под прессом из грунта отжимается жидкость, пока не будет достигнута влажность на границе раската.

Для проведения опыта понадобятся:

• Сушильный шкаф
• Аналитические весы
• Бюксы
• Фарфоровая чаша и ступка с пестиком
• Шпатель
• Сито с ячейками 1 мм
• Фильтровальная бумага
• Хлопчатобумажная ткань
• Деревянные либо металлические пластинки
• Металлический лабораторный шаблон округлой формы толщиной 2 мм и с отверстием по центру (диаметр отверстия 5 см)
• Пресс

Образец готовят таким же образом, как и в предыдущих методиках.

Порядок проведения исследования:

1. Шаблон укладывают на хлопчатобумажную ткань. Отверстие заполняют грунтовой пастой и выравнивают ее поверхность на уровне его края.
2. Далее шаблон убирают, а оставшийся образец сверху накрывают тканью.
3. Затем на грунт снизу и сверху кладут фильтровальную бумагу в ткани.
4. Пробу прижимают пластинками и воздействуют на нее прессом, чтобы создать давление 2 МПа (20 кг/см2). Прессуют пробу 10 минут.
5. После образец вынимают, снимают с него фильтровальную бумагу и ткань.
6. Грунтовую лепешку перегибают пополам. Если на сгибе появилась трещина, значит достигнута влажность на границе раската.
7. Если трещина не появилась, берут новую порцию грунтовой пасты и повторяют опыт. Время давления при этом увеличивается на 10 минут.

При использовании метода прессования около 20% образцов нужно параллельно проверять с помощью раскатывания шнура. Результаты обоих способов должны быть сопоставимыми. Поскольку методика не является полностью самостоятельной и требует большего количества оборудования, она применяется редко.

Расчет числа пластичности

После определения влажности на границе текучести и раската рассчитывают число, или индекс пластичности (Ip) по формуле:

Число пластичности – это основной показатель, по которому оценивают это свойство. На его основе грунты разделяют на глины, суглинки и супеси. Классификация подана в таблице выше.

На основе числа пластичности также рассчитывают предполагаемую деформацию грунта под нагрузками. Поэтому показатель определяют при планировании строительства на глинистых грунтах.

Практическое значение показателя пластичности грунтов

Пластичность – это один из основных показателей, который позволяет оценивать глинистые грунты.

Он влияет на следующие важные характеристики:

Несущую способность
Пластичная и текучая глина имеет более низкую несущую способность, чем твердая. Она сильно деформируется под давлением, проседает. Поэтому следует учитывать, при какой влажности грунт перейдет в пластичное состояние. При этом также смотрят, насколько эта влажность выше, чем естественная, на том или ином участке.

• Склонность к набуханию и усадке
  По пластичности грунта определяют его активность. Чем выше этот показатель, тем сильнее набухает глинистый грунт.
• Структурную прочность
  Прочность грунта падает при переходе от твердого к пластичному и от пластичного к текучему состоянию.

Для строительных грунтов высокое число пластичности – отрицательная характеристика. Это значит, что грунт находится в пластичном состоянии при широком диапазоне влажности. Высокий показатель будет полезен в керамической промышленности, при производстве цемента и в ряде других сфер. В них используются пластичные глины, из которых делают посуду, фарфор и другие материалы.

Также отметим, что с пластичностью связано несколько других показателей, которые характеризуют состояние грунтов при разной влажности. О них вы узнаете дальше.

Другие свойства грунтов, связанные с пластичностью

С пластичностью грунта непосредственно связаны следующие характеристики:

• Показатель текучести
• Консистенция
• Активность грунта

Детальнее об их значении и способах расчета мы расскажем в продолжении этой части статьи.

Показатель текучести

Показатель, или индекс текучести (Il) – это величина, которая рассчитывается по формуле для грунтов с естественной влажностью и нарушенным сложением.

Характеристика помогает предвидеть некоторые механические свойства глинистых грунтов, такие как:

• Влажность, при которой они переходят в текучее состояние
• Степень усадки основания
• Степень деформации под определенным давлением

Индекс текучести рассчитывают по формуле:

В таблице ниже вы найдете классификацию глин, суглинков и супесей в зависимости от показателя текучести. Скажем сразу, что эта типология неофициальная, не закреплена в ГОСТах.

Тип грунта	Индекс текучести (il)
	Меньше 0,01	0,01 — 0,25	0,25 — 0,5	0,5 — 0,75	0,75 — 1	Больше 1
Глины и суглинки	Твёрдые	Полутвёрдые	Тугопластичные	Мягкопластичные	Текучепластичные	Текучие
Супеси	Твёрдые	Пластичные	Пластичные	Пластичные	Пластичные	Текучие

Консистенция

Показатель, или индекс консистенции (Ic) характеризует способность грунта сохранять свою форму и состояние при механическом воздействии и без него. Он включает больше параметров грунта, зависящих от влажности, чем пластичность.

Консистенция бывает жидкой и твердой. Также выделяют ряд переходных форм:

• Текучую
• Текуче-пластичную
• Мягкопластичную
• Тугопластичную
• Пластичную
• Сыпучую

Консистенция определяется в илистых и глинистых грунтах, плодородных почвах. Она зависит от количества и типа влаги, которая находится в грунте. Наибольшее значение имеют связанная и капиллярная вода. При наличии большого количества свободной влаги грунт переходит в текучее состояние.

У торфа и заторфленных грунтов консистенцию не определяют. Их свойства менять свое состояние зависят не столько от воды и мелких частиц, сколько от природных восков и битумов.

Индекс консистенции определяется по формуле:

В зависимости от показателя, грунты делятся на 4 группы:

1. Очень твердые – индекс консистенции больше 1 (литифицированные или окаменевшие глины)
2. Твердые – 0,5-1 (сухие глины и суглинки)
3. Мягкие – 0,05-0,5 (влажные глинистые грунты)
4. Жидкие – меньше 0,05 (водонасыщенные глинистые грунты в текучем состоянии)

Активность грунта

Под активностью глинистого грунта (А) понимают соотношение пластичности и количества глинистых частиц. Показатель дает представление, насколько грунт склонен к набуханию и усадке.

По активности глинистые грунты разделяют на:

• Неактивные глины со слабой склонностью к набуханию (А меньше 0,75)
• Средне активные (А больше 0,75 и меньше 1,25)
• Активные с выраженной склонностью к набуханию (А больше 1,25)

Показатель активности зависит не только от гранулометрического, но и от химического состава.

В таблице даны виды глинистых минералов и показатели их активности (склонности к набуханию).

Тип минерала	Показатель активности (А)
Смектит	1 — 7
Иллит	0,5 — 1,0
Каолинит	0,5
Гидратированный галлуазит	0,1
Дегидратированный галлуазит	0,5
Атгапульгит	0,5 — 1,2
Аллофан	0,5 — 1,2

Вы можете попробовать и самостоятельно определить, какой грунт у вас на участке. Для этого нужно взять комок грунта и увлажнить его до мягкого состояния. Затем необходимо скатать из него шарик и распластать его в лепешку.

Результаты могут быть следующими:

• Глина распластывается в лепешку без трещин
• Суглинок дает трещины по краям
• Супесь распадается

Но такой метод, разумеется, дает очень условные результаты. Они пригодятся для определения типа грунта на вашем участке, чтобы в последующем можно было улучшить его свойства добавлением песка, перегноя или чернозема. Можно ориентироваться на приблизительные данные и при строительстве небольшого помещения для садового инвентаря. Но если вы планируете возводить жилое здание, строить капитальный гараж или сарай, лучше заказать геодезические исследования у специалистов.

Упругость и пластичность. Закон Гука (Лекция №8)

   Действие внешних сил на твердое тело приводит к возникновению в точках его объема напряжений и деформаций. При этом напряженное состояние в точке, связь между напряжениями на различных площадках, проходящих через эту точку, определяются уравнениями статики и не зависят от физических свойств материала. Деформированное состояние, связь между перемещениями и деформациями устанавливаются с привлечением геометрических или кинематических соображений и также не зависят от свойств материала. Для того чтобы установить связь между напряжениями и деформациями, необходимо учитывать реальные свойства материала и условия нагружения. Математические модели, описывающие соотношения между напряжениями и деформациями, разрабатываются на основе экспериментальных данных. Эти модели должны с достаточной степенью точности отражать реальные свойства материалов и условия нагружения.

   Наиболее распространенными для конструкционных материалов являются модели упругости и пластичности. Упругость — это свойство тела изменять форму и размеры под действием внешних нагрузок и восстанавливать исходную конфигурацию при снятии нагрузок. Математически свойство упругости выражается в установлении взаимно однозначной функциональной зависимости между.компонентами тензора напряжений и тензора деформаций. Свойство упругости отражает не только свойства материалов, но и условия нагружения. Для большинства конструкционных материалов свойство упругости проявляется при умеренных значениях внешних сил, приводящих к малым деформациям, и при малых скоростях нагружения, когда потери энергии за счет температурных эффектов пренебрежимо малы. Материал называется линейно-упругим, если компоненты тензора напряжений и тензора деформаций связаны линейными соотношениями.

   При высоких уровнях нагружения, когда в теле возникают значительные деформации, материал частично теряет упругие свойства: при разгрузке его первоначальные размеры и форма полностью не восстанавливаются, а при полном снятии внешних нагрузок фиксируются остаточные деформации. В этом случае зависимость между напряжениями и деформациями перестает быть однозначной. Это свойство материала называется пластичностью. Накапливаемые в процессе пластического деформирования остаточные деформации называются пластическими.

   Высокий уровень нагружения может вызвать разрушение, т. е. разделение тела на части. Твердые тела, выполненные из различных материалов, разрушаются при разной величине деформации. Разрушение носит хрупкий характер при малых деформациях и происходит, как правило, без заметных пластических деформаций. Такое разрушение характерно для чугуна, легированных сталей, бетона, стекла, керамики и некоторых других конструкционных материалов. Для малоуглеродистых сталей, цветных металлов, пластмасс характерен пластический тип разрушения при наличии значительных остаточных деформаций. Однако подразделение материалов по характеру разрушения на хрупкие и пластичные весьма условно, оно обычно относится к некоторым стандартным условиям эксплуатации. Один и тот же материал может вести себя в зависимости от условий (температура, характер нагружены я, технология изготовления и др. ) как хрупкий или как пластичный. Например, пластичные при нормальной температуре материалы разрушаются как хрупкие при низких температурах. Поэтому правильнее говорить не о хрупких и пластичных материалах, а о хрупком или пластическом состоянии материала.

   Пусть материал является линейно-упругим и изотропным. Рассмотрим элементарный объем, находящийся в условиях одноосного напряженного состояния (рис. 1), так что тензор напряжений имеет вид

   При таком нагружении происходит увеличение размеров в направлении оси Ох, характеризуемое линейной деформацией , которая пропорциональна величине напряжения

(1)




Рис.1. Одноосное напряженное состояние

 

   Это соотношение является математической записью закона Гука, устанавливающего пропорциональную зависимость между напряжением и соответствующей линейной деформацией при одноосном напряженном состоянии. Коэффициент пропорциональности E называется модулем продольной упругости или модулем Юнга. Он имеет размерность напряжений.

   Наряду с увеличением размеров в направлении действия; же напряжения происходит уменьшение размеров в двух ортогональных направлениях (рис. 1). Соответствующие деформации обозначим через и , причем эти деформации отрицательны при положительных и пропорциональны :

(2)

   Коэффициент пропорциональности называется коэффициентом Пуассона, который в силу изотропности материала одинаков для обоих ортогональных направлений.

Соотношения, аналогичные (1) и (2), в случае одноосного нагружения в направлении осей Оу, Ог напряжением , , соответственно имеют вид

	(3)
	(4)

   При одновременном действии напряжений по трем ортогональным осям, когда отсутствуют касательные напряжения, для линейно-упругого материала справедлив принцип суперпозиции (наложения решений):

С учетом формул (1 — 4) получим

(5)

   Касательные напряжения вызывают угловые деформации, причем при малых деформациях они не влияют на изменение линейных размеров, и следовательно, на линейные деформации. Поэтому они справедливы также в случае произвольного напряженного состояния и выражают так называемый обобщенный закон Гука.

   Угловая деформация обусловлена касательным напряжением , а деформации и — соответственно напряжениями и . Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости

(6)

которые выражают закон Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига. Существенно, что нормальное напряжение не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними (рис. 1).

   Линейная зависимость существует также между средним напряжением (2.18), пропорциональным первому инварианту тензора напряжений, и объемной деформацией (2.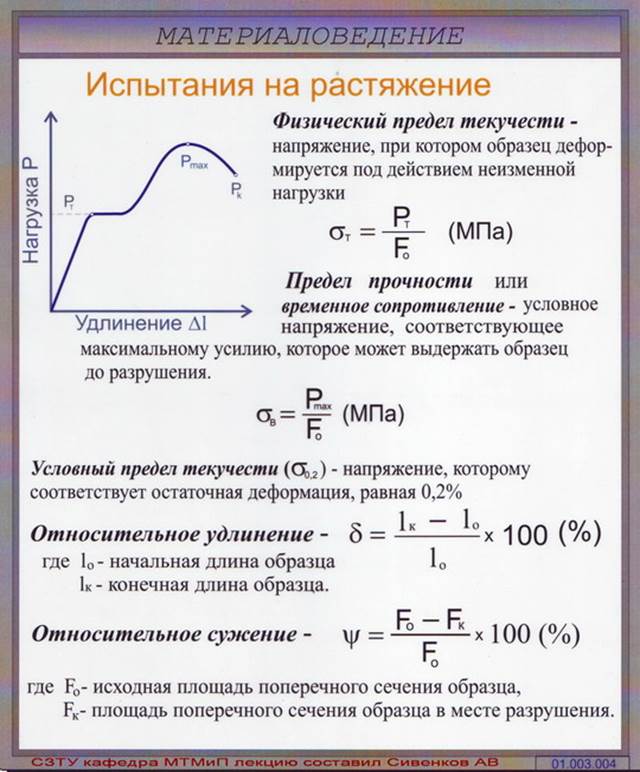 32), совпадающей с первым инвариантом тензора деформаций:

(7)



Рис.2. Плоская деформация сдвига

 

Соответствующий коэффициент пропорциональности К называется объемным модулем упругости.

   В формулы (1 — 7) входят упругие характеристики материала Е, , G и К, определяющие его упругие свойства. Однако эти характеристики не являются независимыми. Для изотропного материала независимыми упругими характеристиками являются две, в качестве которых обычно выбираются модуль упругости Е и коэффициент Пуассона . Чтобы выразить модуль сдвига G через Е и , рассмотрим плоскую деформацию сдвига под действием касательных напряжений (рис. 2). Для упрощения выкладок используем квадратный элемент со стороной а. Вычислим главные напряжения , . Эти напряжения действуют на площадках, расположенных под углом к исходным площадкам. Из рис. 2 найдем связь между линейной деформацией в направлении действия напряжения и угловой деформацией . Большая диагональ ромба, характеризующая деформацию , равна

Для малых деформаций

С учетом этих соотношений

До деформации эта диагональ имела размер . Тогда будем иметь

Из обобщенного закона Гука (5) получим

откуда

Сравнение полученной формулы с записью закона Гука при сдвиге (6) дает

(8)

Сложим три соотношения упругости (5)

(9)

В итоге получим

Сравнивая это выражение с объемным законом Гука (7), приходим к результату

   Механические характеристики Е, , G и К находятся после обработки экспериментальных данных испытаний образцов на различные виды нагрузок. Из физического смысла все эти характеристики не могут быть отрицательными. Кроме того, из последнего выражения следует, что коэффициент Пуассона для изотропного материала не превышает значения 1/2. Таким образом, получаем следующие ограничения для упругих постоянных изотропного материала:

   Предельное значение приводит к предельному значению , что соответствует несжимаемому материалу ( при ). В заключение выразим из соотношений упругости (5) напряжения через деформации. Запишем первое из соотношений (5) в виде

С использованием равенства (9) будем иметь

откуда

Аналогичные соотношения можно вывести для и . В результате получим

(10)

Здесь использовано соотношение (8) для модуля сдвига. Кроме того, введено обозначение

 

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ

   Рассмотрим вначале элементарный объем dV=dxdydz в условиях одноосного напряженного состояния (рис. 1). Мысленно закрепим площадку х=0 (рис. 3). На противоположную площадку действует сила . Эта сила совершает работу на перемещении . При увеличении напряжения от нулевого уровня до значения соответствующая деформация в силу закона Гука также увеличивается от нуля до значения , а работа пропорциональна заштрихованной на рис. 4 площади: . Если пренебречь кинетической энергией и потерями, связанными с тепловыми, электромагнитными и другими явлениями, то в силу закона сохранения энергии совершаемая работа перейдет в потенциальную энергию, накапливаемую в процессе деформирования: . Величина Ф=dU / dV называется удельной потенциальной энергией деформации, имеющей смысл потенциальной энергии, накопленной в единице объема тела. В случае одноосного напряженного состояния




Рис.3. Расчетная схема энергии деформации

 

Рис.4. Линейный закон сопротивления

 

   При одновременном действии напряжений , и на главных площадках (т. е. при отсутствии касательных напряжений) потенциальная энергия равна сумме работ, совершаемых силами на соответствующих перемещениях . Удельная потенциальная энергия равна

.




Рис.5. Расчетная схема сдвигаемой энергии

 

   В частном случае чистого сдвига в плоскости Оху, изображенном на рис. 5, сила совершает работу на перемещении . Соответствующая этому случаю удельная потенциальная энергия деформации равна

Подобные соотношения будут иметь место при сдвиге в других плоскостях.

В общем случае напряженно-деформированного состояния будем иметь

(11)

   Если деформации выразить через напряжения с помощью соотношений упругости (5) и (6), то получим эквивалентную (11) форму записи через компоненты тензора напряжений

(12)

   Выразив напряжения через деформации с использованием соотношений (6) и (10), получим еще одну форму записи для Ф — через компоненты тензора деформаций

   Еще одну форму записи для удельной потенциальной энергии деформации получим, разложив тензоры напряжений и деформаций на шаровые тензоры и девиаторы. В результате (11) можно привести к одной из форм

(13)

   Здесь введены обозначения для — интенсивности касательных напряжений и — интенсивности деформаций сдвига, которые выражаются через вторые инварианты и девиаторов тензора напряжений и тензора деформаций следующим образом:

   Первые слагаемые в (13) соответствуют произведению шаровых составляющих тензоров напряжений и деформаций, а вторые — произведению девиаторных составляющих. Так как шаровой тензор характеризует изменение объема, а девиатор — изменение формы, то соотношения (13) можно интерпретировать как разложение удельной потенциальной энергии на две составляющие: Ф=Ф₀+Ф_ф, где Ф₀ соответствует изменению объема без изменения формы, а Ф_ф — изменению формы без изменения объема. Первая составляющая будет вычисляться через компоненты тензора напряжений следующим образом:

(14)

   Удельную потенциальную энергию изменения формы проще найти не через интенсивность касательных напряжений, а как разность Ф — Ф₀. Вычитая (14) из (12), после преобразований получим

Дальше…

Уравнения изотропной пластичности фон Мизеса — Добро пожаловать на сайт поддержки LS-DYNA

Уравнения изотропной пластичности фон Мизеса https://www.dynasupport.com/tutorial/computational-plasticity/the-equations-for-isotropic-von-mises-plasticity https://www.dynasupport.com/@@site-logo/LS-DYNA-Support-Logo480x80.png

 Эволюция напряжения описывается системой дифференциальных уравнений,

 

, где верхний индекс e означает эластичность. p, а эквивалентное напряжение принимается равным предел текучести,

Поскольку шестимерное пространство напряжений сжимается в одно число, существует множество состояний напряжения, которые будут создавать одно и то же эквивалентное напряжение, и они в совокупности определяют поверхность в пространстве напряжений. Конкретный набор напряжений, удовлетворяющих уравнению 8, определяет поверхность текучести, а нормаль к поверхности текучести определяется как

Пластическое течение происходит, когда напряжение находится на поверхности текучести, а скорость напряжения указывает вне поверхности текучести, 9p = 0. Варианты определения эквивалентного напряжения и пластической деформации не уникальны, но сделанные здесь варианты обычно используются для моделирования металлов. Эквивалентное напряжение представляет собой напряжение фон Мизеса,


Верхний штрих указывает, что напряжение представляет собой девиаторное напряжение, определяемое как

Для одномерного одноосного напряженного состояния (σ 11 = σ и все остальные компоненты равны нулю ), девиаторное напряжение равно

, при этом все остальные компоненты напряжения равны нулю. При подстановке в уравнение 11 эквивалентное напряжение равно

, показывающий, что эквивалентное напряжение равно величине одноосного напряжения. Эквивалентная пластическая деформация является интегралом эквивалентной скорости пластической деформации,

, а эквивалентная скорость пластической деформации определяется через скорость пластической деформации,



. Обратите внимание, что скорость пластической деформации не имеет штриха; тензор скорости пластической деформации в этой модели девиаторный по построению. Пластическое течение в металлах является изохорным, что означает, что объем материала не изменяется при пластическом течении, что соответствует коэффициенту Пуассона 0,5. При одноосном напряжении скорость пластической деформации имеет вид

и все скорости деформации сдвига равны нулю. Сумма членов равна нулю, что свидетельствует о девиаторном характере скорости пластической деформации. Подстановка этой скорости пластической деформации в уравнение 16,

 

показывает, что скорость многомерной деформации сводится к скорости одномерной пластической деформации. p и &lamda получается заменой в определении скорости пластической деформации определением эквивалентной скорости пластической деформации

Для эквивалентного стресса фон Мизес, норму составляет

для линейной изотропной эластичности, выраженной в терминах хромой константы и mue и λ, уравнение скорости становится

. 20 дает

Первый член справа от знака равенства определяет эволюцию девиаторного напряжения, в то время как второй член определяет среднее напряжение, которое является отрицательным значением давления P. Обратите внимание, что среднее напряжение не t появляется в определении эквивалентного напряжения, и его эволюция не зависит от скорости пластической деформации. Это позволяет рассматривать эволюцию девиаторных и средних напряжений независимо друг от друга. Другое определение эквивалентного напряжения (или, что то же самое, поверхности текучести) может привести к связи между всеми терминами. Подводя итог модели пластичности, если ответ эластичный, то

а если пластик то

djb 2005

Математическая формула пластичности: Измерение восприимчивости к изменениям в психическом здоровье и наука о данных

Обзор

. 2023 3 июня; 152:105272.
doi: 10.1016/j.neubiorev.2023.105272. Онлайн перед печатью.

Игорь Бранчи ¹

принадлежность

• ¹ Центр поведенческих наук и психического здоровья, Istituto Superiore di Sanità, Viale Regina Elena, 299, 00161, Рим, Италия. Электронный адрес: [email protected].
• PMID: 37277011
• DOI: 10. 1016/ж.неубиорев.2023.105272

Отзыв

Игорь Бранчи. Neurosci Biobehav Rev. 2023 .

. 2023 3 июня; 152:105272.
doi: 10.1016/j.neubiorev.2023.105272. Онлайн перед печатью.

Автор

Игорь Бранчи ¹

принадлежность

• ¹ Центр поведенческих наук и психического здоровья, Istituto Superiore di Sanità, Viale Regina Elena, 299, 00161, Рим, Италия. Электронный адрес: [email protected].
• PMID: 37277011
• DOI: 10. 1016/ж.неубиорев.2023.105272

Абстрактный

Пластичность все чаще признается важной концепцией в психиатрии и психическом здоровье, поскольку она позволяет реорганизовать нейронные цепи и поведение при переходе от психопатологии к благополучию. Различия в индивидуальной пластичности могут объяснить, почему методы лечения, такие как психотерапевтические и экологические вмешательства, очень эффективны у некоторых, но не у всех пациентов. Здесь я предлагаю математическую формулу для оценки пластичности, т. е. восприимчивости к изменениям, чтобы определить на исходном уровне, какие люди или группы населения с большей вероятностью изменят свои поведенческие результаты в зависимости от терапии или контекстуальных факторов. Формула основана на сетевой теории пластичности, так что при представлении системы (например, психопатологии пациента) в виде взвешенной сети, где узлы представляют собой характеристики системы (например, симптомы), а ребра — связи (т. е. корреляции). ) среди них сила связности сети является обратной мерой пластичности системы: чем слабее связность, тем выше пластичность и больше восприимчивость к изменениям. Прогнозируется, что формула может быть обобщена, измеряя пластичность в нескольких масштабах, от одной клетки до всего мозга, и может применяться в широком спектре областей исследований, включая нейробиологию, психиатрию, экологию, социологию, физику, рынок и финансы.

Ключевые слова: поведенческая пластичность; ограничение; Гибкость; Формула; теория графов; Большая депрессия; Душевное здоровье; Сеть; Нейронная пластичность; неврология; Психиатрия; психопатология; Симптомы; Система.

Copyright © 2023 Elsevier Ltd. Все права защищены.

Похожие статьи

• Добавки фолиевой кислоты и восприимчивость к малярии и ее тяжесть среди людей, принимающих антифолатные противомалярийные препараты в эндемичных районах.

  Крайдер К., Уильямс Дж., Ци Ю.П., Гутман Дж., Юнг Л., Май С., Финкельштейн Дж., Мехта С., Понс-Дюран С., Менендес С., Мораледа С., Роджерс Л., Дэниелс К., Грин П. Крайдер К. и др. Cochrane Database Syst Rev. 2022 Feb 1;2(2022):CD014217. дои: 10.1002/14651858.CD014217. Кокрановская система базы данных, ред. 2022 г. PMID: 36321557 Бесплатная статья ЧВК.

• Пластичность в психическом здоровье: сетевая теория.

  Бранчи И. Бранчи И. Neurosci Biobehav Rev. 2022 Jul; 138:104691. doi: 10.1016/j.neubiorev.2022.104691. Epub 2022 11 мая. Neurosci Biobehav Rev. 2022. PMID: 35568207 Обзор.

• Динамическая парадигма в психопатологии: «теория хаоса», от физики к психиатрии.

  Пезард Л., Нандрино Дж.Л. Пезард Л.