Эпюры — Теория и решение задач

Эпюрами в сопромате называют графическое представление данных о распределении соответствующих факторов по длине либо сечению рассматриваемого бруса.

Различают эпюры внутренних силовых факторов:

а также напряжений и перемещений.

Они наглядно показывают нагруженность участков бруса, положение опасных, с точки зрения прочности, точек сечения, а также направление и величину перемещения сечений.

Для их построения используется метод сечений:

1. Записываются выражения для определения внутренних усилий по каждому силовому участку,
2. Рассчитываются значения соответствующих факторов на границах силовых участков, в характерных сечениях бруса либо точках его поперечного сечения.

Полученные значения откладываются в виде точек от базовой (нулевой) линии в соответствии с их знаком, затем точки соединяются согласно функции определяющей их величину на каждом участке.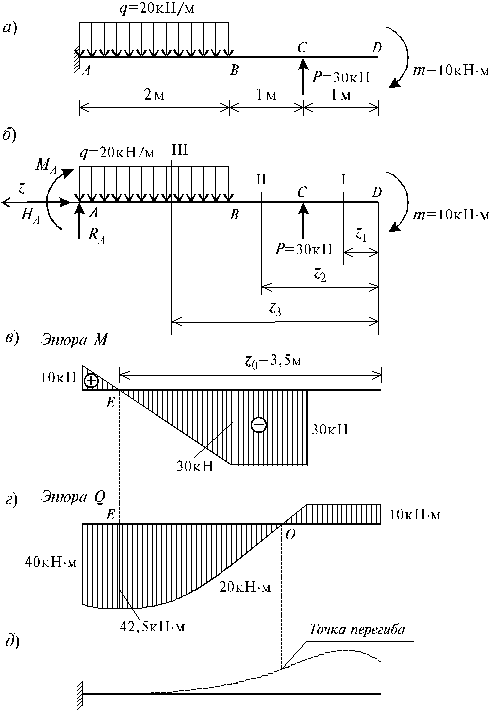

Правила и рекомендации при расчете и построении эпюр:

1. Базовая (нулевая) линия эпюры располагается параллельно продольной оси либо сечению рассматриваемого бруса.
2. Рядом указывается ее обозначение и размерность.
3. Ординаты значений откладываются от базовой линии строго в масштабе в соответствии со знаком.
4. Поле эпюр заштриховывается линиями перпендикулярными к базовой, и проставляется соответствующий знак.
5. В характерных точках эпюры указываются значения ординат.
6. Базовая линия и линии штриховки выполняются тонкими, а линии границ жирными.

Примеры расчета и построения эпюр >
Видеоуроки построения эпюр >
Другие примеры решения задач >

Сохранить или поделиться с друзьями

Уважаемые студенты!
Специалисты нашего сайта готовы оказать помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Подробнее

Сопромат.

Эпюры внутренних усилий [wiki.eduVdom.com]

Построение эпюр внутренних усилий

В балке

Внутренние усилия.

Изгибающий момент в балке равен сумме моментов всех сил, действующих на отсеченную часть относительно точки сечения.

Момент больше нуля, если растянуты нижнее волокно.

Поперечная сила Q численно равна алгебраической сумме проекций всех сил, действующих на отсеченную часть,

на ось, перпендикулярную оси балки ( перпендикулярно оси рамы).

Q>0, если сила вращает отсеченную часть по часовой стрелке.

Q<0, если против часовой стрелки.

Больше нуля — строится вверх и влево, меньше нуля — вниз и вправо.

Эпюра момента имеет максимум там, где Q=0.

Для строительной механики

Изгибающий момент равен сумме моментов всех сил, действующих на отсеченную часть относительно точки сечения.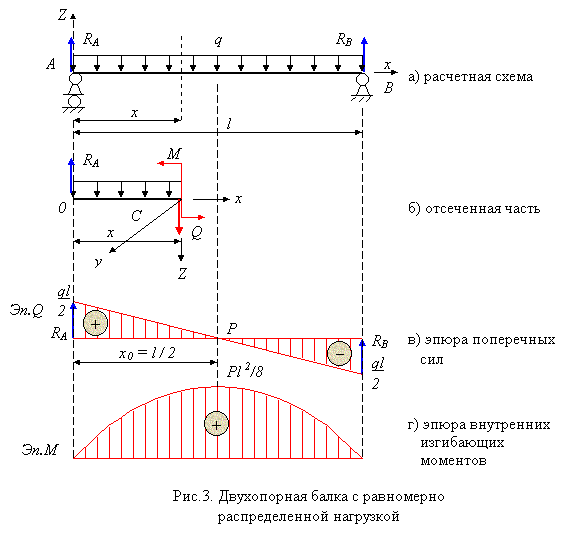

Эпюра моментов откладывается на растянутом волокне.

Если на участке нет нагрузки, то эп М — наклонная линия — прямая.

Если на участке действует распределенная нагрузка Q, то эп М — парабола, расположенная в виде паруса.

Если действует сила P, то эп. М претерпевает излом в сторону действия сил.

Если действует сосредоточенный момент, то — скачок на величину момента.

Проверка :

если Q>0 , то эпюра моментов нисходящая,

если Q<0 , то восходящая.

В шарнире момент равен 0.

Эпюра момента имеет максимум там, где Q=0.

Поперечная сила Q

Поперечная сила Q численно равна алгебраической сумме проекций всех сил, действующих на отсеченную часть,

на ось, перпендикулярную оси балки ( перпендикулярно оси рамы).

Q>0, если сила вращает отсеченную часть по часовой стрелке

Q<0 если против часовой стрелки.

Больше нуля — строится вверх и влево, меньше нуля — вниз и вправо.

Если на участке не действует сила, то Q — константа.

Если действует распр нагрузка q, то эпюра Q — наклонная линия.

Если действует P, то скачок на величину силы.

Если действует М, то эпюра Q не реагирует.

Продольная сила.

Продольная сила N численно равна алгебраической сумме проекций всех сил, действующих на отсеченную часть, на ось параллельно оси балки.

N больше нуля, если балка растянута,

N меньше нуля — если сжата.

Строится эпюра N симметрично с указанием знака

subjects/stroymeh/сопромат. _эпюры.txt · Последние изменения: 2013/08/05 21:03 — ¶

05. Эпюры деформации изгиба — Мастер-класс С.Леонова. Сопромат. Переломы

ЭПЮРЫ ИЗГИБАЮЩЕГО МОМЕНТА (продолжение)

 

В продолжение темы и лучшего усвоения материала предложим Вам следующие примеры.

Балка, опертая по концам (рис.2), но сила внешнего воздействия сместилась к одному из концов балки. Из пройденного материала известно, что при простом изгибе балки, опертой по концам, при изгибе ее под воздействием сосредоточенной силы, эпюры максимальных сжимающих и растягивающих напряжений симметричны (ось симметрии проходит через точки опирания балки, то есть через балку до ее деформации) (рис.1).

Рис.1. Опертая по концам балка, симметричное нагружение

 

Поэтому, чтобы не загружать схему, рассмотрим только эпюру растягивающих напряжений. Строим эпюру максимальных растягивающих напряжений, реализующихся по длине балки: проецируем «главные действующие лица» (точки опоры и место приложения силы) на горизонтальную ось, от точки проекции силы откладываем ее значение (длину) по вертикали и соединяем полученные три точки…(рис. 2).

Рис. 2. Построение эпюры максимальных растягивающих напряжений (балка, опертая по концам, несимметричное нагружение)

 

Непонятно? Предлагаю использовать способ построения эпюры при помощи резинки… Крепим резинку к двум точкам опоры и давим на нее пальцем (рис.3). Получаем эпюру максимального растягивающего напряжения по длиннику балки (самое интересное, что данный способ математически верен)!

Рис.3

 

До этого мы рассматривали, как выглядят максимальные эпюры сжатия и растяжения вдоль оси рассматриваемой балки. Как выглядят эпюры сжатия и растяжения в перпендикулярном сечении, то есть, как выглядит топография напряжений сжатия и растяжения в поперечнике балки (сверху вниз)?

Увеличим балку до цилиндра, переведя ее из схемы в «реальный» объект (рис. 4, б). По нижнему краю цилиндра при изгибе формируются растягивающие напряжения (схема на рис. 4, а), по верхнему краю (из пройденного материала) — сжимающие напряжения. Чтобы сформировалось сжатие, напряжения должны быть направлены к середине балки, а что бы сформировалось растяжение – напряжения должны быть направлены за пределы балки.

Рис.4. Балка, опертая по концам, несимметричное нагружение

 

Почему вектора напряжений (стрелки красного и синего цвета) на рисунке «4 в» только с одного конца цилиндра — спросите Вы? Все верно, с другого конца цилиндра можно расположить аналогичные стрелки красного и синего цвета, симметрично (относительно вертикальной оси) направив красные кнутри, а синие (растягивающие) кнаружи (см. рис.4 б). Однако, вспомнив ранее изложенный материал на простое растяжение и сжатие, вы легко поймете, что достаточно одной пары групп стрелок. В зоне направления красных стрелок (векторов) на всем протяжении будет реализовываться сжатие, а в зоне синих – растяжение.

 

Внимательный читатель давно обратил внимание, что вектора напряжений, как сжимающих, так и растягивающих, имеют наибольшую величину по верхнему и нижнему (соответственно) краям цилиндра, а ближе к центру происходит их уменьшение.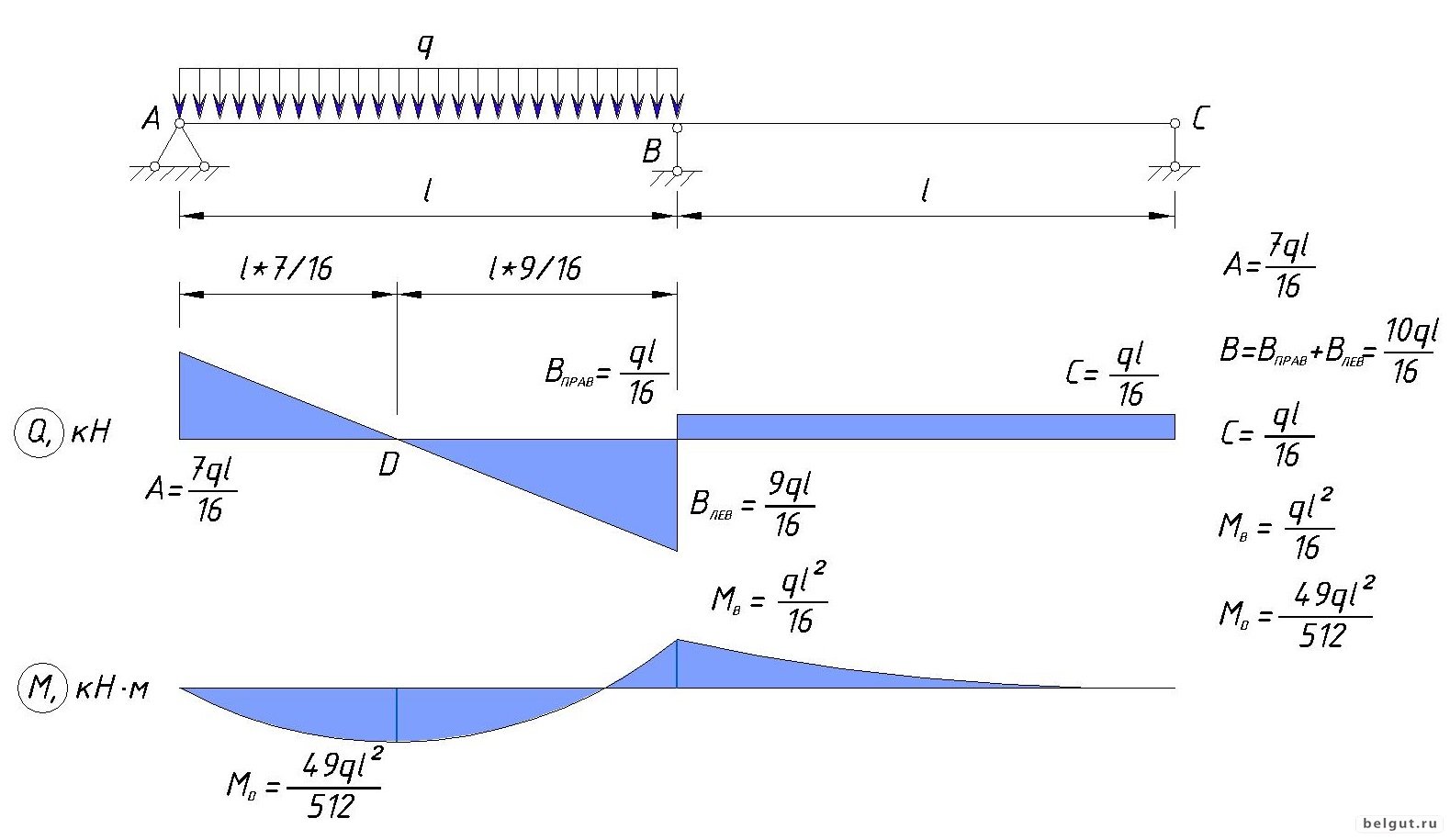

Нулевая точка соответствует оси симметрии балки. Действительно, при деформациях внутренние слои испытывают минимальные напряжения и деформации.

 

Этой особенностью концентрации напряжений активно и умело пользуется природа, обеспечивая минимальный вес конструкции при максимальной прочности. Зачем делать из прочного материала внутренние слои какой-либо конструкции, если эти слои не подвергаются, а значит и не противостоят внешнему воздействию и деформации? Конечно, там лучше убрать материал вовсе! В результате в биологии мы получаем, например диафиз трубчатой кости, а в строительстве швеллер, двутавр и т.д.

 

Высота треугольника эпюры зависит от величины приложенной силы, в нашем случае, достаточно абстрактной. Тем не менее, если силу мы уменьшим в два раза, настолько же уменьшится и высота треугольника эпюры (рис.5).

Рис.5. Балка, опертая по концам, несимметричное нагружение

 

А что происходит в реальности? Правильны ли наши умозаключения?

Метод конечных элементов, компьютерное моделирование позволяют увидеть топографию напряжений.

 

Пример. Рассматривается кость, фиксированная головками к упругой подложке. По кости в средней ее части осуществляется воздействие острого индентора. На рисунке 6 приводятся результаты математического моделирования методом конечных элементов процесса разрушения кости (это один из слайдов).

 

Пусть Вас не пугает смена цветов (на схемах выше мы сжатие отмечали красным, а растяжение синим). Компьютерная программа (если не изменять настроек) наиболее критические состояния отмечает (а они в данном случае в зоне растяжения) оттенками красного цвета.

Рис. 6. Внедрение индентора под углом 90°. Оттенками красного отмечены растягивающие напряжения, оттенками синего – сжимающие

 

Как такой перелом выглядит в реальности? На рисунке 7 представлен полный поперечный (безоскольчатый) перелом большеберцовой кости. Удар нанесен по гребню большеберцовой кости сосредоточенной силой – острым индентором (средней частью лезвия топора).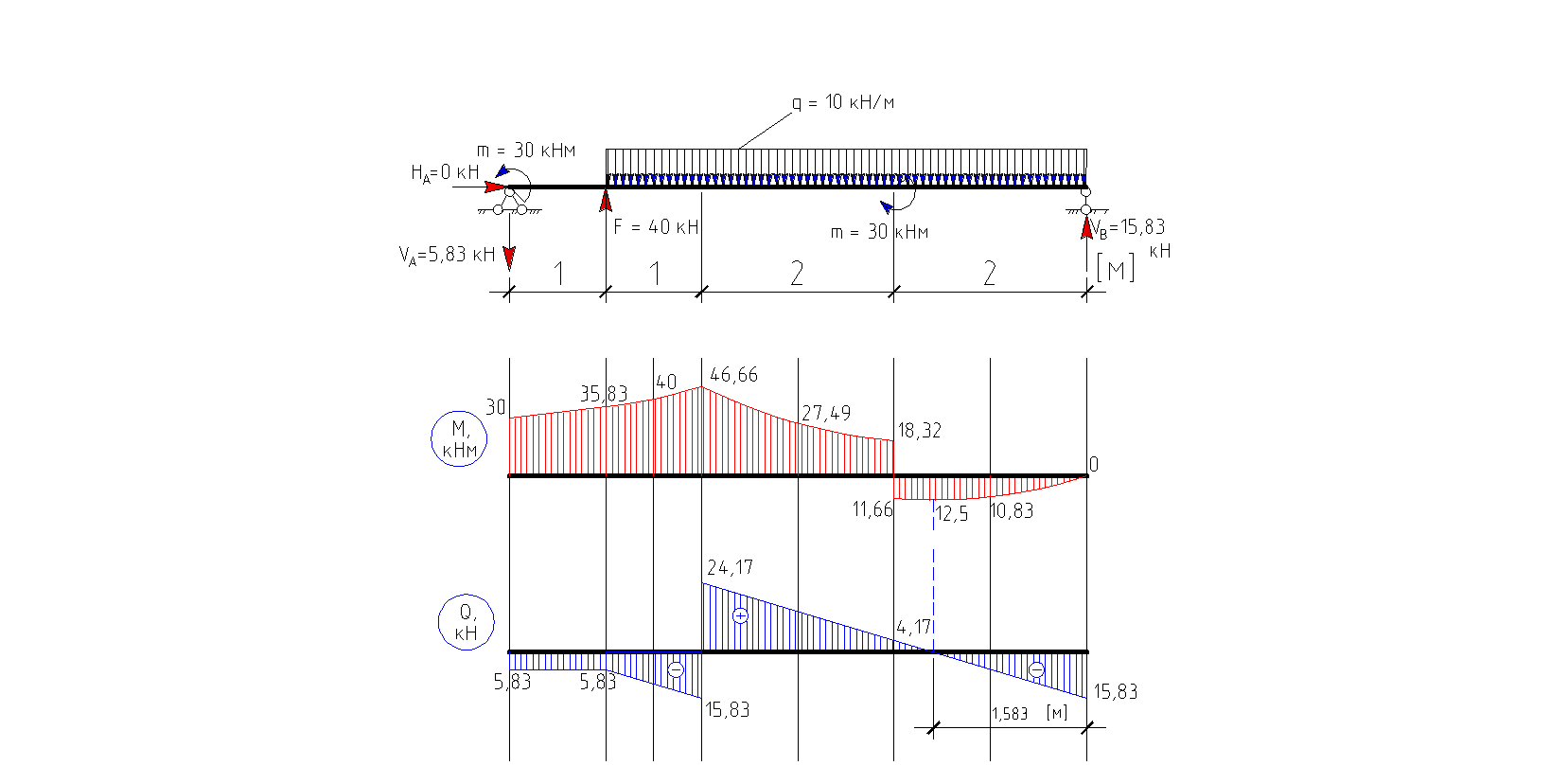

Рис.7. Полный поперечный перелом большеберцовой кости (действие острого индентора)

 

Сосредоточенная сила… кто-то из практических экспертов скажет: «да где ее встретишь, ну тупой топор и что-нибудь подобное…ты нам бампер подавай».

Давайте попробуем разобраться в этом вопросе вместе. Представим, что наезд на пешехода произошел сзади (рис. 8).

Рис. 8. Наезд ТС на пешехода сзади

 

Упрощаем задачу, приняв, что силы трения и инерции тела в сравнении с импульсом удара бампера формируют прочную фиксацию обоих концов балки (ноги), но суставы обеспечивают возможность поворота как минимум в одной плоскости, а бампер автомобиля прямоугольной формы, шириной, например в зоне контакта 5-6 см.

Рассмотреть взаимодействие балки и предмета, которые имеют определенную форму и размеры достаточно сложно. В сопромате этот сложный процесс называется контактной задачей. При ее решении приходится учитывать и силы трения, и форму контактирующих поверхностей. Чтобы упростить такую сложную задачу, заменим бампер группой сил, действующими на определенном ограниченном участке (рис.9).

Рис. 9. Построение схемы нагружения

 

Как будет выглядеть эпюра максимальных растягивающих напряжений в этом случае? Напряжения некоторым образом суммируются, и вершина треугольника получается сглаженной (рис.10)

Рис. 10.

 

Непонятно? Предлагаю призвать на помощь резинку… Крепим резинку к двум точкам опоры и сыпем на нее песок (с единственным допущением, что он распределяется на строго определенном нами участке, соответствующем границам крайних сил и не пересыпается за пунктирные линии рисунка) (рис.11). Получаем эпюру максимального растягивающего напряжения по длиннику балки! (и этот способ математически верен!).

Рис.11.

 

Из построенных эпюр видно, что прогнозируемая зона разрыва должна реализоваться в области «сглаженной» вершины, которую мы вам дали на схеме с «увеличением» на рисунке 9.

А что же происходит на поверхности балки со стороны воздействия индентора? Эпюра напряжений в области контакта индентора и балки имеет следующий вид (рис.12):

Рис. 12

 

Верны ли наши рассуждения? Сравним наши данные с данными моделирования процесса нагружения балки тупым (прямоугольным) индентором. На рисунке 13 наглядно демонстрируются поля напряжений, как в зоне растяжения, так и в зоне сжатия (использованная программная среда не отличает растяжение и сжатия; синим цветом и его оттенками отмечены зоны «спокойствия», а оттенками красного – «критические» участки). Для наглядности к картине полей напряжений мы «прикрепили» индентор и точки опирания.

Рис.13

 

Теперь рассмотрим процесс формирования перелома. В зоне наибольшего растяжения, где-то в области сглаженной вершины, построенной нами, появляются микроразрушения (рис.14,а). Микроскопические разрушения объединяются, и формируется разрыв. Зарождение и разрыв… полукруглая блестящая мелкозернистая поверхность с отвесными краями дает развитие магистральной трещине, появляются касательные напряжения (к ним мы обратимся обязательно, но чуть позже), направленные под углом 45° к нормали.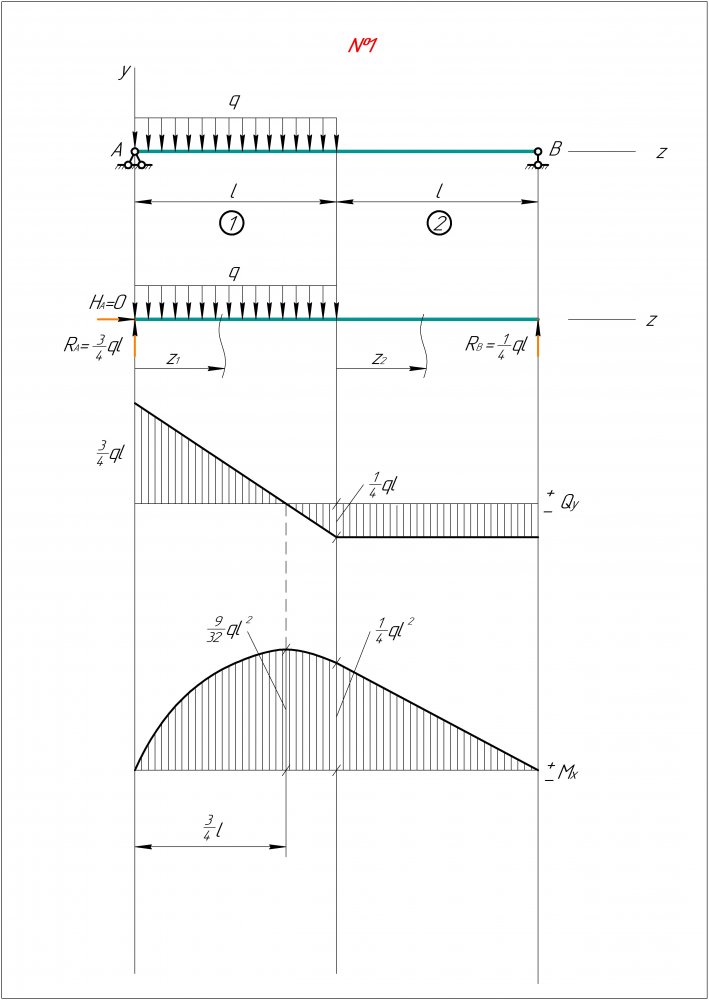 Формируется поверхность излома, на которой регистрируются рубцы в виде шевронов, елочки и т.д. … Куда идти трещине? (на рисунке 14,б мы ее отметили зеленым цветом).

Рис.14.

 

Ровно посредине кости зона растяжения сменяется зоной сжатия (см. рис.3 – эпюра в виде «двух треугольников»). На рисунке 1, и, соответственно в первом абзаце, мы приняли как аксиому, что эпюры максимальных сжимающих и растягивающих напряжений симметричны. Поэтому эпюра максимального сжимающего напряжения аналогична эпюре растягивающего напряжения и имеет форму в виде треугольника со скругленной вершиной (рис.15).

Рис.15.

 

Трещина, определяясь с направлением развития, решает проблему самым энергетически выгодным способом – идет по пути наименьших затрат.

Движение по пути наименьшего сопротивления. Направление наименьшего сопротивления соответствует точкам опоры (поскольку на всем пути напряжения растягивающие, зоны сжатия, которые необходимо преодолевать, не встречаются), но расстояние при этом, которое предстоит преодолеть трещине, наибольшее (рис. 16).

Рис.16.

 

Движение по наикратчайшему пути. Самое короткое расстояние для пересечения толщи кости – это путь от зоны разрыва к точке контакта с индентором (рис.17). Но здесь располагается зона наибольшего сжатия (то же не выгодно). Выход простой – эту зону надо обойти.

Рис.17.

 

Трещина принимает соломоново решение (между «расстоянием» и «сопротивлением»): она берет направление близкое к 45° к длиннику кости (рис.18)

Рис.18.

 

А как же индентор и локальное нагружение? Локальное нагружение трещина воспринимает совершенно реально и обходит его тоже (рис.19).

И если нагружение симметричное, трещина раздваивается и формирует треугольный отломок (рис.19,а), а если не симметричное – косой перелом (рис.19,б) (несимметричное нагружение может быть вызвано отклонением силы от перпендикулярной оси, изменением сечения кости, условиями опирания, всем тем, чего в биосистемах больше, чем достаточно).

Рис.19.

 

В итоге, получаем перелом (рис.20), подобный изображенному на рисунке 19,а.

Рис. 20.

Сопромат для чайников – Что такое сопромат примеры с решением онлайн

Сопромат — это инженерная дисциплина, изучаемая в университетах и колледжах, с технической направленностью и секцией механики.

В ней используются уравнения механики и физики, а также принципы теоретической механики.

При проектировании различных конструкций (сооружений, машин, приборов и др.) необходимо проводить расчеты на прочность. Неправильный расчет самой, на первый взгляд, незначительной детали может повлечь за собой очень тяжелые последствия, привести к разрушению всей конструкции.

• Кроме расчетов на прочность, во многих случаях проектирования производят расчеты на жесткость и устойчивость.

Целью расчетов на жесткость является определение таких размеров элементов конструкций, при которых перемещения (деформации) не превышают заданных (обычно весьма малых) величин, допустимых по условиям нормальной эксплуатации.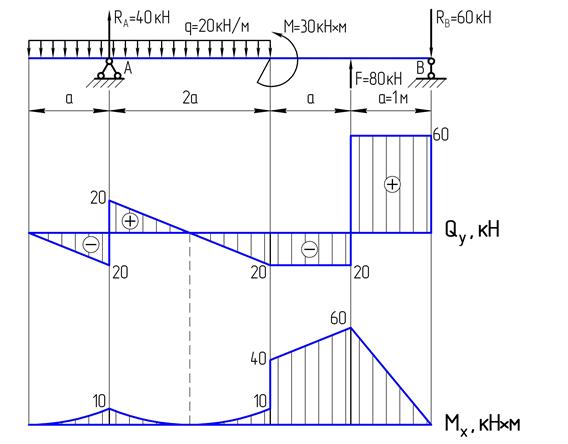

Деформации многих конструкций при действии некоторого вида нагрузок незначительны, пока величины этих нагрузок меньше так называемых критических значений. При нагрузках же, превышающих (даже весьма незначительно) критические значения, деформации конструкций резко возрастают. Простейший пример такого явления представляет так называемый продольный изгиб сжатого стержня — при некотором значении сжимающей силы происходит выпучивание прямолинейного стержня, практически равносильное разрушению. Такое качественное изменение характера деформации конструкции при увеличении нагрузки называется потерей устойчивости. Расчет конструкции, имеющий целью не допустить потери устойчивости, называется расчетом на устойчивость.

Содержание:

1. Расчетная схема. нагрузки
2. Напряжения
3. Деформации и перемещения
4. Продольная сила
5. Напряжения в поперечных и наклонных сечениях бруса
6. Рассмотрим теперь напряжения в наклонных сечениях бруса.
7. Продольные и поперечные деформации
8. Примеры расчета с решением задач
9. Пример решения задачи 1.2.
10. Пример решения задачи 2.2
11. Пример решения задачи 3.2

При проведении расчетов необходимо сочетать надежность работы сооружения с его дешевизной, получать необходимые прочность, жесткость и устойчивость при наименьшем расходе материала.

Совокупность наук о прочности, жесткости и устойчивости сооружений называется строительной механикой*. Одним из разделов строительной механики является сопротивление материалов. Другими ее разделами являются теория упругости (математическая и прикладная), теория пластичности и теория сооружений (включая статику, динамику и устойчивость сооружений **).

По этой ссылке вы найдёте полный курс лекций по сопротивлению материалов:

В сопротивлении материалов рассматриваются вопросы расчета отдельных элементов конструкций и вопросы расчета некоторых простейших конструкций на прочность, жесткость и устойчивость.

В отличие от теоретической механики, в которой все тела рассматриваются как абсолютно твердые, в сопротивлении материалов учитывается, что элементы конструкций при действии внешних сил изменяют свою форму и размеры, т.е. деформируются.

В сопротивлении материалов широко применяются методы теоретической механики (в первую очередь статики) и математического анализа, а также используются данные из разделов физики, в которых изучаются свойства различных материалов.

Сопротивление материалов является экспериментально-теоретической наукой, так как она широко использует опытные данные и теоретические исследования.

Основное внимание в сопротивлении материалов уделяется изучению брусьев, являющихся наиболее распространенными элементами многих конструкций. Брусом (или стержнем) называется элемент, длина которого значительно больше его поперечных размеров (рис. 1.1,а). Горизонтальный (или наклонный) брус, работающий на изгиб, обычно называют балкой.

Ось бруса представляет собой геометрическое место точек, совпадающих с центрами тяжести площадей поперечных сечений бруса, т. е. сечений, расположенных в плоскостях, перпендикулярных к указанной основе.

Элемент конструкции, длина и ширина которого во много раз превышают его толщину, называется оболочкой (рис. 1.1,6).

Геометрическое место точек, равноудаленных от наружной и внутренней поверхностей оболочки, называется срединной поверхностью.

Оболочка, срединная поверхность которой представляет собой плоскость, называется пластинкой (рис. 1.1,в).

Элемент конструкции, размеры которого во всех направлениях мало отличаются друг от друга (например, сплошная опора моста), называется массивным телом (рис. 1.1,г).

Возможно вам будут полезны данные страницы:

Расчетная схема. нагрузки

Нагрузки, действующие на конструкцию, являются по отношению к ней внешними силами. Эти силы приложены к тому или иному элементу конструкции по некоторым участкам его поверхности или распределены по его объему.

В сопротивлении материалов расчет реальной конструкции на действие реальных внешних нагрузок производится с помощью так называемых расчетных схем. При составлении расчетных схем нагрузку, приложенную к небольшим участкам поверхности бруса, все размеры которых малы по сравнению с его длиной, заменяют сосредоточенной силой, т. е. силой, приложенной к точке поверхности, и переносят к оси бруса.

Точки приложения сил на оси бруса сосредоточенных моментов, возникающих при переносе сил, располагают в тех же поперечных сечениях, в которых приложены нагрузки. На расчетной схеме вместо бруса изображается его ось. При составлении расчетной схемы конструкции применяются и другие упрощения, облегчающие ее расчет.

На рис. 2.1,а показан брус и действующие на него (в плоскости чертежа) внешние сосредоточенные силы На рис. 2.1,6 дана расчетная схема этого бруса с сосредоточенными силами и моментами приложенными к его оси.

Указанная схематизация основана на так называемом принципе Сен-Венана, согласно которому распределение напряжений* на достаточно большом расстоянии от места приложения нагрузки, превышающем размеры загруженного участка, не зависит от характера нагрузки, а зависит только от ее статического эквивалента.

Нагрузки, приложенные к участкам больших размеров (например к поверхности бруса на участке, составляющем существенную часть его длины), при составлении расчетной схемы нельзя заменять сосредоточенными силами. Такие нагрузки на расчетной схеме остаются распределенными (не сосредоточенными) по поверхности или приводятся к распределенным по линии***.

Например, нагрузка равномерно распределенная по части поверхности бруса, показанная на рис. 3.1,а, заменяется на расчетной схеме (рис. 3.1,6) нагрузкой равномерно распределенной по длине оси бруса.

При неравномерном распределении сплошной нагрузки или при переменной ширине загруженного участка соответствующая нагрузка на расчетной схеме является неравномерно распределенной.

Нагрузка, распределенная по поверхности, характеризуется ее интенсивностью представляющей собой предел отношения равнодействующей нагрузки приходящейся на весьма малую площадку, к величине этой площадки когда она стремится к нулю, т. е.

Таким образом, интенсивность является мерой нагрузки, распределенной по поверхности сооружения; ее размерность — и т. д.

Мерой нагрузки, распределенной по линии (например, подлине оси бруса —рис. 3.1,6), является ее интенсивность размерность которой и т. д. Такая нагрузка иногда называется погонной.

Сплошная нагрузка, распределенная по линии, изображается обычно в виде графика, показывающего (в определенном масштабе), как изменяется ее интенсивность по длине оси бруса. Такой график называется эпюрой нагрузки. При равномерной нагрузке эпюра ограничена прямой, параллельной оси бруса (рис. 3.1,6), а при неравномерной—прямой, наклонной к оси бруса, или кривой линией (в зависимости от закона изменения интенсивности).

Нагрузки, распределенные по объему тела (например, вес сооружения, силы инерции), называются объемными силами; их интенсивность имеет размерность и т. д.

К внешним силам, действующим на элементы конструкции, кроме нагрузок—активных сил, относятся также реакции связей — реактивные силы.

Нагрузки, распределенные по линии и сосредоточенные в точках, реально не существуют. Их можно получить лишь в результате схематизации реальных нагрузок, распределенных по объему (объемных сил) и по поверхности.

При составлении расчетной схемы в ряде случаев реальные нагрузки нельзя заменить одними лишь сосредоточенными и распределенными силовыми нагрузками. В этих случаях, кроме силовых, появляются и моментные нагрузки (см. рис. 2.1,6) в виде сосредоточенных моментов (пар сил) и моментов, распределенных по линии (длине) или по поверхности. Сосредоточенные моменты имеют размерности и т. д.; моменты, распределенные по линии,— и т. д., а моменты, распределенные по поверхности,— и т. д.

Нагрузки (силовые и моментные) различаются не только по способу их приложения (распределенные и сосредоточенные), но также по длительности действия (постоянные и временные) и характеру воздействия на конструкцию (статические и динамические).

Постоянные нагрузки (например, собственный вес конструкции) действуют на протяжении всего периода эксплуатации конструкции. Временные нагрузки (например, вес поезда) действуют в течение ограниченного промежутка времени. Величина статической нагрузки медленно возрастает от нуля до ее конечного значения, а потому эта нагрузка вызывает в конструкции весьма малые ускорения, в связи с чем возникающими при этом силами инерции можно в расчете пренебречь. Динамическая нагрузка (например, ударная) вызывает в конструкции или отдельных ее элементах большие ускорения, которыми при расчете пренебречь нельзя. Величина этой нагрузки значительно изменяется за малые промежутки времени.

Временная нагрузка может сохранять более или менее постоянную величину в течение всего периода ее действия, а может непрерывно изменяться по некоторому закону; в последнем случае она называется переменной нагрузкой.

Если переменная нагрузка изменяется по циклическому (повторяющемуся) закону, то она называется циклической.

Напряжения

Как уже известно, внешние сосредоточенные (т. е. приложенные в точке) нагрузки реально не существуют.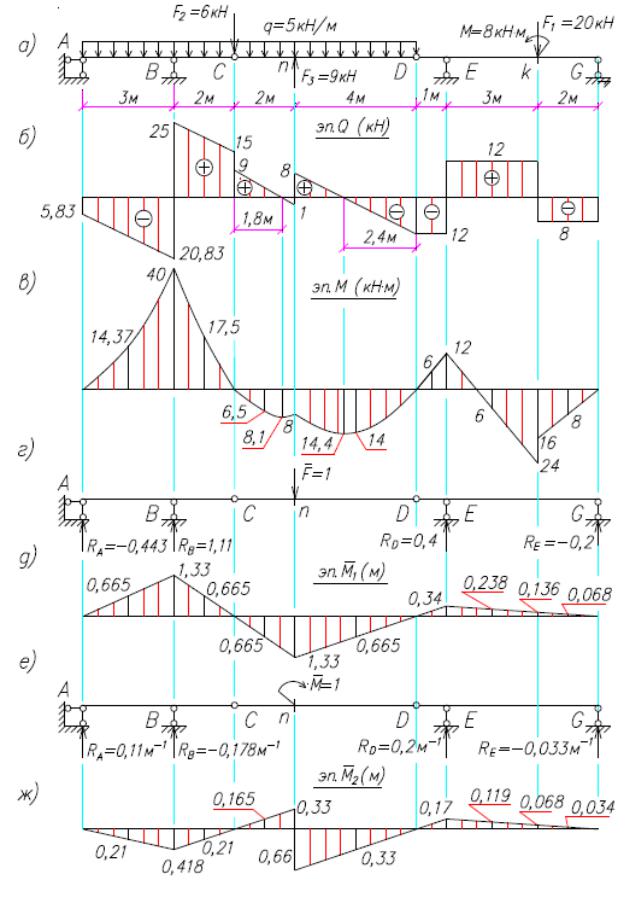 Они представляют собой статический эквивалент распределенной нагрузки.

Аналогично сосредоточенные внутренние силы и моменты, характеризующие взаимодействие между отдельными частями элемента (или между отдельными элементами конструкции), являются также лишь статическим эквивалентом внутренних сил, распределенных

по площади сечения. Эти силы, так же как и внешние нагрузки, распределенные по поверхности, характеризуются их интенсивностью, которая равна

где равнодействующая внутренних сил на весьма малой площадке проведенного сечения (рис. 7.1,а).

Разложим силу на две составляющие: касательную и нормальную из которых первая расположена в плоскости сечения, а вторая перпендикулярна к этой плоскости. Интенсив-

ность касательных сил в рассматриваемой точке сечения называется касательным напряжением и обозначается а интенсивность нормальных сил—нормальным напряжением и обозначается (сигма). Напряжения выражаются формулами

Напряжения имеют размерность и т. д.

Нормальное и касательное напряжения являются составляющими полного напряжения в рассматриваемой точке по данному сечению (рис. 7.1,6). Очевидно, что

Нормальное напряжение в данной точке по определенному сечению характеризует интенсивность сил отрыва или сжатия частиц элемента конструкций, расположенных по обе стороны этого сечения, а касательное напряжение —интенсивность сил, сдвигающих эти частицы в плоскости рассматриваемого сечения. Величины напряжений в каждой точке элемента зависят от направления сечения у проведенного через эту точку.

Совокупность напряжений действующих по различным площадкам проходящим через рассматриваемую точкуу представляет собой напряженное состояние в этой точке.

Нормальные и касательные напряжения имеют в сопротивлении материалов весьма важное значение, так как от их величин зависит прочность сооружения.

Нормальные и касательные напряжения в каждом поперечном сечении бруса связаны определенными зависимостями с внутренними усилиями, действующими в этом сечении. Для получения таких зависимостей рассмотрим элементарную площадку поперечного сечения бруса с действующими по этой площадке нормальными и касательными напряжениями (рис. 8.1). Разложим напряжения на составляющие параллельные соответственно осям На площадку действуют элементарные силы параллельные соответственно осям Проекции всех элементарных сил (действующих на все элементарные площадки сечения на оси и их моменты относительно этих осей определяются выражениями

В левых частях этих выражений указаны внутренние усилия, действующие в поперечных сечениях бруса, а именно: — продольная сила; поперечные силы, параллельные соответственно осям крутящий момент; —изгибающий

момент относительно оси (действующий в плоскости — изгибающий момент относительно оси (действующий в плоскости

Деформации и перемещения

Под действием нагрузки конструкция деформируется, т. е. ее форма и размеры изменяются. Рассмотрим, что представляют собой деформация и перемещение.

Мысленно через точку тела в направлениях осей проведем бесконечно малые отрезки длина которых (рис. 9.1). Обозначим изменения длин этих отрезков

после приложения нагрузки к телу (когда точки переместятся в положения Отношение представляет собой линейную деформацию (эпсилон) в точке т. е. Аналогично

Изменение первоначально прямого угла между отрезками после приложения нагрузки к телу, выраженное в радианах, представляет собой угловую деформацию (гамма) в точке в плоскости Аналогично представляют собой угловые деформации в плоскостях

Деформации конструкции в каждой ее точке по любым направлениям известны, если определены линейные деформации направлениях осей прямоугольной системы координат и угловые деформации в плоскостях

Линейные и угловые деформации—величины безразмерные. Деформацию часто называют относительной линейной деформацией а деформацию —относительным сдвигом.

Совокупность линейных деформаций по различным направлениям и угловых деформаций по различным плоскостям у проходящим через рассматриваемую точку, представляет собой деформированное состояние в этой точке.

Деформации возникающие в каждой точке тела под действием нагрузки, вызывают, как уже отмечалось, изменение его формы и размеров. В результате этого точки тела перемещаются в новые положения, а элементарные (бесконечно малые) отрезки, соединяющие каждую пару близко расположенных друг к другу точек, поворачиваются.

Для примера рассмотрим рис. 10.1, на котором сплошной линией показан брус до приложения к нему нагрузки, а штриховой—деформированный брус. Отметим на брусе произвольную точку и проведем через нее короткий отрезок прямой, соединяющий точки (отрезок В результате деформации бруса точка перейдет в положение а отрезок —в положение

Расстояние представляет собой линейное перемещение (смещение) точки а угол между направлениями отрезков поворот отрезка (угловое перемещение).

Продольная сила

Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние усилия (поперечные силы, изгибающие моменты и крутящий момент) равны нулю.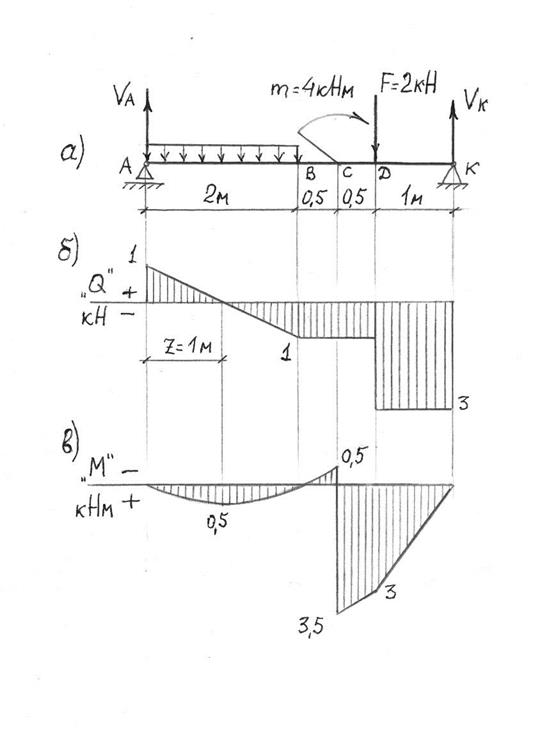 Иногда центральное растяжение (или центральное сжатие) кратко называют растяжением (или сжатием).

На рис. 1.2у а изображен прямой брус, закрепленный одним концом и нагруженный на другом конце силой направленной вдоль его оси.

Во всех поперечных сечениях этого бруса возникают только продольные растягивающие силы и, следовательно, такой брус по всей длине является центрально растянутым. При противоположно направленной силе (рис. 1.2,6) брус по всей длине испытывает сжатие*.

Брус, изображенный на рис. 1.2,6, испытывает центральное растяжение только на участках на участке брус не является центрально растянутым, так как, например, в сечении кроме продольной силы, действуют также поперечная сила и изгибающий момент.

Растягивающие продольные силы принято считать положительнымиу а сжимающие—отрицательными.

На рис. 2.2, а изображен брус, нагруженный силами направленными вдоль его оси, двумя силами параллельными оси и приложенными на равных расстояниях от нее в поперечном сечении а также двумя силами направленными под углом к оси бруса и приложенными в поперечном сечении на равных расстояниях от оси.

На рис. 2.2,6 изображена расчетная схема, полученная путем замены бруса его осью и переноса внешних нагрузок к этой оси.

Силы на расчетной схеме действуют вдоль оси бруса; силы и силы показанные на рис. 2.2, а, приводятся соответственно к силам также направленным вдоль оси. Таким образом, на расчетной схеме (рис. 2.2,6) все внешние силы действуют вдоль оси бруса. Следова-тельно, в поперечных [сечениях рассматриваемого бруса возникают только продольные силы.

Определим в качестве примера продольную силу в сечении (рис. 2.2,6). На рис. 2.2,6, г показаны продольные силы действующие на левую (относительно сечения и на правую части бруса. Направления этих сил приняты в предположении, что они являются растягивающими (т. е. положительными). Если в результате расчета значение получается со знаком «минус», то это означает, что в действительности брус в сечении сжат.

Для определения силы воспользуемся методом сечений. Составим уравнение равновесия в виде суммы проекций на ось бруса всех сил, действующих на левую его часть (рис. 2.2, в):

откуда

Этот же результат можно получить и не составляя уравнения равновесия, а используя то положение, что на основании метода

сечений проекция внутренних сил на ось бруса (т. е. продольная сила), действующих со стороны левой его части на правую, равна сумме проекций на эту же ось всех внешних сил, приложенных к левой части. Следовательно,

Силы взяты со знаком «плюс», потому что их направление совпадает с положительным направлением силы действующей на правую часть бруса.

Аналогично найдем продольные силы в сечениях (рис. 2.2,6), проектируя силы, приложенные слева от этих сечений, на ось бруса:

Очевидно, что на всем участке (между точками приложения сил продольная сила постоянна и равна аналогично и на других участках (между точками приложения внешних сил) продольные силы имеют постоянные значения.

Построим график, показывающий изменение продольных сил по длине оси бруса, называемый эпюрой продольных сил (эпюрой Для этого проведем ось эпюры параллельную оси бруса (рис.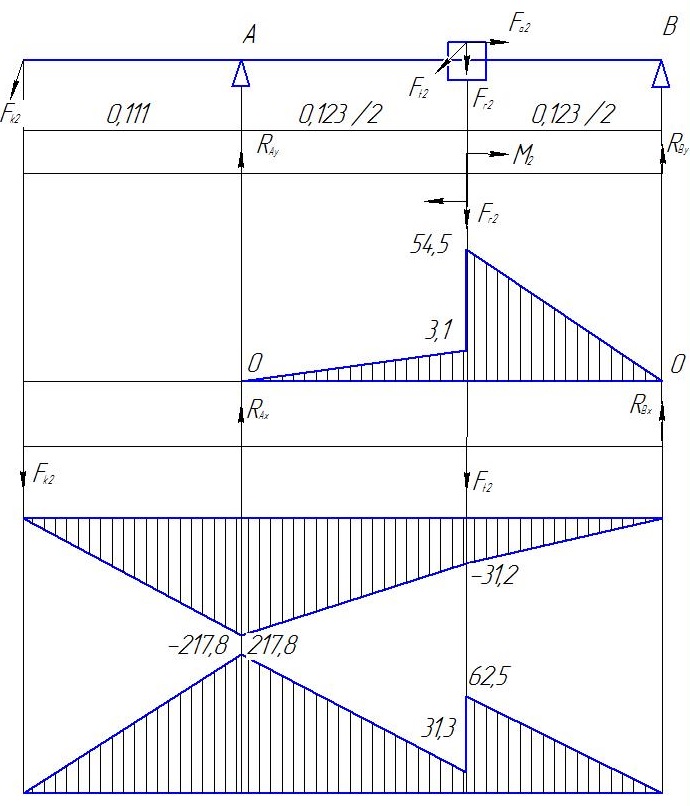 2.2, д), и перпендикулярно к ней отложим ординаты, изображающие в некотором масштабе величины продольных сил в поперечных сечениях бруса.

Полученную таким путем эпюру принято штриховать (так же как и эпюры других внутренних усилий, рассматриваемые в последующих главах курса) прямыми линиями, перпендикулярными к ее оси. Каждая такая линия в принятом масштабе дает величину продольной силы в соответствующем поперечном сечении бруса.

В поперечном сечении у в котором к брусу приложена сосредоточенная сила у не перпендикулярная к его осиу значение продольной силы изменяется скачкообразно: слева от этого сечения, продольная сила имеет одно, а справа—другое значение, отличающееся на величину проекции (на ось бруса) указанной сосредоточенной силы. В соответствии с этим эпюра, изображенная на рис. 2.2, д, имеет скачки (уступы) в точках , равные соответственно величинам и значению реакции опорного закрепления бруса.

Для построения эпюр внутренних усилий, возникающих в поперечных сечениях бруса, нет необходимости изображать и брус с действующими на него нагрузками и расчетную схему, а достаточно привести один из этих чертежей.

Точно так же нет необходимости изображать отдельные части бруса, на которые он расчленяется поперечными сечениями. Например, для решения рассмотренной задачи можно изобразить лишь брус (рис. 2.2у а) или его расчетную схему (рис. 2.2,6), а также эпюру продольных сил (рис. 2.2, д) и мысленно представить остальные схемы, приведенные на рис. 2.2.

При действии на брус внешней распределенной осевой (т. е. направленной вдоль оси бруса) нагрузки продольные силы на участке, на котором такая нагрузка приложена, изменяются непрерывно. Для примера на рис. 3.2,6 показана эпюра продольных сил для бруса, изображенного на рис. 3.2, а. На этот брус, кроме двух сосредоточенных сил действует распределенная нагрузка (собственный вес бруса) интенсивностью Эпюра (рис. 3.2,6) построена на основе уравнений продольных сил, составленных для сечений, отстоящих от верхнего конца бруса на расстоянии

а) для сечения

Напряжения в поперечных и наклонных сечениях бруса

Продольная сила возникающая в поперечном сечении бруса, представляет собой равнодействующую внутренних нормальных сил, распределенных по площади поперечного сечения, и связана с возникающими в этом сечении нормальными напряжениями зависимостью (4. 1):

здесь —нормальное напряжение в произвольной точке поперечного сечения, принадлежащей элементарной площадке площадь поперечного сечения бруса.

Произведение представляет собой элементарную внутреннюю силу, приходящуюся на площадку Величину продольной силы в каждом частном случае легко можно определить при помощи метода сечений, как показано в предыдущем параграфе. Для нахождения же величин напряжений в каждой точке поперечного сечения бруса надо знать закон их распределения по этому сечению.

Закон распределения нормальных напряжений в поперечном сечении бруса изображается обычно графиком, показывающим изменение их по высоте или ширине поперечного сечения. Такой график называют эпюрой нормальных напряжений (эпюрой

Выражение (1.2) может быть удовлетворено при бесконечно большом числе видов эпюр напряжений (например, при эпюрах изображенных на рис. 4.2). Поэтому для выяснения закона распределения нормальных напряжений в поперечных сечениях бруса необходимо провести эксперимент.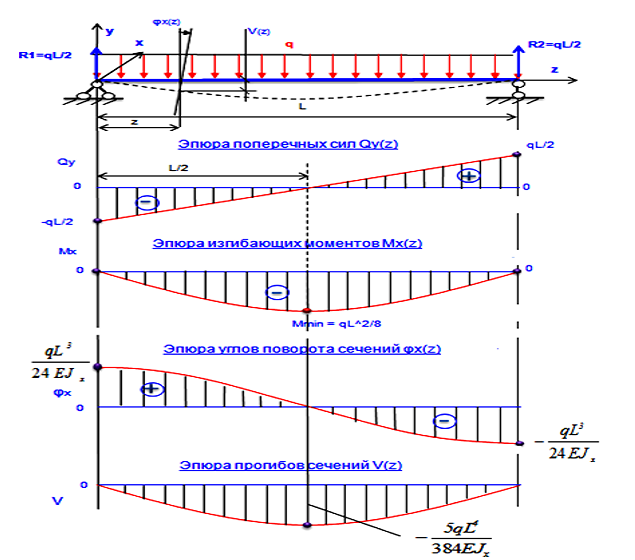

Проведем на бокозой поверхности бруса до его нагружения линии, перпендикулярные к оси бруса (рис. 5.2). Каждую такую линию можно рассматривать как след плоскости поперечного сечения бруса.

При нагружении бруса осевой силой эти линии, как показывает опыт, остаются прямыми и параллельными между собой (их положения после нагружения бруса показаны на рис. 5.2 штриховыми линиями). Это позволяет считать, что поперечные сечения бруса, плоские до его нагружения, остаются плоскими и при действии нагрузки. Такой опыт подтверждает гипотезу плоских сечений (гипотезу Бернулли), сформулированную.

Представим мысленно брус состоящим из бесчисленного множества волокон, параллельных его оси. Два любых поперечных сечения при растяжении бруса остаются плоскими и параллельными между собой, но удаляются друг от друга на некоторую величину; на такую же величину удлиняется каждое волокно. А так как одинаковым удлинениям соответствуют одинаковые напряжения, то и напряжения в поперечных сечениях всех волокон (а следовательно, и во всех точках поперечного сечения бруса) равны между собой. Это позволяет в выражении (1.2) вынести величину за знак интеграла. Таким образом,

откуда

Итак, в поперечных сечениях бруса при центральном растяжении или сжатии возникают равномерно распределенные нормальные напряжения, равные отношению продольной силы к площади поперечного сечения.

При наличии ослаблений некоторых сечений бруса (например, отверстиями для заклепок), определяя напряжения в этих сечениях, следует учитывать фактическую площадь ослабленного сечения равную полной площади уменьшенной на величину площади ослабления

Для наглядного изображения изменения нормальных напряжений в поперечных сечениях стержня (по его длине) строится эпюра нормальных напряжений. Осью этой эпюры является отрезок прямой, равный длине стержня и параллельный его оси. При стержне постоянного сечения эпюра нормальных напряжений имеет такой же вид, как и эпюра продольных сил (она отличается от нее лишь принятым масштабом). При стержне же переменного сечения вид этих двух эпюр различен; в частности, для стержня со ступенчатым законом изменения поперечных сечений эпюра нормальных напряжений имеет скачки не только в сечениях, в которых приложены сосредоточенные осевые нагрузки (где имеет скачки эпюра продольных сил), но и в местах изменения размеров поперечных сечений. Построение эпюры распределения нормальных напряжений по длине стержня рассмотрено в примере 1.2.

Рассмотрим теперь напряжения в наклонных сечениях бруса.

Обозначим угол между наклонным сечением и поперечным сечением (рис. 6.2, а). Угол условимся считать положительным, когда поперечное сечение для совмещения с наклонным сечением надо повернуть на этот угол против часовой стрелки.

Как уже известно, удлинения всех волокон, параллельных оси бруса, при его растяжении или сжатии одинаковы. Это позволяет предполагать, что напряжения во всех точках наклонного (так же как и поперечного) сечения одинаковы.

Рассмотрим нижнюю часть бруса, отсеченную сечением t (рис. 6.2,6). Из условий ее равновесия следует, что напряжения параллельны оси бруса и направлены в сторону, противоположную силе а внутренняя сила действующая в сечении равна Здесь —площадь наклонного сечения равная (где — площадь поперечного сечения бруса).

Следовательно,

откуда

где нормальные напряжения в поперечных сечениях бруса.

Разложим напряжение на два составляющих напряжения: нормальное перпендикулярное к плоскости сечения и касательное параллельное этой плоскости (рис. 6.2, в).

Значения получим из выражений

Нормальное напряжение считается обычно положительным при растяжении и отрицательным при сжатии. Касательное напряжение положительно, если изображающий его вектор стремится вращать тело относительно любой точки С, лежащей на внутренней нормали к сечению, по часовой стрелке.

На рис. 6.2, в показано положительное касательное напряжение а на рис. 6.2, г — отрицательное.

Из формулы (6.2) следует, что нормальные напряжения имеют значения от до нуля Таким образом, наибольшие (по абсолютной величине) нормальные напряжения возникают в поперечных сечениях бруса. Поэтому расчет прочности растянутого или сжатого бруса производится по нормальным напряжениям в его поперечных сечениях.

Из формулы (7.2) следует, что касательные напряжения имеют значения от отрицательный угол а показан на рис.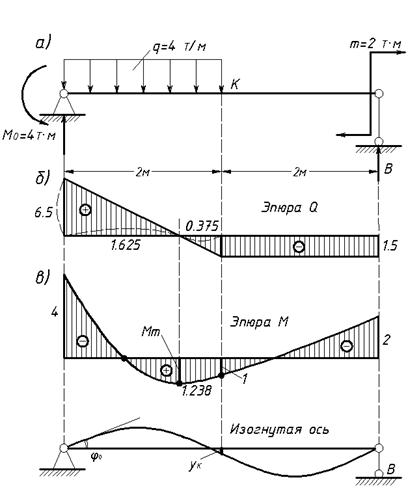 6.2, г. Значение равно нулю при (т. е. в поперечных сечениях бруса) и при Таким образом, в площадках с наибольшими и наименьшими нормальными напряжениями касательные напряжения равны нулю.

Определим значение касательных напряжений в двух наклонных сечениях, перпендикулярных друг к другу (рис. 7.2).

Углы наклона этих сечений к плоскости поперечного сечения бруса находятся между собой в зависимости По формуле (7.2)

Таким образом, касательные напряжения в двух взаимно перпендикулярных площадках равны друг другу по величине и обратны по знаку. Если продольная сила или размеры поперечных сечений бруса переменны по длине его оси, то напряжения в различных точках наклонного сечения имеют различные значения. Они могут определяться по формулам (6.2) и (7.2), но для каждой точки в эти формулы следует подставлять соответствующее значение подсчитанное для поперечного сечения, проходящего через рассматриваемую точку.

Продольные и поперечные деформации

Рассмотрим прямой брус постоянного сечения длимой заделанный одним концом и нагруженный на другом конце растягивающей силой (рис. 8.2, а). Под действием силы брус удлиняется на некоторую величину которая называется полным, или абсолютным, удлинением (абсолютной продольной деформацией).

В любых точках рассматриваемого бруса имеется одинаковое напряженное состояние и, следовательно, линейные деформации для всех его точек одинаковы. Поэтому значение можно определить как отношение абсолютного удлинения к первоначальной длине бруса т. е. Линейную деформацию при растяжении или сжатии брусьев называют обычно относительным удлинением, или относительной продольной деформацией, и обозначают Следовательно,

Относительная продольная деформация измеряется в отвлеченных единицах. Деформацию удлинения условимся считать положительной (рис. 8.2, а), а деформацию сжатия—отрицательной (рис. 8.2,6).

Чем больше величина силы, растягивающей брус, тем больше, при прочих равных условиях, удлинение бруса; чем больше площадь поперечного сечения бруса, тем удлинение бруса меньше. Брусья из различных материалов удлиняются различно. Для случаев, когда напряжения в брусе не превышают предела пропорциональности (см. § 6.1, п. 4), опытом установлена следующая зависимость:

Здесь -—продольная сила в поперечных сечениях бруса; — площадь поперечного сечения бруса; —коэффициент, зависящий от физических свойств материала.

Учитывая, что нормальное напряжение в поперечном сечении бруса получаем

откуда

Абсолютное удлинение бруса выражается формулой

т. е. абсолютная продольная деформация прямо пропорциональна продольной силе.

Впервые закон о прямой пропорциональности между силами и деформациями сформулировал Р. Гук (в 1660 г.). Формулы (10.2)—(13.2) являются математическими выражениями закона Гука при растяжении и сжатии бруса.

Более общей является следующая формулировка закона Гука [см. формулы (11.2) и (12.2)]: относительная продольная деформация прямо пропорциональна нормальному напряжению. В такой формулировке закон Гука используется не только при изучении растяжения и сжатия брусьев, но и в других разделах курса.

Величина входящая в формулы (10.2)—(13.2), называется модулем упругости первого рода (сокращенно—модулем упругости) *. Эта величина—физическая постоянная материала, характеризующая его жесткость. Чем больше значение тем меньше, при прочих равных условиях, продольная деформация.

Произведение назовем жесткостью поперечного сечения бруса при растяжении и сжатии.

В приложении приведены значения модулей упругости для различных материалов.

Формулой (13.2) можно пользоваться для вычисления абсолютной продольной деформации участка бруса длиной лишь при условии, что сечение бруса в пределах этого участка постоянно и продольная сила во всех поперечных сечениях одинакова.

Кроме продольной деформации, при действии на брус сжимающей или растягивающей силы наблюдается также поперечная деформация. При сжатии бруса поперечные размеры его увеличиваются, а при растяжении —уменьшаются. Если поперечный размер бруса до приложения к нему сжимаюших сил обозначить а после приложения этих сил (рис. 9.2), то величина будет обозначать абсолютную поперечную деформацию бруса.

Отношение является относительной поперечной деформацией.

Опыт показывает, что при напряжениях, не превышающих предела упругости (см. § 6.1, п. 3), относительная поперечная деформация прямо пропорциональна относительной продольной деформации но имеет обратный знак:

Коэффициент пропорциональности в формуле (14.2) зависит от материала бруса. Он называется коэффициентом поперечной деформации, или коэффициентом Пуассона, и представляет собой отношение относительной поперечной деформации к продольной, взятое по абсолютной величине, т. е.

Коэффициент Пуассона наряду с модулем упругости характеризует упругие свойства материала.

Величина коэффициента Пуассона определяется экспериментально. Для различных материалов она имеет значения от нуля (для пробки) до величины, близкой к 0,50 (для резины и парафина). Для стали коэффициент Пуассона равен 0,25—0,30; для ряда других металлов (чугуна, цинка, бронзы, меди) он имеет значения от 0,23 до 0,36. Ориентировочные значения коэффициента Пуассона для различных материалов приведены в приложении

Примеры расчета с решением задач

Пример решения задачи 1.2.

Для стального бруса, изображенного на рис. 37.2, а, построить эпюры продольных сил, нормальных напряжений в поперечных сечениях бруса и перемещений этих сечении, а также определить потенциальную энергию деформации. Задачу решить без учета собственного веса бруса. Принять

Продольную силу в поперечном сечении определяем, проектируя внешние силы, приложенные ниже рассматриваемого сечения, на ось бруса:

а) на участках

б) на участке

По полученным значениям строим эпюру продольных сил (рис. 37.2,6).

В поперечных сечениях бруса возникают нормальные напряжения, величины которых определяются по формуле (3.2):

а) на участке

б) на участке

в) на участке

По полученным значениям строим эпюру нормальных напряжений (рис. 37.2, в).

Поперечные сечения бруса под действием нагрузки смещаются по вертикали вниз. Величина смещения сечения, расположенного на расстоянии от верхнего конца бруса, равна деформации участка длиной :

а) для сечений на участке

перемещение сечения (при

для сечении на участке перемещение сечения

в) для сечений на участке

перемещение сечения

Во все полученные выражения координата входит в первой степени, т. е. зависимость между линейная. Это позволяет по подсчитанным перемещениям сечений и по известному перемещению сечения построить эпюру перемещений (рис. 37.2,

Для вычисления потенциальной энергии деформации бруса воспользуемся формулой (28.2):

Пример решения задачи 2.2

Определить напряжения в поперечных сечениях стального бруса, имеющего форму усеченного конуса, изображенного на рис. 38.2, а также перемещение верхнего сечения и потенциальную энергию деформации бруса. Задачу решить без учета собственного веса бруса. Принять

Продольная сила во всех поперечных сечениях бруса одинакова: (сжатие). Нормальные напряжения в поперечном

сечении бруса, отстоящем на расстояние от верхнего конца, определяются по формуле (3.2):

где

Поэтому

Перемещение верхнего конца бруса (вниз) равно укорочению всего бруса и определяется по формуле (18.2):

Потенциальную энергию деформации бруса находим по формуле (31.2):

Проверяем равенство потенциальной энергии деформации работе внешней силы [см. формулу (21.2)]:

Пример решения задачи 3.2

Стальной стержень площадью поперечного сечения закреплен верхним концом и находится под действием собственного веса (рис. 39.2,о). Найти наибольшую, допустимую по условию прочности длину стержня потенциальную энергию деформации этого стержня, а также перемещение его нижнего конца и сечения

Объемный вес стали Допускаемое напряжение на растяжение Модуль упругости

Обозначим расстояние от нижнего конца стержня до произвольного поперечного сечения.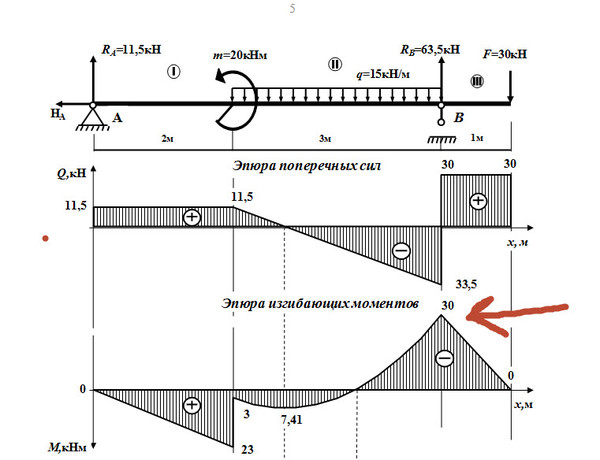 Продольная сила в сечении равна [см. формулу (32.2)]:

где в см.

Нормальные растягивающие напряжения в этом сечении

Наибольшие напряжения возникают в верхнем сечении стержня:

При наибольшей допустимой длине стержня напряжения в опасном (верхнем) сечении должны быть равны допускаемому напряжению; условие прочности для данной задачи имеет вид

откуда

Таким образом, допустимая по условию прочности длина стержня получается очень большой. Поэтому учет собственного веса вертикальных стержней необходим только в редких случаях —при весьма большой их длине, например при расчете тросов подъемников в глубоких шахтах. В большинстве же практических случаев расчет таких стержней производится без учета собственного веса.

Потенциальная энергия деформации стержня на основании формулы (37.2) равна:

где — вес стержня.

Перемещение нижнего конца стержня равно полному его удлинению и может быть определено по формуле (35. 2).

Следовательно, Перемещение сечения стержня равно деформации его верхнего участка длиной Для вычисления этой деформации определяем вес участка стержня ниже сечения и вес верхнего участка

Сила при определении деформации верхнего участка стержня рассматривается как сосредоточенная сила, приложенная к его нижнему концу, а сила является собственным весом этого участка и вызванное ею удлинение определяется по формуле (35.2), т. е. так/ как если бы эта сила была приложена в центре тяжести рассматриваемого участка (рис. 39.2,6). Таким образом,

Nothing found for %25D1%2588%25D0%25Bf%25D0%25Be%25D1%2580%25D1%258B %25D1%2581%25D0%25Be%25D0%25Bf%25D1%2580%25D0%25Be%25D0%25Bc%25D0%25B0%25D1%2582 %25D1%2581%25D0%25Ba%25D0%25B0%25D1%2587%25D0%25B0%25D1%2582%25D1%258C %25D0%25B1%25D0%25B5%25D1%2581%25D0%25Bf%25D0%25Bb%25D0%25B0%25D1%2582%25D0%25Bd%25D0%25Be

Раздел: Инженерная графика /  Дата: 24 Февраль, 2021 в 9:16 /  Просмотров: 3897

Омский институт водного транспорта (филиал) «Новосибирская государственная академия водного транспорта»  КОМПЬЮТЕРНАЯ ГРАФИКА Лабораторная работа № 1 Тема: Построение геометрических тел Цель лабораторной работы: 1) Изучение приемов построени. .. Читать далее

Раздел: Инженерная графика /  Дата: 23 Февраль, 2021 в 12:01 /  Просмотров: 3992

Ухтинский Государственный Технический Университет Инженерная графика и начертательная геометрия — выполнение расчетно-графической работы по начертательной геометрии  для студентов по методическим указаниям: Думицкая Н.Г., Попков О.Н., Ухта, 2006 год. Проекцион… Читать далее

Раздел: Начертательная геометрия /  Дата: 20 Февраль, 2021 в 13:40 /  Просмотров: 85

Омская Государственная Аграрная Академия им. Столыпина МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ к вне аудиторной работе студентов заочников по дисциплине «Начертательная геометрия и инженерная графика», 2006 г. Эпюр №1. Дана плоскость треугольника АВС и точка D. Зад… Читать далее

Раздел: Начертательная геометрия /  Дата: 4 Февраль, 2021 в 9:21 /  Просмотров: 98

Уфимский Государственный Нефтяной Технический Университет Инженерная и компьютерная графика — выполнение расчетно-графической работы по начертательной геометрии для студентов бакалавров заочного обучения по методическим указаниям Тархова Л. М., 2019 г. Лист… Читать далее

Раздел: Без рубрики /  Дата: 7 Сентябрь, 2019 в 9:55 /  Просмотров: 10180

Государственный университет «Московский Политех» (МАМИ) Cодержание расчетно-пояснительной записки: Титульный лист. Введение. Техническое задание. Силовой и кинематический расчет привода. Расчет зацеплений. Расчет ременной или цепной пере… Читать далее

Раздел: Без рубрики /  Дата: 2 Сентябрь, 2019 в 13:19 /  Просмотров: 7174

Начался новый учебный 2019/2020 год, поздравляю всех студентов с 1 сентября и Днем Знаний! Заказы на чертежи по начертательной геометрии инженерной графике, а также и курсовые проекты по предмету «Детали машин» уже принимаются. Обращайтесь, постараюсь помочь всем. Д… Читать далее

Раздел: Начертательная геометрия /  Дата: 16 Март, 2019 в 10:32 /  Просмотров: 16576

Омский институт водного транспорта (филиал) «Новосибирская государственная академия водного транспорта» Т. Л. Копац  СБОРНИК ЗАДАЧ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ИНЖЕНЕРНОЙ ГРАФИКЕ ТЕМА 1: «Проекции точки. Принадлежность точки прямой. Прямые общего и част… Читать далее

Раздел: Начертательная геометрия /  Дата: 13 Ноябрь, 2018 в 16:41 /  Просмотров: 13290

«Нижневартовский государственный университет» Расчетно-графическая работе №1. Задача 1 1. Построить линию пересечения MN плоскости  треугольника Σ(ΔАВС) и Θ(ΔEDK). Показать видимость пересечения плоскости Σ(ΔАВС) с плоскостью Θ(ΔEDK) в проекциях. 2.Опр… Читать далее

Раздел: Инженерная графика /  Дата: 30 Октябрь, 2018 в 12:44 /  Просмотров: 11949

Югорский Государственный Университет Пример выполненных чертежей по начертательной геометрии и инженерной графике для ЮГУ г. Ханты-Мансийск Часть 1. Начертательная геометрия:  5 чертежей по Фролову и одно уникальное задание. Часть 2. Инженерная … Читать далее

Раздел: Инженерная графика /  Дата: 15 Октябрь, 2018 в 13:39 /  Просмотров: 1545

Томский Государственный Университет Систем Управления и Радиоэлектроники  Задание 1 «Проекционное черчение» Задание 2 — Разъемное соединение винтом Задание 3 — Деталирование сборочного чертежа Пример выполнения лабораторной работы… Читать далее

Раздел: Начертательная геометрия /  Дата: 12 Октябрь, 2018 в 16:59 /  Просмотров: 7880

Задача.  Построить проекции шара радиусом 50 мм касательного плоскости треугольника АВС, если дана фронтальная проекция точки D — центра шара. Решение: Т.к. искомый шар касается плоскости треугольника АВС, следовательно, центр шара D удален от плоскости на в.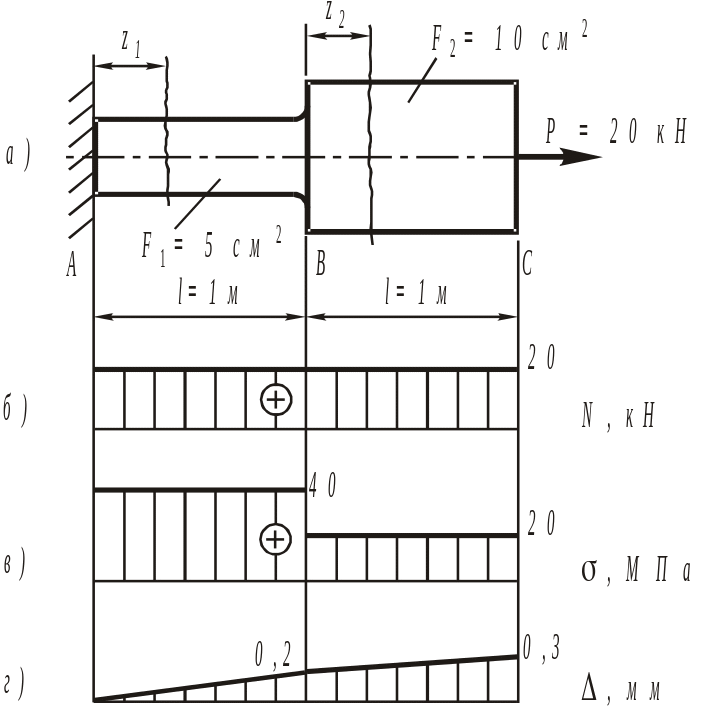 .. Читать далее

Раздел: Начертательная геометрия /  Дата: 8 Октябрь, 2018 в 12:59 /  Просмотров: 3405

Московский государственный университет путей сообщения (МГУПС) Контрольная работа№2  «ПРЕОБРАЗОВАНИЯ ЭПЮРА» Определить проекции и натуральную величину сечения многогранника плоскостью. РЕШЕНИЕ: 1) По заданным координатам в таблице с вариантами строим… Читать далее

Пример решения задачи по сопромату

Ниже приведено условие и решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.

                                                                          № 1

    Построить эпюры нормальной силы, нормальных напряжений и взаимного перемещения сечений. Определить работу внешних сил.

    Дано : F=10 Н ; l=1 м ; A=10 см2.

                                                                  Решение.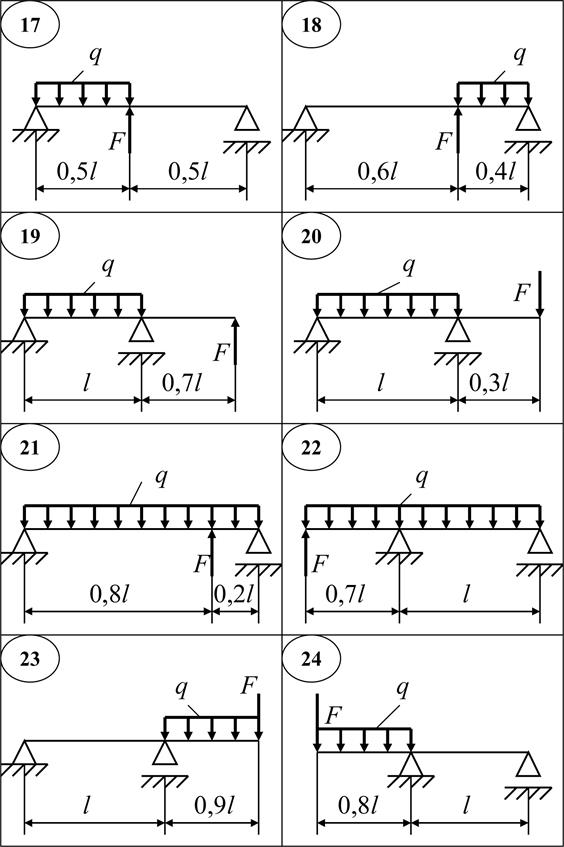

    1. Вычислим продольные силы на участках стержня и построим эпюру N.

    Нормальная сила Nz зависит от величины внешних сил, поэтому границами участков будут сечения, в которых приложены эти силы.

    Пользуясь методом сечений, сделаем на каждом участке  сечение и рассмотрим равновесие отсечённых частей. Из уравнений равновесия получим :

    1 участок AB ;  0≤z1≤ℓ

                      N(z1)=-5F=-50 Н  ; 

    2 участок BC ;  ℓ≤z2≤2ℓ

                      N(z2)=-5F+7F=2F=-50+70=20 Н  ; 

   3 участок CD ; 2ℓ≤z3≤3ℓ

                      N(z3)=-5F+7F-2F=0

    По полученным значениям строим эпюры Nz. Для этого от вертикальной (базисной линии) откладываем значения N, причём положительные значения (со знаком «+») откладываем вверх, а отрицательные (со знаком «-») – вниз.

    Эпюра N построена на рисунке.

    2. Вычислим нормальные напряжения на участках стержня и построим эпюру σ по длине стержня.

    Нормальные напряжения вычисляем по формуле :

                              σ=

    На участке AB :

                              σ1= Па=-0.05 МПа

    На участке BC :

                              σ2= Па=0.02 МПа

    На участке CD :

                              σ3=

    Эпюра нормальных напряжений построена на рисунке.

    3. Вычислим деформации участков стержня и построим эпюру перемещений сечений стержня.

    Вычислим деформации участков.

    Участок AB :

                Δℓ1= м=-2.5×10-4 мм

    где Е – модуль упругости (в задаче не задан) ; для стали Е=2×1011 Па 

    Знак «минус» означает, что участок сжимается.

    Участок BC :

                 Δℓ2= м=1×10-4 мм

    Участок CD :

                 Δℓ3=

    Найдём перемещения характерных сечений стержня. Перемещение любого сечение стержня равно сумме деформаций участков, расположенных между этим сечением и неподвижной опоры.

    Перемещение сечения D :  wD=0

    Перемещение сечения C :

                               wC=wD+Δℓ3=0

    Перемещение сечения B :

                                wB=wC+Δℓ2=0+1×10-4=1×10-4 мм

    Перемещение сечения А :

                                wA=wB+Δℓ1=1×10-4-2.5×10-4=-1.5×10-4 мм

    По вычисленным значениям w строится эпюра перемещений.

    4. Определим работу внешних сил.

    Для определения работы внешних сил воспользуемся формулой :

              A=

    где Ni – продольная сила в поперечном сечении бруса на участке i ; Ai и li — соответственно площадь поперечного сечения бруса на участке i и длина этого участка.

    В нашем случае эта формула примет вид :

               A=

               Дж=7.25 мкДж.

 

 

 

 

Расчет балки — Сопромат — Каталог статей

Расчет балки на прочность и построение эпюр – это вторая расчетно-графическая работа по сопротивлению материалов (РГСУ).

Сейчас мы рассмотрим часть этой расчетно-графической работы, а именно построим эпюры изгибающих моментов и поперечных сил.

Примером будет балка, взятая из условий расчетно-графических работ

Для начала нужно найти опорные реакции, это мы уже делали в прошлых уроках, так что без объяснений, только решение:

∑М_А=0

-q*2*2+Rb*3+m-F*4=0

-12*2*2+3*Rb+18-16*4=0

-48+18-64+3*Rb=0

3*Rb=94

Rb=94/3

Делить не будем, т.к. конечного числа не получается.

∑М_В=0

-Ra*3+q*2*1+m-F*1=0

-3*Ra+12*2*1+18-16*1=0

26=3*Ra

Ra=26/3

Проверка

∑F_Y=0

Ra+Rb-q*2-F=0

26/3+94/3-12*2-16=0

120/3-24-16=0

40-40=0

0=0

Проверка выполнена, опорные реакции найдены правильно.

Что делать дальше? А дальше мы смотрим, на сколько участков разбита наша балка. По идее участок заканчивается где начинает действовать другая сила, но гораздо проще смотреть количество участков по данным нам длинам.

Нам дано 3 длины, значит участка тоже будет три. Приступаем.

Первый участок можно брать хоть слева, хоть справа. Мы пойдем слева направо.

Собственно вот наши участки:

В красном прямоугольнике первый участок, в зеленом – второй, в синем – третий.

И так, первый участок. Мысленно проводим сечение

На чертеже оно, можно сказать, по середине участка, но не стоит забывать, что сечение изменяется от начала участка

До конца

И оно может находится в любом месте, в пределах первого участка.

От начала участка, до сечения расстояние Х₁

Если мы сказали, что сечение может быть в любой точке первого участка, то и Х может принимать разные значения, именно поэтому мы задаем для него границы:

0≤Х≤1   Х может принимать значения от 0 до 1 т.к. весь участок длиной 1.

Теперь мы смотрим, какие же силы действуют на нашем участке.

Кроме реакции опоры Ra ничего не действует (q не попадает в наш участок).

 

Для поперечных сил существует правило знаков:

 

По середине идет сечение.

Смотрим на наше сечение. Все, что левее сечения мы отбрасываем, его как бы нету. На первом участке нас интересует лишь то, что входит в этот участок.

У нас есть Rа, оно направлено вверх (Реакция опоры), прямо как на первом рисунке правил знаков, следовательно знак будет +

Q_Х1=Ra=26/3=8,7 кН (теперь лучше поделить) пишем так же размерность, для Q это килоньютоны.

Далее нам надо найти М на первом участке. Для М есть свое правило знаков:

 

Это правило называют правилом «дождя», если сверху «вылить воду», то на первом рисунке вода останется налита, как в тарелку, а на втором рисунке она просто стечет. Вода осталась, значит у нас есть что попить, а это явный плюс для нас 🙂 . На рисунке два мы остались без воды, а это уж точно не плюс, а скорее минус.

Чистых моментов на первом участке нету. Момент будет давать лишь опорная реакция Ra.

Как помним, момент это сила умноженная на плечо. Плечом у нас будет расстояние X1.

Записываем

М_x1=Ra*X1

Почему знак + ?

Теперь мы смотрим в какую сторону гнет нашу балку эта сила, если она направленна вверх, то по логике она изгибает балку прямо как на первом рисунке правил знаков для моментов, а именно

Теперь вместо X1 мы подставляем пределы нашего участка (0≤Х≤1) которые мы записывали вначале

М_Х1=0=8,7*0=0

М_Х1=1=8,7*1=8,7 кН*м

Первый участок сделан, переходим к участку номер два.

Как и в первом участке пишем пределы

1≤Х2≤3

Почему от 1 до 3 , а не от 0 до 2 ?

Да потому, что мы не можем брать от 0 до 1, т.к. это границы первого участка, а второй участок начинается с 1 и идет до 3.

Q_X2=Ra-q*(X2-1)

Теперь сложный момент с распределенной нагрузкой. В наше сечение попадает лишь его часть:

Если подумать, то она равняется Х2-1  вот тот участок, где действует нагрузка Q. Почему она с минусом: ну во-первых она гнет балку вниз, а во-вторых она противоположна по направлению положительной Ra, следовательно она будет с другим знаком.

Теперь мы подставляем наши границы в получившееся уравнение:

Q_X2=1=8,7-12*(1-1)=8,7 кН

Q_Х2=3=8.7-12(3-1)=-15.3 кН

А вот здесь есть не большой, но важный момент: у нас Q поменял знак на участке с плюса на минус (может менять наоборот), а это значит, что на этом участке момент будет приобретать экстремальное значение и его нам придется найти.

М_Х2=Ra*X2-q*(X2-1)²/2

Почему для моментов такое странное уравнение? Все очень просто: q действует на участке равном (Х2-1) , плечом этой силы будет (Х2-1)/2 и это все нужно перемножить q*(X2-1)*(X2-1)/2

Подставляем значения Х2

М_Х2=1=8,7*1-12*(1-1)²/2=8,7 кН*м

М_Х2=3=8,7*3-12*(3-1)²/2=26,1-24=2,1 кН*м

Теперь нам нужно найти тот самый экстремум, про который говорилось ранее. Для этого нам нужно приравнять 0 уравнение поперечных сил Q для этого участка и найти значение X2:

Q=Ra-q*(X2-1)=0

8,7-12*X2+12=0

20.7=12*X2

X2=1.725

Теперь найденное значение Х2 мы подставляем в уравнение моментов М и находим нужный нам экстремеум. Всю эту процедуру важно запомнить!

М_Х2=1.725=8,7*1,725-12*(1,725-1)²/2=15-3,2=11,8 кН*м (это мы потом укажем на эпюре)

 

Со вторым участком покончено. Остался один. Его можно рассмотреть так же – слева направо, но придется учитывать все опорные реакции, нагрузку и момент, а можно рассмотреть его справа и нам нужно будет учесть только силу F. Так мы и поступим:

Вот он, наш третий участок.

Указываем границы:

0≤Х3≤1  (мы рассматриваем участок справа, а он начинается от 0 и заканчивается 1)

Запишем уравнение поперечных сил:

Q_X3=F=16 кН 

почему плюс?

Смотрим правило знаков:

Смотрим относительно сечения по правилу знаков.

Теперь уравнение моментов:

М_Х3=-F*X3

Знак не такой как в уравнении Q, а кто сказал, что они должны быть всегда одинаковыми?

Мы пользуемся правилами знаков для моментов М:

Наша сила F гнет балку вниз, а значит знак минус.

Подставляем границы:

М_Х3=0=0

М_Х3=1=-16 кН*м

 

Вот мы рассчитали все участки, дальше построение эпюр.

 

Диаграмма деформации

| Обзор прочности материалов в MATHalino

Предположим, что металлический образец помещается в машину для испытания на растяжение-сжатие. Поскольку осевая нагрузка постепенно увеличивается с приращениями, общее удлинение по измерительной длине измеряется при каждом приращении нагрузки, и это продолжается до тех пор, пока не произойдет разрушение образца. Зная исходную площадь поперечного сечения и длину образца, можно получить нормальное напряжение σ и деформацию ε. График этих величин с напряжением σ по оси y и деформацией ε по оси x называется диаграммой напряжение-деформация.Диаграмма «напряжение-деформация» отличается по форме для разных материалов. На приведенной ниже диаграмме показана конструкционная сталь со средним содержанием углерода.

Металлические конструкционные материалы классифицируются как пластичные и хрупкие. Пластичный материал — это материал, имеющий относительно большие деформации при растяжении до точки разрыва, как конструкционная сталь и алюминий, в то время как хрупкие материалы имеют относительно небольшую деформацию до точки разрыва, например, чугун и бетон. Произвольная деформация 0.05 мм / мм часто используется как разделительная линия между этими двумя классами.

Диаграмма деформирования среднеуглеродистой конструкционной стали

Предел пропорциональности (закон Гука)
От начала координат O до точки, называемой пределом пропорциональности, кривая напряжения-деформации представляет собой прямую линию. Эта линейная связь между удлинением и вызывающей осевой силой была впервые замечена сэром Робертом Гук в 1678 году и называется законом Гука, согласно которому в пределах пропорционального предела напряжение прямо пропорционально деформации или

$ \ sigma \ propto \ varepsilon $ или $ \ sigma = k \ varepsilon $

Константа пропорциональности k называется модулем упругости E или модулем Юнга и равна наклону диаграммы напряжение-деформация от O до P.Тогда

$ \ sigma = E \ varepsilon

$

Предел упругости
Предел упругости — это предел, за которым материал больше не будет возвращаться к своей исходной форме при снятии нагрузки, или это максимальное напряжение, которое может возникнуть, так что не будет остаточной или остаточной деформации. когда нагрузка полностью снята.

Диапазон упругости и пластичности
Область на диаграмме «напряжение-деформация» от O до E называется диапазоном упругости.Область от E до R называется пластической областью.

Предел текучести
Предел текучести — это точка, при которой материал будет иметь заметное удлинение или податливость без увеличения нагрузки.

Предел прочности
Максимальная ордината на диаграмме «напряжение-деформация» — это предел прочности или предел прочности при растяжении.

Прочность на вознесение
Прочность на вознесение — это прочность материала при разрыве.Это также известно как предел прочности на разрыв.

Модуль упругости
Модуль упругости — это работа, выполняемая на единицу объема материала при постепенном увеличении силы от O до P, в Н · м / м ³ . Это может быть рассчитано как площадь под кривой напряжения-деформации от начала координат O до предела упругости E (заштрихованная область на рисунке). Устойчивость материала — это его способность поглощать энергию, не создавая постоянных искажений.

Модуль ударной вязкости
Модуль ударной вязкости — это работа, выполняемая на единицу объема материала при постепенном увеличении силы от O до R, в Н · м / м ³ .Это можно рассчитать как площадь под всей кривой напряжения-деформации (от O до R). Прочность материала — это его способность поглощать энергию, не вызывая разрушения.

Рабочее напряжение, допустимое напряжение и коэффициент безопасности
Рабочее напряжение определяется как фактическое напряжение материала при заданной нагрузке. Максимальное безопасное напряжение, которое может выдержать материал, называется допустимым напряжением. Допустимое напряжение должно быть ограничено значениями, не превышающими предела пропорциональности.Однако, поскольку пропорциональный предел трудно определить точно, допустимая прядь берется как предел текучести или предел прочности, деленный на коэффициент безопасности. Отношение этой прочности (предела или предела текучести) к допустимой прочности называется запасом прочности.

Прикладная прочность материалов для инженерных технологий

% PDF-1.7 % 1 0 obj > эндобдж 2 0 obj > поток 2016-11-16T10: 05: 25-08: 002016-11-16T10: 05: 25-08: 002016-11-16T10: 05: 25-08: 00Appligent AppendPDF Pro 5.5uuid: 2afc424e-a45d-11b2-0a00-782dad000000uuid: 2afc877d-a45d-11b2-0a00-f09a2b3ffd7fapplication / pdf

Прикладная прочность материалов для инженерных технологий

Prince 9.0 rev 5 (www.princexml.com) AppendPDF Pro 5.5 Ядро Linux 2.6 64-битная 2 октября 2014 Библиотека 10.1.0 конечный поток эндобдж 5 0 obj > эндобдж 3 0 obj > эндобдж 8 0 объект > эндобдж 9 0 объект > эндобдж 10 0 obj > эндобдж 11 0 объект > эндобдж 12 0 объект > эндобдж 13 0 объект > эндобдж 43 0 объект > эндобдж 44 0 объект > эндобдж 45 0 объект > эндобдж 46 0 объект > эндобдж 47 0 объект > эндобдж 68 0 объект > / MediaBox [0 0 612 792] / Родительский 47 0 R / Ресурсы 74 0 R / Тип / Страница >> эндобдж 69 0 объект > / MediaBox [0 0 612 792] / Родительский 47 0 R / Ресурсы 74 0 R / Тип / Страница >> эндобдж 70 0 объект > / MediaBox [0 0 612 792] / Родительский 47 0 R / Ресурсы 74 0 R / Тип / Страница >> эндобдж 71 0 объект > / MediaBox [0 0 612 792] / Родительский 47 0 R / Ресурсы 74 0 R / Тип / Страница >> эндобдж 72 0 объект > / MediaBox [0 0 612 792] / Родительский 47 0 R / Ресурсы 74 0 R / Тип / Страница >> эндобдж 78 0 объект > поток x] M3h4᫿ $ ˒mr [i ܲ C%? vnmN

Диаграмма механических свойств металла: прочность на сдвиг, предел прочности на разрыв, предел текучести

В последнее время мы получаем много запросов от читателей о таблицах механических свойств для различных металлов , такие как прочность на сдвиг, предел прочности на разрыв, предел текучести и удлинение стали и т. д.

Чтобы удовлетворить потребности наших читателей, мы составили следующие таблицы механических свойств, в которых перечислены различные черные и цветные металлы.

Надеюсь, что это поможет!

Предел текучести
δ
МПа) 901 9030 2060 400 901 301 901 9030 — 9013 9030 390 901
0 320 ~ 440 9013 901 9013 901 9015 9015 9015 с подогревом

Материал	Марка	Материал Статус	Сдвиг Прочность τ (МПа)	Предел прочности Предел прочности σb (МПа)	Относительное удлинение σs (%)	Упругость Модуль упругости Е (МПа)
Промышленное чистое железо для электриков C> 0.025	DT1 DT2 DT3	отожженный	180	230	26
Электротехническая кремниевая сталь	D11 D12 D213 D31 D41 D31 D41 D31 9 3	отожженная	190	230	26
Обычная углеродистая сталь	Q195	неотожженная	260 ~ 320	315 ~ 390 2830	Q215	270 ~ 340	335 ~ 410	26 ~ 31	215
	Q235		310 ~ 380	375 ~ 460	21 ~ 26	235 9013 901 9012 Q2 ~ 420	410 ~ 510	19 ~ 24	255
	Q275		400 ~ 500	490 ~ 610	15 ~ 20	275
	Углеродный инструмент угорь		08F	отожженный	220 ~ 310	280 ~ 390	32	180
			10F		260 ~ 360	330 ~ 450	32 200	330 ~ 450	32 200
15F		220 ~ 340	280 ~ 420		30	190
08		260 ~ 340	300 ~ 440		29	210	198000	198000	198000	198000	198000	250 ~ 370	320 ~ 460	28	—
15		270 ~ 380	340 ~ 480		26	280	202000	360 ~ 510	35	250	21000
25		320 ~ 440	400 ~ 550		34	280	202000
30		360 ~ 480	450 ~ 600	22	300	201000
35		400 ~ 520	500 ~ 650	20	320 20130	12	420 ~ 540	520 ~ 670	18	340	213500
45		440 ~ 560	550 ~ 700	16	36016	нормализованное	440 ~ 580	550 ~ 730	14	380	220000
55		550	≥670	43	390	— 9099	≥700	12	410	208000
65		600	≥730	10	420	—
70		600	≥760	9	430	210000
T7 ~ T12 T7A ~ T12A		отожженный	600	750	T8A	холодная закалка	600 ~ 950	750 ~ 1200	—	—	—
Высококачественная углеродистая сталь		10Mn	отожженная	22	230	211000
		65Mn		600	750	12	400	21000
Легированная конструкционная сталь		25CrMn8 560	500 ~ 700	18	950	—
		30CrMnSiA 30CrMnSi	440 ~ 6000	550 ~ 750	16	1450 850	—
Качественная пружинная сталь		60Si2Mn 60Si2MnA 65SiWA	низкотемпературный отожженный	0	0	холодная закалка	640 ~ 960	800 ~ 1200	10	1400 1600	—
			Нержавеющая сталь	1Cr13	отожженная	320 ~ 380	320 ~ 380	420	210000
2Cr13	320 ~ 400	400 ~ 500		20		450	210000
3 18Cr13	400 ~ 480 500			210000
4Cr13	400 ~ 480	500 ~ 600		15		500	210000
1Cr18Ni19 2Cr18Ni19	термообработка	460 ~ 520		580 ~ 640	35	200	200000
				38	220	200000
1Cr18Ni9Ti	термообработанная смягченная	430 ~ 550		540 ~ 700	40	200	200000

901

Марка стали	Температура нагрева ℃
	200	500	600	700	800	9007
Q195, Q215, 08, 15	360	320	200	110	60 9013 1	30
Q235, Q255, 20, 25	450	450	240	130	90	60
Q275, 30, 35	530 530 530 530	160	90	70
40, 45, 50	600	580	380	190	90	70

Значение сдвига

материал следует брать при температуре штамповки, которая обычно на 150 ~ 200 ℃ ниже температуры нагрева.

Таблица механических свойств цветных металлов

19 90 508 Алюминий-магниевый сплав
Алюминий-магниево-медный сплав 9012 искусственно состаренный 9013 9013 901 9013 901 901 901 901 901 9030 300 9030

9013 901 901 901 901 9030 9030 9013 901 901 901 9030 9013 9013 9013 9013 901 901 9030 450 900-19013 9013 9030 Extra 9030 901 301 901 901 30 901 901 901 901 901 901 9030 560 901 900 900 600 6003 9013 9013 901 901 9030 Мягкий 9013 2401 9050 Никель 9013 9013 9013 TA 901 9030 9099 640 ～ 680 901 901 медь константен 9050n5 900 901 901 901 901 901

Материал	Марка	Состояние материала	Прочность на сдвиг τ (МПа)	Предел прочности при растяжении σb (МПа)	Относительное удлинение σs (%)	Предел текучести Прочность δ (МПа)	Упругость Модуль упругости (МПа)
Алюминий	1070A, 1050A 1200	Отожженный	80	75 ～ 110	72000
		Холодная закалка	100	120 ～ 150		4	120 ～ 240
Алюминиево-марганцевые сплавы	3A21	1		отожженный	50	71000
		Полу-холодная закалка	100 ～ 140	155 ～ 200	13		130
SA02	Отожженный	130 ～ 160	180 ～ 230	—	100	70000
	160131 200	полу-холодная закалка			230 ～ 280		210
Высокопрочный алюминиево-магниево-медный сплав	7A04	Отожженный	170	250	—	—	1	350	500	460	70000
		Магниево-марганцевый сплав	MB1 MB8	Отожженный		120 ～ 140	170 ～ 190	170 ～ 190
Отожженная	170 ～ 190			220 ～ 230	12 ～ 24	140	40000
Холодная закалка	190 ～ 200			240 ～ 250	8 ～ 10	160
Жесткий алюминий	2Al12	Отожженный	105 ～ 150	150 ～ 215	1
		Закалка с естественным старением	280 ～ 310	400 ～ 440	15	368	72000
		Холодная закалка после закалки	280 ～ 320	400 901 901 901	400 901 901
Чистая медь	T1 、 T2 、 T3	Мягкая	160	200	30	70	108000
		Жесткая	240 380131 901 9013 9013 9030 300 9030
Латунь	H62	Мягкий	260	300	35	380	100000
		Полужесткий 9 0131	300	380	20	200	—
		Жесткий	420	420	10	480	—
300	40	100	110000
Полужесткий	280	350		25	—
Жесткий	400	400	400	400	400	400
Свинец латунь	HPb59-1	Мягкий	300	350	25	142	93000
		Жесткий	400
Марганцевая латунь	HMn58-2	Мягкая	340	390	25	170	100000
		Полужесткий	400	450	15	—
		Жесткий	520	600	5
Tin
		QSn4-4-2.5 QSn4-3	Мягкий	260	300	38	140	100000
			Жесткий	480	550	3 ～ 5	650		1 ～ 2	546	124000
Алюминиевая бронза			QAl17	Отожженный	520	600	10	650	5	250	115000 ～ 130000
	Алюминий-марганцевая бронза	QAl9-2		Мягкая	360	450	300 92	480	600	5	500	—
Кремний-марганцевая бронза			QBi3-1 9013 1	Мягкий	280 ～ 300	350 ～ 380	40 ～ 45	239	120000
	Жесткий	480 ～ 520		600 650	3 ～ 5
	Сверхтвердый	560 ～ 600		700 ～ 750	1 ～ 2	—	—
Бериллиевая бронза	QBe2	240	30	250 ～ 350	117000
		Жесткий	520	660	2	1280	132000 ～ 141000
300	25	—	—
Жесткий	360			450	3
Никель-серебро	BZn15-20	280 Мягкий		350	35	207	—
		Жесткий	400	550	1	486	126000 ～ 140000
		901 901 901 901 9030 — экстра-жесткий
Никель	Ni-3 ～ Ni-5	Мягкий	350	400	35	70	—
		Жесткий	470 9013 901	470 9013 901 901	210000 ～ 230000
Немецкое серебро	BZn15-20	Мягкий	300	350	35	—	—
		Жесткий	550	Жесткий
		Сверхтвердый	560	650	1
Цинк	Zn-3 ～ Zn-6	—	120 ～ 200	1 40 ～ 230	40	75	80000 ～ 130000
Свинец	Pb-3 ～ Pb-6	—	20 ～ 30	25 ～ 40	40 ～ 50 10	15000 ～ 17000
Олово	Sn1 ～ Sn4	—	30 ～ 40	40 ～ 50	—	12	41500 ～ 55000	41500 ～ 556	Отожженный	360 480	450 ～ 600	25 ～ 30	—	—
TA3	440 ～ 600	550 ～ 7501
800 ～ 850	15	800 ～ 900	104000
Магниевый сплав	MB1	В холодном состоянии	120 ～ 140	120 ～ 190		40000
	МБ8		150 ～ 180	230 ～ 240	14 ～ 15	220	41000
	MB1	Предварительный нагрев 300 ° C	30 ～ 50	30 ～ 50	1 50	1	40000
	MB8		50 ～ 70	50 ～ 70	58 ～ 62	—	41000
Серебро	—	—	30	81000
Легкосплавный	Ni29Co18	—	400 ～ 500	500 ～ 600	—	—	—
—
Мягкий	—	400 ～ 600	—	—	—
Жесткий	—	650	—	—	6 —	—	—	отожженный	—	720	0	700	312000
неотожженный	—	1491	1 ～ 4	8000000			отожженный	20 30	1400	20 ～ 25	385	280000
неотожженный	32 ～ 34	1600	2 ～16 59306	2 ～16 59306	2 ～16 5

Проверьте эти

Предел текучести — предел текучести

Принципиальная диаграмма кривой напряжения-деформации низкоуглеродистой стали при комнатной температуре показана на рисунке.Есть несколько стадий, демонстрирующих разное поведение, что предполагает разные механические свойства. Для пояснения, материалы могут пропускать одну или несколько стадий, показанных на рисунке, или иметь совершенно разные стадии. В этом случае необходимо различать деформационные характеристики пластичного материала и хрупкого материалов . Следующие пункты описывают различные области кривой напряжения-деформации и важность нескольких конкретных мест.

Предел текучести — предел текучести

Предел текучести — это точка на кривой зависимости напряжения от деформации, которая указывает предел упругого поведения и начало пластического поведения. Предел текучести или предел текучести — это свойство материала, определяемое как напряжение, при котором материал начинает пластически деформироваться, тогда как предел текучести — это точка, в которой начинается нелинейная (упругая + пластическая) деформация. До достижения предела текучести материал будет упруго деформироваться и вернется к своей исходной форме, когда приложенное напряжение будет снято. После достижения предела текучести некоторая часть деформации будет постоянной и необратимой. Некоторые стали и другие материалы демонстрируют поведение, называемое явлением предела текучести.Предел текучести варьируется от 35 МПа для алюминия с низкой прочностью до более 1400 МПа для высокопрочных сталей.

Во многих ситуациях предел текучести используется для определения допустимого напряжения, которому может подвергаться материал. Для компонентов, которые должны выдерживать высокое давление, таких как те, которые используются в реакторах с водой под давлением (PWR), этот критерий неадекватен. Чтобы охватить эти ситуации, теория максимального касательного напряжения была включена в Кодекс ASME (Американское общество инженеров-механиков) по котлам и сосудам под давлением, раздел III, Правила строительства ядерных сосудов под давлением.Эта теория утверждает, что отказ компонента трубопровода происходит, когда максимальное напряжение сдвига превышает напряжение сдвига в пределе текучести при испытании на растяжение.

Характеристики прочности и жесткости

Характеристики прочности и жесткости

Текст подлежит уточнению

Предел пропорциональности: также известный как предел упругости, это точка, в которой кривая напряжения-деформации становится нелинейной. Значения напряжения и деформации в этой точке называются пропорционально-предельным напряжением и деформацией соответственно.Это точка, за которой закон Гука больше не может использоваться для связи напряжения и деформации при осевой или сдвиговой деформации. На рисунке ниже показана точка пропорционального ограничения, связанная с осевой нагрузкой. Аналогичная точка также существует на кривых напряжения-деформации сдвига.

Предел текучести:

Предел текучести соответствует моменту, когда материал начинает иметь постоянную (неустранимую) деформацию.В то время как некоторые материалы имеют четко определенный диапазон текучести (Рисунок A), другие (Рисунок B) — нет. При отсутствии четкого предела текучести используется смещение 0,2% для получения приблизительного предела текучести. Хотя точки предела текучести и пропорционального ограничения близки друг к другу, они не соответствуют одному и тому же положению на кривой напряжения-деформации. Напряжение и деформация, соответствующие пределу текучести, называются соответственно пределом текучести и деформацией текучести.

0.Смещение 2%:

Точка смещения 0,2% определяется путем проведения линии, параллельной линейному участку кривой, начиная с точки 0,002 на оси деформации. Пересечение этой линии и кривой напряжения-деформации определяет предел текучести 0,2%.

Максимальная сила:

Предел прочности на разрыв:

Максимальное растягивающее напряжение, которое может выдержать материал, известно как предельное растягивающее напряжение. Это соответствует наивысшей точке на кривой растяжения.Предел прочности при растяжении обычно обозначается s _tu . Соответствующая деформация известна как предельная деформация растяжения.

Важно помнить, что предельное напряжение растяжения обычно основывается на исходной площади поперечного сечения образца. Таким образом, его значение на инженерной диаграмме «напряжение-деформация» будет отличаться от значения на диаграмме «истинное напряжение-деформация», если образец демонстрирует значительное сужение до разрушения. Обычной практикой является использование значения, связанного с инженерной диаграммой напряжения-деформации.

Предел прочности на сжатие:

Максимальное сжимающее напряжение, которое способен выдержать образец материала, известно как предельное сжимающее напряжение. В отличие от растяжения, реакция образца на сжатие зависит от его формы и длины в поперечном сечении. Чтобы устранить эти геометрические эффекты, сжатые образцы обычно должны быть очень короткими с относительно большой площадью поперечного сечения. Если материал хрупкий, как бетон, то разрушение в конечной точке представляет собой форму разрушения.Если материал пластичный, как алюминий, то разрушение проявляется в виде чрезмерной податливости, и поэтому нет определенного значения для предельного напряжения сжатия пластичного материала. В случае пластичных материалов принято считать, что s _cu = s _tu .

Модуль упругости: это способность материала поглощать энергию в диапазоне упругости. Его значение просто равно площади под упругим участком кривой напряжения-деформации.Для любого линейно упругого материала модуль упругости находится как . U = 0,5 с e e e или U = 0,5 с e 2 / E , где s e — предел упругости или предельное пропорциональное напряжение материала.

Прочность:

Относится к способности материала поглощать энергию до отказа. Его значение равно всей площади под кривой растяжения.В большинстве случаев площадь под упругой частью кривой составляет очень небольшой процент от общей площади, и ее можно не учитывать при вычислении модуля ударной вязкости. Чтобы еще больше упростить расчет, нелинейная часть кривой напряжения-деформации аппроксимируется серией прямых линий, как показано слева. В примере слева модуль ударной вязкости определяется путем суммирования площадей от A 1 до A 4 .

Модуль Юнга: также известный как модуль упругости, это мера сопротивления материала осевой деформации.Его значение получается путем измерения наклона кривой осевого напряжения-деформации в упругой области. Он назван в честь английского ученого Томаса Янга. Обычно обозначается буквой E и имеет единицы Н / м 2 или фунт / дюйм 2 . Поскольку в некоторых материалах модуль Юнга при растяжении отличается от модуля упругости при сжатии, для упрощения различия используется индекс c или t.

Модуль упругости по касательной:

Касательный модуль определяется как наклон линии, касательной к кривой напряжения-деформации в интересующей точке.Модуль касания может иметь разные значения в зависимости от точки, в которой он определяется. Например, касательный модуль равен модулю Юнга, когда точка касания попадает в линейный диапазон кривой напряжения-деформации. Вне области линейной упругости, например, в точке A, показанной, касательный модуль всегда меньше модуля Юнга. Модуль касательной упругости в основном используется для описания жесткости материала в диапазоне пластичности и обозначается E t . Уравнение Рамберга-Осгуда: Он используется для описания зависимости напряжение-деформация в области текучести диаграммы напряжения-деформации.Он использует три различных свойства материала, то есть E — модуль Юнга, s 0,7 — значение напряжения, соответствующее секущему модулю 0,7E, и n-коэффициент формы, описывающий форму диаграммы напряжения-деформации в области текучести. .

Уравнение Рамберга-Осгуда используется при анализе неупругого продольного изгиба колонн и пластин.

Секущий модуль: Секущий модуль — это наклон линии, проведенной из начала диаграммы напряжения-деформации и пересекающей кривую в интересующей точке.Следовательно, секущий модуль может принимать разные значения в зависимости от места пересечения. На рисунке ниже показано, как рассчитывается секущий модуль в точке A на кривой. Секущий модуль может быть выражен в процентах от модуля Юнга (например, 0,7E или 0,85E), и он используется для описания жесткости материала в неупругой области диаграммы напряжения-деформации. Секущий модуль обычно обозначается E s .

Коэффициент Пуассона: отношение поперечной деформации к осевой деформации называется коэффициентом Пуассона материала.Расчет основан на физическом явлении, описанном на рисунке ниже.

Жесткость при сдвиге: также известная как модуль жесткости, это мера сопротивления материала деформации при сдвиге. Его значение равно наклону кривой напряжение-деформация сдвига в упругой области. Обычно обозначается буквой G и имеет единицы Н / м ² или фунт / дюйм ² .

Пластичность: способность материала подвергаться значительной неупругой деформации перед разрушением.Это сильно зависит от рабочей температуры материала. При очень низких температурах материалы имеют тенденцию терять пластичность и становятся хрупкими .

Удлинение:

Мера пластичности материала, она определяется как процентное изменение длины образца в точке разрушения. Обычно обозначается буквой e, его можно получить, умножив деформацию разрушения на 100.

e = (L’-L _o / L _o ) 100

Где L ‘= расчетная длина образца после разрушения, L _o = исходная расчетная длина.Обратите внимание: поскольку процентное удлинение определяется как функция расчетной длины, важно указать расчетную длину при упоминании относительного удлинения.

EngArc — L — Диаграмма напряжение-деформация

EngArc — L — Диаграмма напряжение-деформация

---

---

Схемы

Пример диаграммы напряжения-деформации для пластичного материала

Пластичные материалы могут иметь тенденцию к снижению после достижения максимального напряжения и разрушаться в точке f .Другие, такие как чугуны и высокопрочные стали, разрушаются, пока кривая напряжения-деформации все еще растет, и предел прочности будет равен прочности на излом, например, на рисунке чуть ниже справа, напряжение-деформация кривая для хрупкого материала.

99 Точка A — пропорциональный предел Точка B — предел упругости Точка y — предел текучести Линия определяется методом смещения и используется для определения предела текучести (точка y ) Наклон линии OA равен модулю упругости Линия AB не является идеально прямой линией, даже если образец эластичен в этой области Остальные символы см. В номенклатуре ниже

Кривая напряжение-деформация для пластичного материала

Кривая напряжение-деформация для хрупкого материала

Податливость представляет собой относительно значительную деформацию по отношению к изменению приложенной нагрузки.Эта деформация вызывается проскальзыванием материала по наклонным поверхностям и, следовательно, в первую очередь из-за касательных напряжений. Деформационное упрочнение может повысить предел текучести материала, но сделать его менее пластичным. За счет образования шейки требуются более низкие напряжения, чтобы вызвать дальнейшее удлинение.

Номенклатура

Детали

Из приведенных выше диаграмм предел текучести — это напряжение, при котором начинается текучесть, предел прочности соответствует максимальной нагрузке, приложенной к образцу, а напряжение разрушения соответствует разрыву.

Диаграммы «напряжение-деформация», в которых используются данные испытаний на растяжение, представляют собой инженерные диаграммы «напряжение-деформация», поскольку напряжения и деформации, рассчитанные на основе данных, не являются истинными значениями. Напряжение основано на исходной площади до приложения нагрузки. В действительности, по мере приложения нагрузки площадь уменьшается, так что фактическое или истинное напряжение превышает инженерное напряжение. Чтобы получить истинное напряжение для диаграммы, нагрузка и площадь поперечного сечения должны измеряться одновременно во время испытания.Как правило, истинное напряжение намного выше, чем инженерное напряжение в суженной части. См. Урок: Истинное напряжение, Истинное напряжение, Инженерное напряжение и Инженерное напряжение

Если образец, изготовленный из пластичного материала, был нагружен сжатием, а не растяжением, полученная кривая зависимости напряжения от деформации была бы по существу такой же на его начальном прямолинейном участке и в начале участка, соответствующего текучести и деформационному упрочнению . Особого внимания заслуживает тот факт, что для данной стали предел текучести одинаков как при растяжении, так и при сжатии.При больших значениях деформации кривые растяжения и сжатия «напряжение-деформация» расходятся, и следует отметить, что образование шейки не может происходить при сжатии. Для большинства хрупких материалов предел прочности при сжатии намного превышает предел прочности при растяжении. Это связано с наличием дефектов, таких как микроскопические трещины или полости, которые имеют тенденцию ослаблять материал при растяжении, не влияя заметно на его сопротивление разрушению при сжатии.

Примером хрупкого материала с различными свойствами при растяжении и сжатии является бетон, диаграмма растяжения которого показана.Со стороны растяжения диаграммы находится линейный диапазон упругости, в котором деформация пропорциональна напряжению. После достижения предела текучести деформация увеличивается быстрее, чем напряжение, до тех пор, пока не произойдет разрыв. Поведение материала при сжатии иное. Во-первых, линейный диапазон упругости значительно больше. Во-вторых, разрыва не происходит, когда напряжение достигает максимального значения. Напротив, напряжение уменьшается по величине, в то время как деформация продолжает увеличиваться, пока не произойдет разрыв.Обратите внимание, что модуль упругости, который представлен наклоном кривой напряжения-деформации на ее линейном участке, одинаков при растяжении и сжатии. Это верно для большинства хрупких материалов.

Кривая напряжения-деформации для некоторых низкоуглеродистых сталей показывает двойной предел текучести. Ожидается, что материал будет пластически деформироваться при напряжении σ ₁ . Однако межузельные атомы, сгруппированные вокруг дислокаций, препятствуют скольжению и повышают предел текучести до σ ₂ .Только после приложения более высокого напряжения σ ₂ дислокации скользят. После того, как скольжение начинается при σ ₂ , дислокации удаляются от кластеров небольших атомов и продолжают очень быстро перемещаться при более низком напряжении σ ₁ .

Конструкционная сталь и алюминий, будучи пластичными, имеют разные характеристики текучести. В случае конструкционной стали напряжение остается постоянным в большом диапазоне значений деформации после начала текучести.Позже необходимо увеличить напряжение, чтобы образец продолжал растягиваться до тех пор, пока не будет достигнуто предельное напряжение. Это происходит из-за свойства материала, известного как деформационное упрочнение. Предел текучести конструкционной стали можно определить во время испытания на растяжение, наблюдая за нагрузкой, отображаемой на дисплее испытательной машины. После неуклонного увеличения нагрузка внезапно падает до несколько более низкого значения, которое сохраняется в течение определенного периода, пока образец продолжает растягиваться. В очень тщательно проведенном испытании можно различить верхний предел текучести, который соответствует нагрузке, достигаемой непосредственно перед началом текучести, и нижний предел текучести, который соответствует нагрузке, необходимой для поддержания текучести.Поскольку верхний предел текучести является временным, нижний предел текучести следует использовать для определения предела текучести материала.

---

Таблица выбора материалов — обзор

Решение

Укажите функцию, цель, ограничения и свободные переменные.

Функция в этом случае: стяжка несет растягивающую силу.

Цель: Сведение к минимуму массы.

Ограничения: Должен быть установлен указанный груз.

Свободные переменные: Площадь поперечного сечения стяжки, обычно это геометрические размеры.

Функция объекта описывается формулой

m = Alρ (уравнение для цели)

, где A — площадь поперечного сечения, l — длина, а ρ — плотность.

Длина ( l ) указана и не должна выходить из строя под нагрузкой F (ограничение). Площадь поперечного сечения ( A, ) свободна (произвольная переменная). Подводя итог, функция: рулевая тяга. Цель: минимизировать ограничение массы. Длина указана, не должен разрушаться под нагрузкой F (адекватная вязкость разрушения).

F / A <σy (уравнение для ограничения)

Формула для массы стяжки: плотность ( ρ ) × площадь ( A ) × длина ( l )

Следовательно, площадь (свободная переменная):

(9,4) A = F (Сила) σy (предел текучести)

Более прочные материалы, такие как нержавеющая сталь, требуют небольшой площади поперечного сечения, тогда как более слабые материалы, такие как полимеры, требуют большого поперечного сечения. области, чтобы нести ту же нагрузку. В этой конструкции могут использоваться как малые, так и большие площади поперечного сечения, поскольку они не являются ограничением.Важный вопрос — какой материал даст наименьшую массу для легкого и жесткого луча. Это можно определить как: сгенерировать м в терминах F, G, M . Определим m в терминах любой комбинации F, G, M. Показано, что m = A × l × p. Отсутствующий параметр — F. Определите F в приведенном выше уравнении, F / A = σ _y , исключив область.

Следовательно, индекс эффективности для легкой прочной стяжки составляет

. Выбирайте материал с меньшим размером л .

Первая и вторая скобки содержат указанную нагрузку и указанную длину. Свойство материала, представленное как ( ρ / σ _y ) в последней скобке, предполагает, что самая легкая стяжная шпилька, которая выдержит указанную нагрузку F , принадлежит материалу с наименьшим значением ρ / σ _y . Чтобы максимизировать производительность, член свойств материала ( ρ / σ _y ) инвертирован. Свойство материалов определяется индексом M.В приведенном выше случае M = σ _y / ρ. Самая легкая стяжка будет нести нагрузку F будет с наибольшим значением M.

Аналогично для легкой сильной балки индекс материала M равен

M = σf3 / 2ρ

и масса минимизируется за счет выбора материала с наибольшим значением индекса. В приведенном выше примере ограничениями были l и f .

Типичные примеры показателей материалов приведены в таблице 9.3.

Таблица 9.3. Показатели материала [16]

907 производительность зависит от двух или более свойств материала, которые представлены путем нанесения одного механического свойства или математической комбинации свойств на каждую ось диаграммы материалов.Один из способов рассмотреть материалы для определенного свойства или индекса материала — использовать таблицу выбора материалов. Таблица выбора материала (ρ по сравнению с E ) показана на рис. 9.3. Он показывает модуль растяжения материалов на четыре декады от 0,1 ГПа до 1000 ГПа. Масштаб журнала позволяет отображать большую информацию на небольшом пространстве. Данные для ряда материалов определенного класса сгруппированы и заключены в конверт (жирная линия). Пузырьки в конверте представляют собой подмножество материалов.Например, на рис. 9.3 оболочка инженерных композитов содержит KFRP (полимер, армированный волокном Кельвера), GFRP (полимер, армированный графитовым волокном) и CFRP (полимер, армированный углеродным волокном) в качестве подмножеств материалов в пузыре. Конверт включает в себя всех членов класса и пузырьковые элементы подклассов. В таблицу включен ряд материалов. Эти диаграммы отображают данные по важным свойствам, которые представляют наибольший интерес для определения характеристик материалов и инженерного проектирования.Эти свойства включают плотность, модуль, прочность, ударную вязкость, теплопроводность, коэффициент диффузии и расширение.

Рисунок 9.3. Материалы для весел. Углепластик лучше дерева, потому что структурой можно управлять. (Из Эшби, М.Ф. (1999). Выбор материалов в механическом проектировании , Баттерворт. С любезного разрешения публикации Баттерворта)

Из информации, представленной в таблицах, подмножество материалов, которые максимизируют производительность компонентов после исправления найдены основные ограничения.Устойчивость к коррозии, модуль, прочность и плотность — все это основные ограничения, которые необходимо соблюдать. Ограничения могут исключить несколько классов материалов. Ограничения задаются формулой

P> Pcritical

, где P — свойство, а P _{критическое} — критическое значение, которое нельзя превышать.

Например, если присутствует коррозия, скорость коррозии не должна превышать предписанное критическое значение. Основные ограничения отображаются в виде горизонтальных или вертикальных линий на диаграмме выбора материала.Например, если ограничение E > 10 ГПа и ρ = 3 мг / м ³ , пересечение линий даст область поиска для выбора подходящих материалов.

Из информации, представленной в таблице свойств материалов, материалы, которые обеспечивают максимальную производительность, выбираются из подмножеств, которые соответствуют ограничениям свойств с использованием индексов материалов.

Например, выберите материалы с модулем упругости всего 10 ГПа, при этом значении будет проведена линия (рис.9.4). Все материалы над линией будут показывать набор материалов кандидатов. Если требуемая плотность меньше 2,0 мг / м ³ , на указанном значении плотности проводится линия. Подмножество материалов, отвечающих обоим критериям, можно найти в верхнем левом квадранте.

Рисунок 9.4. Таблица свойств

Индексы материалов Eρ, E1 / 2ρ, E1 / 3ρ для легких и жестких компонентов могут быть нанесены на диаграмму (рис. 9.5).

Рисунок 9.5a. Нормы для E ^1/2 / ρ максимальное значение

Рассмотрим, например, максимизирующий коэффициент для легкой жесткой балки и присвоим ему значение

Взятие бревен с обеих сторон, log E = log ρ + log C, которое представляет собой уравнение прямой линии с наклоном 1.Значение C получается, когда ρ = 1 и равно E , и определяет значение нормативов. Материалы, указанные в нормативных документах, имеют одинаковое значение для E / ρ (удельный модуль).

Для условия:

C = E1 / 2ρ logC = 12logE − logρ logE = 2logρ + 2logC

Таким образом, мы получаем семейство прямых (рис. 9.5a). Другие прямые в семействе будут параллельными линиями с градиентом 2.

Аналогично, для условия:

E1 / 3ρ = C

мы получим другой набор линий с наклоном 3.На рис. 9.5b показаны рекомендации и подмножество материалов. В рекомендациях показаны наклоны семейства параллельных линий для определенного индекса производительности.

Рисунок 9.5b. Линия для E / ρ = 1000

Рассмотрите возможность выбора материала со значениями E / ρ больше, чем, приблизительно, 1000.

log E − log ρ = log 1000log E = log ρ + 3 [log E − log ρ = log C]

Это даст линию с наклоном, равным единице, и точкой пересечения 3 на оси бревна E . Материалы, пересекаемые нормативными требованиями, имеют одинаковое значение E / ρ (удельный модуль).Материалы выше этой линии имеют значения выше, чем C , а материалы ниже имеют более низкие значения и не подходят. Схематическая диаграмма E – ρ , показывающая рекомендации по трем показателям материалов для жесткой и легкой конструкции, показана на рис. 9.6.

Рисунок 9.6. Схема E — ρ , показывающая рекомендации по трем показателям материалов для жесткой и легкой конструкции.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

2019 © Все права защищены.

Функции, цели и ограничения	Максимальный показатель эффективности
1. Стяжки — минимальный вес, предписанная жесткость	Eρ
2. Балка — минимальный вес , предписанная прочность	σy2 / 3ρ
3. Балка — минимальная стоимость, предписанная жесткость	σy2 / 3Cmρ
4. Теплоизоляция — минимальная стоимость, предписанный тепловой поток	1λCmρ