Эпюры внутренних усилий в балках
Эпюрами внутренних усилий в балках называют геометрические образы, применяемые для графического изображения изменения в элементе какого-либо силового фактора либо иных данных.
Примеры построения эпюр
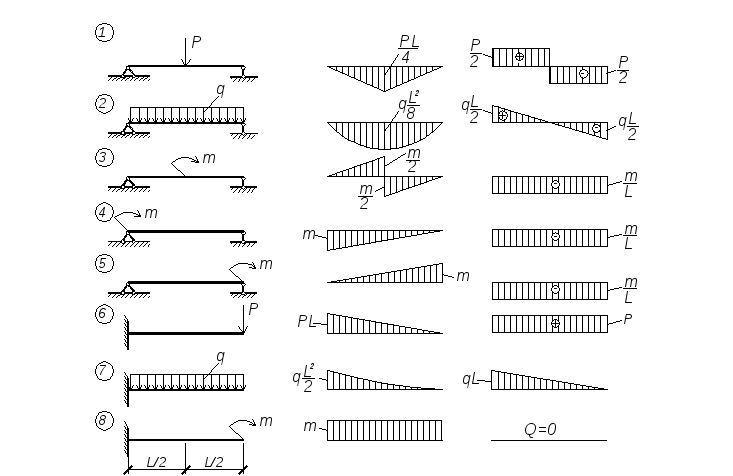
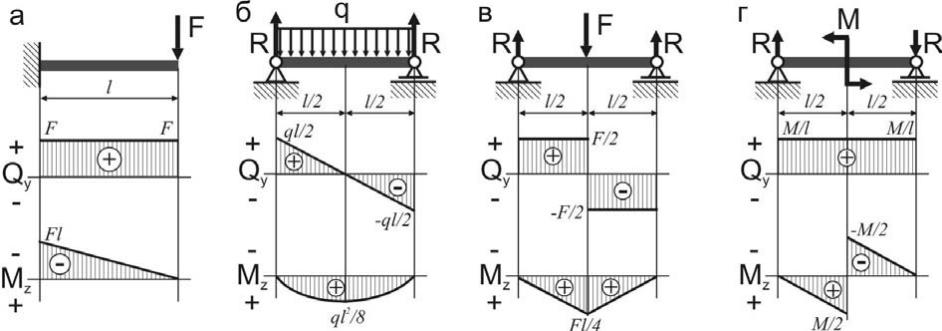
Эпюры внутренних усилий (поперечных сил и изгибающих моментов) для простейших систем показаны на рисунке 3.1.
Рисунок 3.1 – Эпюры внутренних усилий для простейших балок
Отметим, что в строительной механике, на эпюре изгибающих моментов знак, как правило, не ставится, и в отличие от сопромата, она строится со стороны растянутых волокон.
Эпюры для однопролетных балок с консолями строят в следующем порядке:
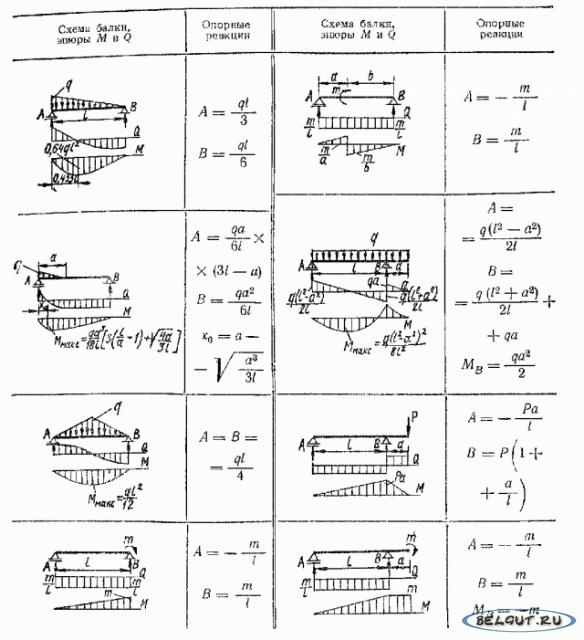
- сначала строят эпюры на консолях, используя таблицы изгибающих моментов для консольных балок (рисунок 3.1), фиксируя при этом консольные моменты;
- отмечая опорные моменты, проводят так называемую линию опорных моментов. Это прямая, соединяющая ординаты моментов над опорами;
- на линию опорных моментов накладывают пролетную балочную эпюру (табличная эпюра М для однопролетной балки) от соответствующего вида загружения;
- все эпюры М строят со стороны растянутых волокон.

Между выражениями для изгибающего момента, поперечной силы и интенсивностью распределенной нагрузки в пределах расчетного силового участка существуют известные из курса «Сопротивление материалов» дифференциальные зависимости.
Они легко выводятся с помощью уравнений равновесия, составленных для вырезанного бесконечно малого элемента (рисунок 3.2):
Рисунок 3.2 – Определение значений поперечной силы
Внутренние силы в основных типах элементов систем:
Понятие о расчетном силовом участке
Расчетным силовым участком называется участок элемента системы с постоянным законом изменения всех внутренних силовых факторов.
В расчетной практике силовые участки определяются их границами.
Граница силового участка − это место приложения какой-либо сосредоточенной нагрузки (силы или момента), начало или конец распределенной нагрузки, место изменения геометрии, механических характеристик конструкции, интенсивности распределенной нагрузки.
В курсе «Строительная механика» принята следующая последовательность определения внутренних усилий (построения эпюр).
Первоначально с помощью уравнений статики в требуемых сечениях определяются изгибающие моменты.
Далее посредством дифференциальной зависимости осуществляется переход к поперечным силам. Последние дают возможность оценить и продольные силы.
Построение эпюры моментов производится по силовым участкам. При этом за расчетный модуль принимается консольная балка (рисунок 3.3).
За начало (В) принимается тот конец силового участка, на котором все внутренние и внешние воздействия определены.
Рисунок 3. 3 – Консольная балка
3 – Консольная балка
Они (воздействия) легко (принцип независимости действия сил) приводятся к алгебраической сумме результатов простейших воздействий.
При построении эпюр внутренних усилий в многопролетных балках, рамах и других конструкциях используются эпюры М и Q в простых однопролетных и консольных балках, которые чаще всего называют табличными эпюрами моментов и поперечных сил (рисунок 3.1).
Последовательность построения эпюр внутренних усилий М, Q, N в статически определимых системах:
1) Кинематический анализ. Напомним, что нас интересуют лишь геометрически неизменяемые системы с нулевым количеством степеней свободы и правильной расстановкой связей.
2) Определение опорных реакций и реакций связи. При этом используются уравнения равновесия, составленные как для всей системы в целом, так и для любого элемента или группы элементов.
3) Построение эпюры изгибающих моментов − М.
По эпюре изгибающих моментов с помощью дифференциальной зависимости Журавского строится эпюра поперечных сил (Q).
На участке с линейной эпюрой изгибающих моментов величина поперечной силы равна тангенсу угла наклона эпюры М.
Q = |tga| — где a угол наклона касательной на эпюре М к оси балки.
Знак Q определяется по направлению кратчайшего совмещения оси участка с эпюрой. Если оно происходит по направлению движения часовой стрелки, поперечную силу считают положительной.
Если же против часовой стрелки, то отрицательной.
При построении эпюры поперечных сил для участков с криволинейной (изменяющейся только по закону квадратной параболы) эпюрой изгибающих моментов пользуются следующей зависимостью:
Q = Qо + (Мпр – Мл)/L
где Qо − поперечная сила от внешней нагрузки, приложенной на рассматриваемый участок, определенная для балки на двух опорах пролета равного L;
Мп, Мл − алгебраические величины изгибающих моментов, соответственно на правом и левом торцах рассматриваемого участка.
Вышеуказанное выражение (3.1) легко получить самостоятельно (рисунок 3.4):
Рисунок 3.4 – Вывод выражения (3)
4) По эпюре поперечных сил строится эпюра продольных сил. При этом рассматривается равновесие всех узлов системы под действием внутренних (продольных и поперечных) и внешних (узловых) сил.
5) Проводится статическая проверка правильности построения эпюр М, Q, N.
Правила для проверки правильности построенных эпюр внутренних усилий:
а) На прямолинейном ненагруженном участке эпюра моментов прямолинейна.
б) В сечении, где приложен сосредоточенный внешний момент, эпюра получает скачок на величину этого момента (рисунок 3.5), а линии эпюры моментов примыкающие к скачку идут параллельно друг другу.
Рисунок 3.5 – Эпюра М на участке с приложенным сосредоточенным моментом
в) В точке приложения сосредоточенной внешней силы Р, перпендикулярной оси стержня, эпюра моментов имеет перелом, направленный острием в сторону действия силы (рисунок 3. 6).
6).
Изменение тангенсов углов наклона эпюры в точке ее перелома равно силе Р. На эпюре Q в этой точке — скачок на величину Р в направлении ее действия.
Рисунок 3.6 – Эпюра М на участке с приложенной сосредоточенной силой Р
г) На участке, где приложена равномерно распределенная нагрузка, эпюра моментов очерчена по параболе второй степени с выпуклостью в сторону действия нагрузки и со стрелкой равной q×L2/8 (рисунок 3.7).
Рисунок 3.7 – Эпюра М на участке с равномерно распределенной нагрузкой
д) В сечениях, где нет сосредоточенной нагрузки, эпюра моментов не имеет перелома.
е) Поперечная сила в сечении стержня положительна, если она стремится вращать разделенные данным сечением части стержня по часовой стрелке (рисунок 3.8).
Рисунок 3.8 – Правило знаков для поперечной силы
Расчет внутренних усилий в рамах >
Примеры решения задач >
2.
 2 Пример построения эпюр внутренних силовых факторов для балки
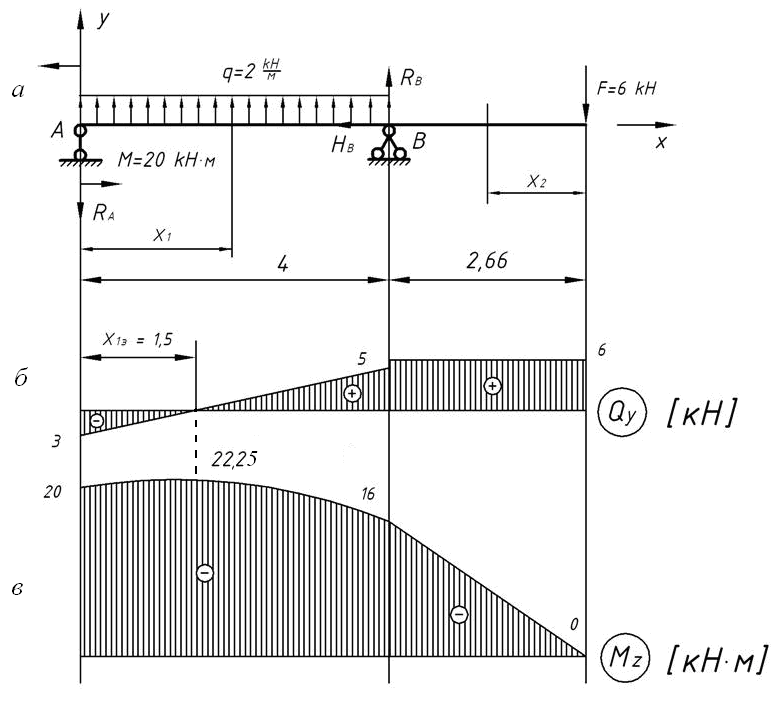
2 Пример построения эпюр внутренних силовых факторов для балкиИсходные данные: расчетная схема балки с указанием численных величин нагрузок и линейных размеров.
Требуется: построить эпюры внутренних силовых факторов.
В поперечных сечениях балки возникают два ВСФ: поперечная сила (Q) и изгибающий момент (M). Вычерчиваем заданную балку с указанием всех нагрузок и линейных размеров. Определяем реакции опор.
;
;
;
;
Проверка правильности определения реакций:
.
Разбиваем
балку на участки, на каждом из которых
проводим произвольное поперечное
сечение на расстоянии z
от начала соответствующего участка
(см. рисунок 2.2, а). Изображаем нулевые
линии для построения эпюр поперечных
сил (эпюра Q)
и эпюры изгибающего момента (эпюра М).
Записываем в общем виде выражения для
определения ВСФ для каждого участка
балки и при помощи полученных уравнений
рассчитываем их численные значения в
характерных сечениях.
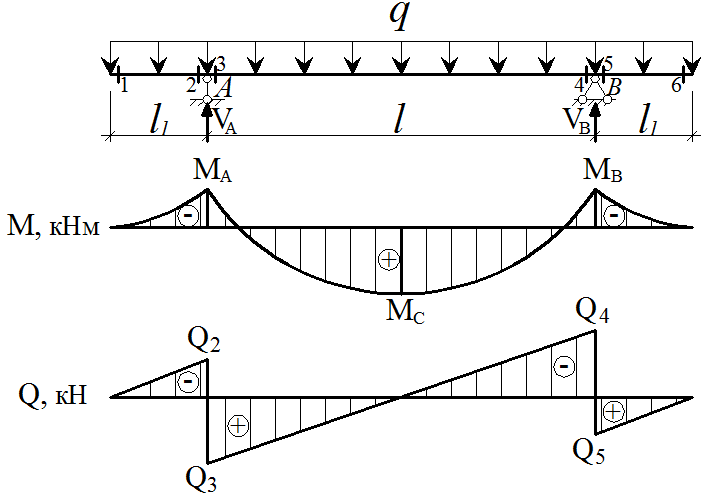
Рисунок 2.2 – Расчетная схема балки и эпюры внутренних силовых факторов
1 участок: .
;
.
2 участок: .
;
Так как на этом участке эпюра Q пересекает нейтральную линию, то в этой точке пересечения изгибающий момент будет иметь экстремальное значение:
;
откуда ;
.
3 участок: .
;
Полученные точки соединяем линиями, замыкающими поле эпюры. В поле эпюры в кружке ставим знак рассматриваемого внутреннего силового фактора и наносим штриховку. Линии штриховки перпендикулярны нулевой линии эпюры (рисунок 2.2, б, в).
Исходные данные: расчетная схема рамы с указанием
численных величин нагрузок и линейных
размеров.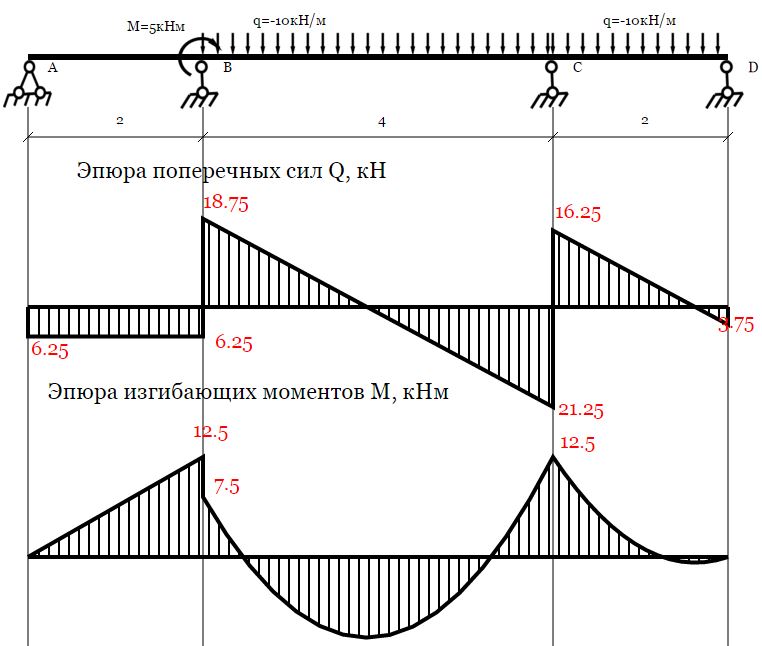
Требуется: построить эпюры внутренних силовых факторов.
Вычерчиваем заданную раму (рисунок 2.3, а) с указанием всех нагрузок и линейных размеров в численном виде. Определяем реакции опор:
;
;
;
;
;
.
Проверка правильности определения реакций:
.
Разбиваем раму на участки, на каждом из которых проводим произвольное поперечное сечение на расстоянии z от начала соответствующего участка (см. рисунок 2.3, а). Изображаем нулевые линии для построения эпюр нормальных (эпюра N) и поперечных (эпюра Q) сил, эпюры изгибающего момента (эпюра М).
Рисунок 2.3 – Расчетная схема рамы и эпюры внутренних силовых факторов
Записываем
в общем виде выражения для определения
ВСФ для каждого участка рамы и при помощи
полученных уравнений рассчитываем их
численные значения в характерных
сечениях рамы.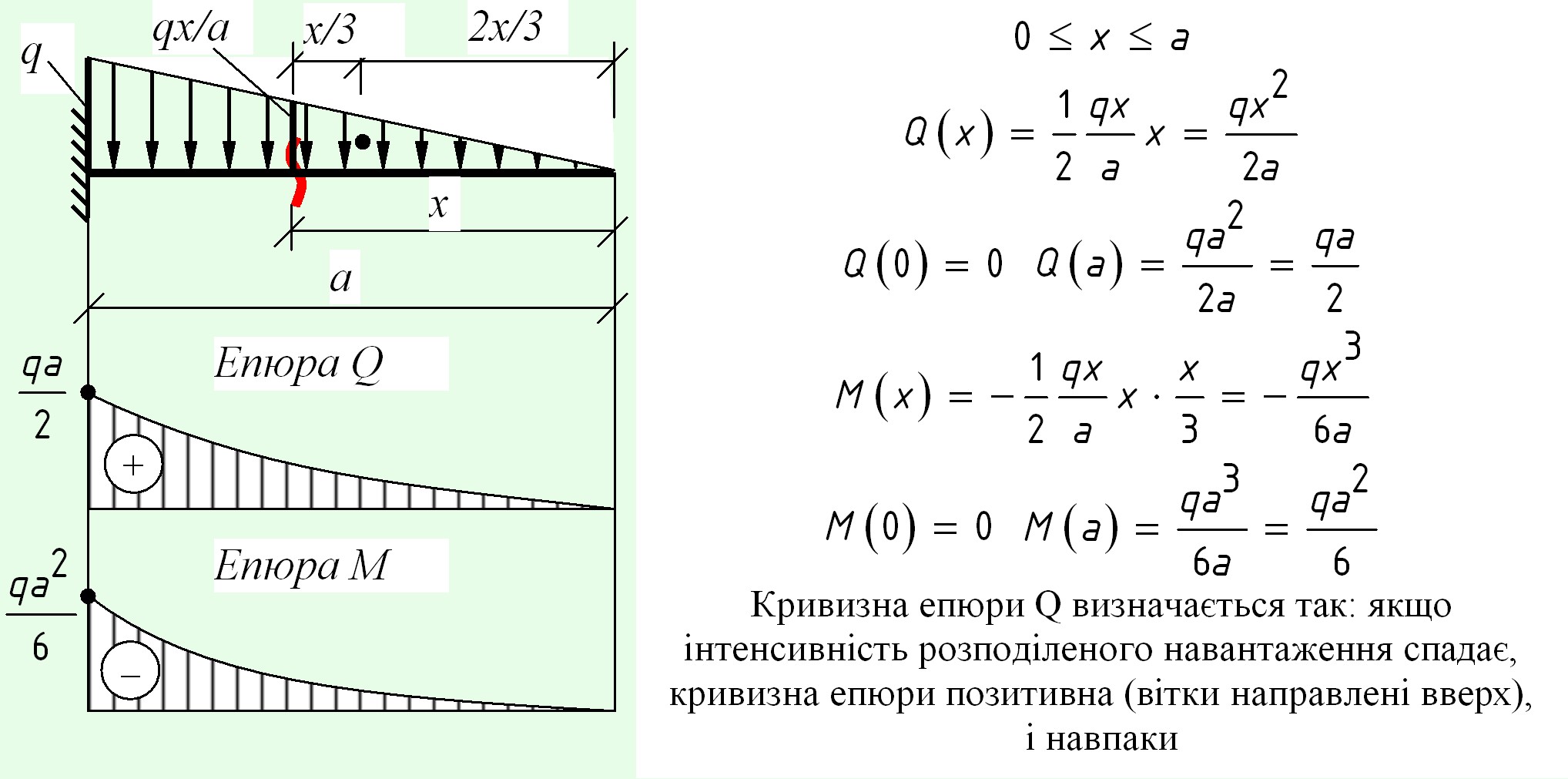
1 участок: .
;
;
.
2 участок: .
;
;
.
3 участок: .
;
;
.4 участок: .
;
;
Так как на четвертом участке эпюра Q пересекает нулевую линию, требуется провести исследование на экстремум:
;
откуда ;
.
Строим эпюры поперечных и продольных сил, изгибающих моментов (рисунок 2.3, б−г). Проверяем равновесие узлов рамы (рисунок 2.3, д) – узлы уравновешены.
| ||||||||||||||||||||||||||||||||||||
| ./../../images/bg_function.png»> | ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
Проверьте диаграмму поперечной силы (SFD) и диаграмму изгибающего момента (BMD) для балочные элементы. | ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
Из Главного Меню выберите Результаты > Силы > Диаграммы балок .
Выберите Результаты
> Силы > Диаграммы балок на вкладке меню Древовидного меню .
Нажмите Диаграммы балок в меню значков . | ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
Варианты нагрузки/сочетания
Выберите желаемое загружение, комбинацию нагрузок или чехол-конверт.
Стадия строительства применима для результат анализа этапа строительства определяется в Select Construction Сцена для отображения или панели инструментов сцены. Щелкните вправо. для ввода новых или изменения существующих сочетаний нагрузок. (См. «Случаи нагрузки / Комбинации»)
Шаг
Примечание
Макс./мин.
Схема
Примечание
Тип дисплея
Определите тип отображения следующим образом:
Расположение секции вывода
Назначить местоположения секций, в которых элемент усилия элементов балки выдаются в числовых значениях.
и : Отображение усилия на стержне в начальном узле (N1) балочного элемента.
Центр : Отображение усилия на стержне в центре балочного элемента.
и : Отображение усилия на стержне в конечном узле (N2) балочного элемента.
Абс Макс. центров балочных элементов.
Мин./макс. : Минимальный и максимальный изгибающие моменты отображаются в числовом виде на соответствующем мест среди 5 точек балочных (4-х секционных) элементов.
Все : Моменты на i-конце и j-конце и изгиб Abs Max или Min/Max моменты выше отображаются в числовом виде.
Генерация пакетного вывода ( , )
Дано типы результатов анализа для графических выходов, генерируемые последовательно графические выходы для выбранных загружений и комбинаций. Общее количество файлов, равных произведениям количества проверенных элементов в создаются три столбца диалогового окна ниже.
Сохраненная строка меню Информация : здесь перечислены базовые файлы. Выберите базовые имена файлов для пакетного вывода.
: Удалить все базовые файлы, выбранные с помощью мыши.
При проведении анализа стадии строительства out, перечислены все этапы строительства. Мы просто выбираем этапы интересов, которые должны быть включены в пакетный вывод. Если нет стадии строительства анализ выполняется, столбец в диалоговом окне становится неактивным и перечисляет условия нагрузки (сочетания).
Ступени
Финальная стадия
Нагрузки
Использовать Сохранено
Этап LCase/LComb
Ступенчатая опция
Сохраненный шаг : Используйте только те шаги, которые использовались для создания базовых файлов .
Все шаги : Используйте все шаги
Опции вывода
Выходной файл
Тип
Описание авто: В левом верхнем углу графических выходов, созданных в пакетном режиме, автоматически сгенерируйте и включите примечания, такие как типы и компоненты анализа результаты, этапы и этапы строительства, условия нагрузки (сочетания), и т. д. Размер шрифта, цвет, тип и т. д. можно изменить, щелкнув значок кнопка .
Выход
Путь
Префикс файла :
Укажите префикс создаваемых графических файлов. Имена файлов будут
состоять из «Префикса»_»Базового имени файла»_»Загрузить
Comb.
: Произвести указанную партию Графические файлы, отражающие содержимое диалогового окна.
/ Производить содержимое ввода данных в Диалоговое окно «Базовые файлы и создание пакетного вывода» в файле двоичного типа (сн. болото). Нажмите кнопку и выберите fn.bog для использования тот же выходной формат.
Примечание
| ||||||||||||||||||||||||||||||||||||
|
SOLIDWORKS Simulation: Диаграммы балок — автоматизированная технология
Знаете ли вы, что в SOLIDWORKS Simulation можно создавать диаграммы сдвига балки и изгибающего момента? Этот полезный тип графика позволяет быстро визуализировать эти результаты по всей длине балки. Я покажу вам функциональность на классическом примере из любого учебника по строительному строительству по сопротивлению материалов, случай свободно опертой балки длиной «L» с центрированной нагрузкой «P», приложенной в центре пролета.
Я покажу вам функциональность на классическом примере из любого учебника по строительному строительству по сопротивлению материалов, случай свободно опертой балки длиной «L» с центрированной нагрузкой «P», приложенной в центре пролета.
В аналитическом решении для сдвига и изгиба по длине балки поперечная сила на каждом конце равна половине приложенной нагрузки и меняет направление в середине пролета.
Изгибающий момент равен нулю на каждом конце и в середине пролета, он достигает пикового значения, равного одной четверти произведения приложенной нагрузки на длину балки.
3D-модель балки показана в SOLIDWORKS с эскизом, представляющим опоры на каждом конце. В нашем случае длина балки «L» составляет 6 метров, а приложенная нагрузка «P» составляет 20 000 ньютонов, поэтому мы ожидаем, что максимальные значения момента сдвига и изгибающего момента составят 10 кН и 30 кН-м соответственно.
После создания статического исследования Simulation на основе этой геометрии вы обнаружите, что по умолчанию для детали задана сетка с использованием твердотельных элементов. Чтобы получить желаемую выходную диаграмму балок, мы указываем программе рассматривать твердое тело как балку, вместо этого щелкнув правой кнопкой мыши деталь в дереве моделирования.
Чтобы получить желаемую выходную диаграмму балок, мы указываем программе рассматривать твердое тело как балку, вместо этого щелкнув правой кнопкой мыши деталь в дереве моделирования.
Для балочных элементов узлы автоматически создаются на каждом конце, и мы можем применять к ним приспособления для обозначения соответствующих условий поддержки.
После создания сетки и решения доступны знакомые графики напряжения и прогиба. Комбинированное осевое и изгибающее напряжение показано ниже.
Перед созданием диаграммы луча нам нужно знать об ориентации луча, чтобы решить, какое направление выбрать при настройке графиков. Самый длинный размер профиля поперечного сечения балки — это Направление 1, а Направление 2 перпендикулярно ему. Чтобы получить визуальное подтверждение этой информации, вы можете щелкнуть правой кнопкой мыши часть балки в дереве моделирования, выбрать «Редактировать определение» и установить флажок, чтобы показать направление балки.



 проверено, одновременно создаются усилия на элемент фермы. Когда осевая сила
(Fx) и установлен флажок «Только усилие фермы», только
создаются усилия на элементах фермы.
проверено, одновременно создаются усилия на элемент фермы. Когда осевая сила
(Fx) и установлен флажок «Только усилие фермы», только
создаются усилия на элементах фермы.

 контур.
контур.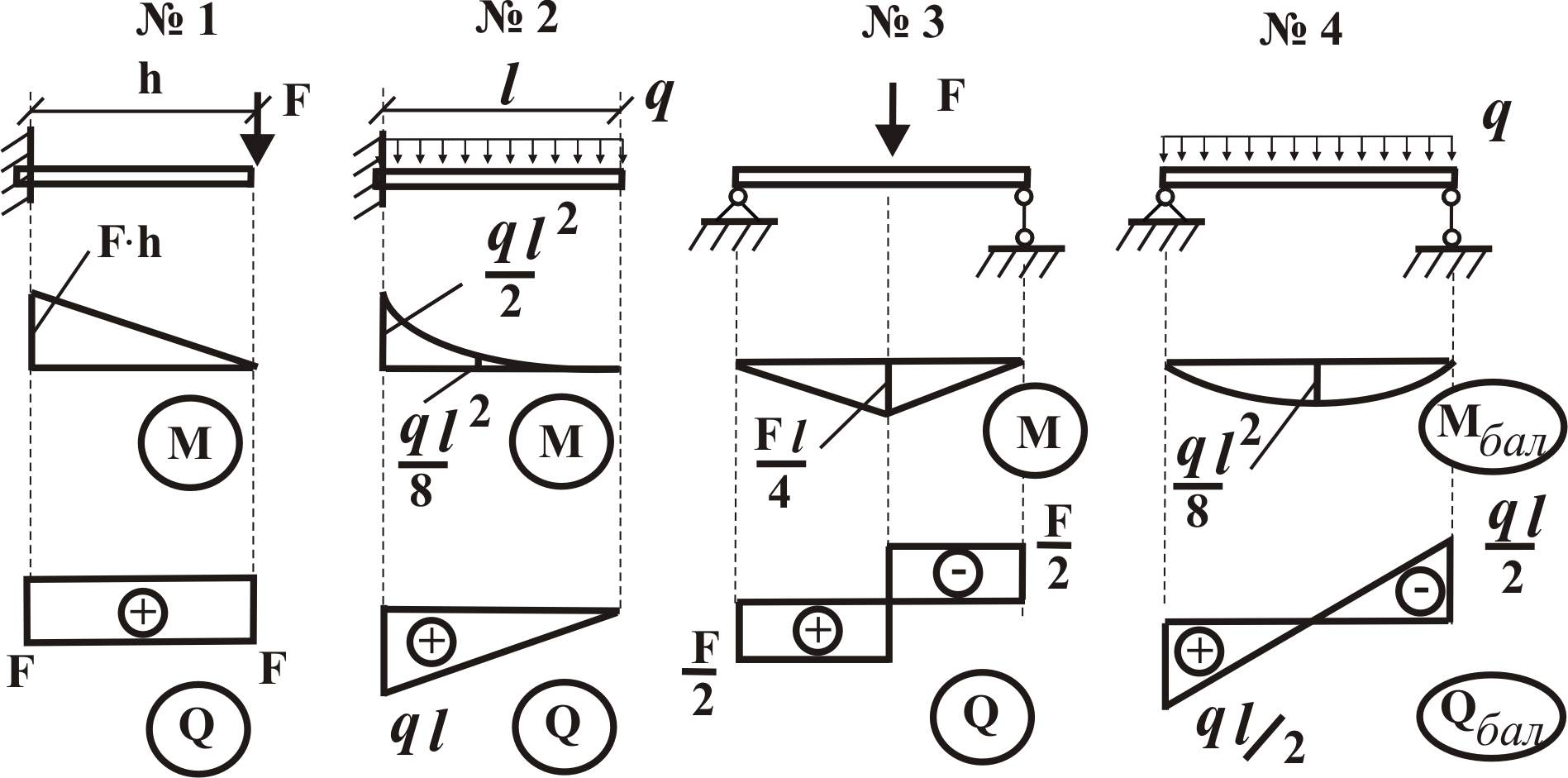 чтобы сократить время, необходимое для представления полного контура.
чтобы сократить время, необходимое для представления полного контура.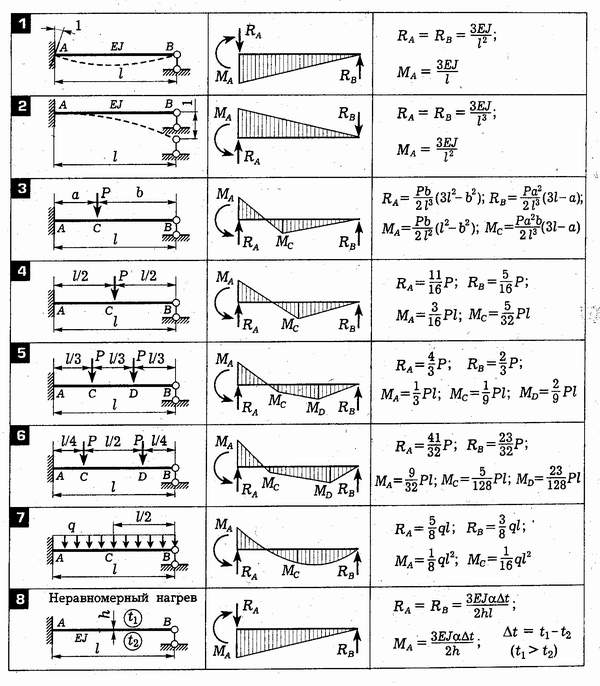



 :
Максимальные абсолютные значения изгибающих моментов среди 5 точек (4-х секционной)
элементы балки отображаются с номером
:
Максимальные абсолютные значения изгибающих моментов среди 5 точек (4-х секционной)
элементы балки отображаются с номером
 Конструкция
этапы перечислены ниже.
Конструкция
этапы перечислены ниже.
 «.bmp(emf) или «Префикс»_»Имя базового файла»_»Этап»_»Этап
LCase»_»Шаг».bmp(emf).
«.bmp(emf) или «Префикс»_»Имя базового файла»_»Этап»_»Этап
LCase»_»Шаг».bmp(emf).