Построение эпюры перемещений.

Министерство образования и науки Российской Федерации

Уфимский государственный авиационный технический университет

Дисциплина: Сопротивление материалов

Расчетно-графическая работа

Вариант № 2489

Выполнил:

студент группы МА 202Т Хабибуллин Р.Р.

Принял: ст. преподаватель Валиев Р. Ш.

Срок выполнения работы по плану:

Фактический срок выполнения:_____________

Туймазы 2014

Задача 1. РАСЧЕТ НА ПРОЧНОСТЬ СТУПЕНЧАТОГО БРУСА

ПРИ ОСЕВОМ РАСТЯЖЕНИИ И СЖАТИИ

Условие задачи

Ступенчатый брус нагружен равномерно распределенными нагрузками интенсивностью q₁ и q₂ и осевыми сосредоточенными силами F₁ и F₂.

Необходимо:

1) построить эпюру нормальных сил;

2) построить эпюру напряжений, отнесенных к площади поперечного сечения;

3) найти площадь из условия прочности;

4) построить эпюру напряжений;

5) построить эпюру перемещений.

Изобразим расчетную схему согласно заданным. На расчетной схеме все внешние силы действуют вдоль оси бруса. Следовательно, в поперечных сечениях рассматриваемого бруса возникают только продольные (нормальные) силы.

Построение эпюры нормальных сил.

Определим нормальные силы с помощью метода сечений. Разобьем брус на три участка, начиная от правого незакрепленного конца. Произвольными сечениями последовательно на каждом участке рассечем мысленно брус на две части. При этом координату проведенного сечения z можно отсчитывать от начала первого участка. Удобнее при построении эпюры нормальных сил пользоваться подвижной системой осей координат, центр которой помещается в начале каждого участка. Тогда координата z на каждом участке бруса отсчитывается от начала этого участка. Отбрасывая закрепленную часть бруса, заменим действие отброшенной части неизвестной нормальной силой N

i (z_i), которую направляем в сторону от рассматриваемого сечения, т. е. считаем положительной (растягивающей). Тогда условие равновесия отсеченной части бруса дает величину и соответствующий знак нормальной силы.

Составим уравнение равновесия в виде суммы проекций на ось бруса всех сил, действующих на правую его часть и найдем на участке I нормальную силу в сечении.

l₁=1.5 м, l₂=2 м, l₃=2 м, q₁=10 кН/м, q₂=0, F₁=30 кН, F₂=20 кН, сталь 30ХМ.

Участок I.

Расстояние от свободного конца до сечения обозначим z₁, z₁ изменяется в интервале [0 ≤z₁<l₁]

∑ZN₁ (z₁)–F₁; N₁ (z₁) F_ кН,

Участок II [0≤z₂<l₂],

ΣZ = N₂ (z₂) –F₁–F₂ – q₁z₂,

отсюда

N₂(z₂ ) = F₁ + F₂ +q₁z₂,

при z₂ = 0:

N₂ (z₂) = F₁ +F₂ = 30+20=50 кН.

при z₂ = l₂:

N₂(z₂ ) = F₁ + F₂ +q₁l₂=30+20+102=70 кН

Участок III [0 ≤z₃<l₃],

ΣZ = N₃ (z₃ ) – F₁– F₂ – q₁l₂

N₃(z₃) =F₁+F₂+q₁l₂=30+20+102=70 кН.

По полученным данным строим эпюру ЭN.

Построение эпюры напряжений.

Определим нормальные напряжения. Поскольку A₀ неизвестна, построим сравнительную эпюру напряжений (сохраним в знаменателе A

₀).

Участок I

Участок II:

при z₂ = 0:

при z₂ = l₂:

На участке III:

Построим сравнительную эпюру напряжений.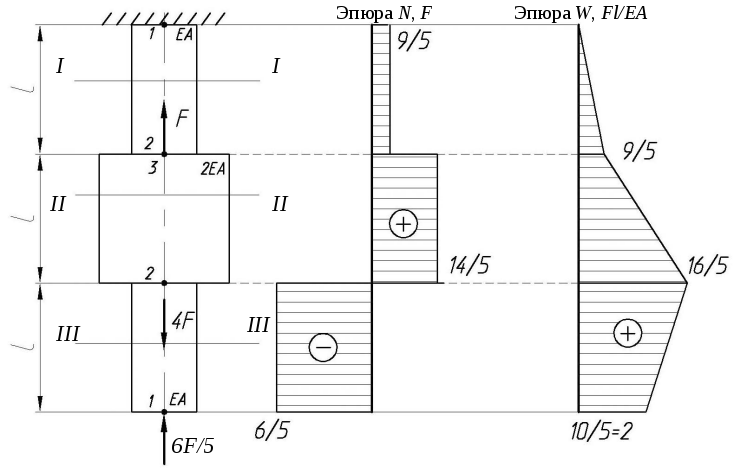

Определение площади поперечного сечения.

Для определения площади поперечного сечения А₀, анализируя построенную сравнительную эпюру напряжений, выявим опасное сечение.

Максимальные напряжения:

Площадь А₀ найдем из условия прочности

σ_max≤[σ],

где [σ] – допускаемое напряжение находится по соотношению (1.3).

Если материал пластичный σ

оп = σ_т, при этом n = 1,5…3.

Если материал хрупкий σ_оп = σ_в , при этом n = 3…5.

Материал ступенчатого бруса сталь 30XM пластичный, так как согласно справочным данным δ >5 %.

Опасным напряжением является предел текучести σ_т = 200МПа; тогда, выбирая коэффициент запаса n = 2, получим допускаемое напряжение

По условию прочности

Тогда минимальный размер площади, обеспечивающий прочность стержня:

Вычислим истинные напряжения по участкам:

Построим эпюру истинных напряжений.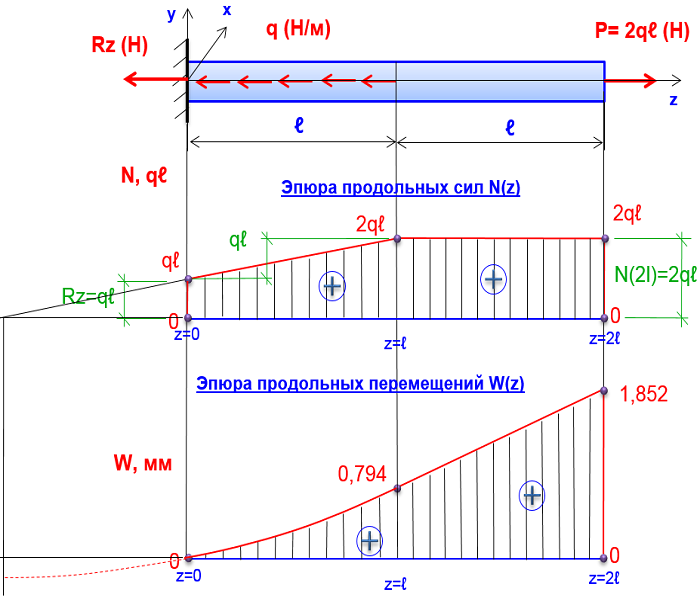

Для построения эпюры продольных перемещений ЭΔl необходимо определить перемещения Δl любых точек оси бруса.

Так как брус имеет ступенчато-переменное сечение, то в условиях рассматриваемого примера, участков, в пределах которых проводят интегрирование, три. Рассмотрим участки в отдельности.

Участок III. Перемещение любого сечения участка может быть выражено соотношением согласно формуле:

Соотношение для нормальной силы примет вид

N₃ (z) = F₁+F₂+q₁l₂,

Δl_III (z₃ = 0) = 0; Δl_III(z₃ = l₃) – удлинение третьего участка или перемещение левой границы третьего участка бруса.

Участок II.

Найдем перемещение произвольного сечения на расстоянии z₂ от правой границы участка, выбирая за начало координат левую границу участка II.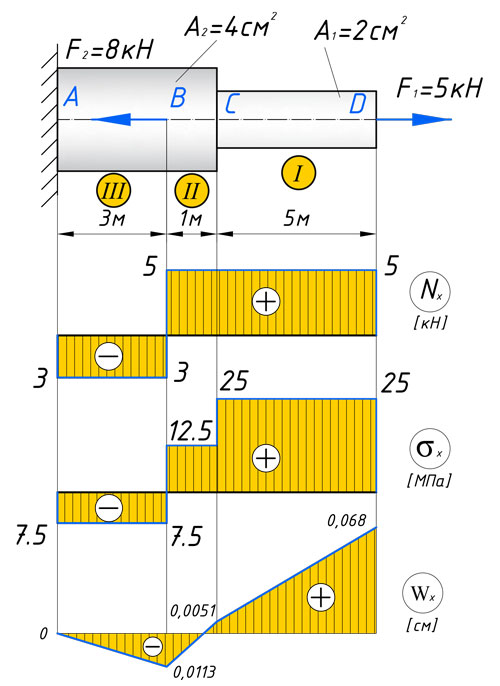

l_II(z₂=l₂) – удлинение второго участка.

l = l_III (l₃ ) +l_II (l₂ ) = 0.59+0.86= 1.45 мм.

Участок I.

Найдем перемещение произвольного сечения на расстоянии z₁ от правой границы участка, выбирая за начало координат левую границу участка I.

так как за начало координат выбрана левая граница участка I, соотношение для нормальной силы примет вид

N₁(z) = F₁ ,

l = l_III (l₃ ) +l_II (l₂ ) +l_I (l₁) = 0.59+0.86+0.27 = 1.72 мм.

По найденным значениям необходимо построить эпюру перемещений.

Задача 2. РАСЧЕТ НА ПРОЧНОСТЬ СТУПЕНЧАТОГО БРУСА

ПРИ КРУЧЕНИИ

Условие задачи

Ступенчатый брус нагружен равномерно распределенным моментом интенсивностью m и сосредоточенными скручивающими моментами М₁, М₂ и М₃. Принять, что сечение, где возникает реактивный момент М₄, неподвижно.

Необходимо:

1) определить реактивный момент М₄, возникающий в неподвижном сечении бруса;

2) построить эпюру крутящих моментов;

3) выбрать опасное сечение бруса из условий прочности;

4) определить диаметр поперечных сечений бруса;

5) построить эпюру максимальных касательных напряжений;

6) построить эпюру относительных углов закручивания;

7) построить эпюру углов закручивания.

Определение реактивного момента.

Исходя из условия равновесия вала, составим уравнение

∑M_z = – M₁ + M₂ – ml₃ + M₃ –М₄ = 0.

Получаем реактивный момент

M₄ = –M₁ + M₂ – ml₃ + M₃.

При указанных выше исходных данных

M₄ = –15 + 0 – 0⋅0,4 +20 = 5 кНм.

Реактивный момент M₄ вращает вал в направлении, указанному на схеме.

Изобразим расчетную схему согласно заданным силам и соотношениям. Покажем на расчетной схеме фактическое направление действия момента M₄.

Построение эпюры крутящих моментов.

Выберем подвижную систему осей координат y, z, при этом первоначально расположим ее в неподвижном сечении.

Рассмотрим участки в отдельности, каждый раз составляя уравнения равновесия рассматриваемой части бруса.

Участок I

Мысленно проведем сечение в начале участка I и из условия равновесия левой отсеченной части вычислим крутящий момент в этом сечении.

z₁ изменяется в интервале [0 ≤ z₁ ≤ l₁]

∑M_z = M_к1–М₁;

М_к1 = М₁ = 15 кН.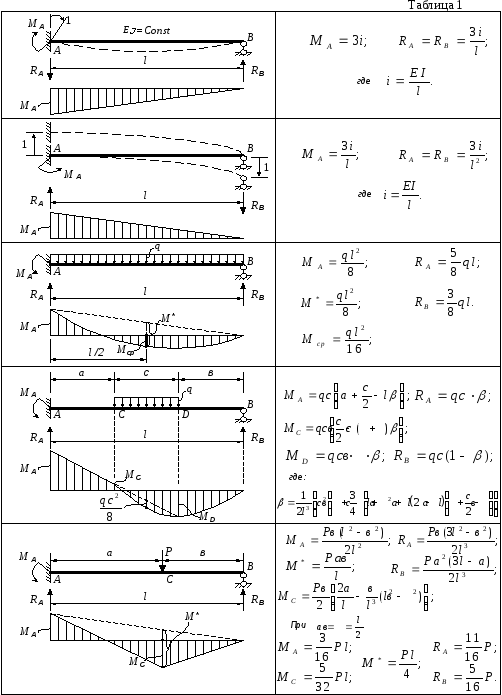

Участок II

В пределах участка z₂ изменяется в интервале [0 ≤ z₂ < l₂]

∑ M_z = M_к2–М₁+М₂=0

M_к2=М₁–М₂=15–0=15 кНм.

Участок III

z₃ изменяется в интервале [0 ≤ z₃≤ l₃]

∑ M_к3–М₁+М₂+М₃=0

M_к3=М₁–М₂–М₃

M_к3=15–0–20= –5 кНм.

Определение опасного сечения.

Найдем моменты сопротивления сечений и значения напряжений по участкам.

Участок I [0 ≤ z₁≤ 1₁]

D_нар=d, D_внут.=0

Участок II [0 ≤ z₂ ≤ l₂]

D_нар=1.2d, D_внут.=0.8d

Участок III [0 ≤ z₃ ≤ l₃]

D_нар=0. 8d, D_внут.=0.5d

Эпюра максимальных значений касательных напряжений, выраженных через параметр d³, показана на рисунке. Наиболее опасными по величине напряжений будут сечения на участке I [0 ≤ z₁ ≤ l₁], где .

Определение диаметра бруса.

Размер d найдем, приравнивая выражение для максимального касательного напряжения в

опасном сечении значению допускаемого напряжения по формуле:

=[] .

Для заданного материала нержавеющей стали Д16 имеем

σ_0,2 =340 МПа и σ_в= 435 МПа.

Так как выбираем запас

n_т = 2.

Тогда τ_0,3 = 0,5  σ_0,2 = 170 МПа согласно,

МПа.

Принимая максимальное значение касательного напряжения _max,max равным допускаемому, получим

=[] ,

= ,

отсюда

,

d=0. 097 м.

Построение эпюры максимальных касательных напряжений.

С помощью полученного значения диаметра d найдем максимальные касательные напряжения по длине бруса.

Участок I [0 ≤ z₁≤ 1₁]

Па= 85 МПа

Участок II [0 ≤ z₂ ≤ l₂]

Участок III [0 ≤ z₃ ≤ l₃]

.

По найденным значениям построим эпюру максимальных касательных напряжений по длине вала.

Построение эпюры относительных углов закручивания.

Эпюру относительных углов закручивания θ получаем из эпюры крутящих моментов М_к.

Для материала сталь Д16, где E = 0.72⋅10⁵ МПа и µ = 0,33, определим G по формуле

МПа.

Для сечений данного бруса значения полярных моментов инерции и относительных углов закручивания при d = 0.097 м имеют вид:

Участок I [0 ≤ z₁≤ 1₁]

D_нар=d=0. 097 м, D_внут.=0

М_к1=15 кНм

1/м

Участок II [0 ≤ z₂ ≤ l₂]

D_нар=1.2d=0.116 м, D_внут.=0.8d=0.078 м

1/м

Участок III [0 ≤ z₃ ≤ l₃]

D_нар=0.8d=0.078 м, D_внут.=0.5d=0.0485 м

1/м

По найденным значениям построим эпюру относительных углов закручивания по длине вала.

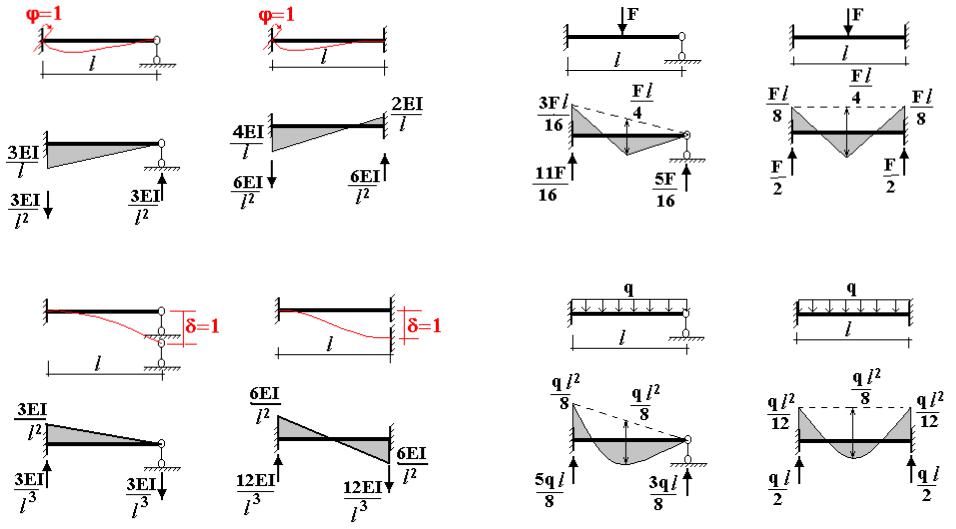
Эпюра перемещений — определение термина

график перемещений по заданному направлению точек осей стержней, отложенных от схемы недеформированного сооружения или от проекции этих точек на прямую, перпендикулярную направлению перемещений.

Научные статьи на тему «Эпюра перемещений»

Определение перемещений в балке и раме Студенты строительных специальностей выполняют расчетно-графические…
Самой первой они рассматривают задачу по определению перемещений в балках и рамах при прямом изгибе. …
В расчетах определяют перемещения, угол поворота, изгибающий момент, поперечную силу….
Для определения перемещений применяют метод Мора, который сводится к поиску интегралов, представляющих…
точках; строим эпюры по полученным значениям.

Статья от экспертов

Рассмотрены вопросы проектирования различных металлических башен необходимых для подержания газоходов. Выявлено, что четырехгранная башня с четырьмя газоотводящими стволами наиболее полно отвечает требованиям тепловых электростанций. Описан ряд преимуществ принятого конструктивного решения, отвечающего производственным требованиям, одно из которых является ключевым — подключение котлов осуществляется к отдельным газоходам, которые позволяют обеспечивать удобство обслуживания и ремонта высотного сооружения. На основе краткого обзора определены цели исследования — установление влияния различных профилей на усилия в элементах и подбор наиболее оптимального профиля для элементов металлической башни с газоходами.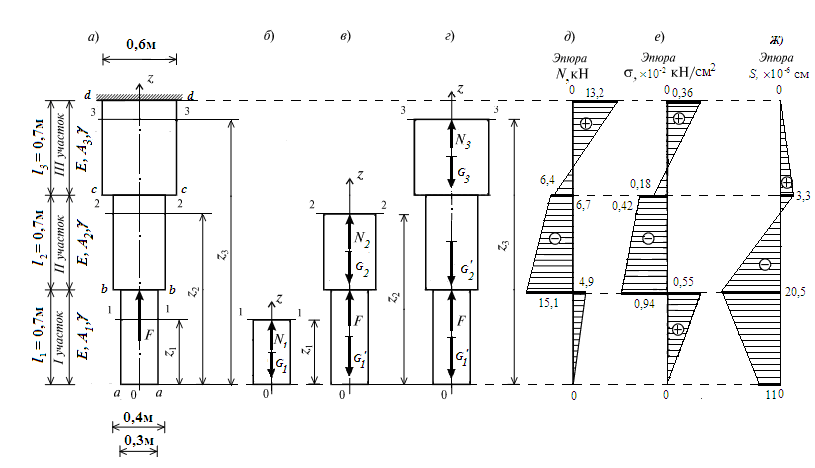 Выполнены расчеты несущих конструкций металлической четырехгранной башни на заданные нагрузки и воздействия с применением метода конечных элементов реализованного в программном комплексе «ЛИРА-САПР». Анализ представленных гистограмм убедительно показал, что по усилиям в элемента…

Creative Commons

Научный журнал

Определение 1 Эпюра – это вид графика, который показывается как распределяется величина нагрузки…
на оцениваемом элементе, например, для стержней расчет эпюр напряжения считается одной из базовых задач…
стержней через отношение жесткости к длине; записываем канонические уравнения; строим в основной системе эпюры…
; умножаем единичную эпюру на грузовую; проверяем правильность окончательной эпюры и поверки равновесия…
При этом перемещения узлов равны перемещениям стержней, деформации определяются перемещениями узлов и

Статья от экспертов

Отверстие охватывающей детали нагружено контактным давлением, методика определения которого изложена в предыдущей работе.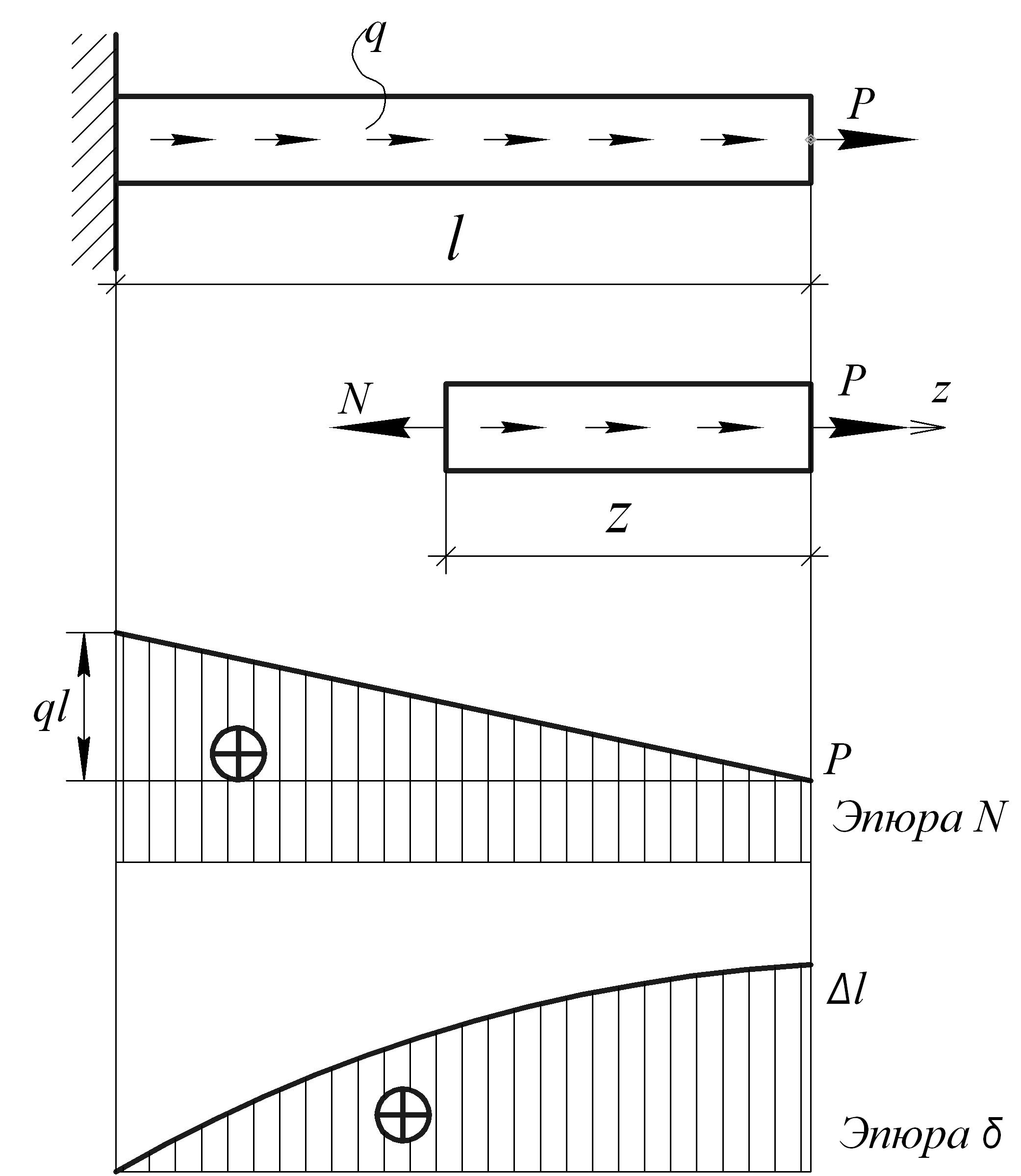 Исследование проводилось методами задачи плоской деформации теории упругости. В результате получены зависимости по определению напряжений, деформаций и перемещений в точках охватывающей детали. Для инженерной методики расчета разработаны графики, позволяющие по значениям полуугла контакта, максимального контактного давления и радиуса отверстия в охватывающей детали определять максимальные эквивалентные напряжения в указанной детали и положение точки, в которой они возникают.

Creative Commons

Научный журнал

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек

Номенклатура кулачков и диаграммы смещения

Номенклатура кулачков номенклатура и диаграммы смещения для различных профилей кулачков

Рис. : Номенклатура кулачков 9000 9

Кулачок Профиль: Контур выработки поверхность кулачка.

Точка трассировки: Точка на острой кромке толкателя, или в центре ролика, или в центре сферической поверхности.

Кривая шага: Путь точки трассировки.

Базовая окружность: Наименьшая окружность, нарисованная по касательной к профилю кулачка, с центром на оси распределительного вала. Размер базовой окружности определяет размер кулачка.

Первичная окружность: Наименьшая окружность, нарисованная по касательной к кривой шага, с центром на оси распределительного вала.

Угол давления: Угол между нормалью к кривой тангажа и направлением движения толкателя в точке контакта.

Типы следящего движения:

Кулачковые следящие системы предназначены для достижения желаемого колебательного движения. Для этой цели должны быть выбраны соответствующие шаблоны смещения до проектирования поверхности кулачка. Предполагается, что кулачок вращается с постоянной скоростью, а толкатель поднимается, останавливается, возвращается в исходное положение и снова останавливается на заданные углы поворота кулачка во время каждого оборота кулачка.

Вот некоторые из стандартных следящих движений:

Следующее движение с,

(a) Равномерная скорость

(b) Модифицированная равномерная скорость

(c) Равномерное ускорение и замедление

(d) Простое гармоническое движение

(e) Циклоидальное движение

Диаграммы смещения: В системе кулачкового толкателя очень важно движение толкателя. Его смещение можно изобразить в зависимости от углового смещения θ кулачка, и это называется диаграммой смещения. Смещение толкателя отложено по оси y, а угловое смещение θ кулачка отложено по оси x. Из диаграммы перемещений также можно построить скорость и ускорение толкателя для различных угловых перемещений θ кулачка. Диаграммы перемещения, скорости и ускорения строятся для одного рабочего цикла, т. е. одного оборота кулачка. Диаграммы перемещений являются основными требованиями к конструкции кулачковых профилей. Построение диаграмм перемещений и расчет скоростей и ускорений толкателей при различных типах движений обсуждаются в следующих разделах.

(a) Движение следящего устройства с равномерной скоростью:

На рис. 2 показаны характеристики перемещения, скорости и ускорения следящего устройства с равноскоростным типом движения. Поскольку толкатель движется с постоянной скоростью, во время подъема и опускания смещение линейно зависит от θ. Кроме того, поскольку скорость изменяется от нуля до конечного значения, теоретически ускорение становится бесконечным в начале и в конце подъема и падения в течение короткого времени.

Рис.2: Движение следящего устройства с равномерной скоростью

(б) Движение следящего устройства с измененной равномерной скоростью:

На диаграммах перемещений следящего устройства с равномерной скоростью становится бесконечным в начале и конце подъема и возврата.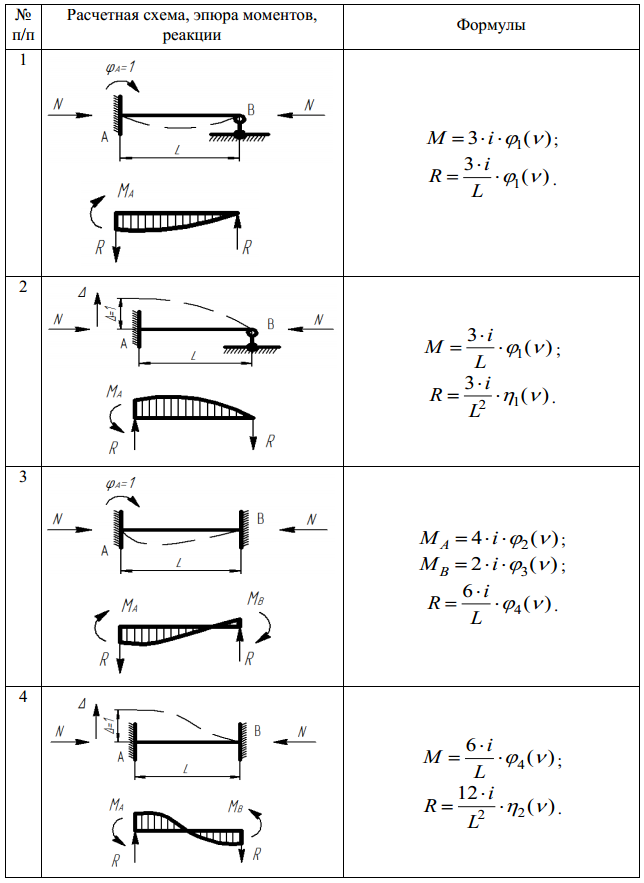 Чтобы этого не допустить, диаграммы водоизмещения несколько видоизменены. В модифицированной форме скорость толкателя изменяется равномерно в начале и в конце каждого хода. Соответственно, перемещение толкателя в эти периоды изменяется параболически. С этой модификацией ускорение становится постоянным в течение этих периодов, а не бесконечным, как в типе движения с равномерной скоростью. Модели перемещения, скорости и ускорения показаны на рис. 3 .

рис.3: Движение следящего устройства с модифицированной равномерной скоростью

(c) Движение следящего устройства с равномерным ускорением и замедлением (UARM):

Здесь перемещение следящего устройства изменяется параболически относительно углового перемещения камеры. Соответственно, скорость толкателя изменяется равномерно по отношению к угловому перемещению кулачка. Соответственно, ускорение/замедление ведомого становится постоянным. Модели перемещения, скорости и ускорения показаны на рис. 4.

Рис.4: Движение следящего устройства с равномерным ускорением и торможением

с = Ход следящего устройства 0128 r = Угловое смещение кулачка при выходе и возврате гладить.

ω = угловая скорость кулачка.

Время, необходимое для выхода толкателя наружу = t _o =

Время, необходимое для возврата толкателя = t _r =

Средняя скорость толкателя =

Средняя скорость толкателя при выходе наружу =

 

vo _мин = 0

= Макс. скорость во время выброса.

 

Средняя скорость толкателя при обратном ходе =

 

vr _мин = 0

 

= Макс. скорость во время обратного хода.

Ускорение толкателя при обратном ходе =

 

Аналогично ускорение толкателя при обратном ходе =

 

(d) Простое гармоническое движение: На рис.5 движение, совершаемое точкой P ^l , которая является проекцией точки P на вертикальный диаметр, называется простым гармоническим движением. Здесь P движется с равномерной угловой скоростью ω _p по окружности радиуса r (r = s/2).

Рис.5: Простое гармоническое движение

Перемещение = ; [d1]

Скорость = ; [d2]

Ускорение = ; [д3]

Рис.6: Диаграмма смещения толкателя с простым гармоническим движением

s= Ход или смещение толкателя.

θ _o = Угловое смещение при прямом ходе.

θ _r = угловое смещение при обратном ходе

ω = угловая скорость кулачка.

t _o = Время, необходимое для прямого хода =

t _r = Время, необходимое для обратного хода =

Макс. скорость толкателя во время выхода = vo _max = rω _p (из d2)

 

vo _max =

Аналогично Макс. скорость толкателя при обратном ходе = , vr _max =

 

Макс. ускорение на выходе = ao _max = rω ² _p (из d3) =

 

Аналогично, макс. ускорение при обратном ходе = ar _max =

 

(e) Циклоидальное движение:

Циклоида — это траектория, образованная точкой на окружности круга, когда круг катится без проскальзывания по прямой/плоской поверхности. Движение, совершаемое толкателем здесь, похоже на проекцию точки, движущейся по цилоидальной кривой, на вертикальную линию, как показано на рисунке 7.

диаграммы перемещений и типовые формы диаграмм скорости и ускорения показаны на рис.8. По сравнению со всеми другими движениями толкателя циклоидальное движение приводит к плавной работе толкателя.

Ниже приведены выражения для максимальных значений скорости и ускорения следящего устройства.

с = Ход или смещение толкателя.

d = диам. образующей циклоиды =

θ _o = Угловое смещение при прямом ходе.

θ _r = угловое смещение при обратном ходе

ω = угловая скорость кулачка.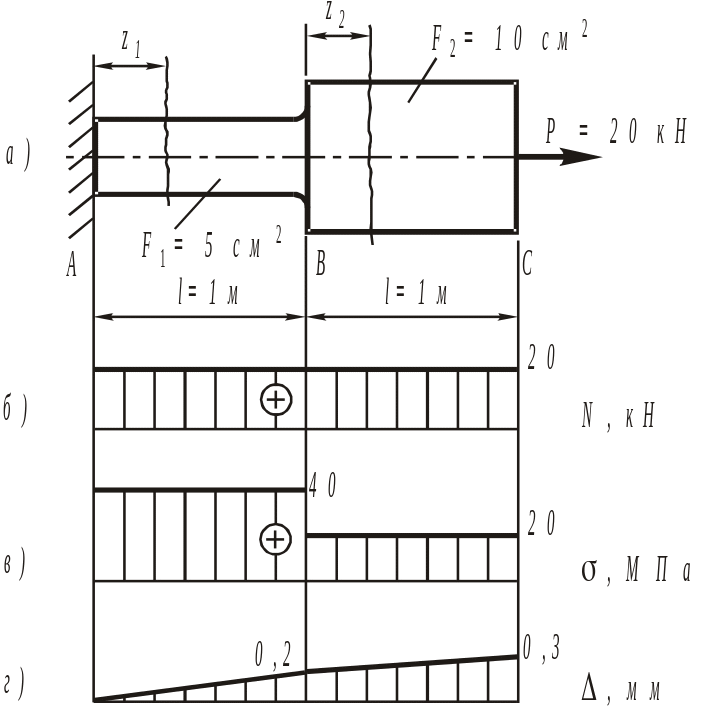

t _o = Время, необходимое для прямого хода =

t _r = Время, необходимое для обратного хода =

или _макс. = макс. скорость толкателя при выходе =

vr _max = Макс. скорость толкателя во время обратного хода =

или _макс. = Макс. ускорение при выходе =

ar _max = Макс. ускорение во время обратного хода =

Рис. 8: Диаграмма смещения толкателя, скорости и ускорения для циклоидального движения

Последнее обновление: воскресенье, 7 декабря 2014 г.

Расстояние и смещение

Расстояние и смещение — это две величины, которые могут показаться одним и тем же, но имеют совершенно разные определения и значения.

• Расстояние — это скалярная величина, которая относится к тому, «сколько земли преодолел объект» во время своего движения.
• Смещение — это векторная величина, указывающая на то, «насколько смещен объект»; это общее изменение положения объекта.

Чтобы проверить свое понимание этого различия, рассмотрите движение, изображенное на диаграмме ниже. Учитель физики проходит 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север.

Несмотря на то, что учительница физики прошла в общей сложности 12 метров, ее перемещение равно 0 метрам. За время своего движения она «преодолела 12 метров земли» (расстояние = 12 м). Тем не менее, когда она заканчивает идти, она не находится «не на своем месте», т. Е. Для ее движения нет смещения (смещение = 0 м). Смещение, будучи векторной величиной, должно учитывать направление. 4 метра на восток отменяет 4 метра на запад; а 2 метра южнее отменяет 2 метра севернее. Векторные величины, такие как смещение, осведомлены о направлении . Скалярные величины, такие как расстояние, не знают направления. При определении общего расстояния, пройденного учителями физики, можно не учитывать различные направления движения.

 

 

Теперь рассмотрим другой пример. На приведенной ниже диаграмме показано положение лыжника в разное время. В каждый из указанных моментов времени лыжник поворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта А в пункт В, затем в пункт С и затем в пункт D.

С помощью диаграммы определите результирующее перемещение и расстояние, пройденное лыжником за эти три минуты. Затем нажмите кнопку, чтобы увидеть ответ.

В качестве последнего примера рассмотрим футбольного тренера, расхаживающего взад-вперед вдоль боковой линии. На приведенной ниже диаграмме показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в обратном направлении. Другими словами, тренер перемещается из позиции A в B, затем в C и затем в D.

Каково результирующее перемещение и пройденное расстояние автобуса? Нажмите кнопку, чтобы увидеть ответ.

 

Чтобы понять различие между расстоянием и смещением, вы должны знать определения.