Эпюры моментов и поперечных сил

Эпюры моментов и поперечных сил

 

         Полную картину распределения поперечных сил и изгибающих моментов по длине балки можно получить, построив эпюры сил и моментов.

         Рассмотрим методику построения эпюр для некоторых простейших случаев нагружения.

На рис. 14.3 показана консольная балка, нагруженная двумя равными поперечными силами. Чтобы получить эпюры сил и моментов на участке а рассмотрим произвольное сечение I-I на этом участке.

Действуя, как показано выше, получим:

        

 

Рис. 14.3.

        

Так как 0 £ x₁ £ a, то 0 £ М_И £ Fa. В соответствии с этим, эпюра поперечных сил на участке а представляет собой горизонтальную линию, отстоящую от оси на положительную величину F.

Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна нулю в начале участка и Fa – в конце.

         Для получения эпюр на участке b рассмотрим произвольное сечение II-II на этом участке. Поперечная внутренняя сила Q равна алгебраической сумме внешних сил слева от сечения, внутренний изгибающий момент M_И равен алгебраической сумме моментов внешних сил F относительно центра сечения:

Значит, на участке b поперечная сила отсутствует, а изгибающий момент постоянен, положителен и равен Fa.

         На рис. 14.4 показана однопролетная двухопорная балка с двумя шарнирными опорами, допускающими поворот сечения балки при изгибных деформациях. 

Причем, левая опора является шарнирно-неподвижной, а правая – шарнирно-подвижной, допускающей поступательное смещение вдоль опорной плоскости. Это бывает необходимо для компенсации возможного изменения длины балки при изгибных или температурных деформациях. Так устанавливаются и длинные валы машин – один из подшипников таких валов может смещаться в осевом направлении, так как не закреплен жестко.

        

 

Рис. 14.4.

 

Балка нагружена поперечной силой F. При такой расчетной схеме необходимо сначала определить реакции в опорах R_A и R_B. Ракцию R_A найдем, приравняв нулю сумму моментов сил относительно точки В:

Отсюда:

                                      (14.1)

Реакцию R_B найдем, приравняв нулю сумму моментов относительно точки А:

Откуда:

                                       (14.2)

Теперь, для получения эпюр поперечных сил и изгибающих моментов, аналогично предыдущему, рассматриваем сечение I-I на участке а:

Причем, так как 0 £ x₁ £ a, то 0 £ М_И £ R_Aa.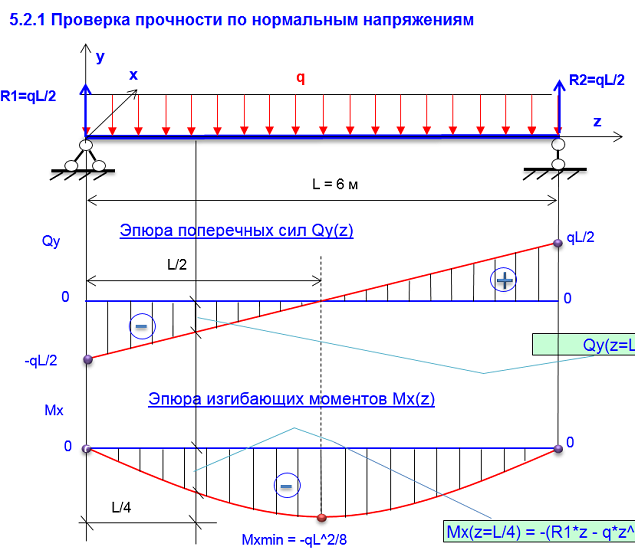 В соответствии с этим, эпюра поперечных сил на участке а представляет собой горизонтальную линию, отстоящую от оси на положительную величину R_A. Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна нулю в начале участка и R_Aa – в конце.

         В сечении II-II на участке b (с учетом (14.1) и (14.2)):

Здесь а £ х

2 £ а + b, следовательно (с учетом (16.1)) R_Aа £ M_И £ 0. Значит, эпюра поперечных сил на участке b представляет собой горизонтальную линию, отстоящую от оси на отрицательную величину      -R_A. Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна R_Aa в начале участка и нулю – в конце.

На рис. 14.5 показана однопролетная двухопорная балка, нагруженная изгибающим моментом М. Сначала определяем реакции в опорах R_A и R_B.

Ракцию R_A найдем, приравняв нулю сумму моментов сил относительно точки В:

Отсюда:

                                       (14. 3)

Реакцию R_Bнайдем, приравняв нулю сумму моментов относительно точки А:

 

 

Рис. 14.5.

 

Откуда:

Теперь, для получения эпюр поперечных сил и изгибающих моментов, аналогично предыдущему, рассматриваем сечение I-I на уча- стке а:

Причем, так как 0 £ x₁ £ a, то 0 £ М_И £ R_Aa. В соответствии с этим, эпюра поперечных сил на участке а представляет собой горизонтальную линию, отстоящую от оси на положительную величину R_A. Эпюра изгибающих моментов – это наклонная прямая, ордината которой равна нулю в начале участка и R_Aa – в конце.

         В сечении II-II на участке b (с учетом (14.1) и (14.2)):

Здесь а £ х₂ £ а + b, следовательно (с учетом (14.

3) -R_Ab £ M_И £ 0. Эпюра поперечных сил на участке b представляет собой горизонтальную линию, отстоящую от оси на положительную величину R_A, так же, как на участке а. Эпюра изгибающих моментов – это наклонная  прямая, ордината которой равна -R_Ab в начале участка и нулю – в конце.

 

 

Строительная механика

Строительная механика

Дарков А. В., Шапошников Н. Н. Строительная механика: Учеб. для строит. спец. вузов. —8-е изд., перераб. и доп. — М.: Высш. шк., 1986. — 607 с. В учебнике отражены вопросы курса строительной механики (статика и динамика сооружений). Изложение материала иллюстрируется конкретными примерами. В отличие от предыдущего издания (7-е— 1976 г.) рассматриваются методы расчета с использованием ЭВМ, указываются особенности этих методов. В учебнике отражено современное состояние строительной механики. Предназначается для студентов строительных специальностей вузов. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ Глава 1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ СООРУЖЕНИЙ § 1.2. УСЛОВИЯ ГЕОМЕТРИЧЕСКОЙ НЕИЗМЕНЯЕМОСТИ СТЕРЖНЕВЫХ СИСТЕМ § 1.3. УСЛОВИЯ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ГЕОМЕТРИЧЕСКИ НЕИЗМЕНЯЕМЫХ СТЕРЖНЕВЫХ СИСТЕМ Глава 2. БАЛКИ § 2.2. ЛИНИИ ВЛИЯНИЯ ОПОРНЫХ РЕАКЦИЙ ДЛЯ ОДНОПРОЛЕТНЫХ И КОНСОЛЬНЫХ БАЛОК § 2.3. ЛИНИИ ВЛИЯНИЯ ИЗГИБАЮЩИХ МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ ДЛЯ ОДНОПРОЛЕТНЫХ И КОНСОЛЬНЫХ БАЛОК § 2.4. ЛИНИИ ВЛИЯНИЯ ПРИ УЗЛОВОЙ ПЕРЕДАЧЕ НАГРУЗКИ § 2.5. ОПРЕДЕЛЕНИЕ УСИЛИЙ С ПОМОЩЬЮ ЛИНИЙ ВЛИЯНИЯ § 2.6. ОПРЕДЕЛЕНИЕ НЕВЫГОДНЕЙШЕГО ПОЛОЖЕНИЯ НАГРУЗКИ НА СООРУЖЕНИИ. ЭКВИВАЛЕНТНАЯ НАГРУЗКА § 2.7. МНОГОПРОЛЕТНЫЕ СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ БАЛКИ § 2.8. ОПРЕДЕЛЕНИЕ УСИЛИЙ В МНОГОПРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ ОТ НЕПОДВИЖНОЙ НАГРУЗКИ § 2. 9. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ ДЛЯ МНОГОПРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК § 2.10. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ С ЛОМАНЫМИ ОСЯМИ ОТ НЕПОДВИЖНОЙ НАГРУЗКИ § 2.11. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ В БАЛКАХ КИНЕМАТИЧЕСКИМ МЕТОДОМ Глава 3. ТРЕХШАРНИРНЫЕ АРКИ И РАМЫ § 3.1. ПОНЯТИЕ ОБ АРКЕ И СРАВНЕНИЕ ЕЕ С БАЛКОЙ § 3.2. АНАЛИТИЧЕСКИЙ РАСЧЕТ ТРЕХШАРНИРНОЙ АРКИ § 3.3. ГРАФИЧЕСКИЙ РАСЧЕТ ТРЕХШАРНИРНОЙ АРКИ. МНОГОУГОЛЬНИК ДАВЛЕНИЯ § 3.4. УРАВНЕНИЕ РАЦИОНАЛЬНОЙ ОСИ ТРЕХШАРНИРНОЙ АРКИ § 3.5. РАСЧЕТ ТРЕХШАРНИРНЫХ АРОК НА ПОДВИЖНУЮ НАГРУЗКУ § 3.6. ЯДРОВЫЕ МОМЕНТЫ И НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ Глава 4. ПЛОСКИЕ ФЕРМЫ § 4.1. ПОНЯТИЕ О ФЕРМЕ. КЛАССИФИКАЦИЯ ФЕРМ § 4.2. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ПРОСТЕЙШИХ ФЕРМ § 4.3. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ СЛОЖНЫХ ФЕРМ § 4.4. РАСПРЕДЕЛЕНИЕ УСИЛИЙ В ЭЛЕМЕНТАХ ФЕРМ РАЗЛИЧНОГО ОЧЕРТАНИЯ § 4.5. ИССЛЕДОВАНИЕ НЕИЗМЕНЯЕМОСТИ ФЕРМ § 4.6. ЛИНИИ ВЛИЯНИЯ УСИЛИИ В СТЕРЖНЯХ ПРОСТЕЙШИХ ФЕРМ § 4.7. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ В СТЕРЖНЯХ СЛОЖНЫХ ФЕРМ § 4. 8. ШПРЕНГЕЛЬНЫЕ СИСТЕМЫ § 4,9. ТРЕХШАРНИРНЫЕ АРОЧНЫЕ ФЕРМЫ И КОМБИНИРОВАННЫЕ СИСТЕМЫ Глава 5. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В УПРУГИХ СИСТЕМАХ § 5.2. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 5.3. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЙ § 5.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ. ИНТЕГРАЛ МОРА § 5.5. ПРАВИЛО ВЕРЕЩАГИНА § 5.6. ПРИМЕРЫ РАСЧЕТА § 5.7. ТЕМПЕРАТУРНЫЕ ПЕРЕМЕЩЕНИЯ § 5.8. ЭНЕРГЕТИЧЕСКИЙ ПРИЕМ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ § 5.9. ПЕРЕМЕЩЕНИЯ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ, ВЫЗЫВАЕМЫЕ ПЕРЕМЕЩЕНИЯМИ ОПОР Глава 6. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ СИЛ § 6.2. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 6.3. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ НА ДЕЙСТВИЕ ЗАДАННОЙ НАГРУЗКИ § 6.4. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ § 6.5. СОСТАВЛЕНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ПРИ РАСЧЕТЕ СИСТЕМ НА ПЕРЕМЕЩЕНИЯ ОПОР § 6.6. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМАХ § 6.7. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ. ПРОВЕРКА ЭПЮР § 6. 8. СПОСОБ УПРУГОГО ЦЕНТРА § 6.9. ЛИНИИ ВЛИЯНИЯ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 6.10. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 6.11. ГРУППИРОВКА НЕИЗВЕСТНЫХ § 6.12. СИММЕТРИЧНЫЕ И ОБРАТНОСИММЕТРИЧНЫЕ НАГРУЗКИ § 6.13. СПОСОБ ПРЕОБРАЗОВАНИЯ НАГРУЗКИ § 6.14. ПРОВЕРКА КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ § 6.15. ПРИМЕРЫ РАСЧЕТА РАМ § 6.16. «МОДЕЛИ» ЛИНИЙ ВЛИЯНИЯ УСИЛИИ ДЛЯ НЕРАЗРЕЗНЫХ БАЛОК Глава 7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДАМИ ПЕРЕМЕЩЕНИЙ И СМЕШАННЫМ § 7.2. ОПРЕДЕЛЕНИЕ ЧИСЛА НЕИЗВЕСТНЫХ § 7.3. ОСНОВНАЯ СИСТЕМА § 7.4. КАНОНИЧЕСКИЕ УРАВНЕНИЯ § 7.5. СТАТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ § 7.6. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ ПЕРЕМНОЖЕНИЕМ ЭПЮР § 7.7. ПРОВЕРКА КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ МЕТОДА ПЕРЕМЕЩЕНИЙ § 7.8. ПОСТРОЕНИЕ ЭПЮР M, Q И N В ЗАДАННОЙ СИСТЕМЕ § 7. 9. РАСЧЕТ МЕТОДОМ ПЕРЕМЕЩЕНИЙ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ § 7.10. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ ПРИ РАСЧЕТЕ РАМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ § 7.11. ПРИМЕР РАСЧЕТА РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ § 7.12. СМЕШАННЫЙ МЕТОД РАСЧЕТА § 7.13. КОМБИНИРОВАННОЕ РЕШЕНИЕ ЗАДАЧ МЕТОДАМИ СИЛ И ПЕРЕМЕЩЕНИЙ § 7.14. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ МЕТОДОМ ПЕРЕМЕЩЕНИЙ Глава 8. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ СТЕРЖНЕВЫХ СИСТЕМ И МЕТОДЫ ЕЕ РЕШЕНИЯ § 8.2. СОСТАВЛЕНИЕ УРАВНЕНИЙ РАВНОВЕСИЯ, СТАТИЧЕСКИЕ УРАВНЕНИЯ. ИССЛЕДОВАНИЕ ОБРАЗОВАНИЯ СИСТЕМ § 8.3. СОСТАВЛЕНИЕ УРАВНЕНИЙ СОВМЕСТНОСТИ, ГЕОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. ПРИНЦИП ДВОЙСТВЕННОСТИ § 8.4. ЗАКОН ГУКА. ФИЗИЧЕСКИЕ УРАВНЕНИЯ § 8.5. СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ. СМЕШАННЫЙ МЕТОД § 8.6. МЕТОД ПЕРЕМЕЩЕНИЙ § 8.7. МЕТОД СИЛ § 8.8. УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ И ИХ СВЯЗЬ С УРАВНЕНИЯМИ СТРОИТЕЛЬНОЙ МЕХАНИКИ Глава 9. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ЭВМ § 9.2. ПОЛУАВТОМАТИЗИРОВАННЫЙ РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ КАЛЬКУЛЯТОРОВ § 9. 3. АВТОМАТИЗАЦИЯ РАСЧЕТА СТЕРЖНЕВЫХ СИСТЕМ. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ ДЛЯ СТЕРЖНЯ § 9.4. МАТРИЦЫ РЕАКЦИЙ (ЖЕСТКОСТИ) ДЛЯ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ СТЕРЖНЕЙ И ИХ ИСПОЛЬЗОВАНИЕ § 9.5. ОПИСАНИЕ УЧЕБНОГО КОМПЛЕКСА ПО РАСЧЕТУ СТЕРЖНЕВЫХ СИСТЕМ. ВНУТРЕННЕЕ И ВНЕШНЕЕ ПРЕДСТАВЛЕНИЕ ИСХОДНЫХ ДАННЫХ. БЛОК-СХЕМА КОМПЛЕКСА ПО РАСЧЕТУ СТЕРЖНЕВЫХ СИСТЕМ Глава 10. УЧЕТ ГЕОМЕТРИЧЕСКОЙ И ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ ПРИ РАСЧЕТЕ СТЕРЖНЕВЫХ СИСТЕМ § 10.2. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С УЧЕТОМ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ § 10.3. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ § 10.4. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С УЧЕТОМ ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ Глава 11. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ (МКЭ) § 11.2. СВЯЗЬ МКЭ С УРАВНЕНИЯМИ СТРОИТЕЛЬНОЙ МЕХАНИКИ § 11.3. ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ РЕШЕНИЯ ПЛОСКОЙ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ § 11.4. ПРЕДЕЛЬНЫЙ ПЕРЕХОД ДЛЯ ПЛОСКОЙ ЗАДАЧИ § 11.5. ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ РЕШЕНИЯ ОБЪЕМНОЙ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ § 11. 6. СЛОЖНЫЕ ЭЛЕМЕНТЫ, ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ ЭЛЕМЕНТОВ С ИСКРИВЛЕННОЙ ГРАНИЦЕЙ § 11.7. ПОСТРОЕНИЕ МАТРИЦ РЕАКЦИЙ ДЛЯ РАСЧЕТА ПЛАСТИНОК И ОБОЛОЧЕК § 11.8. ОСОБЕННОСТИ КОМПЛЕКСОВ ДЛЯ РАСЧЕТА КОНСТРУКЦИЙ ПО МКЭ. СУПЕРЭЛЕМЕНТНЫЙ ПОДХОД Глава 12. ОСНОВЫ ДИНАМИКИ СООРУЖЕНИЙ § 12.2. СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 12.3. РАСЧЕТ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ ДЕЙСТВИИ ПЕРИОДИЧЕСКОЙ НАГРУЗКИ § 12.4. РАСЧЕТ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ ДЕЙСТВИИ ПРОИЗВОЛЬНОЙ НАГРУЗКИ. ИНТЕГРАЛ ДЮАМЕЛЯ § 12.5. ДВИЖЕНИЕ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ. ПРИВЕДЕНИЕ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ К ДВУМ СИСТЕМАМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 12.6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ. УРАВНЕНИЕ ЛАГРАНЖА § 12.7. ПРИВЕДЕНИЕ КИНЕМАТИЧЕСКОГО ВОЗДЕЙСТВИЯ К СИЛОВОМУ § 12.8. СВЕДЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДИНАМИКИ К РАЗДЕЛЯЮЩИМСЯ УРАВНЕНИЯМ С ПОМОЩЬЮ РЕШЕНИЯ ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ § 12.9. МЕТОД ПОСТОЯННОГО УСКОРЕНИЯ И ЕГО ИСПОЛЬЗОВАНИЕ ДЛЯ РЕШЕНИЯ ДИНАМИЧЕСКИХ ЗАДАЧ Глава 13. СВЕДЕНИЯ ИЗ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ, ИСПОЛЬЗУЕМЫЕ В СТРОИТЕЛЬНОЙ МЕХАНИКЕ § 13.2. МАТРИЦЫ, ИХ ВИДЫ, ПРОСТЕЙШИЕ ОПЕРАЦИИ НАД МАТРИЦАМИ § 13.3. ПЕРЕМНОЖЕНИЕ МАТРИЦ. ОБРАТНАЯ МАТРИЦА § 13.4. МЕТОД ГАУССА ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ. РАЗЛОЖЕНИЕ МАТРИЦЫ В ПРОИЗВЕДЕНИЕ ТРЕХ МАТРИЦ § 13.5. ИССЛЕДОВАНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. ОДНОРОДНЫЕ УРАВНЕНИЯ. РЕШЕНИЕ n УРАВНЕНИЙ С m НЕИЗВЕСТНЫМИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА ГАУССА § 13.6. КВАДРАТИЧНАЯ ФОРМА. МАТРИЦА КВАДРАТИЧНОЙ ФОРМЫ. ПРОИЗВОДНАЯ ОТ КВАДРАТИЧНОЙ ФОРМЫ § 13.7. СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ВЕКТОРЫ ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННОЙ МАТРИЦЫ § 13.8. ОДНОРОДНЫЕ КООРДИНАТЫ И ИНТЕГРИРОВАНИЕ ПО ТРЕУГОЛЬНОЙ ОБЛАСТИ § 13.9. СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ, ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ И ЭКСПОНЕНЦИАЛЬНОЙ ФУНКЦИЕЙ ЗАКЛЮЧЕНИЕ ЛИТЕРАТУРА

6.2 Диаграммы сдвигов/моментов – инженерная механика: статика

Глава 6: Внутренние силы

Диаграммы

сдвиг/момент представляют собой графическое представление внутренней поперечной силы и изгибающего момента вдоль всей балки.

 

Источник (изображение): XFEM Skier — собственная работа, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=29178249

Диаграмма силы сдвига

Это графическое представление изменение силы сдвига на части или по всей длине балки или рамы. По соглашению, диаграмму поперечной силы можно рисовать выше или ниже x — центральная ось конструкции, но она должна быть указана, если это положительная или отрицательная сила сдвига.

Диаграмма изгибающего момента

Это графическое изображение изменения изгибающего момента на сегменте или на всей длине балки или рамы. По соглашению положительные изгибающие моменты изображаются над центральной осью конструкции с размерами x , а отрицательные изгибающие моменты изображаются под осью.

Ниже приведен простой пример того, как выглядят диаграммы сдвига и момента, после чего будет обсуждаться связь между нагрузкой на балку и диаграммами. 92}=-w(x)[/латекс]

Или:

[латекс]\Delta M=\int V(x)dx[/латекс]

[латекс]\Delta V=\int w(x)dx[/латекс]

Итак, если есть постоянная распределенная нагрузка, то наклон сдвига будет линейным, а наклон момента будет параболическим.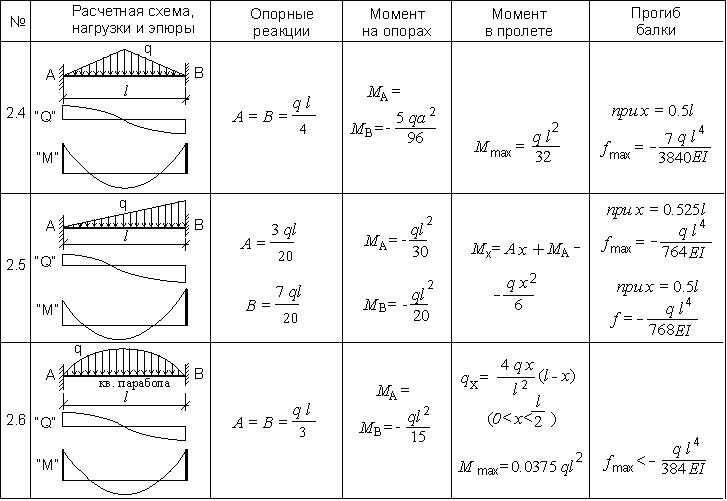 Если распределенная нагрузка равна 0, то сдвиг будет постоянным, а наклон момента будет линейным (как показано в примере 1 в следующем разделе).

 

 

Для вывода соотношений между  w, V и M рассмотрим свободно опертую балку, на которую действует равномерно распределенная нагрузка по всей ее длине, как показано на рисунке ниже. Пусть поперечная сила и изгибающий момент на участке, расположенном на расстоянии x от левой опоры, равны V и M соответственно, а на участке x + dx V 1 + dV и M + dM соответственно. Суммарная нагрузка, действующая через центр бесконечно малой длины, равна 92/2)}[/латекс]

[латекс]M+dM=M+Vdx[/латекс]

или

[латекс]\frac{dM}{dx}=V(x)[/латекс] (Уравнение 6.1)

Уравнение 6.1 подразумевает, что первая производная изгибающего момента по расстоянию равна поперечной силе. Уравнение также предполагает, что наклон диаграммы моментов в конкретной точке равен поперечной силе в той же точке. Уравнение 6.1 предлагает следующее выражение:

[латекс]\Delta M=\int V(x)dx[/латекс] (уравнение 6.2)

Уравнение 6.2 утверждает, что изменение момента равно площади под диаграммой сдвига. Аналогично, усилие сдвига в сечении x + dx  равно:

[латекс]\frac{dV}{dx}=-w(x)[/латекс]  (уравнение 6.3)

Из уравнения 6.3 следует, что первая производная силы сдвига по расстоянию равна интенсивности распределенная нагрузка. Уравнение 6.3 предлагает следующее выражение: 92}=-w(x)[/latex] (уравнение 6.5)

Уравнение 6.5 подразумевает, что вторая производная изгибающего момента по расстоянию равна интенсивности распределенной нагрузки.

Источник: Внутренние силы в балках и рамах, LibreTexts. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

 

 

Существует множество методов, которые можно использовать для решения диаграммы сдвига/моментов. Во-первых, вы можете найти уравнение для каждой части и проинтегрировать, используя приведенные выше уравнения.

Во-вторых, вы можете использовать метод, показанный в предыдущем разделе, для расчета внутренних сил в важных точках (где приложены нагрузки, в начале и в конце распределенных нагрузок, в точках реакции). Нанесите эти точки на графики V и M в местах x, затем соедините точки, используя соответствующий наклон формы (подробнее об этом внизу этой страницы).

В-третьих, вы можете найти уравнения, используя уравнения равновесия (чтобы не было интегрирования/дифференцирования).

1. Адаптировано из оригинального источника https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

   Нарисуйте FBD конструкции

2. Рассчитайте реакции, используя уравнения равновесия (может не потребоваться, если вы выбрали консольную балку и используете свободную сторону для FBD).
3. Сделайте разрез и сложите внутренние силы N V и M, используя положительный знак. В зависимости от количества загрузок может потребоваться несколько разрезов. Вспомним позитивную конвенцию:
4. Для сдвига найдите уравнение (выражение) сдвига, которое равно x расстоянию от начала координат (часто реакции) для каждого разреза.
5. На минутку, найдите уравнение (выражение) сдвига, которое равно x расстоянию от начала координат (часто реакции) для каждого разреза.
6. Нанесите эти уравнения на график друг над другом.

 

В остальной части этого раздела будет использоваться этот метод.

Пример 1

(адаптировано с https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames)

Начертите диаграммы поперечной силы и изгибающего момента для консольной балки, несущей сосредоточенную нагрузку в 5 фунтов на свободном конце на расстоянии 3 фута от стены.

1. Нарисуйте FBD конструкции

 

2. Рассчитайте реакции, используя уравнения равновесия (может не потребоваться, если вы выбрали консольную балку и используете свободную сторону для FBD).

Сначала вычислите реакции на опоре. Так как поддержка в B фиксируется, на этой опоре будет три реакции, а именно B _y , B _x и M _B . Применение условий равновесия предполагает следующее:

[латекс]\сумма F_{x}=0: \quad \underline{B_{x}=0}[/латекс]

[латекс]\сумма F_{y}=0: \quad-5 фунтов+B_{y}=0[/латекс]
[латекс]\qquad \quad \underline{B_{y}=5 фунтов}[/ латекс]

[латекс]\сумма M_{B}=0: \quad(5 фунтов)(3 \mathrm{ft})-M=0[/латекс]
[латекс]\qquad \quad \underline{M=15 футов \cdot lb}[/latex]

 

3. Сделайте разрез и сложите внутренние силы N V и M, используя положительный знак. В зависимости от количества загрузок может потребоваться несколько разрезов

Требуется только 1 рез, поскольку в конце добавляется только 1 нагрузка. (Если бы он был посередине, нужно было бы рассмотреть 2 раздела). Значение x может быть от 0 до 3 футов.

4. Для сдвига найдите уравнение (выражение) сдвига, которое равно x расстоянию от начала координат (часто реакции) для каждого разреза.

x — расстояние от свободного конца консольной балки до выреза. Сила сдвига в этом сечении обусловлена ​​приложенной нагрузкой. Используя уравнения равновесия,

[латекс]\сумма F_y = -5 фунтов — V = 0 \\ \qquad \quad \underline{V = — 5 фунтов} \text{  (- указывает, что V действует в противоположном направлении)}[/latex]

Постоянное число для сдвига означает, что оно не изменяется или изменяется на x. (Если бы была распределенная нагрузка, x был бы частью уравнения).

Знак «минус» указывает, что сдвиг действительно идет в противоположном направлении. (Это связано с тем, что правило знаков для поперечной силы гласит, что направленная вниз поперечная сила слева от рассматриваемого сечения вызовет отрицательное поперечное усилие на этом сечении. )

5. На данный момент найдите уравнение (выражение) сдвига, которое равно x расстоянию от начала координат (часто реакции) для каждого разреза.

Здесь x отсчитывается слева. Используя уравнения суммы моментов, найдите выражение для M. Вы можете суммировать моменты относительно конечной точки, где приложена нагрузка, или вы можете сделать это в движущейся точке x. Оба требуют одинакового усилия для решения этой задачи, поэтому давайте выберем левую сторону, где применяется 5 фунтов.

[латекс]\сумма M_L = -Vx — M = 0[/латекс]

[латекс]\qquad \quad M = + Vx = (-5 фунтов) * x[/латекс]

[латекс]\qquad \quad \underline{M = -(5lb)x } \text{  (знак минус указывает, что стрелка идет в другом направлении.}[/latex]

Полученное выражение справедливо для всей балки (область 0 < x < 3 футов). Отрицательный знак указывает на отрицательный момент, который был установлен из соглашения о знаках для момента, поэтому момент фактически движется в противоположном направлении. Момент из-за силы в 5 фунтов имеет тенденцию вызывать вогнутость сегмента балки с левой стороны сечения вниз, что соответствует отрицательному изгибающему моменту в соответствии с соглашением о знаках для изгибающего момента.

 

6. Нанесите эти уравнения на график друг над другом.

Обратите внимание: поскольку сила сдвига является постоянной величиной, она должна иметь одинаковую величину в любой точке балки. Условно диаграмму поперечных сил наносят выше или ниже линии, соответствующей нейтральной оси балки, но при этом необходимо указывать знак «плюс», если это положительная поперечная сила, и знак «минус», если это положительная поперечная сила. отрицательное усилие сдвига. Способ проверить ответ состоит в том, чтобы убедиться, что сила реакции возвращает проблему к 0. Сдвиг равен -5 до последнего момента, когда сила реакции +5lb возвращает силу к 0,9.0005

Поскольку функция изгибающего момента является линейной, диаграмма изгибающего момента представляет собой прямую линию. Таким образом, достаточно использовать два главных значения изгибающих моментов, определенных при х = 0 футов и при х = 3 фута, чтобы построить диаграмму изгибающих моментов. По соглашению диаграммы отрицательных изгибающих моментов строят ниже нейтральной оси балки, а диаграммы положительных изгибающих моментов строят над осью балки.

Обратите внимание, что единицы измерения включены в оси.

 

Вот второе объяснение того, как создавать диаграммы сдвиг/момент:

Диаграмма сдвига

Для создания диаграммы силы сдвига мы будем использовать следующий процесс.

1. Решите для всех внешних сил, действующих на тело.
2. Нарисуйте диаграмму свободного тела тела по горизонтали . Оставьте все распределенные силы как распределенные силы и не заменяйте их эквивалентной точечной нагрузкой.
3. Нарисуйте ряд осей под диаграммой свободного тела. Ось X будет представлять местоположение (совмещенное с приведенной выше диаграммой свободного тела), а ось Y будет представлять внутреннюю силу сдвига.
4. Начиная с нуля в правой части графика, вы будете двигаться вправо, обратите внимание на силы на диаграмме свободного тела выше. Двигаясь прямо по своему сюжету, держитесь ровно, за исключением…
   • Прыжок вверх по величине силы для любой точечной силы, направленной вверх.
   • Прыжок вниз по величине силы для любой точечной силы, падающей вниз.
   • Для любых равномерно распределенных сил у вас будет линейный наклон , где величина распределенной силы представляет собой наклон линии (положительные наклоны для направленных вверх сил, отрицательные наклоны для направленных вниз сил).
   • Для неравномерно распределенных сил форма графика диаграммы сдвига будет интегралом силовой функции .
   • Вы можете игнорировать любые моменты или горизонтальные силы, действующие на тело.

   К тому времени, когда вы дойдете до левого конца графика, вы всегда должны вернуться к обратно к нулю . Если вы не вернетесь к нулю, вернитесь и проверьте свою предыдущую работу.

Чтобы прочитать график, вам просто нужно найти интересующее место на диаграмме свободного тела выше и прочитать соответствующее значение по оси Y на вашем графике. Положительные числа представляют направленную вверх внутреннюю силу сдвига справа от поперечного сечения и направленную вниз силу слева, а отрицательные числа указывают направленную вниз внутреннюю силу сдвига справа от поперечного сечения и направленную вверх силу слева. Визуальное представление этих сил можно увидеть на диаграмме справа.

 

Диаграмма моментов

Диаграмма моментов отображает внутренний изгибающий момент в горизонтальной балке, на которую действует множество сил и моментов, перпендикулярных длине балки. В практических целях эта диаграмма часто используется в тех же обстоятельствах, что и диаграмма сдвига, и обычно обе диаграммы создаются для анализа в этих сценариях.

Чтобы создать диаграмму момента для вала, мы будем использовать следующий процесс.

1. Решите для всех внешних сил и моментов, создайте диаграмму свободного тела и диаграмму сдвига.
2. Нарисуйте ряд осей под диаграммой сдвига. Ось X будет представлять местоположение (в соответствии с приведенной выше диаграммой сдвига и диаграммой свободного тела), а ось Y будет представлять внутренний изгибающий момент.
3. Начиная с нуля в правой части графика, вы будете двигаться вправо, обратите внимание на диаграмму сдвига и моменты на диаграмме свободного тела выше. По мере того, как вы будете двигаться вправо по своему графику, диаграмма моментов будет в первую очередь 9-й.0268 интеграл диаграммы сдвига , кроме…
   • Прыжок вверх по величине момента для любых отрицательных (по часовой стрелке) моментов.
   • Перейти вниз на величину момента для любых положительных (против часовой стрелки) моментов.
   • Вы можете игнорировать любые силы на диаграмме свободного тела.

   К тому времени, когда вы дойдете до левого конца графика, вы всегда должны вернуться к нулю . Если вы не вернетесь к нулю, вернитесь и проверьте свою предыдущую работу.

Чтобы прочитать график, вам просто нужно найти интересующее место на диаграмме свободного тела выше и прочитать соответствующее значение по оси Y на вашем графике. Положительные внутренние моменты заставят луч изгибаться вниз (представьте себе форму улыбки), а отрицательные внутренние моменты заставят луч изгибаться вверх (представьте себе форму хмурого взгляда). Вы также можете увидеть положительные и отрицательные внутренние моменты на рисунке справа.

 

 

Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/6_internal_forces/6-4_shear_moment_diagrams/shear_moment_diagrams.html

 

 

Пример 2

Начертите диаграммы поперечной силы и изгибающего момента для консольной балки, подвергнутой равномерно распределенной нагрузке по всей ее длине, как показано на рис.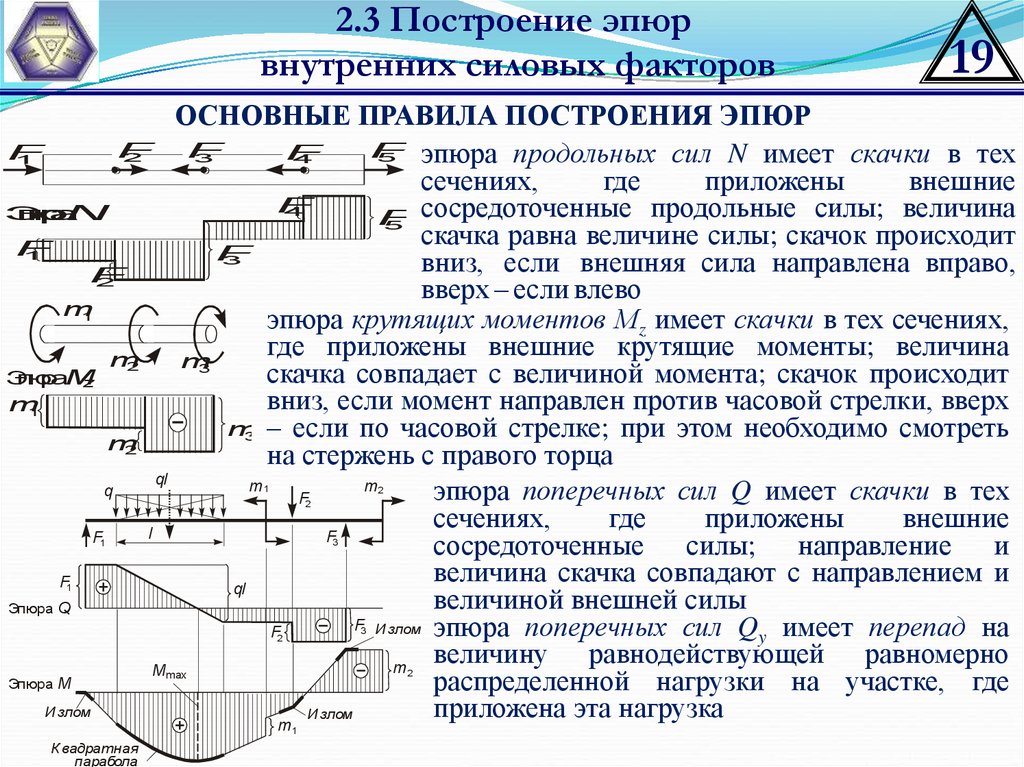 4.5а.

Ответ:

Реакции поддержки.

Сначала вычислите реакции на опоре. Поскольку опора B фиксирована, возможно, на этой опоре будет три реакции, а именно B _y , B _x и M _B , как показано на изображении со свободным телом. диаграмма на рис. 4.4b. Применение условий равновесия предполагает следующее:

 

Функция поперечной силы

Пусть х — расстояние произвольного сечения от свободного конца консольной балки, как показано на рис. 4.5б. Перерезывающая сила всех сил, действующих на отрезок балки слева от сечения, как показано на рис. 4.5д, определяется следующим образом:

Полученное выражение справедливо для всей балки. Знак минус указывает на отрицательную силу сдвига, которая была установлена ​​из правила знаков для силы сдвига. Выражение также показывает, что сила сдвига линейно зависит от длины балки.

Диаграмма поперечной силы. Обратите внимание, что поскольку выражение для поперечной силы является линейным, его диаграмма будет состоять из прямых линий. Сила сдвига при x = 0 м и x = 5 м была определена и использована для построения диаграммы силы сдвига, как показано на рисунке 4.5c. Как показано на диаграмме, перерезывающая сила изменяется от нуля на свободном конце балки до 100 кН на закрепленном конце. Расчетную вертикальную реакцию B _y на опоре можно рассматривать как проверку правильности расчета и диаграммы.

 

Функция изгибающего момента

Выражение для изгибающего момента в сечении на расстоянии x от свободного конца консольной балки выглядит следующим образом:

Знак минус указывает на отрицательный момент, который был установлен из знакового соглашения на данный момент. Как видно на рис. 4.5f, момент из-за распределенной нагрузки приводит к тому, что сегмент балки с левой стороны сечения имеет вогнутость вверх, что соответствует отрицательному изгибающему моменту в соответствии с соглашением о знаках для изгибающий момент.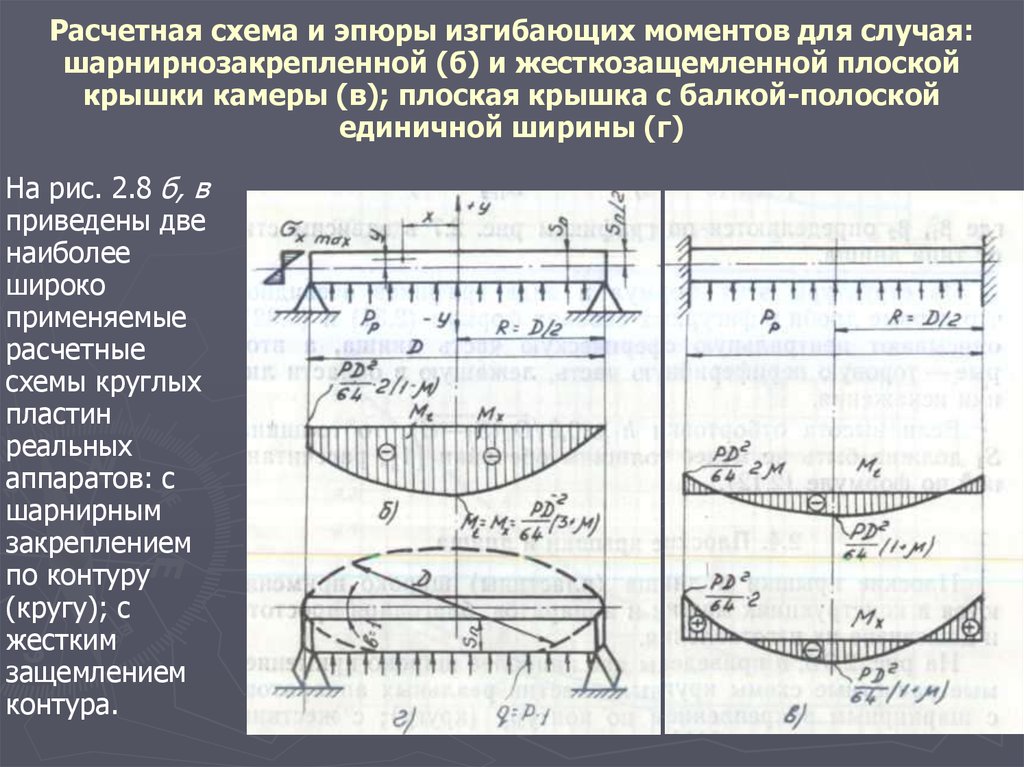

Диаграмма изгибающего момента. Поскольку функция изгибающего момента параболическая, диаграмма изгибающего момента представляет собой кривую. Помимо двух основных значений изгибающего момента при х = 0 м и при х = 5 м, для правильного построения диаграммы изгибающих моментов следует определить моменты в других промежуточных точках. Диаграмма изгибающего момента балки показана на рис. 4.5d.

Источник: Внутренние силы в балках и рамах, Либретексты. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

 

 

В следующих примерах показаны диаграммы сдвига и момента для каждой балки. Подробную информацию о том, как решить каждую из них, см. на странице https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

.

Пример 3

Пример 4

Пример 5

 

Пример 6

Источник: Внутренние силы в балках и рамах, Либретексты. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

 

Хотя есть исключения, эти правила в целом верны:

• +V означает увеличение M
• -V означает уменьшение M
• Когда V = 0, это максимум или минимум M

 

Как начинается/заканчивается каждый сюжет? Реакции только при отсутствии приложенной нагрузки/моментов на концах:

• Консоль:
  • При запуске/реакции: Ненулевые V и M
  • В конце/неподдерживаемом конце: 0 для обоих
• Просто поддерживается
  •   Для V: начало и конец с силами реакции
  •   Для M: начало и конец с нуля
• Где находятся «скачки» или точка перегиба, где линии меняются?
  • В V силы «прыгают» вверх или вниз там, где действуют силы, в соответствии с направлением их приложения (также реакции)
  • В M моменты прыгают вверх или вниз там, где действуют приложенные моменты, в соответствии с направлением
• Связь между графиками
  • При увеличении наклона M сдвиг должен быть положительным
  • При уменьшении наклона M сдвиг должен быть отрицательным
  • Когда V положительно, М должно увеличиваться
  • Когда V отрицательно, M должно уменьшаться
  • Когда интенсивность положительная, V должно увеличиваться
  • Когда интенсивность отрицательная, V должно уменьшаться
  • Точки перегиба на графике M (где наклон линии меняется с отрицательного на положительный и максимальные/минимальные значения) должны быть равны 0 на графике V
  • Нулевое значение на графике V должно давать максимальное или минимальное значение на графике M

На следующем рисунке показано соотношение между производными. Помните, что производная x2 (квадратичная) = x (линейная). Производная x (линейная) является постоянным числом. Производная постоянного числа равна 0. Производная момента — это сдвиг, поэтому, если у вас есть форма момента, используйте эту цифру, чтобы аппроксимировать форму сдвига, спускаясь по графикам.

При переходе от сдвига к моменту верно обратное. Интеграл сдвига есть момент. Интеграл от 0 является постоянным числом. Интеграл постоянного числа линейный. Интеграл от линейного квадратичен. (Интеграл от квадратного кубический). Эта прогрессия перемещает графики снизу вверх.

 

Существует несколько онлайн-программ, которые могут помочь подтвердить найденную форму или помочь вам научиться преобразовывать нагрузки в диаграммы сдвига и момента. Их нельзя использовать на экзамене или в домашних заданиях, и их бесплатные версии ограничены. Это не одобрение какого-либо из сайтов, а просто демонстрация инструментов обучения.

• https://skyciv. com/free-beam-calculator/
• https://clearcalcs.com/freetools/beam-analysis/au
• https://beamguru.com/beam/

 

В основном: Диаграммы сдвига/моментов графически отображают внутренние нагрузки вдоль балки.

Применение : Это может помочь вам определить основные точки напряжения, чтобы обеспечить более безопасную конструкцию.

Глядя в будущее : Вы будете использовать это больше в своем классе структур.

 

Как рисовать диаграммы моментов

← Как рисовать диаграммы сдвига

Расчеты выемки и насыпи земляных работ →

Ширина конструкции

Диаграммы моментов аналогичны диаграммам сдвига, используйте их, чтобы найти местоположение и значение максимального положительного и отрицательного момент или момент в любом конкретном месте.

Самый простой и быстрый способ построить диаграмму моментов — использовать площади областей на диаграмме сдвига. Прежде чем сделать это, вы должны найти все реакции и решить диаграмму сдвига.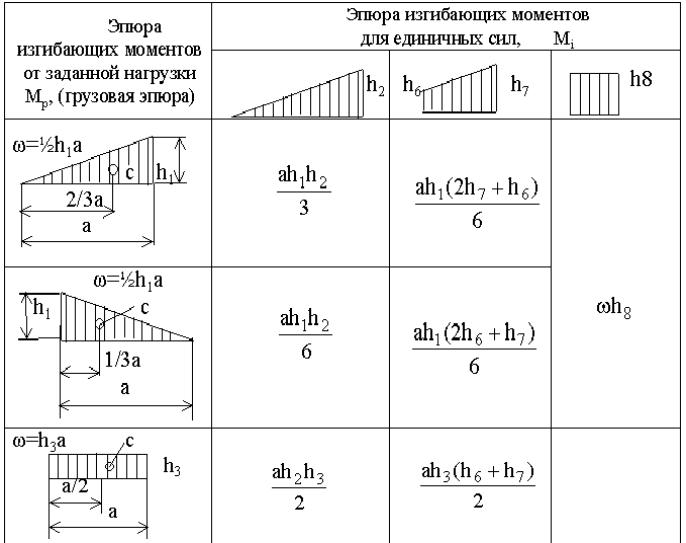

Вот элемент, который переведен в желаемое состояние, чтобы начать работу над диаграммой моментов. Начало диаграммы момента (M) находится ниже существующей диаграммы сдвига (V).

Диаграммы моментов, как и диаграммы сдвига, начинаются и заканчиваются нулем. Момент в каждом сечении является интегралом этого сечения на диаграмме сдвига. Области области диаграммы сдвига помечены ниже и будут упоминаться далее.

Площадь первой области на диаграмме сдвига составляет . Нарисуйте прямую линию от нуля до -50ft*lb  под опорой в точке A. Нарисуйте точку в конечной точке вашей линии, чтобы у вас была цель в поле зрения для каждого сегмента (это серьезно снижает количество ошибок и ускоряет движение).

Линия прямая, потому что сдвиг в этом сегменте постоянен .

Площадь области 2 графика сдвига составляет . Конечная точка на диаграмме моментов для этого участка будет . Поставьте точку в конечной точке ( 8,35 lbft ) и проведите к ней прямую линию (этот отрезок сдвига также постоянен).

Площадь области 3 составляет 8,35 фунт*фут, а сдвиг постоянен, что приводит к линейному моменту. Момент в конце этого отрезка равен 16,35 ft*lb.

Район 4 отличается от остальных, это треугольник, а не прямоугольник. Чтобы найти площадь, мы должны найти, где наклонная линия пересекает ось. Это делается с помощью простого линейного уравнения:

Площадь треугольной области 4 равна , что приводит график к 17,4 фунт-фут . Эта область линейная  , поэтому наш график моментов будет параболическим .

Параболическая секция имеет два варианта, она может изгибаться вверх или вниз. Самый простой способ определить, в какую сторону он будет изгибаться, — это проверить сегмент диаграммы сдвига. Высокая сторона треугольника области 4 находится на левой стороне, поэтому самая крутая часть параболы будет на левой стороне. Эта параболическая секция будет изгибаться вверх/наружу.

Область 5 также является треугольником. Мы знаем расстояние по горизонтали, чтобы быть . Площадь . Сдвиг здесь отрицательный, поэтому общее изменение момента будет отрицательным, и это вернет вас к ноль .

Самая высокая сторона треугольника в области 5 находится на правой стороне  , поэтому самая крутая часть параболы также будет на правой стороне . Эта параболическая секция также будет изгибаться вверх.

Этот последний участок яснее описывает крутой участок параболы. Посмотрите, насколько он крут в конце графика около 0 по сравнению с тем, насколько он пологий в верхней части сегмента около 17,4. Опять же, это связано с тем, что высокая сторона треугольной секции находится в крайнем правом углу.

Это завершает диаграмму моментов для этого примера. Максимальный отрицательный момент составляет -50 фут*фунт на опоре А, а максимальный положительный момент составляет ~17,4 фут*фунт слева от опоры В.