Динамика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Основы динамики
К оглавлению…
Если в кинематике только описывается движение тел, то в динамике изучаются причины этого движения под действием сил, действующих на тело.
Динамика – раздел механики, который изучает взаимодействия тел, причины возникновения движения и тип возникающего движения. Взаимодействие – процесс, в ходе которого тела оказывают взаимное действие друг на друга. В физике все взаимодействия обязательно парные. Это значит, что тела взаимодействуют друг с другом парами. То есть всякое действие обязательно порождает противодействие.
Сила – это количественная мера интенсивности взаимодействия тел. Сила является причиной изменения скорости тела целиком или его частей (деформации). Сила является векторной величиной. Прямая, вдоль которой направлена сила, называется линией действия силы.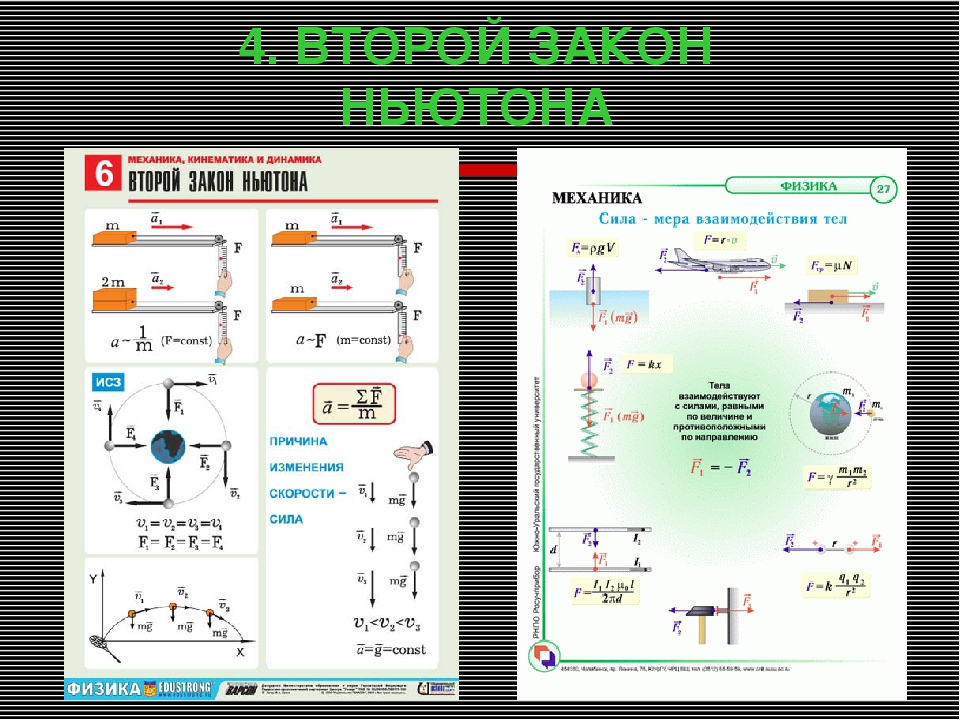
Сила, оказывающая на тело такое же действие, как и все силы, действующие на него, вместе взятые, называется равнодействующей силой. Она равна векторной сумма всех сил, действующих на тело:
Чтобы найти векторную сумму нескольких сил нужно выполнить чертеж, где правильно нарисовать все силы и их векторную сумму, и по данному чертежу с использованием знаний из геометрии (в основном это теорема Пифагора и теорема косинусов) найти длину результирующего вектора.
Виды сил:
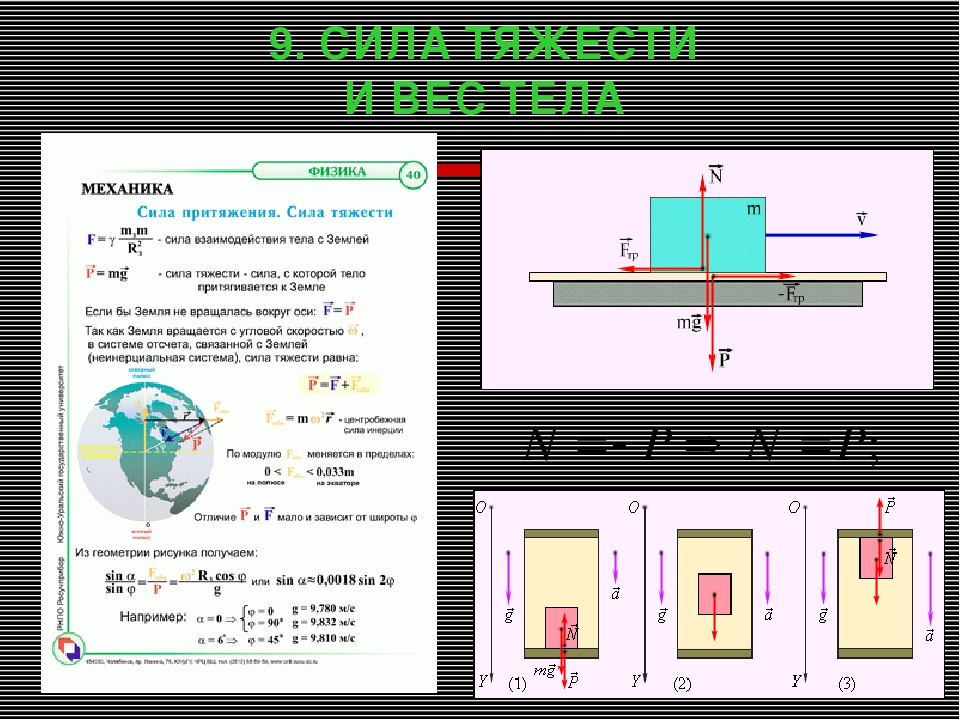
1. Сила тяжести. Приложена к центру масс тела и направлена вертикально вниз (или что тоже самое: перпендикулярно линии горизонта), и равна:
где: g — ускорение свободного падения, m — масса тела. Не перепутайте: сила тяжести перпендикулярна именно горизонту, а не поверхности на которой лежит тело. Таким образом, если тело лежит на наклонной поверхности, сила тяжести по-прежнему будет направлена строго вниз.
Не перепутайте: сила тяжести перпендикулярна именно горизонту, а не поверхности на которой лежит тело. Таким образом, если тело лежит на наклонной поверхности, сила тяжести по-прежнему будет направлена строго вниз.
2. Сила трения. Приложена к поверхности соприкосновения тела с опорой и направлена по касательной к ней в сторону противоположную той, куда тянут, или пытаются тянуть тело другие силы.
3. Сила вязкого трения (сила сопротивления среды). Возникает при движении тела в жидкости или газе и направлена против скорости движения.
4. Сила реакции опоры. Действует на тело со стороны опоры и направлена перпендикулярно опоре от нее. Когда тело опирается на угол, то сила реакции опоры направлена перпендикулярно поверхности тела.
5. Сила натяжения нити. Направлена вдоль нити от тела.
6. Сила упругости. Возникает при деформации тела и направлена против деформации.
Обратите внимание и отметьте для себя очевидный факт: если тело находится в покое, то равнодействующая сил равна нулю.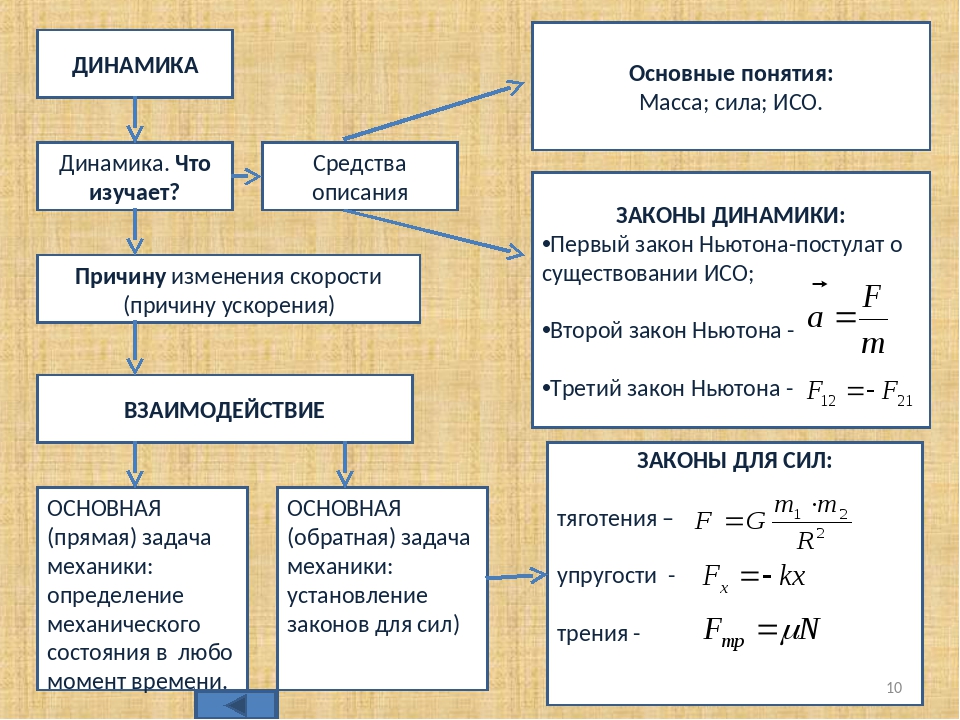
Проекции сил
К оглавлению…
В большинстве задач по динамике на тело действует больше чем одна сила. Для того чтобы найти равнодействующую всех сил в этом случае можно пользоваться следующим алгоритмом:
- Найдем проекции всех сил на ось ОХ и просуммируем их с учетом их знаков. Так получим проекцию равнодействующей силы на ось ОХ.
- Найдем проекции всех сил на ось OY и просуммируем их с учетом их знаков. Так получим проекцию равнодействующей силы на ось OY.
- Результирующая всех сил будет находится по формуле (теореме Пифагора):
При этом, обратите особое внимание на то, что:
- Если сила перпендикулярна одной из осей, то проекция именно на эту ось будет равна нулю.
- Если при проецировании силы на одну из осей «всплывает» синус угла, то при проецировании этой же силы на другую ось всегда будет косинус (того же угла). Запомнить при проецировании на какую ось будет синус или косинус легко.
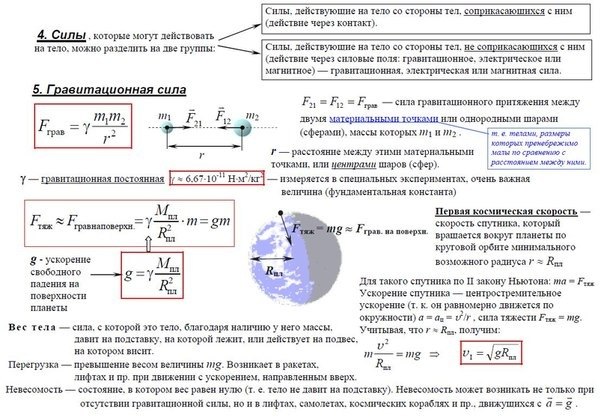 Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус.
Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус. - Если сила направлена в ту же сторону что и ось, то ее проекция на эту ось будет положительной, а если сила направлена в противоположную оси сторону, то ее проекция на эту ось будет отрицательной.
Законы Ньютона
К оглавлению…
Законы динамики, описывающие влияние различных взаимодействий на движение тел, были в одной из своих простейших форм, впервые четко и ясно сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год), поэтому эти законы также называют Законами Ньютона. Ньютоновская формулировка законов движения справедлива только в
Есть и другие ограничения на применимость законов Ньютона. Например, они дают точные результаты только до тех пор, пока применяются к телам, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул (обобщением классической механики на тела, двигающиеся с произвольной скоростью, является релятивистская механика, а на тела, размеры которых сравнимы с атомными — квантовая механика).
Первый закон Ньютона (или закон инерции)
Формулировка: В ИСО, если на тело не действуют никакие силы или действие сил скомпенсировано (то есть равнодействующая сил равна нулю), то тело сохраняет состояние покоя или равномерного прямолинейного движения.
Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Поэтому первый закон Ньютона называют законом инерции. Итак, причиной изменения скорости движения тела целиком или его частей всегда является его взаимодействие с другими телами. Для количественного описания изменения движения тела под воздействием других тел необходимо ввести новую величину – массу тела.
Масса – это свойство тела, характеризующее его инертность (способность сохранять скорость постоянной). В Международной системе единиц (СИ) масса тела измеряется в килограммах (кг). Масса тела – скалярная величина. Масса также является мерой количества вещества:
Второй закон Ньютона – основной закон динамики
Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела и сила.
Формулировка: Ускорение, приобретаемое телом в ИСО, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе этого тела:
Однако при решении задач по динамике второй закон Ньютона целесообразно записывать в виде:
Если на тело одновременно действуют несколько сил, то под силой в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил. Если равнодействующая сила равна нолю, то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения, т.к. ускорение будет нулевым (первый закон Ньютона).
Третий закон Ньютона
Формулировка: В ИСО тела действуют друг на друга с силами, равными по модулю и противоположными по направлению, лежащими на одной прямой и имеющими одну физическую природу:Эти силы приложены к разным телам и поэтому не могут уравновешивать друг друга. Обратите внимание, что складывать можно только силы, которые одновременно действуют на одно из тел. При взаимодействии двух тел возникают силы, равные по величине и противоположные по направлению, но складывать их нельзя, т.к. приложены они к разным телам.
Обратите внимание, что складывать можно только силы, которые одновременно действуют на одно из тел. При взаимодействии двух тел возникают силы, равные по величине и противоположные по направлению, но складывать их нельзя, т.к. приложены они к разным телам.
Алгоритм решения задач по динамике
Задачи по динамике решаются с помощью законов Ньютона. Рекомендуется следующий порядок действий:
1. Проанализировав условие задачи, установить, какие силы действуют и на какие тела;
2. Показать на рисунке все силы в виде векторов, то есть направленных отрезков, приложенных к телам, на которые они действуют;
3. Выбрать систему отсчета, при этом полезно одну координатную ось направить туда же, куда направлено ускорение рассматриваемого тела, а другую – перпендикулярно ускорению;
4. Записать II закон Ньютона в векторной форме:
5. Перейти к скалярной форме уравнения, то есть записать все его члены в том же порядке в проекциях на каждую из осей, без знаков векторов, но учитывая, что силы, направленные против выбранных осей будут иметь отрицательные проекции, и, таким образом, в левой части закона Ньютона они будут уже вычитаться, а не прибавляться. В результате получатся выражения вида:
В результате получатся выражения вида:
6. Составить систему уравнений, дополнив уравнения, полученные в предыдущем пункте, в случае необходимости, кинематическими или другими простыми уравнениями;
7. Провести далее все необходимые математические этапы решения;
8. Если в движении участвует несколько тел, анализ сил и запись уравнений производится для каждого из них по отдельности. Если в задаче по динамике описывается несколько ситуаций, то подобный анализ производится для каждой ситуации.
При решении задач учитывайте также следующее: направление скорости тела и равнодействующей сил необязательно совпадают.
Сила упругости
К оглавлению…
Деформацией называют любое изменение формы или размеров тела. Упругими называют такие деформации, при которых тело полностью восстанавливает свою форму после прекращения действия деформирующей силы. Например, после того, как груз сняли с пружины, её длина в недеформированном состоянии не изменилась. При упругой деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Ее называют силой упругости. Простейшим видом деформации является деформация одностороннего растяжения или сжатия.
При упругой деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Ее называют силой упругости. Простейшим видом деформации является деформация одностороннего растяжения или сжатия.
При малых деформациях модуль силы упругости пропорционален деформации тела. При этом сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации, и может быть рассчитана по формуле:
где: k – жесткость тела, х – величина растяжения (или сжатия, другими словами: деформации тела), она равна модулю разности между конечной и начальной длиной деформируемого тела. Важно, что величина растяжения или сжатия не равна ни начальной, ни конечной длине тела в отдельности. Жесткость не зависит ни от величины приложенной силы, ни от деформации тела, а определяется только материалом, из которого изготовлено тело, его формой и размерами. В системе СИ жесткость измеряется в Н/м.
Утверждение о пропорциональности силы упругости и деформации называют законом Гука.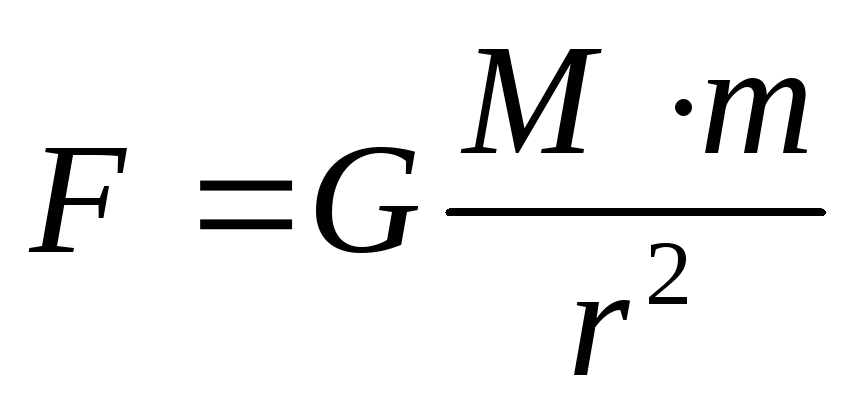 В технике часто применяются спиралеобразные пружины. При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром.
В технике часто применяются спиралеобразные пружины. При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром.
Таким образом, у каждого конкретного тела (а не материала) есть своя жесткость и она не изменяется для данного тела. Таким образом, если у Вас в задаче по динамике несколько раз растягивали одну и ту же пружину Вы должны понимать, что ее жесткость во всех случаях была одна и та же. С другой стороны если в задаче было несколько пружин разных габаритов, но, например, все они были стальные, то тем не менее у них у всех будут разные жесткости. Так как жесткость не является характеристикой материала, то ее нельзя найти ни в каких таблицах. Жесткость каждого конкретного тела будет либо Вам дана в задаче по динамике, либо ее значение должно стать предметом некоторых дополнительных изысканий при решении данной задачи.
При сжатии сила упругости препятствует сжатию, а при растяжении – препятствует растяжению. Рассмотрим также то, как можно выразить жесткость нескольких пружин соединенных определённым образом. При параллельном соединении пружин общий коэффициент жесткости рассчитывается по формуле:
При последовательном соединении пружин общий коэффициент жесткости может быть найден из выражения:
Вес тела
К оглавлению…
Силу тяжести, с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни в неправильном смысле, под весом подразумевается масса, однако это не так.
Весом тела называют силу, с которой тело действует на опору или подвес. Вес – сила, которая, как и все силы, измеряется в ньютонах (а не в килограммах), и обозначается P. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Согласно третьему закону Ньютона вес зачастую равен либо силе реакции опоры (если тело лежит на опоре), либо силы натяжении нити или силе упругости пружины (если тело висит на нити или пружине). Сразу оговоримся — вес не всегда равен силе тяжести.
Сразу оговоримся — вес не всегда равен силе тяжести.
Невесомость – это состояние, которое наступает, когда вес тела равен нолю. В этом состоянии тело не действует на опору, а опора на тело.
Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Перегрузка рассчитывается по формуле:
где: P – вес тела, испытывающего перегрузку, P0 – вес этого же тела в состоянии покоя. Перегрузка – безразмерная величина. Это хорошо видно из формулы. Поэтому не верьте писателям-фантастам, которые в своих книгах измеряют ее в g.
Запомните, что вес никогда не изображается на рисунках. Он просто вычисляется по формулам. А на рисунках изображается сила натяжения нити либо сила реакции опоры, которые по третьему закону Ньютона численно равны весу, но направлены в другую сторону.
Итак, отметим еще раз три существенно важных момента в которых часто путаются:
- Несмотря на то, что вес и сила реакции опоры равны по величине и противоположны по направлению, их сумма не равна нулю.
 Эти силы вообще нельзя складывать, т.к. они приложены к разным телам.
Эти силы вообще нельзя складывать, т.к. они приложены к разным телам. - Нельзя путать массу и вес тела. Масса – собственная характеристика тела, измеряется в килограммах, вес – это сила действия на опору или подвес, измеряется в Ньютонах.
- Если надо найти вес тела Р, то сначала находят силу реакции опоры N, или силу натяжения нити Т, а по третьему закону Ньютона вес равен одной из этих сил и противоположен по направлению.
Сила трения
К оглавлению…
Трение – один из видов взаимодействия тел. Оно возникает в области соприкосновения двух тел при их относительном движении или попытке вызвать такое движение. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело.
Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней вызывающей силе и направлена в противоположную ей сторону. Сила трения покоя не может превышать некоторого максимального значения, которое определяется по формуле:
Сила трения покоя всегда равна по величине внешней вызывающей силе и направлена в противоположную ей сторону. Сила трения покоя не может превышать некоторого максимального значения, которое определяется по формуле:
где: μ – безразмерная величина, называемая коэффициентом трения покоя, а N – сила реакции опоры.
Если внешняя сила больше максимального значения силы трения, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения. Силу трения скольжения можно считать равной максимальной силе трения покоя.
Коэффициент пропорциональности μ поэтому называют также коэффициентом трения скольжения. Коэффициент трения μ – величина безразмерная. Коэффициент трения положителен и меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки их поверхностей. Таким образом коэффициент трения является неким конкретным числом для каждой конкретной пары взаимодействующих тел. Вы не сможете найти его ни в каких таблицах. Для Вас он должен либо быть дан в задаче, либо Вы сами должны найти его в ходе решения из каких-либо формул.
Вы не сможете найти его ни в каких таблицах. Для Вас он должен либо быть дан в задаче, либо Вы сами должны найти его в ходе решения из каких-либо формул.
Если в рамках решения задачи у Вас получается коэффициент трения больше единицы или отрицательный – Вы неправильно решаете эту задачу по динамике.
Если в условии задачи просят найти минимальную силу, под действием которой начинается движение, то ищут максимальную силу, под действием которой, движение ещё не начинается. Это позволяет приравнять ускорение тел к нулю, а значит значительно упростить решение задачи. При этом силу трения полагают равной ее максимальному значению. Таким образом рассматривается момент, при котором увеличение искомой силы на очень малую величину сразу вызовет движение.
Особенности решения задач по динамике с несколькими телами
К оглавлению…
Связанные тела
Алгоритм решения задач по динамике в которых рассматриваются несколько тел связанных нитями:
- Сделать рисунок.

- Записать второй закон Ньютона для каждого тела в отдельности.
- Если нить нерастяжима (а так в большинстве задач и будет), то ускорения всех тел будут одинаковы по модулю.
- Если нить невесома, блок не имеет массы, трение в оси блока отсутствует, то сила натяжения одинакова в любой точке нити.
Движение тела по телу
В задачах этого типа важно учесть, что сила трения на поверхности соприкасающихся тел действует и на верхнее тело, и на нижнее тело, то есть силы трения возникают парами. При этом они направлены в разные стороны и имеют равную величину, определяемую весом верхнего тела. Если нижнее тело тоже движется, то необходимо учитывать, что на него также действует сила трения со стороны опоры.
Вращательное движение
К оглавлению…
При движении тела по окружности независимо от того, в какой плоскости происходит движение, тело будет двигаться с центростремительным ускорением, которое будет направлено к центру окружности, по которой движется тело. При этом понятие окружность не надо воспринимать буквально. Тело может проходить только дугу окружности (например, двигаться по мосту). Во всех задачах этого типа одна из осей обязательно выбирается по направлению центростремительного ускорения, т.е. к центру окружности (или дуги окружности). Вторую ось целесообразно направить перпендикулярно первой. В остальном алгоритм решения этих задач совпадает с решением остальных задач по динамике:
При этом понятие окружность не надо воспринимать буквально. Тело может проходить только дугу окружности (например, двигаться по мосту). Во всех задачах этого типа одна из осей обязательно выбирается по направлению центростремительного ускорения, т.е. к центру окружности (или дуги окружности). Вторую ось целесообразно направить перпендикулярно первой. В остальном алгоритм решения этих задач совпадает с решением остальных задач по динамике:
1. Выбрав оси, записать закон Ньютона в проекциях на каждую ось, для каждого из тел, участвующих в задаче, или для каждой из ситуаций, описываемых в задаче.
2. Если это необходимо, дополнить систему уравнений нужными уравнениями из других тем по физике. Особенно хорошо нужно помнить формулу для центростремительного ускорения:
3. Решить полученную систему уравнений математическими методами.
Так же есть ряд задач на вращение в вертикальной плоскости на стержне или нити. На первый взгляд может показаться, что такие задачи будут одинаковы. Это не так. Дело в том, что стержень может испытывать деформации как растяжения, так и сжатия. Нить же невозможно сжать, она сразу прогибается, а тело на ней просто проваливается.
На первый взгляд может показаться, что такие задачи будут одинаковы. Это не так. Дело в том, что стержень может испытывать деформации как растяжения, так и сжатия. Нить же невозможно сжать, она сразу прогибается, а тело на ней просто проваливается.
Движение на нити. Так как нить только растягиваться, то при движении тела на нити в вертикальной плоскости в нити будет возникать только деформация растяжения и, как следствие, сила упругости, возникающая в нити, будет всегда направлена к центру окружности.
Движение тела на стержне. Стержень, в отличие от нити, может сжиматься. Поэтому в верхней точке траектории скорость тела, прикрепленного к стержню, может быть равна нулю, в отличии от нити, где скорость должна быть не меньше определенного значения, чтобы нить не сложилась. Силы упругости, возникающие в стержне, могут быть направлены как к центру окружности, так и в противоположную сторону.
Поворот машины. Если тело движется по твердой горизонтальной поверхности по окружности (например, автомобиль проходит поворот), то силой, которая удерживает тело на траектории, будет являться сила трения. При этом сила трения направлена в сторону поворота, а не против него (наиболее частая ошибка), она помогает машине поворачивать. Например, когда машина поворачивает направо, сила трения направлена в сторону поворота (направо).
При этом сила трения направлена в сторону поворота, а не против него (наиболее частая ошибка), она помогает машине поворачивать. Например, когда машина поворачивает направо, сила трения направлена в сторону поворота (направо).
Закон всемирного тяготения. Спутники
К оглавлению…
Все тела притягиваются друг к другу с силами, прямо пропорциональными их массам и обратно пропорциональными квадрату расстояния между ними. Таким образом закон всемирного тяготения в виде формулы выглядит следующим образом:
Такая запись закона всемирного тяготения справедлива для материальных точек, шаров, сфер, для которых r измеряется между центрами. Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной. В системы СИ он равен:
Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле или другой планете. Если M – масса планеты, Rп – ее радиус, то ускорение свободного падения у поверхности планеты:
Если M – масса планеты, Rп – ее радиус, то ускорение свободного падения у поверхности планеты:
Если же удалиться от поверхности Земли на некоторое расстояние h, то ускорение свободного падения на этой высоте станет равно (при помощи нехитрых преобразований можно также получить соотношение между ускорением свободного падения на поверхности планеты и ускорением свободного падения на некоторой высоте над поверхностью планеты):
Рассмотрим теперь вопрос об искусственных спутниках планет. Искусственные спутники движутся за пределами атмосферы (если таковая у планеты имеется), и на них действуют только силы тяготения со стороны планеты. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой орбите практически на нулевой высоте над планетой. Радиус орбиты таких спутников (расстояние между центром планеты и точкой где находится спутник) можно приближенно принять равным радиусу планеты Rп. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Скорость спутника на орбите вблизи поверхности (на нулевой высоте над поверхностью планеты) называют первой космической скоростью. Первая космическая скорость находится по формуле:
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу планеты. Для спутников, движущихся по круговым траекториям на значительном удалении от планеты, гравитационное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника в таком случае находится с помощью формулы:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Если речь идёт о планете Земля, то нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6R3 называется геостационарной.
Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6R3 называется геостационарной.
Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике. Тест
Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике. Тест — курсы по физике Skip navigation- Элементы математики
- действия с векторами
- выражение неизвестной
- Физические величины
- Единицы измерения
- внесистемные единицы
- Постоянные величины в физике
- плотность вещества
- предел прочности, модуль Юнга
- скорость звука
- удельная теплота
- диэлектрическая проницаемость
- удельное сопротивление
- электрохимический эквивалент
- Формулы
- I.
 Механика
Механика - Кинематика
- равномерное движение
- относительность движения
- неравномерное движение
- равноускоренное движение
- ускорение свободного падения
- графики движения
- движение по окружности
- параболическое движение
- Динамика
- закон тяготения
- законы Ньютона
- силы в природе
- равнодействующая сила
- Законы сохранения
- импульс тела, импульс силы
- закон сохранения импульса
- работа и мощность
- кинетическая и потенциальная энергии
- закон сохранения энергии
- Статика
- плечо и момент силы
- условия равновесия
- центр тяжести, центр масс
- Колебания и волны
- колебательное движение
- гармонические колебания
- маятники
- превращение энергии при колебаниях
- упругие волны
- звуковые волны
- II.
 Молекулярная физика
Молекулярная физика - Молекулярная физика
- основные положения мкт
- давление
- основное уравнение мкт, температура
- уравнение идеального газа
- изопроцессы
- свойства жидкостей*
- свойства твердых тел
- Термодинамика
- количество теплоты
- работа, внутренняя энергия
- первый закон термодинамики
- второй закон термодинамики
- тепловые двигатели
- III. Основы электродинамики
- Электричество
- электрический заряд
- закон Кулона
- напряженность поля
- потенциал и работа поля
- диэлектрики, проводники
- электроемкость, конденсаторы
- энергия конденсатора
- Электрический ток
- электрический ток, сила и плотность
- закон Ома для участка цепи
- работа и мощность тока
- закон Ома для замкнутой цепи
- электрический ток в различных средах
- электрические явления
- Магнетизм
- магнитное поле
- сила Ампера
- сила Лоренца
- Электромагнетизм
- магнитный поток
- закон электромагнитной индукции
- самоиндукция, энергия поля
- электромагнитные колебания
- электромагнитные волны
- переменный ток
- трансформатор*
- IV.
 Оптика
Оптика - Волновая оптика
- свет как электромагнитные волны
- интерференция
- дифракция
- Геометрическая оптика
- законы распространения света
- линзы, оптические приборы
- V. Теория относительности
- Теория относительности
- постулаты теории относительности
- VI. Квантовая физика
- Световые кванты
- фотон
- фотоэффект
- квантовые постулаты Бора
- излучение и поглощение света
- Атомное ядро
- энергия связи ядра
- ядерные реакции
- закон радиоактивного распада
- элементарные частицы и их свойства
- Современная физика*
- физика элементарных частиц
- мир внутри атомного ядра
- время расщепляем на мгновения
- нанотехнологии и нанофизика
- вещество в экстремальных состояниях
Основные формулы по физике — МЕХАНИКА
Формулы механики. Механика делится на три раздела: кинематику, динамику и статику. В разделе кинематика рассматриваются такие кинематические характеристики движения, как перемещение, скорость, ускорение. Здесь необходимо использовать аппарат дифференциального и интегрального исчисления.
Механика делится на три раздела: кинематику, динамику и статику. В разделе кинематика рассматриваются такие кинематические характеристики движения, как перемещение, скорость, ускорение. Здесь необходимо использовать аппарат дифференциального и интегрального исчисления.
В основе классической динамики лежат три закона Ньютона. Здесь необходимо обратить внимание на векторный характер действующих на тела сил, входящих в эти законы.
Динамика охватывает такие вопросы, как закон сохранения импульса, закон сохранения полной механической энергии, работа силы.
При изучении кинематики и динамики вращательного движения следует обратить внимание на связь между угловыми и линейными характеристиками. Здесь вводятся понятия момента силы, момента инерции, момента импульса и рассматривается закон сохранения момента импульса.
Смотрите также основные формулы по термодинамике
Таблица основных формул по механике
|
Физические законы, формулы, переменные |
Формулы механики |
||||
|
Скорость мгновенная: где r — радиус-вектор материальной точки, t — время;
|
|||||
|
Модуль вектора скорости: где s — расстояние вдоль траектории движения (путь) |
|||||
|
Скорость средняя (модуль): |
|||||
|
Ускорение мгновенное: |
|||||
|
Модуль вектора ускорения при прямолинейном движении: |
|||||
|
Ускорение при криволинейном движении: 1) нормальное где R — радиус кривизны траектории, 2) тангенциальное 3) полное (вектор) 4) (модуль) |
|||||
|
Скорость и путь при движении: 1) равномерном 2) равнопеременном V0— начальная скорость; а > 0 при равноускоренном движении; а < 0 при равнозамедленном движении. |
|
||||
|
Угловая скорость: где φ — угловое перемещение. |
|||||
|
Угловое ускорение: |
|||||
|
Связь между линейными и угловыми величинами: |
|||||
|
Импульс материальной точки: где m — масса материальной точки. |
|||||
|
Основное уравнение динамики поступательного движения (II закон Ньютона): где F — результирующая сила, <> |
|||||
|
Формулы сил: тяжестиP где g — ускорение свободного падения трения Fтр где μ — коэффициент трения, N — сила нормального давления, упругости Fупр где k — коэффициент упругости (жесткости), Δх — деформация (изменение длины тела). |
|
||||
|
Закон сохранения импульса для замкнутой системы, состоящей из двух тел: где — скорости тел до взаимодействия; — скорости тел после взаимодействия. |
|||||
|
Потенциальная энергия тела: 1) поднятого над Землей на высоту h 2) упругодеформированного |
|
||||
|
Кинетическая энергия поступательного движения: |
|||||
|
Работа постоянной силы: где α — угол между направлением силы и направлением перемещения. |
|||||
|
Полная механическая энергия: |
|||||
|
Закон сохранения энергии: силы консервативны силы неконсервативны где W1 — энергия системы тел в начальном состоянии; W2 — энергия системы тел в конечном состоянии. |
|
||||
|
Момент инерции тел массой m относительно оси, проходящей через центр инерции (центр масс): 1) тонкостенного цилиндра (обруча) где R — радиус, 2) сплошного цилиндра (диска) 3) шара 4) стержня длиной l, если ось вращения перпендикулярна стержню и проходит через его середину |
|||||
|
Момент инерции тела относительно произвольной оси (теорема Штейнера): где — момент инерции тела относительно оси, проходящей через центр масс, d — расстояние между осями. |
|||||
|
Момент силы(модуль): где l — плечо силы. |
|||||
|
Основное уравнение динамики вращательного движения: где — угловое ускорение, — результирующий момент сил. |
|||||
|
Момент импульса: 1) материальной точки относительно неподвижной точки где r — плечо импульса, 2) твердого тела относительно неподвижной оси вращения |
|
||||
|
Закон сохранения момента импульса: где L1 — момент импульса системы в начальном состоянии, L2 — момент импульса системы в конечном состоянии. |
|||||
|
Кинетическая энергия вращательного движения: |
|||||
|
Работа при вращательном движении где Δφ — изменение угла поворота. |
Более 40 основных формул по физике с объяснением
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика, термодинамика и молекулярная физика, электричество. Их и возьмем!
Это механика, термодинамика и молекулярная физика, электричество. Их и возьмем!
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Формулы, термодинамикаОсновные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
Далее берем постоянный и переменный ток.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса. Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Автор: Иван
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
+50 формул по физике за 7-11 класс с пояснением
Мы собрали основные формулы по физике с пояснениями в картинках. Более пятидесяти формул, разделенные по категориям физики: кинетика, динамика, статика, молекулярка, термодинамика, электричество, магнетизм, оптика, кинетика. Это не статья, а огромная шпаргалка по физике!
Это не статья, а огромная шпаргалка по физике!
Основные формулы по физике: кинематика, динамика, статика
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Нужна работа? Есть решение!
Более 70 000 экспертов: преподавателей и доцентов вузов готовы помочь вам в написании работы прямо сейчас.
Подробнее Гарантии Отзывы
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:
Это термодинамика:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Основные формулы оптической физики
Переходим к следующему разделу по физике – оптика. Здесь даны 8 основных формул, которые необходимо знать. Будьте уверены, задачи по оптике – частое явление:
Основные формулы элементов теории относительности
И последнее, что нужно знать перед экзаменом. Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Основные формулы световых квантов
Этими формулами приходится часто пользоваться в силу того, что на тему “Световые кванты” попадается немало задач. Итак, рассмотрим их:
Итак, рассмотрим их:
На этом можно заканчивать. Конечно, по физике есть ещё огромное количество формул, но они вам не столь не нужны.
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
P.S. Хватило ли вам 50 формул по физике, или статью нужно дополнить? Пишите в комментариях.
Более 50 основных формул по физике с пояснением обновлено: 22 ноября, 2019 автором: Научные Статьи.Ру
Урок 7. законы динамики ньютона — Физика — 10 класс
Законы динамики Ньютона
Необходимо запомнить
ВАЖНО!
Масса – одна из основных характеристик материи. {n}Fi$.
{n}Fi$.
Первый закон Ньютона: если на тело не действуют другие тела, то тело движется прямолинейно и равномерно: $\overrightarrow{F} = 0$.
Важно! Если есть ИСО, то любая другая система, движущаяся относительно неё прямолинейно и равномерно, также является инерциальной.
Второй закон Ньютон: ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально его массе: $\overrightarrow{a} = \frac{\overrightarrow{F}}{m}$.
Другая запись формулы второго закона Ньютона (основное уравнение динамики): $\overrightarrow{F} = m \overrightarrow{a}$ .
Третий закон Ньютона: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению: $\overrightarrow{F}_{12} = -\overrightarrow{F}_{21}$.
Второй закон Ньютона для системы тел: приращение импульса $\Delta \overrightarrow{P}$ системы тел равно по величине и по направлению импульсу внешних сил, действующих на тело, за то же время: $\Delta \overrightarrow{p} = \overrightarrow{F} \Delta t$.
Границы применимости: справедливы для материальных точек или поступательно движущихся тел; для скоростей много меньше скорости света в вакууме; выполняются в ИСО.
Решение задачи на применение второго закона Ньютона
Физика: механика | Новый физтех. Университет ИТМО
Содержание курса
Лекция 1 Введение
«Современная картина мира. Микро- и макромир. Задачи современной физики.
Понятия пространства и времени. Классическое представление. Эталоны длины и времени. Способы измерения промежутков времени и длины. Границы применимости классической нерелятивистской механики. Система отсчета. Различные системы координат и связь между ними.»
Лекция 2 Нерелятивистская кинематика материальной точки
Основные понятия кинематики материальной точки: радиус-вектор, траектория, перемещение, путь, скорость, ускорение. Выражение скорости и ускорения в различных системах координат. Естественная параметризация движения. Ускорение материальной точки при криволинейном движении, его тангенциальная и нормальная составляющие. Вращательное движение. Циклоида, брахистрона и таутохрона. Баллистическое движение. Кривизная траектории.
Естественная параметризация движения. Ускорение материальной точки при криволинейном движении, его тангенциальная и нормальная составляющие. Вращательное движение. Циклоида, брахистрона и таутохрона. Баллистическое движение. Кривизная траектории.
Лекция 3 Нерелятивистская динамика материальной точки
Основные понятия динамики материальной точки. Понятие инерции. Первый закон Ньютона. Инерциальные системы отсчета. Импульс. Масса как мера инертности. Сила. Импульс. Второй закон Ньютона. Закон сохранения импульса материальной точки. Третий закон Ньютона. Импульс системы материальных точек. Сохранение импульса замкнутой системы. Центр масс системы материальных точек. Система центра масс. Закон движения центра масс. Приведенная масса. Аддитивность и сохранение массы. Уравнение движения. Закон движения. Начальные условия. Прямая и обратная задача динамики.
Лекция 4 Нерелятивистская динамика материальной точки
Интегрирование уравнений движения. Трение. Пример задачи: баллистическое движение с учетом сопротивления воздуха. Движение тел переменной массы. Реактивное движение. Уравнение Мещерского, формула Циолковского. Поворот ракеты.
Движение тел переменной массы. Реактивное движение. Уравнение Мещерского, формула Циолковского. Поворот ракеты.
Лекция 5 Нерелятивистская динамика системы материальных точек
Работа силы. Мощность. Понятие кинетической энергии. Кинетическая энергия системы материальных точек. Преобразование энергии при переходе от одной ИСО к другой и теорема Кенига. Консервативные силы. Потенциальная энергия. Связь потенциальной энергии и силы. Градиент. Закон сохранения полной механической энергии.
Лекция 6 Нерелятивистская динамика
«Эквипотенциальные поверхности и смысл градиента. Примеры потенциалов, встречающихся в физике. Финитное и инфинитное движение.
Столкновения частиц. Упругие столкновения. Векторные диаграммы. Неупругие столкновения. Каналы реакции. Порог реакции.»
Лекция 7 Нерелятивистская динамика
Момент силы и момент импульса материальной точки и системы материальных точек. Уравнение динамики вращательного движения для материальной точки и системы материальных точек.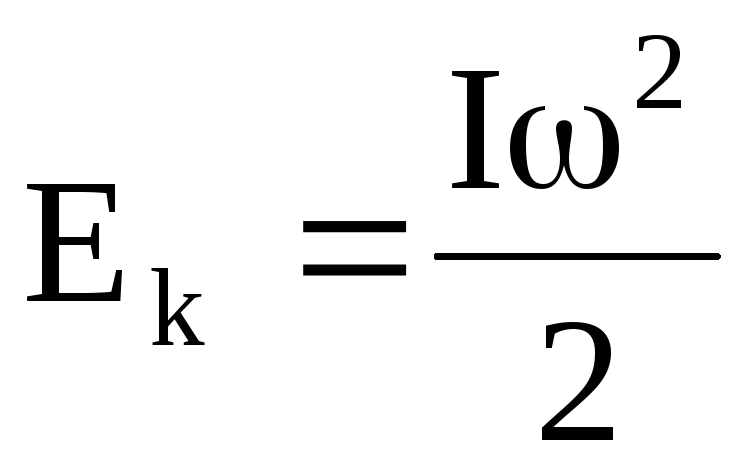 Закон сохранения момента импульса. Момент импульса относительно оси. Вращение относительно движущегося центра. Рассеяние частиц. Формула Резерфорда. Дифференциальное сечение рассеяния.
Закон сохранения момента импульса. Момент импульса относительно оси. Вращение относительно движущегося центра. Рассеяние частиц. Формула Резерфорда. Дифференциальное сечение рассеяния.
Лекция 8 Нерелятивистская динамика
Секториальная скорость. Закон всемирного тяготения. Опыт Кавендиша. Потенциальная и полная энергия гравитационного взаимодействия. Вывод законов Кеплера.
Лекция 9 Гравитационное взаимодействие
«Типы орбит и их связь с полной энергией. Космические скорости. Межпланетные полеты. Приливные силы.
Теорема Гаусса для гравитационного поля, примеры ее применения.»
Лекция 10 Элементы космологии
Элементы космологии. Космологический постулат. Закон Хаббла. Критическая плотность.
Лекция 11 Нерелятивистская динамика в неинерциальных системах отсчета
Неинерциальные системы отсчета. Принцип относительности для НИСО. Силы инерции. Закон движения в НИСО. Частные случаи: поступательное движение НИСО и движение с вращением. Ускорение д’Аламбера, Кориолиса, центробежное. Маятник Фуко.
Маятник Фуко.
Лекция 12 Нерелятивистская динамика в неинерциальных системах отсчета, введение в СТО
«Динамика движения материальной точки в окрестности поверхности Земли. Отклонение отвеса от направления на центр Земли. Связь инертной и гравитационной масс.
Экспериментальные обоснования СТО»
Лекция 13 Релятивистская кинематика материальной точки
Постулаты специальной теории относительности. Относительность одновременности событий. Способы синхронизации часов. Вывод преобразований Лоренца. Интервал. Причинность. Собственное время. Распад мю-мезонов. Лоренцево сокращение продольных размеров объекта и фотосъемка быстро движущихся объектов.
Лекция 14 Релятивистская кинематика материальной точки
Диаграммы Минковского. Парадокс «пенала». Экспериментальная проверка замедления времени. Релятивистский закон преобразования скоростей. Аберрация света. Продольный и поперечный эффект Доплера для периодической последовательности сигналов. Парадокс близнецов, связь с эффектом Доплера.
Лекция 15 Релятивистская динамика
Релятивистский импульс и релятивистская энергия. Четырехвектор энергии-импульса. Энергия покоя. Преобразование энергии и импульса при переходе между инерциальными системами отсчета. Релятивистский закон сохранения энергии. Связь энергии и массы.
Лекция 16 Релятивистская динамика
Столкновения и распад релятивистских частиц. Порог реакции. Ускорители частиц.
Лекция 17 Кинематика АТТ
«Понятие абсолютно твердого тела (АТТ). Элементы кинематики АТТ. Независимость угловой скорости от начала отчета в ТТ. Сложение вращений. Разложение плоского движения на поступательное и вращательное. Мгновенная ось вращения.
Момент импульса и момент инерции твердого тела. Теорема Гюйгенса-Штайнера. Вычисление моментов инерции. Понятие о тензоре инерции.»
Лекция 18 Динамика АТТ
Динамика вращательного движения АТТ вокруг фиксированной оси. Движение относительно центра масс. Маятник Максвелла. Скатывание тел с наклонной плоскости. Кинетическая энергия вращения. Аналогия между вращательным и поступательным движением.
Кинетическая энергия вращения. Аналогия между вращательным и поступательным движением.
Лекция 19 Нерелятивистсткая динамика абсолютно твердого тела
Свободный гироскоп. Приближенная теория движения гироскопа под действием внешних сил. Симметричный волчок. Нутация. Тензор и эллипсоид инерции
Лекция 20 Основы теории колебаний
Гармонические колебания материальной точки. Уравнение колебаний. Общее решение и начальные условия. Понятия фазы, частоты, амплитуды. Энергия коллебаний гармонического осциллятора. Метод комплексных амплитуд. Связь колебательного движения с движением по окружности. Сложение колебаний. Фигуры Лиссажу. Фазовое пространство.
Лекция 21 Основы теории колебаний
Затухающие колебания материальной точки при вязком трении, понятие декремента затухания. Вынужденные колебания затухающего осциллятора: различные режимы. Добротность системы. Понятие резонанса. Лоренцева форма резонанса.
Лекция 22 Основы теории колебаний
Установление колебаний. Биения. Связанные осцилляторы. Резонанс Фано. Колебания со многими степенями свободы. Нормальные колебания. Цепочка связанных осцилляторов. Оптические аналогии.
Биения. Связанные осцилляторы. Резонанс Фано. Колебания со многими степенями свободы. Нормальные колебания. Цепочка связанных осцилляторов. Оптические аналогии.
Лекция 23 Основы теории колебаний
Физический маятник. Приведенная длина и центр качания. Адиабатические инварианты. Нелинейные колебания.
Лекция 24 Элементы теории упругости
Деформация простого растяжения. Модуль Юнга. Коэффициент Пуассона. Плотность энергии упругой деформации. Всестороннее гидростатическое сжатие. Деформация сдвига. Модуль сдвига. Деформация кручения. Модуль кручения.
Лекция 25 Элементы механики сплошных сред
Гидростатика несжимаемой жидкости. Закон Архимеда. Стационарное течение жидкости. Идеальная жидкость. Уравнение Бернулли, примеры. Кинематика вязкой жидкости. Вязкость. Внутреннее трение. Ламинарное течение вязкой жидкости по трубке. Формула Пуазейля.
Лекция 26 Элементы механики сплошных сред
Обтекание тел жидкостью и газом. Лобовое сопротивление. Турбулентное движение. Число Рейнольдса. Подъемная сила. Эффект Магнуса. Элементы теории размерности.
Турбулентное движение. Число Рейнольдса. Подъемная сила. Эффект Магнуса. Элементы теории размерности.
Лекция 27 Элементы теории волн
Кинематика волнового движения. Уравнение плоской и сферической волны. Поляризация механических волн. Волновое уравнение, скорость распространения волн. Волны в цепочках связанных осцилляторов.
Лекция 28 Элементы теории волн
Энергия волн в упругой среде. Поток энергии, вектор Умова. Понятие волнового пакета. Групповая скорость, дисперсия. Упругие возмущения. Динамика струны. Звук.
Dynamics | Физика для идиотов
Динамика — это название правил движения. Это то, что, как вы могли подумать, станет одним из первых, о чем нужно будет разобраться, но не было полностью заблокировано до недавнего времени. При этом правила не сильно изменились и довольно предсказуемы, по крайней мере, в больших масштабах. Кто-то однажды сказал мне, что все, что вам нужно знать для экзамена по динамике, это: и все остальное можно вывести из этого. Я так и не узнал, правы ли они, я узнал и эти на всякий случай:
Я так и не узнал, правы ли они, я узнал и эти на всякий случай:
Если вы уже знакомы с уравнениями, возможно, вы захотите перейти к следующему разделу, иначе я объясню, откуда они взялись и как их использовать.
При работе с измерениями вы можете использовать скалярные или векторные величины.
Скалярные величины:
- Укажите только величину.
- Энергия, Длина, Масса, Скорость, Температура и Время — все это скалярные величины.
Векторные величины:
- Имеют как величину, так и направление
- Смещение, Сила, Скорость, Ускорение и Импульс — все векторные величины.
Иногда может показаться, что скорость и скорость — одно и то же (часто они равны друг другу), но на самом деле они немного отличаются.Скорость — это то, насколько быстро что-то движется, не имеет значения, идет ли он вверх, вниз, влево или вправо, все, что имеет значение, — это то, как далеко он перемещается за установленное время. Вероятно, лучший способ рассматривать скорость — это если вы думаете или обычная ось x, y. Если тело движется горизонтально по прямой со скоростью 10, затем останавливается и движется в совершенно противоположном направлении, при скорости 10, очевидно, произошло изменение, однако скорость этого не отражает. Скорость до разворота такая же, как и после.Однако скорость не та. Если бы мы сказали, что скорость вначале была такой же, как и скорость: 10, тогда, когда тело движется точно в противоположном направлении с той же скоростью, скорость будет -10.
Вероятно, лучший способ рассматривать скорость — это если вы думаете или обычная ось x, y. Если тело движется горизонтально по прямой со скоростью 10, затем останавливается и движется в совершенно противоположном направлении, при скорости 10, очевидно, произошло изменение, однако скорость этого не отражает. Скорость до разворота такая же, как и после.Однако скорость не та. Если бы мы сказали, что скорость вначале была такой же, как и скорость: 10, тогда, когда тело движется точно в противоположном направлении с той же скоростью, скорость будет -10.
Исаак Ньютон был умным парнем. Мы должны благодарить его за гравитацию (я, вероятно, должен добавить, что он открыл, а не изобрел ее, иначе люди начнут обвинять его каждый раз, когда падают). Больше всего Ньютон известен (помимо случая с яблоком) своими законами движения:
- Частица останется в покое или продолжит движение, если на нее не будет действовать внешняя сила.
- Сила, действующая на объект, равна его массе, умноженной на его ускорение ().
- Каждое действие имеет равную и противоположную реакцию.
Все это нормально, но что на самом деле означают эти законы?
1. Частица останется в покое или продолжит свое движение, если на нее не будет действовать внешняя сила.
Это просто означает, что если на частицу не действует внешняя сила, она никоим образом не изменит ее движения. Если бы не было трения или сопротивления воздуха, то частица, движущаяся со скоростью 5, продолжалась бы бесконечно.Очевидно, что в реальной жизни этого не происходит из-за сопротивления воздуха и трения, поэтому практически невозможно иметь внешнюю силу на движущуюся частицу. Однако, если вы думаете о неподвижной частице, это имеет гораздо больший смысл. Если к неподвижной частице не приложить силу, она не начнет двигаться.
2. Сила, действующая на объект, равна его массе, умноженной на его ускорение.
Проще говоря, это, вероятно, одна из самых фундаментальных формул в динамике.Это один из тех, которые часто возникают в Dynamics, и его действительно стоит изучить. Понять это тоже не так уж и сложно. Имеет смысл, что если что-то имеет большую массу, потребуется большая сила, чтобы придать ему такое же ускорение, как и что-то с меньшей массой.
3. Каждое действие имеет равную и противоположную реакцию
Этот закон в основном означает, что если вы толкнетесь о стену, это оттолкнет вас назад, что на самом деле является хорошей работой, потому что в противном случае вы бы прошли прямо!
У них так много разных названий, что иногда сложно угнаться за ними.Возможно, вы слышали, что их называют кинематическими уравнениями, уравнениями движения, уравнениями SUVAT, а может быть, вы вообще не слышали о них. Прежде всего, давайте взглянем на них:
(1)
(2)
(3)
(4)
(5)
Может показаться, что там есть что вспомнить, но поверьте, это не так сложно, как кажется. Как будто эти уравнения невероятно важны в динамике.
SUVAT Equation 1
Как вы, наверное, уже знаете, скорость, разделенная на время, равна ускорению, а скорость, умноженная на время, равна смещению.Это означает, что на графике зависимости скорости от времени уклон линии равен ускорению, а площадь под линией равна смещению.
Если у вас есть начальная скорость и конечная скорость, график будет выглядеть примерно так:
График, показывающий u против tКак я уже сказал, уклон линии равен ускорению. Так . Переставив это так, чтобы получился объект, мы получаем нашу первую формулу постоянного ускорения:
SUVAT Equation 2
Ладно, один проиграл, осталось четыре!
Мы знаем, что площадь под графиком равна смещению.Итак, мы знаем, что умножение на дает нам нижний прямоугольник площади, а деление на 2 дает нам верхний треугольник. Это дает нам:
Теперь мы уже знаем это, поэтому мы можем переставить это, чтобы получить, а затем подставить это в наше уравнение для смещения. Из этого у нас есть. Если мы просто умножим скобку, которая дает нам нашу вторую формулу:
Для тех из вас, кто любит находить математику там, где это возможно, вам может быть интересно узнать, что это интеграл по отношению к.Если для вас это не имеет смысла, почему бы не заглянуть в замечательный раздел «Интеграция», где все станет ясно!
SUVAT Equation 3
Те из вас, кто увлечен поиском закономерностей, возможно, заметили, что это уравнение очень похоже на предыдущее. Это потому, что он очень похож на предыдущий. Те из вас, кто решил не переходить на страницу интеграции, могут пожалеть об этом сейчас.
Если переставить, чтобы сделать тему, то получится:
Теперь вам просто нужно интегрировать этот результат по времени, чтобы получить наше третье уравнение:
SUVAT Equation 4
Мы уже установили, что площадь под графиком (равная смещению) равна:
Если мы умножим скобку, получим:
, что совпадает с:
Наконец, мы просто разложим это на множители, чтобы получить:
SUVAT Equation 5
Можем переставить, сделать тему:
Затем мы просто подставляем это значение в наше предыдущее уравнение:, что дает нам:
, который можно упростить до
, а затем
это в конечном итоге дает нам окончательную форму
Вот и все! Эти уравнения определенно стоит изучить, поскольку они полезны снова и снова.Есть несколько правил, например, их можно использовать только в тех случаях, когда есть постоянное ускорение. Это означает, что если ускорение составляет примерно 12 мс –2 , они в порядке, но если ускорение составляет 12 мс –2 , тогда они не будут работать, поскольку ускорение зависит от.
Большая часть динамики достигается за счет игнорирования сопротивления воздуха, и хотя это значительно упрощает работу, всегда стоит знать, какое влияние это окажет.Силу сопротивления любого объекта, движущегося в жидкости, можно рассчитать по формуле:
— плотность жидкости (998,2071 кг · м для воды при 30 градусах и 1,204 кг · м для воздуха), — скорость объекта, площадь поперечного сечения объекта и коэффициент сопротивления. Коэффициент лобового сопротивления — это число, которое относится к аэродинамике объекта, у куба и шара есть.
Объект, падающий на Землю, в конце концов (если он будет падать достаточно долго) достигнет скорости, при которой сила сопротивления равна силе тяжести, тянущей его вниз.Это называется Конечная скорость , и вы можете получить выражение для этого, приравняв силу сопротивления к, а затем переставив на:
Для человека, падающего в воздухе (сверху), у нас есть 70 кг, площадь 0,5 м и коэффициент лобового сопротивления около 0,8 (приблизительное предположение где-то около углового куба или цилиндра), мы получаем конечную скорость около 53 мс (что оказывается быть довольно хорошей приблизительной оценкой).
Это самый простой экземпляр в динамике.Тело движется по плоской поверхности по прямой. Например:
1. Преподобный ведет свою машину, как вдруг двигатель перестает работать! Если он едет со скоростью 10 мс –1 , а его замедление составляет 2 мс –2 , сколько времени потребуется машине, чтобы остановиться?
Хорошо, с такого рода проблемами всегда полезно перечислить то, что вы знаете. Нам даны начальная скорость, и ускорение,. Мы также знаем, что если машина собирается финишировать в состоянии покоя, эта конечная скорость должна быть 0 мс -1 .Мы хотим узнать время,. Лично я считаю, что лучше всего изложить эту информацию так:
u = 10 мс -1
v = 0 мс -1
a = -2 мс -2
t =? с
Отсюда видно, какое уравнение нам нужно. В этом случае мы видим, что нам нужно уравнение. Мы переставляем это так, чтобы получился объект, давая нам
Наконец, мы помещаем числа в уравнение:
.
2. Майкл выходит на дорогу, в 30 метрах от места, где двигатель не работает.Очки преподобного упали, и он не видит Майкла. Остановится ли машина вовремя, чтобы не сбить Майкла?
Еще раз, лучше всего выложить всю имеющуюся у нас информацию:
u = 10 мс -1
v = 0 мс -1
a = -2 мс -2
t = 5 с
s =? м
На этот раз мы хотим найти смещение s, поэтому нам нужно выбрать уравнение с этим in. Я собираюсь использовать. Я мог бы использовать или, однако, поскольку нам не дали времени, а вместо этого мы разработали это самостоятельно, любая ошибка, сделанная в предыдущих расчетах, будет перенесена в эту.
Я снова перегруппирую уравнение, на этот раз сделав его предметом обсуждения. Это хорошая привычка, теперь это может не иметь большого значения, переставляете ли вы уравнение до или после ввода чисел, но с более сложными формулами это может стать действительно беспорядочным, если вы не измените его сначала. Также в экзаменационных ситуациях, если вы допустили ошибку, вы все равно можете получить оценки по методу, если экзаменатор видит, что вы сделали.
В любом случае, это дает нам
Подставляя числа в уравнение, получаем:
, чтобы Майкла не ударили! (Уф!)
В приведенном выше примере трение полностью проигнорировано.В реальном мире мы не можем этого сделать (очень удачно, потому что мы все время падали, и люди думали, что мы пьяны). А теперь давайте посмотрим на ситуацию с трением. Коэффициент трения обозначается символом μ. Результирующая (нормальная) сила веса уравновешивает вес автомобиля (чтобы он не проезжал по дороге). Сила трения равна μ (или μN).
3. Машина преподобного сломалась на трассе М1. Ему нужно подтолкнуть его к твердому плечу. Автомобиль весит 5000Н.Rev может выдвинуть около 1800N. Коэффициент трения между автомобилем и дорогой составляет 0,6. Сможет ли Rev подтолкнуть машину к твердой обочине?
Хорошо, в такой ситуации сначала хорошо нарисовать небольшой набросок того, что происходит.
Диаграмма сил, показывающая, что происходит в примере 3.Из этого мы знаем, что для того, чтобы машина двигалась, Rev должен толкать с силой не менее μR. Просто умножив коэффициент трения на равнодействующую силу, мы обнаружим, что сила трения составляет 3000 Н, поэтому Rev не сможет толкнуть автомобиль на обочину дороги.
4. Бодибилдер случайно проходит мимо и, пытаясь облегчить заторы на постоянно загруженном М1, он решает помочь. Он может толкать с силой 3200Н. Каким будет ускорение машины с учетом того, что бодибилдер и Rev.NB — Принять массу автомобиля 510 кг
Итак, на самом деле ситуация та же, что и раньше, только на этот раз силы не уравновешиваются и будет ускорение. Мы получили это от очень умного Исаака Ньютона.
Помните, что для определения общей силы необходимо убрать силу трения. Итак, это (3200 + 1800) — 3000. Таким образом, общая сила составляет 2000Н. Снова нам нужно изменить формулу, чтобы на этот раз в качестве испытуемого использовалось и . Это дает нам. Подставляя числа, получаем:
a = 3.9 мс -2 (2 s.f.)
Это очень похоже на движение по плоской поверхности, только одна или две другие переменные … о, и мы больше не будем говорить об автомобиле Rev, так как я не уверен, что это поможет ему подняться в гору!
В любом случае, боюсь, я немного сбился с пути.Введение «наклонной плоскости» или «уклона», как ее называют большинство из нас, означает, что вам придется освежить свою тригонометрию. С другой стороны, вы узнаете, почему люди годами пытались вбить это в вас! Если вы знакомы со старым добрым порядком операций, все будет в порядке.
Итак, давайте начнем с простого простого примера.
Пример наклонной плоскостиНа рисунке выше показан блок, стоящий на склоне. Хорошее место для начала (вероятно, единственное место, с которого можно начать, если вы хотите получить хоть какой-то шанс получить хоть что-нибудь с вопросом), — это объединить силы.Предполагая, что блок находится в состоянии покоя, мы знаем, что он находится в равновесии, поэтому горизонтальные силы должны быть равны, как и вертикальные силы (если это не один из тех прекрасных левитирующих блоков).
Снарядыничем не отличаются от Движения по прямой, просто вместо того, чтобы тело двигалось слева направо, оно также движется вверх или вниз. Сначала рассмотрим типичный пример движения снаряда:
.Мяч брошен под углом 30 °. Имеет начальную скорость 20 мс -1 .Найдите максимальную высоту, которую может достичь мяч.
Ладно, как обычно, рисуем диаграмму:
Пример движения снарядаТеперь давайте перечислим то, что мы знаем:
- u = 20 sin30 мс -1
- v = 0 мс -1
- a = -9,81 мс -2
- с =? м
Теперь мы выбираем одну из кинематических формул, которая даст нам результат наиболее прямым путем:, и переставляем ее так, чтобы получился объект:
Затем, наконец, введите числа в уравнение:
и выскакивает ответ:
Смотри, не так ли сложно было? Вопросы о снарядах иногда могут показаться довольно сложными, но если вы не забудете просто использовать тригонометрию для нахождения компонентов x и y, вы не ошибетесь.
Иногда вы знаете максимальную высоту, но какой-то другой компонент будет отсутствовать. Например, время, когда мяч находится в воздухе … Опять же, это не проблема, вы просто посмотрите, что вы знаете, , , и воспользуйтесь формулами, чтобы вычислить остальное.
Dynamics — The Physics Hypertextbook
Обсуждение
Почему существует эта страница?
Это не страница о каком-то фундаментальном принципе физики. Это страница о решении конкретной (и распространенной) проблемы механики.
Неформально, динамика — это исследование сил и движения. Говоря более формально, динамика — это раздел механики, изучающий влияние сил на движение объектов. Напротив, статика — это изучение сил без движения; или, более формально, раздел механики, который имеет дело с силами при отсутствии изменений в движении. Динамика предполагает изменение. Статика предполагает неизменность. Важное изменение — это ускорение.
Цель этого раздела книги — служить хранилищем проблем в динамике.Ускорение в каждой задаче будет отличным от нуля в одном направлении. Это верно только для этого раздела. Идея состоит в том, чтобы увидеть, каково решать такие проблемы, чтобы вы могли распознать их, когда они появятся позже.
Аккуратная сила
Возьмите первый закон движения Ньютона и разбейте его на две части. «Покоящийся объект имеет тенденцию оставаться в покое, а объект в движении имеет тенденцию продолжать движение с постоянной скоростью…». В этом длинном главном предложении живет статика.«Если только на это не действует чистая внешняя сила». В этом коротком придаточном предложении мы находим динамику.
Слово «чистая» во фразе « чистая сила» означает общую, комбинированную или общую. Это то, что вы получаете, когда все обдумываете. Слово net связано со словом аккуратный. Поиск чистой стоимости — это что-то вроде уборки математического беспорядка (или, по крайней мере, уменьшения беспорядка). Это может быть записано как ∑ F (с использованием греческой буквы сигма для обозначения суммы и жирным шрифтом, чтобы указать, что силы являются векторами) или как F net (используя индексированное слово net, чтобы сделать символ более похожим на разговорный язык и курсив, чтобы указать, что знание величины силы часто имеет значение) или другие подобные варианты.
Сила — это векторная величина, что означает, что направление имеет значение. Используйте положительные значения для сил, которые указывают в предпочтительном направлении, и отрицательные значения для сил, которые направлены в противоположном направлении. Если проблема двумерная, выберите два предпочтительных направления под прямым углом — что-то вроде вверх и вправо. Выбирайте предпочтительные направления, которые облегчат вашу жизнь. Законы физики не заботятся о том, называете ли вы правое положительное или левое положительным. Пространство в математическом смысле изотропно .Он измеряет одинаково во всех направлениях.
Второй закон движения Ньютона описывает, как связаны чистая сила, масса и ускорение. По сути, чистая сила вызывает ускорение, а масса ему сопротивляется. Лучше всего писать не словами, а символами. Примерно так…
| ∑ F = м a | или | F нетто = ма |
Теперь вы готовы начать следующий этап обучения.
Например
Возьмем беспрецедентный пример обычного велосипеда, который безупречно крутил педали по ничем не примечательной ровной и ровной дороге. Какие силы действуют на велосипед и гонщика (вместе в целом)?
Начните с очевидного. Все имеет вес и вес указывает вниз. Велосипед находится на твердой поверхности, поэтому нормальная сила направлена перпендикулярно этой поверхности. Поверхность ровная, нормальное направление — вверх.Всадник крутит педали. Это означает, что есть какая-то сила, толкающая велосипед вперед. Я не хочу чрезмерно анализировать ситуацию, поэтому давайте просто назовем эту силу push . Даже правильно накачанные шины сопротивляются качению, ось может нуждаться в смазке, а может и не нуждаться в смазке, и воздух определенно затягивает движущееся тело. Давайте упростим жизнь и назовем все эти силы вместе трением . Гонщик толкает велосипед вперед, а трение толкает назад.
Готовы сделать свободную схему тела.Нарисуйте рамку, изображающую велосипед и всадника. Нарисуйте четыре стрелки, выходящие из центра прямоугольника, чтобы обозначить четыре силы, действующие на велосипед и гонщика. Хотя это не всегда необходимо, следует попытаться нарисовать стрелки, длина которых соответствует относительным величинам сил. Длинные стрелки для сильных сил. Короткие для слабых.
Начните с легкой пары — весовой и нормальной. В этом сценарии ничего не происходит в вертикальном направлении. Дорога ровная, и гонщик не выполняет трюков.Вес и нормальный вес уравновешивают друг друга. Нарисуйте одну стрелку вниз, а другую вверх и придайте им одинаковую длину.
Закончите несколько менее легкой парой — толчок и трение. Что-то — это , происходящее в горизонтальном направлении. Движение происходит в горизонтальном направлении. Велосипед куда-то едет. Это должно быть для чего-то полезно. Разве не должно?
Извините, но нет. Движение не имеет значения. Изменение движения — вот что важно. Велосипед ускоряется или движется с постоянной скоростью? Ускорение делает ситуацию динамичной.Отсутствие ускорения делает его статичным. Направление чистой силы определяет ускорение. Сила, направленная в направлении чистой силы, будет более сильной из двух.
Если велосипед ускоряется, значит, гонщик толкает велосипед вперед больше, чем трение толкает его назад. Если велосипед движется с постоянной скоростью, то толчок и трение равны. Если велосипед замедляется, сила трения побеждает силу, толкающую велосипед вперед.
Вот несколько рисунков, которые показывают то, что я только что сказал.
Вот набор уравнений, которые показывают то, что я только что сказал. Мне нравится использовать «вверх» и «вправо» в качестве положительных направлений, но это не закон физики. Это просто предпочтение.
| ||||||||||||||
| ||||||||||||||
| ↙ | ↓ | ↘ | ||||||||||||
|
|
|
Идите и решайте проблемы.
Перевернутые (деформированные) координаты
два тела, соединенные струной
Dynamics | Безграничная физика
Инерция вращения
Инерция вращения — это тенденция вращающегося объекта оставаться во вращении, если к нему не приложен крутящий момент.
Цели обучения
Объясните взаимосвязь между силой, массой, радиусом и угловым ускорением
Основные выводы
Ключевые моменты
- Чем дальше от оси приложена сила, тем больше угловое ускорение.2) α — вращательный аналог второго закона Ньютона (F = ma), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr2 аналогично массе (или инерции).
Ключевые термины
- инерция вращения : Тенденция вращающегося объекта оставаться вращающимся, если к нему не приложен крутящий момент.
- крутящий момент : вращательное или скручивающее действие силы; (Единица СИ ньютон-метр или Нм; британская единица измерения фут-фунт или фут-фунт)
Если вы когда-либо крутили колесо велосипеда или катали карусель, вы испытали силу, необходимую для изменения угловой скорости.Наша интуиция надежно предсказывает многие из вовлеченных факторов. Например, мы знаем, что дверь открывается медленно, если мы нажимаем слишком близко к ее петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше от оси приложена сила, тем больше угловое ускорение; другое значение состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона.На самом деле существуют точные вращательные аналоги как силы, так и массы.
Инерция вращения, как показано на рисунке, — это сопротивление объектов изменениям в их вращении. Другими словами, вращающийся объект будет продолжать вращаться, а невращающийся объект останется неподвижным, если на него не будет действовать крутящий момент. Это должно напомнить вам о Первом законе Ньютона.
Инерция вращения : Для вращения колеса велосипеда требуется сила. Чем больше сила, тем больше угловое ускорение.Чем массивнее колесо, тем меньше угловое ускорение. Если вы надавите на спицу ближе к оси, угловое ускорение будет меньше.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу F к точечной массе m, находящейся на расстоянии r от точки поворота. Поскольку сила перпендикулярна r, ускорение [latex] \ text {a} = \ text {F} / \ text {m} [/ latex] получается в направлении F. Мы можем изменить это уравнение так, чтобы F = ma, а затем поищите способы связать это выражение с выражениями для вращательных величин.Заметим, что a = rα, и подставляем это выражение в F = ma, получая:
[латекс] \ text {F} = \ text {mr} \ alpha [/ latex].
Напомним, что крутящий момент — это эффективность силы при повороте. В этом случае, поскольку F перпендикулярно r, крутящий момент просто равен τ = Fr. Итак, если мы умножим обе части приведенного выше уравнения на r, мы получим крутящий момент в левой части. То есть rF = mr 2 α, или
τ = mr 2 α.
Это уравнение является вращательным аналогом второго закона Ньютона (F = ma), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr 2 аналогично массе (или инерции).Величина mr 2 называется инерцией вращения или моментом инерции точечной массы m на расстоянии r от центра вращения.
Объекты различной формы имеют разную инерцию вращения, которая зависит от распределения их массы.
Веб-сайт класса физики
Законы движения Ньютона: обзор набора задач
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять чистую силу по значениям отдельных сил, связывать ускорение с чистой силой и массой, анализировать физические ситуации, чтобы нарисовать диаграмму свободного тела и решить ее. неизвестная величина (ускорение или значение индивидуальной силы) и объединить анализ второго закона Ньютона с кинематикой для определения неизвестной величины (кинематической величины или значения силы).Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синим цветом .
Масса против веса
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять чистую силу по значениям отдельных сил, связывать ускорение с чистой силой и массой, анализировать физические ситуации, чтобы нарисовать диаграмму свободного тела и решить неизвестная величина (ускорение или индивидуальное значение силы), масса — это величина, которая зависит от количества вещества, присутствующего в объекте; обычно выражается в килограммах.Масса материи, которой обладает объект, не зависит от его местоположения во Вселенной. С другой стороны, вес — это сила тяжести, с которой Земля притягивает к себе объект. Поскольку гравитационные силы меняются в зависимости от местоположения, вес объекта на поверхности Земли отличается от его веса на Луне. Вес, как сила, чаще всего выражается в метрических единицах измерения в ньютонах. Каждое место во Вселенной характеризуется постоянной гравитационного поля, представленной символом g (иногда называемое ускорением свободного падения).Вес (или F grav ) и масса ( м ) связаны уравнением:
F grav = m • g
Второй закон движения Ньютона
Второй закон движения Ньютона гласит, что ускорение ( a ), испытываемое объектом, прямо пропорционально чистой силе ( F net ), испытываемой объектом, и обратно пропорционально массе объекта.В форме уравнения можно сказать, что a = F net / m . Чистая сила — это векторная сумма всех индивидуальных значений силы. Если величина и направление отдельных сил известны, то эти силы могут быть добавлены как векторы для определения результирующей силы. Следует обратить внимание на векторную природу силы. Направление важно. Поднимающую силу и прижимающую силу можно добавить, присвоив прижимной силе отрицательное значение, а восходящей силе положительное значение. Аналогичным образом, сила, направленная вправо, и сила, направленная влево, могут быть добавлены путем присвоения левой силе отрицательного значения и правой силы положительного значения.
Уравнение a = F net / m может использоваться как формула для решения проблем, так и как руководство к размышлениям. При использовании уравнения в качестве формулы для решения проблемы важно, чтобы числовые значения двух из трех переменных в уравнении были известны, чтобы найти неизвестную величину. При использовании уравнения в качестве руководства к размышлениям необходимо учитывать прямые и обратные отношения между ускорением и чистой силой и массой. Двукратное или трёхкратное увеличение чистой силы вызовет такое же изменение ускорения, удвоение или утроение его значения.Увеличение массы в два или три раза вызовет обратное изменение ускорения, уменьшив его значение в два или три раза.
Диаграммы свободного тела
Диаграммы свободного тела представляют силы, которые действуют на объект в данный момент времени. Отдельные силы, действующие на объект, представлены векторными стрелками. Направление стрелок указывает направление силы, а приблизительная длина стрелки представляет относительную величину силы.Силы обозначены в соответствии с их типом. Схема свободного тела может оказаться полезным подспорьем в процессе решения проблем. Он обеспечивает визуальное представление сил, действующих на объект. Если величины всех отдельных сил известны, диаграмму можно использовать для определения чистой силы. И если ускорение и масса известны, то можно рассчитать чистую силу, и диаграмму можно использовать для определения значения единственной неизвестной силы.
Коэффициент трения
Объект, который движется (или событие, пытающееся двигаться) по поверхности, встречает силу трения.Сила трения возникает из-за того, что две поверхности плотно прижаты друг к другу, вызывая межмолекулярные силы притяжения между молекулами разных поверхностей. Таким образом, трение зависит от природы двух поверхностей и от степени их прижатия друг к другу. Силу трения можно рассчитать по формуле:
F frict = µ • F norm
Символ µ (произносится как «мью») представляет коэффициент трения и будет отличаться для разных поверхностей.
Смешение законов Ньютона и кинематических уравнений
Кинематика относится к описанию движения объекта и фокусируется на вопросах, как далеко?, Как быстро?, Сколько времени? а с каким ускорением? Чтобы помочь ответить на такие вопросы, в модуле «Одномерная кинематика» были представлены четыре кинематических уравнения. Четыре уравнения перечислены ниже.
- d = v o • t + 0.5 • а • т 2
- v f = v o + a • t
- v f 2 = v o 2 + 2 • a • d
- d = (v o + v f ) / 2 • t
где
- d = рабочий объем
- t = время
- a = ускорение
- v o = исходная или начальная скорость
- v f = конечная скорость
Законы Ньютона и кинематика разделяют один из этих общих вопросов: с каким ускорением? Ускорение (a) F net = m • уравнение — это то же ускорение, что и в кинематических уравнениях.Таким образом, общие задачи включают:
- использование кинематической информации для определения ускорения, а затем использование ускорения в анализе законов Ньютона, или
- использование информации о силе и массе для определения значения ускорения, а затем использование ускорения в кинематическом анализе.
При анализе словесной проблемы физики целесообразно идентифицировать известные величины и систематизировать их либо как кинематические, либо как величины типа F-m-a.
Привычки эффективно решать проблемы
Эффективный решатель проблем по привычке подходит к физическим проблемам таким образом, чтобы отражать набор дисциплинированных привычек. Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …
- …. внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
- … определяет известные и неизвестные величины в организованном порядке, часто записывая их на диаграмме. Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, v o = 0 м / с, a = 2,67 м / с / с, v f = ???).
- …построит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания физических принципов.
- … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
- … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.
Подробнее …
Дополнительная литература / Учебные пособия:
Следующие страницы из учебного пособия по физике могут быть полезны для понимания концепций и математики, связанных с этими проблемами.
Набор задач о законах движения Ньютона
Просмотреть набор задач
Законы Ньютона о движении Решения с аудиосистемой
Ознакомьтесь с аудиогидом решения проблемы:1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30
Законы динамики — Энциклопедия окружающей среды
Закон Ньютона, связывающий силу и ускорение, лежит в основе современной физики.Применяемый к каждому графику жидкости, он лежит в основе моделей прогнозирования погоды и климата. Интуитивное понятие силы использовалось с древних времен для понимания статического равновесия. Это позволяет спроектировать своды в архитектуре, использовать рычаг, чтобы описать баланс жидкости под действием тяги Архимеда. Именно принцип инерции, открытый Галилеем, проложил путь к законам ньютоновской динамики, чей большой успех заключался в объяснении движения планет и спутников, а также приливов и отливов.Это потребовало большого математического опыта, который имеет свои пределы для более сложных систем, таких как атмосфера или океан. Решение уравнений динамики стало возможным только с момента появления компьютерных вычислений. Однако законы сохранения, количества движения, энергии, кинетического момента накладывают глобальные ограничения, позволяющие более непосредственно понять определенные явления.
1. Балансирующие силы
Понятие силы выражает механическое воздействие на объект.Силы имеют четко определенное физическое происхождение, например, гравитационная сила , (вес , вес ), электрическая сила , , действующая на заряженную частицу , , контакт , контакт или напряжение , напряжение , , сила на кабеле, или сила упругости и пружина . Как и многие фундаментальные понятия физики, силу трудно определить сама по себе, но к ней можно подойти с помощью экспериментальных примеров, а также с помощью математических соотношений, которые она имеет с другими величинами.
Рис. 1. Равновесие противоположных сил, а) в пружинном динамометре, б) в воздушном шаре. [Источник: Traité de Physique Elemententaire — DRION et FERNET — 1885] Сила, таким образом, характеризуется своей интенсивностью (или модулем ) и направлением , а также точкой приложения и математически представлена как вектор . Сумма сил, действующих на покоящийся объект, должна нейтрализовать друг друга. Сила может быть измерена по удлинению пружины из ее положения покоя (рис. 1).Экспериментально подтверждается, что это удлинение пропорционально силе путем последовательного добавления нескольких одинаковых грузов. После калибровки этот датчик усилия пружины можно использовать для измерения различных сил. Для воздушного шара, неподвижного в воздухе, общий вес уравновешивается тягой Архимеда , равной и противоположной массе вытесненного объема воздуха. Это не что иное, как результат сил атмосферного давления и , действующих по всей оболочке: из-за уменьшения давления с высотой давление в нижней части оболочки выше, чем в верхней, что выражается в результирующей восходящей силе. .Этот баланс между давлением и силой тяжести фактически применяется к любому объему жидкости в равновесии, известном как гидростатическое равновесие (см. «Давление, температура, тепло»). Именно благодаря этому балансу воздушные участки или водные участки в бассейне не падают на землю под действием силы тяжести. Когда воздух нагревается, его плотность и, следовательно, масса данного объема уменьшается, в то время как давление остается неизменным, поскольку оно контролируется весом окружающего воздуха.Затем равновесие нарушается, что приводит к вертикальному ускорению воздушного шара. В атмосфере воздушная масса, локально нагретая солнечным излучением, также будет иметь тенденцию подниматься: это принцип конвекции .
Рис. 2. Перевернутая модель Собора Святого Семейства Гауди. Форма равновесия такова, что на каждом пересечении проводов векторная сумма сил равна нулю. Каждый элемент балки представлен проволокой, а его масса моделируется грузом. Сила натяжения пряжи обязательно совпадает с пряжей.В реальной перевернутой конфигурации соответствующая сила будет тогда силой сжатия, направленной вдоль балки, что гарантирует ее механическую прочность. [Источник: http://olive-art.weebly.com/uploads/2/6/0/5/26053332/6555663_orig.jpg]. В общем, баланс сил должен быть выражен как векторов , что является Основа для расчета структур в архитектуре, см. Рисунок 2. Для каждой материальной точки, например, узла пересечения проводов, векторная сумма сил должна уравновешивать друг друга в состоянии равновесия, как показано на Рисунке 3a.Это позволяет, например, найти интенсивности сил F1 и F2 , зная силу F3 и углы θ1 и θ2 , либо геометрическим построением, либо численно. путем проецирования векторов по вертикальной и горизонтальной осям. Протяженный объект, например твердое тело , описывается в физике как набор из материальных точек , удерживаемых вместе внутренними силами .Эти силы следует отличать от внешних сил , таких как вес или силы контакта с другими объектами. Сумма внутренних сил компенсируется принципом действия и противодействия , так что равновесие требует отмены суммы внешних сил.
Рисунок 3. Баланс сил на материальной точке а) и баланс моментов на протяженном объекте — рычаге.Но состояние равновесия протяженного объекта также требует отмены полного момента сил, чтобы избежать его вращения.Момент силы относительно оси определяется как произведение силы, проецируемой перпендикулярно оси, на расстояние до оси. Классическим примером является рычаг, показанный на рисунке 3b. В состоянии равновесия или квазиравновесия для медленного движения для компенсации моментов требуется, чтобы F1d1 = F2d2 (силы здесь перпендикулярны оси), что позволяет увеличить силу, действующую в обратном отношении расстояния до оси (согласно обычному соглашению мы отмечаем здесь F1 интенсивность силы, а F1 представляет вектор силы).Обычно моменты рассматривают относительно оси рычага, потому что момент силы реакции R земли компенсируется сам собой. Однако тот же результат можно получить, вычислив момент относительно любой математической оси, добавив момент реакции R , который является равным вектором и противоположен сумме двух сил F1 и F2 . .
2. Силы и ускорение
Теперь, покидая область статики, ускорение объекта связано с общей силой F , которая действует на него по знаменитому закону ньютоновской динамики , F = мг , где м — это масса объекта, а г, — его вектор ускорения.Это позволяет определить единицу силы, Ньютон (Н), как силу, создающую ускорение в 1 (м / с) / с над массой 1 кг, что записывается как 1 Н = 1 кг · м · с-2. .
В отсутствие силы объект движется с постоянной скоростью, это принцип инерции , впервые сформулированный Галилеем (1564–1642). В то время этот принцип был не очень интуитивно понятным, потому что в повседневной жизни любое движение имеет тенденцию останавливаться без усилия. Это замедление (отрицательное ускорение) теперь приписывается трению и силам, которые противоположны скорости.Но трение становится незначительным в межпланетной пустоте, и большой успех Ньютона (1643-1727) заключался в том, чтобы математически описать движение планет и спутников на основе простого закона универсальной гравитационной силы , убывающей как величина, обратная квадрату расстояния r. .
Применение закона Ньютона потребовало изобретения математической концепции производной , определяющей понятия скорости и ускорения. Отметим скорость v = dz / dt, где dz — небольшое смещение во временном интервале dt.Фактически, мы считаем предел из очень коротким временным интервалом. Точно так же ускорение обозначается как g = dv / dt. Для постоянного ускорения g скорость пропорциональна времени, v = gt , и легко продемонстрировать, что расстояние падения (разница между начальной высотой z0 и высотой z ) будет тогда z0- z = (1/2) gt2 . Таким образом, на Земле под действием силы тяжести г = 9,8 м / с объект достигает скорости 9.8 м / с (35 км / ч) за 1 секунду, падает с высоты 4,9 м.
Закон Ньютона применяется в более общем плане в векторной форме : объект может падать вертикально, как было сказано ранее, сохраняя при этом свою горизонтальную составляющую скорости по инерции. При достаточно высокой горизонтальной скорости необходимо принять во внимание кривизну Земли и получить круговое движение спутника , см. Рисунок 4. В этом случае скорость постоянна по модулю, но вектор скорости вращается на такая же угловая скорость [1], что и у спутника.Ускорение тогда перпендикулярно скорости и направлено к центру Земли со значением g = v2 / r , как показано на рисунке 4. Таким образом, для спутника, близкого [2] к Земле, g = 9,8 мс-2, r = 6500 км, что приводит к: скорости v = (gr ) 1/2 = 8 км / с, времени обращения (длина 40 000 км) T = 5000 с (1 ч 23 мин).
Рисунок 4. a) Движение запущенного тела с увеличивающейся горизонтальной скоростью до спутника на круговой орбите (8000 м / с) и выброс Земли (11000 м / с) [Источник: иллюстрация теории Ньютона, опубликованная в «Popular Astronomy» ].(б) Закон динамики применяется к круговому движению спутника: за короткий промежуток времени dt спутник поворачивается на угол dq = (v / r) dt, а вектор скорости поворачивается на тот же угол dq = (g / v) dt, откуда выводится g = (v2 / r), что позволяет рассчитать скорость спутника v = 8000 м / с у поверхности Земли (r = 6500 км, g = 9,81 м / с-2). ). Если теперь сила тяжести g уменьшается на 1 / r2, скорость v = (gr ) 1/2 от круговое движение уменьшается на 1 / r1 / 2, а период вращения равен 2πr / v , увеличивается на r3 / 2 .Таким образом Луна удалена от Земли r = 384 000 км, т.е. е. В 60 раз больше радиуса Земли, он должен вращаться за время в 465 раз дольше, чем ближайший спутник, т.е. е. 27 дн. Это согласуется с наблюдениями [3]. Закон роста времени обращения в r3 / 2 был открыт Кеплером (1571-1630) для планет, вращающихся вокруг Солнца. Помимо частного случая круговой орбиты, Ньютон смог продемонстрировать, что общее движение следует за эллипсом (или гиперболой за пределами скорости истечения), и он смог найти три закона, ранее установленные Кеплером, на основе точных измерений положения планет.
Бывает, что сила тяжести сама по себе пропорциональна массе, так что возникающее ускорение не зависит от нее: все тела падают с одинаковым ускорением в одном и том же месте. Это равенство между тяжелой массой и инертной массой было заявлено Галилеем и проиллюстрировано его знаменитыми экспериментами (возможно, только воображаемыми) с падающими объектами с Пизанской башни. Это было сделано снова с большой точностью в вакууме, избегая трения воздуха. В качестве демонстрации для публики был снят фильм, сравнивающий падение молотка и пера на Луне во время полета Аполлона XV [4], и аналогичный эксперимент был снят на Земле в огромной вакуумной камере [5].Именно из-за этого принципа эквивалентности все объекты плавают в невесомости на спутнике, каждый движется по одной и той же орбите вокруг Земли. Эта эквивалентность сейчас проверяется с относительной точностью 10-13 (1/10 триллиона), а точность 10-15 ожидается от недавно запущенного спутника «Микроскоп». Эти сверхточные измерения предназначены для проверки отклонений от принципа эквивалентности, предсказываемого новыми теориями гравитации.
3. Кинетическая и потенциальная энергия
В приведенном выше примере свободного падения можно отметить, что mg (z0-z ) = m (1/2 ) g2t2 = (1/2 ) mv2 .Это соответствует более общему свойству сохранения полной энергии, состоящему из кинетической энергии (1/2 ) mv2 и потенциальной энергии mgz . Когда объект падает, его кинетическая энергия увеличивается, но его потенциальная энергия также уменьшается, так что полная механическая энергия сохраняется (при отсутствии трения). В общем случае кинетическая энергия (1/2 ) mv2 выражается как функция модуля скорости. Сохранение механической энергии становится все более распространенным в случае спутника, но выражение потенциальной энергии затем должно быть изменено, чтобы учесть уменьшение силы тяжести.Эта потенциальная энергия зависит только от положения объекта, так что он принимает то же значение после вращения, и кинетическая энергия также имеет такое же значение в соответствии с тем фактом, что движение планеты сохраняется бесконечно. Гравитационный потенциал определяется путем деления этой потенциальной энергии на массу объекта. Этот потенциал характеризует гравитационное поле независимо от объекта, вращающегося вокруг него (до тех пор, пока объект мал и не приводит планету в движение посредством реакции).
Сохранение механической энергии требует особой формы законов силы. Силы трения, в отличие от силы тяжести, уменьшают механическую энергию, так что спутник в конечном итоге входит в контакт с остаточной атмосферой. Однако потерянная механическая энергия преобразуется в тепло, так что общая энергия сохраняется (см. «Энергия»). Тепло по существу соответствует неупорядоченной кинетической энергии молекул газа. Для однородной сферической планеты потенциал изменяется в пределах -1 / r, так что эквипотенциалы представляют собой концентрические сферы.Однако эти сферы слегка деформированы из-за вращения Земли и неоднородностей. Равновесная форма поверхности океана является таким эквипотенциалом (см. «Морская среда»). В самом деле, объект, движущийся по эквипотенциалу, сохраняет ту же потенциальную энергию, и, поскольку его полная энергия сохраняется, он не может приобретать (или терять) скорость под действием только силы тяжести. И наоборот, если форма океана отклоняется от эквипотенциальной, поверхностная вода имеет тенденцию течь в области с более низким потенциалом, пока она не заполнит их и не достигнет состояния равновесия, при котором поверхность является эквипотенциальной.Поверхность твердой Земли также приближается к эквипотенциальности из-за эрозии и пластичности мантии Земли.
4. Количество движения
Количество движения элементарной массы (рассматриваемой как точечная) определяется как произведение массы и скорости, определение, которое может быть распространено на любую физическую систему, добавляя (векторно) количества движения каждой из ее элементарные массы. Легко продемонстрировать, что величина движения равна величине движения центра инерции (центр тяжести ) системы, на которую воздействует ее общая масса.Затем закон динамики Ньютона указывает, что производная от количества движения по времени равна сумме сил, действующих на систему.
Согласно фундаментальному принципу физики, количество движения изолированной системы сохраняется. Другими словами, его центр инерции движется поступательно с постоянной скоростью, и только внешние силы могут изменить эту скорость. Другой эквивалентной формулировкой является принцип действие и противодействие , который предусматривает, что любое тело A, оказывающее силу на тело B, испытывает силу равной интенсивности, но в противоположном направлении, действующую со стороны тела B.Затем закон динамики указывает, что эти внутренние силы не изменяют величину движения глобальной системы A + B. Это обобщает рассмотренное выше условие статического равновесия.
Зная начальные массы m1 и m2 и начальные скорости u1 и u2 каждой массы, вычисляется величина движения до удара m1u1 + m2u2 , которая должна сохраняться после удара , таким образом, обеспечивая ограничение на конечные скорости.Если дополнительно предположить, что ударная волна упругая , т.е. е. что кинетическая энергия (1/2 ) m1u12 + (1/2 ) m2u22 сохраняется, мы можем вывести две конечные скорости. Для двух равных масс мы имеем обмен скоростями (рис. 5а). В случае полностью неупругого удара массы остаются связанными после удара с конечной скоростью, равной средневзвешенному значению начальных скоростей m1u1 + m2u2 / (m1 + m2 ) при сохранении количества движение.Применительно к молекулам газа эти ударные свойства позволяют интерпретировать явление вязкости, которое уравнивает количество движений быстрой и медленной зон внутри жидкости, сохраняя при этом общее количество движений.
Привод ракет или самолетов — еще один классический пример: величина движения, передаваемого транспортному средству, прямо противоположна движению выбрасываемого газа, независимо от задействованных сложных механизмов. Это также относится к силам гравитации: Луна притягивает Землю с силой, равной силе тяжести Земли, действующей на Луну, и противоположной ей.Таким образом, Земля вращается вокруг центра инерции системы Земля-Луна так же, как и молотковая установка, которая должна вращаться, чтобы компенсировать реакцию вращающегося шара (см. «Приливы»). Именно этот центр инерции описывает эллиптическую орбиту вокруг Солнца, а не саму Землю.
Рисунок 5-а. Choc élastique entre deux masses égales [Источник: Саймон Штайнманн (собственная работа) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5)]] Рис. 5-b.Choc élastique entre deux masses inégales [Источник: Саймон Штайнманн (собственная работа) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5) через Wikimedia Commons] Рисунок 5-c. Отличное неэластичное блюдо из двух масс [Источник: Par Raul Roque (персонал Travail) [CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5)], через Wikimedia Commons]
5. Угловой момент
Угловой момент относительно оси определяется для точечной массы как произведение расстояния до оси на величину ее движения, проецируемого перпендикулярно этой оси.Это определение обобщается на протяженное тело, например твердое тело, путем деления его мыслью на элементарные массы и сложения их угловых моментов. Мы демонстрируем из закона динамики, что производная кинетического момента по времени равна суммарному моменту сил (также называемых «крутящий момент »), действующих на систему. Это обобщает закон статики, который требует, чтобы полный момент сил был равен нулю.
Закон сохранения кинетического момента гласит, что полный момент внутренних сил уравновешивается, и поэтому только момент внешних сил может изменить кинетический момент.Таким образом, в твердом состоянии внутренние силы сцепления не вмешиваются в баланс кинетического момента, так же как они не вмешиваются в величину движения. Это фундаментальный закон физики, отличный от принципа действия и противодействия и дополняющий его.
Другими словами, система не может начать самопроизвольное вращение или потерять свое начальное вращение без действия внешних сил. Однако его скорость вращения может измениться в случае сжатия или растяжения.Действительно, для точечной массы это произведение , скорости u на расстояние r до оси, которая сохраняется, поэтому скорость u увеличивается обратно пропорционально расстоянию r , и его угловая скорость u / r обратно пропорциональна квадрату этого расстояния.
Классический пример — фигурист, а в естественной среде — образование торнадо и циклонов (см. «Торнадо: мощные разрушительные водовороты»).Само вращение Земли является результатом увеличения угловой скорости при аккреции вещества, которое привело к ее образованию. Самый яркий пример — пульсары, чрезвычайно плотные звезды, вращающиеся с периодом от нескольких секунд до нескольких миллисекунд. Эти объекты возникают в результате коллапса массивной звезды, обычно в радиусе от 1 миллиона км до 10 км. Такое сжатие увеличивает угловую скорость вращения в 10 миллиардов раз (часть углового момента выбрасывается вместе с газом, испускаемым взрывом).
Момент количества движения на самом деле является вектором, выровненным с осью вращения [6], и поэтому он сохраняется как по направлению, так и по модулю. Это принцип работы гироскопа . Точно так же ось вращения Земли остается выровненной по отношению к звездам, а Северный полюс по-прежнему указывает на область, близкую к Полярной звезде.
Рисунок 6. Прецессия фрезера: вес создает разрез, ориентированный перпендикулярно рисунку и горизонтальный. Таким образом, результирующее изменение вектора кинетического момента перпендикулярно этому вектору, что приводит к прецессионному движению, показанному на рисунке.Аналогичное явление происходит с вращением Земли под действием крутящего момента из-за лунного притяжения (однако прецессия происходит в противоположном направлении, поскольку крутящий момент имеет противоположный знак по отношению к вершине). Источник: http: //hyperphysics.phy astr.gsu.edu/hbase/mechanics/imgmechs/imgmech/topp.gif]Это верно только для изолированной системы, а точнее при отсутствии крутящего момента (или момента) от внешние силы. Крутящий момент, перпендикулярный оси вращения, вызывает вращение оси вращения без какого-либо изменения угловой скорости: это явление прецессии , наблюдаемое на маршрутизаторе, см. Рисунок 6 (точно так же, как ускорение, перпендикулярное скорости, производит вращение скорости без изменения ее модуля).Аналогичный эффект происходит с Землей из-за ее уплощенной формы на полюсе: крутящий момент возникает из-за более сильного притяжения Луны на части около бусинки, чем на ее противоположной части. Это приводит к медленному прецессионному движению вращения Земли в течение 26 000 лет (см. Рисунок 6). Таким образом, направление полюса медленно перемещается по небесной сфере на протяжении столетий. Это приводит к смещению орбиты Земли относительно положения равноденствий, когда ось вращения Земли ориентирована перпендикулярно направлению Солнца.Вот почему это явление получило название « прецессия равноденствий ». Связанное с этим изменение солнечного света происходит при изменении климата между ледниковым и умеренным периодами.
Ссылки и примечания
Фотография на обложке. Автор http://creativecommons.org/licenses/by-sa/2.0 (загружен на Flickr как обычный jfpds) [CC BY-SA 2.0 (极 博 双 板 滑雪 俱乐部)] через Wikimedia Commons.
[1] Угловая скорость Ω — это угол, пройденный за единицу времени, обычно выражаемый в радианах / с, так что Ω = v / r.Радиан определяется как угол, пересекающий дугу окружности, равную радиусу, так что полный оборот (окружность 2πr ) представляет 2π радиан, а период вращения равен T = 2π / Ω = 2πr / v .
[2] Высота должна составлять несколько сотен километров, чтобы избежать атмосферного трения, но ускорение свободного падения остается близким к ускорению земной поверхности, а радиус орбиты мало отличается от радиуса Земли.
[3] Это сидеральная революция, i.е. относительно звезд, в то время как время между двумя полными лунами, равное 29,5 дня, является синодическим оборотом, i. e . по отношению к Солнцу.
[4] Молот и перо Аполлона 15 — Youtube
[5] Брайан Кокс посещает самую большую в мире вакуумную камеру — Вселенная человека: обзор серии 4 — BBC Two — Youtube
[6] Угловой момент более точно определяется относительно исходной точки O. Для точки массой м в точке M это векторное произведение на вектор OM на величину движения м и массы в точке М.Для осесимметричного твердого тела, такого как маршрутизатор или Земля, кинетический момент выровнен по оси вращения со значением, пропорциональным угловой скорости и моменту инерции .
Экологическая энциклопедия окружающей среды Ассоциации энциклопедий окружающей среды и энергии (www.a3e.fr), по контракту связана с Университетом Гренобль-Альп и ИЯФ Гренобля и спонсируется Французской академией наук .
Для цитирования: SOMMERIA Joël (2021), Законы динамики, Энциклопедия окружающей среды, [онлайн ISSN 2555-0950] URL: https://www.encyclopedie-environnement.org/en/physics/laws-of -динамика /.
Статьи в Энциклопедии окружающей среды доступны в соответствии с условиями лицензии Creative Commons BY-NC-SA, которая разрешает воспроизведение при условии: цитирования источника, не коммерческого использования их, использования идентичных исходных условий, воспроизведения в при каждом повторном использовании или распространении эта лицензия Creative Commons BY-NC-SA упоминается.
3.4 Движение с постоянным ускорением — University Physics Volume 1
Учебные цели
К концу этого раздела вы сможете:
- Определите, какие уравнения движения следует использовать для решения неизвестных.
- Используйте соответствующие уравнения движения для решения задачи о преследовании двух тел.
Можно предположить, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени.Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.
Обозначение
Во-первых, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением.Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, принятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x0x0 — это начальная позиция , а v0v0 — начальная скорость . Мы не ставим индексы на окончательные значения. То есть t — это конечный момент времени , x — конечная позиция , а v — конечная скорость . Это дает более простое выражение для затраченного времени: Δt = tΔt = t.Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение постоянно .Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
a– = a = постоянная. a– = a = постоянная.Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения. Во-первых, ускорение равно постоянным в большом количестве ситуаций.Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
Замена упрощенных обозначений для ΔxΔx и ΔtΔt дает
v– = x − x0t.v– = x − x0t.Решение x дает нам
x = x0 + v – t, x = x0 + v – t,3,10
, где средняя скорость
v– = v0 + v2.v– = v0 + v2.3,11
Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой простое среднее значение начальной и конечной скоростей. Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:
v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.В части (b) ускорение не является постоянным. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рисунок 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv. Средняя скорость равна 12 (v0 + v) = 60 км / ч22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.Решение для окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает
а = v − v0t (константа). a = v − v0t (константа).Решение для v дает
v = v0 + at (constanta). v = v0 + at (constanta).3,12
Пример 3.7
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70.0 м / с, а затем ускоряется против движения со скоростью 1,50 м / с 2 за 40,0 с. Какова его конечная скорость?Стратегия
Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.
Решение
Подставьте известные значения и решите: v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.Рисунок 3.19 представляет собой эскиз, показывающий векторы ускорения и скорости.
Рис. 3.19. Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы самолет остановился и начал движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.Помимо полезности при решении задач, уравнение v = v0 + atv = v0 + at дает нам представление о взаимосвязях между скоростью, ускорением и временем.Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательно, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение для конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает
v0 + v2 = v0 + 12at. v0 + v2 = v0 + 12at.Поскольку v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем
v– = v0 + 12at.v– = v0 + 12at.Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает
х = х0 + v0t + 12at2 (константа).х = х0 + v0t + 12at2 (константа).3,13
Пример 3.8
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с 2 . Предположим, драгстер ускоряется из состояния покоя с этой скоростью в течение 5,56 с. Рис. 3.20. Как далеко он пролетит за это время?Рисунок 3.20. Пилот Top Fuel в армии США Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фото любезно предоставлено США.Армия.)
Стратегия
Сначала нарисуем набросок Рис. 3.21. Нас просят найти смещение, которое составляет x , если мы возьмем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 когда мы идентифицируем v0v0, aa и t из постановки задачи.Рис. 3.21. Эскиз разгоняющегося драгстера.
Решение
Во-первых, нам нужно определить известные.Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с 2 и t задается как 5,56 с.Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
x = x0 + v0t + 12at2.x = x0 + v0t + 12at2.Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
Подстановка идентифицированных значений на и t дает
x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м. x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:
- Смещение зависит от квадрата истекшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
- Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.
Расчет конечной скорости по расстоянию и ускорению
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим v = v0 + atv = v0 + at для t , мы получим
Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем
v2 = v02 + 2a (x − x0) (constanta). v2 = v02 + 2a (x − x0) (constanta).3,14
Пример 3.9
Расчет конечной скорости
Рассчитайте конечную скорость драгстера в Примере 3.8 без использования информации о времени.Стратегия
Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.Решение
Сначала мы идентифицируем известные значения. Мы знаем, что v 0 = 0, поскольку драгстер запускается из состояния покоя. Мы также знаем, что x — x 0 = 402 м (это был ответ в примере 3.8). Среднее ускорение было равно , а = 26.0 м / с 2 .Во-вторых, мы подставляем известные в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :
v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).Таким образом,
v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.Значение
Скорость 145 м / с составляет около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость не достигает рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:
- Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
- При фиксированном ускорении автомобиль, который едет вдвое быстрее, не просто останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.
Сводка кинематических уравнений (константа
a ) х = х0 + v0t + 12at2x = x0 + v0t + 12at2 v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.Переставляя уравнение 3.12, получаем
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико, приближаясь к нулю в том пределе, когда начальная и конечная скорости равны. Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.
Аналогичным образом, переставляя уравнение 3.14, мы можем выразить ускорение в терминах скоростей и смещения:
а = v2-v022 (х-х0).а = v2-v022 (х-х0).Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример 3.10
Как далеко уезжает машина?
На сухом бетоне автомобиль может ускоряться противоположно движению со скоростью 7,00 м / с 2 , тогда как на мокром бетоне он может ускоряться противоположно движению со скоростью всего 5 м / с.00 м / с 2 . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.Стратегия
Для начала нам нужно нарисовать набросок Рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.Рис. 3.22. Пример эскиза для визуализации ускорения, противоположного движению и тормозному пути автомобиля.
Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30,0 м / с, v = 0 и a = −7,00 м / с 2 ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Возьмем x 0 равным нулю. Ищем смещение ΔxΔx, или x — x 0 .
Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования — v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0). Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x : x − x0 = v2 − v022ax − x0 = v2 − v022a и подставляем известные значения: х − 0 = 02− (30.0 м / с) 22 (-7,00 м / с2). X-0 = 02- (30,0 м / с) 22 (-7,00 м / с2). Таким образом, x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне. - Эта часть может быть решена точно так же, как (a). Единственное отличие состоит в том, что ускорение составляет −5,00 м / с 2 . Результат xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону.
- Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки.Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы, опять же, определяем известные и то, что мы хотим решить. Мы знаем, что v– = 30,0 м / sv– = 30,0 м / с, treaction = 0,500streaction = 0,500s и areaction = 0areaction = 0. Примем x0-реакцию x0-реакцию равной нулю. Ищем xreactionxreaction.
Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение — x , что мы и хотим найти.
В-третьих, мы подставляем известные для решения уравнения: x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем если бы он реагировал мгновенно.
Наконец, мы добавляем смещение во время реакции к смещению при торможении (рис. 3.23), xbraking + xreaction = xtotal, xbraking + xreaction = xtotal, и найдите (a) равным 64,3 м + 15,0 м = 79.3 м в сухом виде и (b) должно составлять 90,0 м + 15,0 м = 105 м во влажном состоянии.
Рис. 3.23. Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося со скоростью 30,0 м / с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.
Значение
Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важен общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.Пример 3.11
Время расчета
Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м. Если его начальная скорость равна 10,0 м / с, а он ускоряется со скоростью 2,00 м / с 2 , сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)Стратегия
Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время t . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобную физическую связь (то есть уравнение с одной неизвестной, t .)Рис. 3.24. Эскиз автомобиля, ускоряющегося на съезде с автострады.
Решение
Опять же, мы идентифицируем то, что нам известно, и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2,00 м / с2 и x = 200 м.
Нам нужно решить для т . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t , затем подставив известные значения в уравнение:
200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t с, где t — величина времени, а s — единица измерения. Остается
Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,
t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,, что дает два решения: t = 10.0 и t = −20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.Проверьте свое понимание 3.5
Ракета ускоряется со скоростью 20 м / с 2 во время пуска.Сколько времени нужно, чтобы ракета достигла скорости 400 м / с?
Пример 3.12
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с 2 за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.Решение
Сначала мы решаем для v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:
v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также увидели общий подход к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на Рисунке 3.25.
Рис. 3.25. Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.
Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В тот момент, когда газель проходит мимо гепарда, гепард из состояния покоя ускоряется со скоростью 4 м / с 2 , чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, — это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно посмотрим на проблему, становится ясно, что общим параметром для каждого животного является их положение x в более позднее время t . Поскольку оба они начинаются с x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает смещение для каждого животного, мы можем затем установить уравнения, равные друг другу, и решить для неизвестного, то есть времени.Решение
- Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0: x = x0 + v – t = v – t. x = x0 + v – t = v – t. Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2. Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a.x = v – t = 12at2t = 2v – a. Газель имеет постоянную скорость 10 м / с, что составляет ее среднюю скорость.Ускорение гепарда составляет 4 м / с 2 . Оценивая t , время, за которое гепард достигнет газели, имеем t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.
- Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны дать одинаковый ответ.
Смещение гепарда: x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. Водоизмещение газели: x = v – t = 10 м / с (5) = 50 м. x = v – t = 10 м / с (5) = 50 м.Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.Проверьте свое понимание 3.6
Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и начинает бежать, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?
Модуль 03: Динамика — AP Physics 1 Online
Цели:
Понятия силы и чистой силы
- Студент должен уметь (а) соотносить силу с движением и (б) объясните, что подразумевается под чистой или неуравновешенной силой.
- Студент должен уметь (а) сформулировать и объяснить закон Ньютона инерции (1-й закон движения) и, (b) описывают инерцию и ее отношение к массе.
- Учащиеся должны уметь анализировать ситуации, в которых частица остается в покое, или движется с постоянной скоростью под действием нескольких сил.
- Учащийся должен уметь (а) сформулировать и объяснить закон Ньютона ускорения (2-й закон движения), (б) применить его к физическому ситуации и (c) различать вес и массу.
- Учащиеся должны понимать взаимосвязь между силой, действующей на объект, и результирующим изменением скорости объекта, чтобы они могли:
- Рассчитать, для объекта, движущегося в одном измерении, изменение скорости, которое приводит к когда постоянная сила F действует в течение заданного интервала времени.
- Определить, для объекта, движущегося в плоскости, вектор скорости которого испытывает указанное изменение за указанный интервал времени, средняя сила, которая действовали на объект.
- Студенты должны понимать, как Второй закон Ньютона , F = ma , применяется к объекту, подверженному таким силам, как гравитация, натяжение струн или контактные силы, чтобы они могли:
- Нарисовать колодец- маркированная диаграмма свободного тела, показывающая все действительные силы, действующие на объект.
- Написать вниз по векторному уравнению, полученному в результате применения Второго закона Ньютона к объекту, и возьмите компоненты этого уравнения вдоль соответствующих топоры.
- Студенты должны уметь анализировать ситуации в объект движется с заданным ускорением под действием одна или несколько сил, чтобы они могли определить величину и направление чистая сила или одна из сил, составляющих чистую силу, например, движение вверх или вниз с постоянным ускорением.
- Учащиеся должны уметь (а) сформулировать и объяснить закон Ньютона закон действия-противодействия (3-й закон движения), и (б) определить пары сила действия-противодействия.
- Студенты должны понимать Третий закон Ньютона так что для данной системы они могут идентифицировать пары сил и объекты, на которые они действуют, и указывают величину и направление каждого сила.
- Студенты должны уметь применять третий закон Ньютона при анализе силы контакта между двумя объектами, которые вместе ускоряются по горизонтали или вертикальной линией или между двумя скользящими поверхностями.
- Студенты должны уметь решать задачи в котором применение законов Ньютона приводит к двум или трем совместные линейные уравнения, включающие неизвестные силы или ускорения.
- Студенты должны уметь (а) применять законы Ньютона в анализ различных ситуаций с использованием диаграмм свободного тела, и (б) понять концепцию поступательного равновесия.
- Студенты должны знать, что напряжение постоянна в легкой струне, которая проходит через безмассовый шкив и должны уметь использовать этот факт при анализе движения системы два объекта, соединенных строкой.
- Учащиеся должны уметь объяснять (а) причины трение, и (б) как трение описывается с помощью коэффициентов трение.
- Учащиеся должны понимать значение коэффициента трения , чтобы они могли:
- Записать соотношение между нормальными силами и силами трения на поверхности.
- Проанализируйте ситуации, в которых объект движется по неровной наклонной плоскости или горизонтальной поверхности.
- Проанализируйте, при каких обстоятельствах объект начнет скользить, или рассчитайте величину силы статического трения.
- Учащиеся должны понимать влияние сил сопротивления на движение объекта, чтобы они могли:
- Найти конечную скорость объекта, движущегося вертикально под действием замедляющей силы, зависящей от скорости.
Постоянное понимание 1.C:
Объекты и системы обладают свойствами инертной массы и гравитационной массы, которые экспериментально подтверждены, чтобы быть одинаковыми и которые удовлетворяют принципам сохранения.
Essential Knowledge 1.C.1:
Инерционная масса — это свойство объекта или системы, которое определяет, как изменяется его движение при взаимодействии с другими объектами или системами.
Цель обучения (1.C.1.1):
Учащийся может разработать эксперимент для сбора данных, чтобы определить взаимосвязь между чистой силой, действующей на объект, его инерционной массой и его ускорением.
[См. Научную практику 4.2]
Основные знания 1.C.3:
Объекты и системы обладают
свойствами инертной массы и гравитационной массы, которые экспериментально подтверждены как одинаковые и удовлетворяют принципам сохранения.
Цель обучения (1.C.3.1):
Учащийся может разработать план сбора данных для измерения гравитационной массы и измерения инертной массы, а также провести различие между двумя экспериментами.
[См. Научную практику 4.2]
Векторы силы
Устойчивое понимание 3.A:
Все силы обладают некоторыми общими характеристиками, если их рассматривать наблюдателями в инерциальных системах отсчета.
Основные знания 3.A.2:
Силы описываются векторами.
- Силы обнаруживаются по их влиянию на движение объекта.
- Силы имеют величину и направление .
Цель обучения (3.A.2.1): Нарисуйте и рассчитайте
Учащийся может представить силы на диаграммах или математически , используя соответствующим образом обозначенные векторы с величиной, направлением и единицами измерения во время анализа ситуации. .
[См. Научную практику 1.1]
Силы заставляют вещи ускоряться
Существенные знания 3.A.3:
Сила , приложенная к объекту , всегда возникает из-за взаимодействия этого объекта с другим объектом.
- Объект не может воздействовать на себя силой.
- Даже если объект находится в состоянии покоя, на него могут действовать силы со стороны других объектов.
- Ускорение объекта, но не обязательно его скорость, всегда происходит в направлении результирующей силы, прикладываемой к объекту другими объектами.
Цель обучения (3.A.3.1):
Учащийся может анализировать сценарий и выдвигать утверждения (развивать аргументы, обосновывать утверждения) о силах, действующих на объект другими объектами для различных типов сил. или
составляющих сил.
[См. Научные практики 6.4 и 7.2]
Цель обучения (3.A.3.2):
Учащийся может оспорить утверждение о том, что объект может оказывать на себя силу.
[См. Научную практику 6.1]
Цель обучения (3.A.3.3):
Учащийся может описать силу как взаимодействие между двумя объектами и идентифицировать оба объекта для любой силы.
[См. Научную практику 1.4]
Третий закон движения Ньютона
Основные знания 3.A.4:
Если один объект оказывает силу на второй объект, второй объект всегда оказывает силу равной величины на первом объекте в обратном направлении
.
Цель обучения (3.A.4.1):
Учащийся может построить объяснения физических ситуаций, связанных с взаимодействием тел, используя третий закон Ньютона и представление пар сил действие-противодействие.
[См. Научные практики 1.4 и 6.2]
Задача обучения (3.A.4.2):
Учащийся может использовать третий закон Ньютона для заявлений и прогнозов о парах действие-реакция сил при взаимодействии двух объектов.
[См. Научные практики 6.4 и 7.2]
Цель обучения (3.A.4.3):
Учащийся может анализировать ситуации , связанные с взаимодействием между несколькими объектами , используя диаграммы свободного тела , которые включают приложение третьего закона Ньютона для определения сил.
[См. Научную практику 1.4]
Второй закон движения Ньютона
Постоянное понимание 3.B:
Классически ускорение объекта, взаимодействующего с другими объектами, можно предсказать, используя ΣF = ma .
Essential Knowledge 3.B.1:
Если интересующий объект взаимодействует с несколькими другими объектами, чистая сила является векторной суммой отдельных сил.
Цель обучения (3.B.1.1):
Учащийся может предсказать движение объекта с учетом сил, действующих от нескольких объектов, используя второй закон Ньютона в различных физических ситуациях с ускорением в одно измерение.
[См. Научную практику 6.4 и 7.2]
Цель обучения (3.B.1.2):
Учащийся может разработать план сбора и анализа данных движения (статического, постоянного или ускоряющегося) на основе измерений силы и переноски. провести анализ, чтобы определить взаимосвязь между чистой силой и векторной суммой отдельных сил.
[См. Научные практики 4.2 и 5.1]
Задача обучения (3.B.1.3):
Учащийся может перевыразить диаграмму свободного тела в математическое представление и решить математическое представление для ускорения объекта.
[См. Научные практики 1.5 и 2.2]
Диаграммы свободного тела
Основные знания 3.B.2: Диаграммы свободного тела — полезные инструменты для визуализации сил, действующих на отдельный объект, и написания уравнений которые представляют физическую ситуацию.
- Объект можно нарисовать так, как если бы он был извлечен из его среды, и взаимодействия с ней идентифицированы.
- Сила, действующая на объект, может быть представлена в виде стрелки, длина которой представляет величину силы, а направление показывает направление силы.
- Система координат с одной осью, параллельной направлению ускорения, упрощает перевод от диаграммы свободного тела к алгебраическому представлению.
Цель обучения (3.B.2.1):
Учащийся может создавать и использовать диаграммы свободного тела, чтобы анализировать физические ситуации решать задачи с движением качественно и количественно .
[См. Научную практику 1.1, 1.4 и 2.2]
Откуда берутся силы?
Постоянное понимание 3.C:
На макроскопическом уровне силы можно разделить на дальнодействующих (действие на расстоянии) сил или контактных сил .
Essential Knowledge 3.C.4:
Контактные силы возникают в результате взаимодействия одного объекта с другим объектом, и они возникают из межатомных электрических сил . Эти силы включают натяжение, трение, нормальные, пружинные (Физика 1) и плавучие (Физика 2).
Цель обучения (3.C.4.1):
Учащийся может утверждать о различных контактах сил между объектами на основе микроскопической причины этих сил.
[См. Научную практику 6.1]
Цель обучения (3.C.4.2):
Учащийся может объяснить контактные силы (натяжение, трение, нормальное давление, пружина), возникающие из-за межатомных электрических сил и что они поэтому есть определенные направления.
[См. Научную практику 6.2]
Фундаментальные силы
Постоянное понимание 3.G:
Определенные типы сил считаются фундаментальными.
Essential Knowledge 3.G.1:
Гравитационные силы действуют во всех масштабах и преобладают на самых больших масштабах расстояний и масс.
Цель обучения (3.G.1.1):
Учащийся может сформулировать ситуации , когда сила тяжести является доминирующей силой, а электромагнитные, слабые и сильные силы можно игнорировать.
[См. Научную практику 7.1]
Центр масс
Постоянное понимание 4.A:
Ускорение центра масс системы связано с чистой силой, действующей на систему, где ΣF = ma .
Границы:
Physics 1 не включает вычислений центров масс; уравнение не предоставляется до Физики 2. Однако, без проведения расчетов, студенты Физики 1, как ожидается, смогут определить центр масс высокосимметричных распределений масс, таких как однородный стержень или куб с однородной плотностью, или две сферы равная масса.
Essential Knowledge 4.A.1:
Линейное движение системы можно описать с помощью смещения, скорости и ускорения ее центра масс.
Цель обучения (4.A.1.1):
Учащийся может использовать представления центра масс изолированной двухобъектной системы для качественного и полуколичественного анализа движения системы.
[См. Научные практики 1.2, 1.4, 2.3 и 6.4]
Основные знания 4.A.2:
Ускорение равно скорости изменения скорости во времени, а скорость равна скорости изменения положения во времени.
- Ускорение центра масс системы прямо пропорционально чистой силе, прилагаемой к нему всеми объектами, взаимодействующими с системой, и обратно пропорционально массе системы.
- Сила и ускорение являются векторами с ускорением в том же направлении, что и результирующая сила.
Цель обучения (4.A.2.1):
Учащийся может делать прогнозы о движении системы на основе того факта, что ускорение равно изменению скорости в единицу времени, а скорость равна изменению положения на единицу. время.
[См. Научную практику 6.4]
Цель обучения (4.A.2.2):
Учащийся может оценить, используя предоставленные данные , были ли задействованы все силы в системе или все части системы идентифицированы.
[См. Научную практику 5.3]
Цель обучения (4.A.2.3):
Учащийся может создавать математические модели и анализировать графические взаимосвязи для ускорения, скорости и положения центра масс системы и используйте их для вычисления
свойств движения центра масс системы.
[См. Научные практики 1.4 и 2.2]
Кинематические уравнения
Основные знания 4.A.3:
Силы, которые системы оказывают друг на друга, возникают из-за взаимодействий между объектами в системах.