Простейшие связи и их реакции
Связи, которые рассматриваются в статике, реализуются при помощи твердых и гибких тел. Сила, с которой данное тело действует на связь, и реакция связи по аксиоме А3 являются противоравными силами.
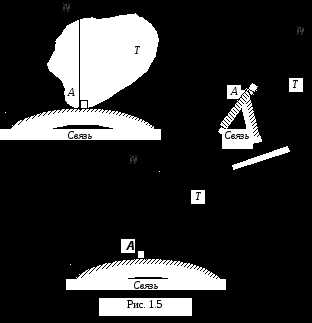
Идеально гладкая поверхность (рис. 1.5)
Тело Т опирается в точке А на гладкую поверхность, которая является
для него связью. Реакция  гладкой поверхности приложена в точкеА и направлена по общей нормали к телу и
гладкой поверхности (рис. 1.5).
гладкой поверхности приложена в точкеА и направлена по общей нормали к телу и
гладкой поверхности (рис. 1.5).
2) Цилиндрический шарнир (рис. 1.6)
Вцилиндрическое отверстие телаТ вставляется цилиндрический болт (заштрихован) несколько меньшего диаметра, чем отверстие. Тело
 цилиндрического шарнира лежит в
плоскости, перпендикулярной оси болта,
проходит через центр болта и точку
касания с телом. Таким образом, направление
реакции
цилиндрического шарнира лежит в
плоскости, перпендикулярной оси болта,
проходит через центр болта и точку
касания с телом. Таким образом, направление
реакции неизвестно и определяется в зависимости
от приложенных к телу сил. Часто, чтобы
не вводить неизвестный угол,
определяющий направление реакции
неизвестно и определяется в зависимости
от приложенных к телу сил. Часто, чтобы
не вводить неизвестный угол,
определяющий направление реакции  ,
ее заменяют двумя другими составляющими
по взаимно ортогональным направлениям:
,
ее заменяют двумя другими составляющими
по взаимно ортогональным направлениям:.
3) Цилиндрическая шарнирно-подвижная опора (подвижной каток) (рис. 1. 7)
ТелоТ опирается на гладкую поверхность через
шарнир, поставленный на катки. Реакция  шарнирно-подвижной опоры направлена
перпендикулярно опорной поверхности.
шарнирно-подвижной опоры направлена
перпендикулярно опорной поверхности.
4) Цилиндрическая шарнирно-неподвиж-ная опора (рис.1.8)
ТелоТ прикреплено с помощью шарнира к
неподвижной поверхности. Направление
реакции  опоры может быть любым, в зависимости
от приложенных сил. Как и в случае 2),
чтобы не вводить неизвестный угол,
реакцию
опоры может быть любым, в зависимости
от приложенных сил. Как и в случае 2),
чтобы не вводить неизвестный угол,
реакцию  раскладывают по двум взаимно ортогональным
направлениям.
раскладывают по двум взаимно ортогональным
направлениям.
5) Гибкая нерастяжимая нить (рис. 1.9)
Реакция
нити  ,
называемая натяжением нити, направлена
вдоль нити к точке подвеса.
,
называемая натяжением нити, направлена
вдоль нити к точке подвеса.
6) Невесомый шарнирно-закрепленный на концах стержень (рис. 1.10)
Реакция  невесомого стержня направлена вдоль
стержня. При этом стержень может быть
как сжат, и тогда реакция стержня
направлена от стержня к телу
невесомого стержня направлена вдоль
стержня. При этом стержень может быть
как сжат, и тогда реакция стержня
направлена от стержня к телу
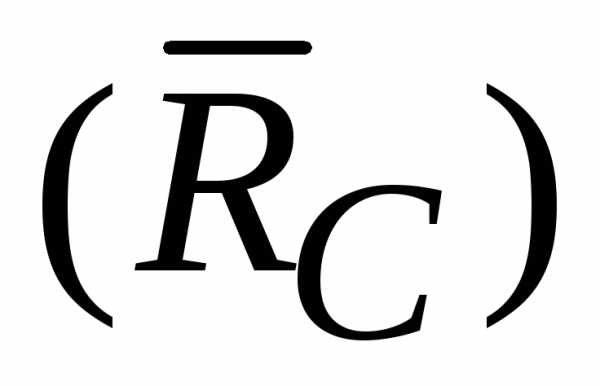 .
.7) Жесткая заделка (рис. 1.11)
Конец
балкиАВ жестко заделан в стену. При нагрузке на
балку в заделке возникают реакции,
состоящие из реакции заделки 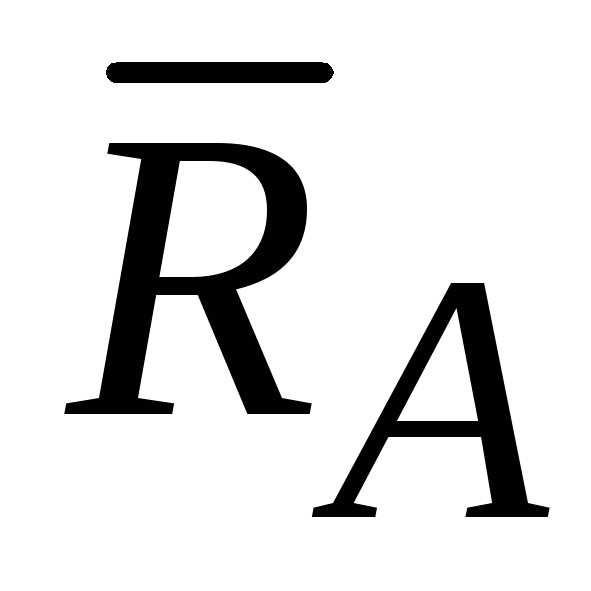 и пары с реактивным моментом заделки
и пары с реактивным моментом заделки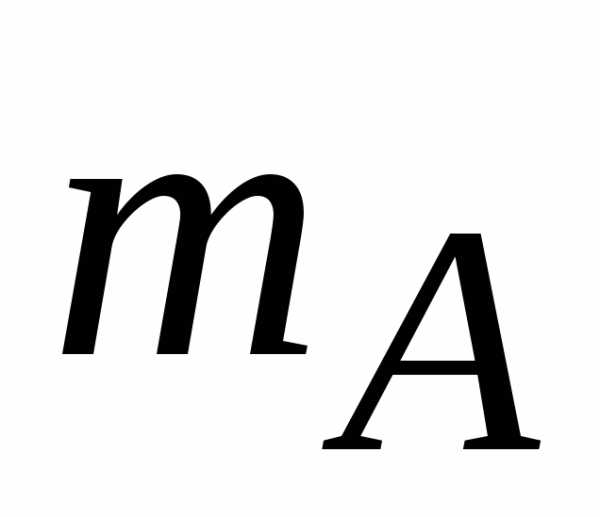 .
Так как направление реакции заделки
.
Так как направление реакции заделки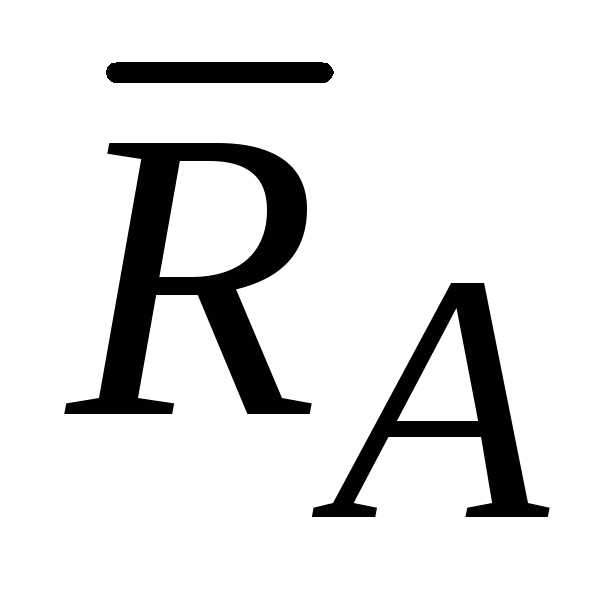 неизвестно, ее обычно раскладывают по
двум взаимно ортогональным направлениям
неизвестно, ее обычно раскладывают по
двум взаимно ортогональным направлениям
.
Рис. 1.11
ЛЕКЦИЯ 2
ТЕОРИЯ ПАРДля решения основной задачи статики – определения условий равновесия твердых тел, находящихся под действием системы сил, необходимо ввести понятия моментов силы.
Момент силы относительно точки
Пусть
на твердое тело в точкеА действует сила  .
Выберем произвольную точку пространстваО и укажем линию действия силы
.
Выберем произвольную точку пространстваО и укажем линию действия силы  .
.
Точка О и линия определяют в пространстве
плоскость. Заштрихуем ее. Восстановим
перпендикуляр к этой плоскости в точке О.
Вдоль этой прямой в точке О направим вектор, который обозначим  направив его в ту сторону, откуда сила
видна, стремящейся повернуть тело, к
которому она приложена против хода
часовой стрелки. Опустим из точки
направив его в ту сторону, откуда сила
видна, стремящейся повернуть тело, к
которому она приложена против хода
часовой стрелки. Опустим из точки
 так, чтобы он равнялся
так, чтобы он равнялся ,
где
,
где назовем плечом силы относительно точкиО.
назовем плечом силы относительно точкиО.Определение. Моментом силы относительно произвольной точки пространства О называют вектор, построенный в точке О перпендикулярно к плоскости, содержащей силу и точку О, направленный в ту сторону, откуда сила видна, стремящейся повернуть тело против хода часовой стрелки и равной произведению модуля силы на ее плечо.
Вектор  зависит как от самой силы
зависит как от самой силы ,
так и от выбора точки О. Это связанный
с точкойО вектор, единицей измерения модуля
которого в системе СИ является Н м= кг
м 2/с2.
,
так и от выбора точки О. Это связанный
с точкойО вектор, единицей измерения модуля
которого в системе СИ является Н м= кг
м 2/с2.
studfiles.net
Вторая группа связей
Ко второй группе относятся связи, по конструктивным особенностям которых ничего нельзя сказать заранее о направлениях реакций. Известна только точка приложения, а искомыми являются неизвестные составляющие силы реакции.
3.3.8 Связь в виде шероховатой поверхности
Пример 1. Тело А находится на шероховатой опорной поверхности (на рисунке 35 а изображено тело А до освобождения от связи).
а) б)
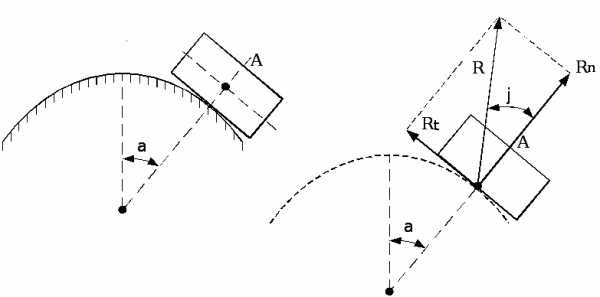
Рис. 35
В этом случае реакция поверхности
Пример 2. На рисунке 36 а изображен стержень АВ веса Р, опирающийся концами на шероховатую поверхность. Кроме веса стержня Р и нормальных реакций опорной поверхности NА и NВ, на стержень действуют силы трения FА и FВ (на рисунке 36 б изображен стержень АВ, освобожденный от связей).
а) б)

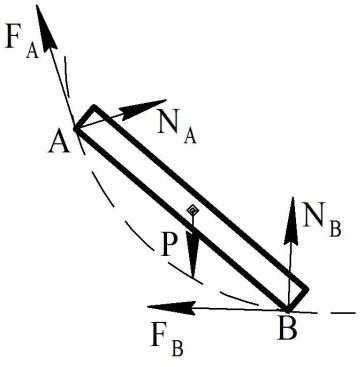
Рис. 36
3.3.9 Шарнирная связь
Решения многих задач статики сводятся к определению реакций опор, с помощью которых закрепляются балки, мостовые фермы и т.д. К ним относятся:
1. Гладкий цилиндрический шарнир или подшипник
(шарнирно-неподвижная опора
В данном случае, цилиндрический шарнир (или просто шарнир) осуществляет такое соединение двух тел, при котором одно тело может вращаться по отношению к другому вокруг общей оси называемой осью шарнира (например, как две половины ножниц).
По своей конструкции цилиндрический шарнир представляет собой опирание цилиндрического стержня (на рисунке 37 а и б его сечение залито и заштриховано, ось цилиндра перпендикулярна плоскости чертежа) на внутреннюю поверхность цилиндрического отверстия тела А.
Соприкосновение этих тел происходит по какой-либо образующей цилиндрической поверхности, которая в сечении, перпендикулярном оси цилиндра, проектируется в «точку контакта» В (рис. 37 б). Реакция связи (на рисунке 37 а левое тело считаем связью для правого) проходит через ось шарнира и располагается в плоскости, перпендикулярной этой оси. Так как в зависимости от действующих сил «точка контакта» цилиндрических поверхностей тел будет меняться, то для реакции R в этом случае не известны ни её модуль (R), ни её направление (рис. 37 б). Поэтому при освобождении тела от шарнирной связи реакцию RА раскладывают на две составляющие XА и YА, параллельные осям координат в плоскости, перпендикулярной оси шарнира.
В процессе решения задачи эти составляющие всегда направляем в сторону положительного направления осей; если в результате решения задачи для XА и YА получатся отрицательные значения, то это означает, что в действительности составляющие реакции направлены в стороны, противоположные направлению осей координат. По составляющим
; 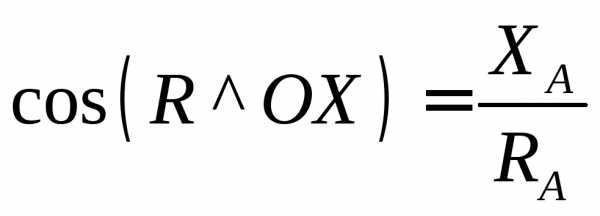 ;
; 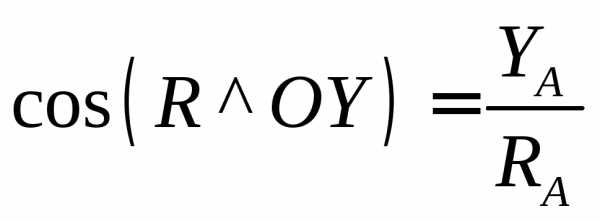 .
.
На рисунке 38 а показан цилиндрический шарнир (подшипник) В, ось которого совпадает с осью y.
а) б)

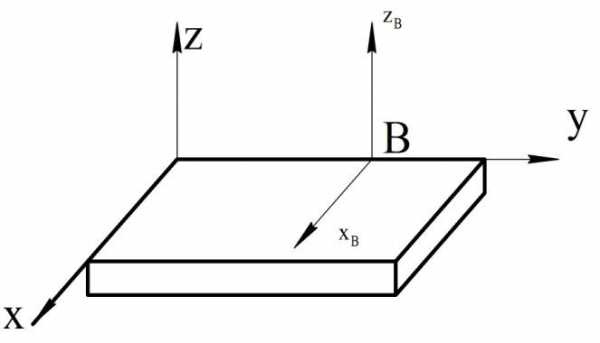
Рис. 38
Подшипник В препятствует повороту тела вокруг осей x и z и не препятствует вращению тела вокруг оси y и скольжению вдоль этой оси. Если трением пренебречь, то реакция RВ подшипника (реакция цилиндрической поверхности его стенок) пересекает ось вращения тела и лежит в плоскости, перпендикулярной к этой оси (ХВ и ZВ – составляющие этой реакции, рис. 38 б). Так как подшипник не препятствует скольжению тела вдоль оси вращения, то нет и реакции, направленной вдоль этой оси.
Модуль и направление полной реакции определяется аналогично.
studfiles.net
Гладкий цилиндрический шарнир или подшипник
⇐ ПредыдущаяСтр 8 из 9Следующая ⇒
(шарнирно-неподвижная опора, плоский случай)
В данном случае, цилиндрический шарнир (или просто шарнир) осуществляет такое соединение двух тел, при котором одно тело может вращаться по отношению к другому вокруг общей оси называемой осью шарнира (например, как две половины ножниц).
По своей конструкции цилиндрический шарнир представляет собой опирание цилиндрического стержня (на рисунке 37 а и б его сечение залито и заштриховано, ось цилиндра перпендикулярна плоскости чертежа) на внутреннюю поверхность цилиндрического отверстия тела А.
Соприкосновение этих тел происходит по какой-либо образующей цилиндрической поверхности, которая в сечении, перпендикулярном оси цилиндра, проектируется в «точку контакта» В (рис. 37 б). Реакция связи (на рисунке 37 а левое тело считаем связью для правого) проходит через ось шарнира и располагается в плоскости, перпендикулярной этой оси. Так как в зависимости от действующих сил «точка контакта» цилиндрических поверхностей тел будет меняться, то для реакции Rв этом случае не известны ни её модуль (R), ни её направление (рис. 37 б). Поэтомупри освобождении тела от шарнирной связи реакцию RА раскладывают на две составляющие XА и YА, параллельные осям координат в плоскости, перпендикулярной оси шарнира.
В процессе решения задачи эти составляющие всегда направляем в сторону положительного направления осей; если в результате решения задачи для XАиYА получатся отрицательные значения, то это означает, что в действительности составляющие реакции направлены в стороны, противоположные направлению осей координат. По составляющим XАиYА находят модуль и направление полной реакции:
; ; .
На рисунке 38 а показан цилиндрический шарнир (подшипник) В, ось которого совпадает с осью y.
а) б)
Рис. 38
Подшипник Впрепятствует повороту тела вокруг осей x и z и не препятствует вращению тела вокруг оси y и скольжению вдоль этой оси. Если трением пренебречь, то реакция RВподшипника (реакция цилиндрической поверхности его стенок) пересекает ось вращения тела и лежит в плоскости, перпендикулярной к этой оси (ХВ и ZВ – составляющие этой реакции, рис. 38 б). Так как подшипник не препятствует скольжению тела вдоль оси вращения, то нет и реакции, направленной вдоль этой оси.
Модуль и направление полной реакции определяется аналогично.
2. Сферический шарнир(пространственный случай)
Для свободного твердого тела не возникает никаких ограничений на повороты тела относительно любой оси и его перемещений вдоль этих осей. В этом случае для какой-либо точки тела (А), связанной с осями координат x, y и z, будем иметь: XА = 0; YА= 0; ZА = 0; МAx = 0; МAy = 0; МAz = 0,
где XА, YАи ZА– проекции реакции RA,
МAx , МAyи МAz– проекции опорного момента МА.
Если твердое тело закреплено на сферической шарнирной опоре, то такая опора не накладывает никаких ограничений на повороты тела относительно любой оси, поэтому составляющие проекции опорного момента остаются равными нулю: МАх = МАу = МАz = 0.
Решение вопроса о том, какие из составляющих реакции RА тождественно равны нулю, а какие не равны нулю и являются неизвестными, зависит от свойств кинематического закрепления основания опоры.
Классическим примером такой опоры является шаровой шарнир (рис. 39): шар вставлен в обойму, обойма закреплена неподвижно, а с шаром жестко соединено тело балки или некоторой конструкции. Поверхности шара и обоймы обычно полагаются идеальными.
Реакция такой опоры RА проходит через центр шара, её величина и направление неизвестны, поэтому при решении практических задач её разлагают на три составляющих XА, YАи ZА, направляя их в сторону осей х, y и z. Все три проекции реакции RА в общем случае будут не равны нулю:
XА ≠ 0; YА ≠ 0; ZА ≠ 0.
Модуль этой реакции определяют по формуле:
Рис. 39
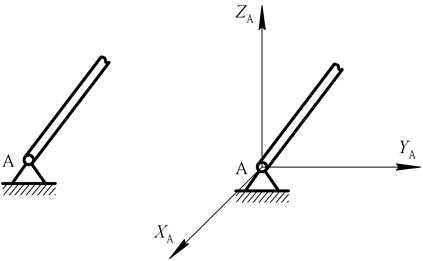
Рис. 40
На рисунке 40 показано условное обозначение неподвижной сферической шарнирной опоры и направления ее реакций связей.
3. Подпятники
Подпятник А представляет собой соединение цилиндрического шарнира с опорной плоскостью, препятствующей осевым перемещениям тел (рис. 41). Подпятник служит для укрепления пяты стойки и допускает только одно поворотное движение тела, а именно вращение этого тела вокруг оси стойки.
Рис. 41
Основание подпятника препятствует перемещению тела по вертикали вниз (вдоль оси стойки), а стенки подпятника препятствуют перемещению тела в плоскости, перпендикулярной к оси стойки.
Реакции подпятника направляются также, как и реакции сферического шарнира; однако следует иметь в виду, что составляющая ZА, действующая вдоль оси подпятника, может быть направлена только к телу.
Для подпятника, показанного на рисунке 42 в плоской системе сил, реакцию связи нужно разложить на две составляющие ХА и YА.
Рис. 42
Рекомендуемые страницы:
lektsia.com
ШАРНИР ЦИЛИНДРИЧЕСКИЙ — это… Что такое ШАРНИР ЦИЛИНДРИЧЕСКИЙ?
- ШАРНИР ЦИЛИНДРИЧЕСКИЙ
- шарнир, допускающий поворот соединяемых элементов вокруг определённой оси
(Болгарский язык; Български) — цилиндрична става
(Чешский язык; Čeština) — neposuvný [pevný] válcový kloub
(Немецкий язык; Deutsch) — Zapfengelenk
(Венгерский язык; Magyar) — görgő csukló
(Монгольский язык) — бортгон нугас
(Польский язык; Polska) — przegub walcowy
(Румынский язык; Român) — articulaţie cilindrică
(Сербско-хорватский язык; Српски језик; Hrvatski jezik) — cilindrični zglob
(Испанский язык; Español) — articulación cilindrica
(Английский язык; English) — cylindrical hinge
(Французский язык; Français) — charnière cylindrique
Источник: Терминологический словарь по строительству на 12 языках
Строительный словарь.
- ШАРНИР ПЛАСТИЧЕСКИЙ
- ШАТЁР
Смотреть что такое «ШАРНИР ЦИЛИНДРИЧЕСКИЙ» в других словарях:
шарнир цилиндрический — Шарнир, допускающий поворот соединяемых элементов вокруг определённой оси [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики строительная механика, сопротивление материалов EN cylindrical hinge DE… … Справочник технического переводчика
шарнир — подвижное соединение двух деталей, которые могут совершать относительное вращение вокруг оси (цилиндрический шарнир) или вокруг точки (шаровой шарнир). Цилиндрический шарнир представляет собой вал, вращающийся в подшипнике скольжения или качения; … Энциклопедия техники
Шарнир — [hinge] подвижное соединение двух тел, при которых их относительное движение вращение вокруг оси (цилиндрический шарнир) или вокруг точки (шаровой шарнир). Цилиндрический шарнир в механизмах называется вращательной кинетической парой и… … Энциклопедический словарь по металлургии
Шарнир — Цилиндрический шарнир Шарнир (нем. Scharnier, от фр. charniere, от лат. c … Википедия
Шарнир — (нем. Scharnier, от франц. charniere, от лат. cardo дверная петля) подвижное соединение двух тел, при котором их относительное движение есть вращение вокруг оси (цилиндрический Ш.) или вокруг точки (шаровой Ш.). Цилиндрический Ш. в… … Большая советская энциклопедия
Кинематическая пара — … Википедия
Суста́вы — (articulationes; синоним сочленения) подвижные соединения костей скелета, которые участвуют в перемещении отдельных костных рычагов относительно друг друга, в локомоции (передвижении) тела в пространстве и сохранении его положения. Различают… … Медицинская энциклопедия
Теория механизмов и машин — Теория машин и механизмов (ТММ) это научная дисциплина об общих методах исследования, построения, кинематики и динамики механизмов и машин и о научных основах их проектирования. Содержание 1 История развития дисциплины 2 Основные понятия … Википедия
ГОСТ 23537-79: Лопатки авиационных осевых компрессоров и турбин. Термины и определения — Терминология ГОСТ 23537 79: Лопатки авиационных осевых компрессоров и турбин. Термины и определения оригинал документа: Антивибрационная полка Ндп. Бандажная полка пера Определения термина из разных документов: Антивибрационная полка 21.… … Словарь-справочник терминов нормативно-технической документации
МУФТОВЫЕ СОЕДИНЕНИЯ — устройства, соединяющие концы двух валов с целью передачи вращения. МЕХАНИЧЕСКИЕ СОЕДИНИТЕЛЬНЫЕ МУФТЫ Механические соединительные муфты это постоянные разъемные соединения. Очень длинные валы, например гребные валы судов, разделяют на секции,… … Энциклопедия Кольера
dic.academic.ru
Шарнир цилиндрический
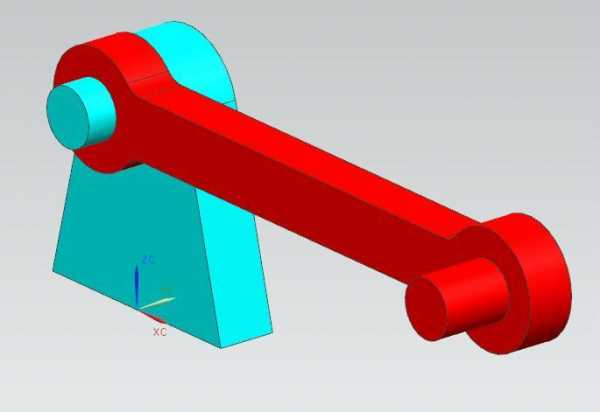


Рис.40 рис.41 рис.42 рис.43 рис.44
Шарнир вращательный (рис.40) отличается от шарнирацилиндрического (рис.41) тем, что первый имеет толькоодну степеньсвободы — вращение вокруг указанной оси, а второй имеетдве степенисвободы: вращение вокруг оси, и перемещение вдоль оси.
Диалоговое окно цилиндрического шарнира почти такое же (рис.42). Также, если одно тело вращается относительно неподвижного основания, то поле Базовыйможно не заполнять.
А вот на закладке Движитель(рис.43) для этой связи можно задать перемещение и вокруг указанной оси вращения, и вдоль этой оси.
Представление строки данной кинематической пары в навигаторе перемещений, в разделе Jointsпоказано на рис.44 (строкаJ002).
Попробуйте самостоятельно выполнить несложный пример с цилиндрическимшарниром (рис.41).
Винтовая пара

Рис.45 рис.47 рис.48 рис.49
При оформлении Винтовой пары(рис.47) в диалоговом окне вы обычным способом должны указать только гайку (поскольку вал неподвижен),задать привязку(произвольную точку), иуказать ориентацию(ось вращения гайки относительно вала).
И ещё в нижней части этого окна вы должны указать Отношение винтарис.48. Это отношение показывает — насколько миллиметров в длину переместится гайка за один её поворот.
Представление строки данной кинематической пары в навигаторе перемещений, в разделе Jointsпоказано на рис.49 ( строкаJ003).
Попробуйте самостоятельно выполнить несложный пример с винтовой парой(рис.45). Исходные данные для этого примера возьмите из учебной директорииPrim_Vint.
Универсальный узел (кардан)
Пример данного соединения показан на рис.50, 51. Это так называемое карданное соединение, обеспечивающее для ответной детали кардана сложное перемещение в двух плоскостях.
Ещё на этапе создания статической сборки важно задать нужные ограничения сборки, чтобы правильно ориентировать обе детали кардана. А именно, оси обеих половинок карданного механизма (рис.52) должны быть перпендикулярны друг другу, и пересекаться строго посередине. Для достижения этого эффекта можно, например, использовать соответствующие ссылочные наборы.
Строка Универсального узлав навигаторе перемещений показана на рис. 53 (J002). Диалоговое окно такой кинематической пары представлено на рис. 54. Обратите внимание на то, что в этойсвязиможно задать только трение.
В диалоговом окне (рис.54) нет ничего необычного, но здесь важно правильно указывать соединяемые тела. Есть некоторые особенности:
Первое звено указываем с помощью его ребра, направленноговдоль осикардана (рис.55), ив обратную сторонуот кардана (будущая ось Х).
Точку привязки задаём как середину между парой отверстий (рис.56, 57). Это будет центр кардана.
Ориентацию – вдоль оси кардана и опять в обратную сторону. Это будет ось Х первой половины кардана .
При указании второго звена обратите внимание на то, что в диалоговом окне для второго звена выделено два поля: звено и ориентация (рис.54).


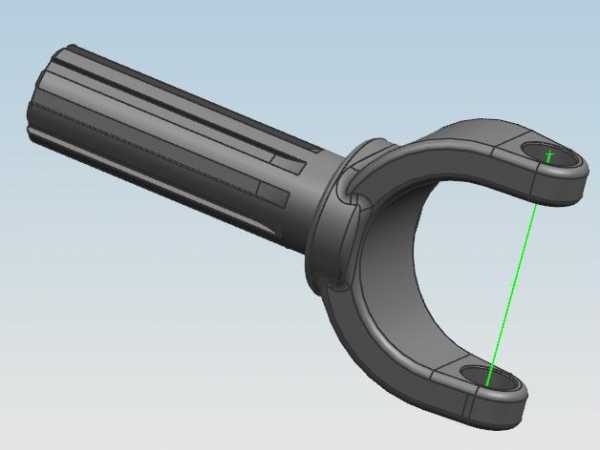
Рис.50 рис.51 рис.52 рис.53 рис.54

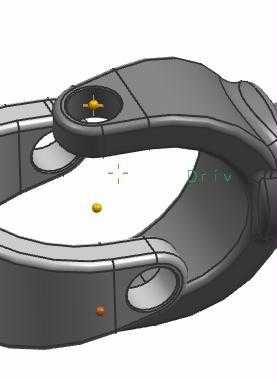

рис.55 рис.56 рис.57 рис.58
При указании второго звена мы укажем грань соответствующего отверстия (рис.59). Система поймет, что это грань отверстия, ось которого определит основание второй «чашки».
А ориентацию второго звена нужно указать как на рис.60. В итоге оси Х обеих «чашек» должны указывать в противоположные стороны (рис.60).


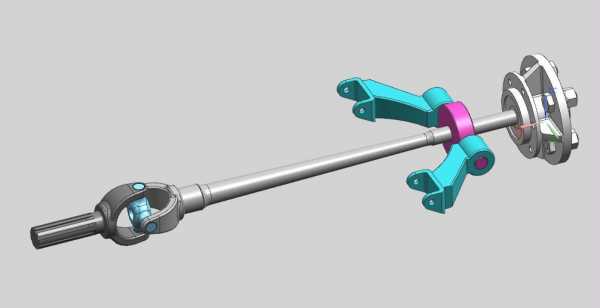
рис.59 рис.60 рис.61 рис.62
Пример
Повторите из учебной директории пример Prim_Kardan(рис.61). В этой директории присутствуют все необходимые детали и готоваястатическая сборка. Загрузите сразу готовуюстатическую сборку.
Навигатор сборки этого механизма показан на рис.62. Здесь включены:
Вращательный шарнир между левым (ведущим) звеном кардана и неподвижным основанием (рис.63). У этого шарнира включен постоянный движитель со скоростью 300 град / сек.;
Вращательный шарнир между голубой скобой и неподвижным основанием (рис.64). У этого шарнира включен гармонический движитель с параметрами, представленными на рис.65;
Вращательный шарнир между голубой скобой и малиновым звеном;
Цилиндрический шарнир между малиновым звеном и ведомым звеном кардана;
Универсальный шарнир между ведущим и ведомым звеньями кардана.
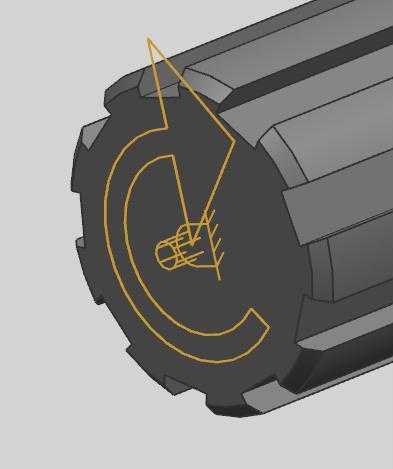
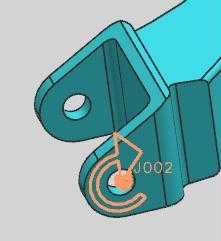
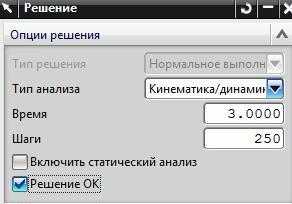
Рис.63 рис.64 рис.65 рис.66
studfiles.net
Цилиндрический шарнир
По умолчанию КЭ оболочки (стены и плиты) сопрягаются друг с другом жестко.
Для моделирования шарнирного опирания плиты перекрытия на стены необходимо создать цилиндрический шарнир помощью функции объединение перемещений – создать шарнир с расшивкой узлов
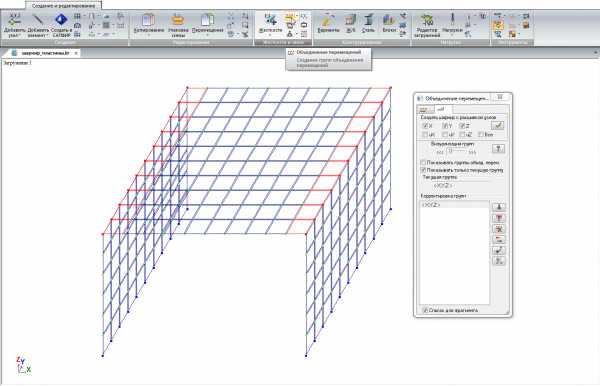
Шарнир в пластинах алгоритмически организуется при помощи расшивки схемы по соответствующей линии узлов, как правило, ориентированной вдоль одной из осей глобальной системы координат. Расшивка сопровождается раздвоением узлов на линии расшивки (в одних и тех же координатах появляется по два узла). Чтобы не допустить полного нарушения совместности, новым узлам должно быть дано указание, к каким именно элементам они должны принадлежать.
В связи с этим моделирование шарнира в пластине рекомендуется производить в следующем порядке:
- Отметить на схеме узлы, лежащие на линии расшивки.
- Отметить на схеме элементы, которым должны принадлежать новые узлы (элементы, примыкающие к отмеченным узлам).
- Создать для линии узлов расшивки группу объединения соответствующих перемещений и с помощью установки соответствующих флажков зафиксировать нужные перемещения -X, Y, Z, UX, UY, UZ. Так, например, если на линии расшивки необходимо создать шарнир вокруг оси Y, то в группу объединения войдут все перемещения, кроме UY.
- Занести созданную группу в поле ввода текущей группы и в поле накопления групп при помощи команды Применить.
В результате выполнения команды произойдет раздвоение всех узлов на линии стыка. Узлы с большими номерами будут принадлежать отмеченным ранее элементам.
Мозаика изгибающих моментов в КЭ(справа схема с созданным шарниром)
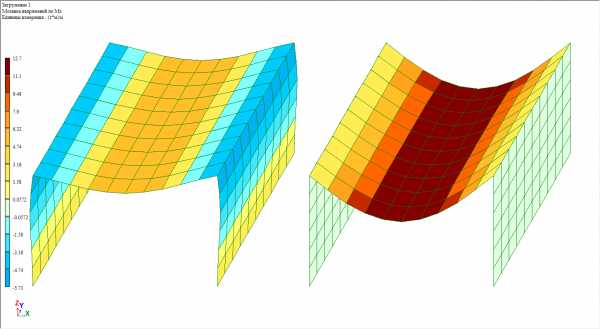
Используя объединение перемещений, не забывайте во время упаковки указывать «Не сшивать узлы с объединением перемещений»
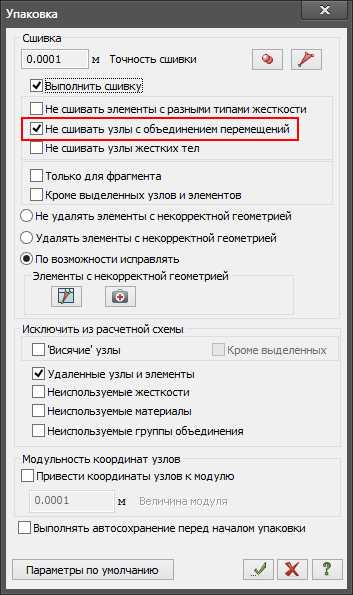
rflira.ru
2) Цилиндрический шарнир (рис. 1.6)
Вцилиндрическое отверстие телаТ вставляется цилиндрический болт
(заштрихован) несколько меньшего
диаметра, чем отверстие. Тело Т может вращаться вокруг оси болта. Реакция  цилиндрического шарнира лежит в
плоскости, перпендикулярной оси болта,
проходит через центр болта и точку
касания с телом. Таким образом, направление
реакции
цилиндрического шарнира лежит в
плоскости, перпендикулярной оси болта,
проходит через центр болта и точку
касания с телом. Таким образом, направление
реакции неизвестно и определяется в зависимости
от приложенных к телу сил. Часто, чтобы
не вводить неизвестный угол,
определяющий направление реакции
неизвестно и определяется в зависимости
от приложенных к телу сил. Часто, чтобы
не вводить неизвестный угол,
определяющий направление реакции  ,
ее заменяют двумя другими составляющими
по взаимно ортогональным направлениям:
,
ее заменяют двумя другими составляющими
по взаимно ортогональным направлениям:
.
Цилиндрическая шарнирно-подвижная опора (подвижной каток) (рис. 1. 7)
Тело Т опирается на гладкую поверхность через
шарнир, поставленный на катки. Реакция  шарнирно-подвижной опоры направлена
перпендикулярно опорной поверхности.
шарнирно-подвижной опоры направлена
перпендикулярно опорной поверхности.
4) Цилиндрическая шарнирно-неподвиж-ная опора (рис. 1.8)
ТелоТ прикреплено с помощью шарнира к
неподвижной поверхности. Направление
реакции  опоры может быть любым, в зависимости
от приложенных сил. Как и в случае 2),
чтобы не вводить неизвестный угол,
реакцию
опоры может быть любым, в зависимости
от приложенных сил. Как и в случае 2),
чтобы не вводить неизвестный угол,
реакцию  раскладывают по двум взаимно ортогональным
направлениям.
раскладывают по двум взаимно ортогональным
направлениям.
5) Гибкая нерастяжимая нить (рис. 1.9)
Реакция
нити  ,
называемая натяжением нити, направлена
вдоль нити к точке подвеса.
,
называемая натяжением нити, направлена
вдоль нити к точке подвеса.
6) Невесомый шарнирно-закрепленный на концах стержень (рис. 1.10)
Реакция  невесомого стержня направлена вдоль
стержня. При этом стержень может быть
как сжат, и тогда реакция стержня
направлена от стержня к телу
невесомого стержня направлена вдоль
стержня. При этом стержень может быть
как сжат, и тогда реакция стержня
направлена от стержня к телу ,
так и растянут. Тогда реакция стержня
направлена в сторону от тела к стержню
,
так и растянут. Тогда реакция стержня
направлена в сторону от тела к стержню .
.
7) Жесткая заделка (рис. 1.11)
Конец
балки АВ жестко заделан в стену. При нагрузке на
балку в заделке возникают реакции,
состоящие из реакции заделки  и пары с реактивным моментом заделки
и пары с реактивным моментом заделки .
Так как направление реакции заделки
.
Так как направление реакции заделки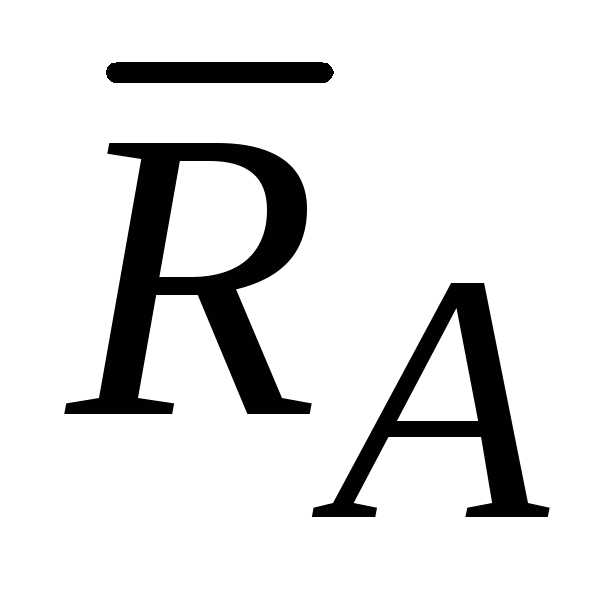 неизвестно, ее обычно раскладывают по
двум взаимно ортогональным направлениям:
неизвестно, ее обычно раскладывают по
двум взаимно ортогональным направлениям:
.
Моменты сил. Главный вектор и главный момент системы сил
Для решения основной задачи статики – определение условий равновесия твердых тел, находящихся под действием системы сил, необходимо ввести понятия моментов силы.
Момент
силы  относительно произвольной точки О,
обозначаемый
относительно произвольной точки О,
обозначаемый 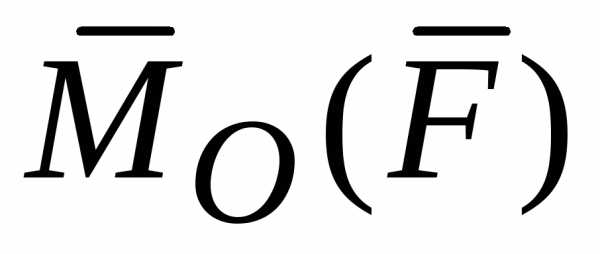 ,
определяется как вектор, равный векторному
произведению
,
определяется как вектор, равный векторному
произведению
,
где  — радиус-вектор точки приложения силыА относительно точки О (рис. 1.12).
— радиус-вектор точки приложения силыА относительно точки О (рис. 1.12).
Модуль момента силы относительно точки О вычисляется по формуле
,
где
длина перпендикуляра h,
опущенного из точки О на линию действия силы, называется плечом
силы.
Направление вектора  определяется по правилу векторного
произведения.
определяется по правилу векторного
произведения.
Момент
силы  относительно осиl,
обозначаемый
относительно осиl,
обозначаемый 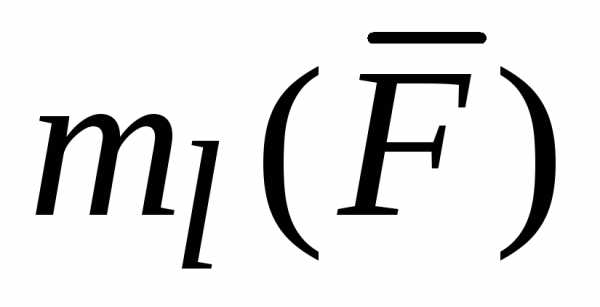 ,
— это скалярная величина, равная
произведению модуля проекции силы
,
— это скалярная величина, равная
произведению модуля проекции силы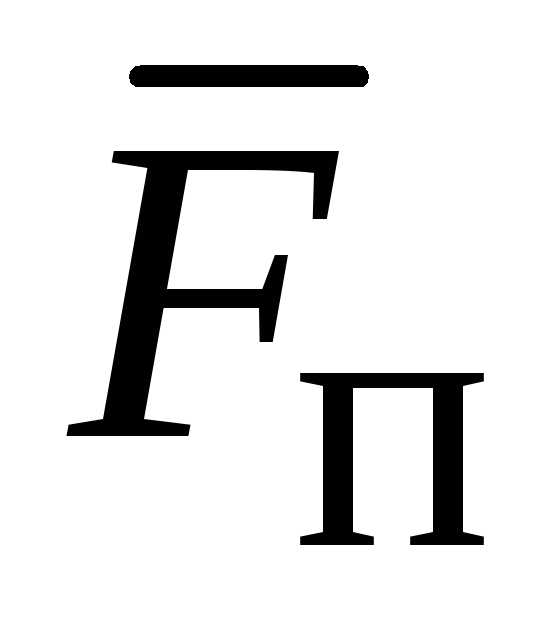 (рис. 1.13) на плоскость П, перпендикулярную
осиl,
на плечо hп этой проекции относительно точки О пересечения оси и плоскости, взятая со
знаком плюс при стремлении силы повернуть
тело, к которому она приложена, против
хода часовой стрелки и со знаком минус
– в противоположном случае, если смотреть
с конца оси.
(рис. 1.13) на плоскость П, перпендикулярную
осиl,
на плечо hп этой проекции относительно точки О пересечения оси и плоскости, взятая со
знаком плюс при стремлении силы повернуть
тело, к которому она приложена, против
хода часовой стрелки и со знаком минус
– в противоположном случае, если смотреть
с конца оси.
Из формулы (1.1) видно, что момент силы относительно оси равен нулю, если либо сила параллельна оси (Fп = 0), либо сила пересекает ось (hп = 0).
(1.1)
Существует связь между моментом силы относительно точки О и моментом силы относительно оси, проходящей через эту точку: момент силы относительно оси равен проекции момента силы относительно точки оси на эту ось.
Главным вектором системы сил называется вектор, равный геометрической сумме векторов всех сил системы. Главный вектор не является силой. Это свободный вектор, полученный формальным сложением перенесенных в любую точку векторов сил системы:
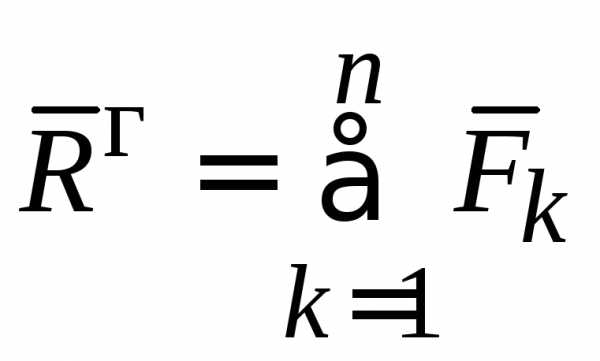 .
.
(1.2)
Главным моментом системы сил относительно некоторой точки О называется приложенный в этой точке вектор, равный геометрической сумме моментов всех сил системы относительно этой точки:
 .
.
(1.3)
studfiles.net