Составные балки и перемещения при изгибе (Лекция №21)

ПОНЯТИЕ О СОСТАВНЫХ БАЛКАХ

   Работу составных балок проиллюстрируем на простом примере трехслойной балки прямоугольного поперечного сечения. Если слои между собой не связаны и силы трения между ними отсутствуют, то каждый из них деформируется как отдельная балка, имеющая свой нейтральный слой (рис. 1, а). Нагрузка между этими балками распределяется пропорционально их жесткостям при изгибе (в данном примере поровну). Это означает, что моменты инерции и моменты сопротивления трех независимо друг от друга деформирующихся балок должны быть просуммированы

   Если скрепить балки сваркой, болтами или другим способом (рис. 1, б), то с точностью до пренебрежения податливостью наложенных связей сечение балки будет работать как монолитное с моментом инерции и моментом сопротивления, равным

   Как видно, при переходе к монолитному сечению жесткость балки возрастает в девять раз, а прочность—в три раза.

В инженерной практике наиболее распространены сварные двутавровые балки.

б)

а) несвязанная конструкция, б) связанная сварная конструкция
Рис.1. Расчетные схемы составных балок:

 

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПРЯМОГО ИЗГИБА ПРИЗМАТИЧЕСКОГО СТЕРЖНЯ

   Определено, что мерой деформации призматического стержня при прямом чистом изгибе является кривизна нейтрального слоя. Можно показать, что с достаточной для инженерных расчетов точностью этим тезисом можно пользоваться и в случае прямого поперечного изгиба стержня. Однако для практических целей кроме кривизны необходимо определить вертикальные перемещения центров тяжести отдельных поперечных сечений — прогибов балки v, а иногда и углы поворота этих сечений (рис. 2). Вследствие гипотезы плоских сечений угол поворота сечения ( оказывается равным углу наклона касательной к изогнутой оси балки, который в силу малости

(1)

   Тогда возникает геометрическая задача: составить уравнение для функции прогиба , зная закон изменения ее кривизны.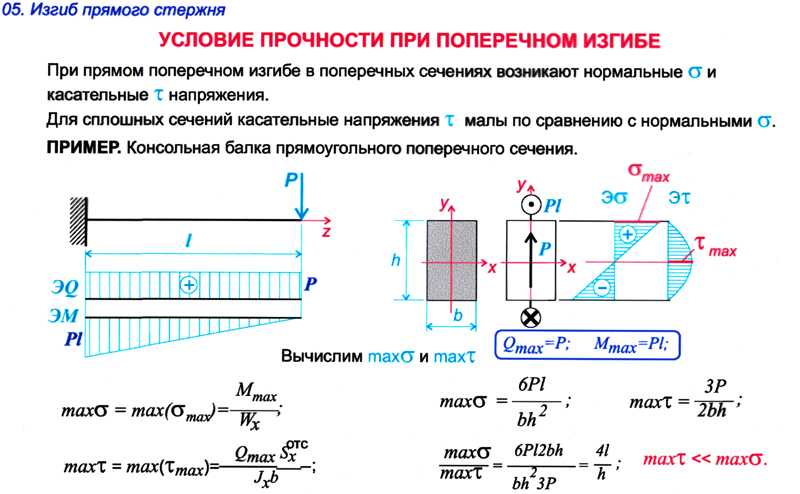

Рис.2. Расчетная схема определения перемещений при изгибе

 

   Воспользуемся известным из дифференциальной геометрии выражением для кривизны в прямоугольных декартовых координатах:

(2)

   Однако, учитывая, что в инженерной практике применяются достаточно жесткие балки, для которых наибольший прогиб f (рис.2) мал по сравнению с длиной (

f / l << 1), а первая производная от прогиба имеет порядок

и, следовательно, величиной (dv / dz)²<<1, стоящей в знаменателе (2), можно пренебречь, выражение для кривизны упрощается

(3)

   Тогда, подставив это выражение в полученную ранее связку кривизны и изгибающего мометна — , условившись что ось Oy направлена вверх и согласовав знаки и М_х, приходим к дифференциальному уравнению прямого изгиба балки

(4)

известному также как дифференциальное уравнение упругой кривой.

Если учесть точное выражение для кривизны по формуле (2), то точное уравнение упругой кривой

является нелинейным дифференциальным уравнением. Поэтому линейное дифференциальное уравнение, описывающее малые прогибы балки, иногда называют линеаризованным уравнением упругой кривой.

   Решение уравнения получаем путем двукратного почленного интегрирования. При первом интегрировании получаем выражение

(5)

которое с учетом , дает также закон изменения углов поворота поперечных сечений по длине балки. Повторным интегрированием получаем функцию прогиба

(6)

Постоянные интегрирования С и D должны быть найдены из граничных условий.

   Во всех приведенных выше уравнениях функция изгибающего момента

М_х(г) предполагалась известной, что возможно лишь для статически определимых балок. Простейшие варианты статически определимых однопролетных балок и соответствующие граничные условия показаны на рис. 3. Условия, накладываемые на прогиб и угол поворота сечения, получили название кинематических граничных условий. Как видно, для шарнирно опертой балки требуется, чтобы прогиб на опорах v(0) =v(l) =0, а для консольной балки прогиб и угол поворота сечения в заделке

Рис.3. Примеры граничных условий: а) двухопорная, б) консольная балки

 

   Дифференциальное уравнение неприменимо для расчета статически неопределимых балок, так как содержит неизвестный изгибающий момент М_x появившийся в результате двукратного интегрирования уравнения четвертого порядка

(7)

В этом уравнении нагрузка q известна, поэтому его можно получить, учитывая, что

   При интегрировании уравнения необходимо задать четыре граничных условия (по два на каждом конце балки) в том числе так называемые силовые граничные условия — условия, накладываемые на силовые величины (изгибающий момент и поперечную силу), которые выражаются через производные от прогиба. Так как

а с учетом дифференциального соотношения Q_y=dM_x/dz, получаем

(8)

   Вернемся к интегрированию уравнения второго порядка. Если имеется несколько участков, для которых правая часть уравнения исходного

f(z)=M_x/EJ_x, содержит разные аналитические выражения, то интегрирование усложняется. На рис. 4 приведена эпюра М_x, содержащая п участков. Для каждого участка независимое интегрирование дает по две константы, а при п участках требуется определить 2n постоянных. Добавляя к двум граничным условиям на опорах 2(n—1) условия непрерывности и гладкости упругой кривой на границе; смежных участков, заключающиеся в равенстве прогибов v и углов поворота сечений dv/dz на этих границах

получим 2п граничных условий, необходимых для нахождения постоянных интегрирования.

Рис.4. Расчетная схема балки, содержащая n

углов

 

   Рекомендую для практики решения дифференциальных уравнений второго порядка воспользоваться системой входных тестов Т-4, приведенных в ПРИЛОЖЕНИИ.

Дальше…

Сопромат чистый изгиб

 

 

Основные положения, характеризующие деформацию чистого изгиба

 

Заказать решение

 

Исследование напряженного состояния балок мы начнем с простейшего случая, так называемого чистого изгиба.

Чистый изгиб есть частный случай изгиба, при котором в сечениях балки поперечная сила равна нулю. Чистый изгиб может иметь место только в том случае, когда собственный вес балки настолько мал, что его влиянием можно пренебречь. Для балок на двух опорах примеры нагрузок, вызывающих чистый

 

 

 

изгиб, представлены на рис. 88. На участках этих балок, где Q = 0 и, следовательно, М= const; имеет место чистый изгиб.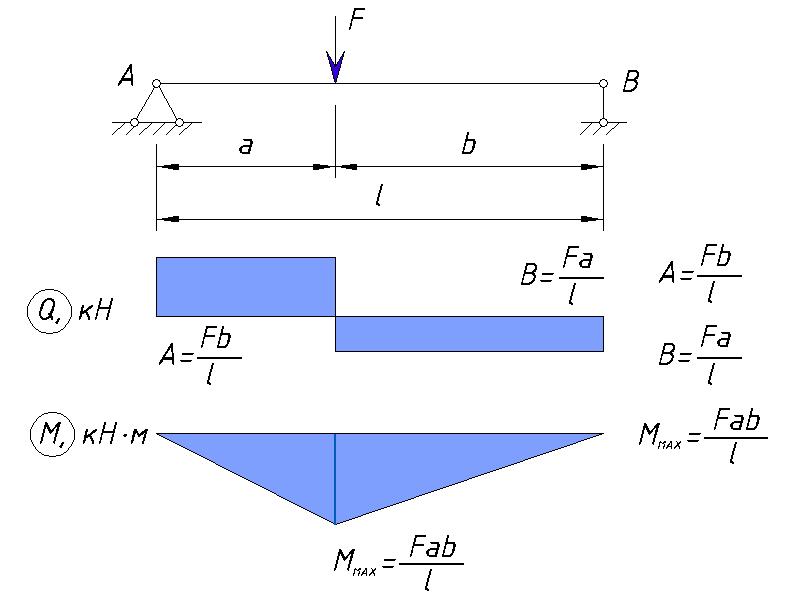

 

Усилия в любом сечении балки при чистом изгибе сводятся к паре сил, плоскость действия которой проходит через ось бал­ки, а момент постоянен.

 

Напряжения могут быть определены на основании следую­щих соображений.

 

1. Касательные составляющие усилий по элементарным пло­щадкам в поперечном сечении балки не могут быть приведены к паре сил, плоскость действия которой перпендикулярна к пло­скости сечения. Отсюда следует, что изгибающее усилие в сече­нии является результатом действия по элементарным площадкам

лишь нормальных усилий, а потому при чистом изгибе и напряжения сводятся только к нормальным.

 

2.  Чтобы усилия по элементарным площадкам свелись только к паре сил, среди них должны быть как положительные, так и отрицательные. Поэтому должны существовать как растянутые, так и сжатые волокна балки.

 

 

3.  Ввиду того, что усилия в различных сечениях одинаковы, то и напряжения в соответственных точках сечений одинаковы.

 

Рассмотрим какой-либо элемент вблизи поверхности (рис. 89, а). Так как по нижней его грани, совпадающей с по­верхностью балки, силы не приложены, то на ней нет и напря­жений. Поэтому и на верхней грани элемента нет напряжений, так как иначе элемент не находился бы и равновесии, Рассмат­ривая соседний с ним по высоте элемент (рис. 89,б), придем к

 

 

­такому же заключению и т. д. Отсюда следует, что по горизон­тальным граням любого элемента напряжения отсутствуют. Рас­сматривая элементы, входящие в состав горизонтального слоя, начиная с элемента у поверхности балки (рис. 90), придем к за­ключению, что и по боковым вертикальным граням любого эле­мента напряжения отсутствуют. Таким образом, напряженное состояние любого элемента (рис. 91,а), а в пределе и волокна, должно быть представлено так, как это показано на рис. 91,б, т. е. оно может быть либо осевым растяжением, либо осевым сжатием.

 

4. В силу симметрии приложения внешних сил сечение по середине длины балки после деформации должно остаться пло­ским и нормальным к оси балки (рис. 92, а). По этой же причине и сечения в четвертях длины балки тоже остаются плоскими и нормальными к оси балки (рис. 92,б), если только крайние се­чения балки при деформации остаются плоскими и нормальными к оси балки. Аналогичное заключение справедливо и для сечений в восьмых длины балки (рис. 92, в) и т. д. Следовательно, если при изгибе крайние сечения балки остаются плоскими, то и для любого сечения остается

справедли­вым утверждение, что оно после де­формации остается плоским и нор­мальным к оси изогнутой балки. Но в таком случае очевидно, что изменение удлинений волокон балки по ее высоте должно происходить не только непре­рывно, но и монотонно. Если назвать слоем совокупность волокон, имеющих одинаковые удлинения, то из сказан­ного следует, что растянутые и сжатые волокна балки должны располагаться по разные стороны от слоя, в котором удлинения волокон равны нулю. Бу­дем называть волокна, удлинения ко­торых равны нулю, нейтральными; слой, состоящий из нейтральных воло­кон, — нейтральным слоем; линию пе­ресечения нейтрального слоя с плоскостью поперечного сечения балки — нейтральной линией этого сечения. Тогда на основании предыдущих рассуждений можно утверждать, что при чистом изгибе балки в каждом ее сечении имеется нейтральная линия, которая делит это сечение на две части (зоны): зону растяну­тых волокон (растянутую зону) и зону сжатых волокон (сжа­тую зону). Соответственно с этим в точках растянутой зоны се­чения должны действовать нормальные растягивающие напря­жения, в точках сжатой зоны — сжимающие напряжения, а в точках нейтральной линии напряжения равны нулю.

 

Таким образом, при чистом изгибе балки постоянного се­чения:

 

1)  в сечениях действуют только нормальные напряжения;

 

2) все сечение может быть разбито на две части (зоны) — растянутую и сжатую; границей зон является нейтральная линия сечения, в точках которой нормальные напряжения равны нулю;

 

3) любой продольный элемент балки (в пределе любое во­локно) подвергается осевому растяжению или сжатию, так что соседние волокна друг с другом не взаимодействуют;

 

4) если крайние сечения балки при деформации остаются плоскими и нормальными к оси, то и все ее поперечные сечения остаются плоскими и нормальными к оси изогнутой балки.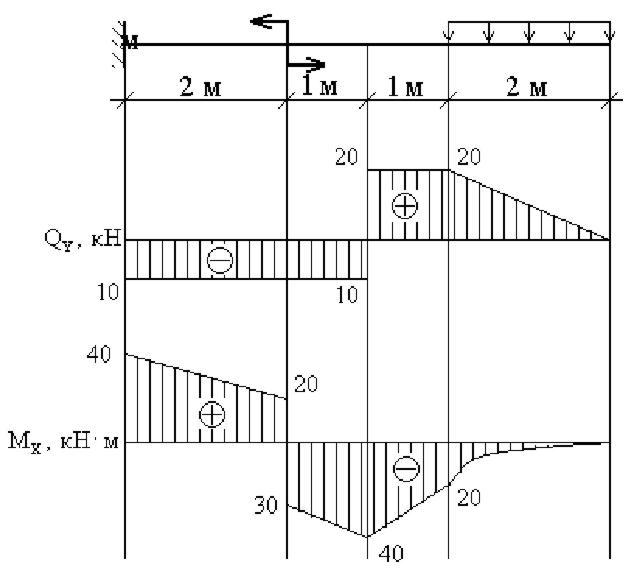

 

Напряженное состояние балки при чистом изгибе

 

Рас­смотрим элемент балки, подверженной чистому изгибу, заклю­ченный между сечениями m— m и n — n, которые отстоят одно от дру­гого на бесконечно малом расстоя­нии dx (рис. 93). Вследствие по­ложения (4) предыдущего пункта, сечения m— m и n — n, бывшие до деформации параллельными, после изгиба, оставаясь плоскими, будут составлять угол dQ и пересекаться по прямой, проходящей через точ­ку С, которая является центром кривизны нейтрального волокна NN. Тогда заключенная между ними часть АВ волокна, находящегося на расстоянии z от нейтрального во­локна (положительное направление оси z принимаем в сторону выпук­лости балки при изгибе), превра­тится после деформации в дугу А’В’.Отрезок нейтрального волокна О1О2, превратившись в дугу О1О2 не изменит своей длины, тогда как волокно АВ получит удлинение:

 

 до деформации

после деформации

где р — радиус кривизны нейтрального волокна.

Поэтому абсолютное удлинение отрезка АВ равно

 

и относительное удлинение

 

 

Так как согласно положению (3) волокно АВ подвергается осевому растяжению, то при упругой деформации

Отсюда видно, что нормальные напряжения по высоте балки распределяются по линейному закону (рис. 94). Так как равно­действующая всех усилий по всем элементарным площадкам се­чения должна равняться нулю, то

                      

откуда, подставляя значение из (5.8), найдем

Но последний интеграл есть статический момент относительно оси Оу, перпендикулярной к плоскости действия изгибающих уси­лий.

Вследствие равен­ства его нулю эта ось должна проходить через центр тяжести О сечения. Тамим образом,нейтраль­ная линия сечения балки есть прямая уу, перпен­дикулярная к плоскости действия изгибающих усилий. Ее называют ней­тральной осью сечения балки. Тогда из (5.8) следует, что напряжения в точках, лежа­щих на одинаковом расстоянии от нейтральной оси, одинаковы.

Случай чистого изгиба, при котором изгибающие усилия действуют только в одной плоскости, вызывая изгиб только в этой плоскости, является плоским чистым изгибом. Если названная плоскость проходит через ось Oz, то момент элементарных уси­лий относительно этой оси должен быть равен нулю, т. е.

Подставляя сюда значение σ из (5.8), находим

Стоящий в левой части этого равенства интеграл, как изве­стно, является центробежным моментом инерции сеченияотноси­тельно осей у и z, так что

Оси, относительно которых центробежный момент инерции сечения равен нулю, называют главными осями инерции этого сечения. Если они, кроме того, проходят через центр тяжести сечения, то их можно назвать главными центральными осями инерции сечения. Таким образом, при плоском чистом изгибе направление плоскости действия изгибающих усилий и нейтраль­ная ось сечения являются главными центральными осями инер­ции последнего. Иными словами, для получения плоского чи­стого изгиба балки нагрузка к ней не может прикладываться произвольно: она должна сводиться к силам, действующим в плоскости, которая проходит через одну из главных центральных осей инерции сечений балки; при этом другая главная централь­ная ось инерции будет являться нейтральной осью сечения.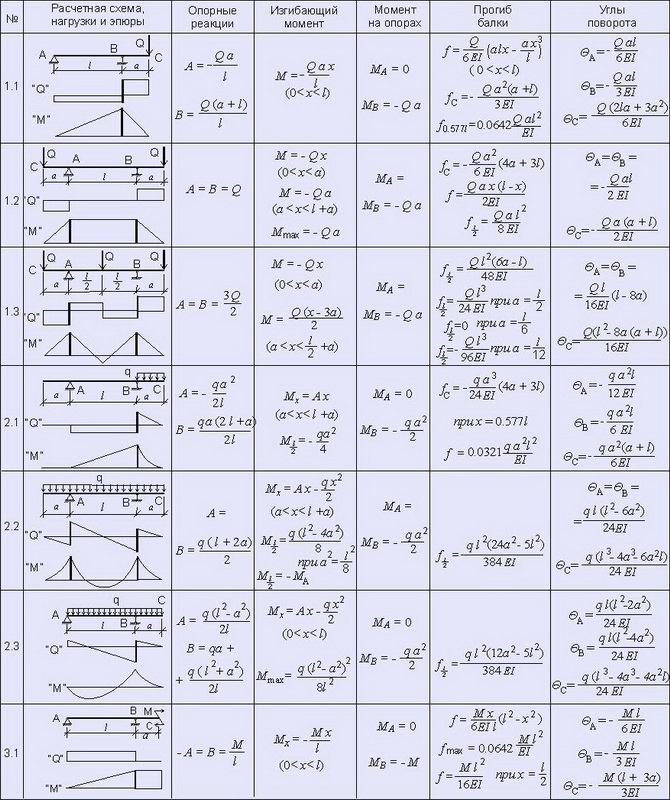

 

Как известно, в случае сечения, симметричного относительно какой-либо оси, ось симметрии является одной из главных цент­ральных осей инерции его. Следовательно, в этом частном случае мы заведомо получим чистый изгиб, приложив соответствующие анагрузки в плоскости, проходящей через продольную ось балки я ось симметрии ее сечения. Прямая, перпендикулярная к оси симметрии и проходящая через центр тяжести сечения, является при этом нейтральной осью этого сечения.

 

Установив положение нейтральной оси, нетрудно найти и ве­личину напряжения в любой точке сечения. В самом деле, так как сумма моментов элементарных усилий относительно нейт­ральной оси уу должна равняться изгибающему моменту, то

откуда, подставляя значение σ из (5.8), найдем

Так как интеграл  является. моментом инерции сечения относительно оси уу, то

и из выражения (5.8) получим

Произведение ЕI_Уназывают жесткостью балки при изгибе.

Наибольшее растягивающее и наибольшее по абсолютной величине сжимающее напряжения действуют в точках сечения, для которых абсолютная величина z наибольшая, т. е. в точках, наиболее удаленных от нейтральной оси. При обозначениях, рис. 95 имеем

 

 

Величину Jy/h2 называют моментом сопротивления сечения рас­тяжению и обозначают Wyр; аналогично, Jy/h3называют моментом сопротивления сечения сжатию

и обозначают Wyc,так что

и поэтому

 

Если нейтральная ось является, осью симметрии сечения, то h2 = h3 = h/2 и, следовательно, Wyp = Wyc, так что их различать нет надобности, и пользуются одним обозначением:

называя W_yпросто моментом сопротивления сечения.Следова­тельно, в случае сечения, симметричного относительно нейтраль­ной оси,

 

Все приведенные выше выводы получены на основании допу­щения, что поперечные сечения балки, при изгибе остаются пло­скими и нормальными к ее оси (гипотеза плоских сечений). Как было показано, это допущение справедливо только в том случае, когда крайние (концевые) сечения балки при изгибе остаются плоскими. С другой стороны, из гипотезы плоских сечений сле­дует, что элементарные усилия в таких сечениях должны распре­деляться по линейному закону. Поэтому для справедливости по­лученной теории плоского чистого изгиба необходимо, чтобы из­гибающие моменты на концах балки были приложены в виде элементарных сил, распределенных по высоте сечения по линей­ному закону (рис. 96), совпадающему с законом распределения напряжений по высоте сечения балки. Однако на основании принципа Сен-Венана можно утверждать, что изменение способа приложения изгибающих моментов на концах балки вызовет лишь местные деформации, влияние которых скажется лишь на некотором расстоянии от этих концов (приблизительно равном высоте сечения). Сечения же, находящиеся во всей остальной части длины балки, останутся плоскими. Следовательно, изложенная теория плоского чистого изгиба при любом способе приложения изгибающих моментов справедлива только в пределах средней части длины балки, находящейся от ее концов на расстояниях, при­близительно равных высоте сечения. Отсюда ясно, что эта тео­рия заведомо неприменима, если высота сечения превосходит половину длины или пролета балки.

Заказать решение

Доступ к en.sopromat.org. Сопротивление материалов онлайн

Доступ en.sopromat.org. Сопротивление материалов онлайн

Первый ответ

515 мс

Ресурсы загружены

1,7 с

Отрисовка страницы

89 мс

О веб-сайте

Добро пожаловать на главную страницу en.sopromat.org. Информация – приготовьтесь ознакомиться с лучшими материалами En Sopromat для России прямо сейчас или после того, как узнаете эти важные сведения о en.sopromat.org

Сопротивление материалов онлайн: расчеты балок онлайн . Рассчитать прогиб балки, изгиб балки, прочность на растяжение, прочность на сдвиг и другие. Рассчитайте балку на прочность с помощью мобильного телефона.

Посетите en.sopromat.org

Ключевые выводы

Мы проанализировали время загрузки страницы En.sopromat.org и обнаружили, что первое время ответа составляло 515 мс, а затем потребовалось 1,8 с, чтобы загрузить все ресурсы DOM и полностью отобразить веб-страницу. Это довольно хороший результат, так как только 30% веб-сайтов могут загружаться быстрее.

имя

значение

оценка

вес

FCP (First Contentful Paint)

Value1.1 s

99/100

10%

0002 LCP (самая большая довольная краска)

Value1,4 S

100/100

25%

SI (индекс скорости)

Значение 2,1 S

99/100

10%

TBT (общая блокировка

Значение 360 мс

72/100

30%

CLS (сдвиг совокупного макета). с

100/100

10%

en.sopromat.org

515 мс

ourigine_style.css

257 MS

Watch.js

1 MS

B1.gif

791 MS

. сделал в общей сложности 7 запросов на загрузку всех элементов на главной странице. Выяснилось, что 71% из них (5 запросов) были адресованы оригинальному En.sopromat.org, 14% (1 запрос) — Mc.yandex.ru и 14% (1 запрос) — Top100-images. rambler.ru. Менее отзывчивый или самый медленный элемент, загрузка которого заняла больше всего времени (791 мс) относится к внешнему источнику Top100-images.

rambler.ru.

Размер содержимого

23,2 КБ

После оптимизации

14,5 кБ

На самом деле общий размер главной страницы En.sopromat.org составляет 23,2 кБ. Этот результат попадает в обширную категорию (1 000 000 лучших) тяжеловесных, вероятно, неоптимизированных и, следовательно, медленно загружаемых веб-страниц. Лишь небольшому количеству веб-сайтов требуется меньше ресурсов для загрузки. Изображения занимают 11,8 КБ, что составляет большую часть объема сайта.

Оптимизация HTML

-65%

Потенциальное уменьшение на 5,5 КБ

• Оригинал 8,5 КБ
• После минификации 8,3 КБ
• После сжатия 3,0 КБ

HTML-контент может быть уменьшен и сжат сервером веб-сайта. Наиболее эффективным способом является сжатие контента с помощью GZIP, что уменьшает объем данных, передаваемых по сети между сервером и браузером. HTML-код на этой странице хорошо минимизирован. Настоятельно рекомендуется, чтобы содержимое этой веб-страницы было сжато с помощью GZIP, так как это может сэкономить до 5,5 КБ или 65% исходного размера.

Оптимизация изображения

-8%

Потенциальное снижение на 950 Б

• Оригинал 11,8 КБ
• После минификации 10,8 КБ

Оптимизация размера изображения может ускорить загрузку веб-сайта. На графике выше показана разница между размером до и после оптимизации. Однако изображения En Sopromat хорошо оптимизированы.

Оптимизация CSS

-77%

Потенциальное сокращение на 2,2 КБ

• Оригинал 2,9 КБ
• После минификации 2,2 КБ
• После сжатия 665 Б

Минимизация файлов CSS очень важна для сокращения времени рендеринга веб-страницы. Чем быстрее могут загружаться файлы CSS, тем раньше может быть отображена страница. En.sopromat.org требует минимизации и сжатия всех файлов CSS, поскольку это может сэкономить до 2,2 КБ или 77% исходного размера.

Запросы сейчас

5

После оптимизации

5

Браузер отправил 5 запросов CSS, Javascript, AJAX и изображений, чтобы полностью отобразить главную страницу En Sopromat.

По нашей аналитике все запросы уже оптимизированы.

EN.SOPROMAT.ORG

EN.SOPROMAT.ORG

515 MS

Origin_style.css

Origin_style.css

257 MS

Watch.js

Watch.JS

10005

.0005

B1.GIF

B1.GIF

791 MS

LOGO.JPG

LOGO.JPG

130 MS

RUS.GIF

RUS.GIF

130 МС

.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.J.JPG49 .jpg

258 мс

Проблемы доступности

Это возможность улучшить читаемость вашего контента.

Высокий

Цвета фона и переднего плана не имеют достаточной контрастности.

Это возможности для улучшения навигации с помощью клавиатуры в вашем приложении.

Высокий

Элементы заголовков расположены не в порядке последовательного убывания

Это возможность улучшить интерпретацию вашего контента пользователями в разных регионах.

Высокий

Элемент не имеет атрибута [lang]

Это возможность улучшить семантику элементов управления в вашем приложении. Это может улучшить работу пользователей вспомогательных технологий, таких как программа чтения с экрана.

Высокий

Элементы изображения не имеют атрибутов [alt]

Высокий

Элементы формы не имеют связанных меток

Высокий

Ссылки не имеют различимого имени

Области улучшения

High

не используют HTTPS

Низкий

Убедитесь, что CSP вступает в силу против Attachs XSS

High

Сервится изображения с низким разрешением

High

. Используемый Apis

High

. вошли в консоль

Советы по поисковой оптимизации

Чтобы появиться в результатах поиска, поисковым роботам необходим доступ к вашему приложению.

Высокий

Ссылки не сканируются

Отформатируйте HTML таким образом, чтобы сканеры могли лучше понять содержимое вашего приложения.

Высокий

Элементы изображения не имеют атрибутов [alt]

Язык и кодировка

• Обнаружен язык

  ЕН

• Заявленный язык

  Н/Д

• Кодировка

  UTF-8

Язык, указанный в метатеге HTML, должен соответствовать языку, который фактически используется на веб-странице. В противном случае En.sopromat.org может быть неверно истолкован Google и другими поисковыми системами. Наш сервис обнаружил, что на странице используется английский язык, и ни этот язык, ни какой-либо другой не были заявлены в тегах или. Наша система также обнаружила, что заявленная кодировка главной страницы En.sopromat.org — utf-8. Использование этого формата кодировки является наилучшей практикой, так как у посетителей главной страницы со всего мира не будет проблем с транскрипцией символов.

Оптимизация обмена в социальных сетях

en.sopromat.org

Описание Open Graph не обнаружено на главной странице En Sopromat. Отсутствие описания Open Graph может быть контрпродуктивным для их присутствия в социальных сетях, поскольку такое описание позволяет преобразовать домашнюю страницу веб-сайта (или другие страницы) в красивые, богатые и хорошо структурированные сообщения, когда они публикуются на Facebook и другие социальные сети. Например, добавление следующего фрагмента кода в HTML-тег поможет правильно представить эту веб-страницу в социальных сетях:

Laser – Расчеты на изгиб структурных балок – Yuji Tomita

Перейти к содержимому

Это первый пост в категории Лазер. Я написал «Сгибание структурного луча», потому что я имею в виду не лазерный луч, а алюминиевый луч в моем лазере.

Мне потребовалось некоторое время, чтобы вернуться к поезду инженерных концепций. В последний раз я делал какие-либо преобразования единиц измерения, по крайней мере, 5 лет назад. 94 или 416 231,4256

В отличие от программирования, физическая информация не так легко доступна в легко усваиваемых форматах. Я расскажу о своем опыте, чтобы помочь всем, кто наткнется на этот блог.

Для расчета отклонения балки:

Найдите момент инерции материала, модуль упругости и расстояние до самого дальнего волокна.

Мои детали поставляются Misumi, поэтому их техпаспорт выглядит так:

Момент инерции для двух осей четко показан. Модуль упругости — это свойство материала, и я не смог найти точную марку алюминия, которую использует Misumi, поэтому я поискал в Интернете средние значения, и они варьировались от 9 доот 000 000 фунтов на квадратный дюйм до 11 000 000 фунтов на квадратный дюйм.

Расстояние до самого дальнего волокна — это максимальное расстояние от нейтральной оси луча, поэтому я интерпретирую его как 1/2 ширины. Это может быть неправильно.

Сначала запустите BeamBoy и введите длину вашей балки.

Введите свойства вашей балки, как описано выше: момент инерции, модуль упругости и расстояние до самого дальнего волокна.

Затем добавьте две опоры к вашей конструкции, я просто добавил опоры в начале и конце моей балки.

Добавьте распределенную нагрузку по длине вашей балки, равную весу на расстояние (в моем случае, фунт/фут), чтобы имитировать вес самой балки.

При необходимости добавьте к балке распределенную или точечную нагрузку. Я хотел максимальное отклонение для данного веса, поэтому я использовал точечную нагрузку в «худшем» месте: в центре, вдали от моих двух опорных конструкций.

Нажмите рассчитать и посмотрите результат!

PS: Я пытался сделать это в Solidworks Beam Modeler, но результаты не кажутся точными.