Армирование бетонной лестницы арматурой — Sibear.ru
Армирование бетонной лестницы арматурой
Для сборки бетонной лестницы нужно выполнить следующие шаги: сначала собрать опалубку, затем произвести бетонирование. Как это можно сделать самостоятельно, описано в статье «Бетонная лестница своими руками». Для армирования простых в форме бетонных лестниц хорошо подходит стержневая арматура. Чтобы понять, для чего нужно армировать, рассмотрим силы, возникающие на одномаршевой лестнице.
Содержание статьи:
Выбор схемы армирования лестницы
Сборка арматурного каркаса лестницы
Это будет сила тяжести от собственного веса лестницы, её пешеходов, заносимых вещей и прочего тяжелого имущества. Все перечисленное давит на лестницу сверху. При этом в верхней части плиты лестницы бетон сжимается, а в нижней растягивается. Всё это значит, что бетон, который непрочный при растяжении, нужно армировать в нижней части плиты лестницы. В верхней же части плиты лестницы, в данном случае, армировать бетон незачем, там бетон будет прекрасно противостоять сжимающим усилиям и без всякой арматуры. Нужно заметить, что некоторые частные застройщики при сборке арматурных каркасов лестниц закладывают в опалубку по бокам стальные швеллеры, уголки, балки и т.д. Конечно, хуже от этого не будет, но это совершенно бесполезная трата недешевого нынче металла. Армирование бетонной лестницы арматурой в нижней части более чем достаточно для восприятия растягивающих усилий.
В верхней же части плиты лестницы, в данном случае, армировать бетон незачем, там бетон будет прекрасно противостоять сжимающим усилиям и без всякой арматуры. Нужно заметить, что некоторые частные застройщики при сборке арматурных каркасов лестниц закладывают в опалубку по бокам стальные швеллеры, уголки, балки и т.д. Конечно, хуже от этого не будет, но это совершенно бесполезная трата недешевого нынче металла. Армирование бетонной лестницы арматурой в нижней части более чем достаточно для восприятия растягивающих усилий.
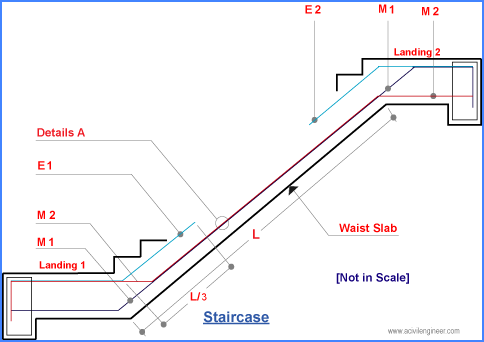
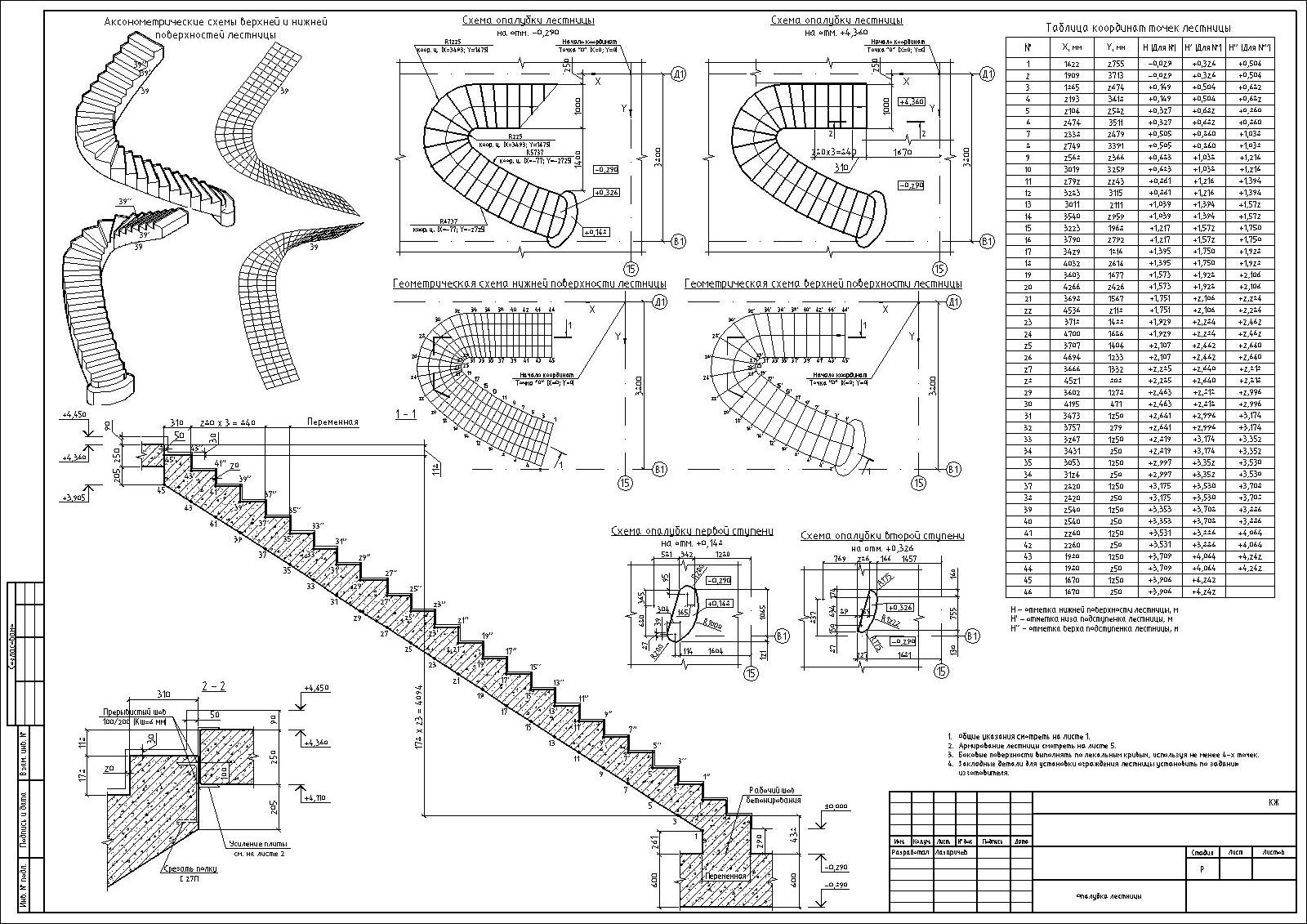
На рисунке изображена схема армирования простой одномаршевой лестницы. Видно, что одномаршевая монолитная лестница (без монолитной площадки или забежных ступеней) армируется только в нижней части плиты, то есть там, где сосредотачиваются растягивающие усилия. Иногда можно встретить проекты, где верх лестницы возле верхней поверхности бетона армируются стальной сеткой 100х100х5 мм. Такая сетка практически ни как не увеличивает жесткость монолитной лестницы, а лишь защищает ступеньки при случайных сильных ударах от сколов.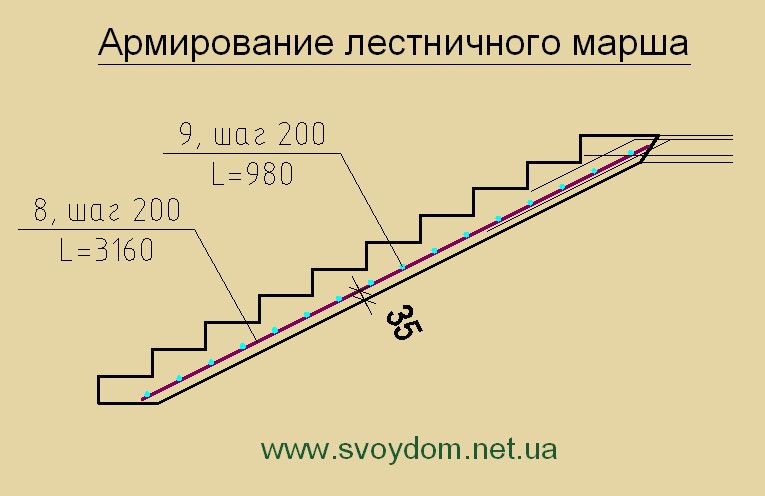
акой несложный характер воздействий на простую одномаршевую лестницу позволяет для составления схемы армирования использовать упрощенную методику. Определить оптимальную схему армирования таких простых монолитных лестниц вполне можно самостоятельно.
Обозначения на рисунке схемы армирования бетонной лестницы: рабочая высота плиты монолитной лестницы (H), длинна лестничного марша (L). Расстояние между поперечной арматурой (Е) обычно выбирают равным 40 см. В качестве поперечной арматуры используется прутки диаметром 10 мм. Оптимальное расстояние силовой арматуры до поверхности 3 см. Высота рабочей плиты лестницы (Н), диаметр продольной арматуры и расстояние между прутками продольной арматуры (I) выбирается по табл. 1 в зависимости от свободного пролёта лестничного марша (L).
Таблица 1. Определение продольного армирования одномаршевой бетонной лестницы
Длинна пролёта лестницы (L), м | Максимальное расстояние между прутками (I), см | Минимальная высота рабочей плиты лестницы, см | Диаметр арматуры, мм |
| 2 | 10 | 10 | |
| 3 | 17 | 15 | 10 |
| 4 | 15 | 20 | 12 |
| 4,5 | 13 | 22 | 12 |
| 5 | 12 | 25 | 12 |
| 5,5 | 11 | 27 | 14 |
| 6 | 10 | 30 | 14 |
В случае двухмаршевой лестницы с монолитной площадкой усилия, которые возникают в конструкции монолитной лестницы, схема армирования бетонной лестницы усложняется.
На картинке видно, что в отличие от обычной одномаршевой лестницы без площадки собственный и полезный вес лестницы хочет как бы обломить площадки, вызывая растягивающие усилия в верхних частях монолитных площадок. Этому, отчасти, помогают усадочные напряжения. Поэтому монолитные площадки армируются и снизу, и сверху, а верхняя арматура в площадках частично продолжается и в лестнице. Параметры верхнего арматурного каркаса выбираются аналогично нижнему армированию.
Площадки двухмаршевых лестниц испытывают большие усилия от веса лестницы, и поэтому должны быть прочно закреплены в стене. На практике для закрепления монолитных площадок чаще всего используют железобетонные венцы, которые формируются углублениями в стенах с размерами в среднем 20х20 см. Таким образом, для того чтобы закрепить монолитную бетонную площадку, нужны прочные и толстые стены, например, из бетона, бетонных блоков или кирпича. При стен из кирпича в них оставляют свободные углубления, а в случае возведения толстых стен из монолитного бетона к опалубке в месте размещения площадки закладываются деревянные трапеции или пенопластовые изделия соответствующего размера.
Если стены строятся по технологии монолитного литья «термодом», то практичнее всего монолитить лестничные марши и площадку на этапе возведения стен. Лестницы с монолитными площадками для увеличения конструктивной жесткости должны крепиться сверху к арматурному каркасу верхней и нижней арматурой.
Что касается схем армирования бетонных лестниц своими руками с забежными ступенями и спиральных лестниц, то их схемы армирования стержневой арматурой слишком сложные и индивидуальные. Для их составления, как минимум, придётся воспользоваться специальными программами для расчётов и проектирования железобетонных конструкций. Поэтому проект схемы армирования таких лестниц лучше всего доверить профессиональным проектировщикам, тем более что сам по себе проект будет относительно недорогим в общей стоимости сложной лестницы.
Чтобы стержни арматурного каркаса сохраняли своё проектное положение в соответствии со схемой армирования, нужно скрепить все прутки арматуры вместе. Для скрепления арматурных сеток можно применять либо точечную сварку, либо вязку. Бытует мнение, что сварка приводит к снижению прочности арматуры, однако это верно лишь в случае использования специальной высокопрочной арматуры. В этом случае, действительно, высокопрочная закалённая арматура из-за термической обработки в местах сварки превращается в обычную строительную арматуру. Такая высокопрочная арматура,стоит дорого и выпускается лишь несколькими заводами в СНГ по спецзаказу. Для обычной же строительной арматуры сварка ни как не вредит и является основным способом соединения арматурных каркасов в промышленности.
Для скрепления арматурных сеток можно применять либо точечную сварку, либо вязку. Бытует мнение, что сварка приводит к снижению прочности арматуры, однако это верно лишь в случае использования специальной высокопрочной арматуры. В этом случае, действительно, высокопрочная закалённая арматура из-за термической обработки в местах сварки превращается в обычную строительную арматуру. Такая высокопрочная арматура,стоит дорого и выпускается лишь несколькими заводами в СНГ по спецзаказу. Для обычной же строительной арматуры сварка ни как не вредит и является основным способом соединения арматурных каркасов в промышленности.
Сборка арматурного каркаса лестницы
Если под рукой нет сварочного аппарата, то арматурную сетку можно просто связывать отожженной вязальной проволокой с помощью крючка. Крючок для быстроты связывания удобно зажать в электрический шуруповёрт.
Ещё удобнее скреплять арматурные каркасы с помощью электротехнических пластиковых хомутов. Правда о таком способе соединения арматуры пока что умалчивают отечественные СНиПы, но такой способ связки уже во всю применяется заграницей и на частных стройках.
Чтобы выдержать расстояние между нижней частью опалубки и арматурой 3 см, удобно пользоваться пластиковыми фиксаторами, которые продаются в строительных супермаркетах. Для монолитной лестницы предпочтительнее применять фиксатор по форме напоминающий «стул».
Иногда не получается собрать арматурных каркас из непрерывных прутков нужной длины. Сложно это выполнить при соединении на загибах, так как без гибочного аппарата гнуть арматуру не удобно. В таком случае можно силовую арматуру соединять из кусков. Соединение производят сваркой или связкой. В качестве сварки проще всего применить ручную электродуговую шовную сварку между прутками арматуры. При сварочном способе прутков внахлёст с двух сторон стыка должно быть не менее 6 диаметров, а при сварном шве только с одной стороны не менее 12 диаметров.
В случае двухмаршевой лестницы с монолитной площадкой диаметр проволки, который берётся для закрепления двух арматурных сеток, должен быть не менее 6 мм.Если же силовая арматура соединяется между собой при помощи связывания, то нахлёст должен быть (в среднем) равным 50 диаметров соединяемой арматуры.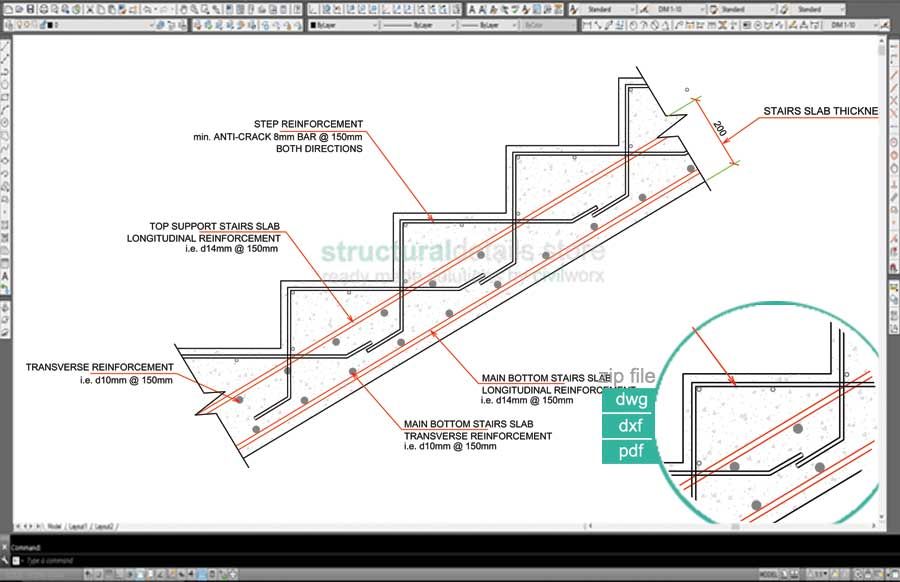 Если соединяемых стыков несколько, то их располагают в шахматном порядке, чтобы они были друг от друга на расстоянии 0,7–1 м.
Если соединяемых стыков несколько, то их располагают в шахматном порядке, чтобы они были друг от друга на расстоянии 0,7–1 м.
Какие есть лестницы на второй этаж?
Виды лестниц на второй этаж по типу несущего элемента
- Лестницы на тетиве Классическая тетива — представляет собой наклонную балку из древесины, в которой сделаны отверстия-пазы с внутренней стороны. …
- Лестницы на косоуре …
- Лестницы на больцах …
- Консольные лестницы …
- Радиальные лестницы …
- Монолитные лестницы
Сколько слоев арматуры?
Количество слоев арматуры зависит от конкретного строительного проекта и требований к нагрузкам на конструкцию. Обычно, при укладке арматуры в монолитные конструкции, используют не менее двух слоев. Первый слой укладывают на расстоянии около трети толщины плиты от нижней грани, второй слой — на расстоянии от верхней грани около половины толщины плиты. При этом между слоями арматуры должен быть расстояние не менее 2-3 см.
Армирование лестничного марша: чертеж и схема ступеней
Дата: 10 ноября 2018
Просмотров: 5222
Содержание
- Достоинства
- Рекомендации по проектированию и разработке документации
- Монтаж опалубки
- Работы по армированию
- Заливка бетоном
- Итоги
Несмотря на то, что среди застройщиков популярны лестницы из древесины и металла, при строительстве частных зданий часто применяются монолитные сооружения, идеально подходящие для создания межэтажных переходов. Марш бетонной лестницы может быть установлен как внутри помещения, так и с уличной стороны.
Лестница представляет собой архитектурное решение, предназначенное для удобного передвижения между этажами постройки и входа в помещение с наружной стороны. К лестничным сооружениям предъявляют комплекс требований по обеспечению безопасности, надежности, длительности ресурса эксплуатации, эстетичности и удобству при пользовании.
Лестнице из бетона не страшны нагрузки. Ее срок эксплуатации значительно превосходит период использования других конструкций. Такие лестницы получили распространение благодаря высокой прочности и комплексу положительных моментов. Изготовленные с учетом строительных требований, они могут стать настоящим украшением помещения и в полном объеме выполнять возложенные на них функции.
Несмотря на высокий уровень популярности деревянных или железных лестниц, при строительстве частных домов нередко используются и монолитные конструкции
Рассмотрим более детально:
- положительные черты бетонной лестницы;
- особенности ее расчета при разработке чертежа;
- требования к монтажу опалубки;
- армирование монолитной лестницы;
- выполнение бетонирования.
Достоинства
Лестничная конструкция из бетонного монолита обеспечивает следующий комплекс положительных моментов:
- Повышенную степень надежности, связанную с тем, что армирование лестницы увеличивает срок службы изделия, которое при эксплуатации объекта не нуждается в ремонте, за исключением внешней отделки.
 Такая конструкция объединяет основание здания с плитами перекрытия, усиливает всю постройку.
Такая конструкция объединяет основание здания с плитами перекрытия, усиливает всю постройку. - Облегчение строительных мероприятий за счёт того, что лестничный пролет формируется на стадии возведения здания. Это упрощает поднос к месту работ строительных материалов и способствует облегчению технологии строительных мероприятий.
- Обеспечение в дальнейшем различных дизайнерских решений, улучшающих эстетическое восприятие и способствующих реализации замыслов клиента. Принцип создания и усиления бетонных конструкций позволяет обустраивать как традиционные маршевые лестницы, так и пространственные винтового типа.
Монолитная лестница из бетона массивная и материалоемкая, но при этом надежная и прочная
Широкий ассортимент отделочных материалов позволяет обеспечить индивидуальный колорит и гармонично вписаться в интерьер помещения.
Рекомендации по проектированию и разработке документации
В зависимости от особенностей проекта каждая лестничная конструкция отличается размерами, углом наклона, количеством ступенек и формой.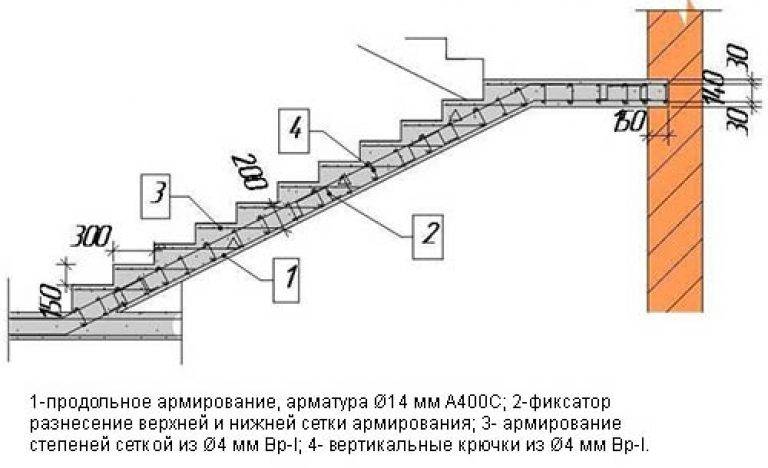 Разрабатывая чертеж, обеспечьте соблюдение следующих характеристик:
Разрабатывая чертеж, обеспечьте соблюдение следующих характеристик:
- угол наклона не должен превышать 35 градусов;
- оптимальная высота ступени – 150-180 мм;
- ширина лестничного прохода – не меньше 1 метра;
- размер опорной части ступени – 280-300 мм.
Осуществляя проектирование, выполняйте все расчёты и эскизы на бумаге, учитывайте чистовые размеры помещения, в том числе высоту полов с учетом финишной отделки.
Для того чтобы понять принцип армирования бетонной лестницы, необходимо рассмотреть силы, влияющие на ступени простой одномаршевой конструкции
Разрабатывая различные лестницы из бетона, помните, что выполнение работ по их возведению включает следующие стадии:
- Монтаж опалубки.
- Армирование лестничного марша.
- Бетонирование.
Рассмотрим детально эти три главных этапа.
Монтаж опалубки
Для усиления будущего лестничного марша необходимо возвести опалубку. Это серьезный этап формирования бетонной лестницы, выполняя который соблюдайте рекомендации:
Это серьезный этап формирования бетонной лестницы, выполняя который соблюдайте рекомендации:
- начертите после окончания проектных работ на поверхности стены расположение ступеней, чтобы избежать ошибок;
- располагайте первую ступеньку так, чтобы она превышала фактический уровень пола на толщину стяжки вместе с материалом будущего покрытия;
- используйте для изготовления опалубки фанеру, а для несущих – нагрузку направляющих применяйте брус сечением 5х15 сантиметров;
- установите подпорки, применяя металлические опорные стойки или брусья;
- обеспечьте герметичность деревянного каркаса, заполняя щели монтажной пеной.
Опалубку специалисты считают самым сложным этапом возведения монолитных лестниц
Общие рекомендации по установке опалубки для лестницы, подлежащей армированию и заливке, распространяются на различные лестничные конструкции. Ознакомиться с ними подробнее:
- Прямой одномаршевый вариант, отличающийся простотой и увеличенной до 5,5 метров длиной.
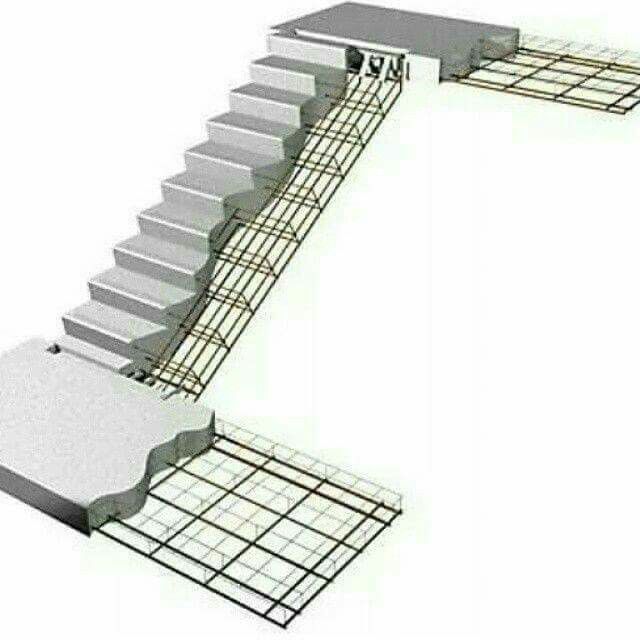 Сборка каркаса осуществляется на подпертой снизу упорами фанерной основе. С боковых сторон устанавливаются борта, а по длине с равным шагом вертикальные планки ступеней прямой или радиусной формы. Связанная сеткой арматура располагается на основании ложемента.
Сборка каркаса осуществляется на подпертой снизу упорами фанерной основе. С боковых сторон устанавливаются борта, а по длине с равным шагом вертикальные планки ступеней прямой или радиусной формы. Связанная сеткой арматура располагается на основании ложемента. - Прямая двухмаршевая схема с прямоугольной переходной площадкой распространена в многоэтажных зданиях и частных постройках. Ее отличают простота, удобство, безопасность. В качестве основы опалубки используются зашитые досками или фанерой щиты, которые опираются на предварительно установленную, горизонтальную площадку. После установки телескопических опор монтируются борта, к которым вертикально крепятся планки ступеней размером 5х15 см.
- Прямая двухмаршевая схема с радиусным изгибом похожа на предыдущую конструкцию, но отличается отсутствием прямоугольной площадки. Установка опалубки осуществляется аналогично предшествующей схеме сборки. Отличие – прикрепленная тонкая изогнутая фанера толщиной до 10 миллиметров и использование цельных прутков арматуры без стыков в зоне поворота.
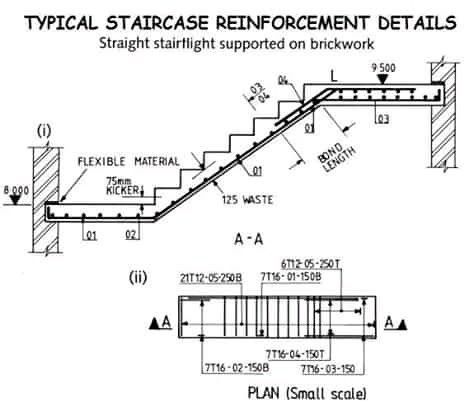
- Лестничная конструкция с радиусными ступеньками предусматривает выполнение шаблона из фанеры, в соответствии с которым деформируется тонкая 6 мм фанера, применяемая для ступеней. Крепление элементов опалубки осуществляется шурупами. Для такой лестницы армирование соответствует по стандартному варианту.
- Винтовой вариант отличается сложной конструкцией опалубки, которая достаточно часто изготавливается сварной из стальных листов, формирующих цельный винтовой контур. Устанавливая силовые прутки в каркас, не допускайте их прерывания по длине.
Первое, что нужно рассмотреть при определении рабочих нагрузок – это схема и чертеж лестницы
Работы по армированию
Если опалубка собрана, можно приступать к армированию конструкции. Комплекс работ по усилению лестничного марша предусматривает следующие стадии работ:
- подготовку необходимых материалов, инструмента;
- разработку схемы усиления;
- сборку силового каркаса.
Для выполнения работ понадобятся:
- Строительная арматура диаметром 10-14 мм.

- Проволока для вязания каркасов усиления.
- Четырехмиллиметровая сетка для усиления ступенек с ячейкой 10х10 см.
- Хомуты из пластика для фиксации.
- Электрошуруповерт.
- Сварочное оборудование.
Если всё подготовлено, начинайте работы по сборке каркаса из арматуры.
Схему армирования составляйте с учетом рекомендаций, приведённых в справочных источниках. Строительные нормы регламентируют, какая будет применяться арматура в каркасе усиления в зависимости от протяженности пролета, высоты лестничной плиты и интервала между прутками.
Проблема бетонных конструкций без арматурного каркаса известна всем – хрупкость
Например, при длине лестничного пролета 3 метра, диаметре арматуры 10 миллиметров и высоте плиты 15 сантиметров, расстояние между прутками должно быть 17 сантиметров. Руководствуясь табличными данными, выбрать параметры продольного усиления несложно.
Для понимания процесса армирования, рассмотрим усилия, возникающие в обычной одномаршевой лестнице, связанные с силой тяжести.
Ее величина зависит от массы конструкции, передвигающихся по ней людей, а также веса переносимых предметов.
Под воздействием усилий, нижняя часть бетонного монолита растягивается, а верхняя – стремится сжаться. Бетон не отличается высокой прочностью на растяжение. Именно поэтому усиление лестничной конструкции производится с использованием стальной арматуры. Для одномаршевых решений применяется проверенная на практике схема усиления, при которой стальной каркас устанавливается в нижней плоскости опалубки.
Для более нагруженных двухмаршевых схем с монолитной площадкой каркас возводится в двух уровнях конструкции – верхнем и нижнем.
Производя армирование, выполняйте следующие правила:
- соблюдайте интервал между стальными прутками усиления в соответствии с рекомендациями;
- укладываете прутки каркаса на основание опалубки, согласно эскизам, формируя ячейки необходимых размеров;
- производите фиксацию стержней для сохранения правильного положения каркаса с использованием вязальной проволоки или сварочного аппарата.
 Применяйте специальный крючок, установленный в шуруповерт для вязки элементов каркаса, если не используется сварка;
Применяйте специальный крючок, установленный в шуруповерт для вязки элементов каркаса, если не используется сварка;
- используйте пластиковые элементы крепления для фиксации стержней арматуры;
- обеспечьте интервал от основания опалубки до прутков – 3 см, используя фиксаторы, установленные в местах соединения прутков;
- соблюдайте величину нахлеста арматуры не меньше 50 диаметра прутков при объединении в каркас силовых элементов;
- зафиксируйте к стене каркас усиления, что позволит добиться увеличения прочности.
Заливка бетоном
К выполнению этапа приступают, когда арматурный каркас установлен. Для заливки подойдет, как заказной бетон, так и приготовленный самостоятельно, непосредственно на месте работ. Производя заливку, придерживайтесь следующих правил:
- Формируйте бетонную поверхность лестницы одновременно с заливкой плиты перекрытия.

- Работы выполняйте в один прием, начиная с нижней части и постепенно передвигаясь вверх.
- Обеспечьте густую консистенцию бетона, он не должен «сползать».
- Уплотняйте массив, применяя вибратор.
- Спланируйте поверхность ступеней, используя мастерок.
- Увлажняйте после заливки поверхность.
- Демонтируйте опалубку не раньше, чем через полмесяца после бетонирования.
Итоги
Производя армирование с учетом технических требований, вы обеспечите прочность лестничного марша, длительный ресурс эксплуатации.
Филонцев Виктор Николаевич
На сайте: Автор и редактор статей на сайте pobetony.ru
Образование и опыт работы: Высшее техническое образование. Опыт работы на различных производствах и стройках — 12 лет, из них 8 лет — за рубежом.
Другие умения и навыки: Имеет 4-ю группу допуска по электробезопасности. Выполнение расчетов с использованием больших массивов данных.
Текущая занятость: Последние 4 года выступает в роли независимого консультанта в ряде строительных компаний.
n-шаговое обучение с подкреплением — Введение в обучение с подкреплением
Результаты обучения
Вручную применить n-шаговое приближение обучения с подкреплением для решения небольших задач MDP
Разработка и внедрение многоступенчатого обучения с подкреплением для решения проблемы MDP среднего масштаба автоматически
Аргументация сильных и слабых сторон n-шагового обучения с подкреплением
Обзор
Эти два метода имеют некоторые недостатки в этом базовом формате:
В отличие от методов Монте-Карло, которые получают вознаграждение, а затем распространять это вознаграждение обратно, методы TD используют загрузку (они оценить будущее вознаграждение со скидкой, используя \(Q(s,a)\)), что означает что для проблем с редкими наградами может потребоваться много времени, чтобы чтобы награды распространялись по Q-функции.
Вознаграждения могут быть скудными, а это означает, что мало состояний/действий, которые привести к ненулевым вознаграждениям. Это проблематично, потому что изначально Алгоритмы обучения с подкреплением ведут себя совершенно случайно и будут бороться за хорошие награды.
Оба метода оценивают Q-функцию \(Q(s,a)\), и самый простой способ модель это через Q-таблицу. Однако это требует от нас поддержания таблица размера \(|A| \times |S|\), которая непозволительно велика для любого нетривиальная проблема.
Использование Q-таблицы требует посещения каждого достижимого состояния много раз. раз и применяйте каждое действие много раз, чтобы получить точную оценку \(Q(s,a)\). Таким образом, если мы никогда не посещаем состояние \(s\), у нас нет оценки из \(Q(s,a)\), даже если мы посетили состояния, очень похожие на \(с\).
Чтобы обойти ограничения 1 и 2, мы рассмотрим n-шаговое обучение временной разнице: методы «Монте-Карло» выполняют целые трассы, а затем распространяют вознаграждение, в то время как базовые методы TD рассматривают только вознаграждение на следующем шаге.
n-шаговое обучение TD исходит из идеи, использованной на изображении ниже, от Sutton and Barto (2020). В методах Монте-Карло используются «глубокие резервные копии», когда выполняются целые трассировки, а вознаграждение передается обратно. Такие методы, как Q-обучение и SARSA, используют «неглубокие резервные копии», используя только вознаграждение за 1 шаг вперед. n-шаговое обучение находит золотую середину: обновляйте Q-функцию только после изучения вперед \(n\) шагов.
Рис. 1 Подходы к обучению с подкреплением (из Sutton and Barto (2020))
n-шаговое обучение TD
Мы рассмотрим n-шаговое обучение с подкреплением, в котором \(n\) — это параметр,
определяет количество шагов, которые мы хотим заглянуть вперед перед обновлением Q-функции. Таким образом, для \(n=1\) это просто «обычное» TD-обучение, такое как Q-обучение или SARSA.
Когда \(n=2\), алгоритм смотрит на один шаг дальше непосредственной награды, \(n=3\) он смотрит на два шага дальше и т. д.
Таким образом, для \(n=1\) это просто «обычное» TD-обучение, такое как Q-обучение или SARSA.
Когда \(n=2\), алгоритм смотрит на один шаг дальше непосредственной награды, \(n=3\) он смотрит на два шага дальше и т. д.
И Q-learning, и SARSA имеют n-шаговую версию. Мы рассмотрим n-шаговое обучение в более общем виде, а затем покажем алгоритм для n-шагового обучения. САРСА. Версия для Q-learning аналогична. 93 r_4+\ldots\]
Мы можем переписать это как:
\[ G_t = r_1 + \gamma(r_2 + \gamma(r_3 + \gamma(r_4 + \ldots))) \]
Если \(G_t\) значение, полученное на временном шаге \(t\), то
\[ G_t = r_t + \gamma G_{t+1} \]
В методах TD(0), таких как Q-learning и SARSA, мы не знаем \(G_{t+1}\) при обновлении \(Q(s,a)\), поэтому мы оцениваем с помощью начальной загрузки:
\[ G_t = r_t + \gamma \cdot V(s_{t+1}) \]
То есть награда
все будущее с шага \(t\) оценивается как вознаграждение в \(t\) плюс
расчетное (дисконтированное) будущее вознаграждение от \(t+1\). \(V(s_{t+1})\) есть
оценивается с использованием максимальной ожидаемой отдачи (Q-обучение) или
оценочное значение следующего действия (SARSA). 9n_t\) — это полное вознаграждение, усеченное в \(n\)
шагов, в момент времени \(t\).
\(V(s_{t+1})\) есть
оценивается с использованием максимальной ожидаемой отдачи (Q-обучение) или
оценочное значение следующего действия (SARSA). 9n_t\) — это полное вознаграждение, усеченное в \(n\)
шагов, в момент времени \(t\).
Основная идея n-шагового обучения с подкреплением заключается в том, что мы не обновляем Q-значение сразу после выполнения действия: ждем \(n\) шагов и обновляем его на основе n-шагового возврата.
Если \(T\) шаг завершения и \(t + n \geq T\), то мы просто используем полный награда.
В методах Монте-Карло мы идем до конца эпизода. Поиск по дереву Монте-Карло является одним из таких методов Монте-Карло, но есть другие, которые мы не покрываем. 9nQ(s_{\tau+n}, a_{\tau+n}).\]
Добавляет будущую ожидаемую награду, если мы не в конце эпизода (если \(\tau+n < T\)).
Наконец, мы обновляем Q-значение:
\[Q(s_{\tau}, a_{\tau}) \leftarrow Q(s_{\tau}, a_{\tau}) + \alpha[G — Q(s_{\tau}, a_{\ тау}) ]\]
В приведенном выше правиле обновления мы используем обновление SARSA, но аналогичное обновление Q-learning.
N-шаг SARSA
Хотя концептуально это не так уж сложно, алгоритм для выполнения n-шагового обучения должен хранить награды и наблюдаемые состояния для \(n\) шагов, а также отслеживать, какой шаг нужно обновить. Алгоритм для n-шагового SARSA показан ниже.
Алгоритм – n-шаговый SARSA
Ввод: MDP \(M = \langle S, s_0, A, P_a(s’ \mid s), r(s,a,s’)\rangle\), число шагов \(n\)
Вывод: Q-функция \(Q\)
Инициализация \(Q\) произвольно; например, \(Q(s,a)=0\) для всех \(s\) и \(a\)
Повторить (для каждого эпизода)
\(\quad\quad\) Выбрать действие \(a\ ) для применения в \(s\) с использованием Q-значений в \(Q\) и алгоритма многорукого бандита, такого как \(\epsilon\)-жадный
\(\quad\quad\) \(ss = \ лангле с\рангле\)
\(\quad\quad\) \(as = \langle a\rangle\)
\(\quad\quad\) \(rs = \langle \rangle\)
\(\quad\quad\) Пока \ (ss\) не пусто
\(\quad\quad\quad\quad\) Если \(s\) не конечное состояние, то:
\(\quad\quad\quad\quad\quad\quad\) Выполнить действие \(a\) в состоянии \(s\)
\(\quad\quad\quad\quad\quad\quad\) Наблюдать за вознаграждением \(r\) и новым состоянием \(s’\)
\( \quad\quad\quad\quad\quad\quad\) \(rs \leftarrow rs + \langle r\rangle\)
\(\quad\quad\quad\quad\quad\quad\) Если \(s’ \) не является терминальным состоянием, то: 9n Q(s’, a’)\)
\(\quad\quad\quad\quad\quad\quad\) \(Q(ss_0, as_0) \leftarrow Q(ss_0, as_0) + \alpha[G — Q(ss_0, as_0)]\)
\(\quad\quad\quad\quad\quad\quad\) \(rs \leftarrow rs_{[1 : n + 1]}\)
\(\quad\quad \quad\quad\quad\quad\) \(ss \leftarrow ss_{[1 : n + 1]}\)
\(\quad\quad\quad\quad\quad\quad\) \(as \leftarrow as_ {[1 : n + 1]}\)
\(\quad\quad\quad\quad\) \(s \leftarrow s’\)
\(\quad\quad\quad\quad\) \(a \ стрелка влево а’\)
Это похоже на стандартную SARSA, за исключением того, что мы сохраняем последние \(n\) состояния, действия и награды; а также расчет вознаграждений за последние пять вознаграждений, а не только за одно.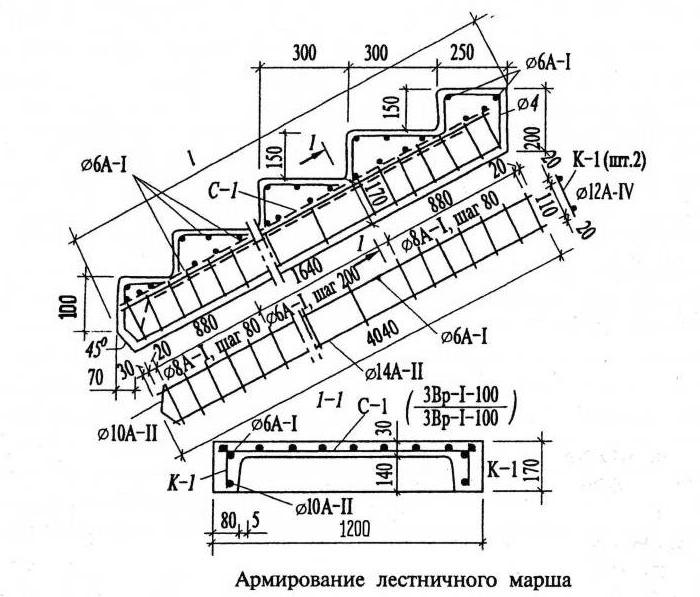 n\) вместо \(\gamma\). Почему? Это связано с тем, что предполагаемое вознаграждение в будущем составляет \(n\) шагов от состояния \(ss_0\). Награда \(n-step\) в \(G\) бывает первой. Затем мы выполняем фактическое обновление, которое обновляет пару состояние-действие \((ss_0, as_0)\), то есть \(n\)-шагов назад. 9{th}\) шаги эпизода; и отсутствие TD-оценки будущего вознаграждения на последних \(n\) шагах эпизода.
n\) вместо \(\gamma\). Почему? Это связано с тем, что предполагаемое вознаграждение в будущем составляет \(n\) шагов от состояния \(ss_0\). Награда \(n-step\) в \(G\) бывает первой. Затем мы выполняем фактическое обновление, которое обновляет пару состояние-действие \((ss_0, as_0)\), то есть \(n\)-шагов назад. 9{th}\) шаги эпизода; и отсутствие TD-оценки будущего вознаграждения на последних \(n\) шагах эпизода.
С вычислительной точки зрения это не намного хуже, чем одноэтапное обучение. Нам нужно сохранить последние \(n\) состояний, но пошаговое вычисление для n-шагов небольшое и единообразное, как и для 1-шага.
Пример — \(n\)-шаг обновления SARSA
Рассмотрим нашу простую задачу 2D-навигации, в которой мы не знаем вероятности переходов и награды. Первоначально алгоритм обучения с подкреплением должен будет выполнять поиск случайным образом, пока не найдет вознаграждение. Распространить это вознаграждение обратно на n шагов будет полезно.
Представьте себе первый эпизод, состоящий из следующего (очень удачного!) следа:
Предполагая, что \(Q(s,a)=0\) для всех \(s\) и \(a\), если мы пройдем эпизод помеченный эпизод, как будет выглядеть наша Q-функция для 5-шагового обновить с помощью \(\alpha=0. 4 rs_3 = 0,90 \cdot 1 = 1\\
& & Q((2,2, справа) = 0 + 0,5[1 \cdot 1 — 0] = 0,5
\конец{массив}
\)
4 rs_3 = 0,90 \cdot 1 = 1\\
& & Q((2,2, справа) = 0 + 0,5[1 \cdot 1 — 0] = 0,5
\конец{массив}
\)
В этот момент больше не осталось состояний для обновления, поэтому внутренний цикл завершается, и мы начинаем новый эпизод.
Реализация
Ниже приведена реализация на Python n-шагового обучения временным различиям. Сначала мы реализуем абстрактный суперкласс NStepReinforcementLearner , который содержит большую часть кода, который нам нужен, за исключением той части, которая определяет значение состояния \(s’\) в обновлении Q-функции, которое оставлено подклассу, чтобы мы могли поддержка как n-шагового Q-обучения, так и n-шагового SARSA:
класс NStepReinforcementLearner:
def __init__(self, mdp, bandit, qfunction, n, альфа=0.1):
self.mdp = mdp
self.bandit = бандит
self.alpha = альфа
self.qфункция = qфункция
селф.n = n
def выполнить (я, эпизоды = 100):
для _ в диапазоне (эпизоды):
состояние = self.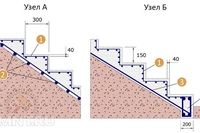 mdp.get_initial_state()
действия = self.mdp.get_actions (состояние)
action = self.bandit.select(состояние, действия, self.qfunction)
награды = []
состояния = [состояние]
действия = [действие]
в то время как len(состояния) > 0:
если не self.mdp.is_terminal (состояние):
(следующее_состояние, вознаграждение) = self.mdp.execute (состояние, действие)
награды += [награда]
next_actions = self.mdp.get_actions (следующее_состояние)
если не self.mdp.is_terminal(next_state):
next_action = self.bandit.select(
next_state, next_actions, self.qfunction
)
состояния += [next_state]
действия += [следующее_действие]
если len(вознаграждения) == self.n или self.mdp.is_terminal(состояние):
n_step_rewards = сумма(
[
self.
mdp.get_initial_state()
действия = self.mdp.get_actions (состояние)
action = self.bandit.select(состояние, действия, self.qfunction)
награды = []
состояния = [состояние]
действия = [действие]
в то время как len(состояния) > 0:
если не self.mdp.is_terminal (состояние):
(следующее_состояние, вознаграждение) = self.mdp.execute (состояние, действие)
награды += [награда]
next_actions = self.mdp.get_actions (следующее_состояние)
если не self.mdp.is_terminal(next_state):
next_action = self.bandit.select(
next_state, next_actions, self.qfunction
)
состояния += [next_state]
действия += [следующее_действие]
если len(вознаграждения) == self.n или self.mdp.is_terminal(состояние):
n_step_rewards = сумма(
[
self. mdp.discount_factor ** i * вознаграждение[i]
для i в диапазоне (len (вознаграждения))
]
)
если не self.mdp.is_terminal (состояние):
следующее_состояние_значение = self.state_value(следующее_состояние, следующее_действие)
n_step_rewards = (
n_step_rewards
+ self.mdp.discount_factor ** self.n * next_state_value
)
q_value = self.qfunction.get_q_value(
состояния[0], действия[0]
)
self.qfunction.update(
состояния [0],
действия[0],
self.alpha * (n_step_rewards - q_value),
)
награды = награды [1 : self.n + 1]
состояния = состояния [1 : self.n + 1]
действия = действия [1 : self.
mdp.discount_factor ** i * вознаграждение[i]
для i в диапазоне (len (вознаграждения))
]
)
если не self.mdp.is_terminal (состояние):
следующее_состояние_значение = self.state_value(следующее_состояние, следующее_действие)
n_step_rewards = (
n_step_rewards
+ self.mdp.discount_factor ** self.n * next_state_value
)
q_value = self.qfunction.get_q_value(
состояния[0], действия[0]
)
self.qfunction.update(
состояния [0],
действия[0],
self.alpha * (n_step_rewards - q_value),
)
награды = награды [1 : self.n + 1]
состояния = состояния [1 : self.n + 1]
действия = действия [1 : self. n + 1]
состояние = следующее_состояние
действие = следующее_действие
""" Получить значение состояния """
def state_value (я, состояние, действие):
абстрактный
n + 1]
состояние = следующее_состояние
действие = следующее_действие
""" Получить значение состояния """
def state_value (я, состояние, действие):
абстрактный
Мы наследуем от этого класса для реализации n-шагового алгоритма Q-обучения:
из импорта n_step_reinforcement_learner NStepReinforcementLearner
класс NStepQLearning (NStepReinforcementLearner):
def state_value (я, состояние, действие):
(_, max_q_value) = self.qfunction.get_max_q (состояние, self.mdp.get_actions (состояние))
вернуть max_q_value
Пример — 1-этапное Q-обучение против 5-этапного Q-обучения
Используя интерактивную графику ниже, мы сравниваем одноэтапное и пятиэтапное Q-обучение в течение первых 20 эпизодов обучения в задаче GridWorld. При использовании одноэтапного Q-обучения достижение награды информирует только о состоянии, из которого оно было достигнуто в первом эпизоде; тогда как для 5-шагового Q-обучения он информирует о предыдущих пяти шагах. Затем, во втором эпизоде, если какое-либо действие достигает состояния, которое было посещено, оно может получить доступ к TD-оценке для этого состояния. В 5-этапном Q-обучении есть пять таких состояний; и только одно в 1 шаге Q-обучения. На всех последующих итерациях больше шансов встретить состояние с TD-оценкой, и эти оценки лучше информированы. Конечным результатом является то, что оценки «распространяются» по Q-таблице быстрее:
Затем, во втором эпизоде, если какое-либо действие достигает состояния, которое было посещено, оно может получить доступ к TD-оценке для этого состояния. В 5-этапном Q-обучении есть пять таких состояний; и только одно в 1 шаге Q-обучения. На всех последующих итерациях больше шансов встретить состояние с TD-оценкой, и эти оценки лучше информированы. Конечным результатом является то, что оценки «распространяются» по Q-таблице быстрее:
Значения
nМожем ли мы просто увеличить \(n\) до бесконечности, чтобы получить вознаграждение за всю трассировку? Выполнение этого, которое называется симуляцией Монте-Карло , на практике работает не так хорошо. По сути, у нас больше не будет оценок TD в правиле обновления, что приводит к большей дисперсии в обучении.
Каково тогда лучшее значение для \(n\)? К сожалению, теоретически лучшего значения для \(n\) не существует. Это зависит от конкретного приложения и функции вознаграждения, которая обучается. На практике кажется, что значения \(n\) около 4-8 дают хорошие обновления, потому что мы можем легко присвоить значение каждому из 4-8 действий; то есть мы можем сказать, повлияли ли 4-8 действий в прогнозе на оценку, потому что мы используем оценки TD.
На практике кажется, что значения \(n\) около 4-8 дают хорошие обновления, потому что мы можем легко присвоить значение каждому из 4-8 действий; то есть мы можем сказать, повлияли ли 4-8 действий в прогнозе на оценку, потому что мы используем оценки TD.
Резюме
n-ступенчатое обучение с подкреплением распределяет вознаграждение по \(n\) шагам, чтобы помочь в обучении.
Концептуально это довольно просто, но реализация требует много «бухгалтерского учета».
Выбор значения \(n\) для домена требует экспериментов и интуиции.
Дополнительная литература
N-ступенчатая начальная загрузка. Это часть 7 руководства по RL… | Саги Шайер
Опубликовано в·
Чтение: 5 мин.·
21 ноября 2020 г.Второе издание.» Ричард С. Саттон и Эндрю Г. Барто. Эта книга доступна бесплатно здесь
Изображение с Pexels [ссылка]Эта статья является частью серии. Смотрите полную серию: Часть 1, Часть 2, Часть 3, Часть 4, Часть 5, Часть 6 и Часть 7!
Глава 7 — n-шаговая начальная загрузка
В этой главе основное внимание уделяется объединению методов одношаговой временной разности (TD) и методов Монте-Карло (MC).
Идея состоит в том, что ни одношаговый TD, ни MC не всегда подходят лучше всего. Скорее, если вы подумаете о спектре, где один шаг TD находится на одном конце, а MC — на другом, мы найдем что-то среднее между ними.
n-шаговое TD-предсказание
Самый простой способ понять, какие методы находятся между MC и TD, — это следующее изображение:
Рассмотрите возможность оценки функции ценности Vπ по некоторым выборочным эпизодам.
1-шаговые методы TD будут выполнять обновление для каждого состояния, используя следующее вознаграждение и оценочное значение следующего состояния в качестве приближения для следующих вознаграждений. Методы
MC, с другой стороны, будут выполнять обновление, используя всю последовательность наград, которую он наблюдал от начального состояния до конца эпизода.
Таким образом, довольно легко увидеть, что находится между ними: например, 2-шаговый TD выполнит обновление на основе следующих 2-х вознаграждений и оценочного значения соответствующего состояния (на 2 шага вперед).
Обратите внимание, что эти n-шаговые методы по-прежнему являются методами TD, поскольку они изменяют предыдущее оценочное значение на основе другого его отличия от следующего оценочного значения.
Более формально, возврат метода MC:
MC return [ref]Где T — последний временной шаг.
Возврат в 1-шаговый метод TD:
1-шаговый TD-возврат [ref]Возврат в 2-шаговый TD-метод:
2-шаговый TD-возврат [ref]Наконец, возврат для n-шагового TD-метода:
n-шаг TD return [ref]n шаг алгоритма TD [ref] n-ступенчатая сарса
В предыдущей главе мы обсуждали сарсу (0), или 0-шаговую сарсу. Напомню, что в Sarsa нас интересовали значения пар состояние-действие, а не только значения состояний.
Так что очень похоже на описанную выше технику с методом n шагов TD:
Обратите внимание, что ожидается n шагов Sarsa имеет немного другой последний шаг, о котором я расскажу позже.
Итак, теперь наша прибыль выражается только в расчетных значениях действий:
Возврат [ссылка]И наша пара действие-значение:
Пара действие-значение [ссылка]n шаг Алгоритм Сарса [ссылка]Пример:
Пример выбора пути [ссылка] Рассмотрим путь, показанный в левой сетке.
1 шаг Sarsa будет обновлять значения действий, основываясь исключительно на последнем действии в последовательности действий.
10 шагов Sarsa будет обновлять значения действий на основе последних 10 действий в последовательности действий.
Как видно из схемы резервного копирования Sarsa для шага n, ожидаемый Sarsa имеет другой последний шаг. В нем мы взвешиваем вероятности каждого действия, которое произойдет в соответствии с политикой. Таким образом, все шаги до последнего аналогичны n шагу Сарсы.
Возврат [ref] На последнем шаге мы взвешиваем вероятности действий [ref] n-step off policy Learning
Вспомните, что в on-policy мы отбираем и обновляем одну политику, а при off-политике мы отбираем действия из политики поведения b и стремимся улучшить нашу целевую политику π.
Мы будем делать то же самое, что и в предыдущей главе, где мы использовали коэффициент выборки важности для взвешивания результатов, за исключением того, что теперь нас интересуют только n действий.
Коэффициент выборки по важности [ссылка]Таким образом, наше обновление для n шагов TD:
Обратите внимание, что мы взвешиваем результаты с коэффициентом выборки важности [ref]И обновление для Sarsa:
Обновление Sarsa [ref] Off policy n step Sarsa [ref]Off policy Learning Без выборки по важности: алгоритм резервного копирования дерева из n шагов
В этом разделе представлен алгоритм, который работает с n шагами без выборки по важности — алгоритм резервного копирования дерева
Схема резервного копирования дерева из 3 шагов [ref] просто обновив наше оценочное значение верхнего узла, используя вознаграждения со скидкой, которые он получил по пути, а также значения нижних узлов, мы также собираемся добавить оценочные значения узлов действия в каждом из состояний, которые мы проходим.