Примеры решения задач по сопротивлению материалов
В этом разделе рассмотрены примеры решения задач по сопромату, с необходимыми пояснениями и графическими иллюстрациями.
- Определение опорных реакций
- Расчеты на прочность
- Построение эпюр
- Расчет балки
- Расчет напряжений
- Проверка на прочность
- Расчет деформаций и перемещений
- Расчеты на жесткость
- Растяжение-сжатие
- Кручение
- Изгиб
- Другие примеры
- Олимпиадные задачи
Задачи по условию
Определение опорных реакций
Примеры определения опорных реакций при растяжении-сжатии и плоском поперечном изгибе, определение неизвестного крутящего момента для вала.
Расчеты на прочность
Примеры решения задач по расчету стержней, балок и валов на прочность.
Построение эпюр
Примеры построения эпюр внутренних усилий, напряжений и перемещений при растяжении-сжатии, кручении, изгибе и других видах деформации.
Расчет напряжений
Примеры расчетов нормальных, касательных и главных напряжений при различных видах деформации. Рассмотрены аналитические и графический способ (круг Мора) определения напряжений.
Расчет деформаций и перемещений
Примеры расчетов деформации бруса при различных видах нагружения.
Задачи по видам нагружения
Растяжение-сжатие
Примеры решения задач и расчетно-графических работ по теме растяжение-сжатие стержней и стержневых систем.
Кручение
Примеры решения задач и РГР на тему кручение валов.
Изгиб
Примеры решения задач и РГР по теме плоский поперечный изгиб балок.
Расчет балки
Примеры расчетов двухопорных и консольных балок.
Примеры решения задач для олимпиад по сопротивлению материалов.
Другие задачи
- Определение положение центра тяжести сложного сечения
- Определение положения центра тяжести составной фигуры, расчет главных центральных моментов и радиусов инерции, построение эллипса инерции
- Определение реакций в опорах рамы
- Построение эпюр N, Q и M для рамы
- Проверка построенных эпюр в рамах
- Перемещение точки нити перекинутой через блок
isopromat.ru
Примеры решения задач по сопромату.
Решение задач по сопромату
Примеры решения задач по сопротивлению материалов
Как и в предыдущей статье, на этой странице приведены основные принципы решения задач технической механики на примере простейших заданий, в которых необходимо определить какие-либо силовые факторы, возникающие в конструкциях и телах напряжения, построить эпюры и т. п. Сопротивление материалов является базовой основой для решения вопросов наиболее практического раздела технической механики — «Детали машин».
Решение задачи на растяжение и сжатие
Построить эпюру напряжений в ступенчатом круглом брусе, нагруженном продольными силами и указать на наиболее напряженный участок.
Весом бруса пренебречь.
Исходные данные:
Силы:
F1 = 100 кН;
F2 = 400 кН;
Площадь сечения бруса: А = 0,1 м2.
Решение:
При построении эпюры напряжений используем метод сечений, рассматривая отдельные участки бруса, как самостоятельные его элементы, находящиеся в состоянии равновесия под действием реальных и условных нагрузок. При этом исследование сечений начинаем со стороны свободного конца бруса, т. е. со стороны, где приложены известные нам силы.
Для каждого из участков определяем нормальные напряжения в сечениях по формуле σ = F/A, где: F — величина продольной силы в сечении, А — площадь сечения. При этом следует учитывать знаки: если сила растягивающая, то ее условно считают положительной, если сжимающая — отрицательной. Соответственно, напряжения будут иметь такие же знаки, как и силы.
После подсчетов получим:
σI = F1/A = -100×103/0,1 = -1000000 Па (-1 МПа),
σIII = (F2 — F1)/A = (400 — 100)×103/0,1 = 3000000 Па (3 МПа).
Построение эпюры напряжений начинаем с проведения линии, параллельной оси бруса (эта линия условно изображает брус и является нулевой ординатой графика эпюры). Затем, начиная от свободного конца бруса, откладываем от линии, как от нулевой ординаты, величины напряжений по каждому участку с учетом их знаков.
На брусе, приведенном в задании, величина напряжений в каждом сечении отдельных участков будет одинакова, и лишь в граничных (расположенных между соседними участками) сечениях появится скачок напряжения в виде ступени (здесь используется принцип Сен-Венана, условно полагающий, что в месте приложения нагрузки напряжение изменяется скачкообразно).
Построение эпюры завершается указанием на ее площадках знаков напряжения в кружках, проведением тонких линий перпендикулярно оси (нулевой ординаты) эпюры (эти линии условно изображают сечения бруса) и расстановкой величины напряжений на внешних углах графика (на внутренних углах цифровые обозначения не наносятся). Слева от эпюры указывается, что на ней изображено (в нашем случае — Эпюра σ)
В результате построений мы получим график (эпюру) распределения напряжений по каждому сечению бруса, визуальное исследование которого позволяет определить наиболее напряженный участок. Для бруса, представленного в задаче, максимальные напряжения возникают в сечениях участка III (см. схему). Поскольку эти напряжения положительны, они являются растягивающими
Задача решена.
***
Решение задачи с использованием закона Гука
Определить величину растягивающей силы F, если известно, что под ее действием брус удлинился на величину ΔL.
Исходные данные:
Удлинение бруса ΔL = 0,005 мм;
Площадь сечения бруса A = 0,01 м2;
Размеры бруса и точка приложения силы F приведены на схеме.
Решение:
Решить задачу можно, используя известную зависимость между линейными удлинениями и нагрузками (закон Гука).
Согласно закону Гука, представленному в расширенном виде:
ΔL = FL/(EA), откуда: F = (ΔLEA)/L.
Поскольку сила F приложена не к крайнему сечению бруса, а к его середине, то удлинился лишь участок между жесткой заделкой и сечением, к которому приложена растягивающая сила, имеющий длину L1 = 2 м.
Учитывая это, определяем силу, вызвавшую удлинение бруса (не забываем привести все величины к единицам системы СИ):
F = (ΔLEA)/L1 = (0,005×10-3×2×1011×0,01)/2 = 5000 Н = 5,0 кН.
Задача решена.
***
Решение задачи на срез и смятие
Венец зубчатого колеса прикреплен к ступице болтовыми соединениями из шести болтов с гайками, размещенными равномерно по окружности диаметром D.
Определить касательные напряжения сдвига (среза), действующие в каждом из болтов при номинальной нагрузке.
При расчете не учитывать ослабление стержня болта впадинами резьбы.
Исходные данные:
Номинальный крутящий момент на валу шестерни: Мкр = 10 Нм;
Диаметр окружности, на которой размещены болтовые соединения D = 0,4 м;
Диаметр стержня болта d = 10 мм.
Решение:
Для решения задачи воспользуемся зависимостью между напряжением среза, внешней нагрузкой и площадью сечения по плоскости среза:
τср = Fокр /A,
где: τср — касательное напряжение среза, Fокр — окружная сила на расстоянии от оси вращения до центра болта,
Окружную силу можно определить, зная крутящий (вращающий) момент на валу зубчатого колеса и расстояние от оси вращения зубчатого колеса до центра болта:
Fокр = 2Мкр/D.
Площадь сечения одного болта: А(1) = πd2/4, шести болтов: А = 3πd2/2 .
Подставив эти значения в исходную формулу, определим касательное напряжение сдвига (среза) болта:
τср = Fокр /A = (2Мкр/D) / (3πd2/2) = (2×10/0,4) / (3×3,14 0,012/2) ≈ 106 000 Па (или 0,106 МПа).
Задача решена.
***
Решение задачи на срез и смятие шпонки
Произвести проверочный расчет призматической шпонки на смятие.
Исходные данные:
Вращающий момент на валу Т = 120 Нм;
Радиус сечения вала r = 30 мм;
Рабочая длина шпонки lр= 30 мм;
Допускаемое напряжение на смятие [σ]см = 200 МПа
Решение:
Решение задачи сводится к определению напряжения смятия, возникающего в продольном сечении шпонки, выступающем над канавкой вала (рабочая площадь шпонки). Это напряжение можно определить из формулы:
σсм = Fокр /Aраб (1)
где: σсм — искомое напряжение смятия,
Fокр — окружная сила, действующая на рабочую поверхность шпонки: Fокр = Т/r.
Учитывая, что высота рабочей поверхности шпонки невелика, можно принять для расчета напряжения окружную силу, действующую на расстоянии r от оси вращения вала (радиус вала). Если необходимо выполнить более точный расчет, следует к радиусу вала прибавить половину высоты рабочей поверхности шпонки (в нашем случае — h/4).
Aраб — площадь шпонки, подвергаемая смятию: Aраб = hlр /2 (здесь lр — рабочая длина шпонки).
Подставив полученные значения окружной силы и площади шпонки, работающей на смятие, в формулу (1), получим:
σсм = Fокр /Aраб = (Т/r) / (hlр /2) = (120/0,03) / (0,003×0,03/2) = 88 900 000 Па (или 88,9 МПа).
Полученное напряжение сравниваем с допускаемым напряжением смятия [σсм] = 200 МПа, и делаем вывод, что шпонка выдержит нагрузку.
Задача решена.
***
Решение задачи на кручение
Построить эпюру вращающих моментов для круглого однородного бруса, представленного на схеме. Указать наиболее нагруженный участок бруса и определить напряжение в его сечениях.
Исходные данные:
Вращающие моменты:
Т1 = 150 Нм;
Т2 = 400 Нм;
Т3 = 50 Нм;
Диаметр бруса d = 0,05 м.
Решение:
Построение эпюр вращающих (крутящих моментов) начинаем со стороны свободного конца бруса, откладывая величины крутящих моментов от оси абсцисс (нулевой ординаты) бруса с соблюдением знаков моментов (см. схему).
Из эпюры очевидно, что максимальный крутящий момент возникает в сечениях участка I: Мкр = 500 Нм. Для определения напряжения (при кручении возникает касательное напряжение), воспользуемся зависимостью, полученной ранее:
τmax = Мкр / Wr ,
где: Wr ≈ 0,2d3 — момент сопротивления круглого сечения кручению (или полярный момент сопротивления круглого сечения).
Подставив полученные зависимости и их числовые значения в формулу, получим максимальное напряжение τmax, возникающее в сечениях участка I при кручении бруса:
τmax≈ Мкр / 0,2d3 ≈ 500/0,2×0,053≈ 200 000 000 Па (или 200 МПа).
Задача решена.
С правилами и примерами построения эпюр при деформации кручения можно ознакомиться здесь.
***
Решение задачи на изгиб
Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой, если к свободному концу бруса приложена поперечная сила F.
Вес бруса не учитывать.
Поперечная сила F = 1000 Н;
Длина бруса L = 5 м;
Диаметр бруса d = 0,1 м.
Решение:
Изгибающий момент силы F и возникающие в сечениях бруса напряжения зависят от расстояния между линией приложения (вектором) силы и плоскостью рассматриваемого сечения (очевидно, что величина изгибающего момента находится в прямо пропорциональной зависимости от расстояния до вектора силы). Поэтому для данного бруса изгибающий момент достигает максимального значения в сечении рядом с жесткой заделкой:
Миmax = FL = 1000×5 = 5000 Нм.
Максимальные нормальные напряжения в этом сечении можно определить по формуле:
σmax = Миmax / W,
где: W ≈ 0,1d3 — момент сопротивления круглого сечения изгибу (или осевой момент сопротивления круглого сечения). Подставив зависимости и их величины в формулу, получим:
σmax≈ Миmax / 0,1d3≈ 5000/0,1х0,13≈ 50 000 000 Па (или 50 МПа).
Задача решена.
***
Решение задачи на изгиб с построением эпюр
Построить эпюру поперечных сил и изгибающих моментов, действующих на защемленный одним концом брус (см. схему).
Исходные данные:
Поперечная сила F = 50 Н;
Распределенная нагрузка q = 10 Н/м;
Длина бруса L = 12 м;
Вес бруса не учитывать.
Решение:
Для построения эпюр определим границы участков бруса, в пределах которых внешние нагрузки и размеры сечений одинаковы. Для данного бруса можно выделить два таких участка (см. схему).
Далее, используя метод сечений, строим эпюру поперечных сил, учитывая знаки. Очевидно, что на первом участке поперечная сила будет постоянной во всех сечениях, и эпюра представляет собой горизонтальную линию, отстоящую от оси эпюры на величину -F (сила отрицательная).
В среднем сечении бруса начинает действовать распределенная нагрузка, которая линейно увеличивается и суммируется с поперечной силой F в каждом последующем сечении бруса по направлению к жесткой заделке. Поскольку эпюра поперечных сил на втором участке представляет собой отрезок наклонной прямой, то для ее построения достаточно определить величину поперечной силы в середине бруса (очевидно, что здесь F = 50 Н) и величину поперечной силы в сечении рядом с жесткой заделкой:
F2 = -FL — 6q = -50 — 10×6 = -110 Н.
По полученным значениям строим эпюру поперечных сил F (см. схему).
Построение эпюры изгибающих моментов строится аналогично эпюре поперечных сил — при помощи метода сечений. При этом учитывается расстояние от сечения, в котором приложена поперечная сила, до рассматриваемого сечения (плечо силы).
Очевидно, что изгибающий момент от силы F будет увеличиваться прямо пропорционально по мере удаления от сечения, к которому она приложена, причем в крайнем сечении (где приложена сила) момент этой силы равен нулю (поскольку плечо силы равно нулю).
В среднем сечении бруса изгибающий момент достигает значения: Ми = FL/2 = -50×6 = -300 Нм .
Начиная с середины бруса начинает действовать изгибающий момент от распределенной нагрузки q, который в каждом сечении определяется, как произведение приведенной силы Fпр = ql на половину расстояния l (здесь l — расстояние от рассматриваемого сечения до начала действия распределенной нагрузки).
Очевидно, что по мере удаления от среднего сечения к жесткой заделке изгибающий момент от распределенной нагрузки q изменяется по квадратичной зависимости, и линия эпюры изгибающих моментов на втором участке представляет собой параболу.
Чтобы построить параболу недостаточно двух точек, необходимо определить величину изгибающего момента в нескольких сечениях бруса (на втором участке). При этом следует учитывать изгибающий момент от силы F, который суммируется с изгибающим моментом от распределенной нагрузки q на данном участке бруса.
Максимальной величины изгибающий момент достигает в сечении рядом с жесткой заделкой:
Миmax = — FL + [-q×(L/2)×(L/4)] = -50×12 + [-10×(12/2)×(12/4)] = -780 Нм.
Выполнив необходимые подсчеты, строим эпюру изгибающих моментов, начиная со свободного конца бруса (см. схему).
Задача решена.
***
Пример расчета бруса (стержня)
Сопротивление материалов
k-a-t.ru
Примеры решения задач по сопромату
Приветствую тебя, читатель сайта — sopromats.ru, на котором размещено много полезной и интересной информации о сопромате и не только. Сегодня я решил написать большую статью о примерах решения задач по сопромату, которые размещены на этом ресурсе. Все примеры было решено классифицировать на три категории: по виду деформации, по виду рассчитываемого объекта и по типу расчета. Эти категории имеют три уровня вложенности. Например, в категории — по виду деформации входят задачи, связанные с изгибом, кручением, растяжением (сжатием) и сложным сопротивлением. В свою очередь, решения на изгиб классифицируются на статически определимые и неопределимые. Для того, чтобы найти нужную категорию перемещайтесь по указанным ссылкам на страничках. Также хотелось бы отметить, что на данный момент на сайте преобладают рукописные примеры решения. Но наша команда, активно работает над добавлением электронных материалов: с качественными схемами и набранными в цифровом виде расчетами. По мере развития сайта, все рукописные записи, планируется заменить цифровыми. Ну что же перейдем непосредственно к нашим примерам.
Классификация по виду деформации
Как уже говорилось выше, здесь все примеры отсортированы по виду деформации: растяжению и сжатию, кручению, изгибу и сложному сопротивлению. В категорию задач на сложное сопротивление попадают такие популярные решения на такие темы как изгиб с кручением, внецентренное растяжение (сжатие), косой изгиб. Теперь давайте перейдем непосредственно к категориям и не забывайте переходить по ссылкам на интересующую вас подкатегории.
Что можно найти в данной категории задач?
- определение реакций в опорах из уравнений равновесия статики;
- расчет ВСФ методом сечений;
- вычисление продольной и поперечной силы;
- расчет изгибающего момента;
- расчет нормальных и касательных напряжений;
- вычисление перемещений поперечных сечений;
- раскрытие статической неопределимости с использованием уравнения совместности деформации.
Растяжение и сжатие
Задачи на растяжение и сжатие, разделены следующим образом:
- статически определимые брусья;
- статически неопределимые брусья;
- статически определимые стержневые системы;
- статически неопределимые стержневые системы.
Кручение
Примеры задач на кручение распределены по 2 основным категориям:
- статически определимое кручение;
- статически неопределимое кручение.
Изгиб
Задачи на изгиб подразделяются по тем же признакам:
- статически определимый изгиб;
- статически неопределимый изгиб.
Классификация по типу рассчитываемого объекта
В этом разделе все решения распределены по типу рассчитываемого объекта: на балки, рамы, фермы и т. д. Каждая представленная здесь категория имеет укрупненную классификацию, которую можно изучить, перейдя по соответствующим ссылкам.
Балки
Примеры данной категории можно разделить на две основные подкатегории:
- статически определимые балки;
- статически неопределимые балки.
Валы
Данные задачи можно поделить на два основных вида:
- статически определимые валы;
- статически неопределимые валы.
Рамы
Данные решения можно классифицировать на 2 основные категории:
- статически определимые рамы;
- статически неопределимые рамы.
Фермы
Все примеры про фермы решено было поместить в одну большую категорию. В этой категории можно встретить задачи на:
- определение реакций в опорах фермы;
- определение продольных усилий в стержнях методом вырезания узлов, либо методом Риттера.
- построение линий влияния.
Сечения
В разделе про сечения, связанные с расчетом геометрических характеристик, принята следующая классификация:
- симметричные и несимметричные сечения, состоящие из геометрических примитивов;
- симметричные и несимметричные сечения, состоящие из металлопрокатных профилей.
Классификация по типу расчета
В этом разделе материалы разделены по типу расчета. Сюда попали расчеты на прочность, жесткость и устойчивость. Здесь же находятся задачи, связанные с расчетом напряжений, эпюр внутренних силовых факторов и другие.
Прочность
В этой категории находятся задачи, связанные с расчетом прочности, при различных видах деформации: изгибе, кручении, растяжении (сжатии) и сложном сопротивлении. Здесь можно встретить как проверочные, так и проектировочные расчета. Найти расчеты на грузоподъемность какой-либо системы.
Жесткость
В расчетах на жесткость, можно найти задачах, в которых исследуются различные элементы конструкций: балки, рамы, валы и другие. Во всех задачах проверяется жесткость, путем сравнения расчетных значений перемещений с допустимыми значениями.
Устойчивость
В примерах на устойчивость, можно найти задачи, связанные с подбором сечения стоек из условия устойчивости, либо расчетом грузоподъемности.
Эпюры
Данная категория, связанна с расчетом эпюр внутренних силовых факторов, при различных видах деформации: растяжении и сжатии, кручении, изгибе и сложном сопротивлении. Есть эпюры, которые откладываются со стороны растянутых волокон (строителям) и сжатых волокон (машиностроителям).
sopromats.ru
Примеры решения задач по сопромату
Статья посвящена решению сопромата, в частности основным разделам по которым решаются задачи. Дано краткое описание того, что необходимо делать, находить, определять в этих задачах каждого раздела. Также собраны ссылки на примеры решения задач по основным разделам сопромата:
На данной страничке собраны ссылки на основные рубрики данного сайта с примерами решения задач по сопромату.
- Стержневые системы
- Пространственные системы (рамы)
- Валы
Классификация по виду деформации:
- Изгиб
- Кручение
- Изгиб с кручением
- Растяжение (сжатие)
Примеры решения задач на геометрические характеристики
 При решении задач, связанных с геометрическими характеристиками, для плоских сечений могут определяться такие вещи как центр тяжести, осевой момент инерции, момент сопротивления, радиус инерции и т.д. Причем задачи могут сильно разница по сложности, все зависит от самого поперечного сечения. Например, для плоского сечения, у которого имеется две оси симметрии, можно сразу сказать, где у него находится центр тяжести, соответственно и положение главных центральных осей. Можно сразу определить главные моменты инерции, потом и момент сопротивления, и радиус инерции.
При решении задач, связанных с геометрическими характеристиками, для плоских сечений могут определяться такие вещи как центр тяжести, осевой момент инерции, момент сопротивления, радиус инерции и т.д. Причем задачи могут сильно разница по сложности, все зависит от самого поперечного сечения. Например, для плоского сечения, у которого имеется две оси симметрии, можно сразу сказать, где у него находится центр тяжести, соответственно и положение главных центральных осей. Можно сразу определить главные моменты инерции, потом и момент сопротивления, и радиус инерции.
Для сечения, у которого только одна ось симметрии, центр тяжести будет лежать на этой оси, но не лежать на другой оси, одну из координат придется вычислять, затем также определять остальные важные геометрические характеристики. Но в задачах могут встречаться и совсем не симметричные поперечные сечения. У простых сечений, которых есть хотя бы одна ось симметрии, вертикальная и горизонтальная осевые линии, проходящие через центр тяжести, являются главными центральными осями, то есть осями относительно которых осевой момент максимален и минимален. У сложных поперечных сечений, без осей симметрий, главные центральные оси проходят через центр тяжести, но находятся под некоторым углом к вертикальной или горизонтальной оси. Для решения такой задачи, необходимо сначала определить моменты инерции относительно вертикальной и горизонтальной оси проходящей через центр тяжести, центробежный момент инерции, затем уже можно определить тот самый угол, и численные значения главных центральных моментов инерции.
Но в задачах могут встречаться и совсем не симметричные поперечные сечения. У простых сечений, которых есть хотя бы одна ось симметрии, вертикальная и горизонтальная осевые линии, проходящие через центр тяжести, являются главными центральными осями, то есть осями относительно которых осевой момент максимален и минимален. У сложных поперечных сечений, без осей симметрий, главные центральные оси проходят через центр тяжести, но находятся под некоторым углом к вертикальной или горизонтальной оси. Для решения такой задачи, необходимо сначала определить моменты инерции относительно вертикальной и горизонтальной оси проходящей через центр тяжести, центробежный момент инерции, затем уже можно определить тот самый угол, и численные значения главных центральных моментов инерции.
 На тему растяжения (сжатия) можно выделить 4 основных типа задач: статически определимый и неопределимый брус, статически определимая и неопределимая стержневая система. Во всех данных типах задач обязательно вычисляется внутреннее усилие – продольная сила, возникающая в нагруженных элементах при центральном растяжении (сжатии).
На тему растяжения (сжатия) можно выделить 4 основных типа задач: статически определимый и неопределимый брус, статически определимая и неопределимая стержневая система. Во всех данных типах задач обязательно вычисляется внутреннее усилие – продольная сила, возникающая в нагруженных элементах при центральном растяжении (сжатии).
В статически неопределимых задачах, перед тем как определить продольные силы обязательно раскрывается статическая неопределимость. После определения продольных усилий в решении задачи может:
- Вычисляться площадь / площади поперечных сечений конструкции из условия прочности.
- Вычисляться нормальное напряжение / напряжения. По вычисленным напряжениям делается вывод о прочности конструкции путем сравнения расчетного максимального напряжения с допустимым напряжением.
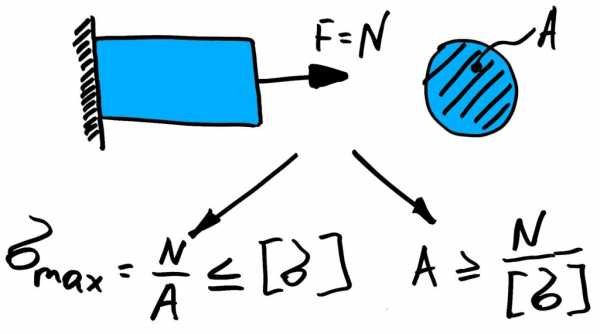
Часто по условию задачи требуется определить осевое перемещение поперечного сечения, найти удлинение (укорочение) стержня.
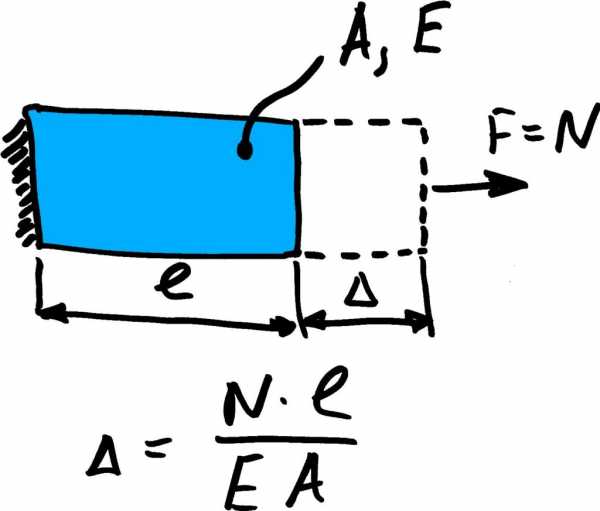
В условии задач обычно требуют строить эпюры от описываемых выше величин: продольной силы, нормального напряжения и перемещения.

Примеры решения задач на кручение
 Задачи на чистое кручение сильно схожи с задачами растяжение (сжатие). В элементах, работающих на кручение, чаще всего валов, возникает также как и при растяжении один внутренний силовой фактор, только не продольная сила, а крутящий момент. Соответственно вместо нормальных напряжений, уже появляются касательные напряжения, которые распределены в поперечном сечении не равномерно, в отличие от нормальных напряжений, появляющихся при растяжении (сжатии). Как видно из рисунка, максимальные напряжения находятся в наиболее удаленных точках сечения.
Задачи на чистое кручение сильно схожи с задачами растяжение (сжатие). В элементах, работающих на кручение, чаще всего валов, возникает также как и при растяжении один внутренний силовой фактор, только не продольная сила, а крутящий момент. Соответственно вместо нормальных напряжений, уже появляются касательные напряжения, которые распределены в поперечном сечении не равномерно, в отличие от нормальных напряжений, появляющихся при растяжении (сжатии). Как видно из рисунка, максимальные напряжения находятся в наиболее удаленных точках сечения.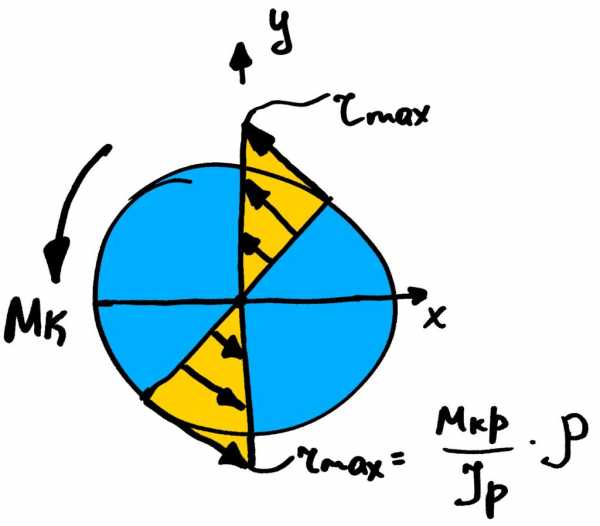
Задачи могут быть проектировочными и проверочными. В первых определяются оптимальные размеры детали, удовлетворяющие условию прочности, а во вторых проверяется прочности детали работающей под заданной нагрузкой.
Помимо крутящих моментов, касательных напряжений, в задачах часто требуют определять относительные углы закручивания или углы поворота поперечных сечений.
Задачи на кручение могут быть как статически определимыми, так и неопределимыми. Статическая неопределимость раскрывается точно так же, как и при центральном растяжении. Составляется дополнительное уравнение совместности деформаций к уравнению равновесия, и выражаются реактивные моменты.
Задачи на поперечный изгиб очень разнообразны, перейдя по ссылке выше можно посмотреть примеры задач на этот вид деформации. В рамках этого блока будем говорить именно о поперечном изгибе, его еще называют плоским или прямым. О более сложных видах изгиба (изгиб с кручением, косой изгиб) поговорим ниже, в рамках раздела – сложное сопротивление. При поперечном изгибе деталей в их поперечных сечениях появляются два внутренних силовых фактора: поперечная сила и изгибающий момент.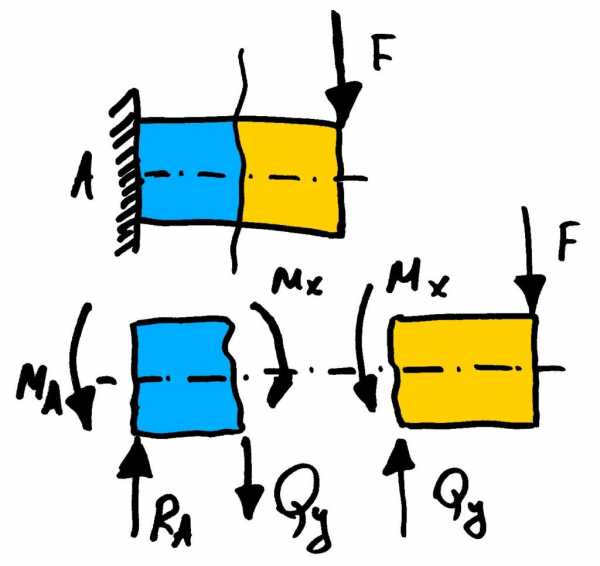
А значит и два типа напряжений: касательные и нормальные. При проведении прочностных расчетов учитываются оба вида напряжений, но особую важность представляют напряжения нормальные, т.к. они, чаще всего, в несколько раз превосходят касательные. Нормальные напряжения можно определить по изгибающему моменту, а касательные определяют с помощью формулы Журавского по поперечной силе.
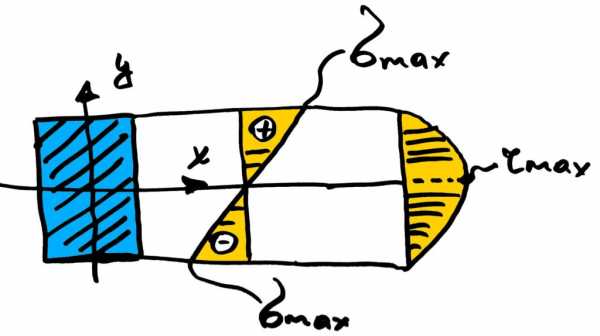
Расчеты на прочность при поперечном изгибе могут быть проверочными и проектировочными. Также часто производят расчеты на грузоподъемность, то есть вычисляют нагрузку, которую может выдержать конструкция, работающая на изгиб.
При решении задач на изгиб могут производиться расчеты на жесткость. Для этого определяют максимальное перемещение или угол поворота поперечного сечения различными методами: Мора-Верещагина, Мора-Симпсона, методом начальных параметров, методом конечных разностей, методом Кастильяно и д.р. После определения перемещений их сравнивают с допустимыми перемещениями. Также иногда в задачах требуют определить размеры конструкции из условия жесткости.
ssopromat.ru
Задачи на изгиб | ПроСопромат.ру
Проектный и проверочный расчеты. Для балки с построенными эпюрами внутренних усилий подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано:
Покажем балку с построенными эпюрами Q и М
Согласно эпюре изгибающих моментов опасным является сечение С, в котором МС=Мmax=48,3кНм.
Условие прочности по нормальным напряжениям для данной балки имеет вид σmax=MC/WX≤σadm. Требуется подобрать сечение из двух швеллеров.
Определим необходимое расчетное значение осевого момента сопротивления сечения:
Для сечения в виде двух швеллеров согласно сортаменту прокатной стали принимаем два швеллера №20а, момент инерции каждого швеллера Ix=1670см4, тогда осевой момент сопротивления всего сечения:
Перенапряжение (недонапряжение) в опасных точках посчитаем по формуле: Тогда получим недонапряжение:
Теперь проверим прочность балки, исходя из условия прочности по касательным напряжениям. Согласно эпюре поперечных сил опасными являются сечения на участке ВС и сечение D. Как видно из эпюры, Qmax=48,9 кН.
Условие прочности по касательным напряжениям имеет вид:
Для швеллера №20 а: статический момент площади Sx1=95,9 см3, момент инерции сечения Ix1=1670 см4, толщина стенки d1=5,2 мм, средняя толщина полки t1=9,7 мм, высота швеллера h1=20 см, ширина полки b1=8 см.
Для поперечного сечения из двух швеллеров:
Sx= 2Sx1=2·95,9=191,8 см3,
Ix=2Ix1=2·1670=3340 см4,
b=2d1=2·0,52=1,04 см.
Определяем значение максимального касательного напряжения:
τmax=48,9·103·191,8·10−6/3340·10−8·1,04·10−2=27МПа.
Как видно, τmax <τadm (27МПа<75МПа).
Следовательно, условие прочности выполняется.
Проверяем прочность балки по энергетическому критерию.
Из рассмотрения эпюр Q и М следует, что опасным является сечение С, в котором действуют MC=Mmax=48,3 кНм и QC=Qmax=48,9 кН.
Проведем анализ напряженного состояния в точках сечения С

Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Определим нормальные и касательные напряжения на нескольких уровнях (отмечены на схеме сечения)
Уровень 1-1: y1-1=h1/2=20/2=10см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 2−2: y2-2=h1/2−t1=20/2−0,97=9,03см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 3−3: y3-3=h1/2−t1=20/2−0,97=9,03см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 4−4: y4-4=0.
Нормальные и касательные напряжения:(в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 5−5:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 6−6:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 7−7:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
В соответствии с выполненными расчетами эпюры напряжений σ, τ, σ1, σ3, τmax и τmin представлены на рис. Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Анализ этих эпюр показывает, что в сечении балки опасными являются точки на уровне 3-3 (или 5-5), в которых:
Используя энергетический критерий прочности, получим
Из сравнения эквивалентного и допускаемого напряжений следует, что условие прочности также выполняется
(135,3 МПа<150 МПа).
prosopromat.ru
Задачи на растяжение и сжатие (задачи по сопромату)
Пример решения задачи на растяжение и сжатие
.Условие задачи на растяжение и сжатие
 Стальной стержень (модуль Юнга кН/см2) с размерами см; см, см и площадью поперечного сечения нижнего участка см2, а верхнего – см2 нагружен внешними осевыми силами кН и кН. Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Стальной стержень (модуль Юнга кН/см2) с размерами см; см, см и площадью поперечного сечения нижнего участка см2, а верхнего – см2 нагружен внешними осевыми силами кН и кН. Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Расчетная схема для задачи на растяжение и сжатие
рис 3.2
Решение пример задачи на растяжение и сжатие
Определяем значение опорной реакции , возникающей в заделке
Учитывая, что , направим опорную реакцию вниз. Тогда из уравнения равновесия находим:
кН.
Строим эпюру продольных сил
Разбиваем длину стержня на три участка. Границами участков являются сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений. Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Cечение 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. 3.2, б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила уравновесит внешнюю силу . Поэтому очевидно, что
кН.
Сечение 2 – 2. Внешняя сила растягивает рассматриваемую нами нижнюю часть стержня, а сила ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила , противодействующая сжатию, то есть направленная к сечению. Она равна:
кН.
Сечение 3 – 3. Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю (реактивную) сжимающую силу . Поэтому она направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействует сжатию. Она равна:
кН.
При построении эпюры продольных сил будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию. Оно вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому кН.
Для построения эпюры продольных сил проводим тонкой линией ось, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. 3.2, д, никак не сказывается на характере эпюры .
Строим эпюру нормальных напряжений
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и – продольная сила и площадь k–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
кН/см2,
во втором –
кН/см2,
в третьем –
кН/см2.
Строим по вычисленным значениям эпюру (рис. 3.2, е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
Оцениваем прочность стержня
Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем случае
кН/см2 > кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
Вычисляем удлинение всего стержня
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
,
где E – модуль Юнга, а – длина соответствующего участка стержня.
Тогда
см.
Таким образом, длина стержня уменьшается на мм.
Задача по сопромату на растяжение и сжатие для самостоятельного решения
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) находится под действием внешних осевых сил и (рис. 3.1). Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Схемы для задачи на растяжение и сжатие

Исходные данные к задаче на растяжение и сжатие
Номер схемы | F, см2 | a, м | b, м | c, м | P, кН |
1 | 2,0 | 1,2 | 1,4 | 1,6 | 11 |
2 | 2,2 | 1,4 | 1,6 | 1,4 | 12 |
3 | 2,4 | 1,8 | 1,6 | 1,2 | 13 |
4 | 2,6 | 1,6 | 2,0 | 1,0 | 14 |
5 | 2,8 | 2,0 | 1,8 | 1,2 | 15 |
6 | 3,0 | 2,2 | 1,6 | 1,4 | 16 |
7 | 3,2 | 2,4 | 1,4 | 1,6 | 17 |
8 | 3,4 | 2,6 | 1,2 | 1,8 | 18 |
9 | 3,6 | 2,8 | 1,0 | 1,4 | 19 |
0 | 3,8 | 2,4 | 1,6 | 1,2 | 20 |
sopromato.ru
Прямой поперечный изгиб (задачи по сопромату)
Пример решения задачи «прямой поперечный изгиб» №1
Условие примера задачи на прямой поперечный изгиб
Для консольной балки, нагруженной распределенной нагрузкой интенсивностью кН/м и сосредоточенным моментом кН·м (рис. 3.12), требуется: построить эпюры перерезывающих сил и изгибающих моментов , подобрать балку круглого поперечного сечения при допускаемом нормальном напряжении кН/см2 и проверить прочность балки по касательным напряжениям при допускаемом касательном напряжении кН/см2. Размеры балки м; м; м.
Расчетная схема для задачи на прямой поперечный изгиб
 Рис. 3.12
Рис. 3.12
Решение задачи «прямой поперечный изгиб»
Определяем опорные реакции
Горизонтальная реакция в заделке равна нулю, поскольку внешние нагрузки в направлении оси z на балку не действуют.
Выбираем направления остальных реактивных усилий, возникающих в заделке: вертикальную реакцию направим, например, вниз, а момент – по ходу часовой стрелки. Их значения определяем из уравнений статики:
.
Составляя эти уравнения, считаем момент положительным при вращении против хода часовой стрелки, а проекцию силы положительной, если ее направление совпадает с положительным направлением оси y.
Из первого уравнения находим момент в заделке :
кН·м.
Из второго уравнения – вертикальную реакцию :
кН.
Полученные нами положительные значения для момента и вертикальной реакции в заделке свидетельствуют о том, что мы угадали их направления.
Строим эпюры перерезывающих сил и изгибающих моментов
В соответствии с характером закрепления и нагружения балки, разбиваем ее длину на два участка. По границам каждого из этих участков наметим четыре поперечных сечения (см. рис. 3.12), в которых мы и будем методом сечений (РОЗУ) вычислять значения перерезывающих сил и изгибающих моментов.
Сечение 1. Отбросим мысленно правую часть балки. Заменим ее действие на оставшуюся левую часть перерезывающей силой и изгибающим моментом . Для удобства вычисления их значений закроем отброшенную нами правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением.
Напомним, что перерезывающая сила, возникающая в любом поперечном сечении, должна уравновесить все внешние силы (активные и реактивные), которые действуют на рассматриваемую (то есть видимую) нами часть балки. Поэтому перерезывающая сила должна быть равна алгебраической сумме всех сил, которые мы видим.
Приведем и правило знаков для перерезывающей силы: внешняя сила, действующая на рассматриваемую часть балки и стремящаяся «повернуть» эту часть относительно сечения по ходу часовой стрелки, вызывает в сечении положительную перерезывающую силу. Такая внешняя сила входит в алгебраическую сумму для определения со знаком «плюс».
В нашем случае мы видим только реакцию опоры , которая вращает видимую нами часть балки относительно первого сечения (относительно края листка бумаги) против хода часовой стрелки. Поэтому
кН.
Изгибающий момент в любом сечении должен уравновесить момент, создаваемый видимыми нами внешними усилиями, относительно рассматриваемого сечения. Следовательно, он равен алгебраической сумме моментов всех усилий, которые действуют на рассматриваемую нами часть балки, относительно рассматриваемого сечения (иными словами, относительно края листка бумаги). При этом внешняя нагрузка, изгибающая рассматриваемую часть балки выпуклостью вниз, вызывает в сечении положительный изгибающий момент. И момент, создаваемый такой нагрузкой, входит в алгебраическую сумму для определения со знаком «плюс».
Мы видим два усилия: реакцию и момент в заделке . Однако у силы плечо относительно сечения 1 равно нулю. Поэтому
кН·м.
Знак «плюс» нами взят потому, что реактивный момент изгибает видимую нами часть балки выпуклостью вниз.
Напомним, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении (то есть левый край листка бумаги нами мысленно представляется жесткой заделкой).
Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки. Теперь, в отличие от первого сечения, у силы появилось плечо: м. Поэтому
кН; кН·м.
Сечение 3. Закрывая правую часть балки, найдем
кН;
кН·м.
Сечение 4. Закроем листком левую часть балки. Тогда
кН;
кН·м.
Сечение 5. По-прежнему закроем левую часть балки. Будем иметь
кН;
кН·м.
Сечение 6. Опять закроем левую часть балки. Получим
.
По найденным значениям строим эпюры перерезывающих сил (рис. 3.12, б) и изгибающих моментов (рис. 3.12, в).
Под незагруженными участками эпюра перерезывающих сил идет параллельно оси балки, а под распределенной нагрузкой q – по наклонной прямой вверх. Под опорной реакцией на эпюре имеется скачок вниз на величину этой реакции, то есть на 40 кН.
На эпюре изгибающих моментов мы видим излом под опорной реакцией . Угол излома направлен навстречу реакции опоры. Под распределенной нагрузкой q эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре – экстремум, поскольку эпюра перерезывающей силы в этом месте проходит здесь через нулевое значение.
Определяем требуемый диаметр поперечного сечения балки
Условие прочности по нормальным напряжениям имеет вид:
,
где – момент сопротивления балки при изгибе. Для балки круглого поперечного сечения он равен:
.
Наибольший по абсолютному значению изгибающий момент возникает в третьем сечении балки: кН·см.
Тогда требуемый диаметр балки определяется по формуле
см.
Принимаем мм. Тогда
кН/см2 кН/см2.
«Перенапряжение» составляет
,
что допускается.
Проверяем прочность балки по наибольшим касательным напряжениям
Наибольшие касательные напряжения, возникающие в поперечном сечении балки круглого сечения, вычисляются по формуле
,
где – площадь поперечного сечения.
Согласно эпюре , наибольшее по алгебраической величине значение перерезывающей силы равно кН. Тогда
кН/см2 кН/см2,
то есть условие прочности и по касательным напряжениям выполняется, причем, с большим запасом.
Пример решения задачи «прямой поперечный изгиб» №2
Условие примера задачи на прямой поперечный изгиб
Для шарнирно опертой балки, нагруженной распределенной нагрузкой интенсивностью кН/м, сосредоточенной силой кН и сосредоточенным моментом кН·м (рис. 3.13), требуется построить эпюры перерезывающих сил и изгибающих моментов и подобрать балку двутаврового поперечного сечения при допускаемом нормальном напряжении кН/см2 и допускаемом касательном напряжении кН/см2. Пролет балки м.
Пример задачи на прямой изгиб – расчетная схема
 |
Решение примера задачи на прямой изгиб
Определяем опорные реакции
Для заданной шарнирно опертой балки необходимо найти три опорные реакции: , и . Поскольку на балку действуют только вертикальные нагрузки, перпендикулярные к ее оси, горизонтальная реакция неподвижной шарнирной опоры A равна нулю: .
Направления вертикальных реакций и выбираем произвольно. Направим, например, обе вертикальные реакции вверх. Для вычисления их значений составим два уравнения статики:
; .
Напомним, что равнодействующая погонной нагрузки , равномерно распределенной на участке длиной l, равна , то есть равна площади эпюры этой нагрузки и приложена она в центре тяжести этой эпюры, то есть посредине длины.
Тогда
кН;
;
кН.
Делаем проверку: .
Напомним, что силы, направление которых совпадает с положительным направлением оси y, проектируются (проецируются) на эту ось со знаком плюс:
,
то есть верно.
Строим эпюры перерезывающих сил и изгибающих моментов
Разбиваем длину балки на отдельные участки. Границами этих участков являются точки приложения сосредоточенных усилий (активных и/или реактивных), а также точки, соответствующие началу и окончанию действия распределенной нагрузки. Таких участков в нашей задаче получается три. По границам этих участков наметим шесть поперечных сечений, в которых мы и будем вычислять значения перерезывающих сил и изгибающих моментов (рис. 3.13, а).
Сечение 1. Отбросим мысленно правую часть балки. Для удобства вычисления перерезывающей силы и изгибающего момента , возникающих в этом сечении, закроем отброшенную нами часть балки листком бумаги, совмещая левый край листка бумаги с самим сечением.
Перерезывающая сила в сечении балки равна алгебраической сумме всех внешних сил (активных и реактивных), которые мы видим. В данном случае мы видим реакцию опоры и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
кН.
Знак «плюс» взят потому, что сила вращает видимую нами часть балки относительно первого сечения (края листка бумаги) по ходу часовой стрелки.
Изгибающий момент в сечении балки равен алгебраической сумме моментов всех усилий, которые мы видим, относительно рассматриваемого сечения (то есть относительно края листка бумаги). Мы видим реакцию опоры и погонную нагрузку q, распределенную на бесконечно малой длине. Однако у силы плечо равно нулю. Равнодействующая погонной нагрузки также равна нулю. Поэтому
.
Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки. Теперь мы видим реакцию и нагрузку q, действующую на участке длиной . Равнодействующая погонной нагрузки равна . Она приложена посредине участка длиной . Поэтому
кН;
кН·м.
Напомним, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении (то есть левый край листка бумаги нами мысленно представляется жесткой заделкой).
Сечение 3. Закроем правую часть. Получим
кН;
кН·м.
Сечение 4. Закрываем листком правую часть балки. Тогда
кН;
кН·м.
Теперь, для контроля правильности вычислений, закроем листком бумаги левую часть балки. Мы видим сосредоточенную силу P, реакцию правой опоры и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
кН;
кН·м.
То есть все верно.
Сечение 5. По-прежнему закроем левую часть балки. Будем иметь
кН;
кН·м.
Сечение 6. Опять закроем левую часть балки. Получим
кН;
.
По найденным значениям строим эпюры перерезывающих сил (рис. 3.13, б) и изгибающих моментов (рис. 3.13, в).
Убеждаемся в том, что под незагруженным участком эпюра перерезывающих сил идет параллельно оси балки, а под распределенной нагрузкой q – по прямой, имеющей наклон вниз. На эпюре имеется три скачка: под реакцией – вверх на 37,5 кН, под реакцией – вверх на 132,5 кН и под силой P – вниз на 50 кН.
На эпюре изгибающих моментов мы видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой интенсивностью q эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. Под сосредоточенным моментом – скачок на 60 кН ·м, то есть на величину самого момента. В сечении 7 на эпюре – экстремум, поскольку эпюра перерезывающей силы для этого сечения проходит через нулевое значение (). Определим расстояние от сечения 7 до левой опоры.
Перерезывающая сила
.
Отсюда
м.
Экстремальное значение изгибающего момента в сечении 7 равно:
кН·м.
Определяем требуемый момент сопротивления балки из условия прочности по нормальным напряжениям
Согласно эпюре , максимальный по алгебраической величине изгибающий момент возникает в третьем поперечном сечении балки: кН·см. Тогда
см3.
По сортаменту (см. прил. 1, табл. П1.3) подбираем двутавр № 30а, имеющий см3.
Проверяем прочность балки по наибольшим касательным напряжениям
Наибольшие касательные напряжения, возникающие в поперечном сечении двутавровой балки, вычисляются по формуле
.
По сортаменту для выбранного нами двутавра определяем, что статический момент половины сечения относительно нейтральной оси см3, момент инерции относительно нейтральной оси см4, а толщина стенки см.
Согласно эпюре , наибольшее по алгебраической величине значение перерезывающей силы кН. Тогда
кН/см2 кН/см2,
то есть условие прочности по касательным напряжениям выполняется.
Варианты задач по теме «прямой поперечный изгиб» для самостоятельного решения
Условие задачи на прямой изгиб для самостоятельного решения
Для двух заданных схем балок (рис. 3.11) требуется:
1. построить эпюры перерезывающих сил и изгибающих моментов ;
2. подобрать из условия прочности по нормальным напряжениям ( кН/см2) балку круглого поперечного сечения для схемы a и балку двутаврового поперечного сечения для схемы б;
3. проверить прочность подобранных балок по касательным напряжениям (кН/см2).
Варианты расчетных схем
Рис. 3.11
 |
Варианты исходных данных к задаче для самостоятельного решения «прямой поперечный изгиб»
Номер схемы (рис. 3.11) | l, м | M, кН·м | P, кН | q, кН/м | |||
1 | 3 | 0,2 | 0,6 | 0,2 | 8 | 5 | 10 |
2 | 4 | 0,3 | 0,5 | 0,3 | 7 | 6 | 11 |
3 | 5 | 0,4 | 0,4 | 0,3 | 6 | 7 | 12 |
4 | 6 | 0,5 | 0,3 | 0,2 | 5 | 8 | 13 |
5 | 3 | 0,6 | 0,7 | 0,2 | 4 | 9 | 14 |
6 | 4 | 0,7 | 0,5 | 0,3 | 8 | 10 | 9 |
7 | 5 | 0,8 | 0,4 | 0,6 | 7 | 5 | 10 |
8 | 6 | 0,2 | 0,6 | 0,3 | 6 | 6 | 11 |
9 | 3 | 0,3 | 0,5 | 0,4 | 5 | 7 | 12 |
0 | 4 | 0,4 | 0,4 | 0,2 | 4 | 8 | 8 |
sopromato.ru