Примеры решения задач

1.2.1. Расчет статически неопределимого составного стержня, работающего на растяжение-сжатие (задача № 4) Условие задачи

Рис. 1.8. Схема нагрузки на стержень

в задаче № 4

Стержень переменного сечения с заданным соотношением площадей поперечного сечения, выполненный из разного материала, загружен силойF(рис. 1.8). Между правым концом стержня и стенкой существует зазор.

Требуется:

1. определить продольные силы, напряжения на каждом участке и проверить прочность стержня от действия заданной нагрузки F.

2. найти дополнительные напряжения, возникающие в стержне при его нагревании на температуру и проверить прочность стержня от температурного воздействия.

Решение

1. Определение напряжений от заданной нагрузки

Прежде всего надо убедиться, что заданная система является статически неопределимой. Найдем абсолютную деформацию стержня, показанного на рис. 1.8, предполагая сначала, что правая стенка отсутствует. Тогда, используя метод сечений, определим продольные силы на трех участках стержня:

на первом участке длиной ;

на втором и третьем участках .

Полное удлинение стержня, равное в общем случае , в данной задаче равно удлинению первого участка и, следовательно, по (1.3)

.

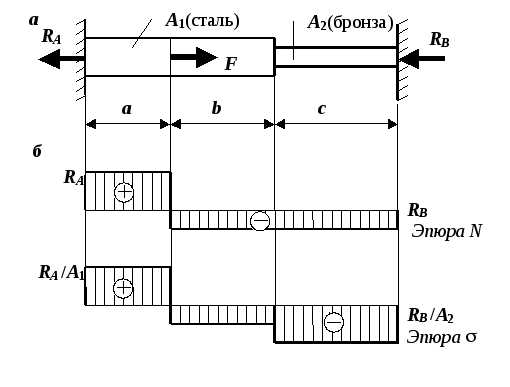
Рис. 1.9. К решению задачи № 4:

а – план сил от действия F,

б – эпюры продольной силы и напряжений от F

Если под действием нагрузки абсолютная деформациястержня будет больше заданного зазора, то стержень упрется правым концом в стенку и возникнут опорные реакции как в левом защемлении (), так и в правом опорном закреплении () (рис. 1.9,

а). Для заданной системы можно составить только одно независимое уравнение статики. Таким образом, две неизвестные опорные реакции нельзя найти из одного уравнения, и система в процессе деформации становится один раз статически неопределимой.

Для раскрытия статической неопределимости используем расчет по упругой стадии деформаций и запишем три группы уравнений:

1. уравнения равновесия. Из них получим:

• для всего стержня ;

• для отсеченных частей стержня Заметим, что при составлении уравнений равновесия отсеченных частей стержня сделано предположение, что первая и вторая части стержня растянуты, а третья часть – сжата;

1. уравнение совместности деформаций, смысл которого в данной задаче очень простой: полная деформация стержня равна заданному зазору. При составлении уравнения совместности деформаций важно, чтобы знаки абсолютных деформаций соответствовали сделанным предположениям о направлении усилий. В нашем примере ;

2. физические уравнения

.

Решив полученную систему уравнений, найдем продольные силы, а затем напряжения в разных частях стержня и построим эпюры их распределения по длине стержня (рис. 1.9, б). Если знак усилия после решения системы уравнений получился отрицательным, это означает, что сделанное предположение о направлении продольной силы не подтвердилось. В рассмотренной задаче отрицательным должно получиться усилие, т. е. второй участок длинойb не растянут, а сжат. ЗнакиNиsна эпюрах ставим в соответствии с правилом знаков для продольной силы.

После определения напряжений производим проверку прочности по формулам (1.5) или (1.7) так же, как в статически определимой системе. Если условие прочности на каком-нибудь участке стержня не будет выполняться, измените значение

Fтак, чтобы условие прочности соблюдалось.

2. Определение температурных напряжений

Найдем удлинение стержня от температурного воздействия и убедимся в том, что это удлинение больше заданного зазора.

.

Рис. 1.10. К решению задачи № 4: а – план сил от действия ,

б – эпюры продольной силы и напряжений от

Если>, то система является один раз статически неопределимой и раскрытие статической неопределимости производим по той же схеме, что и в предыдущей части задачи:

Из уравнений равновесия следует, что и. Здесь в соответствии с рис. 1.10,

апредполагаем, что стержень всюду сжат. (СилуF при определении температурных напряжений считаем равной нулю.)

Уравнение совместности деформации показывает, что абсолютная деформация стержня, равная разности удлинения стержня от температурного воздействияи укорочения от действия сжимающих продольных силне может быть больше заданного зазора:

,

где .

Укорочение стержня от действия продольных сил найдем, используя физические уравнения (закон Гука):

и.

После решения полученной системы уравнений найдем усилия в обеих частях стержня. Полученный положительный знак должен подтвердить предположение о том, что стержень сжат. Строим эпюры продольной силы и напряжений (рис. 1.10, б) от температурного воздействия.

Проверяем прочность стержня и в случае невыполнения условия прочности на каком-нибудь участке находим новое значение , при котором условие прочности будет соблюдаться на всех участках.

studfiles.net

Сопромат задачи на растяжение сжатие примеры решения

В треугольнике ABC AC=BC, AD высота, угол BAD равен 28. Найдите угол C. Решение: AC=BC треугольник ABC равнобедренный, углы A и B равны. Найдем угол B из прямоугольного треугольника ABD 90-28=62 180-62-62=56. Ответ: 56. Отправить по электронной почтеНаписать об этом в.

Примеры решения задач по сопромату

Приветствую тебя, читатель сайта — sopromats. ru, на котором размещено много полезной и интересной информации о сопромате и не только. Сегодня я решил написать большую статью о примерах решения задач по сопромату, которые размещены на этом ресурсе. Все примеры было решено классифицировать на три категории: по виду деформации, по виду рассчитываемого объекта и по типу расчета. Эти категории имеют три уровня вложенности. Например, в категории — по виду деформации входят задачи, связанные с изгибом, кручением, растяжением (сжатием) и сложным сопротивлением. В свою очередь, решения на изгиб классифицируются на статически определимые и неопределимые. Для того, чтобы найти нужную категорию перемещайтесь по указанным ссылкам на страничках. Также хотелось бы отметить, что на данный момент на сайте преобладают рукописные примеры решения. Но наша команда, активно работает над добавлением электронных материалов: с качественными схемами и набранными в цифровом виде расчетами. По мере развития сайта, все рукописные записи, планируется заменить цифровыми. Ну что же перейдем непосредственно к нашим примерам.

Классификация по виду деформации

Как уже говорилось выше, здесь все примеры отсортированы по виду деформации: растяжению и сжатию, кручению, изгибу и сложному сопротивлению. В категорию задач на сложное сопротивление попадают такие популярные решения на такие темы как изгиб с кручением, внецентренное растяжение (сжатие), косой изгиб. Теперь давайте перейдем непосредственно к категориям и не забывайте переходить по ссылкам на интересующую вас подкатегории.

Что можно найти в данной категории задач?

определение реакций в опорах из уравнений равновесия статики; расчет ВСФ методом сечений; вычисление продольной и поперечной силы; расчет изгибающего момента; расчет нормальных и касательных напряжений; вычисление перемещений поперечных сечений; раскрытие статической неопределимости с использованием уравнения совместности деформации.

Растяжение и сжатие

статически определимые брусья; статически неопределимые брусья; статически определимые стержневые системы; статически неопределимые стержневые системы.

Примеры задач на кручение распределены по 2 основным категориям:

статически определимое кручение; статически неопределимое кручение.

Задачи на изгиб подразделяются по тем же признакам:

статически определимый изгиб; статически неопределимый изгиб.

Классификация по типу рассчитываемого объекта

В этом разделе все решения распределены по типу рассчитываемого объекта: на балки, рамы, фермы и т. д. Каждая представленная здесь категория имеет укрупненную классификацию, которую можно изучить, перейдя по соответствующим ссылкам.

Решения, связанные с балками, можно разделить на две основные подкатегории:

статически определимые балки; статически неопределимые балки.

статически определимые валы; статически неопределимые валы.

статически определимые рамы; статически неопределимые рамы.

Все примеры решения задач, связанные с расчетом ферм, решено было поместить в одну большую категорию. В этой категории можно встретить задачи на:

определение реакций в опорах фермы; определение продольных усилий в стержнях методом вырезания узлов, либо методом Риттера; построение линий влияния.

В разделе про сечения, связанные с расчетом геометрических характеристик, принята следующая классификация:

симметричные и несимметричные сечения, состоящие из геометрических примитивов; симметричные и несимметричные сечения, состоящие из металлопрокатных профилей.

Классификация по типу расчета

В этом разделе материалы разделены по типу расчета. Сюда попали расчеты на прочность, жесткость и устойчивость. Здесь же находятся задачи, связанные с расчетом напряжений, эпюр внутренних силовых факторов и другие.

В этой категории находятся задачи, связанные с расчетом прочности, при различных видах деформации: изгибе, кручении, растяжении (сжатии) и сложном сопротивлении. Здесь можно встретить как проверочные, так и проектировочные расчета. Найти расчеты на грузоподъемность какой-либо системы.

В расчетах на жесткость, можно найти задачах, в которых исследуются различные элементы конструкций: балки, рамы, валы и другие. Во всех задачах проверяется жесткость, путем сравнения расчетных значений перемещений с допустимыми значениями.

Устойчивость

В примерах на устойчивость, можно найти задачи, связанные с подбором сечения стоек из условия устойчивости, либо расчетом грузоподъемности.

Данная категория, связанна с расчетом эпюр внутренних силовых факторов, при различных видах деформации: растяжении и сжатии, кручении, изгибе и сложном сопротивлении. Есть эпюры, которые откладываются со стороны растянутых волокон (строителям) и сжатых волокон (машиностроителям).

Сопромат задачи на растяжение сжатие примеры решения

Растяжение и сжатие. Усилия в поперечном сечении стержня.

Центральным растяжением или сжатием в сопромате называется такой вид деформации, при котором в поперечных сечениях стержня возникает только продольная сила N, а все остальные усилия равны нулю.

Продольная сила N — равнодействующая внутренних сил в поперечном сечении стержня. В сопротивлении материалов она определяется из условия равновесия отсеченной части, и численно равна сумме проекций на продольную ось стержня всех внешних сил, расположенных по одну сторону от сечения.

При растяжении продольная сила направлена от сечения и считается положительной. При сжатии она направлена к сечению и считается отрицательной.

Эпюра продольных сил — график величин этих усилий для всех поперечных сечений стержня.

Пример Решения задачи по сопромату на растяжение — сжатие. Построить эпюру продольных сил для стержня, изображенного на рис. 4,а.

Решение. Проводим сечение 1-1 в пределах первого участка и отбрасываем правую часть стержня. К оставшейся левой части прикладываем неизвестную силу N1, предполагая ее положительной и направляя от сечения. Из уравнения равновесия отсеченной части получим N1-3P=0 => N1=3P

2-ой участок N2 – P – 3P =0 N2=4P

3-й участок N3 +6P-P-3P=0 N3= -2P

4-й участок N4-4P+6P-P-3P=0 N4=2P

Для контроля определим N4 из рассмотрения правой части стержня.

По найденным значениям N на рис. 4, в построена эпюра продольных сил. Из эпюры следует, на участках 1,2 и 4 стержень растянут, а на участке 3 сжат. Так ведется решение задач на растяжение и сжатие в сопромате.

Напряжения и деформации. Растяжение и сжатие. Сопромат решение задач

При растяжении-сжатии стержня с постоянными поперечными размерами в любом поперечном сечении возникают нормальные напряжения, равномерно распределенные по сечению и равные

Где N — продольная сила в сечении;

А — площадь поперечного сечения.

Эта формула справедлива только для поперечных сечений, отстоящих от места приложения нагрузки на расстоянии не меньшем поперечного размера стержня (принцип Сен-Венана).

Вблизи места приложения нагрузки напряжения распределяются

В случае однородного стержня, растянутого или сжатого силами, приложенными на концах, напряжения остаются постоянными как по сечению, так и по длине, т. е. одинаковы для всех точек объема стержня

Такое напряженное состояние в сопромате называется однородным.

Продольную деформацию стержня характеризуют следующие величины (рис. 5).

Абсолютная продольная деформация (удлинение при растяжении и укорочении при сжатии) ^ l = l1-l

Где 1 — первоначальная длина стержня;

L1 — конечная длина.

Поперечную деформацию стержня В сопротивление материаловХарактеризуют следующие величины:

Абсолютная поперечная деформация ^b = b – b1,

Где b — первоначальный поперечный размер,

B1 — поперечный размер после деформации

Относительная поперечная деформация e 1 = ^b / b

При растяжении продольную деформацию можно считать положительной (е > 0), а поперечную отрицательной (е 1 < 0).

При сжатии, наоборот e < 0, е 1 > 0.

Абсолютная величина отношения e1 к е называется коэффициентом Пуассона,

Коэффициент Пуассона M (мю) — величина безразмерная и его значение

Для различных материалов колеблется в пределах от 0 до 0,5. Объемная деформация характеризуется относительным изменением объема

Где ^V — абсолютное изменение объема;

V — Первоначальный объем стержня.

Закон Гука о = e Е,

Где Е — коэффициент пропорциональности, называемый модулем продольной упругости, который имеет размерность Па, кПа, мПа.

Закон Гука справедлив, пока напряжения не превосходят определенной для каждого материала величины, называемой пределом пропорциональности.

Абсолютное удлинение стержня постоянного сечения при постоянном по его длине значении продольной силы определяется по формуле: ^l = Nl / EA — закон Гука

Где ЕА – жесткость сечения. Эта формула очень важна в курсе изучения сопротивления материалов вообще и в решении задач по сопромату в частности.

Для продолжения скачивания необходимо собрать картинку:

Сопромат задачи на растяжение сжатие примеры решения

Техническая механика

Решение задач по сопромату

Примеры решения задач по сопротивлению материалов

Как и в предыдущей статье, на этой странице приведены основные принципы решения задач технической механики на примере простейших заданий, в которых необходимо определить какие-либо силовые факторы, возникающие в конструкциях и телах напряжения, построить эпюры и т. п. Сопротивление материалов является базовой основой для решения вопросов наиболее практического раздела технической механики — «Детали машин».

Решение задачи на растяжение и сжатие

Построить эпюру напряжений в ступенчатом круглом брусе, нагруженном продольными силами и указать на наиболее напряженный участок.

Весом бруса пренебречь.

Площадь сечения бруса: А = 0,1 м 2 .

При построении эпюры напряжений используем метод сечений, рассматривая отдельные участки бруса, как самостоятельные его элементы, находящиеся в состоянии равновесия под действием реальных и условных нагрузок. При этом исследование сечений начинаем со стороны свободного конца бруса, т. е. со стороны, где приложены известные нам силы.

Сначала разбиваем весь брус на однородные участки, границами которых служат точки приложения силовых факторов и (или) изменение размеров сечения. Для нашего бруса можно выделить три таких однородных участка — I, II, III (см. схему 2) .

Для каждого из участков определяем нормальные напряжения в сечениях по формуле σ = F/A, где: F — величина продольной силы в сечении, А — площадь сечения. При этом следует учитывать знаки: если сила растягивающая, то ее условно считают положительной, если сжимающая — отрицательной. Соответственно, напряжения будут иметь такие же знаки, как и силы.

После подсчетов получим:

Построение эпюры напряжений начинаем с проведения линии, параллельной оси бруса (эта линия условно изображает брус и является нулевой ординатой графика эпюры) . Затем, начиная от свободного конца бруса, откладываем от линии, как от нулевой ординаты, величины напряжений по каждому участку с учетом их знаков.

На брусе, приведенном в задании, величина напряжений в каждом сечении отдельных участков будет одинакова, и лишь в граничных (расположенных между соседними участками) сечениях появится скачок напряжения в виде ступени (здесь используется принцип Сен-Венана, условно полагающий, что в месте приложения нагрузки напряжение изменяется скачкообразно) .

Построение эпюры завершается указанием на ее площадках знаков напряжения в кружках, проведением тонких линий перпендикулярно оси (нулевой ординаты) эпюры (эти линии условно изображают сечения бруса) и расстановкой величины напряжений на внешних углах графика (на внутренних углах цифровые обозначения не наносятся) . Слева от эпюры указывается, что на ней изображено (в нашем случае — Эпюра σ )

В результате построений мы получим график (эпюру) распределения напряжений по каждому сечению бруса, визуальное исследование которого позволяет определить наиболее напряженный участок. Для бруса, представленного в задаче, максимальные напряжения возникают в сечениях участка III (см. схему) . Поскольку эти напряжения положительны, они являются растягивающими

Решение задачи с использованием закона Гука

Определить величину растягивающей силы F , если известно, что под ее действием брус удлинился на величину ΔL .

Модуль продольной упругости балки Е = 2,0×10 5 МПа;

Площадь сечения бруса A = 0,01 м 2 ;

Размеры бруса и точка приложения силы F приведены на схеме.

Решить задачу можно, используя известную зависимость между линейными удлинениями и нагрузками (закон Гука).

Согласно закону Гука, представленному в расширенном виде:

ΔL = FL/(EA) , откуда: F = (ΔLEA)/L.

Поскольку сила F приложена не к крайнему сечению бруса, а к его середине, то удлинился лишь участок между жесткой заделкой и сечением, к которому приложена растягивающая сила, имеющий длину L1 = 2 м.

Учитывая это, определяем силу, вызвавшую удлинение бруса (не забываем привести все величины к единицам системы СИ):

F = (ΔLEA)/L1 = (0,005×10 -3 ×2×10 11 ×0,01)/2 = 5000 Н = 5,0 кН.

Решение задачи на срез и смятие

Венец зубчатого колеса прикреплен к ступице болтовыми соединениями из шести болтов с гайками, размещенными равномерно по окружности диаметром D .

При расчете не учитывать ослабление стержня болта впадинами резьбы.

Диаметр окружности, на которой размещены болтовые соединения D = 0,4 м;

Диаметр стержня болта d = 10 мм.

Для решения задачи воспользуемся зависимостью между напряжением среза, внешней нагрузкой и площадью сечения по плоскости среза:

Где: τср — касательное напряжение среза, Fокр — окружная сила на расстоянии от оси вращения до центра болта, A — площадь сечения (в нашем случае — площадь поперечного сечения 6 болтов) .

Окружную силу можно определить, зная крутящий (вращающий) момент на валу зубчатого колеса и расстояние от оси вращения зубчатого колеса до центра болта:

Подставив эти значения в исходную формулу, определим касательное напряжение сдвига (среза) болта:

Τср = Fокр /A = (2Мкр/D) / (3πd 2 /2) = (2×10/0,4) / (3×3,14 0,01 2 /2) ≈ 106 000 Па (или 0,106 МПа) .

Решение задачи на срез и смятие шпонки

Произвести проверочный расчет призматической шпонки на смятие.

Радиус сечения вала r = 30 мм;

Высота шпонки h = 6 мм;

Рабочая длина шпонки lр = 30 мм;

Допускаемое напряжение на смятие [σ]см = 200 МПа

Решение задачи сводится к определению напряжения смятия, возникающего в продольном сечении шпонки, выступающем над канавкой вала (рабочая площадь шпонки) . Это напряжение можно определить из формулы:

Где: σсм — искомое напряжение смятия,

Fокр — окружная сила, действующая на рабочую поверхность шпонки: Fокр = Т/r.

Учитывая, что высота рабочей поверхности шпонки невелика, можно принять для расчета напряжения окружную силу, действующую на расстоянии R от оси вращения вала (радиус вала). Если необходимо выполнить более точный расчет, следует к радиусу вала прибавить половину высоты рабочей поверхности шпонки (в нашем случае — h/4).

Aраб — площадь шпонки, подвергаемая смятию: Aраб = hlр /2 (здесь lр — рабочая длина шпонки) .

Подставив полученные значения окружной силы и площади шпонки, работающей на смятие, в формулу (1) , получим:

Полученное напряжение сравниваем с допускаемым напряжением смятия [σсм] = 200 МПа, и делаем вывод, что шпонка выдержит нагрузку.

Решение задачи на кручение

Построить эпюру вращающих моментов для круглого однородного бруса, представленного на схеме. Указать наиболее нагруженный участок бруса и определить напряжение в его сечениях.

Диаметр бруса d = 0,05 м.

Построение эпюр вращающих (крутящих моментов) начинаем со стороны свободного конца бруса, откладывая величины крутящих моментов от оси абсцисс (нулевой ординаты) бруса с соблюдением знаков моментов (см. схему) .

Из эпюры очевидно, что максимальный крутящий момент возникает в сечениях участка I: Мкр = 500 Нм. Для определения напряжения (при кручении возникает касательное напряжение), воспользуемся зависимостью, полученной ранее:

Где: Wr ≈ 0,2d 3 — момент сопротивления круглого сечения кручению (или полярный момент сопротивления круглого сечения).

Подставив полученные зависимости и их числовые значения в формулу, получим максимальное напряжение τmax, возникающее в сечениях участка I при кручении бруса:

Τmax ≈ Мкр / 0,2d 3 ≈ 500/0,2×0,05 3 ≈ 200 000 000 Па (или 200 МПа).

С правилами и примерами построения эпюр при деформации кручения можно ознакомиться Здесь.

Решение задачи на изгиб

Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой, если к свободному концу бруса приложена поперечная сила F .

Вес бруса не учитывать.

Изгибающий момент силы F и возникающие в сечениях бруса напряжения зависят от расстояния между линией приложения (вектором) силы и плоскостью рассматриваемого сечения (очевидно, что величина изгибающего момента находится в прямо пропорциональной зависимости от расстояния до вектора силы) . Поэтому для данного бруса изгибающий момент достигает максимального значения в сечении рядом с жесткой заделкой:

Максимальные нормальные напряжения в этом сечении можно определить по формуле:

Где: W ≈ 0,1d 3 — момент сопротивления круглого сечения изгибу (или осевой момент сопротивления круглого сечения). Подставив зависимости и их величины в формулу, получим:

Решение задачи на изгиб с построением эпюр

Построить эпюру поперечных сил и изгибающих моментов, действующих на защемленный одним концом брус (см. схему).

Вес бруса не учитывать.

Для построения эпюр определим границы участков бруса, в пределах которых внешние нагрузки и размеры сечений одинаковы. Для данного бруса можно выделить два таких участка (см. схему) .

Далее, используя метод сечений, строим эпюру поперечных сил, учитывая знаки. Очевидно, что на первом участке поперечная сила будет постоянной во всех сечениях, и эпюра представляет собой горизонтальную линию, отстоящую от оси эпюры на величину — F (сила отрицательная).

В среднем сечении бруса начинает действовать распределенная нагрузка, которая линейно увеличивается и суммируется с поперечной силой F в каждом последующем сечении бруса по направлению к жесткой заделке. Поскольку эпюра поперечных сил на втором участке представляет собой отрезок наклонной прямой, то для ее построения достаточно определить величину поперечной силы в середине бруса (очевидно, что здесь F = 50 Н) и величину поперечной силы в сечении рядом с жесткой заделкой:

По полученным значениям строим эпюру поперечных сил F (см. схему) .

Построение эпюры изгибающих моментов строится аналогично эпюре поперечных сил — при помощи метода сечений. При этом учитывается расстояние от сечения, в котором приложена поперечная сила, до рассматриваемого сечения (плечо силы).

Очевидно, что изгибающий момент от силы F будет увеличиваться прямо пропорционально по мере удаления от сечения, к которому она приложена, причем в крайнем сечении (где приложена сила) момент этой силы равен нулю (поскольку плечо силы равно нулю) .

В среднем сечении бруса изгибающий момент достигает значения: Ми = FL/2 = -50×6 = -300 Нм.

Начиная с середины бруса начинает действовать изгибающий момент от распределенной нагрузки Q, который в каждом сечении определяется, как произведение приведенной силы Fпр = ql на половину расстояния L (здесь L — расстояние от рассматриваемого сечения до начала действия распределенной нагрузки) .

Очевидно, что по мере удаления от среднего сечения к жесткой заделке изгибающий момент от распределенной нагрузки Q изменяется по квадратичной зависимости, и линия эпюры изгибающих моментов на втором участке представляет собой параболу.

Чтобы построить параболу недостаточно двух точек, необходимо определить величину изгибающего момента в нескольких сечениях бруса (на втором участке) . При этом следует учитывать изгибающий момент от силы F, который суммируется с изгибающим моментом от распределенной нагрузки Q на данном участке бруса.

Максимальной величины изгибающий момент достигает в сечении рядом с жесткой заделкой:

Выполнив необходимые подсчеты, строим эпюру изгибающих моментов, начиная со свободного конца бруса (см. схему) .

Главная страница

Техническая механика

Заочное отделение

Учебно-методические документы

Экзаменационные вопросы

КГБПОУ «Каменский агротехнический техникум»

poiskvstavropole.ru

Задачи по сопромату на растяжение-сжатие с решением

Площадь боковой поверхности усеченной пирамиды можно найти, зная апофему (высоту грани) – то есть высоту трапеции в данном случае, и стороны оснований – пирамиды и трапеции одновременно. Имея эти данные, мы найдем площадь одной грани по формуле площади трапеции и умножим на.

Примеры решения задач по сопромату

Приветствую тебя, читатель сайта — sopromats. ru, на котором размещено много полезной и интересной информации о сопромате и не только. Сегодня я решил написать большую статью о примерах решения задач по сопромату, которые размещены на этом ресурсе. Все примеры было решено классифицировать на три категории: по виду деформации, по виду рассчитываемого объекта и по типу расчета. Эти категории имеют три уровня вложенности. Например, в категории — по виду деформации входят задачи, связанные с изгибом, кручением, растяжением (сжатием) и сложным сопротивлением. В свою очередь, решения на изгиб классифицируются на статически определимые и неопределимые. Для того, чтобы найти нужную категорию перемещайтесь по указанным ссылкам на страничках. Также хотелось бы отметить, что на данный момент на сайте преобладают рукописные примеры решения. Но наша команда, активно работает над добавлением электронных материалов: с качественными схемами и набранными в цифровом виде расчетами. По мере развития сайта, все рукописные записи, планируется заменить цифровыми. Ну что же перейдем непосредственно к нашим примерам.

Классификация по виду деформации

Как уже говорилось выше, здесь все примеры отсортированы по виду деформации: растяжению и сжатию, кручению, изгибу и сложному сопротивлению. В категорию задач на сложное сопротивление попадают такие популярные решения на такие темы как изгиб с кручением, внецентренное растяжение (сжатие), косой изгиб. Теперь давайте перейдем непосредственно к категориям и не забывайте переходить по ссылкам на интересующую вас подкатегории.

Что можно найти в данной категории задач?

определение реакций в опорах из уравнений равновесия статики; расчет ВСФ методом сечений; вычисление продольной и поперечной силы; расчет изгибающего момента; расчет нормальных и касательных напряжений; вычисление перемещений поперечных сечений; раскрытие статической неопределимости с использованием уравнения совместности деформации.

Растяжение и сжатие

статически определимые брусья; статически неопределимые брусья; статически определимые стержневые системы; статически неопределимые стержневые системы.

Примеры задач на кручение распределены по 2 основным категориям:

статически определимое кручение; статически неопределимое кручение.

Задачи на изгиб подразделяются по тем же признакам:

статически определимый изгиб; статически неопределимый изгиб.

Классификация по типу рассчитываемого объекта

В этом разделе все решения распределены по типу рассчитываемого объекта: на балки, рамы, фермы и т. д. Каждая представленная здесь категория имеет укрупненную классификацию, которую можно изучить, перейдя по соответствующим ссылкам.

Решения, связанные с балками, можно разделить на две основные подкатегории:

статически определимые балки; статически неопределимые балки.

статически определимые валы; статически неопределимые валы.

статически определимые рамы; статически неопределимые рамы.

Все примеры решения задач, связанные с расчетом ферм, решено было поместить в одну большую категорию. В этой категории можно встретить задачи на:

определение реакций в опорах фермы; определение продольных усилий в стержнях методом вырезания узлов, либо методом Риттера; построение линий влияния.

В разделе про сечения, связанные с расчетом геометрических характеристик, принята следующая классификация:

симметричные и несимметричные сечения, состоящие из геометрических примитивов; симметричные и несимметричные сечения, состоящие из металлопрокатных профилей.

Классификация по типу расчета

В этом разделе материалы разделены по типу расчета. Сюда попали расчеты на прочность, жесткость и устойчивость. Здесь же находятся задачи, связанные с расчетом напряжений, эпюр внутренних силовых факторов и другие.

В этой категории находятся задачи, связанные с расчетом прочности, при различных видах деформации: изгибе, кручении, растяжении (сжатии) и сложном сопротивлении. Здесь можно встретить как проверочные, так и проектировочные расчета. Найти расчеты на грузоподъемность какой-либо системы.

В расчетах на жесткость, можно найти задачах, в которых исследуются различные элементы конструкций: балки, рамы, валы и другие. Во всех задачах проверяется жесткость, путем сравнения расчетных значений перемещений с допустимыми значениями.

Устойчивость

В примерах на устойчивость, можно найти задачи, связанные с подбором сечения стоек из условия устойчивости, либо расчетом грузоподъемности.

Данная категория, связанна с расчетом эпюр внутренних силовых факторов, при различных видах деформации: растяжении и сжатии, кручении, изгибе и сложном сопротивлении. Есть эпюры, которые откладываются со стороны растянутых волокон (строителям) и сжатых волокон (машиностроителям).

Задачи по сопромату на растяжение-сжатие с решением

Примеры решения задач по сопромату

Приветствую тебя, читатель сайта — sopromats. ru, на котором размещено много полезной и интересной информации о сопромате и не только. Сегодня я решил написать большую статью о примерах решения задач по сопромату, которые размещены на этом ресурсе. Все примеры было решено классифицировать на три категории: по виду деформации, по виду рассчитываемого объекта и по типу расчета. Эти категории имеют три уровня вложенности. Например, в категории — по виду деформации входят задачи, связанные с изгибом, кручением, растяжением (сжатием) и сложным сопротивлением. В свою очередь, решения на изгиб классифицируются на статически определимые и неопределимые. Для того, чтобы найти нужную категорию перемещайтесь по указанным ссылкам на страничках. Также хотелось бы отметить, что на данный момент на сайте преобладают рукописные примеры решения. Но наша команда, активно работает над добавлением электронных материалов: с качественными схемами и набранными в цифровом виде расчетами. По мере развития сайта, все рукописные записи, планируется заменить цифровыми. Ну что же перейдем непосредственно к нашим примерам.

Классификация по виду деформации

Как уже говорилось выше, здесь все примеры отсортированы по виду деформации: растяжению и сжатию, кручению, изгибу и сложному сопротивлению. В категорию задач на сложное сопротивление попадают такие популярные решения на такие темы как изгиб с кручением, внецентренное растяжение (сжатие), косой изгиб. Теперь давайте перейдем непосредственно к категориям и не забывайте переходить по ссылкам на интересующую вас подкатегории.

Что можно найти в данной категории задач?

определение реакций в опорах из уравнений равновесия статики; расчет ВСФ методом сечений; вычисление продольной и поперечной силы; расчет изгибающего момента; расчет нормальных и касательных напряжений; вычисление перемещений поперечных сечений; раскрытие статической неопределимости с использованием уравнения совместности деформации.

Растяжение и сжатие

статически определимые брусья; статически неопределимые брусья; статически определимые стержневые системы; статически неопределимые стержневые системы.

Примеры задач на кручение распределены по 2 основным категориям:

статически определимое кручение; статически неопределимое кручение.

Задачи на изгиб подразделяются по тем же признакам:

статически определимый изгиб; статически неопределимый изгиб.

Классификация по типу рассчитываемого объекта

В этом разделе все решения распределены по типу рассчитываемого объекта: на балки, рамы, фермы и т. д. Каждая представленная здесь категория имеет укрупненную классификацию, которую можно изучить, перейдя по соответствующим ссылкам.

Решения, связанные с балками, можно разделить на две основные подкатегории:

статически определимые балки; статически неопределимые балки.

статически определимые валы; статически неопределимые валы.

статически определимые рамы; статически неопределимые рамы.

Все примеры решения задач, связанные с расчетом ферм, решено было поместить в одну большую категорию. В этой категории можно встретить задачи на:

определение реакций в опорах фермы; определение продольных усилий в стержнях методом вырезания узлов, либо методом Риттера; построение линий влияния.

В разделе про сечения, связанные с расчетом геометрических характеристик, принята следующая классификация:

симметричные и несимметричные сечения, состоящие из геометрических примитивов; симметричные и несимметричные сечения, состоящие из металлопрокатных профилей.

Классификация по типу расчета

В этом разделе материалы разделены по типу расчета. Сюда попали расчеты на прочность, жесткость и устойчивость. Здесь же находятся задачи, связанные с расчетом напряжений, эпюр внутренних силовых факторов и другие.

В этой категории находятся задачи, связанные с расчетом прочности, при различных видах деформации: изгибе, кручении, растяжении (сжатии) и сложном сопротивлении. Здесь можно встретить как проверочные, так и проектировочные расчета. Найти расчеты на грузоподъемность какой-либо системы.

В расчетах на жесткость, можно найти задачах, в которых исследуются различные элементы конструкций: балки, рамы, валы и другие. Во всех задачах проверяется жесткость, путем сравнения расчетных значений перемещений с допустимыми значениями.

Устойчивость

В примерах на устойчивость, можно найти задачи, связанные с подбором сечения стоек из условия устойчивости, либо расчетом грузоподъемности.

Данная категория, связанна с расчетом эпюр внутренних силовых факторов, при различных видах деформации: растяжении и сжатии, кручении, изгибе и сложном сопротивлении. Есть эпюры, которые откладываются со стороны растянутых волокон (строителям) и сжатых волокон (машиностроителям).

Задачи по сопромату на растяжение-сжатие с решением

Решение задач по сопротивлению материалов

Сопромат является одной из основных, если не самой главной дисциплиной, которая преподаётся на специальностях, связанных с механикой. Это основа всех предметов, которые будут изучаться студентами в дальнейшем и камень преткновения, о который спотыкаются многие в начале своего обучения. Наверное любой был озадачен многоэтажными формулами и непонятными рамами и конструкциями, изображенными в учебниках.

Решение задач по теме «Растяжение и сжатие»

Это базовые задания, решение которых оказывается под силу почти каждому. Необходимо определить внутренние усилия, возникающие в балке прямоугольного сечения при растяжении её силами, приложенными вдоль оси балки.

Решение производится следующим образом:

Разбиваем балку на участки, границами которых являются точки приложения сил либо точки, в которых изменяется площадь поперечного сечения балки. Определяем суммарные усилия на каждом участке, сложив проекции всех сил на ось балки. Определяем нормальные напряжения на участках. Определяем относительные удлинения и перемещения на границах участков если того требует задание. Строим эпюры по полученным данным.

Вариантом этого задания может быть решение статически неопределимой системы. В этом случае необходимо принять реакцию дополнительной опоры за неизвестную величину и составить с ней уравнение перемещений.

Решение задач по теме «Кручение»

Здесь необходимо определить крутящие моменты и угловые перемещения элементов конструкции, возникающие под действием внешних усилий.

В целом подобные задачи аналогичны задачам на растяжение, разница в том что линейные перемещения заменяются угловыми, а роль модуля упругости играет величина, называемая модулем сдвига.

Решение задач по теме «Изгиб»

Задачи на изгиб немного выше предыдущих по сложности, однако, если придерживаться несложных правил, решение окажется быстрым.

Вначале необходимо определить тип опор балки (шарнирно-подвижная, шарнирно-неподвижная, консольная заделка) и их количество. Исходя из этого, определяется количество реакций опор, которые необходимо рассчитать.

Далее проводится расчет в следующем порядке:

Разбиваем балку на участки, границами которых являются опоры или точки приложения сил. Определяем величину поперечных сил и изгибающих моментов на каждом участке. Для этого составляем уравнения равновесия, приравнивая сначала сумму сил, а затем моментов к нулю и решая получившиеся уравнения. Необходимо руководствоваться следующим правилом: поперечные силы и изгибающие моменты направляются так, чтобы они растягивали нижние волокна балки. Из получившихся величин моментов выбираем максимальный изгибающий момент. Исходя из условия прочности, определяем необходимый момент сопротивления поперечного сечения балки. При заданной форме поперечного сечения определяем его площадь.

Задачи на изгиб являются одними из основных, и сейчас существует множество программ и интернет-ресурсов для автоматизации расчета. Однако преподавателю по-прежнему необходимо предоставить порядок расчета.

Решение задач по теме: «Продольный изгиб»

Продольный изгиб возникает в стержне под действием сжимающих сил, приложенных вдоль его оси. При превышении силой некоего критического значения стержень теряет свою устойчивость. Данное значение и предлагается определить в задачах на устойчивость.

Задача решается следующим образом:

Пользуясь заданной формой поперечного сечения стержня, определяем его площадь в относительных величинах, так как абсолютные необходимо найти. Определяем осевые моменты инерции и находим минимальный из них. Пользуясь формулой, с учетом коэффициента приведения длины, находим гибкость стержня. Путем последовательных приближений находим величину поперечного сечения стержня. Для этого задаем первоначальную величину коэффициента формулы φ равной 0,5 и вычисляем величину условной единицы площади и гибкость стержня при этом значении. По найденной величине гибкости λ определяем табличное значение коэффициента φ и вычисляем разницу между вычисленным и табличным значением. Если разница оказывается больше 5%, повторяем вычисления, принимая новое значение φ равным среднему арифметическому между табличным и вычисленным. Повторяем вычисления пока разница не станет меньше 5%. Затем подставляем найденную величину условной единицы площади в формулу и находим площадь поперечного сечения стержня. Находим величину критической силы.

Если научиться решать эти основные разновидности задач по сопромату, то остальные не доставят особых хлопот.

Литература

Наиболее полезной и понятной литературой по сопромату являются методические указания, составляемые преподавателями вузов. Из учебников же можно порекомендовать пособие «Сопротивление материалов» А. В Даркова, и Г. С. Шпиро.

Платное решение задач по сопромату на заказ

Ввиду невозможности научить решать задачи в рамках одной статьи, предлагаем вам более простое решение проблемы. Заказать решение задач по сопротивлению материалов можно у нас на сайте. Специалисты подробно распишут решение, так чтобы вам была понятна его суть. Сделать заказ на решение можно на этой странице.

poiskvstavropole.ru

Сопромат. Растяжение-сжатие — Botva-Project

Рассмотрим типовую статически определимую задачу на растяжение сжатие

 

 

 

 

 

 

 

Как  и в любой другой задаче по сопромату, первым делом определяем реакции в опорах. Отбрасываем заделку, заменяем ее реакцией. Для осевого растяжения-сжатия реакция только одна – осевая сила

 

 

 

 

 

 

 

Направление можно выбирать в любую сторону. Записываем условие равновесия стержня – сумма всех сил должна быть равна 0. Силы, которые смотрят вправо, пишем с плюсом, влево – с минусом

 

 

Отсюда выражается сила R

 

 

Получили реакцию со знаком минус, значит, сила направлена не вправо, как мы ее нарисовали, а влево. Получаем следующую расчетную схему

 

 

 

 

 

 

Сечениями, где приложены сосредоточенные силы, или на границах распределенной нагрузки, или в местах изменения профиля сечения, стержень разбивается на участки. У нас их четыре.

 

 

 

 

 

 

Применяем метод сечений для каждого участка. Разрезаем стержень по середине участка, отбрасываем то, что находится справа от сечения, заменяем отброшенную часть внутренним усилием. Для первого участка это выглядит так.

Разрезали

 

 

 

 

 

 

 

 

 

 

Отбросили

 

 

 

 

 

 

 

 

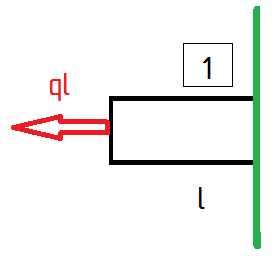
Заменили

 

 

 

 

 

 

 

Силу N всегда направляем вправо, в направлении, которое считаем положительным.

Записываем уравнение равновесия для данного участка стержня

 

 

 

Отсюда выражаем силу N₁

 

 

 

Это и есть внутреннее усилие на первом участке. Как видим, это усилие постоянно по всей длине участка и положительно, т.е. первый участок испытывает растяжение.

Повторим для второго участка.

Разрезали

 

 

 

 

 

 

 

Отбросили

 

 

 

 

 

 

 

 

Заменили

 

 

 

 

 

 

 

 

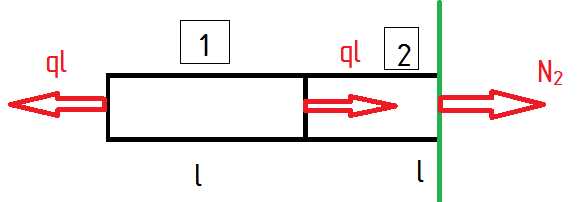
Уравновесили

 

 

 

Отсюда выражаем силу N₂

 

 

Получается, второй участок не нагружен.

Для третьего участка

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

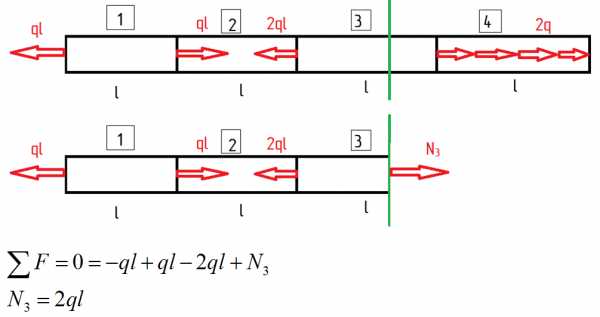
Третий участок тоже растягивается.

На четвертом участке нас ждет небольшая засада в виде распределенной нагрузки. Из-за нее нагрузка внутри участка непостоянна и меняется по длине участка. Делаем то же, что и с предыдущими участками, но вводим локальную координату z. Она начинается от начала участка и заканчивается местом сечения, т.е. меняется от 0 до l.

 

 

 

 

 

 

 

 

 

Отбрасываем правую часть

 

 

 

 

 

 

 

 

 

Заменяем внутренней силой

 

 

 

 

 

 

 

 

 

Уравнение равновесия

 

 

 

 

 

Внутреннее усилие N₄ непостоянно и меняется по длине участка от 2ql (при z=0) до 0 (при z=l)

Запишем все выражения для найденных усилий в один столбик

 

 

 

 

 

 

 

 

 

 

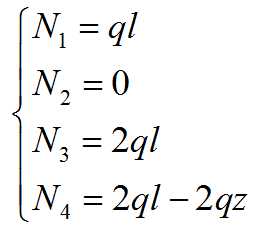
По данным зависимостям можно построить эпюру внутренних усилий N(z). Удобно делать это под общей расчетной схемой

 

 

 

 

 

 

 

 

 

 

 

Посмотрим на эпюру и проверим ее на адекватность. В сечениях, где приложены сосредоточенные силы, эпюра должна совершать скачок на величину этой силы. На участках с распределенной нагрузкой эпюра идет под углом. На концах стержня без нагрузки эпюра равна нулю. Все выполняется, значит, задача решена верно. Максимальной величины нагрузка достигает на третьем участке.

 

Если у Вас есть вопросы по решению данной задачи (или любой другой), пишите на наш e-mail [email protected], поможем.

С уважением,

Botva-Project

 

botva-project.ru

Задача | ПроСопромат.ру

Определить грузоподъемность (допускаемую нагрузку [F]) шарнирно-стержневой системы для двух случаев:

1. Если материал стержней пластичный (сталь – 3, [σ]=160 МПа),
2. Если материал стержней хрупкий (чугун — [σ_р]=20 МПа, [σ_с]=80МПа).

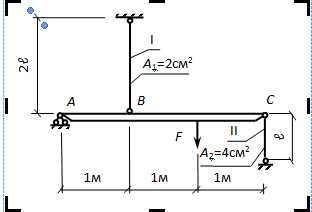
Сначала необходимо найти усилия в стержнях, оставляя нагрузку в общем (буквенном) виде. Начинаем с использования метода сечений: делаем сквозной (замкнутый) разрез и рассматриваем равновесие средней части (неизвестные усилия при этом предполагаем положительными, т.е. растягивающими):

∑х = Н = 0,       (1)

∑у = R+N₁— F—N₂=0,    (2)

∑М(А)= N₁·1 — F·2 – N₂·3=0, (3)

В этих трёх уравнениях статики содержатся 4 неизвестных, следовательно, задача один раз статически неопределима. Для раскрытия статической неопределимости придётся составить одно дополнительное уравнение, но уже не статическое, а геометрическое, которое выражало бы условие совместности деформаций всех упругих элементов системы. С этой целью следует рассмотреть систему в деформированном состоянии с тем, чтобы «связать» друг с другом абсолютные деформации первого и второго стержней. Картина возможной деформации системы:

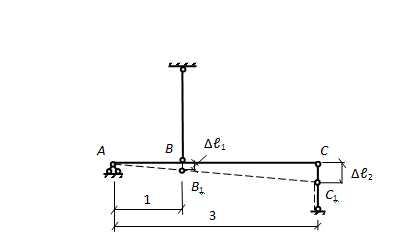
Очевидно, что ВВ₁ – удлинение первого стержня (∆ℓ₁), а СС₁ – укорочение второго (∆ℓ₂). Из подобия треугольников

или

По формуле Гука:

(знак «плюс» соответствует деформации удлинения), а

(знак «минус» соответствует деформации укорочения). После подстановки получим необходимое нам дополнительное уравнение:

      (4)

Т.к. ℓ₁=2ℓ, ℓ₂=ℓ, А₁= 2см², А₂= 4см², то

,

откуда N₂=-12N₁. Подставляя это соотношение в уравнение (3), имеем: N₁·1- F·2 — (-12N₁) 3=0, откуда

(растяжение), и тогда

(сжатие).

Напряжения в стержнях будут:

Для определения допускаемой нагрузки используем условия прочности при растяжении-сжатии.

Случай 1. Оба стержня из пластичного материала, который одинаково сопротивляется как растяжению, так и сжатию. Для него достаточно одного условия прочности:

|_maxσ| ≤ [σ].

Наибольшим по абсолютной величине оказывается напряжение во втором стержне. Его и вводим в условие прочности. Допускаемая нагрузка (или грузоподъёмность) – это такая величина нагрузки, при которой напряжение в точности равно допускаемому значению (т.е. в условии прочности необходимо оставить знак равенства)

Случай 2. Оба стержня из хрупкого материала. В этом случае требуется выполнение двух условий прочности: а) по растяжению: _maxσ_р ≤ [σ_р],

б) по сжатию |_maxσ_с| ≤ [σ_с].

Начинать можно с любого из них. Например, из первого условия:

найдём одно значение допускаемой нагрузки (по растяжению):

Если принять это значение за допускаемую нагрузку, то во втором стержне возникает напряжение

Это напряжение превышает допускаемое значение по сжатию: |σ_II| =120МПа > [σ_р]=80МПа, следовательно, нагрузка [F_р] не является допускаемой для всей конструкции. Поэтому будем определять допускаемую нагрузку из второго условия прочности: Остается лишь убедиться, что при такой нагрузке в первом стержне условие прочности будет выполнено.

что меньше допускаемого по растяжению напряжения [σ_р]=20МПа. Итак, для варианта стержней из хрупкого материала допускаемая нагрузка [F]=49,333 кН.

 

prosopromat.ru

Статически определимые задачи. Р-С | ПроСопромат.ру

Стальной ступенчатый брус нагружен силами. Для статически определимого стального ступенчатого бруса построить эпюры: продольных сил, нормальных напряжений и перемещений.

1)   Прежде всего брус «разбивается» на участки, границами которых являются:– точки приложения внешних сил (отмечены крестиком),– места резкого изменения размеров поперечных сечений,– места, где меняется вид материала.

1)                 Определяем опорную реакцию. С этой целью на схеме бруса следует обязательно задаться направлением реакции и принять для нее буквенное обозначение. Например, А (см.схему)

∑у = ─ F₁+ F₂─ F₃─А=0,

откуда А=─ F₁+ F₂─ F₃=─50+60─30=─20кН.

Чрезвычайно важно правильно отреагировать на отрицательный знак реакции. Он означает, что истинное направление реакции противоположно предполагаемому. Поэтому следует зачеркнуть (!) и вектор, и буквенное обозначение (двумя наклонными линиями), а затем показать противоположный вектор и рядом указать абсолютную величину реакции без всякого буквенного обозначения и в дальнейших выкладках «бывшая» отрицательная реакция нигде не должна появляться!

2)   С целью построения эпюры продольных сил (N) необходимо определять ее не в конкретных сечениях, а в произвольных сечениях каждого участка (чтобы иметь функциональную зависимость). Для этого приходится применять метод сечений для произвольного сечения каждого участка:

— на I участке:

∑у = ─F₁─N₁=0,

N₁=─F₁=─50кН (сжатие).

— на II участке:

∑у = ─F₁+ F₂─N₂ =0

N₂=─F₁+ F₂=─50+60=10кН (растяжение)

— на III участке:

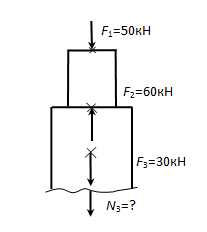
∑у = ─ F₁+ F₂─ F₃─N₃=0,

N₃=─F₁+ F₂─ F₃=─50+60─30=─20 кН (сжатие)

или еще проще:

∑у =N₃+20=0   N₃=─20кН (сжатие).

N.B.: неизвестное усилие всегда (!) следует предполагать положительным и направлять в соответствии с принятым правилом знаков. В частности положительная продольная сила растягивающая и потому должна направляться «от сечения».

3)  Напряжения при  растяжении-сжатии вычисляются по формуле:

,

причем знак напряжения повторяет знак продольной силы N.

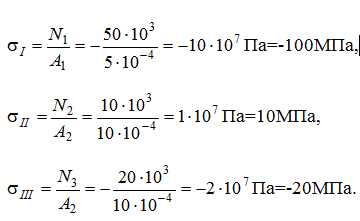
4)                 При построении эпюры перемещений следует вспомнить, что любая ее ордината означает смещение сечения, расположенного под этой ординатой, по отношению к неподвижному сечению.

А поэтому построение и начинается с неподвижного сечения. В нашем случае неподвижным является нижнее сечение, расположенное в опоре. Обозначим его номером (0): δ₍₀₎=0.

Перемещение сечения (1)  на границе между III и II участками бруса будет равно абсолютной деформации III^го участка:

Перемещение сечения (2) на границе II и I^го участков складывается из смещения сечения (1) и абсолютной деформации участка II:

Перемещение верхнего сечения (3) сложится из смещения сечения (2) и абсолютной деформации I^го участка:

Заметим: все эпюры штрихуются только перпендикулярно к оси, поскольку наклонные штрихи не имеют физического смысла!

 

 

 

 

prosopromat.ru

Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.

Сопротивление материалов

Решение задач на растяжение и сжатие



Расчеты на прочность при растяжении и сжатии

В результате проведения механических испытаний устанавливают предельные напряжения, при которых происходит нарушение работы или разрушение деталей конструкции.
Предельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких — предел прочности.
Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации наибольшие напряжения были меньше предельных.

Отношение предельного напряжения к напряжению, возникающему в процессе работы детали, называют коэффициентом запаса прочности и обозначают буквой s:

s = σ_пред / σ,

где σ = N / А – реальное напряжение, возникающее в элементе конструкции.

Недостаточный коэффициент запаса прочности может привести к потере работоспособности конструкции, а избыточный (слишком высокий) — к перерасходу материала и утяжелению конструкции. Минимально необходимый коэффициент запаса прочности называют допускаемым, и обозначают [s].
Отношение предельного напряжения к допускаемому запасу прочности называют допускаемым напряжением, и обозначают [σ]:

[σ] = σ_пред / [s].

Условие прочности в деталях и конструкциях заключается в том, что наибольшее возникающее в ней напряжение (рабочее напряжение) не должно превышать допускаемого:

σ_max≤ [σ], или в другом виде: s ≥ [s].

Если допускаемые напряжения при растяжении и сжатии различны, их обозначают [σ_р] и [σ_с].

Расчетная формула при растяжении и сжатии имеет вид:

σ = N / А ≤ [σ]

и читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле σ = N /А, не должно превышать допустимое.

На практике расчеты на прочность проводят для решения задач:

— проектный расчет, при котором определяются минимальные размеры опасного сечения;
— проверочный расчет, при котором определяется рабочее напряжение и сравнивается с предельно допустимым;
-определение допускаемой нагрузки при заданных размерах опасного сечения.

***

Растяжение под действием собственного веса

Если ось бруса вертикальна, то его собственный вес вызывает деформацию растяжения или сжатия.
Рассмотрим брус постоянного сечения весом G, длиной l, закрепленный верхним концом и нагруженный только собственным весом G (рис.1).
Для определения напряжений в поперечном сечении на переменном расстоянии z от нижнего конца применим метод сечений.
Рассмотрим равновесие нижней части бруса и составим уравнение равновесия:

Σ Z = 0;     N_z — G_z = 0,    откуда:

N_z = G_z = γ А z,

где γ — удельный вес материала бруса, А – площадь его поперечного сечения, z — длина части бруса от свободного конца до рассматриваемого сечения.

Напряжения, возникающие в сечениях бруса, нагруженного собственным весом, определяются по формуле:

σ_z = N_z / А = γ А z / А = γ z,

т. е. для нагруженного собственным весом бруса нормальное напряжение не зависит от площади поперечного сечения. Очевидно, что опасное сечение будет находиться в заделке:

σ_max = γ l.

Эпюра распределения напряжений вдоль оси бруса представляет собой треугольник.
Если требуется определить максимальную длину бруса, нагруженного собственным весом, используют расчет по предельному допустимому напряжению в сечении:

l_пр = [σ] / γ.

***



Статически неопределимые задачи

Иногда в практике расчета конструкций требуется определить неизвестные силовые факторы (например, реакции связей или внутренние силы), при этом количество неизвестных силовых факторов превышает количество возможных уравнений равновесия для данной конструкции, и расчет произвести рассмотренными ранее способами не представляется возможным.

Задачи на расчет конструкций, в которых внутренние силовые факторы не могут быть определены с помощью одних лишь уравнений равновесия статики, называют статически неопределимыми. Подобные задачи нередко встречаются при расчете конструкций, подверженных температурным деформациям.
Для решения таких задач помимо уравнений равновесия составляют уравнение перемещений или деформаций.

Рассмотрим невесомый стержень постоянного сечения площадью А, длиной l, жестко защемленный по концам (см. рис. 2).
При нагревании в стержне возникают температурные напряжения сжатия.
Попробуем определить эти напряжения.

Составим для стержня уравнение равновесия:

Σ Z = 0; R_С — R_В = 0,

откуда следует, что реакции R_С и R_В равны между собой, а применив метод сечений установим, что продольная сила N в сечениях стержня равна неизвестным реакциям:

N = R_С = R_В.

Составим дополнительное уравнение, для чего мысленно отбросим правую заделку и заменим ее реакцией R_В, тогда дополнительное уравнение деформации будет иметь вид:

Δl_t = Δl_СВ

т. е. температурное удлинение стержня равно его укорочению под действием реакции R_B, так как связи предполагаются абсолютно жесткими.

Температурное удлинение стержня определяется по формуле: Δl_t = αtl, где α — коэффициент линейного расширения стержня.

Укорочение стержня под действием реакции: Δl_СВ = R_B l / (EА).

Приравняв правые части равенств, получим:

αtl = R_B l / (EА), откуда R_B = αtEА.

Температурные напряжения в реальных конструкциях могут достигать значительных величин. Чтобы исключить их отрицательное влияние на прочность конструкций, прибегают к различным методам. Мосты, например, закрепляют лишь на одном конце (на одном берегу), а второй конец оставляют подвижным.
В длинных трубопроводах, подверженных температурным напряжениям, делают компенсирующие карманы, петли и т. д.

***

Материалы раздела «Растяжение и сжатие»:

Срез

№ вопроса	1	2	3	4	5	6	7	8	9	10
Правильный вариант ответа	2	1	1	3	3	2	1	3	2	1

k-a-t.ru