Удельная прочность металлов: таблица. Механические свойства металлов
Использовать металлы в повседневной жизни начали еще вначале развития человечества. Медь – это первый их представитель. Она доступна в природе и прекрасно обрабатывается. При археологических раскопках часто находят изготовленные из нее предметы домашнего обихода и разные изделия.  В процессе развития человек обучался объединять разные металлы, производя сплавы большей прочности. Из них делали орудия труда, а позже использовали для изготовления оружия. Опыты продолжаются и в наше время, создаются сплавы с удельной прочностью металлов, пригодные для возведения современных конструкций.
В процессе развития человек обучался объединять разные металлы, производя сплавы большей прочности. Из них делали орудия труда, а позже использовали для изготовления оружия. Опыты продолжаются и в наше время, создаются сплавы с удельной прочностью металлов, пригодные для возведения современных конструкций.
Виды нагрузок
К механическим свойствам металлов и сплавов относятся такие, которые способны оказывать сопротивление действию на них внешних сил или нагрузок. Они могут быть самыми разнообразными и по своему воздействию различают:
- статические, которые неспешно возрастают от нулевого значения до максимума, а затем остаются постоянными или незначительно меняются;
- динамические – возникают вследствие удара и действуют короткий промежуток.
Виды деформации
Деформация – это видоизменение конфигурации твердого тела под воздействием прилагаемых к нему нагрузок (внешних сил). Деформации, после которых материал возвращается в прежнюю форму и сохраняет первоначальные размеры, считают упругими, в противном случае (форма изменилась, материал удлинился) – пластическими или остаточными. Существует несколько видов деформации:
- Сжатие. Уменьшается объем тела в результате действия на него сдавливающих сил. Такую деформацию испытывают фундаменты котлов и машин.
- Растяжение. Увеличивается длина тела, когда к его концам прилагаются силы, направление которых совпадает с его осью. Растяжению подвергаются тросы, приводные ремни.
- Сдвиг или срез. В этом случае силы направлены навстречу друг другу и при определенных условиях наступает срез. Примером служат заклепки и болты стяжки.
- Кручение. Пара сил, противоположно направленных, действует на закрепленное одним концом тело (валы двигателей и станков).
- Изгиб. Изменение кривизны тела при воздействии внешних сил. Такое действие характерно для балок, стрел подъемных кранов, железнодорожных рельсов.
Определение прочности металла
Одно из основных требований, которое предъявляют к металлу, применяемому для производства металлических конструкций и деталей, является прочность. Для ее определения берется образец металла и растягивается на испытательной машине. Эталон становится тоньше, площадь поперечного сечения уменьшается с одновременным увеличением его длины. В определенный момент образец начинает растягиваться лишь в одном месте, образуя «шейку». А через некоторое время происходит разрыв в области самого тонкого места. Так ведут себя исключительно вязкие металлы, хрупкие: твердая сталь и чугун растягиваются незначительно и у них не образуется шейка.
 Нагрузка на образец определяется специальным прибором, который носит название силоизмеритель, он вмонтирован в испытательную машину. Для вычисления основной характеристики металла, называемой пределом прочности материала, надо максимальную нагрузку, выдержанную образцом до разрыва, разделить на величину площади поперечного сечения до растяжения. Эта величина необходима конструктору для того, чтобы определиться с размерами изготовляемой детали, и технологу назначить режимы обработки.
Нагрузка на образец определяется специальным прибором, который носит название силоизмеритель, он вмонтирован в испытательную машину. Для вычисления основной характеристики металла, называемой пределом прочности материала, надо максимальную нагрузку, выдержанную образцом до разрыва, разделить на величину площади поперечного сечения до растяжения. Эта величина необходима конструктору для того, чтобы определиться с размерами изготовляемой детали, и технологу назначить режимы обработки.
Самые прочные металлы в мире
К высокопрочным металлам можно отнести следующие:
Титан находит применение в медицине, военной промышленности, кораблестроении, авиации.
- Уран. Самый известный и прочный металл в мире, является слабым радиоактивным материалом. Встречается в природе в чистом виде и в соединениях. Он относится к тяжелым металлам, гибкий, ковкий и относительно пластичный. Широко используется в производственных сферах.
- Вольфрам. Расчет прочности металла показывает, что это самый прочный и тугоплавкий металл, не поддающийся химическому воздействию. Хорошо куется, его можно вытянуть в тонкую нить. Используется для нити накаливания.
- Рений. Тугоплавкий, имеет высокую плотность и твердость. Очень прочный, не подвержен перепадам температуры. Находит применение в электронике и технике.
- Осмий. Твердый металл, тугоплавкий, стойкий к механическим повреждениям и агрессивным средам. Применяют в медицине, используют для ракетной техники, электронной аппаратуры.
- Иридий. В природе в свободном виде встречается редко, чаще – в соединениях с осмием. Механической обработке поддается плохо, имеет высокую стойкость к химическим веществам и прочность. Сплавы с металлом: титаном, хромом, вольфрамом, используют для изготовления ювелирных изделий.
- Бериллий. Высокотоксичный металл с относительной плотностью, имеющий светло-серый цвет. Находит применение в черной металлургии, атомной энергетике, лазерной и аэрокосмической технике. Имеет высокую твердость и используется для легирования сплавов.
- Хром. Очень твердый металл с высокой прочностью, бело-голубого цвета, обладает стойкостью к щелочам и кислотам. Прочность металла и сплавов позволяют их использовать для изготовления медицинского и химического оборудования, а также для металлорежущих инструментов.

- Тантал. Металл серебристого цвета, имеет высокую твердость, прочность, обладает тугоплавкостью и стойкостью к коррозии, пластичен, легко обрабатывается. Находит применение при создании ядерных реакторов, в металлургии и химической промышленности.
- Рутений. Принадлежит к металлам платиновой группы. Обладает высокой прочностью, твердостью, тугоплавкостью, химической стойкостью. Из него изготовляют контакты, электроды, острые наконечники.
Как определяют свойства металлов?
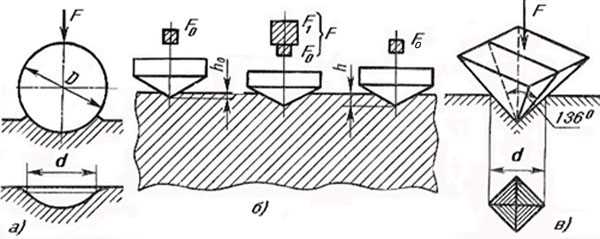
Для испытания металлов на прочность применяют химические, физические и технологические методы. Твердость определяет, как сопротивляются материалы деформациям. Стойкий металл имеет большую прочность и детали, изготовленные из него, меньше снашиваются. Для определения твердости вдавливают шарик, алмазный конус или пирамидку в металл. Значение твердости устанавливают по диаметру отпечатка или по глубине вдавливания предмета. Более крепкий металл меньше деформируется, и глубина отпечатка будет меньше.
А вот образцы на растяжение испытываются на разрывных машинах с плавно нарастающей при растягивании нагрузкой. Эталон может иметь в сечении круг или квадрат. Для проверки металла противостоять нагрузкам ударного характера проводят испытания на удар. В середине специально изготовленного образца делают надрез и устанавливают его напротив ударного устройства. Разрушение должно происходить там, где слабое место. При испытании металлов на прочность структуру материала исследуют рентгеновскими лучами, ультразвуком и при помощи мощных микроскопов, а также используют травление химическими веществами.
 К технологическим относятся самые простые виды испытаний на разрушение, пластичность, ковку, сварку. Испытание на выдавливание дает возможность определить, способен ли листовой материал подвергаться холодной штамповке. С помощью шарика в металле выдавливают лунку, пока не появится первая трещина. Глубина ямки до появления разрушения и будет характеризовать пластичность материала. Испытание на изгиб дает возможность определить способность листового материала принимать нужную форму. Это испытание используют для оценки качества швов при сварке. Для оценки качества проволоки используется проба на перегиб. Трубы испытывают на расплющивание и изгиб.
К технологическим относятся самые простые виды испытаний на разрушение, пластичность, ковку, сварку. Испытание на выдавливание дает возможность определить, способен ли листовой материал подвергаться холодной штамповке. С помощью шарика в металле выдавливают лунку, пока не появится первая трещина. Глубина ямки до появления разрушения и будет характеризовать пластичность материала. Испытание на изгиб дает возможность определить способность листового материала принимать нужную форму. Это испытание используют для оценки качества швов при сварке. Для оценки качества проволоки используется проба на перегиб. Трубы испытывают на расплющивание и изгиб.
Механические свойства металлов и сплавов
К механическим свойствам материалов из металла относятся следующие:
- Прочность. Она заключается в способности материала оказывать сопротивление разрушению под воздействием сил извне. Вид прочности зависит от того, как действуют внешние силы. Ее разделяют на: сжатие, растяжение, кручение, изгиб, ползучесть, усталость.
- Пластичность. Это способность металлов и их сплавов под воздействием нагрузки менять форму, не подвергаясь разрушению, и сохранять ее после окончания воздействия. Пластичность материала из металла определяют при его растяжении. Чем больше происходит удлинение, при одновременном уменьшении сечения, тем пластичнее металл. Материалы, обладающие хорошей пластичностью, прекрасно обрабатываются давлением: ковке, прессованию. Пластичность характеризуют двумя величинами: относительное сужение и удлинение.
- Твердость. Такое качество металла заключается в способности оказывать сопротивление проникновению в него инородного тела, имеющего более значительную твердость, и не получить при этом остаточных деформаций. Износоустойчивость и прочность – это основные характеристики металлов и сплавов, которые тесно связаны с твердостью. Материалы с такими свойствами находят применение для изготовления инструментов, применяемых для обработки металлов: резцы, напильники, сверла, метчики. Нередко по твердости материала определяют его износоустойчивость. Так твердые стали при эксплуатации изнашиваются меньше, чем более мягкие сорта.
- Ударная вязкость. Особенность сплавов и металлов сопротивляться влиянию нагрузок, сопровождающихся ударом. Это одна из важных характеристик материала, из которого изготовлены детали, испытывающие ударную нагрузку, во время работы машины: оси колес, коленчатые валы.
- Усталость. Это состояние металла, который находится под постоянным воздействием нагрузок. Усталость металлического материала происходит постепенно и может закончиться разрушением изделия. Способность металлов оказывать сопротивление разрушению от усталости называют выносливостью. Это свойство находится в зависимости от природы сплава или металла, состояния поверхности, характера обработки, условий работы.
Классы прочности и их обозначения
Нормативными документами по механическим свойствам крепежных изделий введено понятие класс прочности металла и установлена система обозначения. Каждый класс прочности обозначается двумя цифрами, между которыми ставится точка. Первое число означает предел прочности, уменьшенный в 100 раз. Например, класс прочности 5.6 означат, что предел прочности будет 500. Второе число увеличено в 10 раз – это отношение предела текучести к временному сопротивлению, выраженному в процентах (500х0,6=300), т. е. 30 % составляет минимальный предел текучести от предела прочности на растяжение. Все изделия, используемые для крепежа, классифицируются по назначению применения, форме, используемому материалу, классу прочности и покрытию. По назначению использования они бывают:
- Лемешные. Их используются для сельскохозяйственных машин.
- Мебельные. Применяются в строительстве и мебельном производстве.
- Дорожные. Ими крепят металлоконструкции.
- Машиностроительные. Применяют в машиностроительной промышленности и приборостроении.
Механические свойства крепежных изделий зависят от стали, из которой они изготовлены и качества обработки.
Удельная прочность
Удельная прочность материала (формула ниже) характеризуется отношением предела прочности к плотности металла. Эта величина показывает прочность конструкции при данной его массе. Наибольшую важность она представляет для таких отраслей, как авиастроение, ракетостроение и производство космических аппаратов.
 По величине удельной прочности сплавы из титана самые прочные из всех применяемых технических материалов. Титановые сплавы вдвое превышают удельную прочность металлов, относящихся к легированным сталям. Они не поддаются коррозии на воздухе, в кислотной и щелочной среде, не боятся морской воды и обладают хорошей теплоустойчивостью. При высоких температурах их прочность выше, чем у сплавов с магнием и алюминием. Благодаря этим свойствам их применение, как конструкционного материала, все время увеличивается и находит широкое использование в машиностроении. Недостаток титановых сплавов заключается в их низкой обрабатываемости резанием. Это связано с физическими и химическими свойствами материала и особой структурой сплавов.
По величине удельной прочности сплавы из титана самые прочные из всех применяемых технических материалов. Титановые сплавы вдвое превышают удельную прочность металлов, относящихся к легированным сталям. Они не поддаются коррозии на воздухе, в кислотной и щелочной среде, не боятся морской воды и обладают хорошей теплоустойчивостью. При высоких температурах их прочность выше, чем у сплавов с магнием и алюминием. Благодаря этим свойствам их применение, как конструкционного материала, все время увеличивается и находит широкое использование в машиностроении. Недостаток титановых сплавов заключается в их низкой обрабатываемости резанием. Это связано с физическими и химическими свойствами материала и особой структурой сплавов. 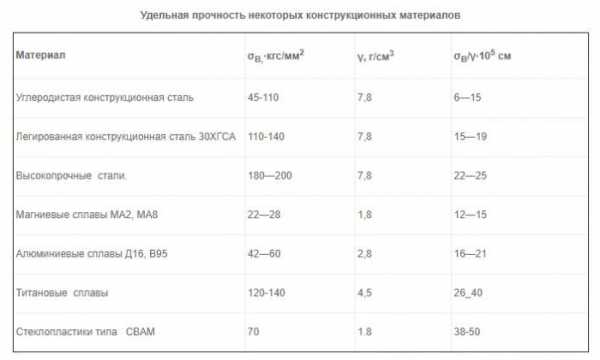 Выше приведена таблица удельной прочности металлов.
Выше приведена таблица удельной прочности металлов.
Использование пластичности и прочности металлов
Очень важными свойствами металла являются пластичность и прочность. Эти свойства находятся в прямой зависимости друг от друга. Они не позволяют металлу изменять форму и препятствуют макроскопическому разрушению при воздействии на него внешних и внутренних сил.
Металлы, обладающие высокой пластичностью, под воздействием нагрузки разрушаются постепенно. Вначале у них появляется изгиб и только затем он начинает постепенно разрушаться. Пластичные металлы легко меняют форму, поэтому их широко используют для изготовления кузовов автомобилей. Прочность и пластичность металлов зависит от того, как направлены приложенные к нему силы и в каком направлении проводилась прокатка при изготовлении материала. Установлено, что при прокатке кристаллы металла удлиняются в ее направлении больше, чем в поперечной направленности. У листовой стали прочность и пластичность значительно больше в направлении прокатки. В поперечном же направлении прочность уменьшается на 30 %, а пластичность на 50 %, по толщине листа эти показатели еще ниже. Например, появление излома на стальном листе при сваривании можно объяснить параллельностью оси шва и направления прокатки. По пластичности и прочности материала устанавливают возможность его использования для изготовления различных деталей машин, сооружений, инструментов, приборов.
Нормативное и расчетное сопротивление металла
Одним из основных параметров, которые характеризуют сопротивление металлов воздействиям силы, является нормативное сопротивление. Оно устанавливается по нормам проектирования. Расчетное сопротивление получается в результате деления нормативного на соответствующий коэффициент надежности по данному материалу. В некоторых случаях учитывают еще и коэффициент условий работы конструкций. В вычислениях, имеющих практическое значение, в основном используют расчетное сопротивление металла.
Пути повышения прочности металла
Существует несколько способов повышения прочности металлов и сплавов:
- Создание сплавов и металлов, имеющих бездефектную структуру. Имеются разработки по изготовлению нитевидных кристаллов (усов) в несколько десятков раз превышающих прочность обыкновенных металлов.
- Получение объемного и поверхностного наклепа искусственным путем. При обработке металла давлением (ковка, волочение, прокатка, прессование) образуется объемный наклеп, а накатка и дробеструйная обработка дает поверхностный наклеп.
- Создание легированного металла, используя элементы из таблицы Менделеева.
- Очищение металла, от имеющихся в нем примесей. В результате этого улучшаются его механические свойства, распространение трещин значительно уменьшается.
- Устранение с поверхности деталей шероховатости.
Интересные факты
- Сплавы из титана, удельный вес которых превышает алюминиевые примерно на 70 %, прочнее их в 4 раза, поэтому, по удельной прочности сплавы, содержащие титан, выгоднее использовать для самолетостроения.
- Многие алюминиевые сплавы превышают удельную прочность сталей, содержащих углерод. Сплавы из алюминия имеют высокую пластичность, коррозийную стойкость, прекрасно обрабатываются давлением и резанием.
- У пластмасс удельная прочность выше, чем у металлов. Но из-за недостаточной жесткости, механической прочности, старения, повышенной хрупкости и малой термостойкости ограничены в применении слоистые пластики, текстолиты и гетинаксы, особенно в крупногабаритных конструкциях.
- Установлено, что по выносливости к коррозии и удельной прочности, металлы черные, цветные и многие их сплавы уступают стеклопластикам.
 Механические свойства металлов являются важнейшим фактором использования их в практических нуждах. Проектируя какую-то конструкцию, деталь или машину и подбирая материал, обязательно рассматривают все механические свойства, которыми он обладает.
Механические свойства металлов являются важнейшим фактором использования их в практических нуждах. Проектируя какую-то конструкцию, деталь или машину и подбирая материал, обязательно рассматривают все механические свойства, которыми он обладает.
fb.ru
Условия прочности и жесткости. Виды расчетов
Расчет растянутого или сжатого стержня на прочность и жесткость может осуществляться по участкам (в этом случае стержень будет иметь ступенчатую форму сечений) или для всего стержня (стержень постоянной жесткости).
В первом случае вычисляют рабочие напряжения, которые возникают в поперечных сечениях каждого участка стержня по известной формуле (9.2):
(9.2)
Во втором случае по той же формуле вычисляют:
— наибольшие по модулю напряжения, если стержень изготовлен из упруго-пластических материалов (различных марок стали)
;
— наибольшие растягивающие и наибольшие по модулю сжимающие напряжения, если стержень изготовлен из хрупких материалов (из чугуна, бетона, железобетона).
Эти напряжения не должны превышать определенной величины, установленной номами или техническими условиями для каждого вида материала и каждого вида деформирования элемента конструкции. В зависимости от метода расчета эту величину называют допускаемым напряжением или расчетным сопротивлением.
Если расчет осуществляется по методу допускаемых напряжений, то рабочее напряжение не может превышать допускаемого напряжения, которое обозначается символом .
Допускаемые напряжения определяются отношением опасного напряжения к коэффициенту запаса прочности. За опасное напряжение принимается предел текучести для пластичных материалов, или предел прочности для хрупких материалов.
Величины опасных напряжений определяют в результате испытания стандартных образцов пластичных материалов на растяжение, или в результате испытания стандартных образцов хрупких материалов на сжатие.
Коэффициент запаса прочности при растяжении бруса обозначается буквой , а при его сжатии буквой . Эти коэффициенты имеют значения больше единицы и, в зависимости от условий эксплуатации конструкции, принимаются равными, в пределах: ; .
Тогда, согласно приведенным выше определениям, допускаемое напряжение можно найти по формулам:
; .
Допускаемые напряжения регламентируются специальными нормами. Например, для различных марок стали, они имеют значения: — 180 МПа.
В результате получаем следующее условие прочности стержня по методу допускаемых напряжений:
(9.16)
Примечание: Условие (3.16) используется для материалов, которые имеют одинаковую прочность при растяжении и сжатии, то есть имеет равные значения допускаемых напряжений при растяжении и при сжатии. Если допускаемые значения напряжений при растяжении и сжатия имеют разные значения, то нужно рассматривать два условия прочности на растяжение и сжатие отдельно:
(9.17)
(9.18)
Изложенный метод расчета в настоящее время практически не применяется, но он имеет историческую ценность и содержится в абсолютном большинстве учебников и учебных пособий по сопротивлению материалов.
Если расчет осуществляется по методу расчетных сопротивлений, то рабочее напряжение не может превышать расчетного сопротивления , которое, как и допускаемое напряжение , определяется с использованием предела текучести или временного сопротивления, принимаемых за нормативное сопротивление .
Расчетное сопротивление определяется с использованием трех коэффициентов (коэффициента условий работы, коэффициента однородности материала и коэффициента перегрузки). Это приводит к более экономному расходу материала конструкции, так как значение расчетного сопротивления имеет больше значение чем допускаемое напряжение.
Например, для низкоуглеродистых сталей расчетное сопротивление принимается равным в пределах 210-240 МПа, тогда как допускаемое напряжение равно 160-180 МПа.
Условия прочности при растяжении (сжатии) приводятся к следующему виду:
, , (9.19)
В дальнейшем расчеты на прочность при любых видах деформирования стержней будем осуществлять по методу расчетных сопротивлений.
Условие прочности связывает между собой три величины:
— продольную силу N;
— площадь поперечного сечения А;
— расчетное сопротивление ,
В соответствии с этим возможные три вида расчета стержня на прочность:
1. Проверочный расчет. Если известны все три величины: N, А, , но отсутствуют расчеты стержня, то осуществляется проверка выполнения условия прочности. При выполнении этого условия стержень можно использовать по назначению, а при невыполнении условия прочности нужно увеличить площадь сечения стержня, или уменьшить нагрузку.
2. Определение размеров поперечного сечения:
. (9.20)
В зависимости от заданной формы сечения находятся его размеры.
3. Определение допускаемой нагрузки. В этом случае известны площадь поперечного сечения А и расчетное сопротивление . Тогда из условия прочности находим допускаемую продольную силу (допускаемую нагрузку на стержень):
. (9.21)
Условие жесткости стержня. В случае растяжения или сжатия стержень получает абсолютное удлинение или укорочение . Величина этой деформации не может быть больше допускаемой деформации , то есть
,или(9.22)
Это условие называется условием жесткости стержня при растяжении или сжатии. Оно позволяет выполнить три вида расчетов стержня на жесткость, аналогично, как и при использовании условия прочности, то есть:
1. Осуществить проверку выполнения условия жесткости;
2. Определить размеры поперечного сечения;
3. Определить допускаемую нагрузку на стержень.
Похожие статьи:
poznayka.org
Механические свойства
Механические свойства характеризуют поведение материалов под действием нагрузки. В рамках данной статьи рассмотрим 5 основных механических свойств материалов: прочность, упругость, пластичность, хрупкость и твердость.
Что такое Прочность?
Прочностью называется способность разнообразных материалов без разрушения воспринимать напряжение под внешним воздействием различных сил. Прочность зависит не только от того, какой материал, но и имеет зависимость от типа состояния напряжения — например, это может быть сжатие, растяжение или изгиб. Также непосредственное влияние на прочность оказывают условия, при которых материал эксплуатируется — воздействия извне, температура окружающей среды.
Испытания на прочность
Существует понятие предела прочности, который является основной количественной характеристикой прочности и численно равен разрушающему напряжению для конкретного материала. Предел прочности для каждого материала определяется средним результатом серии испытаний, так как основные материалы, используемые в строительстве, характеризуются неоднородностью.
Если происходит статическая нагрузка для выявления прочности проводится испытание образцов определенного стандарта (как правило речь идет об образцах, имеющих сечение круглой формы, реже прямоугольной), диаграмма таким образом отражает зависимость относительного удлинения от величины действующего на образец напряжения.
О так называемой усталости материала (в частности, металла) говорят если при большом числе циклически повторяющихся внешних напряжений разрушение происходит даже при напряжениях меньших чем предел прочности. В этом случае рассчитывается циклическая прочность, т.е. обоснование прочности материала, проводящееся с учетом нагрузки, которая меняется с определенным циклом.
Упругость
Если материал самопроизвольно восстанавливает форму, после того как внешняя сила прекращает действовать, то такое механическое свойство называется упругостью материала. Если после снятия внешней нагрузки, деформация полностью исчезает, то следует говорить об обратимой упругой деформации.
От чего зависит упругость?
Упругость материала непосредственно связана с силами взаимодействия, происходящими между отдельными атомами. В твёрдых телах при температуре равной абсолютному нулю и при отсутствии какого-либо внешнего воздействия атомы занимают положения, называемые равновесными. Потенциальная энергия тела увеличивается при воздействии внешнего напряжения, и атомы смещаются из равновесного положения. Соответственно, когда прекращается внешнее напряжение, конфигурация неравновесных атомов деформированного материала постепенно становится неустойчивой и возвращается в равновесное состояние. Помимо силы притяжения и отталкивания, которые действуют на каждый атом материала со стороны остальных, существуют и угловые силы, они непосредственно связаны с валентными углами, наблюдающимися между прямыми, которые соединяют атомы между собой. Естественно, это характерно исключительно для макроскопических тел и молекул, содержащих много атомов. Угловые силы уравновешиваются при равновесных значениях валентных углов. Когда говорят о количественной характеристике упругости материала, то используется модуль упругости, зависящий от напряжения воздействующего на материал и определяется производной зависимости напряжения от деформации, что применимо для области упругой деформации.
Пластичность
Пластичностью называется механическое свойство материалов под влиянием внешней нагрузки изменять форму и размер, а после того как нагрузка перестает действовать — сохранять ее в измененном виде.
Пластичность является важным свойством, учитывающееся когда происходит выбор материала несущей конструкции, либо же определения технологии (методики) изготовления разнообразных изделий. Для конструкций важно сочетание высокой пластичности материала и большого показателя упругости. Эта комбинация свойств предотвращает внезапное разрушение материала. В целом пластичность в физике материалов противопоставляется как упругости, так и хрупкости — пластичный материал сохраняет форму, которую придают ему внешние воздействия.
Пластичность — важное механическое свойство
Изучение пластичности важно при прогнозировании долговечности и прочности какой-либо конструкции, так как пластичность зачастую предшествует разрушению и важно рассмотреть деформационные процессы, возникающие в материале. Измерение пластичности, являющейся важным свойством металлов, очень важно при обработке под давлением — ковке и прокатке. Это свойство металлов непосредственно зависит от тех условий, в которых происходит деформирование — температуры, давления и т.д. Пластичность металлов влияет на такие характеристики как удлинение (абсолютное и относительное) и сужение материала. При удлинении происходит увеличение длины образца под воздействием происходящего растяжения, а при сужении, соответственно, от растяжения образца происходит уменьшение площади поперечного сечения.
Хрупкость
Хрупкость относится к механическим свойствам материалов противоположным пластичности. Те процессы, которые повышают пластичность, соответственно, снижают хрупкость, и наоборот. Материалы, отличающиеся хрупкостью при статическом испытании разрушаются без пластической деформации. Это характерно, например, для стекла. Если при статическом испытании материал характеризуется пластичностью, но при динамическом испытании разрушается, то речь идет о так называемой ударной хрупкости. Причиной ударной хрупкости могут быть пределы текучести (то есть зависимость скорости деформации и сопротивления) и пределы прочности (изменение сопротивления разрушению). Хрупкое разрушение материала происходит если сопротивление деформации равно или больше сопротивления отрыву. Соответственно, пластичность материала уменьшается, если рост сопротивления деформации происходит быстрее роста сопротивления разрушению.
Фактором, от которого непосредственно зависит хрупкое состояние материала является однородность напряженного состояния. Материал переходит от пластичности к хрупкости при неоднородном напряженном состоянии. Расчет сопротивления хрупкому разрушению является важным обоснованием прочности конструкции.
Твёрдость
Механическое свойство материала при внешнем воздействии не испытывать пластической деформации называется твёрдостью. В первую очередь оно зависит от механических характеристик материала, в частности структуры, модуля упругости, предела прочности и т.д. Количественную связь твердости от данных характеристик устанавливает общая физическая теория упругости.
Методы, с помощью которых экспериментально устанавливают твердость бывают как статическими (например, в поверхность вдавливается твердый предмет или же она царапается), так и динамическими. К статическим методам также относятся измерения твёрдости по Бринеллю (вдавление шарика в поверхность), Виккерсу (вдавление алмазного наконечника) и Роквеллу (для материалов с высокой твердостью используется алмазный конус, с низкой — шарик из стали). Также к статическим методам относится склерометрия — царапание алмазной структурой в виде конуса, пирамиды, или же карандашом различной твердости — оценивается нагрузка, которую необходимо приложить, чтобы создать царапину, а также размеры созданной царапины.
При динамических методах установления твердости материала благодаря ударной нагрузке наносится отпечаток шариком (по принципу маятника) и величина твердости характеризуется тем, как материал сопротивляется деформации от удара или же параметрами отскока шарика от поверхности, в том числе затуханию маятниковых колебаний.
sopromats.ru
Прочность
Испытание образца на прочность при сжатии.
Прочность — способность материала сопротивляться необратимый ( пластической, вязкой) деформации и разрушению (разделению на части) под действием нагрузок или других факторов (усадка, неравномерное температурное поле и т. д.). Потеря прочности или превышение ее предельного значения приводит к разрушению материала и детали или конструкции из него изготовленной.
Различают прочность собственно материала и конструкционную прочность, а по способу приложения нагрузки: кратковременную, длительную и прочность в условиях циклических нагрузок и усталости.
Показатели прочности: временное сопротивление или предел прочности, граница упругости, предел текучести, граница длительной прочности, предел выносливости.
1. Допустимые напряжения
Наибольшие напряжения в материале детали из условия надежной ее работы следует ограничивать допустимыми значениями. При растяжении и сжатии допустимые напряжения обозначают соответственно и . При смещении — .
Если известны допустимые напряжения и есть формулы, определяющие напряжение через усилия и моменты в сечении, то можно, в принципе, рассчитать на прочность любую деталь.
2. Оценка прочности при различных видах деформации
При растяжении или сжатия стержня находят опасные сечения, в которых напряжения достигают наибольших по модулю значений, и для этих сечений записывают условие прочности в виде:
Для случая сдвига (среза)
При сгибании
При кручении
При поверхностном смятии деталей
В этих уравнениях:
Для случая сложного напряженного состояния, когда вектор напряжения в материале произвольно направлен в трехмерных координатах, эквивалентное напряжение и условие наступления предельного состояния определяют руководствуясь теориями прочности.
3. Прочностные испытания материалов
3.1. Образцы для испытаний

Важной характеристикой материала является предел прочности, которую определяют в результате разрушения образцов при статических испытаний на специальных разрывных машинах. Чаще всего испытывают на растяжение, реже на сжатие, изгиб или кручения. В случае растяжения стандартный образец круглого (реже прямоугольного) сечения нагружают двумя одинаковыми и противоположно направленными силами вдоль его оси. Эти силы плавно растут до тех пор, пока образец не разрушится. Чаще используют длинные образцы, в которых отношение длины к поперечному диаметру l / d = 10, реже — короткие, в которых l 0 / d 0 = 5, где l 0 — начальная расчетная длина и d 0 — начальный диаметр образца; S 0 — начальная площадь поперечного сечения образца). Перед испытанием вроде наносят отметки, которыми обозначают величину l 0, затем измеряют l 0 и d 0.
3.2. Диаграмма растяжения
Диаграмма растяжения металлического образца
На основе испытаний образцов на разрывных машинах строится диаграмма растяжения ( диаграмма деформирования) в координатах напряжение — деформация. Характер диаграммы зависит от свойств испытуемого материала. Типичный такой диаграммы изображен на рисунке. Диаграмма растяжения имеет ряд характерных участков.
С начала погрузки до определенного значения напряжений имеет место прямо пропорциональна зависимость между напряжением и деформацией. На этой стадии растяжения справедливый закон Гука.
Далее эта линейная зависимость теряется и предел называется граница пропорциональности. Итак границей пропорциональности называется напряжение, после которого нарушается закон Гука.
При дальнейшем увеличении нагрузки, в материале появляются остаточные деформации, не исчезающие после разгрузки. Наибольшее напряжение, к которому остаточная деформация не оказывается, называется пределом упругости.
Дальнейшее увеличение нагрузки приводит к появлению горизонтальной площинкы текучести на диаграмме деформирования. Такой процесс деформации называют текучестью материала сопровождается остаточным удлинением, не исчезающей после разгрузки. Итак, пределом текучести (Yield Strength) σ Т называется наименьшее напряжение, при котором деформация образца происходит при постоянном растягивающие напряжения.
Начало пластической деформации соответствует наступлению некоторого критического состояния, которое можно обнаружить не только за появлением остаточных деформаций, но и за повышением температуры, изменением электропроводности и магнитных свойств при этом. После стадии текучести материал снова приобретает способность увеличивать сопротивление (Strain Hardening) в некоторой границы. Напряжение, соответствующее максимальному сопротивлению материала называется временное сопротивление или предел прочности (Ultimate Strenght) и обозначается σ в.
Дальнейшее растяжение образца сопровождается появлением шейки (локализации деформации), его разупрочнения и разрушением (Fracture).
Граница (предел) прочности при сжатии плотных изверженных и метаморфических горных пород составляет около 100 МПа, а для особо прочных пород, например, базальтов, достигает 500 МПа. Прочность осадочных пород существенно зависит от ихнои структуры и пористости и лежит в пределах 5-200 МПа. Теории прочности разрабатывались многими учеными, среди которых были Галилео Галилей, Сен-Венана, Кулон, Максвелл, Мор, Риттингер и др..
См.. также
Литература
nado.znate.ru
Механические свойства строительных материалов
Основные характеристики стройматериалов
Прочность — свойство материала сопротивляться разрушению под действием напряжений, возникающих от приложенных нагрузок. Прочность строительных материалов можно охарактеризовать пределом прочности при механическом воздействии: срезе, изгибании, растяжении, сжатии, срезе.
Предел прочности — напряжение соответствующей нагрузки, при которой происходит разрушение образца. Предел прочности — минимальная величина воздействия, при которой материал начинается разрушаться.
Прочность устанавливается в качестве маркировки. Предельную величину определяют путем проведения различных испытаний образца материала. Среди стройматериалов наименьшим пределом прочности обладают тор-фоплиты — всего 0,5 Мпа. Самый прочный материал — это высококачественная сталь — до 1000 Мпа.
Упругость — свойство материала под воздействием нагрузок деформироваться и принимать после снятия напряжения исходные форму и размеры (резина). В отличии от хрупких тел упругие под воздействием внешних сил не разрушаются, а только деформируются. При прекращении действия материал приобретает первоначальную форму. Ярким примером является резина. Если взять кусок этого материала и растянуть в разные стороны, то он удлинится, но стоит отпустить одну сторону — резина приобретет начальные размеры.
Пластичность — свойство материала под воздействием нагрузки принимать другую форму и сохранять ее после снятия нагрузки.
Хрупкость — свойство материала мгновенно разрушаться под действием сил (стекло, керамика). Под хрупкостью понимают способность вещества мгновенно разрушаться при незначительной деформации. Иными словами механическое воздействие на тело приводит к появлению трещин или раскалыванию. Примером хрупких материалов является стекло и керамика.
Сопротивление удару — способность сопротивляться воздействию ударных нагрузок.
Твердость — свойство материала сопротивляться проникновению в него другого более твердого материала (по шкале Мооса). Под твердостью понимается способность одного вещества оказывать сопротивление воздействию другого, более твердого. Для оценивания данного показатели принято использовать десятибалльную шкалу. Минимальную твердость имеет тальк-1, самый твердый материал — алмаз, с максимальным значением в 10 балов.
Износ — разрушение материала под совместным воздействием ударных и истирающих усилий. Измеряется потерей массы в %.
Стираемость. Способность материала под действием силы трения терять свою массу и объем. Зачастую эту способность учитывают при организации дорожного покрытия, а также укладке полов в общественных местах.
При строительстве и ремонте зданий очень важно учитывать все свойства используемых материалов, так как от них будет зависеть срок службы и надежность конструкций.
Основные свойства стройматериалов:
Плотность. Представляет собой отношение массы материала к его объему в стандартных условиях, то есть с учетом пустот и пор. Чем больше количество пор, тем, соответственно меньше плотность вещества.
Плотность определяет массу строительной конструкции, ее теплопроводность и прочность.
2) Прочность строительного материала. Свойство вещества оказывать сопротивление нагрузке. Конструкции здания постоянно испытывают нагрузки разного рода, под которыми они сжимаются, растягиваются или сгибаются. Строительный материал ни в коем случае не должен терять свою структуру или разрушаться.
3) Теплопроводность. Характеризуется количеством тепла, которое проходит через толщину материала в один метр при разнице внешней и внутренней температуры в один градус по Цельсию.
Основными факторами, которые влияют на теплопроводность вещества — это показатель плотности степень влажности. Чем меньше их значение, тем меньше тепла пропускает материал.
4) Влажность. Количество влаги, которое содержится в порах материала, называют влажностью. Она рассчитывается в процентном соотношении к массе идеально сухого материала. Чем выше показатель влажности, тем меньше прочность материала и выше теплопроводность.
5) Водопроницаемость. Данный показатель показывает количество воды, которое может пройти через материал площадью один сантиметр за один час. Для расчета данного показателя используют специальные камеры, в которых создают условия приближенные к реальным. Например, чтобы рассчитать водопроницаемость наружных плит их помещают под установку, которая имитирует косой дождь. Кровельные материалы испытывают на выносливость: то есть помещают под струю воды и рассчитывают время, через которое на другой стороне вещества появятся следы влаги.
6) Морозоустойчивость. Свойство влажного материала сохранять свою структуру при неоднократной заморозке. Испытания проходят по такому алгоритму: материал напитывают влагой и помещают в морозильную камеру. Далее процесс заморозки чередуется с разморозкой. В зависимости от количества циклов, которое может выдержать вещество ем присваивается соответствующие значения при маркировке.
7) Огнестойкость. Способность материала сохранять свою структуру при воздействии высоких температур. Предел огнестойкости определяется как время, через которое конструкция уже не сможет сохранять свою прочность.
Строительные материалы классифицируют по нескольким параметрам в зависимость от их способности гореть, воспламеняться и тлеть.
- Трудносгораемые материалы. Вещества, которые прекращают процесс тления и горения, если убрать источник огня.
- Несгораемые. Материала, которые не горят и не обугливаются.
- Сгораемые. Все остальные материалы.
Фирменный Таркетт ламинат по самой низкой цене в магазине Floors.

knep.ru
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ | Энциклопедия Кругосвет
Содержание статьиСОПРОТИВЛЕНИЕ МАТЕРИАЛОВ, раздел механики твердого тела, изучающий напряжения и деформации, которые обусловлены силами, действующими на твердые тела – элементы конструкции. Эту дисциплину можно характеризовать и как науку о методах расчета элементов конструкции на прочность, жесткость и устойчивость.
Напряжение, создаваемое в твердом теле внешними нагрузками, есть мера (с размерностью силы на единицу площади) интенсивности внутренних сил, действующих со стороны одной, мысленно отсекаемой, части тела на другую, оставшуюся (метод сечений). Внешние нагрузки вызывают деформацию тела, т.е. изменение его размеров и формы. В сопротивлении материалов исследуются соотношения между нагрузками, напряжениями и деформациями, причем исследования ведутся, с одной стороны, путем математического вывода формул, связывающих нагрузки с вызываемыми ими напряжениями и деформациями, а с другой – путем экспериментального определения характеристик материалов, применяемых в строениях и машинах. См. также МЕТАЛЛОВ МЕХАНИЧЕСКИЕ СВОЙСТВА; МЕТАЛЛОВ ИСПЫТАНИЯ. По найденным формулам с учетом результатов испытания материалов рассчитываются размеры элементов строений и машин, обеспечивающие сопротивление заданным нагрузкам. Сопротивление материалов не относится к точным наукам, так как многие его формулы выводятся на основе предположений о поведении материалов, которые не всегда точно выполняются. Тем не менее, пользуясь ими, грамотный инженер может создавать надежные и экономичные конструкции.
С сопротивлением материалов тесно связана математическая теория упругости, в которой тоже рассматриваются напряжения и деформации. Она позволяет решать те задачи, которые с трудом поддаются решению обычными методами сопротивления материалов. Однако между сопротивлением материалов и теорией упругости нет четкой границы. Хотя почти все задачи о распределении напряжений решены методами математического анализа, при сложных условиях эти решения требуют трудоемких выкладок. И тогда на помощь приходят экспериментальные методы анализа напряжений.
НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ
Виды напряжений.
Самое важное понятие в сопротивлении материалов – это понятие напряжения как силы, действующей на малую площадку и отнесенной к площади этой площадки. Напряжения бывают трех видов: растяжения, сжатия и сдвига.
Если на металлическом стержне подвешен груз, как показано на рис. 1,а, то такой стержень называется растянутым или работающим на растяжение. Напряжение S, создаваемое силой P в растянутом стержне с площадью поперечного сечения, равной A, дается выражением S = P/A. Если вес груза равен 50 000 Н, то растягивающая сила тоже равна 50 000 Н. Далее, если ширина стержня равна 0,05 м, а толщина – 0,02 м, так что площадь поперечного сечения составляет 0,001 м2, то растягивающее напряжение равно 50 000/0,001 = 50 000 000 Н/м2 = 50 МПа. Растянутый стержень длиннее, чем до приложения растягивающих сил.
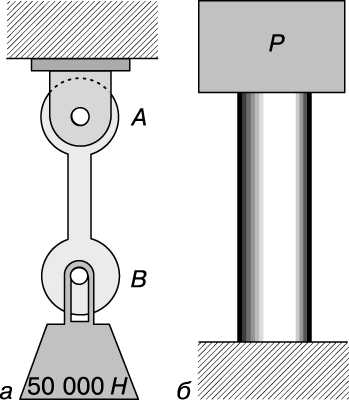
Рассмотрим короткий цилиндр (рис. 1,б), на верхний торец которого положен груз. При этом во всех поперечных сечениях цилиндра действуют напряжения сжатия. Если напряжение равномерно распределено по всему сечению, то справедлива формула S = P/A. Сжатый цилиндр короче, чем в отсутствие деформаций.
Напряжение сдвига возникает, например, в болте (рис. 2,а), на котором верхним концом держится растянутый стержень AB с грузом 50 000 Н (рис. 1,а). Болт удерживает стержень, действуя с силой 50 000 Н, направленной вверх, на ту часть стержня, которая расположена непосредственно над отверстием в стержне, а стержень в свою очередь давит на среднюю часть болта с силой 50 000 Н. Силы, действующие на болт, приложены так, как показано на рис. 2,б. Если бы болт был сделан из материала с низким пределом прочности на сдвиг, например из свинца, то он был бы срезан по двум вертикальным плоскостям (рис. 2,в). Если же болт стальной и достаточно большого диаметра, то он не срежется, но в двух его вертикальных поперечных сечениях будут существовать напряжения сдвига. Если напряжения сдвига равномерно распределены, то они даются формулой S = P/A. Полная сила сдвига, действующая в каждом из поперечных сечений, равна 25 000 Н, и если диаметр болта равен 0,02 м (площадь поперечного сечения равна приблизительно 0,0003 м2), то напряжение сдвига Ss будет составлять 25 000 Н/0,0003 м2, т.е. немногим более 80 МПа.
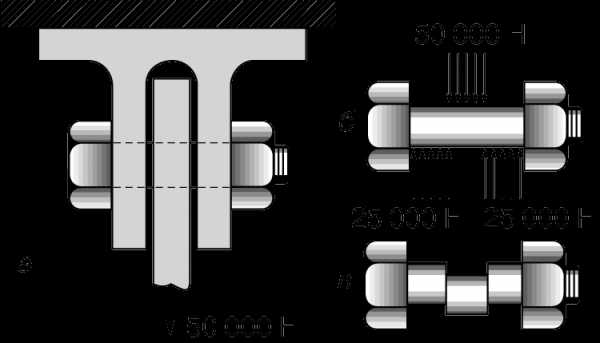
Напряжения растяжения и сжатия направлены по нормали (т.е. вдоль перпендикуляра) к площадке, в которой они действуют, а напряжение сдвига – параллельно площадке. Поэтому напряжения растяжения и сжатия называются нормальными, а напряжения сдвига – касательными.
Деформация.
Деформацией называется изменение размера тела под действием приложенных к нему нагрузок. Деформация, отнесенная к полному размеру, называется относительной. Если изменение каждого малого элемента длины тела одинаково, то относительная деформация называется равномерной. Относительную деформацию часто обозначают символом d, а полную – символом D. Если относительная деформация постоянна по всей длине L, то d = D/L. Например, если длина стального стержня до приложения растягивающей нагрузки равна 2,00 м, а после нагружения – 2,0015 м, то полная деформация D равна 0,0015 м, а относительная – d = 0,0015/2,00 = 0,00075 (м/м).
Почти для всех материалов, применяемых в строениях и машинах, относительная деформация пропорциональна напряжению, пока оно не превысит т.н. предела пропорциональности. Это очень важное соотношение называется законом Гука. Оно было экспериментально установлено и сформулировано в 1678 английским изобретателем и часовых дел мастером Р.Гуком. Данное соотношение между напряжением и деформацией для любого материала выражается формулой S = Ed, где E – постоянный множитель, характеризующий материал. Этот множитель называют модулем Юнга по имени Т.Юнга, который ввел его в 1802, или же модулем упругости. Из обычных конструкционных материалов наибольший модуль упругости у стали; он равен примерно 200 000 МПа. В стальном стержне относительная деформация, равная 0,00075, из приводившегося ранее примера вызывается напряжением S = Ed = 200 000 ґ 0,00075 = 150 МПа, что меньше предела пропорциональности конструкционной стали. Если бы стержень был из алюминия с модулем упругости около 70 000 МПа, то, чтобы вызвать ту же самую деформацию 0,00075, достаточно было бы напряжения немногим более 50 МПа. Из сказанного ясно, что упругие деформации в строениях и машинах очень малы. Даже при сравнительно большом напряжении 150 МПа из приведенного выше примера относительная деформация стального стержня не превышает одной тысячной. Столь большая жесткость стали – ее ценное качество.
Чтобы наглядно представить деформацию сдвига, рассмотрим, например, прямоугольную призму ABCD (рис. 3). Ее нижний конец жестко заделан в твердое основание. Если на верхнюю часть призмы действует горизонтальная внешняя сила F, она вызывает деформацию сдвига, показанную штриховыми линиями. Смещение D есть полная деформация на длине (высоте) L. Относительная деформация сдвига d равна D/L. Для деформации сдвига тоже выполняется закон Гука при условии, что напряжение не превышает предела пропорциональности для сдвига. Следовательно, Ss = Esd, где Es – модуль сдвига. Для любого материала величина Es меньше E. Для стали она составляет около 2/5 E, т.е. приблизительно 80 000 МПа. Важный случай деформации сдвига – деформация в валах, на которые действуют внешние скручивающие моменты.
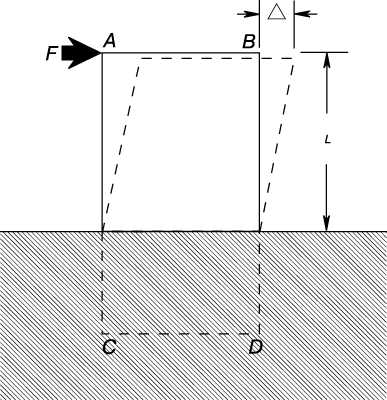
Выше речь шла об упругих деформациях, которые вызываются напряжениями, не превышающими предела пропорциональности. Если же напряжение выходит за предел пропорциональности, то деформация начинает расти быстрее, чем напряжение. Закон Гука перестает быть справедливым. В случае конструкционной стали в области, лежащей чуть выше предела пропорциональности, небольшое увеличение напряжения приводит к увеличению деформации во много раз по сравнению с деформацией, соответствующей пределу пропорциональности. Напряжение, при котором начинается столь быстрый рост деформации, называется пределом текучести. Материал, в котором разрушению предшествует большая неупругая деформация, называется пластичным.
ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ
Допускаемое (допустимое) напряжение – это значение напряжения, которое считается предельно приемлемым при вычислении размеров поперечного сечения элемента, рассчитываемого на заданную нагрузку. Можно говорить о допускаемых напряжениях растяжения, сжатия и сдвига. Допускаемые напряжения либо предписываются компетентной инстанцией (скажем, отделом мостов управления железной дороги), либо выбираются конструктором, хорошо знающим свойства материала и условия его применения. Допускаемым напряжением ограничивается максимальное рабочее напряжение конструкции.
При проектировании конструкций ставится цель создать конструкцию, которая, будучи надежной, в то же время была бы предельно легкой и экономной. Надежность обеспечивается тем, что каждому элементу придают такие размеры, при которых максимальное рабочее напряжение в нем будет в определенной степени меньше напряжения, вызывающего потерю прочности этим элементом. Потеря прочности не обязательно означает разрушение. Машина или строительная конструкция считается отказавшей, когда она не может удовлетворительно выполнять свою функцию. Деталь из пластичного материала, как правило, теряет прочность, когда напряжение в ней достигает предела текучести, так как при этом из-за слишком большой деформации детали машина или конструкция перестает соответствовать своему назначению. Если же деталь выполнена из хрупкого материала, то она почти не деформируется, и потеря ею прочности совпадает с ее разрушением.
Запас прочности.
Разность напряжения, при котором материал теряет прочность, и допускаемого напряжения есть тот «запас прочности», который необходимо предусматривать, учитывая возможность случайной перегрузки, неточностей расчета, связанных с упрощающими предположениями и неопределенными условиями, наличия не обнаруженных (или не обнаружимых) дефектов материала и последующего снижения прочности из-за коррозии металла, гниения дерева и пр.
Коэффициент запаса.
Коэффициент запаса прочности какого-либо элемента конструкции равен отношению предельной нагрузки, вызывающей потерю прочности элемента, к нагрузке, создающей допускаемое напряжение. При этом под потерей прочности понимается не только разрушение элемента, но и появление в нем остаточных деформаций. Поэтому для элемента конструкции, выполненного из пластичного материала, предельным напряжением является предел текучести. В большинстве случаев рабочие напряжения в элементах конструкции пропорциональны нагрузкам, а поэтому коэффициент запаса определяется как отношение предела прочности к допускаемому напряжению (коэффициент запаса по пределу прочности). Так, если предел прочности конструкционной стали равен 540 МПа, а допускаемое напряжение – 180 МПа, то коэффициент запаса равен 3.
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ
В сопротивлении материалов большое внимание уделяется выводу соотношений между заданными нагрузками, размерами и формой элемента конструкции, несущего эти нагрузки или сопротивляющегося им, и напряжениями, возникающими в определенных сечениях элемента конструкции. Как правило, цель расчетов состоит в том, чтобы найти необходимые размеры элемента, при которых максимальное рабочее напряжение в нем не будет превышать допускаемого.
В элементарном курсе сопротивления материалов рассматривается ряд типичных случаев равномерного распределения напряжений: растянутые стержни, короткие сжатые стержни, тонкостенные цилиндры, работающие под давлением внутренней среды (котлы и резервуары), заклепочные и сварные соединения, температурные напряжения и такие статически неопределимые системы, как растянутые стержни из нескольких разных материалов.
Если напряжение одинаково во всех точках поперечного сечения, то S = P/A. Конструктор находит необходимую площадь поперечного сечения, поделив заданную нагрузку на допускаемое напряжение. Но нужно уметь отличать случаи, в которых напряжение действительно распределено равномерно, от других, сходных случаев, в которых этого нет. Необходимо также (как в задаче о заклепочных соединениях, в которых существуют напряжения и растяжения, и сжатия, и сдвига) находить плоскости, в которых действуют напряжения разного вида, и определять максимальные местные напряжения.
Тонкостенный цилиндр.
Такой резервуар выходит из строя (разрывается), когда напряжение растяжения в его оболочке становится равным пределу прочности материала. Формулу, связывающую толщину стенки t, внутренний диаметр резервуара D, напряжение S и внутреннее давление R, можно вывести, рассмотрев условия равновесия кольца, вырезанного из его оболочки двумя поперечными плоскостями, разделенными расстоянием L (рис. 4,а). Внутреннее давление действует на внутреннюю поверхность полукольца с направленной вверх силой, равной произведению RDL, а напряжения в двух горизонтальных концевых сечениях полукольца создают две направленные вниз силы, каждая из которых равна tLS. Приравнивая, получаем
RDL = 2tLS, откуда S = RD/2t.
Заклепочное соединение.
На рис. 4,б представлено двухзаклепочное соединение двух полос внахлестку. Такое соединение может выйти из строя из-за перерезывания обеих заклепок, разрыва одной из полос в том месте, где она ослаблена отверстием под заклепку, или из-за слишком больших напряжений смятия по площади соприкосновения заклепки с полосой. Напряжение смятия в заклепочном соединении вычисляется как нагрузка на одну заклепку, деленная на диаметр заклепки и на толщину полосы. Допускаемой для такого соединения принимается наименьшая из нагрузок, соответствующих допускаемым напряжениям трех указанных видов.
Вообще говоря, напряжение, действующее в поперечном сечении растянутого или короткого сжатого стержня, можно с полным основанием считать равномерно распределенным, если равные и противоположно направленные нагрузки приложены так, что равнодействующая каждой из них проходит через центр тяжести рассматриваемого поперечного сечения. Но нужно иметь в виду, что ряд задач (и к ним относится задача о напряжениях смятия в заклепочном соединении) решается в предположении о равномерном распределении напряжения, хотя это заведомо не соответствует действительности. Допустимость такого подхода проверяется опытным путем.
НЕРАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ
Многие элементы строений и детали машин нагружаются так, что напряжения во всех их поперечных сечениях распределены неравномерно. Чтобы вывести формулы для расчета напряжений в таких условиях, мысленно разрезают элемент плоскостью, которая дает нужное поперечное сечение, на две части и рассматривают условия равновесия одной из них. На эту часть действуют одна или несколько заданных внешних сил, а также силы, эквивалентные напряжениям в данном поперечном сечении. Действующие напряжения должны удовлетворять условиям равновесия и соответствовать деформациям. Эти два требования составляют основу для решения задачи. Второе из них подразумевает справедливость закона Гука. Типичными элементами с неравномерным распределением напряжений являются нагруженные балки, валы под действием скручивающих сил, растянутые или сжатые стержни с дополнительным изгибом и колонны.
БАЛКИ.
Балка – это длинный стержень с опорами и нагрузками, работающий в основном на изгиб. Поперечное сечение балки обычно одинаково по всей ее длине. Силы, с которыми опоры действуют на балку, называются реакциями опор. Наиболее распространены два вида балок: консольная (рис. 5,а) и балка с двумя опорами, называемая простой (рис. 5,б). Под действием нагрузок балка прогибается. При этом «волокна» на ее верхней стороне сокращаются, а на нижней – удлиняются. Очевидно, что где-то между верхней и нижней сторонами балки имеется тонкий слой, длина которого не изменяется. Он называется нейтральным слоем. Изменение длины волокна, расположенного между верхней (или нижней) стороной балки и ее нейтральным слоем, пропорционально расстоянию до нейтрального слоя. Если справедлив закон Гука, то напряжения тоже пропорциональны этому расстоянию.
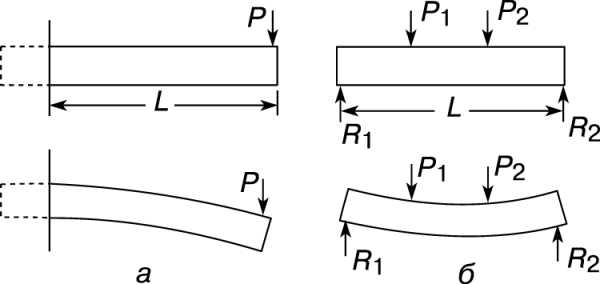
Формула изгиба.
На основе указанного распределения напряжений, дополненного условиями статики, выведена т.н. формула изгиба, в которой напряжение выражается через нагрузки и размеры балки. Она обычно представляется в виде S = Mc/I, где S – максимальное напряжение в рассматриваемом поперечном сечении, c – расстояние от нейтрального слоя до наиболее напряженного волокна, M – изгибающий момент, равный сумме моментов всех сил, действующих по одну сторону от этого сечения, а I – момент инерции поперечного сечения (определенная функция формы и размеров последнего). Характер изменения нормальных напряжений в поперечном сечении балки показан на рис. 6.
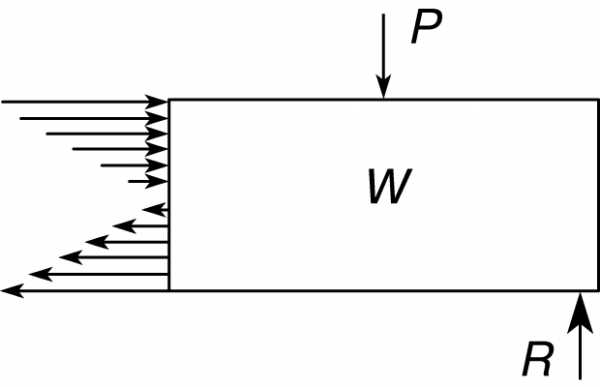
В поперечных сечениях балок действуют также касательные напряжения. Их вызывает равнодействующая всех вертикальных сил, приложенных по одну сторону поперечного сечения горизонтальной балки. Сумма всех внешних сил и реакций, действующих на одну из двух частей балки, называется сдвигом в сечении балки и обычно обозначается через V. Касательные напряжения неравномерно распределены по сечению: они равны нулю на верхнем и нижнем краях сечения и почти всегда максимальны в нейтральном слое.
Прогиб балки.
Часто требуется рассчитать прогиб балки, вызванный действием нагрузки, т.е. вертикальное смещение точки, лежащей в нейтральном слое. Это очень важная задача, поскольку прогиб и кривизну балки нужно знать при решении задач, относящихся к широкому кругу т.н. статически неопределимых систем.
Еще в 1757 Л.Эйлер вывел формулу для кривизны изогнутой балки. В этой формуле кривизна балки выражается через переменный изгибающий момент. Чтобы найти ординату упругой кривой (прогиб), необходимо брать двойной интеграл. В 1868 О.Мор (Германия) предложил метод, основанный на эпюрах изгибающих моментов. Этот графоаналитический метод имеет огромное преимущество перед прежними методами, так как позволяет свести все математические вычисления к сравнительно простым арифметическим выкладкам. Он дает возможность вычислять прогиб и наклон в любой точке балки при любой нагрузке.
Статически неопределимые балки.
Многие балки, используемые в строениях и машинах, имеют более двух опор или только две опоры, но с заделкой одного из концов, исключающей возможность поворота. Такие балки называются статически неопределимыми, поскольку уравнений статики недостаточно для определения реакций в опорах и моментов в заделке. Чаще всего рассматриваются подобные балки трех типов: с одним заделанным (защемленным) концом и одной опорой, с заделанными обоими концами и неразрезные балки, имеющие более двух опор (рис. 7).
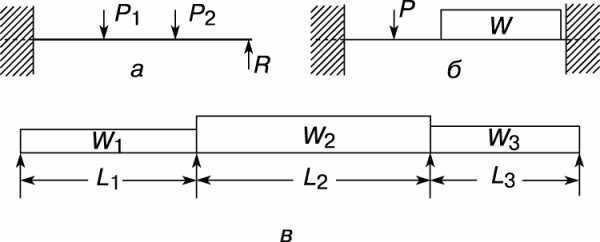
Первое решение задачи о неразрезных балках было опубликовано французским инженером Б.Клапейроном в 1857. Он доказал т.н. теорему о трех моментах. Уравнение трех моментов представляет собой соотношение между изгибающими моментами в трех последовательных опорах одной неразрезной балки. Например, в случае неразрезной балки с равномерной нагрузкой на каждом пролете это уравнение имеет вид
MAL1 + 2MB (L1 + L2) + MCL2 = – (W1L13)/4 – (W2L23)/4.
Здесь MA, MB и MC – изгибающие моменты в трех опорах, L1 и L2 – длины левого и правого пролетов, W1 – нагрузка на левый пролет, а W2 – нагрузка на правый пролет. Нужно написать такое уравнение для каждой пары смежных пролетов, а затем решить полученную систему уравнений. Если число пролетов равно n, то число уравнений будет равно n – 1.
В 1930 Х.Кросс опубликовал свой метод расчета широкого круга статически неопределимых рам и неразрезных балок. Его «метод распределения моментов» позволяет обходиться без решения систем уравнений, сводя все вычисления к сложению и вычитанию чисел.
НАПРЯЖЕНИЕ ПРИ КРУЧЕНИИ.
Если к концам вала приложены равные, но противоположно направленные внешние скручивающие моменты, то во всех его поперечных сечениях существуют только касательные напряжения, т.е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. В круговом поперечном сечении вала деформации сдвига и касательные напряжения равны нулю в центре и максимальны на краю; в промежуточных точках они пропорциональны расстоянию от центра тяжести сечения. Обычная формула для максимального касательного напряжения при кручении такова: S = Tc/J, где T – скручивающий момент на одном конце, c – радиус вала и J – полярный момент сечения. Для круга J = pr4/2. Эта формула применима только в случае кругового поперечного сечения. Формулы для валов с поперечным сечением другой формы выводятся путем решения соответствующих задач методами математической теории упругости с привлечением в некоторых случаях методов экспериментального анализа.
СЛОЖНОЕ СОПРОТИВЛЕНИЕ.
Нередко приходится рассчитывать балки, на которые в дополнение к поперечным нагрузкам действуют продольные силы растяжения или сжатия, приложенные к концам. В таких случаях напряжение в любой точке поперечного сечения равно алгебраической сумме нормального напряжения, создаваемого продольной нагрузкой, и изгибного напряжения, создаваемого поперечными нагрузками. Общая формула для напряжения в случае совместного действия изгиба и растяжения-сжатия такова: S = ± (P/A) ± (Mc/I), где знак «плюс» относится к растягивающему напряжению.
КОЛОННЫ.
Каркасы зданий и фермы мостов состоят в основном из растянутых стержней, балок и колонн. Колонны – это длинные сжатые стержни, примером которых в каркасах зданий могут служить вертикальные стержни, несущие межэтажные перекрытия.
Если длина сжатого стержня более чем в 10–15 раз превышает его толщину, то под действием критических нагрузок, приложенных к его концам, он, потеряв устойчивость, изогнется, даже если нагрузки номинально приложены по его оси (продольный изгиб). Вследствие такого изгиба нагрузка оказывается внецентренной. Если эксцентриситет в среднем поперечном сечении колонны равен D, то максимальное сжимающее напряжение в колонне будет равно (P/A) + (PDc/I). Отсюда видно, что допускаемая нагрузка для колонны должна быть меньше, чем для короткого сжатого стержня.
Формулу для устойчивости гибких колонн вывел в 1757 Л.Эйлер. Максимальная нагрузка P, которую может нести гибкая колонна высотой L, равна mEA /(L/r)2, где m – постоянный множитель, зависящий от конструкции основания, A – площадь поперечного сечения колонны, а r – наименьший радиус инерции поперечного сечения. Отношение L/r называется гибкостью (при продольном изгибе). Как нетрудно видеть, допускаемая нагрузка быстро убывает с увеличением гибкости колонны. В случае колонн с малой гибкостью формула Эйлера непригодна, и конструкторы вынуждены пользоваться эмпирическими формулами.
В строениях часто встречаются внецентренно нагруженные колонны. В результате точного теоретического анализа таких колонн были получены «формулы секанса». Но расчеты по этим формулам весьма трудоемки, а потому часто приходится прибегать к эмпирическим методам, дающим хорошие результаты.
СЛОЖНЫЕ НАПРЯЖЕННЫЕ СОСТОЯНИЯ
Напряжение в какой-либо точке той или иной плоскости нагруженного тела, вычисленное по обычным формулам, не обязательно будет наибольшим в этой точке. Поэтому важное значение имеет вопрос о соотношениях между напряжениями в разных плоскостях, проходящих через одну точку. Такие соотношения являются предметом раздела механики, посвященного сложным напряженным состояниям.
Соотношения между напряжениями.
Напряженное состояние в некоторой точке любого нагруженного тела можно полностью охарактеризовать, представив напряжения, действующие на грани элементарного куба в этой точке. Часто встречаются случаи, к которым относятся и рассмотренные выше, двухосного (плоского) напряженного состояния с напряжениями, равными нулю, на двух противоположных гранях куба. Напряжения, существующие в точке тела, неодинаковы в плоскостях с разным наклоном. Исходя из основных положений статики, можно сделать ряд важных выводов о соотношении между напряжениями в разных плоскостях. Приведем три из них:
1. Если в некоторой точке заданной плоскости имеется касательное напряжение, то точно такое же напряжение имеется в проходящей через эту точку плоскости, перпендикулярной заданной.
2. Существует плоскость, в которой нормальное напряжение больше, чем в любой другой.
3. В плоскости, перпендикулярной этой плоскости, нормальное напряжение меньше, чем в какой-либо другой.
Максимальное и минимальное нормальные напряжения, о которых говорится в п. 2 и 3, называются главными напряжениями, а соответствующие плоскости – главными плоскостями.
Необходимость в анализе главных напряжений на основе указанных соотношений не всегда возникает, так как простые формулы, которыми обычно пользуются инженеры, в большинстве случаев дают именно максимальные напряжения. Но в некоторых случаях, например при расчете вала, сопротивляющегося одновременно скручивающему и изгибающему моментам, нельзя обойтись без соотношений для сложного напряженного состояния.
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ
В задачах, о которых говорилось выше, рассматривались напряжения либо равномерно распределенные, либо линейно меняющиеся с удалением от нейтральной оси, где напряжение равно нулю. Однако во многих случаях закон изменения напряжения более сложен.
В качестве примера задач с нелинейным распределением напряжений можно привести искривленные балки, толстостенные сосуды, работающие под высоким внутренним или наружным давлением, валы некругового поперечного сечения и нагруженные тела с резкими изменениями поперечного сечения (канавками, буртиками и т.д.). Для таких задач рассчитываются коэффициенты концентрации напряжений.
Кроме того, выше речь шла только о статических нагрузках, постепенно прилагаемых и снимаемых. Переменные же и периодически меняющиеся нагрузки, многократно повторенные, могут приводить к потере прочности, даже если они не превышают статического предела прочности рассматриваемого материала. Такие отказы называются усталостными, а проблема их предотвращения приобрела важное значение в наш век машин и механизмов, работающих на необычайно высоких скоростях. См. также СТАТИКА; ПРОЧНОСТНОЙ РАСЧЕТ КОНСТРУКЦИЙ; КОНСТРУКЦИОННЫЕ И СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ.
www.krugosvet.ru
Прочность древесины на изгиб и сжатие + таблица
Определение прочности и виды нагрузок
Одним из важных механических свойств древесины является ее устойчивость к разрушающим механическим воздействиям, то есть прочность. Зависит она от разных факторов, самые важные из которых:
- Плотность;
- Влажность;
- Присутствие пороков;
- Порода древесины;
- Наличие разрушающих нагрузок в разных направлениях (например, поперек или вдоль волокон), то одно и тоже дерево будет иметь разную прочность.
 На прочности дерева отражается содержание влаги в клеточных оболочках – связанная влага. Чем больше влажность, тем меньше прочность. Однако это правило действует до показателя влажности 30 %, который является пределом гигроскопичности. После достижения этого предела прочность остается неизменной даже при увеличении количества влаги. При определении показателей прочности образцы древесины должны иметь одинаковую влажность. Продолжительность разрушающей нагрузки также сильно отражается на показателе прочности.
На прочности дерева отражается содержание влаги в клеточных оболочках – связанная влага. Чем больше влажность, тем меньше прочность. Однако это правило действует до показателя влажности 30 %, который является пределом гигроскопичности. После достижения этого предела прочность остается неизменной даже при увеличении количества влаги. При определении показателей прочности образцы древесины должны иметь одинаковую влажность. Продолжительность разрушающей нагрузки также сильно отражается на показателе прочности.
Нагрузки различают по силе, направлению и времени воздействия. Статические действуют с постоянной силой или с постепенным увеличением, а динамические очень недолго, только в момент соприкосновения с поверхностью дерева. Эти нагрузки принято называть разрушительными, поскольку от их действия структура древесины нарушается. Крайние показатели прочности, при которых древесина способна сохранить свою структуру, называют пределом прочности. Единица измерения прочности – Па/см2 или иначе кгс на 1 кв. см.
Прочность измеряют во всех направлениях – продольном, радиальном и тангенциальном. При испытаниях применяют силы растяжения и сжатия, а также испытывают на изгиб и скалывание. Ниже приведена таблица механических свойств древесины.
Прочность на сжатие имеет большое значение в строительных конструкциях, таких, как опоры и стойки. Ее измеряют в разных направлениях.
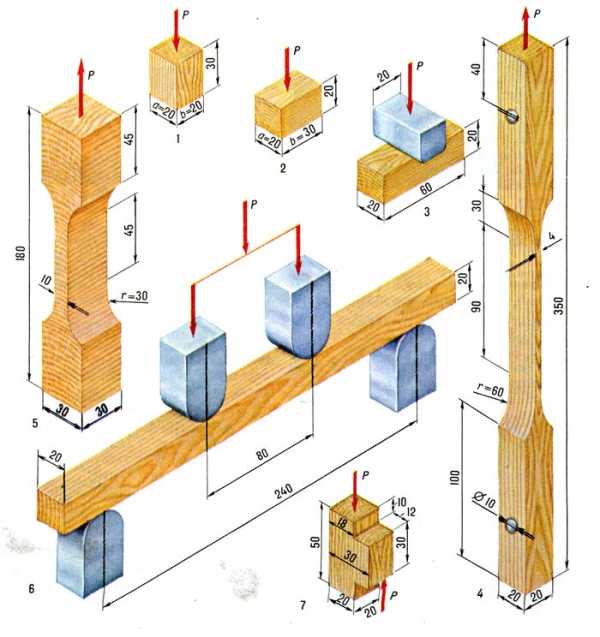
Испытание механических свойств древесины на сжатие
Прочность на сжатие проверяют в продольном и поперечном по отношению к волокнам направлению. При этом при продольном сжатии происходит уменьшение длины образца. При испытании образца древесины мягких сортов с высокой влажностью торцы начинают сминаться, а боковые части выпирают в сторону. Древесина твердая и сухая при продольном сжатии начинает разрушаться и части образца сдвигаются в разные стороны.
Усредненное значение предела прочности продольного сжатия для всех видов древесины около 500 кгс на 1 кв. см.
Величина прочности при поперечном сжатии намного меньше, чем при продольном и их соотношение друг к другу составляет 1:8. Момент, в который происходит разрушение древесины при поперечном сжатии не легко определить, как и силу давления, при которой оно происходит.
Обычно проверяют прочность на поперечное сжатие в двух направлениях – радиальном и тангенциальном. При этом лиственные породы имеют прочность в 1.5 раза больше при сжатии в радиальном направлении, нежели при тангенциальном. Прочность древесины хвойных пород при сжатии в радиальном направлении ниже, чем при тангенциальном сжатии.
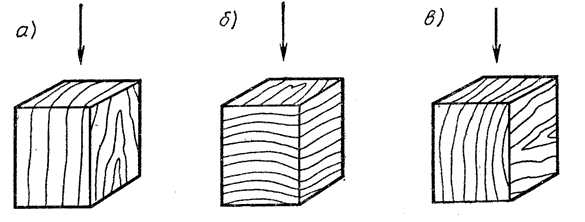
Испытание механических свойств древесины на сжатие: а — вдоль волокон; б — поперек волокон — радиально; в — поперек волокон — тангенциально.
Прочность древесины на растяжение
Прочность древесины при растяжении вдоль волокон колеблется в пределах 1100 – 1400 кгс/см2, правда использование ее в деталях, работающих на растяжение затруднено в связи с тем, что она не выдерживает нагрузок в местах крепления. В этих местах на древесину действуют силы сжатия и скалывания, а они имеют более низкие значения. Ярким примером использования древесины с работой на растяжение являются оглобли в конных повозках.
В поперечном направлении прочность на растяжение низкая и ее значение не превышает 5% от предела прочности на растяжение в продольном направлении. Поэтому в тех случаях, когда деталь из древесины работает на растяжение, применяют только древесину с продольным расположением волокон.
Величина поперечной прочности древесины на растяжение учитывается при резке и сушке материала, режимы этих операций подбираются в прямой зависимости от прочности.
Испытание механических свойств древесины на изгиб
Усредненная прочность всех пород деревьев при изгибе принято считать равной 1000 кгс/см2, что в два раза больше прочности на сжатие и примерно на 30% меньше прочности при продольном растяжении. При изгибе разные слои древесины испытывают разное напряжение — верхний слой получает сжатие, а нижний, напротив, — растяжение. В средней части образца, подвергаемого изгибу, находится нейтральная область, которая не испытывает никаких напряжений. Зона, испытывающая напряжение растяжения, начинает разрушаться в первую очередь – крайние волокна древесины разрываются.
Визуально определить прочность древесины на изгиб можно по характеру излома – качественные образцы будут иметь неровный излом с наличием большого количества щепы, а дефектная – почти ровный, без выступов и вмятин.
При изгибе одна часть заготовки подвергается сжатию, другая – растяжению, поэтому показатель сопротивления изгибу находится между показателями сопротивлений сжатия и растяжения. Отношение сопротивления сжатия к сопротивлению растяжения колеблется от 1.7 до 2.2 у разных пород дерева.
Влажность дерева также отражается на показателе сопротивления статическому изгибу – при изменении влажности на 1%, сопротивление изменяется на 4%.
По величине сопротивления ударному изгибу можно определить вязкость или хрупкость древесины. Если сопротивление невелико, древесина хрупкая, а высокий показатель сопротивления говорит о большой вязкости древесины.
Измеряют сопротивление ударному изгибу с помощью маятника, замеряя работу Q кг/м, которая требуется маятнику определенного веса для того, чтобы сломать испытуемый брусок. Само сопротивление вычисляют по формуле A = Q/bh3, в которой b и h – соответственно ширина и высота сечения образца в сантиметрах.
Испытание механических свойств древесины на изгиб
Прочность древесины при сдвиге
Смещение в заготовке одной части древесины относительно другой называется сдвигом. Сдвиги образуются под действием внешних нагрузок разного характера. Выделяют сдвиги, возникающие от скалывания вдоль или поперек волокон и от распила (перерезания).
Прочность при скалывании меньше прочности продольного сжатия примерно в 5 раз. А если сравнивать прочность скалывания вдоль и поперек волокон в одном образце, то предел прочности при продольном скалывании в два раза выше, чем при поперечном. Прочность древесины при перерезании выше прочности при скалывании раза в четыре.
Самая прочная древесина
Все породы деревьев различаются по прочности. Из хвойных деревьев наиболее прочной считается лиственница. Это дерево обладает уникально твердой и долговечной древесиной, устойчивой к гниению и влагостойкой. Смолистая и прочная, она замечательна еще и тем, что, находясь в воде способна приобретать прочность камня. Древесина лиственницы используется в производстве мебели и в строительстве. В строительстве подводных сооружений ей практически нет альтернативы. Успешно применяется в кораблестроении.
Из лиственных пород, используемых человеком, первое место по прочности занимает дуб. Древесина очень долговечная, гибкая, имеет великолепные декоративные качества и применяется во многих областях промышленности. Из нее делают дорогую мебель, паркет, хороша для поделок.
До настоящего времени в Литве, в маленькой деревушке Стелмуж, растет дуб, возраст которого более 1500 лет. На высоте человеческого роста диаметр ствола составляет 4 метра, а обхват дерева на трехметровой высоте равен 13.5 метров. Этот дуб является памятником природы, он – самый старый представитель дубовых деревьев во всей Европе.
В мире есть несколько образцов деревьев с «железной» древесиной. Амазонское дерево в Бразилии, азобе в Африке, темир-агач в Азербайджане и Иране. Закавказские леса и леса Северной Ирландии – место произрастания персидской парротии, которая также поражает своей прочностью. К сожалению, все перечисленные деревья редко встречаются в природе, и их находки – это настоящее чудо.
Посетители, просмотревшие эту статью, также заинтересовались следующими:
o-drevesine.ru