Уравнения равновесия для балки | Лекции и примеры решения задач механики

Для плоской системы нагружения, при определении опорных реакций и внутренних силовых факторов исходя из условия равновесия системы, можно составить только три уравнения статики.

Ранее были показаны примеры составления уравнений равновесия для пространственной и плоской систем сил.

При плоском поперечном изгибе можно записать только два уравнения. Это частный случай плоского нагружения. В этом случае все силы приложенные к балке расположены нормально к ее оси, т. е. не дают проекций на ось балки.

В результате имеем следующие уравнения статики:

1. Сумма проекций всех сил на вертикальную ось равна нулю
   
2. Сумма моментов относительно любой точки системы тоже равна нулю.
   

Эти уравнения являются уравнениями равновесия рассматриваемой балки находящейся под действием комплекса нагрузок.

Рассмотрим пример плоского поперечного изгиба, когда все внешние силы имеют исключительно вертикальное направление.

Уравнения статики

Сумма проекций всех сил на ось Y:

Здесь силы и нагрузки записаны в соответствии с правилом знаков для проекций сил.

Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.

Проекции сил на ось Z в данном случае равны нулю:

Сумма моментов всех нагрузок, например, относительно точки A:

Правило знаков для моментов.

Дополнительные материалы

• Порядок определения момента от распределенной нагрузки.
• Правила знаков при составлении уравнений статики для систем находящихся в равновесии.

Совместное решение системы полученных уравнений позволяет определить величину и направление двух неизвестных усилий.

Уравнения равновесия >
Примеры решения задач >
Краткая теория >

isopromat.ru

Уравнения равновесия для рамы | Лекции и примеры решения задач механики

Рассмотрим порядок составления уравнений равновесия для плоской системы нагрузок, например в рамах.

Ранее уже был показан порядок составления уравнений равновесия для пространственной системы сил.

В сопротивлении материалов при определении опорных реакций и внутренних силовых факторов для плоской схемы нагружения, исходя из условий равновесия, можно составить только три уравнения статики:

Равенство нулю суммы проекций всех сил на вертикальную и горизонтальную оси

И так же нулю равна сумма моментов относительно произвольной точки системы

Частный случай составления уравнений статики для балки при плоском поперечном изгибе рассмотрен здесь.

Рассмотрим пример действия плоской системы сил, удерживающего Т-образную раму в равновесии.

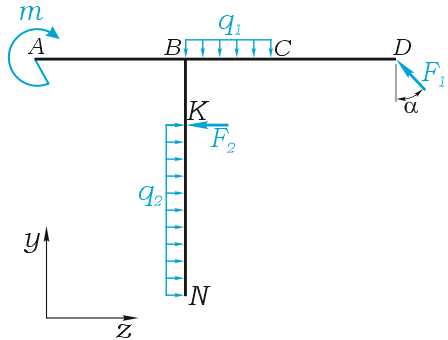
Уравнения равновесия

Сумма проекций всех сил и нагрузок на ось Y (с учетом соответствующего правила знаков):

Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.

Проекции на ось Z:

Сумма моментов всех нагрузок, например, относительно точки A (с учетом правила знаков для моментов):

Порядок определения момента распределенной нагрузки показан здесь.

Правила знаков при составлении уравнений статики для систем находящихся в равновесии.

Совместное решение системы трех полученных уравнений позволяет определить величину и направление до трех неизвестных усилий.

Уравнения равновесия >
Примеры решения задач >
Краткая теория >

isopromat.ru

Равновесие составных конструкций | Лекции и примеры решения задач механики

В случае системы твердых тел, соединенных между собой, силы, действующие на эту систему, можно подразделить на две группы:

1. внешние силы;
2. внутренние силы.

Внутренними силами называются силы взаимодействия между телами, входящими в данную систему. По закону равенства действия и противодействия внутренние силы всегда попарно равны по модулю и прямо противоположны по направлению, но приложены к двум разным взаимодействующим между собой телам системы.

Рис. 1

Внешними силами называются те силы, с которыми тела, не входящие в данную систему, действуют на тела этой системы.

Рассмотрим, например, систему, изображенную на рис.1.

Балка AB весом P_x может вращаться вокруг оси A неподвижного цилиндрического шарнира и концом B опирается свободно на другую балку CD весом P₂, которая подперта в точке E и соединена со стеной шарниром D.

В данном случае система состоит из двух тел: балки AB и балки CD.

Внутренними силами для данной системы являются силы взаимодействия между балками, т. е. сила N₂ давления балки AB

на балку CD и сила N₁, с которой балка CD действует на балку AB. По закону равенства действия и противодействия силы N₁ и N₂ равны по модулю и противоположны по направлению, т. е. N₁ = — N₂.

Веса P₁ и P₂ балок представляют собой силы, с которыми эти балки притягиваются к Земле, и, следовательно, для данной системы являются силами внешними, так как Земля по отношению к этой системе есть внешнее тело.

Реакции R_A и R_D шарнирных опор A и D, а также реакция R_E опоры E являются для данной системы тоже внешними силами, так как шарнирные опоры A и D и опора E не принадлежат к рассматриваемой системе, состоящей только из двух балок.

При решении задач на равновесие системы тел необходимо учесть, что все внешние и внутренние силы, приложенные к каждому телу в отдельности, уравновешиваются. Следовательно, в случае плоской системы сил можно составить по три уравнения равновесия для каждого из этих тел в отдельности.

Таким образом, для системы, состоящей из n тел, можно составить всего 3n уравнений равновесия. Поэтому, если число неизвестных сил в данной задаче не более 3n, то такая задача является статически определимой.

Если же число неизвестных в задаче окажется больше 3n, то такая задача не может быть разрешена только на основании уравнений статики абсолютно твердого тела и потому является статически неопределимой.

Так как внутренние силы попарно равны по величине и направлены по одной прямой в противоположные стороны, то алгебраическая сумма их моментов относительно любой точки равна нулю и сумма их проекций на любую ось также равна нулю.

Поэтому, если составим уравнение равновесия (уравнение моментов относительно какой-либо точки, или уравнение проекций на какую-либо ось) для каждого тела в отдельности и затем все эти уравнения сложим, то в полученном уравнении члены, содержащие внутренние силы, попарно уничтожаются и, следовательно, в это уравнение будут входить только внешние силы.

Таким образом, если система тел находится в равновесии, то внешние силы, приложенные к этой системе, удовлетворяют тем же трем уравнениям равновесия, что и в случае равновесия одного абсолютно твердого тела. Эти уравнения представляют собой условия равновесия внешних сил, действующих на систему.

Из этих уравнений можно найти все внешние реакции, если число этих внешних реакций не больше трех. Если же число внешних реакций окажется больше трех или если в задаче, кроме внешних реакций, требуется найти неизвестные внутренние силы, то необходимо применять метод расчленения системы, т. е. нужно рассматривать равновесие каждого тела системы в отдельности и для каждого из этих тел составлять уравнения равновесия, учитывая при этом все силы, приложенные к рассматриваемому телу.

Если система состоит, например, из двух твердых тел, то, применяя метод расчленения, получим в общем случае всего шесть уравнений равновесия (по три уравнения для каждого тела).

Для составления шести уравнений равновесия можно применять еще и другой прием, а именно: составить сначала три уравнения для всей системы в целом (как для одного абсолютно твердого тела) и затем к этим трем уравнениям присоединить три уравнения равновесия, составленные только для одного из двух тел данной системы.

Этот второй прием нередко предпочтительнее, так как в уравнения равновесия, составленные для всей системы в целом, входят только внешние силы и потому эти уравнения обычно оказываются проще.

Задачи, относящиеся к равновесию системы твердых тел, в зависимости от вида соединения этих тел между собой можно разделить на следующие четыре типа:

1. Задачи, где тела, входящие в систему, опираются свободно друг на друга.
2. Задачи, где тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем,  концы которого прикреплены к этим телам при помощи шарниров.
3. Задачи, где тела, входящие в систему, соединены между собой при помощи шарнира.
4. Задачи, относящиеся к определению усилий в стержнях плоской фермы.

>> Равновесие твердого тела при наличии трения

isopromat.ru

Правила знаков для сил и моментов в уравнениях равновесия

При составлении уравнений статики для систем находящихся в равновесии (например при определении опорных реакций) правила знаков могут быть упрощены до следующего вида:
Нагрузки направленные в одну сторону принимаются положительными, а соответственно, нагрузки обратного направления записываются со знаком минус.

Знаки проекций сил

То есть, для уравнений сумм проекций сил на оси:
Проекции сил и нагрузок на координатную ось имеющие одинаковое направление принимаются положительными, а проекции усилий противоположного направления – отрицательными.

Например, для такой схемы нагружения:

уравнение суммы сил имеет вид

А так как суммы проекций разнонаправленных сил равны, то данное уравнение можно записать и так:

Здесь F(q) – равнодействующая от распределенной нагрузки, определяемая произведением интенсивности нагрузки на ее длину.

Знаки моментов

Сосредоточенные моменты и моменты сил стремящиеся повернуть систему относительно рассматриваемой точки по ходу часовой стрелки записываются в уравнения с одним знаком, и соответственно моменты, имеющие обратное направление с противоположным знаком.

Например, для суммы моментов относительно точки A

получаем

или, что одно и то же

Здесь m(F) – моменты сил F относительно точки A.
M(q) – моменты распределенных нагрузок q относительно рассматриваемой точки.

Примеры решения задач >

isopromat.ru

Статически неопределимая балка | Лекции и примеры решения задач механики

Статически неопределимыми называют балки, для которых при определении опорных реакций и внутренних силовых факторов недостаточно одних только уравнений равновесия.

Другими словами, СН балки имеют «лишние» опоры, которые дают дополнительные связи, сверх необходимых для удержания системы в равновесии.

СН балки – частный случай статически неопределимых систем.

Примеры статически неопределимых балок

Для удержания балки в геометрически неизменяемом и неподвижном положении (в равновесии) требуется одна заделка (рис. 1 а) либо две шарнирные опоры (рис. 1 б) одна из которых подвижная другая неподвижная.

а

б

Рис. 1 Статически определимые балки

В этих случаях балка статически определима.

Добавление еще одной опоры (Рис. 2) упрочнит балку, но при этом она станет статически неопределимой.

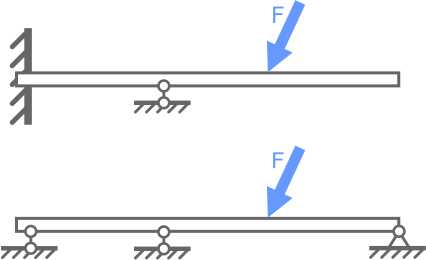
Рис. 2 Статически неопределимые балки

Усилия в дополнительных опорах являются лишними неизвестными при решении систем уравнений статики.

Степень статической неопределимости балки

Количество дополнительных связей показывает степень статической неопределимости балки, которую можно определить по формуле:

k=m-n

где m – общее количество неизвестных реакций связи балки,
n – количество возможных уравнений равновесия которые можно составить для данной системы (для плоской – 3, пространственной – 6).

Балки с одной дополнительной связью называют однажды (один раз) неопределимыми, с двумя – дважды неопределимыми и т.д.

Раскрытие статической неопределимости

Расчет величины и направления лишних связей называют раскрытием статической неопределимости.

Так как для статически неопределимых балок возможных уравнений равновесия всегда меньше чем неизвестных усилий для их расчета требуются дополнительные зависимости.

В качестве таковых используются условия отсутствия соответствующих линейных и угловых перемещений на опорах.

Существуют теоретические и практические методы раскрытия статической неопределимости.

Раскрыть статическую неопределимость балки можно с помощью метода начальных параметров или методом сил.

Практический метод определения лишней опорной реакции подробно рассмотрен здесь.

Примеры решения задач >>

isopromat.ru

Уравнения равновесия системы сходящихся сил

Сходящаяся система сил находится в равновесии в случае замкнутости силового многоугольника. Величина равнодействующей при этом равна нулю (R = 0).

Проекции равнодействующей системы сходящихся сил на координатные оси равны суммам проекций составляю­щих сил на те же оси, т. е.

Модуль равнодействующей определится по формуле:

Оба слагаемых, стоящих под знаком корня, во всех случаях положительны как величины, возведенные в ква­драт. Поэтому R = 0 только при выполнении условий:

Таким образом, равнодействующая плоской системы сходящихся сил равна нулю только в том случае, когда алгебраические суммы проекций ее слагаемых на каждую из двух координатных осей равны нулю.

Формулы Σх=0 (сумма проекций всех сил на ось Х равна нулю),  Σy=0 (сумма проекций всех сил на ось Y равна нулю) называют уравнениями равновесия плоской системы сходящихся сил и используют при аналитическом решении задач.

Следовательно, для решения задач на равновесие плоской системы сходящихся сил мы имеем два уравне­ния. Эти уравнения позволяют определить две неизвест­ные величины.

Если же задача содержит неизвестные в количестве, превышающем число уравнений равнове­сия, то эту задачу нельзя решить методами статики абсо­лютно твердого тела. Задачи подобного типа называют статически неопределимыми. Их решение возможно только при отказе от допущения об абсолютной твердости тел; помимо уравнений равновесия для решения их составляют дополнительные уравнения, основанные на рассмотрении деформаций тел. Методы решения таких задач рассматриваются в курсе сопротивления материалов.

prosopromat.ru

Сопромат статически определимые и статически неопределимые системы

 

В сопромате система называется статически определимой, если число неизвестных в ней равно числу полезных уравнений равновесия.

 

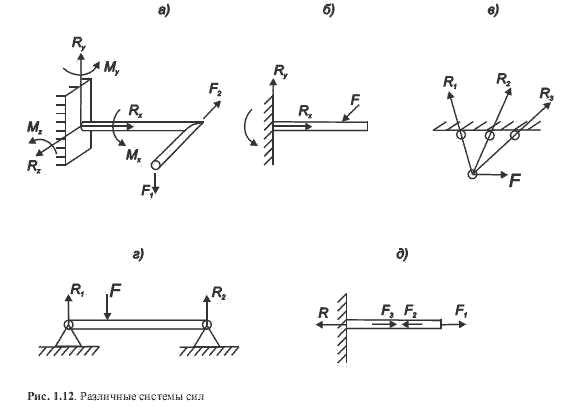
Для всякой пространственной системы сил (рис. 1.12, а) можно составить систему из 6-и уравнений равновесия и, решив ее, найти 6 неизвестных сил. Однако среди этих уравнений могут быть тождества, обращающиеся в нуль при любых значениях нагрузок. Это бесполезные уравнения и, следовательно, число неизвестных сил должно быть равно числу уравнений минус число тождеств.

 

Для произвольной плоской системы сил (рис. 1.12, б) можно составить 3 уравнения, не являющихся тождествами, например, сумму проекций всех сил на 2 любые оси и одну сумму моментов всех сил, относительно какой-либо точки.

 

Для плоской системы сходящихся сил (рис.1.12, в) можно составить лишь 2 уравнения, не являющихся тождествами. Сумма моментов всех сил относительно точки их пересечения тождественно равна нулю. Из 2-х уравнений (любых) можно определить лишь 2 неизвестные силы.

 

Для плоской системы параллельных сил (рис.1.12, г) бесполезной оказывается сумма проекций на ось, перпендикулярную силам. Соответственно из 2-х любых уравнений равновесия можно найти лишь 2 неизвестные силы.

 

Для системы коллинеарных сил (действующих вдоль одной прямой линии) (рис. 1.12, д) можно составить лишь одно полезное уравнение — сумму проекций всех сил на эту прямую, которая равна просто сумме сил.

 

Система называется статически неопределимой, если число неизвестных в ней больше числа полезных уравнений равновесия.

 

Степень статической неопределимости равна разности между числом неизвестных и числом полезных уравнений равновесия.

 

Для раскрытия статической неопределимости существуют разные способы, которые будут рассмотрены далее. Заметим лишь, что всякая реакция возникает в местах наложения внешних связей (ограничений движения системы). Нет ограничения — нет реакции. Есть ограничение — есть реакция. В то же время любая наложенная связь (любое ограничение движения) позволяет составить дополнительное уравнение, называемое уравнением совместности перемещений В результате появляется возможность сделать число уравнений равным числу неизвестных и решить систему уравнений.

На рис. 1.13 приведены примеры различных систем.

Рис. 1.13. Статически определимые и статически неопределимые системы

 

Схема а) — стержень недостаточно закреплен, он может свободно вращаться под действием силы. Это механизм. Такие задачи требуют учета сил инерции и рассматриваются в курсе теории машин и механизмов.

Схема б) — система из 2-х стержней статически-определимая, два усилия в 2-х стержнях определяются из 2-х уравнений равновесия.

Схема в) — система из трех стержней 1 раз статически-неопределима: неизвестных усилий — 3, полезных уравнений равновесия—2, степень статической неопределимости 3-2=1.

Схема г) — система 3 раза статически-неопределима: неизвестных усилий — 5, полезных уравнений равновесия—2, степень статической неопределимости 5-2=3.

 

При большом количестве опор и шарниров определить степень статической неопределимости довольно трудно. Проще это сделать следующим образом:

Мысленно отбрасываем связи по одной до тех пор, пока система не превратится в механизм. Верните на место одну связь (любую). Система станет статически определимой. В таком виде число отброшенных связей равно степени статической неопределимости системы.

Решение статически-неопределимых задач в сопромате значительно более сложная и трудоемкая проблема. Практически без использования компьютера можно решить лишь 2 — 3 раза cтатически — неопределимые задачи.

funnystudy.ru