Строительная механика | ПроСопромат.ру

Статически определимая ферма. Задача. Определить усилия в стержнях фермы второй панели слева и стойки справа от панели, а также срединной стойки аналитическими методами. Дано: d=2м; h=3м; ℓ=16м; F=5кН.

Рассмотрим ферму с симметричным загружением.

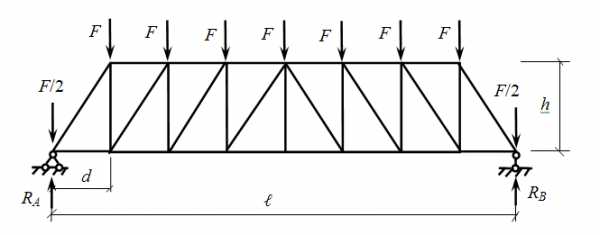
Сначала обозначим опоры буквами А и В, нанесем опорные реакции R_А и R_В.

Определим реакции из уравнений статики. Поскольку загрузка фермы симметрична, реакции будут равны между собой:

Если загрузка фермы несимметричная, то реакции определяются как для балки с составлением уравнений равновесия

∑М_А=0 (находим R_В), ∑М_В=0 (находим R_А), ∑у=0 (проверка).

Теперь обозначим элементы фермы:

«О» — стержни верхнего пояса (ВП),

«U» — стержни нижнего пояса (НП),

«V» — стойки,

«D» — раскосы.

С помощью этих обозначений удобно называть усилия в стержнях, н.р., О₄ — усилие в стержне верхнего пояса; D₂ – усилие в раскосе и т.д.

Затем обозначим цифрами узлы фермы. Узлы А и В уже обозначены, на остальных расставим цифры слева направо с 1 по 14.

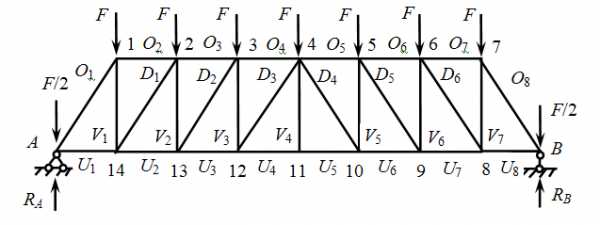
Согласно заданию, нам предстоит определить усилия в стержнях О₂, D₁, U₂ (стержни второй панели), усилие в стойке V₂, а также усилие в срединной стойке V₄ . Существуют три аналитических метода определения усилий в стержнях.

1. Метод моментной точки (метод Риттера),
2. Метод проекций,
3. Метод вырезания узлов.

Первые два метода применяется только тогда, когда ферму можно рассечь на две части сечением, проходящим через 3 (три) стержня. Проведем сечение 1-1 во второй панели слева.

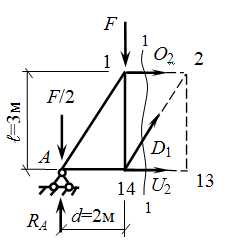
Сеч. 1-1 рассекает ферму на две части и проходит по трем стержням — О₂, D₁, U₂. Рассматривать можно любую часть – правую или левую, неизвестные усилия в стержнях направляем всегда от узла, предполагая в них растяжение.

Рассмотрим левую часть фермы, покажем ее отдельно. Направляем усилия, показываем все нагрузки.

Сечение проходит по трем стержням, значит можно применить метод моментной точки. Моментной точкой для стержня называется точка пересечения двух других стержней, попадающих в сечение.

Определим усилие в стержне О₂.

Моментной точкой для О₂будет т.14, т.к. именно в ней пересекаются два других стержня, попавших в сечение, — это стержни D₁

и U₂ .

Составим уравнение моментов относительно т. 14 (рассматриваем левую часть).

О₂мы направили от узла, полагая растяжение, а при вычислении получили знак «-», значит, стержень О₂ – сжат.

Далее в скобках будет указывать деформацию стержня – сжат или растянут.

Определяем усилия в стержне U₂. Для U₂  моментной точкой будет т.2, т.к. в ней пересекаются два других стержня — О₂ и D₁.

Теперь определяем моментную точку для D₁. Как видно из схемы, такой точки не существует, поскольку усилия О₂ и U₂

не могут пересекаться, т.к. параллельны. Значит, метод моментной точки неприменим.

Воспользуемся методом проекций. Для этого спроецируем все силы на вертикальную ось У. Для проекции на данную ось раскоса D₁ потребуется знать угол α. Определим его.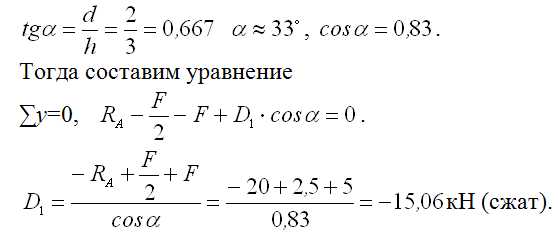

Определим усилие в правой стойке V₂. Через эту стойку можно провести сечение, которое проходило бы по трем стержням. Покажем сечение 2-2, оно проходит через стержни  О₃, V₂, U₂. Рассмотрим левую часть.

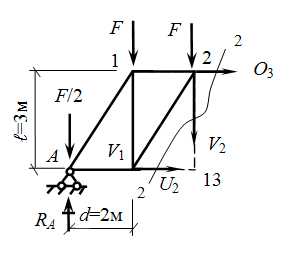
Как видно из схемы, метод моментной точки в данном случае неприменим

, применим метод проекций. Спроектируем все силы на ось У.

Теперь определим усилие в срединной стойке V₄. Через эту стойку нельзя провести сечение, чтобы оно делило ферму на две части и проходило бы через три стержня, значит, методы моментной точки и проекций здесь не подходят. Применим метод вырезания узлов. Стойка V₄ примыкает к двум узлам – узлу 4 (вверху) и к узлу 11 (внизу). Выбираем узел, в котором наименьшее количество стержней, т.е. узел 11. Вырезаем его и помещаем в координатные оси таким образом, чтобы одно из неизвестных усилий проходило бы по одной из осей (в данном случае V₄ направим по оси У). Усилия, как и прежде, направляем от узла, предполагая растяжение.

Узел 11.

Проецируем усилия на координатные оси

∑х=0,   —U₄+ U₅=0,   U₄= U₅

∑у=0,    V₄=0.

Таким образом, стержень V₄ — нулевой.

Нулевым стержнем называется стержень фермы, в которой усилие равно 0.

Правила определения нулевых стержней — смотреть здесь.

Если в симметричной ферме при симметричном загружении требуется определить усилия во всех стержнях, то следует определить усилия любыми методами в одной части фермы, во второй части в симметричных стержнях усилия будут идентичны.

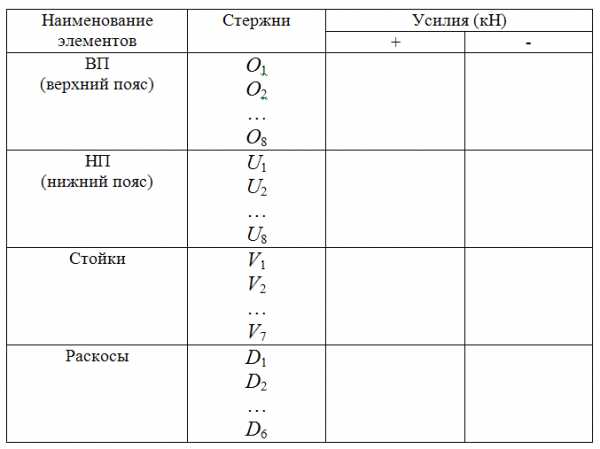
Все усилия в стержнях удобно свести в таблицу (на примере рассматриваемой фермы). В графе «Усилия» следует проставить

значения.

prosopromat.ru

Строительная механика | ПроСопромат.ру | Страница 2

Как рассчитать неразрезную балку. Уравнение 3-х моментов.

Неразрезная балка нагружена во всех пролетах. Построить эпюры Q и M для неразрезной балки.

Схема неразрезной балки

1. Определяем степень статической неопределимости балки по формуле:

n= Соп -3= 5-3 =2, где Соп – число неизвестных реакций, 3 – число уравнений статики. Для решения данной балки требуется два дополнительных уравнения.

2. Обозначим номера опор с нулевой по порядку (0,1,2,3)

3. Обозначим номера пролетов с первого по порядку (

ι_1,ι_2,ι₃)

4. Каждый пролет рассматриваем как простую балку и строим для каждой простой балки эпюры Q и M. То, что относится к простой балке, будем обозначать с индексом «0», то, что относится к неразрезной балке, будем обозначать без этого индекса. Таким образом,  — это поперечная сила и изгибающий момент для простой  балки.

Рассмотрим балку 1^го пролета

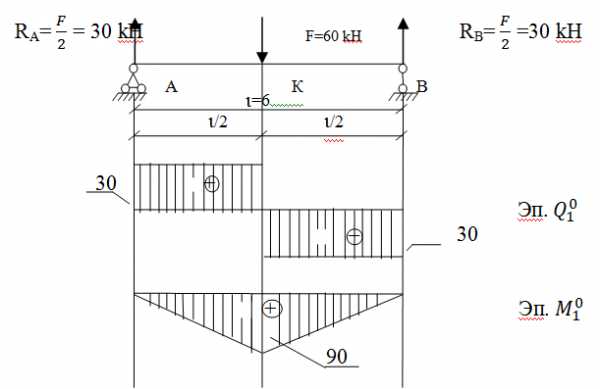
Определим фиктивные реакции для балки первого пролета по табличным формулам (см.таблицу «Фиктивные опорные реакции….»)

Балка 2^го пролета

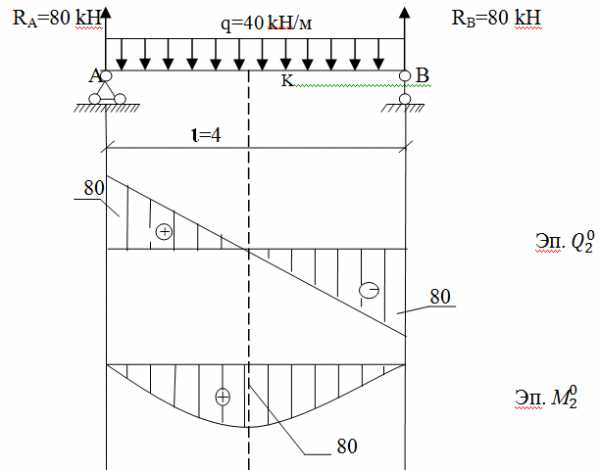
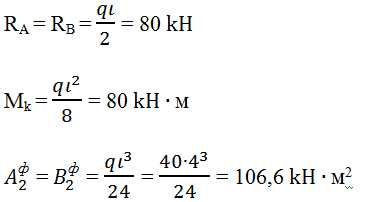
Балка 3^го пролета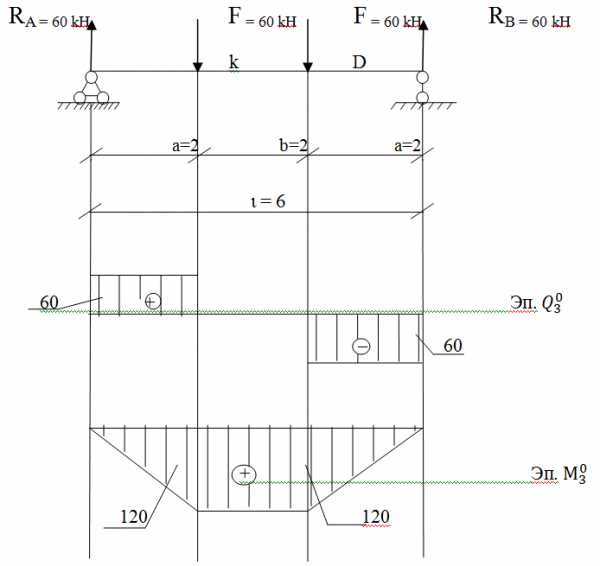

5. Составляем уравнение 3^х моментов для двух точек ­­– промежуточных опор ­– опора 1 и опора 2.  Это и будут два недостающих уравнения для решения задачи.

Уравнение 3х моментов в общем виде:

Для точки (опоры) 1 (n=1):

Для точки (опоры) 2 (n=2):

Подставляем все известные величины, учитываем, что момент  на нулевой опоре и на третьей опоре равны нулю,  M₀=0; M₃=0

Тогда получим:

Поделим первое уравнение на сомножитель 4 при M₂ 

Второе уравнение поделим на сомножитель 20 при M₂   

Решим эту систему уравнений:

Из первого уравнения вычтем второе, получим:

Подставляем это значение в любое из уравнений и находим

M₂

Итак, нашли опорные моменты:

6. Построение эпюры поперечной силы Q для неразрезной балки

Формула для определения Q в любом сечении неразрезной балки:, где n – пролет

1) Построение эп. Q в первом пролете:

Эта запись означает, что поперечная сила в неразрезной балке в первом пролете будет такая же, как в простой балке с разницей ординат на – 9 . 

На эпюрах должны прослеживаться скачки на величину сил.

2) Построение эп. Q во втором пролете:

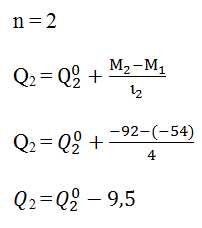Поперечная сила в неразрезной балке во втором пролете будет такая же, как в простой балке с разницей ординат на – 9,5.    

3)Построение эп. Q в третьем пролете:

Поперечная сила в неразрезной балке в третьем пролете будет такая же, как в простой балке с разницей ординат на +15,3.  

Строим эпюру поперечных сил для неразрезной балки.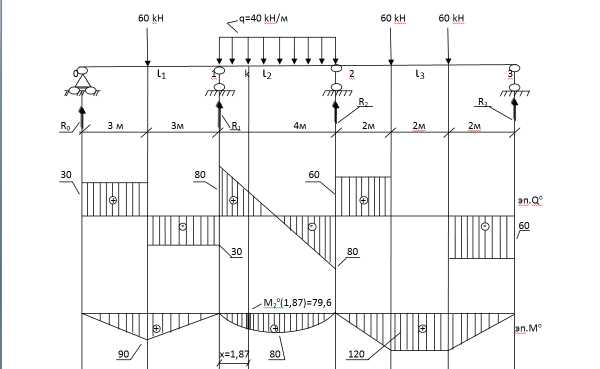 

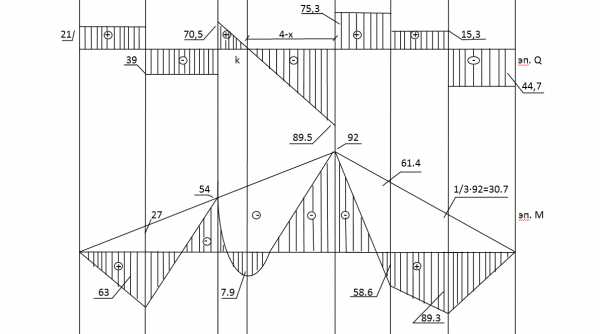
7.  Построение эпюры изгибающего момента для неразрезной балки. Сначала откладываем на опорах значения опорных моментов,   соединяем их линией опорных моментов. Это эпюра опорных моментов.

Эпюру М для неразрезной балки можно построить:

1 вариант – методом «подвешивания».  К эпюре опорных моментов  «подвешиваем»  эпюру M⁰  по разницам ординат. К примеру, в середине первого пролета на эпюре M⁰  ордината равна 90,  а на эпюре опорных моментов -27. В итоге получим 90-27=63. Это значение и откладываем.

2 вариант – формула для определения изгибающего M в любом сечении неразрезной балки:

, где n-пролет , x — расстояние.

Для той же точки первого пролета, которую рассматривали в методе «подвешивания»:

Построение эп. М во 2^ом пролете, загруженном равномерно распределенной нагрузкой

Определим положения т. К. по эпюре Q — это точка экстремума.

Определим М неразрезной балки во 2^ом пролете в этой точке: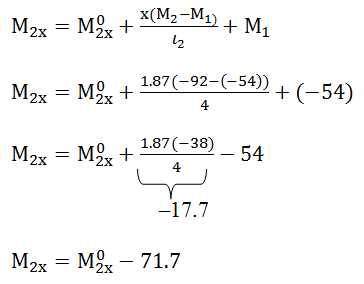 Теперь нужно определить в этой точке К изгибающий момент М в простой балке:

Таким образом, момент в точке К для неразрезной балки:

Строим эпюру М.

8. Выполним проверку опорных реакций. Покажем реакции   на схеме балки на опорах, направив их вверх. Значения этих реакций определим по скачкам эпюры Q. Таким образом получим:

Спроецируем все силы, приложенные к балке, и реакции на вертикальную ось, выполним проверку.

Подставим значения, получим 340-340=0

Проверка верна.

 

 

prosopromat.ru

Методы построения эпюр в статически определимых и статически неопределимых системах Введение

Это пособие в значительной степени соответствует курсу лекций, на протяжении многих лет читаемых в Санкт-Петербургском государственном аграрном университете для студентов строительной специальности.

Пособие состоит из четырех глав, в которых достаточно подробно рассматриваются методы построения эпюр внутренних силовых факторов статически определимых и статически неопределимых стержневых системах.

В большинстве изданных учебников и учебных пособий по строительной механике этот важнейший вопрос излагается поверхностно, или вообще отсутствует.

В главе 1 рассматривается построение эпюр в различных стержневых системах: балках, рамах, плоскопространственных и др.

В главе 2 приводятся различные общие методы определения перемещений, что имеет самостоятельное значение, а также является базой для двух последующих глав.

В главе 3 дается подробное изложение метода сил применительно к расчету статически неопределимых балок и рам. Рассмотрены все проверки метода, а также использование симметрии.

Глава 4 посвящена изложению метода перемещений. Приведенный здесь материал в лекционном курсе, как правило, не излагается в связи с ограниченностью во времени. Тем не менее метод перемещений очень важен, так как, во-первых, является мощным инструментом для расчета статически неопределимых систем, а во-вторых, используется студентами в дисциплинах, читаемых на старших курсах.

Книга снабжена большим количеством примеров.

Глава 1 Построение эпюр внутренних силовых факторов

1.1 Внутренние силы упругости. Метод сечений

Рассмотрим тело произвольной формы в “спокойном”, ненагруженном состоянии. Между его частицами всегда существуют силы взаимодействия, которые стремятся сохранить его как единое целое, то есть препятствуют изменению взаимного расположения частиц. При нагружении тела произвольной внешней нагрузкой силы взаимодействия между частицами изменяются, появляются дополнительные силы взаимодействия, которые приводят к изменению взаимного расположения частиц тела, то есть к его деформации.

Эти дополнительные силы взаимодействия называются внутреннимисилами упругости (ВСУ)и являются предметом изучения сопротивления материалов.

Анализ характера распределения внутренних сил упругости осуществляется при помощи метода сечений. Рассмотрим тело произвольной формы, нагруженное самоуравновешенной системой сил (рис.1,а). В интересующем нас сечении мысленно рассечем его плоскостью на две части (рис.1,б)

Рис. 1

Внутренние силы упругости определяют взаимодействие между частицами тела, расположенными по разные стороны от мысленно проведенного сечения. В разных сечениях тела возникают разные внутренние силы упругости, но по принципу действия и противодействия они всегда взаимны. Правая отсеченная часть тела действует на левую точно так же, как и левая на правую, а это означает, что равнодействующая внутренних сил может определяться из условий равновесия как левой отсеченной части тела, так и правой.

Из курса теоретической механики известно, что любую произвольную систему сил можно привести к центру тяжести сечения. В результате внутренние силы упругости, действующие в рассматриваемом сечении, приводятся к главному векторуиглавному моменту. Выберем прямоугольную систему координат OXYZ так, что ось Z будет направлена по нормали к поперечному сечению, а оси X и Y лежат в плоскости сечения. Проектируя главный векторна каждую из осей, а главный моментна каждую из координатных плоскостей, получим шесть величин — 3 силы и 3 момента, — которые называютсявнутренними силовыми факторами(рис.2).

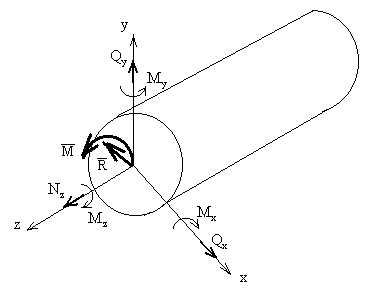
Рис. 2

Полученные таким образом 6 внутренних силовых факторов (ВСФ) имеют строго определенные названия:

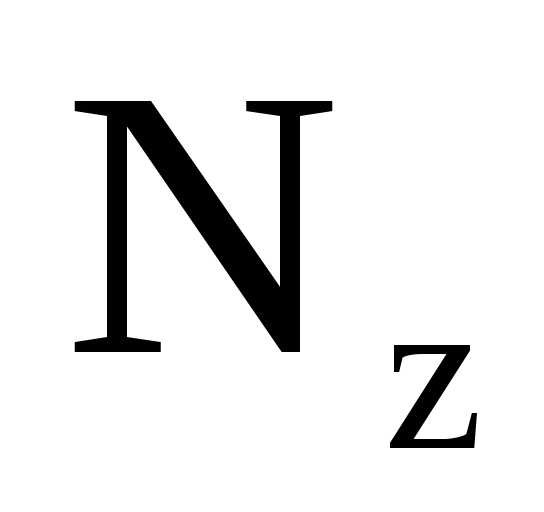— продольная (нормальная) сила;

-поперечная (перерезывающая) сила;

— изгибающий момент;

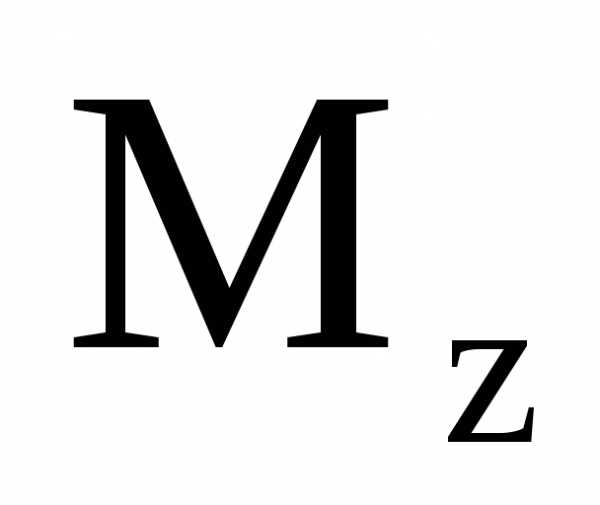— крутящий момент.

Иногда обозначение 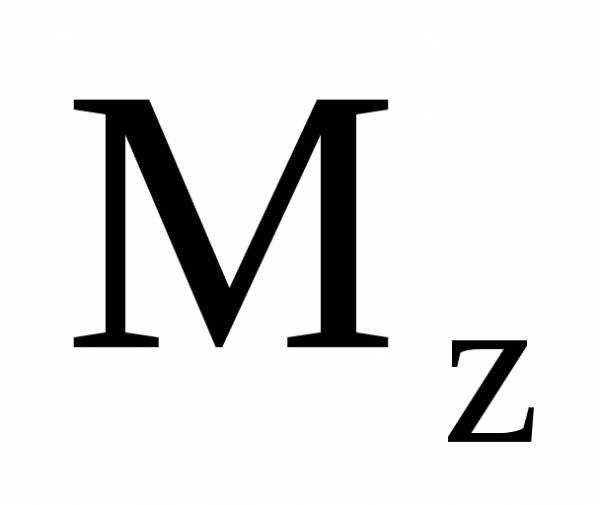заменяют на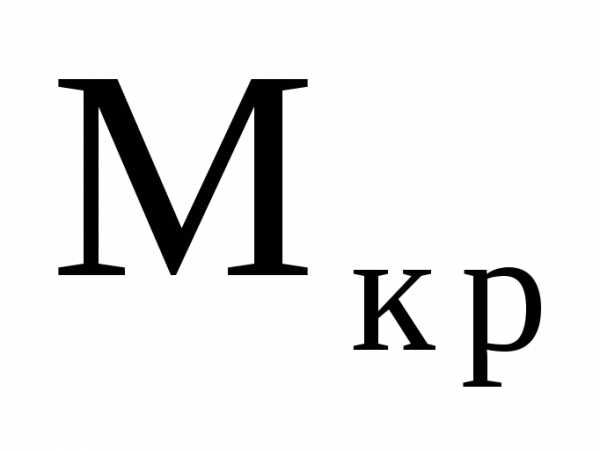или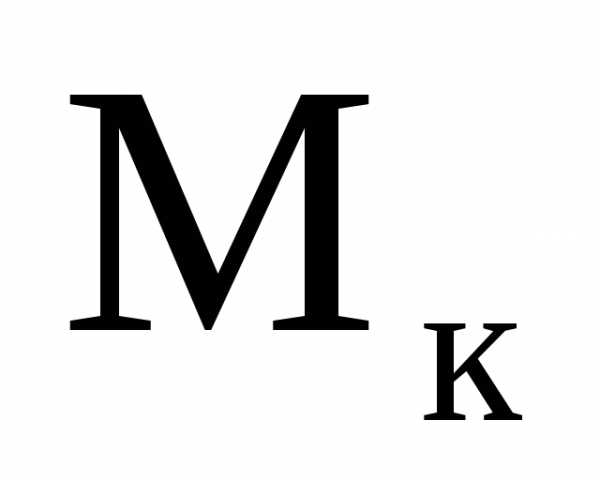, более точно отвечающие физическому смыслу этой величины.

График, показывающий как меняется внутренний силовой фактор по длине рассматриваемого тела, называется эпюрой.

Правильность построения эпюры обеспечивается, в первую очередь, надлежащим выбором характерных сечений, то есть тех сечений, в которых величина внутреннего силового фактора обязательно должна быть определена.

К характерным сечениям относятся:

1. сечения, расположенные бесконечно близко по обе стороны от точек приложения сосредоточенных сил и моментов;

2. сечения, расположенные в начале и в конце каждого участка с распределенной нагрузкой;

3. сечения, расположенные бесконечно близко к опорам, а также на свободных концах.

studfiles.net

Метод сил в сопромате

 

 

Заказать решение           Способ оплаты

 

При решении задач сопромата, статически неопределимой называется такая система, которая не может быть рассчитана при помощи одних только уравнений статики, так как имеет лишние связи. Для расчета таких систем составляются дополнительные уравнения, учитывающие деформации системы.

Оговоримся, что здесь и далее понятие “расчет” подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а не расчет на прочность, жесткость и т.д.

Статически неопределимые системы обладают рядом характерных особенностей:

1. Статически неопределимые конструкции являются более жесткими, чем соответствующие статически определимые, так как имеют дополнительные связи.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Нарушение лишних связей в статически неопределимой системе не всегда приводит к разрушению, в то время как потеря связи в статически определимой системе делает ее геометрически изменяемой.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Основными методами расчетастатически неопределимых систем являются:

 

1. Метод сил. Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.
2.Метод перемещений. Неизвестными являются деформационные факторы – углы поворотов и линейные смещения.
3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитичеких методов при расчете особо сложных систем используются различные численные методы.

 

Канонические уравнения метода сил

 

Для получения дополнительных уравнений, о которых говорилось в предыдущем параграфе, нужно прежде всего превратить заданную, n раз статически неопределимую систему, в статически определимую, удалив из нее лишние связи. Полученная статически определимая система называется основной. Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этого пособия. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.

В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения.

Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:

 

 

где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е. — это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи; — перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.

В методе сил реакцию k-ой связи принято обозначать через Xk. С учетом этого обозначения и в силу справедливости закона Гука перемещения можно представить в виде:

 

 

где — единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией т.е. реакцией, совпадающей по направлению с Xk, но равной единице.

Подставляя (2) в (1), получим:

 

 

Физический смысл уравнения (3): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю.

Записывая выражения, аналогичные (3), для всей совокупности отброшенных связей, получим систему канонических уравнений метода сил:

 

 

Вид уравнения (4), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

 

Коэффициенты системы канонических уравнений (4) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр. Все эти коэффициенты, как указывалось выше, представляют собой перемещения; коэффициенты, стоящие при неизвестных – единичные перемещения, а свободные члены – грузовые. Единичные перемещения делятся на главные, расположенные по главной диагонали и имеющие одинаковые индексы и побочные (). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е. .

 

Алгоритм расчета методом сил

 

Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:

1. Определить степень статической неопределимости.
2. Выбрать основную систему.
3. Сформировать эквивалентную систему.
4. Записать систему канонических уравнений.
5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.
6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.
7. Построить суммарную единичную эпюру.
8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.
9. Решить систему (4), т.е. определить реакции лишних связей.
10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).
11. Выполнить статическую и кинематическую проверки.
Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной.
Остановимся подробнее на некоторых из вышеперечисленных этапов расчета.

 

Выбор основной системы

 

Это важнейший этап расчета, так как рациональный выбор основной системы существенно упрощает вычислительную работу. Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.

1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.1,б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.1,а).

2.Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n=3 (рис.2,а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.2,б).

3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.2,в). В частных случаях (рис.2,г) рассечение стержня по шарниру освобождает две связи (рис.2,д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.2,е).

 

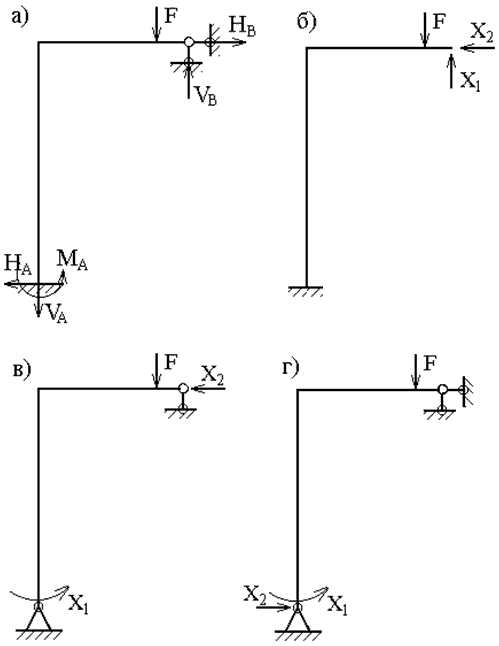
рис. 1

 

Среди связей статически неопределимой системы различают абсолютно необходимые и условно необходимые. К абсолютно необходимым относятся связи, при удалении которых система становится геометрически изменяемой. Для абсолютно необходимой связи характерна статическая определимость усилия в ней, т.е. реакция такой связи может быть вычислена из условия равновесия. При выборе основной системы абсолютно необходимые связи отбрасывать нельзя.

 

 

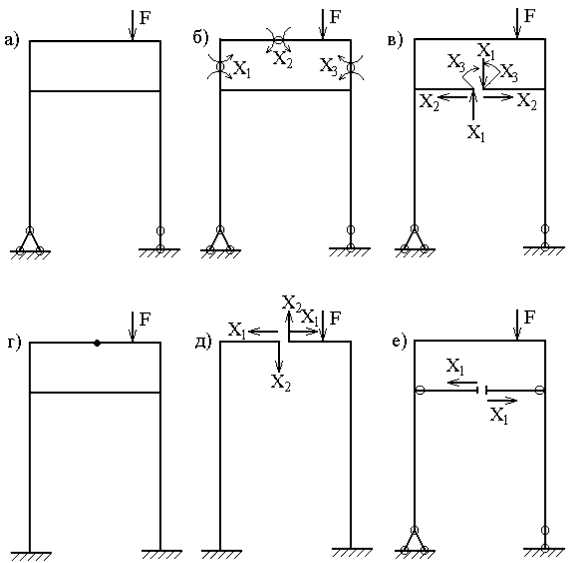
рис. 2

 

Связи, при удалении которых система продолжает оставаться геометрически неизменяемой, называются условно необходимыми. Система, у которой удалили такую связь, может являться основной системой метода сил.

 

Вычисление коэффициентов и свободных членов канонических уравнений

 

Этому этапу расчета предшествует построение единичных и грузовых эпюр внутренних силовых факторов (для балок и рам – эпюр изгибающих моментов). Единичные эпюры строятся от действия безразмерной единичной силы или безразмерного единичного момента, совпадающих по направлению с направлением соответствующей лишней неизвестной в эквивалентной системе, и обозначаются через , а единичная эпюра – через .

 

Грузовая эпюра строится от внешней нагрузки, приложенной к основной системе. При этом можно строить одну эпюру от одновременного действия всех внешних нагрузок или несколько эпюр, отдельно от каждой из приложенных нагрузок. Такое разбиение одной грузовой эпюры на несколько  более простых, как правило, целесообразно только тогда, когда среди действующих нагрузок есть равномерно распределенная, и эпюра моментов на соответствующем участке под ней является знакопеременной. При этом в каждом каноническом уравнении число свободных членов будет равно числу построенных грузовых эпюр.

Единичные и грузовые перемещения (коэффициенты и свободные члены канонических уравнений) в общем случае можно вычислить методом Мора. Для балок и рам это можно сделать при помощи правила Верещагина.

 

Универсальная проверка коэффициентов и свободных членов канонических уравнений

 

Для выполнения универсальной проверки необходимо построить суммарную единичную эпюру — эпюру моментов от одновременного действия всех единичных сил, приложенных к основной системе:

 

Перемножим суммарную единичную эпюру с эпюрой :

 

 

Таким образом результат перемножения суммарной и i-ой единичной эпюр — это перемещение по направлению i-ой связи от совместного действия единичных лишних неизвестных. Это перемещение равно сумме коэффициентов i-го канонического уравнения:

 

 

Такая проверка называется построчной и выполняется для каждого канонического уравнения.
Вместо n построчных проверок чаще всего выполняется одна – универсальная поверка, которая состоит в перемножении суммарной единичной эпюры самой на себя и проверке условия:

 

 

Если универсальная проверка выполняется, значит единичные перемещения вычислены правильно; если нет – необходимо выполнить построчные проверки, что позволит уточнить перемещение, при вычислении которого допущена ошибка.

Для выполнения проверки грузовых перемещений необходимо перемножить суммарную единичную и грузовую эпюры изгибающих моментов:

 

 

Таким образом, проверка свободных членов системы канонических уравнений (4) состоит в выполнении условия:

 

 

Построение окончательных эпюр внутренних силовых факторов

 

Окончательные эпюры можно построить двумя способами.

Так как при найденных значениях лишних неизвестных Xi выполняются условия совместности деформаций, то из расчета основной системы можно получить все искомые внутренние усилия заданной системы. На основании принципа независимости действия сил для изгибающих моментов получим:

 

или, учитывая, что

 

 

приходим к выражению:

 

 

Аналогично определяется продольные и поперечные силы:

 

Второй способ основан на том, что в результате вычисления реакций лишних связей Xi исходная статически неопределимая система приведена к статически определимой системе, загруженной внешними нагрузками и реакциями лишних связей. Поэтому окончательные эпюры внутренних силовых факторов можно построить для эквивалентной системы, вычислив предварительно (и то не всегда) из условий равновесия опорные реакции последней.

Недостатком первого способа является то обстоятельство, что для его реализации необходимо дополнительно построить эпюры Qi, Ni (i=1, 2, …,n), Qf, Nf, которые не используются в расчете методом сил и поэтому не были построены ранее.

В связи с этим для построения окончательных эпюр более рациональным представляется второй способ, а условие (8) можно использовать в качестве дополнительной проверки.

 

Проверка окончательной эпюры изгибающих моментов

 

Эта проверка выполняется в двух вариантах: статическая и кинематическая.

При статической проверке, выполняемой обычно для рам, вырезаются узлы и записываются условия их равновесия под действием узловых сосредоточенных моментов и изгибающих моментов на концах стержней. Эта проверка является вспомогательной и выполняется автоматически при правильных эпюрах изгибающих моментов в основной системе и при выполнении кинематической проверки.

Статическая проверка эпюр Q и N состоит в том, что для любой отсеченной части рамы сумма проекций на две оси всех действующих сил – внешних нагрузок и  внутренних усилий – должна быть равна нулю.

Основной проверкой окончательной эпюры моментов в методе сил является кинематическая проверка, которая может быть построчной или универсальной.<br /> При построчной проверке каждая единичная эпюра моментов перемножается с окончательной эпюрой моментов М:

 

 

Таким образом, в результате перемножения каждой единичной эпюры с окончательной эпюрой моментов получим ноль:

 

Вариантом построчной проверки является проверка по замкнутомуконтуру, состоящая в том, что сумма приведенных (т.е. деленных на жесткость соответствующего стержня или его участка) площадь эпюры М, находящихся внутри каждого замкнутого бесшарнирного контура, должна быть равна сумме приведенных площадей, находящихся снаружи этого контура.

Суммируя выражения типа (11) для всех n, получим выражение, служащее для универсальной кинематической проверки окончательной эпюры изгибающих моментов:

 

 

Формулу (12) можно интерпретировать следующим образом: условное перемещение эквивалентной, или, что то же самое, заданной системы по направлению всех неизвестных от действия всех неизвестных и внешних нагрузок, равно нулю.

 

Определение перемещений в статически неопределимых системах

 

Для определения перемещения в статически неопределимой системе используется тождественность заданной и эквивалентной систем в том смысле, что если условия совместности деформаций выполняются, т.е. справедливы уравнения (4), то перемещения в эквивалентной системе соответствуют перемещениям заданной системы. Тогда, построив для основной системы эпюру изгибающих моментов от единичной силы (или единичного момента) приложенной в направлении искомого перемещения, величину перемещения находим по формуле:

 

 

 

где М – эпюра изгибающих моментов от внешней нагрузки, построенная для статически неопределимой системы.

Отметим, что при вычислении перемещения можно поступить и наоборот: единичную эпюру моментов построить в статически неопределимой заданной системе, а эпюру моментов от внешних нагрузок М – в основной (статически определимой) системе.

 

Пример расчета

 

Построить эпюры продольных, поперечных сил и изгибающих моментов для плоской рамы (рис.3,а).

Степень статической неопределимости рамы:

n = r — s = 4 — 3 = 1

 

Выбираем основную систему, отбрасывая на правой опоре горизонтальный стержень (рис.3,б),  т.е. заменяем шарнирно-неподвижною опору на шарнирно-подвижную. На базе основной системы формируем эквивалентную систему (рис.3,в).

Заменяя реакцию лишней связи соответствующей единичной силой, (рис. 3,г) строим эпюру моментов M1 (рис.3,д).

Грузовая эпюра моментов (рис.3,ж), построенная от одновременного действия всех внешних нагрузок (рис.3,е), является знакопеременной на участке, где действует нагрузка q. Это создает определенные трудности (хотя и не непреодолимые!) при ее перемножении с единичной эпюрой M1. В связи с этим целесообразно построить две грузовых эпюры – отдельно от нагрузки q (эпюра Mq) и от совместного действия F и M (эпюра MF). Эти варианты нагружения и эпюры представлены на рис.3,з и рис.3,а,б,в.

При таком разбиении внешней нагрузки каноническое уравнение метода сил содержит два грузовых перемещения и имеет вид:

 

 

Вычислим коэффициенты канонического уравнения:

 

 

Реакция лишних связи:

 

Эпюры Nz, Qy, Mx для заданной системы, загруженной нагрузками F, M, q и X1 (рис.3,г) представлены на рис.3,д,е,ж.

Как уже говорилось, при построении эпюр Nz и Q в рамах ординаты можно откладывать в любую сторону, но обязательно указывать знаки; а при построении эпюр Mx знаки можно не указывать, но обязательно откладывать ординаты со стороны сжатых волокон соответствующих элементов.

В рассмотренном примере универсальная проверка правильности вычисления коэффициентов канонического уравнения и свободных членов не выполнялась, так как рама имеет степень статической неопределимости n = 1, а, значит, суммарная единичная эпюра (если ее построить) совпадет с единичной эпюрой M1. В этом случае можно (и желательно!) проверить правильность выполнения расчета при помощи универсальной кинематической проверки окончательной эпюры моментов Mx.

Выполним эту проверку для рамы, рассмотренной в последнем примере (рис.3,а). Должно выполняться условие:

 

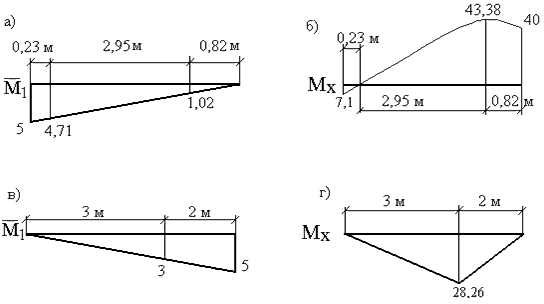
Покажем отдельно фрагменты перемножаемых эпюр (рис.3,д и рис.4,ж) для ригеля (рис.5,а,б) и стойки (рис.5,в,г) с указанением всех характерных размеров и соответствующих им ординат. Причем стойка (на рис.5,в,г) показана в горизонтальном положении.

Точка пересечения кривой на ригеле эпюры  Mx с осью (рис.5,б) определяется следующим образом. Обозначим координату произвольного сечения, отсчитываемую от правого конца ригеля, через z, тогда момент Mx определяется в виде:

 

 

откуда z = 3,77 м (второй корень этого уравнения лишен физического смысла).

 

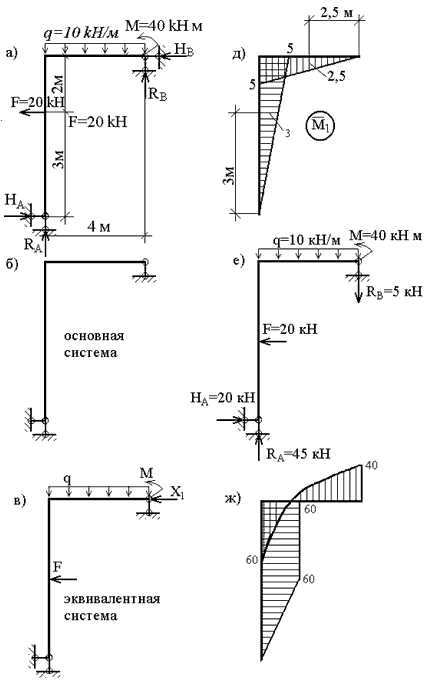
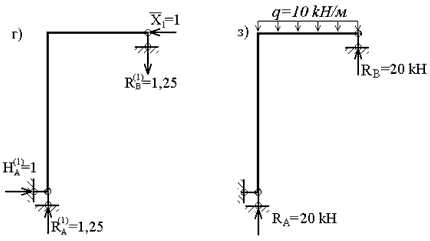
рис. 3

 

 

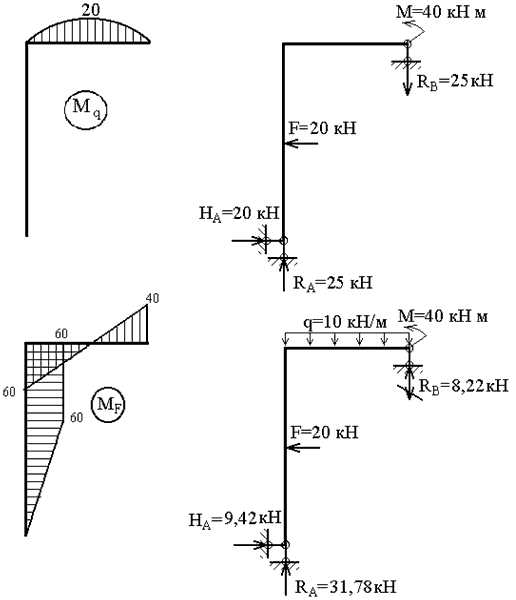
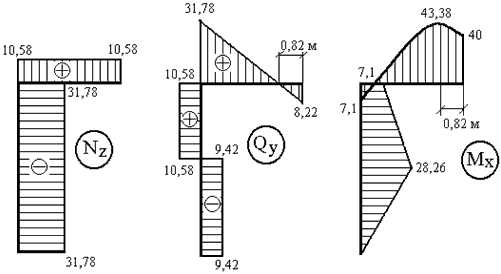
рис. 4

 

 

следовательно, расчет выполнен правильно.

 

 

 

Заказать решение

funnystudy.ru

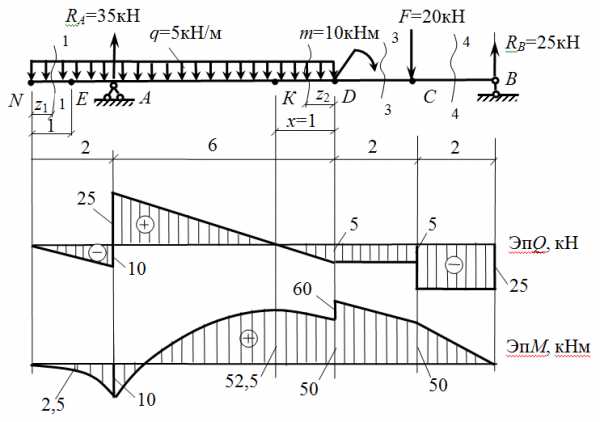
Задача на построение эпюр Q и M в балке

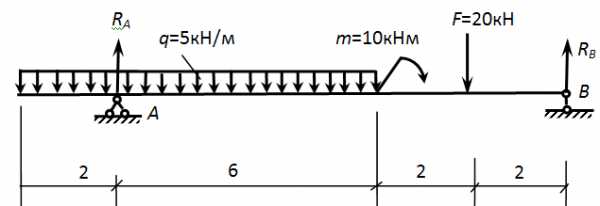
Для балки определить  опорные реакции и построить эпюры изгибающих моментов (М) и поперечных сил (Q).

1. Обозначаем опоры буквами А и В и направляем опорные реакции R_А и R_В.

Составляем уравнения равновесия.

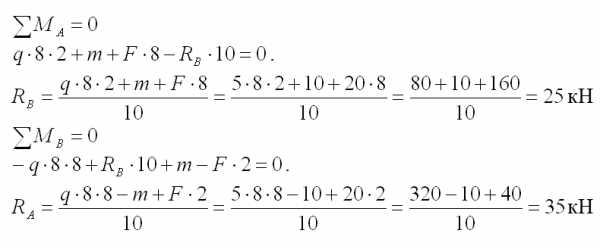
Проверка

Записываем значения R_А и R_В на расчетную схему.

2. Построение эпюры поперечных сил методом сечений. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 4 участка, 4 сечения.

сеч. 1-1   ход слева.

Сечение проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z₁ влево от сечения до начала участка. Длина участка 2 м. Правило знаков для Q — см. здесь.

Строим по найденным значением эпюру Q.

сеч. 2-2   ход справа.

Сечение вновь проходит по участку равномерно распределенной нагрузкой, отмечаем размер z₂  вправо от сечения до начала участка. Длина участка 6 м.

Строим эпюру Q.

сеч. 3-3   ход справа.

сеч. 4-4   ход справа.

Строим эпюру Q.

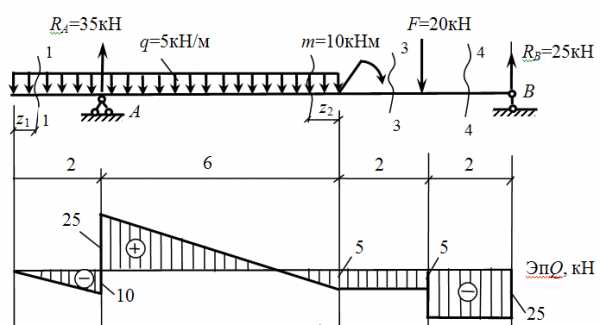
3. Построение эпюры М методом характерных точек.

Характерная точка – точка, сколь-либо заметная на балке. Это точки А, В, С, D, а также точка К, в которой Q=0 и изгибающий момент имеет экстремум. Также в середине консоли поставим дополнительную точку Е, поскольку на этом участке под равномерно распределенной нагрузкой эпюра М описывается кривой линией, а она строится, как минимум, по 3 точкам.

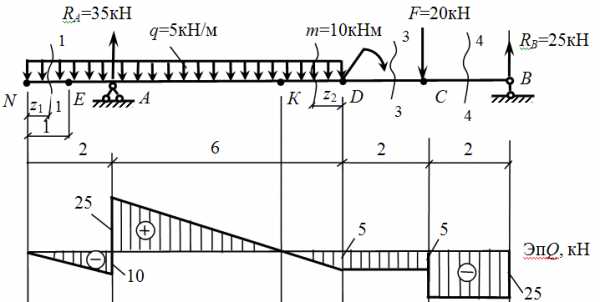
Итак, точки расставлены, приступаем к определению в них  значений изгибающих моментов. Правило знаков — см. здесь.

Участки NA, AD – параболическая кривая (правило «зонтика» у механических специальностей или «правило паруса» у строительных ), участки DС, СВ – прямые наклонные линии.

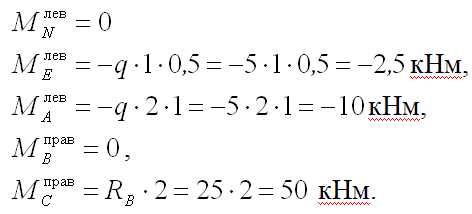
Момент в точке D следует определять как слева, так и справа от точки D. Сам момент в эти выражения не входит. В точке D получим два значения с разницей на величину m – скачок на его величину.

Теперь следует определить момент в точке К (Q=0). Однако сначала определим положение точки К, обозначив расстояние от нее до начала участка неизвестным х.

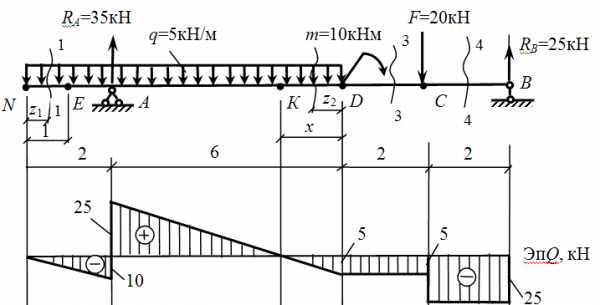
Т. К принадлежит второму характерному участку, его уравнение для поперечной силы (см. выше)

Но поперечная сила в т. К равна 0, а z₂ равняется неизвестному х.

Получаем уравнение:

Теперь, зная х, определим  момент в точке К с правой стороны.

Строим эпюру М. Построение выполним для механических специальностей, откладывая положительные значения вверх от нулевой линии и используя правило «зонтика».

prosopromat.ru

Ломаные стержни

 

  Систему, состоящую из жестко соединенных между собой стержней, оси которых не лежат в одной плоскости в сопромате называют ломаным стержнем. При этом ограничимся рассмотрением только таких ломаных стержней, отдельные элементы которых стыкуются друг с другом под прямыми углами, а внешние нагрузки приложены перпендикулярно к осям стержней (рис.17,а,б).

 

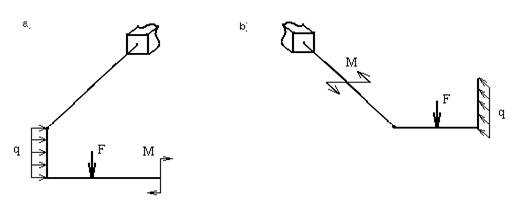
Рис.17

В общем случае нагружения в поперечных сечениях ломаных стержней могут возникать все 6 известных внутренних силовых факторов: продольная сила , поперечные силы , изгибающие моменты , крутящий момент. Очень часто, особенно в машиностроительных конструкциях, отдельные элементы ломаного стержня имеют незначительную длину, иногда соизмеримую с размерами поперечного сечения, то есть являются «короткими» стержнями. В этом случае не только внутренние моменты,, но и внутренние силы (,) существенно влияют на напряженно-деформированное состояние конструкции, поэтому для ломаных стержней будем строить эпюры всех шести внутренних силовых факторов.

Для правильного построения эпюр здесь обязательным является использование скользящей системы координат, о которой уже говорилось при рассмотрении плоско-пространственных систем (см.1.17).

  Пример 12. Рассмотрим простейший случай нагружения ломанного стержня — двумя взаимноперпендикулярными сосредоточенными силами, приложенными на свободном конце (рис.18,а).

Выбираем скользящую систему координат (рис.18,б). Ось z всегда направлена вдоль продольной оси того или иного участка ломаного стержня, а при переходе с одного участка на другой координатные оси поворачиваются на 90 градусов, но никогда не вращаются вокруг оси z. Удобнее всего начинать выбор скользящей системы координат с горизонтального участка ломаного стержня, который параллелен плоскости чертежа или лежит в этой плоскости (участок ВС на рис.18,б).
На этом участке (а он аналогичен обычной балке) ось y  направляется вертикально (вверх или вниз), ось z — вдоль продольной оси участка, а ось  x — перпендикулярно плоскости yoz, после чего система координат передвигается на остальные участки ломаного стержня.

 Построение эпюры .

Построение этой и всех последующих эпюр ведем от свободного конца. Правило знаков для  остается таким же, как и для других систем, а именно: растяжению соответствует знак «+», сжатию — «-«.

Участок АВ имеет нулевую продольную силу, так как  перпендикулярны продольной оси этого участка:

.
Участок ВС растягивается силой :

.
Участок СД сжимается силой :

.

Построение эпюр  и .

Поперечную силу  формируют только те силы, которые параллельны оси x на данном участке, а поперечную силу — силы, параллельные оси y. Здесь также сохраняется обычное для Q правило знаков: , если внешняя сила, приложенная к отсеченной части, стремится повернуть рассматриваемое сечение по часовой стрелке и — в противоположном случае. С учетом сказанного в характерных сечениях имеем:

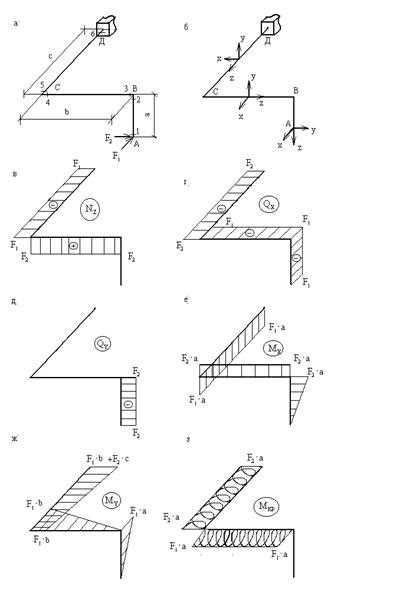
Рис.18

 

Построение эпюр .

Ординаты эпюр изгибающих моментов будем, как обычно, откладывать со стороны сжатых волокон, не указывая знаков, причем ориентировать эпюры нужно так, чтобы плоскость эпюры совпадала с плоскостью действия пары того изгибающего момента, для которого она построена. Иначе говоря, эпюра  на всех участках ломаного стержня располагается в плоскости yoz, а эпюра — в плоскости xoz.

Начнем с построения эпюры . Здесь нас будет интересовать изгиб каждого участка в плоскости yoz (см. скользящую систему координат на
рис.18,б) и, соответственно, плечо каждой действующей на отсеченную часть нагрузки нужно измерять в этой плоскости.

На участке АВ плоскость yoz — вертикальная плоскость, параллельная плоскости чертежа. В этой плоскости стержень АВ изгибается только силой , так как  перпендикулярна плоскости yoz :

;
 (сжаты правые волокна).

На участке ВС плоскость yoz  ориентирована так же, как и на участке АВ, причем, все точки ВС равноудалены от линии действия силы , поэтому:
 (сжаты верхние волокна).

На участке СД плоскость yoz — вертикальная плоскость, перпендикулярная плоскости чертежа. В этой плоскости стержень СД изгибается только силой , так как  перпендикулярна yoz ; все точки участка СД равноудалены (в рассматриваемой плоскости) от линии действия силы , следовательно:

 (сжаты нижние волокна).

Рассуждая аналогичным образом, будем строить эпюру , но теперь нужно рассматривать изгиб каждого участка ломаного стержня в плоскости xoz.

На участке АВ плоскость xoz — вертикальная плоскость, перпендикулярная плоскоси чертежа. В этой плоскости стержень АВ изгибается только силой , так как  перпендикулярна плоскости xoz:

;
 (сжаты дальние от наблюдателя волокна).

На участке ВС плоскость xoz — горизонтальная плоскость. В этой плоскости сила  приложена вдоль продольной оси стержня ВС и к изгибу привести не может, поэтому:

;
 (сжаты дальние от наблюдателя волокна).

На участке СД плоскость xoz — это так же горизонтальная плоскость. Здесь к изгибу стержня СД приводят обе силы: плечо силы   постоянно и равно b, а плечо силы  равно нулю в сечении 5 и равно с в сечении 6:

  (сжаты правые волокна).

Иногда при построении эпюр изгибающих моментов в ломанных стержнях возникают затруднения в определении участия той или иной нагрузки в изгибе стержня или в определении плеча той или иной нагрузки. В этих случаях всегда можно использовать простой, но эффективный прием: спроектировать конструкцию и действующие нагрузки на ту плоскость в которой изгибается стержень, переходя тем самым от пространственной конструкции к ее проекции, что позволяет легко определить плечи каждой из нагрузок и их «вклад» в изгиб рассматриваемого участка. Проследим использование этого приема например, при построении эпюры  на участке СД (рис.18,а,б). На этом участке плоскость xoz, в которой нужно рассматривать изгиб стержня при построении — горизонтальная плоскость, следовательно, для реализации описываемого приема необходимо спроектировать конструкцию на горизонтальную плоскость, то есть изобразить вид сверху (рис.19).

Рис.19

При этом сила  будет видна направленной вдоль стержня ВС, сила — перпендикулярно ВС, а стержень ВА проектируется в точку. Теперь совершенно очевидно, что все точки стержня СД равноудалены от линии действия силы , что приводит к постоянному моменту , а сила  имеет нулевое плечо в сечении 5 и плечо, равное с, — в сечении 6:

В обоих сечениях сжаты  правые волокна, то есть получен тот же результат, что и ранее, но в более наглядном виде.

funnystudy.ru

Внутренние усилия. Правила построения их эпюр.

 

Внешняя нагрузка, действуя на составные части любого строительного сооружения, приводят к возникновению в элементах конструкции внутренние напряжения и деформации. В строительной механике рассчитывают следующие характеристики напряжений и деформаций – внутренние усилия и перемещения.

В элементах стержневой системы на плоскости могут возникать три вида внутренних усилий: продольная сила N, поперечная сила Q, изгибающий момент M. Положительные значения указанных усилий в зависимости от направления внутренних усилий определяются как на рисунке, приведенном ниже:

 

Правило знаков при построении эпюр

Изгибающий момент (М) – это сумма моментов, создаваемых силами, расположенными слева (или справа) относительно рассматриваемой точки (момент создается относительно оси z).

Поперечная сила (Q) – это сумма проекций всех сосредоточенных сил, расположенных слева (или справа) относительно рассматриваемой точки, на ось y.

Продольная сила (N) – это сумма проекций всех сосредоточенных сил, расположенных слева (или справа) относительно рассматриваемой точки, на ось x.

При построении эпюр для Q и N ординаты со знаком «+» откладывают вверх от нейтральной оси эпюры, а отрицательные – вниз. Эпюра М всегда изображается на стороне растянутого волокна балки, т.е. значения со знаком «+» откладываются вниз от нейтральной оси эпюры, а отрицательные – вверх.

Между эпюрами изгибающего момента (М) и поперечной силы (Q) существует прямая зависимость – поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки (теорема Журавского).

 

Q=dM/dx

 

Правила для проверки правильности построения эпюр:

1. На участках стержня, на которые действует равномерно распределенная нагрузка q эпюра изгибающих моментов М имеет вид выпуклой (вогнутой) кривой (выпуклость этой кривой направлена в ту сторону, куда направлена распределенная нагрузка), эпюра Q – наклонной прямой.

2. В местах расположения на стержне сосредоточенной силы P на эпюре поперечной силы Q всегда будет перепад на величину этой сосредоточенной силы. В месте расположения сосредоточенного момента на эпюре изгибающих моментов  М также всегда будет перепад на величину этого сосредоточенного момента.

3. Если эпюра поперечной силы (Q) имеет один знак, то эпюра изгибающего момента (М) или возрастает или убывает (если знак Q «– » ординатами эпюры М слева на право увеличиваются).

4. Величина поперечной силы (Q) равна тангенсу угла между касательной к эпюре изгибающего момента (М) и нейтральной осью эпюры.

5. В точках балки, в которых эпюра поперечной силы (Q) пересекает нейтральную ось (Q=0) на эпюре изгибающего момента (М) располагается максимум или минимум.

6. По виду линии эпюры изгибающего момента (М) можно определить знак эпюры поперечной силы (Q). Для этого нейтральную ось эпюры M необходимо повернуть до совпадения с касательной к линии эпюры М. Если поворот будет по часовой стрелке, Q будет со знаком «+», а если против часовой стрелки, то со знаком «–». При этом угол поворота должен быть меньше 90°.

 

Примеры задач с решениями.

5stroymeh.ru