Напряжения и характер деформаций при растяжении и сжатии

Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила.
Брусья с прямолинейной осью, работающие на растяжение или сжатие, часто называются стержнями.

Рассмотрим невесомый, защемленный левым концом прямой брус, вдоль оси которого действуют активные силы F и 2F (рис. 1). Части бруса постоянного сечения, заключенные между поперечными плоскостями (сечениями), в которых приложены одинаковые внешние силы (нагрузки или реакции связей) будем называть участками. Т. е. участок — это однородный кусок бруса и по форме, и по нагрузкам, и по площади сечения.

Изображенный на рис. 1 брус состоит из двух участков – от защемленного конца до места приложения силы F, и от силы F до свободного конца, к которому приложена сила

∑ Z = 0, следовательно: 2F – F – N₁ = 0, откуда N₁ = 2F – F = F.

Очевидно, что для сохранения равновесия части бруса достаточно приложить продольную силу. Нетрудно понять, что на втором участке бруса продольная сила в сечении 2-2 будет иметь другое значение: N₂ = 2F.
Таким образом, продольная сила в поперечном сечении бруса равна алгебраической сумме внешних сил, расположенных по одну сторону от рассматриваемого сечения и в пределах каждого участка имеет одинаковое значение.
Последнее утверждение не совсем справедливо, поскольку в местах приложения внешних сил внутренние силы распределяются по сложным закономерностям, но с учетом рассмотренного ранее принципа смягчения граничных условий (принципа Сен-Венана), мы допускаем некоторую условную погрешность, незначительно влияющую на итоговый результат расчета.

При определении величины продольной силы алгебраическим сложением внешних сил следует обращать внимание на знаки (векторные значения) этих сил. При расчетах в сопромате обычно принимают растягивающие нагрузки (направленные от сечения) положительными, а сжимающие – отрицательными.

При изучении ряда деформаций мы будем мысленно представлять брусья состоящими из бесконечного количества волокон, расположенных параллельно оси бруса, и предполагать, что при деформации растяжения и сжатия эти волокна не надавливают друг на друга (гипотеза о не надавливании волокон).

Чтобы понять характер напряжений и деформаций, возникающих в сжимаемом или растягиваемом брусе, представим себе прямой брус из резины, на котором нанесена сетка из продольных и поперечных линий. Если такой брус подвергнуть деформации растяжения, можно заметить, что:

• поперечные линии на брусе остаются ровными и перпендикулярными оси бруса, а расстояния между ними увеличатся;
• продольные линии останутся прямыми, а расстояния между ними уменьшатся.

Из этого эксперимента следует, что при растяжении справедлива гипотеза плоских сечений (гипотеза Бернулли), и, следовательно, все волокна бруса удлинятся на одну и ту же величину. Все это позволяет сделать вывод, что при растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению. Эти напряжения можно определить по формуле:

σ = N / А,

где N – продольная сила, А – площадь поперечного сечения бруса.

Очевидно, что при растяжении и сжатии форма сечения бруса на величину напряжений не влияет.
Для наглядного изображения распределения продольных сил и нормальных напряжений вдоль оси бруса строят графики, называемые эпюрами (от французского «epure» — чертеж, график) , при этом на эпюрах при построении учитывают знаки (векторные значения) продольных сил и напряжений.

Для ступенчатого бруса, к которому приложены сжимающая 2F и растягивающая 3F силы на рис. 2 показаны соответствующие эпюры продольных сил N и нормальных напряжений σ.

Порядок построения эпюр таков: сначала под чертежом бруса проводят прямую линию, параллельную оси бруса (эта линия условно представляет брус), затем напротив каждого сечения бруса откладывают по этой линии величину силовых факторов: для положительных – вверх, для отрицательных — вниз. Масштаб при этом выбирается произвольный. Разумеется, перед построением эпюры необходимо подсчитать величину силовых факторов (сил, моментов сил или напряжений) в каждом участке бруса.
На полученном графике в кружках указываются знаки силовых факторов по участкам, на наружных углах ступенчатых переходов ставятся числовые значения этих силовых факторов, а вся площадь графика заштриховывается тонкими линиями, перпендикулярными оси.

По эпюрам, представленным на рис. 2 можно заметить, что в местах приложения внешних нагрузок и реакций внутренние силовые факторы изменяются скачкообразно (принцип Сен-Венана).
Визуальное исследование эпюры позволяет определить критические участки бруса, находящиеся в наиболее напряженном состоянии. Так, по представленным на рис. 2 эпюрам напряжений, возникающих в брусе, можно определить, что критическим является 2-й участок, поскольку здесь возникает наибольшее напряжение (по эпюре видно, что это напряжение сжатия, т. к. оно имеет отрицательное значение).

Кроме того, эпюра любого силового фактора позволяет (без применения лишних расчетов) определить силу или момент, действующие на брус со стороны, например, заделки, поскольку после построения эпюры со стороны свободного конца бруса эти силовые факторы отобразятся графически, без вычислений.

Ниже размещен видеоролик, в котором подробно объясняется порядок построения эпюр продольных сил и напряжений, возникающих в брусе при растяжении и сжатии, а также выводы, которые можно сделать на основе визуального анализа графиков.
Видеоурок ведет преподаватель ГОУ СПО «Нижнетагильский горно-металлургический колледж» Чирков А. С.

***

Материалы раздела «Растяжение и сжатие»:

Смятие

k-a-t.ru

Что такое растяжение и сжатие?

Растяжение и сжатие является первым разделом с которым знакомятся студенты в рамках сопромата. Растяжение (сжатие) – это такой способ воздействия на стержень при котором в его поперечных сечениях возникает только одно внутреннее усилие – продольная сила.

Какие существуют виды растяжения и сжатия?

Указанное выше определение относится только к центральному растяжению или сжатию, то есть все внешние силы, в этом случаем, прикладываются к центру тяжести поперечных сечений, то есть они направленны вдоль оси стержней. В сопромате есть более сложный вид растяжения при котором силы прикладываеются внеценртенно, а в поперечных сечениях в ответ появляется сразу несколько внутренних силовых факторов. Для решения задач на данную тематику потребуются знания сразу нескольких разделов сопромата, поэтому будем продвигаться постепенно, начиная с более простых тем, данная статья будет посвященна только центральному растяжению и сжатию.

Метод сечений и растяжение (сжатие)

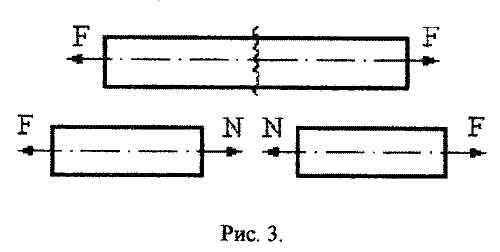
Как говорилось выше, в центрально растянутых или сжатых элементах конструкций возникают только продольные усилия. Как узнать численное значение этих сил? Для их определения сопроматчики пользуются методом сечений. В чем собственно этот метод заключается? Если тело нагружено внешними силами находится в равновесии, то и отдельные части этого тела будут находится в равновесии. Данный метод позволяет устанавливать связь между внутренними и внешними силами. Рассмотрим этот метод в действии на примере бруса, который растягивается какой-то внешней силой.

Например, если мы хотим узнать продольное усилие в поперечном сечении, находящемся справа от свободно торца бруса на расстоянии x, мысленно рассекаем брус в намеченном месте, компенсируем действие одной части бруса на другую прикладывая силы N, то есть уравновешиваем одну часть и другую, тем самым сила N и будет той искомой внутренней продольной силой, не трудно догадаться что эта сила будет численно равна внешней силе F.

Отличием здесь служит только направление этих сил. Так же очевидно, что в каком бы месте бруса мы не делали сечение и находили продольную силу, она бы всегда была равна внешней. Отсюда, формулируем полезное правило, которое в дальнейшем обязательно пригодится: если в пределах участка нагруженного стержня действует только постоянная внешняя сила, то в поперечных сечениях стержня на данном участке будут возникать одинаковые внутренние усилия, которые численно будут равны внешней силе.

На практике в стержнях по всей длине могут возникать различные по величение продольные силы. Для того чтобы отслеживать их величину по всей длине, сопроматчики придумали строить так называемые эпюры продольных сил.

Эпюра в сопромате – это график показывающий распределение какой-либо величины по длине нагруженного элемента.

sopromats.ru

Растяжение и сжатие. Усилия в поперечном сечении стержня.

 Центральным растяжением или сжатием  в сопромате называется такой вид деформации, при котором в поперечных сечениях стержня возникает только продольная сила N, а все остальные усилия равны нулю.

 Продольная сила N — равнодействующая внутренних сил в поперечном сечении стержня. В сопротивлении материалов она определяется из условия равновесия отсеченной части, и численно равна сумме проекций на продольную ось стержня всех внешних сил, расположенных по одну сторону от сечения.

  При растяжении продольная сила направлена от сечения и считается положительной. При сжатии она направлена к сечению и считается отрицательной.

  Эпюра продольных сил — график величин этих усилий для всех поперечных сечений стержня.

 Пример решения задачи по сопромату на растяжение — сжатие. Построить эпюру продольных сил для стержня, изображенного на рис. 4,а.

 Решение. Проводим сечение 1-1 в пределах первого участка и отбрасываем правую часть стержня. К оставшейся левой части прикладываем неизвестную силу N1, предполагая ее положительной и направляя от сечения. Из уравнения равновесия отсеченной части получим      N1-3P=0   =>  N1=3P

 Проводя сечения 2-2, 3-3 и т.д. на остальных участках и составляя уравнения равновесия для отсеченных частей, определим продольные силы (рис.4,б).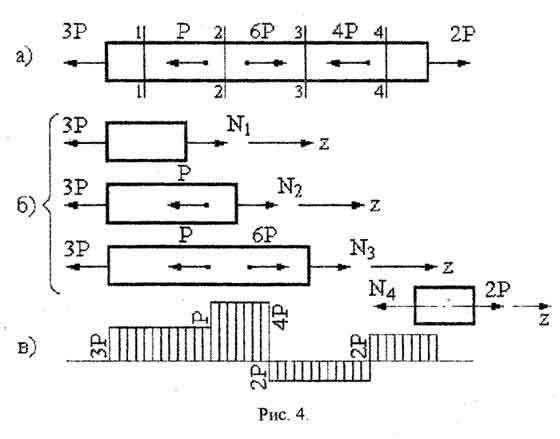

2-ой участок   N2 – P – 3P =0     N2=4P

3-й участок    N3 +6P-P-3P=0     N3= -2P

4-й участок     N4-4P+6P-P-3P=0   N4=2P

Для контроля определим N4 из рассмотрения правой части стержня.

  2P – N4=0    N4=2P

 По найденным значениям N на рис. 4, в построена эпюра продольных сил. Из эпюры следует, на участках 1,2 и 4 стержень растянут, а на участке 3 сжат. Так ведется решение задач на растяжение и сжатие в сопромате.

Напряжения и деформации. Растяжение и сжатие. Сопромат решение задач

При растяжении-сжатии стержня с постоянными поперечными размерами в любом поперечном сечении возникают нормальные напряжения, равномерно распределенные по сечению и равные

o = N/A

где N — продольная сила в сечении;

       А -площадь поперечного сечения.

Эта формула справедлива только для поперечных сечений, отстоящих от места приложения нагрузки на расстоянии не меньшем поперечного размера стержня (принцип Сен-Венана).

   Вблизи места приложения нагрузки напряжения распределяются

неравномерно.

В случае однородного стержня, растянутого или сжатого силами, приложенными на концах, напряжения остаются постоянными как по сечению, так и по длине, т.е. одинаковы для всех точек объема стержня

   Такое напряженное состояние в сопромате называется однородным.

Продольную деформацию стержня характеризуют следующие величины (рис. 5).

  Абсолютная продольная деформация (удлинение при растяжении и укорочении при сжатии)  ^ l = l1-l

где 1 -первоначальная длина стержня;

       l1 — конечная длина.

Относительная продольная деформация (относительное удлинение). e = ^ l / l 

Поперечную деформацию стержня в сопротивление материаловхарактеризуют следующие величины:

Абсолютная поперечная деформация   ^b = b – b1,

где b -первоначальный поперечный размер,

      b1 — поперечный размер после деформации

Относительная поперечная деформация  e 1 = ^b / b

 При растяжении продольную деформацию можно считать положительной (е > 0), а поперечную отрицательной (е 1 < 0).

 При сжатии, наоборот e < 0, е 1 > 0.

Абсолютная величина отношения e1  к  е называется коэффициентом Пуассона, 

                         M = [e1/e]

Коэффициент Пуассона  M (мю) — величина безразмерная и его значение

для различных материалов колеблется в пределах от 0 до 0,5. Объемная деформация характеризуется относительным изменением объема

 ev = ^V / V

 где ^V — абсолютное изменение объема;

         V — Первоначальный объем стержня.

    Закон Гука о = e Е,

где Е — коэффициент пропорциональности, называемый модулем продольной упругости, который имеет размерность Па, кПа, мПа.

  Закон Гука справедлив, пока напряжения не превосходят определенной для каждого материала величины, называемой пределом пропорциональности.

  Абсолютное удлинение стержня постоянного сечения при постоянном по его длине значении продольной силы определяется по формуле:     ^l = Nl / EA  — закон Гука

 где ЕА – жесткость сечения. Эта формула очень важна в курсе изучения сопротивления материалов вообще и в решении задач по сопромату в частности.

studfiles.net

Центральное (осевое) растяжение (сжатие) стержней

Растяжение  (сжатие) – это такой   вид нагружения стержня, при котором в его поперечном сечении возникает внутренняя продольная сила Ν, действующая вдоль центральной оси z.

Продольная сила Ν – это равнодействующая всех внутренних нормальных сил в сечении. Для вычисления продольной силы применяется метод сечений.

Продольная сила Ν численно равна алгебраической сумме проекций всех сил, действующих по одну сторону от рассматриваемого сечения,  на продольную ось бруса.

Правило знаков для продольной силы Ν: при растяжении продольная сила положительна, при сжатии – отрицательна.

График изменения продольных сил по длине стержня называется эпюрой. Эпюра N строится методом сечений на характерных участках бруса. Строится эпюра для использования ее при расчете бруса на прочность. Она дает возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.

При растяжении (сжатии) возникают только нормальные напряжения. Согласно гипотезе Я. Бернулли (или гипотеза плоских сечений) в поперечных сечениях, удаленных от места приложения нагрузок, нормальные напряжения распределяются по сечению практически равномерно, а сами сечения, перпендикулярные к оси стержня z, остаются плоскими в процессе нагружения.

Нормальные напряжения в сечении при  растяжении (сжатии) вычисляются по формуле

где А – площадь поперечного сечения.

Правило знаков для σ совпадает с правилом знаков для N.

В наклонном сечении, нормаль к которому составляет угол α с осью стержня z,

При растяжении в продольном направлении стержень удлиняется, а его поперечные размеры уменьшаются, при сжатии, напротив, в продольном направлении стержень укорачивается, а его поперечные размеры увеличиваются; Δℓ — абсолютное удлинение или укорочение участка стержня длиной ℓ, Δb – абсолютная поперечная деформация.

Относительное удлинение или укорочение участка стержня длиной ℓ, называемое линейной деформацией, определяется следующим образом

ε=Δℓ/ℓ.

Экспериментально установлено, что в определенной области нагрузок при упругом поведении материала между нормальными напряжениями и линейными деформациями существует линейная зависимость (закон Гука для напряжений)

σ=εЕ,

где Е – модуль продольной упругости или модуль Юнга, это физическая const. Для каждого из материалов величина модуля упругости имеет свое значение:

сталь, Е = 2^.10⁵ МПа,

медь, Е = 1^.10⁵ МПа,

алюминий, Е = 0,7^.10⁵ МПа.

Значение модуля упругости устанавливается экспериментально.

Согласно закону Гука (данную запись называют законом Гука для деформаций)

Δℓ=Νℓ/ЕА

Произведение ЕА – называется жесткостью стержня при растяжении – сжатии.

Перемещение произвольного сечения ступенчатого стержня

w=∑Δℓ_i

Относительная поперечная деформация:

ε′=Δb/b

где b – поперечный размер стержня.

Эксперименты также показывают, что в упругой стадии деформирования между продольной и поперечной деформациями существует взаимосвязь

μ  =│ε′⁄ε│ — const,

где   μ —  коэффициент Пуассона, берется по модулю ,поскольку у продольной и поперечной деформации разные знаки (при растяжении продольные волокна увеличиваются, а поперечные уменьшаются в размере).

Для твердых материалов имеет значения коэффициент Пуассона

0≤μ ≤0,5

Изменение температуры стержня вызывает его удлинение (при нагревании) или укорочение (при охлаждении)

где — a- коэффициент линейного температурного расширения; Δtº=(tº_к-tº_н) — изменение температуры между значениями начальным (tº_н) и конечным (tº_к).

Статически неопределимыми называют системы, имеющие лишние связи – внешние или внутренние.

Для определения внутренних усилий в таких системах недостаточно рассматривать только уравнения равновесия.

В этом случае требуются дополнительные уравнения, число которых равно количеству лишних связей. Дополнительные уравнения составляются на основе анализа картины деформирования системы и использования законов деформирования ее элементов.

Алгоритм решения подобных задач включает следующее:

1)   Статическая часть. Составляются уравнения равновесия с включением неизвестных усилий, действующих по направлению лишних связей.

2)    Геометрическая часть. Составляются уравнения, описывающие взаимосвязь перемещений характерных точек, удлинений и укорочений отдельных стержней между собой.

3)   Физическая связь. Записываются законы деформирования отдельных стержней системы.

Порядок расчета статически неопределимых брусьев

1.  Задаться направлениями возможных опорных реакций и составить уравнение      статики для всей системы в целом.
2. Определить степень статической неопределимости и использовать метод сечений с целью выразить неизвестные усилия через неизвестные опорные реакции. При этом неизвестные продольные силы (N) следует предполагать положительными и поэтому направлять «от сечения».
3. Сформулировать условие совместности деформаций участков бруса.
4. В процессе превращения условия совместности в уравнение совместности деформаций различий в характере деформаций участков не учитывать.

Порядок расчета статически неопределимых шарнирно-стержневых систем

1. Задаться направлениями опорных реакций, но уравнений равновесия для всей системы не составлять, а сразу использовать метод сечений и составить уравнения статики для выделенной части системы.
2. Определить степень статической неопределимости как разницу между количеством всех неизвестных, оказавшихся в уравнениях статики, и числом самих этих уравнений.
3. Рассмотреть (изобразить) любую возможную картину деформаций системы и из ее анализа сформулировать условия совместности деформаций стержней системы (столько, какова степень статической неопределимости).
4. В процессе преобразования условий совместности в уравнения совместности деформаций обязательно учитывать различие в характере деформаций стержней (т.е. вводить удлинение со знаком «плюс», а укорочение со знаком «минус») в соответствии с той картиной деформации, которую мы рассматриваем.

prosopromat.ru

Условие прочности при растяжении-сжатии | Лекции и примеры решения задач механики

При продольном осевом нагружении (растяжении-сжатии) в поперечных сечениях бруса имеют место только нормальные напряжения σ. Поэтому для обеспечения прочности стержней и стержневых систем достаточно выполнение условия:

Здесь
σ_max – максимальные расчетные нормальные напряжения в стержне,
N – внутренние продольные силы (принимаются с построенных эпюр),
А – соответствующая площадь поперечного сечения бруса,
[σ] – допустимые напряжения (расчетное сопротивление) для материала стержня, определяемое как:

n – коэффициент запаса прочности, устанавливаемый нормативными документами.

Данное условие означает что для того чтобы стержень при растяжении-сжатии оставался прочным, напряжения σ в его сечениях не должны превышать допустимых значений [σ].

В случаях, когда для материала стержней допустимые напряжения на растяжение [σ]_р и на сжатие [σ]_сж отличаются, при сравнении необходимо учитывать знак напряжений σ, который зависит только от знака соответствующих внутренних сил N.

Так, положительные значения напряжений σ сравниваются с [σ]_р, отрицательные напряжения по модулю не должны превышать значения [σ]_сж.

Три задачи расчета на прочность

Данное условие прочности позволяет решать три основных задачи сопротивления материалов и технической механики:

Проверка на прочность.

В случае, когда известны внешние нагрузки, а также размеры и материал стержня можно выполнить проверку его прочности. Для этого по каждому участку рассчитывается величина нормальных напряжений σ, после чего максимальная из них сравнивается с заданным допустимым значением [σ].

Ответ в данной задаче дается в виде заключения:

• если σ_max ≤ [σ] стержень прочный,
• если σ_max > [σ] стержень непрочный.

Подбор размеров сечения (проектировочный расчет)

Эта задача является основной в технической механике. Здесь, по известным схеме нагружения и материалу стержня определяется минимально необходимая площадь поперечного сечения A обеспечивающая его прочность.

Для этого условие прочности записывается относительно искомой величины.

Полученные размеры в случае необходимости можно только увеличивать. Уменьшение размеров приведет к превышению напряжениями допустимых значений.

Определение грузоподъемности стержня.

Данная формула позволяет по известным размерам и материалу рассчитать величину допустимой внутренней силы, которую может выдержать стержень, оставаясь прочным.

В данном случае условие прочности записано относительно внутренней силы N.

Напряжения при растяжении-сжатии >
Расчеты на прочность при растяжении-сжатии >

isopromat.ru

Внецентренное растяжение или сжатие | ПроСопромат.ру

Рассмотрим важный частный случай изгиба с растяжением или сжатием. Этот вид деформации получится, если к стержню будут приложены две равные и противоположно направленные силы Р, линия действия которых не будет совпадать с центральной осью стержня, а будет ей параллельна.

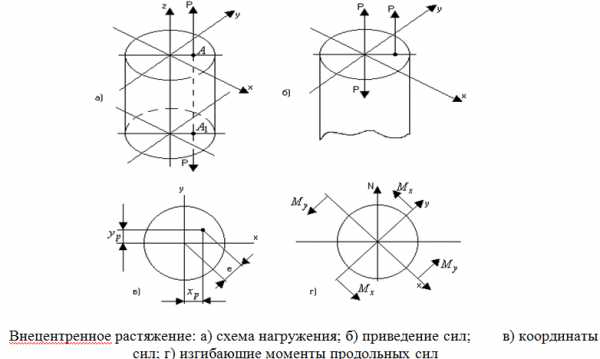
Эксцентриситет (е) линии действия силы:

В результате переноса получаем три силовых фактора: нормальная сила Р, изгибающий момент вокруг оси Х, М_х=Р^.уp и изгибающий момент М_у= – Р^.х_р. Нормальные напряжения будут определяться по формуле:

перепишем эти формулы в другом виде

Если площадь А вынести за скобки

 (1)

По этим формулам  можно вычислить напряжения в любой точке сечения.

Положение нулевой (нейтральной) линии определим, приравнивая (1) к нулю:

По этому уравнению можно определить отрезки, отсекаемые нулевой линией на осях координат. Обозначим эти отрезки через а_хи а_у. Положим а_х=0, получим:

 (2)

Нейтральная линия не проходит через ту четверть, где приложена сила Р, так как здесь знаки компоненты нормального напряжения одинаковы.

Очевидно, что если точка приложения силы будет передвигаться по прямой, параллельной одной из главных осей инерции, то нейтральная линия будет поворачиваться вокруг некоторой точки, лежащей на другой оси.

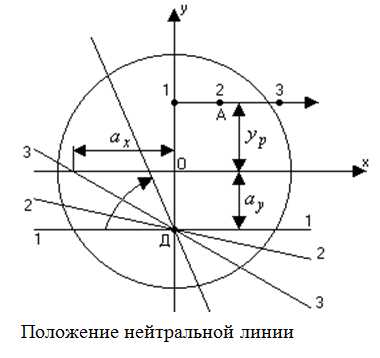
Если координата у_р=const, а а_хменяется, то нейтральная линия, меняя своё положение в сечении, все время проходит через точку Д на оси Y. Когда х_р=0 (точка 1 на оси у), то  нейтральная линия параллельна оси Х.

Если точка приложения силы будет перемещаться по прямой, наклонённой к обеим осям главных  моментов инерции сечения, то нейтральная линия опять-таки будет поворачиваться вокруг некоторой точки, но уже не лежащей в этом случае ни на одной из главных осей.

Нейтральная линия проходит через точку Н и поворачивается вокруг неё.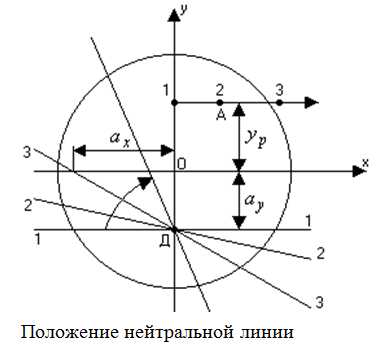

Ядро сечения

Из формул (2) видно, что с уменьшением  координат точки приложения силы  расстояния а_­уи а_х­ увеличиваются, то есть точки пересечения нейтральной линии с осями координат удаляются от центра. При некоторых значениях у_ри х_р нейтральная линия окажется за пределами сечения, тогда во всём сечении напряжения будут иметь один знак.

Хрупкие материалы, как известно, плохо работают на растяжение. Между тем, части сооружений подвергаются действию сжимающей нагрузки, нередко их делают из хрупких материалов. Для того, чтобы и при внецентренном приложении сжимающей нагрузки в материале  не возникало растягивающих напряжений, нужно ограничить величину эксцентриситета нагрузки, не выводить точку приложения за пределы некоторой области в сечении.

Область, расположенная вокруг центра сечения, в пределах которой должна находиться точка приложения продольной сжимающей или растягивающей силы, чтобы напряжения  в сечении были одного знака, называется ядром сечения:

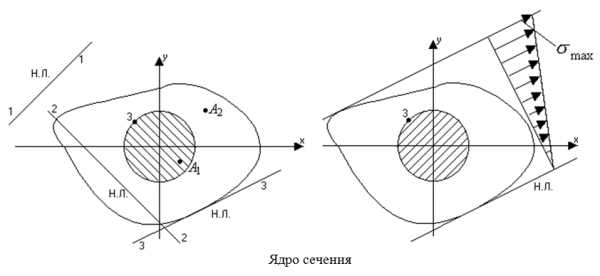
Границы ядра сечения определяются из (2).

prosopromat.ru

Растяжение и сжатие

Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплён в стене (закрепление «заделка») (рис. 30.)
Делим брус на участки закрепления.

Участком закрепления считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.
Расчёт начинаем со свободного конца бруса, чтобы не определять величины реакции в опорах.
Участок 1 :

Продольная сила положительна, участок 1 растянут. Участок 2:

=F. Продольная сила положительна, участок 2 растянут.
Участок .’
Продольная сила отрицательна, участок з сжат. Полученное значение равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис.31.).
Эпюра продольной силы строится только под брусом.

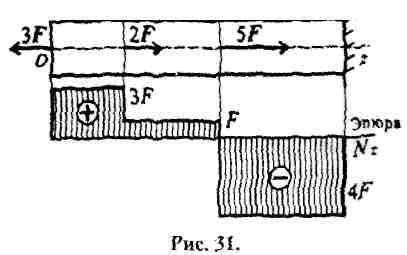
Эпюрой продольной силы называется график распределения продольной силы вдоль от бруса.
Ось эпюры параллельна продольной оси. Нулевая линия проводится тонкой линией. Значения чисел откладывают от оси, положительные — вверх, отрицательные вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Правило контроля: в месте приложения внешней силы на эпюре должен быть скачек на величину приложенной силы.
На эпюре проставляют значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и обводится поперёк оси.
Принцип смягчения граничных условий гласит: в точках тела, удалённых от мест нагрузки, модуль внутренних сил мало зависит от способа закрепления Опытный тамада на свадьбу по низкой цене. . Поэтому при решении задач не уточняют способ закрепления.

www.ostemex.ru