Cтержневые системы в сопромате

 

В сопромате рамой называют конструкцию, состоящую из стержней, которые работают, в основном, на изгиб и кручение. Рамы принято делить на плоские, плоско-пространственные и пространственные.

Плоской называется рама, у которой оси всех ее элементов и действующие нагрузки (включая реакции опор) лежат в одной плоскости. В этой же плоскости лежит одна из главных центральных осей каждого поперечного сечения.

Плоско-пространственной называется рама, оси всех элементов которой и одна из главных осей каждого поперечного сечения лежат в одной плоскости, а внешняя нагрузка — в перпендикулярной плоскости.

 

К пространственным относят все прочие виды рам.
Рамные конструкции, используемые в машиностроении, могут быть статически определимыми и статически неопределимыми.

 
Статически неопределимой называется такая рама, для которой опорные реакции и внутренние силовые факторы не могут быть найдены только из уравнений статики. При этом разность между числом неизвестных (реакций опор и внутренних силовых факторов) и числом независимых уравнений равновесия определяет степень статической неопределимости рамы.

Число связей системы, при котором достигается ее кинематическая неизменяемость, называется необходимым числом связей. Для плоских систем необходимое число связей равно трем, для пространственных — шести. Всякая связь сверх необходимых называется дополнительной. Эти дополнительные связи и обуславливают статическую неопределенность системы, т.е. число дополнительных связей равно степени статической неопределимости.

Связи, наложенные на раму, делят на внешние и внутренние.

Под внешними понимают такие связи, которые накладывают ограничения на перемещения всей системы как жесткого целого.
Под внутренними связями понимают ограничения, накладываемые на взаимные смещения элементов рамы. Поясним сказанное на примере плоской рамы.

 

Рис.4.1

Рама, изображенная на рис.4.1,а является статически определимой, так как на нее наложены в точке

а три связи, а внутренние силовые факторы в любом сечении могут быть определены но методу сечений. Заметим, что сечения B и C имеют возможность взаимного поворота и смещений по горизонтали и вертикали.

 Рама на рис.4.1,5 отличается от рамы на рис.4.1,а тем, что в точке d наложены еще две внешние связи. Общее число внешних связей стало равным 5, причем любые две из них могут рассматриваться как дополнительные. Кроме того, сечения В и С теперь не имеют возможности взаимного поворота и смещений но горизонтали и вертикали, так как в замкнутом контуре добавлены еще три внутренние связи, запрещающие взаимный поворот, взаимные горизонтальное и вертикальное перемещения. Таким образом, данная рама пять раз статически неопределима: два раза внешне и три раза внутренне.

Для решения статически неопределимых задач часто используется метод сил, заключающийся в замене дополнительных связей неизвестными силовыми факторами, которые определяются из условия отсутствия перемещений в направлении отброшенных связей. После нахождения неизвестных силовых факторов рама становится статически определимой, и внутренние силовые факторы определяются по методу сечений.

Перемещения в статически неопределимых системах так же, как и в статически определимых, могут быть определены по методу Мора — Верещагина перемножением эпюры от заданных сил на эпюру от единичного фактора, приложенного в направлении искомого перемещения с последующим делением результата перемножения на соответствующую жесткость. Если единичный фактор прикладывается к заданной статически неопределимой системе, то вновь возникает вопрос о раскрытии статической неопределимости. Однако этого можно избежать, если определять перемещения не в заданной, а в основной системе (а она статически определима), т.к. перемещения в заданной и основной системах одинаковы. Для определения перемещения можно использовать любую основную систему.

Для проверки полученного решения статически неопределимой задачи (суммарной эпюры) можно воспользоваться несколькими способами:

1. Решать задачу заново, используя другую основную систему. Это наиболее трудоемкий способ проверки.

 

1. Определить перемещение, заведомо равное нулю. С этой целью нужно перемножить суммарную эпюру на эпюру от единичного фактора, приложенного к основной системе в этом направлении. В частности, перемножение суммарной эпюры на любую единичную, использованную при раскрытии статической неопределенности, должно дать результат, равный нулю.

 

1. Перемещения одних и тех же сечений (абсолютные или взаимные), вычисленные в различных основных системах, должны быть равными.

funnystudy.ru

Глава 7. Статически неопределимые стержневые системы

7.1. Введение

Под стержневой системой в общем случае понимается любая конструкция, состоящая из элементов имеющих форму бруса. Стержневые системы принято разделять на статически определимые и статически неопределимые. В статически определимых системах все усилия определяются только с помощью уравнений равновесия. В статически неопределимых системах для определения усилий уравнений статики недостаточно.

7.2. Классификация стержневых систем. Системы статической неопределимости

Стержневые системы можно разделить на три группы: плоские; плоскопространственные; пространственные. Рассмотрим только плоские системы. В них все стержни и внешние силы лежат в одной плоскости. К ним относятся: фермы, балки, рамы (рис. 7.1).

Рис. 7.1

Ферма (рис.7.1, а) — стержневая конструкция, элементы которой работают преимущественно на продольную силу. Нагрузка прикладывается в узлах фермы. Балка — прямой брус, работающий на изгиб (рис. 7.1, б). Рама — стержневая система, элементы которой работают преимущественно на изгиб (рис. 7.1, в).

Степень статической неопределимости — число “лишних связей”, удаление которых делают систему статически определимой и геометрически (кинематически) неизменяемой. Геометрически неизменяемой называют систему, изменение формы которой происходит только в связи с деформацией ее элементов.

Известно, что положение бруса в пространстве определяется шестью независимыми координатами, т.е. брус обладает шестью степенями свободы.

На брус могут быть наложены связи, фиксирующие его положение на плоскости (рис.7.2). Если на левый конец балки наложено условие, запрещающее вертикальные перемещения (рис. 7.2, а), то в этой точке имеется одна внешняя связь. Если запрещено как вертикальное, так и горизонтальное, то наложены две связи (рис. 7.2, б). Заделка полностью фиксирует положение стержня в плоскости (рис. 7.2, в).

Рис. 7.2

Примеры определения степени статической неопределимости.

Ферма (рис.7.1,а)

,

где — степень статической неопределимости;

—число стержней, включая и опорные;

—число узлов фермы.

. Следовательно, данная ферма один раз статически неопределимая.

Балка (рис. 7.1, б)

,

где — число опорных реакций, тогда, т.е. данная балка два раза статически неопределимая.

Рама (рис. 7.1,в)

,

где — число замкнутых контуров;

—число врезанных шарниров.

Первая рама внешним образом статически неопределимая, для нее . Вторая рама имеет замкнутый контур и врезанный шарнир, для нее.

7.3. Метод сил. Выбор основной системы

Одним из наиболее распространенных методов расчета статически неопределимых систем (С.Н.С.) является метод сил. Он заключается в том, что заданная С.Н.С. освобождается от «лишних» связей, а их действие заменяются неизвестными силами и моментами. Величина их подбирается так, чтобы перемещения в основной (эквивалентной) системе были равны перемещениям в заданной системе. Основной называется статически определимая, геометрически (кинематически) неизменяемая система, полученная из заданной путем отбрасывания лишних связей и заданных нагрузок. Как правило, для одной статически неопределимой системы можно подобрать сколько угодно основных систем.

Рассмотрим плоскую раму (рис. 7.3). Степень статической неопределенности «» равно. Выберем несколько вариантов основных систем, отбрасывая каждый раз семь «лишних» связей. Например, для данной рамы можно предложить основные системы а), б), ………., которые получены путем отбрасывания семи связей в различных комбинациях.

Рис. 7.3

Эквивалентная система — получается из основной, путем загружения неизвестными реакциями отброшенных связей, а также заданной внешней нагрузкой (рис. 7.4).

Рис. 7.4

Там, где запрещены линейные перемещения, приложены силы, где угловые — моменты, где взаимные — взаимные моменты и силы.

Теперь остается составить уравнения для определения неизвестных .

studfiles.net

Расчет стержневой системы на прочность

Задача

Стержневая система, состоящая из трех одинаковых стержней разной длины, нагружена сосредоточенной силой F=100кН приложенной горизонтально в точке B.

Все стержни системы состоят из двух равнополочных уголков 80×8мм.

Допустимые напряжения для материала стержней:

• на растяжение [σ_р]=50МПа,
• на сжатие [σ_сж]=120МПа.

Требуется: проверить стержневую систему на прочность.

Решение

Как известно, система считается прочной, только если прочны все составляющие ее элементы.

Поэтому в данной задаче, для проверки на прочность требуется определить напряжения во всех трех стержнях системы и сравнить полученные значения с соответствующими допустимыми.

Другими словами, напряжения в растягиваемых стержнях должны быть не больше допустимых на растяжение, а в сжимаемых соответственно не больше [σ_сж].

Под действием внешней силы, стержни, очевидно, испытывают продольное нагружение (растяжение либо сжатие), следовательно, для расчета напряжений используем соответствующие условия прочности:

Площадь поперечного сечения A всех стержней одинакова. Рассчитаем ее.

Для этого по сортаменту прокатной стали для равнополочных уголков найдем площадь сечения одного уголка и удвоим ее значение (т.к. стержни состоят из двух уголков):

Внутренние продольные усилия в стержнях составляют:

N_AB=125кН (сжатие)
N_BC=75кН (растяжение)
N_AC=100кН (растяжение)

Расчет внутренних сил в стержнях данной системы подробно показан здесь.

Осталось рассчитать напряжения в стержнях и сравнить их с соответствующими допустимыми значениями.

Так как напряжения во всех стержнях системы не превышают соответствующих допустимых значений система является прочной.

Другие примеры решения задач >

isopromat.ru

Внутренние силы в стержневых системах

Задача

Стержневая система, состоящая из трех стержней (AB, BC и AC) соединенных между собой шарнирно, нагружена сосредоточенной силой F=100кН приложенной горизонтально в точке B.

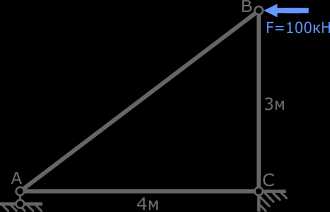
Требуется определить величину и знак продольных усилий в стержнях системы.

Решение

Под действием заданной внешней силы стержни, очевидно, испытывают продольное нагружение (растяжение или сжатие), следовательно, в них возникают внутренние продольные силы N.

Есть все основания полагать, что внутренние силы в стержнях могут отличаться, причем как по величине, так и по знаку.

Для их расчета вычертим заданную схему в масштабе, определим длину стержня AB, покажем систему координат x-y и обозначим любой из углов (например, A) буквой α.

Так как данная система статически определима, внутренние усилия определим методом сечений из условия ее статичности.

Зная, что вся система неподвижна, можно утверждать, что будет также неподвижным любой ее фрагмент, включая шарнирные узлы A, B и C.

Начнем с узла B к которому приложена заданная сила F.

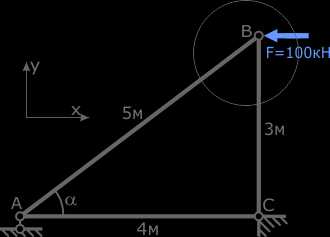
Мысленно вырежем область точки B системы и рассмотрим ее равновесие, заменив отброшенную часть продольными внутренними силами.

Вдоль стержней AB и BC покажем линии действия сил N_AB и N_BC соответственно.

На рисунке показаны их истинные направления.

Для определения двух неизвестных сил требуется два уравнения.

Запишем систему уравнений статики для рассматриваемого фрагмента системы.

Отсюда находим величину внутренних сил:

Обратите внимание на знаки найденных сил. Положительная величина здесь указывает лишь на то, что мы изначально направили их верно.

А вот направление сил показывает их физический смысл:

Внутренняя сила N_AB является сжимающей, а N_BC – растягивающей, что говорит о том что стержень AB сжимается а BC соответственно растягивается.

Внутреннее усилие в стержне AC можно определить, рассматривая один из оставшихся узлов, например A.

Заметим, что ранее найденное внутреннее усилие N_AB на данном фрагменте тоже показываем сжимающим.

Здесь уже достаточно одного уравнения

откуда

Внутренняя сила в стержне AC — растягивающая.

Все усилия в стержнях системы определены.

Проверка стержневой системы на прочность >

Другие примеры решения задач >

isopromat.ru

Расчет стержневой системы при растяжении (сжатии)

Стержневые системы в сопромате могут быть статически определимыми и статически неопределимыми.

Статически определимая стержневая система

Для успешного решения такой задачи понадобятся лишь знания статики, изучаемой в курсе теоретической механики. Обычно в задаче дана абсолютно жесткая балка, то есть не деформируемая, какие бы силы к ней не прикладывались. Эта балка закреплена с помощью шарнира, либо опоры, либо стержней. В этой задаче обязательно будут определяться внутренние продольные усилия в стержнях, необходимые для решения задачи. Усилия находятся из уравнений статики.

Что может требоваться сделать в этой задаче?

1. Подобрать размер поперечного сечения для стержня.
2. Определить удлинение или укорочение стержня.
3. Вычислять напряжение в поперечных сечениях стержня.
4. Определить коэффициент запаса прочности для стержня.
5. Определить перемещение жесткой балки.

Статически неопределимая стержневая система.

В этой задаче сначала придется раскрыть статическую неопределимость. Как правило, дана система один раз статически неопределимая. Для нее составляется дополнительно уравнение совместности деформации. Решая вместе, это уравнение с уравнением статики находят продольные усилия в стержнях. А затем уже находят то, что требуется в условии задачи, будь это напряжение в стержнях или удлинение.

ssopromat.ru

Сопротивление материалов – заочно Примеры решения задач Задача 1. Стержневая система

 

Два стальных стержня, шарнирно соединенных в точке А, находятся под действием силы Р .Первый стержень имеет длину с и площадь поперечного сечения F, второй длину a и площадь 2F.

Требуется найти: 1) величину нормальный напряжений, действующих в стержнях. 2) абсолютную и относительную деформации стержней. Исходные данные: Р = 130 кН,с = 1,5 м,а = 2 м,F = 12 см^2. Решение. Стержни прикреплены к стене и соединены между собой шарнирами (точках В ,С иА ). Шарниры предполагаются идеальными, т. е. такими, трение в которых отсутствует. НагрузкаР приложена в узлеА . Поэтому стержни будут испытывать только продольные (растягивающие или сжимающие) усилия, т.е. в поперечных сечениях стержней возникает только один внутренний силовой фактор — продольная силаN . 1. Для определения усилий используем метод сечений .Рассечем стержни,отбросим часть, содержащую опорные точки.Заменяя действие отброшенной части, приложим в сечениях неизвестные продольные усилияN 1 иN 2 .Полагая оба стержня растянутыми, направим усилияN 1 , иN 2 так, как показано на рис.(1.2).

Уравновесим отсеченную часть. Для сходящейся плоской системы сил можно составить два независимых уравнения равновесия — в виде сумм проекции всех сил на две осих иу (рис. 1.2).

Тогда уравнения равновесия представятся в виде:

Для определения ирассмотрим стержневую систему(рис.1.1). Из точкиА опустим перпендикулярА D на прямуюВС , получим два прямоугольных треугольникаABD иАDC .

Из треугольника ABD определимAD : м. Из треугольника AD С получим: , . Теперь определим неизвестные усилия N 1 , иN 2 из системы двух линейных уравнений(1.1). Перепишем уравнения в следующем виде:

(1.2)

Решим систему (1.2), используя, например, метод Крамера.

 

2. Определим нормальные напряжения, действующие в стержнях.

Напряжения в стержнях определяются по формуле

Для первогостержня

МПа,

для второгостержня

МПа,

3. Найдем абсолютную и относительную деформации стержней.

Абсолютная деформация стержня длиной lопределяется из закона Гука:

Абсолютная деформация первого стержня

м.

Абсолютная деформация второго стержня

м.

Относительную деформацию определим из закона Гука

.

Относительная деформация первого стержня

,

относительная деформация второго стержня

.

Литература: 1 § 1.2 – 8.2

Задача 2. Статически неопределимая стержневая система

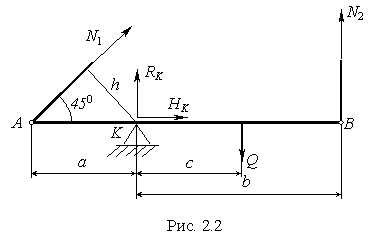
Абсолютно жесткий брус шарнирно закреплен на неподвижной опоре и поддерживается двумя стержнями (рис. 2.1).

Требуется найти: 1)  усилия и напряжения в стержнях, выразив их через силу ; 2)  допускаемую нагрузку [ ], приравняв большее из напряжений в двух стержнях допускаемому напряжению= 160 МПа; 3)  предельную грузоподъемность системы Q пр и допускаемую нагрузку [Q пр ], если предел текучестит = 240 МПа и запас прочностиn = 1,5; 4) сравнить величины допускаемых нагрузок [ Q ] и [Q пр ]. Исходные данные: а = 2,1 м,b = 2,4 м,с = 1,5 м,F = 12см 2 .

Решение.

1. Рассечем стержни АА 1 иВВ 1 , усилияN 1 , иN 2 в стержняхАА 1 , иВВ 1 , направим вдоль осей стержней как показано на рис.2.2. Реакция опорыК имеет горизонтальную составляющуюН К , и вертикальную составляющуюR К , так как эта опора препятствует горизонтальному и вертикальному перемещению точкиК бруса. Таким образом, всего имеется четыре неизвестные реакции (рис.2.2), а независимых уравнений равновесия для плоской системы сил можно составить всего три. Следовательно, данная система один раз статически неопределима Статически неопределимые системы рассчитывают путем совместного решения уравнений, полученных в результате рассмотрения статической, геометрической и физической сторон задачи.

Статическая сторона задачи. По условию задачи необходимо определить усилияN 1 иN 2 , a в определении реакцийН К иR К нет необходимости. Поэтому достаточно из трех возможных уравнений равновесия использовать одно, в которое не входили бы реакцияН К иR К . Таким является уравнение суммы моментов всех сил относительно шарнираК :

где (м).

Подставляя в уравнение значения h ,b ис , получим

(2.1)

Геометрическая сторона задачи . Под действием внешней силы абсолютно жесткий брус повернется вокруг точкиК . ШарнирыА иВ после деформации переходят в положениеА 2 иВ 2 соответственно, т.е. перемещаются по вертикали на величины1 и2(рис.2.3).

откуда

или с учетом равенства (2.2)

(2.3)

Физическая сторона задачи . Используя закон Гука, записанный для абсолютных деформаций, выразим деформации стержней через усилия

(2.4)

Подставим выражения (2.3) в условие (2.4)

после сокращения получим

Решаем совместно уравнения статики (2.1) и уравнение(2.5):

Определяем напряжения в стержнях 1 и 2:

Па,

Па.

2. Найдем допускаемую нагрузку [ ], приравняв большее по модулю напряжение допускаемому напряжению= 160 МПа.

,

откуда

Н.

3. Найдем нагрузки предельную — Q пр и допускаемую — [Q пр ], если предел текучестиТ = 240 МПа и запас прочностиn = 1,5.

При увеличении нагрузки Q c верх значения [Q ] напряжения в обоих стержнях сначала увеличивается прямо пропорционально нагрузке. При увеличении нагрузки до некоторой величиныQ > [ Q ] напряжение2 во втором стержне достигают предела текучестиТ , а усилиеN 2 — предельного значенияN 2пр =Т ·F . При этом напряжение1 сжатия в первом стержне остается меньшеТ . При дальнейшем увеличении нагрузки, напряжения во втором стержне остаются постоянными, равными пределу текучести, а в первом — возрастают, пока также не достигаютТ , усилиеN 1 при этом равно

N 1пр = –Т ·2F . Это состояние системы называется предельным, соответствующим исчерпанию ее грузоподъемности. Дальнейшее, даже незначительное увеличение нагрузки связано с весьма большими деформациями системы. Величину силыQ , вызываюшую предельное состояние, обозначаютQ пр и называют предельной силой.

Для вычисления Q пр подставим в уравнение (2.1) значения предельных продольных усилий, возникающих в стержняхN 1 =N 1пр ,N 2 =N 2пр :

откуда

Н.

4. Сравним величины допускаемых нагрузок [ Q ] и [ Q пр ]

= 1,38.

Литература: 1, §9.2.

studfiles.net

Статически неопределимые системы | Лекции и примеры решения задач механики

Статически неопределимыми называют системы, в которых для определения опорных реакций либо внутренних усилий одних только уравнений статики недостаточно.

Статическая неопределимость возникает из-за наличия дополнительных или «лишних» связей.

Здесь под словом «лишние» понимаются дополнительные опоры (связи) добавление которых не влияет на геометрическую неизменяемость системы в целом.

Дополнительные опоры увеличивают прочность и жесткость систем, что позволяет делать их более экономичными.

Степень статической неопределимости систем

Степень статической неопределимости n определяется по формуле:

n=k-m

где,
k – количество неизвестных усилий (реакций связи),
m – количество уравнений равновесия которые можно составить для данной системы.

Системы, для которых n=1 называют однажды статически неопределимыми, n=2 – дважды СН и т.д.

Примеры статически неопределимых систем

В качестве примера рассмотрим следующий случай:

Консольная балка, закрепленная только в жесткой заделке – статически определима, так как в опоре данной схемы могут иметь место не более трех опорных реакций (вертикальная и горизонтальная силы и момент).

Как известно из курса теоретической механики для плоской системы сил можно составить только три уравнения равновесия. Трех уравнений для определения трех неизвестных вполне достаточно.

Теперь, если добавим к рассматриваемой схеме еще одну опору, например шарнирно-подвижную, то балка становится статически неопределимой, так как количество неизвестных связей увеличилось до четырех, а уравнений равновесия по-прежнему можно составить только три.

В данном случае для расчета опорных реакций не хватает еще одного уравнения, т.е. система один раз (однажды) статически неопределима.

Если к данной системе последовательно добавлять опоры, то степень неопределимости также будет возрастать.

В таких случаях для расчета величины и направления неизвестных усилий потребуются дополнительные уравнения.

Другие примеры СНС

Примеры однажды статически неопределимых систем (n=1):

Статически неопределимый стержень

Трехопорная балка

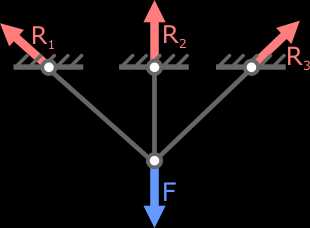
Статически неопределимая стержневая система

Раскрытие статической неопределимости

Расчет усилий в лишних связях называется раскрытием статической неопределимости системы.

Существует несколько способов раскрытия статической неопределимости, принцип которых основан на:

1. равенстве нулю соответствующих перемещений точек системы на опорах;
2. зависимости (совместности) деформаций элементов системы.

Наиболее универсальным из них является метод сил.

Примеры решения задач >>

isopromat.ru