Сопромат расчет стержневой системы

Содержание

Расчет статически определимой стержневой системы. Подбор сечения.

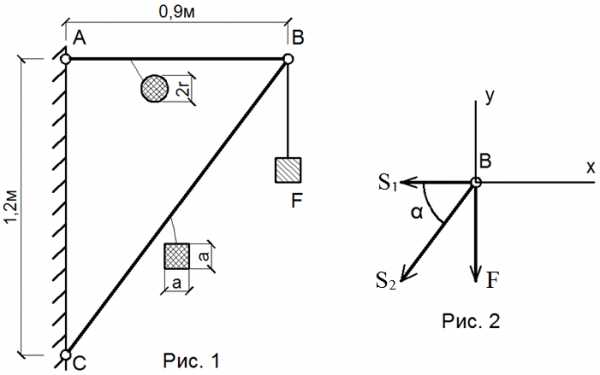
Груз весом F=10кН (рис. 1) удерживается с помощью стального стержня AB круглого сечения (расчетное сопротивление материала Rс=180МПа, допускаемое удлинение [Δc]=1мм, модуль упругости Eс=200000Мпа) и деревянной подпорки BC квадратного сечения (расчетное сопротивление материала Rд=4МПа, допускаемое удлинение [Δд]=2мм, модуль упругости Eд=10000Мпа). Из условий прочности и жесткости подобрать размеры поперечных сечений стержней (r и a).

Решение.

Рассмотрим равновесие узла А (рис. 2). Составим два уравнения равновесия

Здесь

Из уравнений (1) найдем усилия в стержнях системы

Первый стержень растянут, второй сжат. Запишем для стального стержня условия прочности и жёсткости

Из условий (2) получим

Из двух значений выбираем наибольшее

Аналогично подберем сечение деревянной распорки. Условия прочности и жесткости для неё будут иметь вид

Отсюда найдем

Выбирая наибольшее значение, получим

Проверим выполнение условий прочности и жесткости для стального стержня

и деревянной распорки

Условия прочности и жесткости выполняются для обоих стержней.

Замечание. Распорка сжата, поэтому для неё необходимо выполнить проверку на устойчивость.

sopromat.pro

Уфимский государственный авиационный — Расчет стержневых систем на прочность и жесткость

Расчет стержневых систем на прочность и жесткость
скачать (442.2 kb.)

Доступные файлы (1):

содержание

Курсовая по сопромату.doc

Реклама MarketGid:
Уфимский государственный авиационный

технический университет

Кафедра сопротивления материалов

КУРСОВАЯ РАБОТА

по сопротивлению материалов

Тема: расчет стержневых систем на прочность

и жесткость

	Должность / группа	Ф. И. О.	Дата	Подпись
Выполнил
Проверил
Принял

УФА 2007

СОДЕРЖАНИЕ

1.1. Выбор материала и допускаемых напряжений. 3

1.1.1. Расчет физико-химических характеристик материала. 3

1.1.2. Расчет допускаемых напряжений. 3

1.2.1. Построение эпюры продольных сил. 4

1.2.2. Построение эпюры напряжений. 5

1.2.3. Расчет на прочность. Подбор сечения. 5

1.3.1. Построение эпюр продольных сил и перемещений. 6

1.3.2. Расчет на жесткость. 8

1.4. Расчет на прочность статически неопределимой стержневой системы при растяжении – сжатии. 9

1.4.1. Уравнения равновесия. 9

1.4.2. Уравнения совместности деформаций. 9

1.4.3. Физические уравнения. 10

1.4.4. Расчет усилий в стержнях. 10

1.4.5. Расчет на прочность. 10

2.1. Проектировочный расчет на прочность ступенчатого стержня. 11

2.1.1. Построение эпюры крутящих моментов. 11

2.1.2. Построение эпюры напряжений. 12

2.1.3. Расчет на прочность. Подбор сечения. 13

2.2. Расчет на жесткость стержня постоянного сечения. 14

2.2.1. Построение эпюры углов закручивания. 14

2.2.2. Расчет на жесткость. 15

3.1. Проверочный расчет балки из прокатных профилей. 16

3.1.1. Расчет геометрических характеристик сечения. 16

3.1.2. Построение эпюр внутренних силовых факторов. 16

3.1.3. Расчет на прочность. 17

3.3. Проектировочный расчет на прочность плоской рамы. 21

3.3.1. Построение эпюр внутренних силовых факторов. 21

3.3.2. Расчет на прочность. 22

1.1.1. Расчет физико-химических характеристик материала.

Диаграмма растяжения стали 30ХГСА изображена на рис. 1.1. Образец длиной l₀=60мм и диаметром d₀=6мм разрушился с образованием шейки d₁=4,45мм, что свидетельствует о том, что материал пластичный.

Площадь поперечного сечения

образца до испытаний:

;

после разрушения:

Относительное остаточное удлинение:

Относительное остаточное сужение:

Определим основные характеристики прочности.

Предел пропорциональности:

Условный предел текучести:

Предел прочности (временное сопротивление σ_вр)

^
Допускаемое напряжение [] выбираем, как некоторую долю предельного напряжения _пред, то есть

где n – коэффициент запаса прочности.

Рекомендуемые значения n = 1,5  2,5. Примем n =1,5, тогда

.
^
Для ступенчатого стержня, представленного на рис. 1.2, необходимо построить эпюру продольных сил, эпюру напряжений, отнесенную к площади А₀, найти А₀ из условия прочности.

^
Составим уравнение равновесия системы (рис. 1.3 а):

откуда

Разобьем стержень на три участка AB, BC и CD, проведем на каждом из них произвольные сечения 1-1, 2-2, 3-3 с координатами z₁, z₂, z₃(рис 1.3 а).

Участок AB (0z₁l₂) (рис 1.4 а). Из равновесия оставленной верхней части следует, что

На участке ВС (l₁z₂2l₂) (рис 1.4 б). Из условия равновесия получим

На участке СD (0z₃l₃) (рис 1.4 в). Отбросим нижнюю часть, её действие заменим продольной силой N₃. Из уравнения равновесия следует

По полученным данным строим эпюру ЭN (рис. 1.3 б). Эпюра показывает, что на участке АВ – растяжение, а на участках ВС и СD – сжатие. Скачок в сечении А равен силе Р₁=35кН, в сечении D – продольной силе N₃.

^
Нормальные напряжения (z) распределяются равномерно по сечению:

где N(z) – продольная сила, A(z) – площадь поперечного сечения.

Для определения положения опасного сечения стержня, в котором возникают максимальные напряжения, определим напряжения в долях 1/А₀.

Участок АВ (0z₁l₂), нормальные напряжения

На участке ВС (l₁z₂2l₂):

Участок СD (0z₃l₃):

По полученным данным строим эпюру ЭА₀(рис. 1.3 в).

^
По эпюре напряжений видно, что опасным является сечение В

Условие прочности при растяжении-сжатии имеет вид:

где [] – допускаемое напряжение, которое определено выше для материала Ст30 и равно []=563,8 Мпа.

Тогда условие прочности примет вид

откуда А₀:

Определим напряжения, действующие в сечениях при выбранном значении А₀.

Участок АВ:

Участок ВС:

Участок CD:

По полученным данным строим эпюру действующих в стержне нормальных напряжений Э (рис. 1.3 г).

^
Для стержня из стали 30Х, площадью поперечного сечения А=8см², представленного на рис. 1.5, необходимо построить эпюры продольных сил и осевых перемещений, выполнить расчет на жесткость.

^
Построение эпюры продольных сил. Направим вдоль оси стержня ось z (рис.1.5). Составим уравнение равновесия системы:

Разобьем стержень на 3 участка АВ, ВС и CD, проведем на каждом из них произвольные сечения 1-1, 2-2, 3-3 с заданными координатами этих сечений z₁, z₂, z₃.

Участок АВ (0z₁l₁):

Участок ВС (0z₂l₂):

На участке DC (0z₃l₃) отбросим левую часть, ее действие заменим продольной силой N₃:

По полученным данным строим эпюру ЭN (рис. 1.5).
Построение эпюры перемещений. Запишем уравнения для перемещений w(z) сечений, считая площади сечений известными:

где w₀ – перемещение в начале участка, определяемое начальными условиями; l(z) – удлинение участка (абсолютная деформация участка стержня).

Если продольная сила N(z) зависит от координат сечения z, то:

Для стали 30Х Е=2*10⁵ МПа. В расчетах примем жесткость сечения при растяжении-сжатии ЕА=2*10⁵*8*10²=16*10⁷Н=16*10⁴кН.

Рассмотрим участок АВ (0z₁l₁):

Функция w(z₁) – квадратичная парабола. Так как в сечении А – заделка, то w₀=0 и w₁=0,0026мм. Так как в пределах участка АВ продольная сила N₁ не меняет знака, то парабола в пределах участка не имеет экстремума.

Участок ВС (0z₂l₂):

Функция w(z₂) – квадратичная парабола. Так как в пределах участка ВС продольная сила N₂ не меняет знака, то парабола в пределах участка не имеет экстремума.

На участке DC (0z₃l₃):

Функция w(z₁) – линейная.

По полученным данным строим эпюру Эw (рис. 1.5).

^
Условие жесткости при растяжении-сжатии

где L – удлинение стержня, [l] – допускаемое удлинение. В данном случае условие жесткости должно выполняться для участка CD:

Величина [l]=0,001L принимается в долях от суммарной длины L,

Запишем условие жесткости:

Условие жесткости выполняется.
^
Стержневая система, состоящая из жесткого стержня АЕ и двух других стержней ВС и ВК, нагружена силой Р=35кН (рис 1.6). Определить коэффициент запаса прочности стержневой системы, если =45⁰, l₁=0,6м, l₂=0,3м, l₃=0,6м, А=800мм², k=1,2, материал – сталь 30Х с пределом текучести _т=845,7МПа.

При известной площади сечения выполняется проверочный расчет на прочность по напряжениям. Величина фактического коэффициента запаса где _пред– предельное значение напряжения для заданного материала. _max – максимальное рабочее напряжение, возникающее в заданной стержневой системе от приложенных нагрузок. Сталь 30Х пластичный материал, тогда _пред=_т, следовательно

^
Составим уравнения статического равновесия (рис. 1.7):

Для дальнейшего решения применяем уравнение (3), так как реакции заделки А для оценки прочности не нужны. Преобразуем (3), подставляя значения углов и длин, получим

Полученное уравнение содержит две неизвестные величины N_CB и N_DB.Сопоставляем дополнительное уравнение, которое вытекает из условия совместности перемещений.

^
Составим уравнения совместимости деформаций (рис. 1.8): l_CB=B’B’₁; l_DB=B’B’₂. Из BB’B’₁ имеем BB’=B’B’₁/sin2; из BB’B’₂ получим BB’=B’B’₂/sin, приравняем отрезки

подставляя данные углы, получим l_DB=0,7l_CB_(5).

^
Составим физические уравнения. По закону Гука

Подставляя в уравнение совместности перемещений, с учетом длин стержней, соотношений площадей и материала, получим

умножим на ЕА и подставим данные

после вычислений получим

. (6)

^
Статическое уравнение (4) и дополнительно преобразованное уравнение (6) совместности перемещений дают систему разрешающих уравнений:

Из решения системы уравнений получим N_DB=1,11P; N_CB=3,77P.

^
Напряжения в стернях

Видно, что максимальные напряжения возникают в стержне СВ:

_max_{=_св=164,9МПа.}

Условие прочности имеет вид

_max[]=_т/n,

где N – коэффициент запаса прочности. Для сталей n=1,52,5, примем n=2. Тогда допускаемые напряжения []=845,7/2=422,85МПа.

Условие прочности для заданной стержневой системы выполняется:

_max=164,9МПа<[]=422,85МПа.
^
Для ступенчатого стержня из стали 30Х, представленного на рис. 2.1, необходимо построить эпюру крутящих моментов, эпюру условных касательных напряжений как функцию параметра сечения d, из условия прочности найти искомое значение d.

^
Направим ось z вдоль оси стержня (рис. 2.2). Из условия равновесия находим значение М₄:

Участок AB (0z₁l₁) (рис. 2.3 а):

Участок BC (0z₂l₂) (рис. 2.3 б):

Участок BC (0z₃l₃) (рис. 2.3 в):

По полученным данным строим эпюру крутящих моментов ЭМ (рис. 2.2).

^
Наибольшие напряжения при кручении возникают на внешних волокнах и определяются как

где — полярный момент сопротивления, I_p – полярный момент инерции сечения, r_max_{– максимальный радиус. Определим геометрические характеристики сечений:}

Участок АВ:

Участок ВС:

Участок CD:

Определим опасное сечение, в котором возникают наибольшие напряжения, в долях 1/d³:

Участок AB (0z₁l₁):

Участок BC (0z₂l₂):

Участок CD (0z₃l₃):

По полученным данным строим Эd³ (рис. 2.2).

^
На эпюре Эd³ видно, что опасными являются сечения на участке CD, де действуют наибольшие напряжения.

Условие прочности при кручении имеет вид:

где [] – допускаемое касательное напряжение.

Примем для материала Ст30 []=0,5[]=0,5*563,8=281,9МПа.

Тогда условие прочности примет вид:

Из условия прочности находим оптимальное значение диаметра:

Примем (из ряда Ra40 по ГОСТ 6636-69) d=48мм.

Определим напряжения, действующие в сечениях при выбранном значении d.

Участок AB:

Участок BC:

Участок CD:

По полученным данным строим эпюру действующих на валу касательных напряжений Э (рис. 2.2).

^
Для стержня постоянного сечения (рис. 2.4) необходимо построить эпюру углов закручивания и из условия жесткости найти искомое значение диаметра стержня d. Материал стержня – сталь, G=80Гпа.
^
Разобьем стержень на участки AB и BC (рис. 2.5). В пределах каждого участка возьмем произвольные сечения z₁ и z₂ соответственно.

Из условия равновесия определим момент в заделке:

Участок AB (0z₁l₁+ l₂):

Участок BC (l₁+ l₂z₂ l₁+ l₂+l₃):

Находим углы закручивания в долях 1/GI_p.

На участке АВ:

ввиду наличия заделки в точке В.

Функцией угла закручивания на участке АВ является парабола, вторая производная от которой отрицательна, следовательно, парабола выпуклая.

На участке ВС:

По полученным данным строим эпюру углов закручивания Э в долях от GI_p_{(рис. 2.5).}

^
По условию жесткости, максимальный угол поворота не должен превышать допускаемый []=0,001рад/м, то есть _max[]. Из эпюры углов поворота, построенной в долях от GI_p видно, что максимальный угол поворота находится в сечении А Полярный момент инерции сечения откуда найдем диаметр стержня:

Примем (из ряда Ra40 по ГОСТ 6636-69) d=160мм.

Окончательно рассчитывая углы поворота в каждом сечении, получаем _А=-0,32*10^-3рад/м; _В=0 рад/м; _С=0,24*10^-3рад/м;

По полученным данным строим эпюру углов закручивания Э (рис .2.5).
^

3.1.1. Расчет геометрических характеристик сечения.

Исходные данные для расчета балки из прокатных профилей показаны на рис. 3.1. Сечение балки изображено на рис. 3.2.

Рассчитаем геометрические характеристики сечения. Осевой момент инерции для двутавра профиля №20 I_x_{_I=115см⁴ (по ГОСТ 8240-56).}

Осевой момент сопротивления W_xI=W_yI=23,1см³.

Осевой момент инерции для равнобокого уголка профиля №9 I_x_{_L=82,1см⁴ (по ГОСТ 8240-56).}

Для составного сечения:

^
Найдем реакцию в заделке D (рис. 3.1):

Построим эпюры перерезывающих сил и изгибающих моментов. Возьмем произвольное сечение на первом участке DC (0z₁l₃). Запишем уравнения для перерезывающей силы и изгибающего момента в произвольном сечении в пределах этого участка и рассчитаем их значения в характерных точках:

Возьмем произвольное сечение на первом участке CB (0z₂l₂). На данном участке:

Для участка ВА (0z₃l₁), уравнения имеют вид:

^
Материал двутавра и уголков Ст30. Допускаемые напряжения []=282МПа. Рассчитаем максимальные напряжения, возникающие в балке, они находятся в сечении, где изгибающий момент достигает наибольшего значения M_max=7,92кНм:

Условие прочности имеет вид _max[]. Условие прочности не выполняется _max=342,9МПа > []=282МПа. Необходимо взять профиль больших размеров. Для этого, исходя из условия прочности, определим необходимое минимальное значение осевого момента сопротивления:

Выберем двутавр – ближайший из ряда двутавр №22 W_x=28,6см³, тогда Откуда максимальные напряжения

— условие прочности выполняется.
^

Исходные данные и расчетная схема балки из прокатных профилей представлена на рис. 3.3. Возьмем произвольные сечения z₁, z₂ и z₃, как показано на рисунке. При это продлим распределенную нагрузку на участке АС до конца балки, а ее действие на участке CD компенсируем аналогичной распределенной нагрузкой противоположного знака (выделены на рисунке серым цветом).

Участок АВ (0z₁l₁):

Участок ВC (l₁+z₂l₁+ l₂):

Участок CD (l₁+ l₂+z₃l₁+ l₂+l₃):

Ввиду заделки в точке D ₃(l₁+ l₂+l₃)=0:

y₃(l₁+ l₂+l₃)=0:

Углы закручивания на участках BC и CD на длине z=l₁+l₂должны быть равны –

₂(l₁+ l₂)=₃(l₁+ l₂):

Прогибы на участках BC и CD на длине z=l₁+l₂также должны быть равны –

y₂(l₁+ l₂)=y₃(l₁+ l₂):

Углы закручивания на участках AB и BC на длине z=l₁должны быть равны –

₁(l₁)=₂(l₁):

Прогибы на участках AB и BC на длине z=l₁также должны быть равны –

y₁(l₁)=y₂(l₁):

Итак:

_А=0,129 рад; _В=0,133 рад; _С=0,096 рад; _D=0 рад;

y_A=-0,001 м; y_В=-0,00023 м; y_С=-0,0003 м; y_A=-0,001 м; y_D=0 м;

Допускаемые перемещения и углы поворота определяется из условия жесткости

Условие жесткости по перемещениям в сечениях А, В, С и по углам поворота на участках А, В, С не выполняются. Необходимо провести мероприятия по увеличению жесткости конструкции.
^

3.3.1. Построение эпюр внутренних силовых факторов.

Исходные данные для расчета плоской рамы представлены на рис. 3.4. Определим реакции, возникающие в заделке:

Для построения эпюр внутренних силовых факторов рассмотрим три произвольных сечения на участках АВ, ВС и CD (рис. 3.5).

На участке АВ (0z₁l₃) (рис. 3.5 а):

На участке ВС (0z₂l₂) (рис. 3.5 б):

На участке CD (0z₃l₁) (рис. 3.5 в):

По полученным данным строим эпюры продольной, перерезывающей силы и изгибающего момента (рис. 3.6).

^
Рассчитаем диаметр стержней, исходя из условия прочности, при этом М_max=10,8кНм, материал стержня Сталь 30, допускаемые напряжения где n – коэффициент запаса, тогда диаметр стержня:

Примем (из ряда Ra20 по ГОСТ 6636-69) d=80мм.

^
1. В. К. Качурин «Сборник задач по сопротивлению материалов», -М.:Наука, 1970.-432стр.

2. В. И. Анурьев «Справочник по машиностроению», электронное издание.

Скачать файл (442.2 kb.)

gendocs.ru

Сопротивление материалов и расчет конструкций

1	О расчете балок, лежащих на упругом основании	Крылов А.Н.	1931
2	Расчет балок на упругом основании	Жемочкин Б.Н.	1937
3	Осесимметричная задача теории упругости	Соляник-Красса К.В.	1987
4	Сборник задач по сопротивлению материалов	Качурин В.К. (ред.), Беляев Н.М., Белявский Л.А., Кипнис Я.И.	1970
5	Прочность и колебания элементов конструкций	Тимошенко С.П.	1975
6	Сопротивление материалов на базе MathCad	Макаров Е.Г.
7	Расчет сооружений с учетом пластических свойств материалов	Ржаницын А.Р.	1954
8	Устойчивость и колебания сооружений	Смирнов А.Ф.	1958
9	Статическая и динамическая устойчивость сооружений	Смирнов А.Ф.	1947
10	Динамическая устойчивость упругих систем	Болотин В.В.	1956
11	Работа сжатых стоек	Стрелецкий Н.С.	1959
12	Сопротивление материалов	Горшков А.Г., Трошин В.Н., Шалашилин В.И.	2005
13	Сопротивление материалов	Гуле Ж.	1985
14	Расчет строительных конструкций с учетом ползучести	Арутюнян Н.Х., Зевин А.А.	1988
15	Несущая способность тонкостенных конструкций	Дехтярь А.С., Рассказов А.О.	1990
16	Прикладная теория упругости	Тимошенко С.П., Лессельс Дж.	1931
17	Техническая механика: Теоретическая механика. Сопротивление материалов: Учеб. для машиностр. спец. техникумов	Эрдеди А.А., Медведев Ю.А., Эрдеди Н.А.	1991
18	Основы строительной механики стержневых систем	Леонтьев Н.Н., Соболев Д.Н., Амосов. А.А.	1996
19	Строительная механика. Учебное издание	Дарков А.В., Шапошников Н.Н.	1986
20	Расчет коробчатых конструкций на изгиб и кручение	Вольфсон Б.П.	1968
21	Формулы расчета рам	Глушков Г.С., Егоров И.Р., Ермолов В.В.	1958
22	Расчет на кручение балочных и рамных систем из тонкостенных составных стержней на планках	Борисов М.Д.	1970
23	Прочность и устойчивость стержневых систем. Упругие рамы, фермы и комбинированные системы	Корноухов Н.В.	1949
24	Статика и динамика зданий с листовым каркасом	Гоши Б.	1984
25	Новые методы расчета строительных конструкций	Ржаницын А.Р.	1971
26	Статически неопределимые железобетонные конструкции	Дыховичный А.А.	1978
27	Сопротивление материалов	Биргер И.А., Мавлютов Р.Р.	1986
28	Строительная механика стержневых систем. Часть 2 и 3	Винокуров Л.П.	1961
29	Сопротивление материалов	Александров А.В., Потапов В.Д., Державин В.П.	2003
30	Прикладная теория упругости	Ван Цзи-Де	1959
31	Устойчивость деформируемых систем	Вольмир А.С.	1967
32	Устойчивость упругих систем	Вольмир А.С.	1963
33	Нелинейная динамика пластинок и оболочек	Вольмир А.С.	1972
34	Гибкие пластинки и оболочки	Вольмир А.С.	1956
35	Основы расчета тонкостенных конструкций (прочность, устойчивость и колебания)	Карякин Н.И.	1960
36	Справочник по динамике сооружений	Коренев Б.Г.	1972
37	Теория расчета строительных конструкций на надежность	Ржаницын А.Р.	1978
38	Статически неопределимые фермы наименьшего веса	Радциг Ю.А.	1969
39	Расчет пространственных конструкций (метод конечных элементов)	Немчинов Ю.И.	1980
40	Особенности расчета стержневых пространственных конструкций	Лившиц И.Е.	1968
41	Расчет строительных конструкций на основе моделирования	Питлюк Д.А.	1965
42	Линейная алгебра и ее применения	Стренг Г.	1980
43	Зеркальные функции и их применение при решении задач строительной механики	Радциг Ю.А., Колупаев А.Н.	1980
44	Строительная механика. Руководство к практическим занятиям	Бутенко Ю.И.	1984
45	Строительная механика	Снитко Н.К.	1972
46	Устойчивость стержневых систем в упруго-пластической области	Снитко Н.К.	1968
47	Теория упругости	Тимошенко С.П., Гудьер Дж.	1975
48	Курс теории упругости	Тимошенко С.П.	1972
49	Изгибно-крутильные деформации тонкостенных стержней открытого профиля	Ягн Ю.И.	1952
50	Избранные задачи и вопросы по сопротивлению материалов	Феодосьев В.И.	1996
51	Механика деформируемого твердого тела	Работнов Ю.Н.	1979
52	Заглубленные сооружения: статическая и динамическая прочность	Балсон Ф.С.	1991
53	Строительная механика. Тонкостенные пространственные системы	Александров А.В., Лащеников Б.Я., Шапошников Н.Н.	1983
54	Экспериментальная механика. тома 1 и 2	Кобаяси А.	1990
55	Расчёт конструкций на динамические специальные нагрузки	Попов Н.Н.	1992
56	Практические методы расчета статически неопределимых систем	Снитко И.К.	1964
57	Пластичность при переменных нагружениях	Москвитин В.В.	1965
58	Оптимизация элементов конструкций по механическим характеристикам	Гринев В.Б., Филиппов А.П.	1975
59	Циклические нагружения элементов конструкций	Москвитин В.В.	1981
60	Сопротивление материалов	Подскребко М.Д.	2007
61	Справочник по сопротивлению материалов	Фесик С.П.	1970
62	Устойчивость стержней пластин и оболочек	Тимошенко С.П.	1971
63	Пособие к решению задач по сопротивлению материалов	Миролюбов И.Н.	1967
64	Воздействие ветра на здания и сооружения	Симиу Э., Сканлан Р.	1984
65	Расчет и конструирование частей жилых и общественных зданий	Вахненко П.Ф., Хилобок В.Г., Андрейко Н.Т., Яровой М.Л.	1987
66	Динамика сооружений	Новацкий В.	1963
67	Устойчивость и динамика сооружений	Завриев К.С., Карцивадзе Г.Н.	1959
68	Исследования по динамике сооружений	Рабинович И.М.	1947
69	Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Расчетно-теоретический	Уманский А.А.	1960
70	Кручение и изгиб тонкостенных авиаконструкций	Уманский А.А.	1939
71	Элементы строительной механики тонкостенных конструкций	Кан С.Н., Пановко Я.Г.	1952
72	Вопросы теории статического расчета сооружений с односторонними связями	Рабинович И.М.	1975
73	Динамический расчет специальных инженерных сооружений и конструкций	Коренев Б.Г., Смирнов А.Ф.	1986
74	Вопросы расчета и конструирования специальных сооружений	Попов Н.Н., Расторгуев Б.С.	1980
75	Расчет строительных конструкций на динамическую нагрузку	Френкель П.М.	1958
76	Расчет железобетонных конструкций за пределом упругости на действие ударной волны на ЭЦВМ	Котляревский В.А., Сенюков А.В., Бродецкая Л.А.	1965
77	Строительная механика	Довнар Е.П., Коршун Л.И.	1986
78	Руководство к решению задач по сопротивлению материалов	Ицкович Г.М., Минин Л.С., Винокуров А.И.	1999
79	К динамическому расчету сооружений за пределом упругости	Рабинович И.М.	1947
80	Теория составных стержней строительных конструкций	Ржаницын А.Р.	1948
81	Изгиб и статически неопределимые системы	Дарков А.В., Лащеников Б.Я., Ломакин Е.В., Пановко Я.Г., Постное В.А., Феодосьев В.И., Яковенко М.Г.	1981
82	Расчет балок и плит на упругом основании за пределом упругости	Синицын А.П.	1976
83	Проблема оптимального проектирования в строительной механике	Виноградов А.И.	1973
84	Основы теории балок и плит на деформируемом основании	Леонтьев Н.Н. и др.	1982
85	Расчет конструкций на основе теории риска	Синицын А.П.	1985
86	Коэффициенты концентрации напряжений, графики и формулы для расчета конструктивных элементов на прочность	Петерсон Р.	1977
87	Расчет рам	Жемочкин Б.Н.	1965
88	Прочность и устойчивость стержневых систем	Коноухов Н.В.	1949

proektia.ru

Решение типовых задач по сопромату.

Пример решения задачи на расчет статически неопределимых систем при растяжении и сжатии

Расчет статически неопределимых систем при растяжении и сжатии – условие задачи

Для статически неопределимой системы, изображенной на рис. 3.4, а (см2; см2; м; м; м; м, м), требуется определить усилия и напряжения в стальном ( кН/см2; кН/см2) и в медном ( кН/см2; кН/см2) стержнях, выразив их через силу P, а также найти допускаемую нагрузку .

Расчет статически неопределимых систем при растяжении и сжатии – расчетная схема

рис. 3.4

Расчет статически неопределимых систем при растяжении и сжатии – решение задачи

Находим усилия и напряжения, возникающие в стержнях

Рассечем стержни и изобразим систему в деформированном состоянии (рис. 3.4, б). Под действием силы P абсолютно жесткий на изгиб брус повернется на некоторый малый угол, оставаясь прямолинейным. Поскольку угол поворота абсолютно жесткого на изгиб бруса мал, можно предположить, что его точки В и С будут перемещаться не по дуге окружности, а по вертикали вниз. Деформированное положение системы показано на рис. 3.4, б наклонной прямой линией АС1. Очевидно, что оба стержня, поддерживающие брус, растянутся. Поэтому внутренние усилия и , возникающие в поперечных сечениях этих стержней, направим от сечения. Удлинение медного стержня равно отрезку , а стального – отрезку .

Для плоской системы параллельных сил мы имеем два независимых уравнения статики. Неизвестных же у нас три: , и . Следовательно, заданная система является один раз статически неопределимой.

Чтобы исключить из дальнейшего рассмотрения реакцию , возникающую в шарнире A, составим следующее уравнение равновесия:

. (3.1)

В него входят две неизвестные и , поэтому для их определения (то есть для раскрытия статической неопределимости) нам необходимо составить еще одно, дополнительное, уравнение.

Очевидно, что удлинения стержней и связаны между собой. Из подобия треугольников ABB1 и AСС1 следует, что

Или, учитывая закон Гука,

. (3.2)

Полученное нами дополнительное уравнение (3.2), связывающее деформации стержней, называется уравнением совместности деформаций.

Подставив в (3.1) и (3.2) исходные данные задачи и выполнив несложные преобразования, получим следующую систему уравнений относительно неизвестных внутренних усилий и :

Отсюда находим, что усилия в стержнях равны:

Тогда напряжения

Определяем допускаемую нагрузку

Из условия прочности медного стержня

кН/см2

находим, что

кН.

Из условия прочности стального стержня

кН/см2

следует, что

кН.

Принимая меньшее из найденных выше двух значений, находим, что допускаемая нагрузка для заданной системы равна кН.

Расчет статически неопределимых систем при растяжении и сжатии – задача для самостоятельного решения

Расчет статически неопределимых систем — условие задачи для самостоятельного решения

Горизонтальный абсолютно жесткий на изгиб брус, нагруженный силой P, опирается на шарнирно неподвижную опору и поддерживается двумя упругими стержнями, прикрепленными к нему и к основаниям с помощью шарниров. Один из упругих стержней стальной ( кН/см2; кН/см2), а другой медный ( кН/см2; кН/см2) (рис. 3.3). Требуется определить усилия и напряжения, возникающие в стержнях, выразив их через силу P , а также найти допускаемую нагрузку .

Расчет статически неопределимых систем при растяжении и сжатии – расчетные схемы к задаче для самостоятельного решения

Расчет статически неопределимых систем при растяжении и сжатии – исходные данные для самостоятельного решения

Номер схемы	Fст, см2	Fм, см2	lст, м	lм, м	a, м	b, м	c, м
1	1,0	2,0	1,0	1,0	1,0	1,0	0,5
2	1,0	2,0	1,0	0,8	1,0	0,8	0,6
3	2,0	4,0	1,0	1,0	1,0	1,0	1,2
4	3,0	5,0	1,6	1,4	1,6	1,4	1,0
5	4,0	6,0	1,8	1,4	1,8	1,4	1,0
6	2,0	4,0	1,2	1,2	1,2	1,2	0,6
1	2,0	3,0	1,2	1,0	1,2	1,0	0,8
2	3,0	4,0	1,0	1,0	1,0	1,0	1,4
3	4,0	5,0	1,8	1,6	1,8	1,6	1,2
4	5,0	6,0	2,0	1,6	2,0	1,6	1,2
5	3,0	4,0	1,4	1,4	1,4	1,4	0,7
6	3,0	5,0	1,4	1,0	1,4	1,0	0,8
1	4,0	5,0	1,2	1,2	1,2	1,2	1,6
2	5,0	7,0	2,0	1,8	2,0	1,8	1,4

sopromato.ru