Рамы | ПроСопромат.ру

Рама — это система, состоящая из стоек и ригелей, жестко связанных между собой. Рамы применяются в каркасах зданий и сооружений. Вертикальные или близкие к ним стержни называются стойками. Горизонтальные или близкие к ним стержни называются ригелями. Они могут быть прямолинейными, ломаными или криволинейными.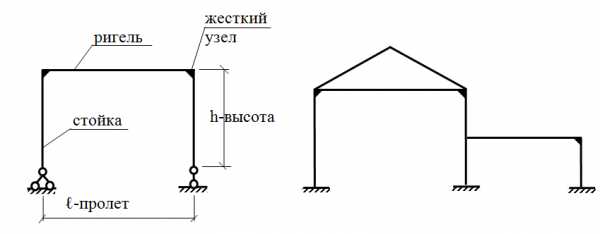

Расстояние между осями стоек называется пролетом. Расстояние между осью опоры и осью ригеля называется высотой рамы или высотой этажа. По числу пролетов и этажей рамы бывают одно- , двух- и многопролетными, одно- , двух- и многоэтажными. Почти все рамы, встречающиеся на практике, являются пространственными. В расчете их обычно расчленяют на плоские.

Кинематический анализ рамы делают по формуле:

n = ЗД — 2Ш — С_оп .

Если n < О, рама геометрически неизменяемая и статически неопределимая, то есть имеет лишние связи. Если n = 0, рама геометрически неизменяемая и статически определимая. В элементах рамы возникают три вида внутренних силовых факторов: продольная и поперечная сила, изгибающий момент (N, Q, М). При построении эпюр наблюдателя помещают внутри контура рамы. При этом придерживаются следующих правил:

1. Ось стержня принимается за ось абсцисс.
2. Вычисленные ординаты эпюр откладываются перпендикулярно к продольной оси стержней.
3. Положительные ординаты эпюры Q откладываются вверх от оси ригеля и влево от оси стойки.
4. Ординаты эпюры М откладываются со стороны растянутых волокон элементов рамы.
5. Ординаты эпюры N откладываются, как правило, симметрично по обе стороны от оси рассматриваемого стержня. Знак на эпюре N обязателен.
6. Штриховка на эпюре производится перпендикулярно к оси соответствующего стержня.

Опорные реакции рамы определяют так же, как в балке, из уравнений равновесия: ∑М_А =0;    ∑М_в =0;    ∑X =0;  проверка:  ∑Y =0.

Если в раме имеется шарнир на ригеле или на стойке, для определения горизонтальных опорных реакций составляют дополнительные уравнения равновесия:

∑М^ш_лев=0;  или  ∑М^ш_пр=0;

проверка:∑X =0: ∑Y =0.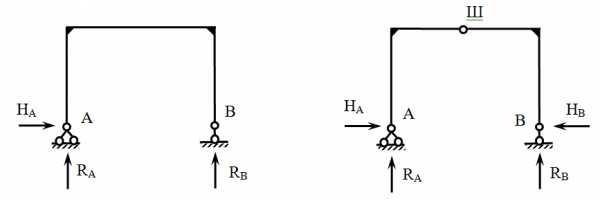

Поперечная сила Q в рассматриваемом сечении численно равна алгебраической сумме проекций внешних сил, приложенных с одной стороны от сечения, на плоскость сечения. Правило знаков такое же, как в балке.

Изгибающий момент М в любом сечении рамы численно равен алгебраической сумме моментов внешних сил, действующих по одну сторону от сечения, относительно центра тяжести сечения. Правило знаков такое же, как в балке.

Продольная сила N в любом сечении рамы численно равна алгебраической сумме проекций всех внешних сил на продольную ось стержня. Правило знаков: если сила направлена от сечения, растягивает стержень, знак «+», стержень растянут.

Контроль правильности построения эпюр выполняют вырезанием жестких узлов. Рассматривают сечения, бесконечно близкие к узлу. Значения внутренних силовых факторов снимают с эпюр и прикладывают к узлу, составляют уравнения равновесия:

∑Х=0; Q_ст  —  N_р  =  0

∑Y=0; N_ст   —  Q_р =  0

∑М=0; М_р  —  М_ст = 0

.

 

 

 

 

 

prosopromat.ru

Рамы. — Сопротивление материалов.

Как сделать заказ:
1)  С любого электронного почтового адреса на почту [email protected] высылается условие задачи; указываете, какой расчёт Вам нужен — численный или аналитический;

2) Обратно на этот адрес приходит счёт, оплатить который можно прямо из письма;

3) После оплаты счёта в течении трёх рабочих дней (для численного расчёта) или недели (для расчёта аналитического) по почте высылается результат.

 

Численный результат служит студенту для проверки правильности собственного расчёта.

Аналитический — это и есть студенческая работа.  

 Круглые рамы.

 

Расчёт выполняется так же, как это показано в примере

K-07.

Результат — три рисунка:

 

Расчётная схема. Моменты изображаются своими векторами — двуглавыми стрелками. Нагрузки подписываются коэффициентами перед формулами. На минусы не обращайте внимания.

Силовая схема. Вектор реактивной силы — малиновая стрелка, вектора реактивных моментов — фиолетовые двуглавые стрелки. Реакции также подписываются коэффициентами перед формулами.

Эпюра внутреннего изгибающего момента. Она подписывается коэффициентами и их размерностями

Расчёт выполняется так же, как это показано в примере K-07.

 

 Рамы, нагруженные только сосредоточенными силами и моментами.

 

Расчёт выполняется так же, как это показано в примерах K-02 и K-03. Результат — три рисунка:

 

Расчётная схема.

Силовая схема.

Эпюра внутреннего изгибающего момента Mx.

Расчёт выполняется так же, как в примерах K-02 и K-03.

 Рамы c шарнирами и/или распределёнными нагрузками.

 

Расчёт выполняется так же, как это показано в примерах K-04, K-05 и K-06.

 

Расчётная схема.

Силовая схема.

Эпюра внутреннего изгибающего момента Mx.

Расчёт выполняется так же, как в примере K-04, K-05 и K-06.

www.tychina.pro

Расчет статически неопределимой рамы по методу сил

Рассчитать статически неопределимую раму методом сил. Для рамы построить эпюры M_ок,Q, N со всеми проверками.

Дано: l=h=2 м, q=10 кН/м, F=20 кН, I₁/I₂=½

Зададимся соотношением моментов инерции. Пусть первый

I₁=I  , тогда  второй I₂=2 I

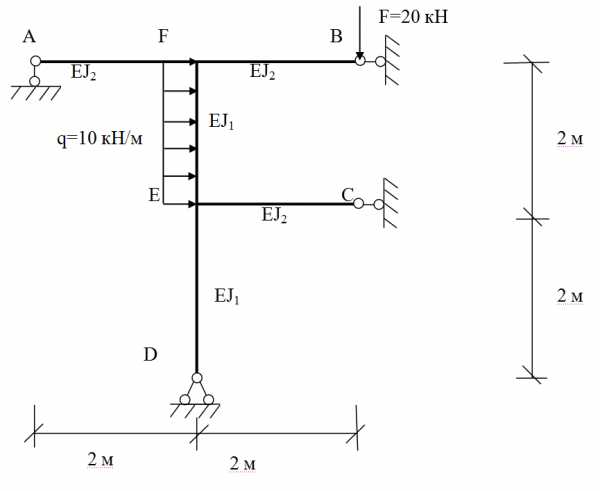
1) определим степень статической неопределимости системы:

 λ=Соп-3=5-3=2

где Соп – число опорных реакций

3 – число  уравнений статики 

то есть, система дважды статически неопределима. т.е. для ее решения требуются два дополнительных уравнения. Это будут канонические уравнения метода сил.

Тогда система канонических уравнений будет:     

δ₁₁∙Х₁+ δ₁₂Х₂+ Δ_1F=0,

δ₂₁∙Х₁+ δ₂₂Х₂+ Δ

2_F=0.

 2) построим основную систему, отбросив некоторое число опор, суммарное количество реакций которых должно соответствовать значению статической неопределимости (т.е. в нашем случае – 2 реакции). Отбросим опоры В и С. Действие опор заменим двумя неизвестными силами —  X_{1    ,}   X_2.

2) загружаем основную систему заданной нагрузкой, определяем реакции опор и строим эпюру изгибающих моментов — грузовую эпюру.

Построим грузовую эпюру моментов  (все значения откладываются на сжатых волокнах):

Посчитаем так же момент в середине действия распределённой нагрузки

3) По направлению предполагаемых реакций отброшенных опор к основной системе поочерёдно прикладываем единичные силы х₁=1 и  х₂=1, строим единичные эпюры М₁ и М₂  

Построим эпюру M₁   от действия x₁=1.

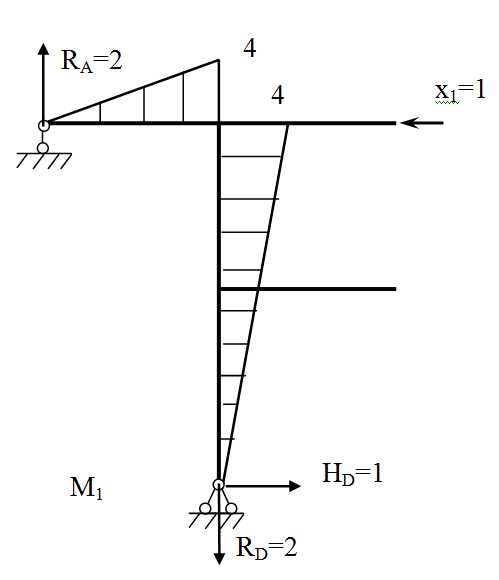
Сначала определим опорные реакции

 ∑X=0   -x₁ + H_D = 0       H_D=1

∑M_D:  R_A2-x₁4=0      R_A=2

∑M_А:  R_Д2- H_D4=0     R_D=2

Проверка  ∑Y=0    R_A— R_D= 0     верно

Теперь определим моменты в характерных точках

M_A=M_D=0 

M_F^лев=R_A2=22=4 (сжатые волокна сверху).  Строим эпюру M₁

Построим эпюру M₂   от действия x₂=1.

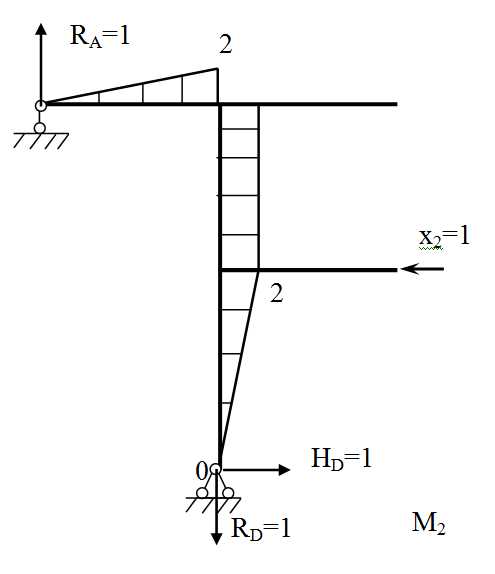
Сначала определим опорные реакции

 ∑X=0   -x₂ + H_D = 0       H_D=1

∑M_D:  R_A2-x₂2=0      R_A=1

∑M_А:  R_Д2- H_D4+x₂2=0     R_D=1

Проверка  ∑Y=0    R_A— R_D= 0     верно

Моменты в характерных точках

M_A=M_D=0 

M_F^лев=R_A2=12=2 (сжатые волокна сверху)

4) определяем коэффициенты канонических уравнений перемножением эпюр по формуле Симпсона.

Следует помнить о соотношении жесткостей стержней.

Знак минус перед слагаемыми в грузовых коэффициентах ставим потому, что эпюры на грузовой и единичной эпюрах расположены по разные стороны стержней.

5) подставляем значения перемещений в канонические уравнения, сокращаем на EI, находим значения x₁ и x₂ :

26,7X₁ +17,33X₂  -513, 33=0

17,33X₁ +12X₂  -333 ,32 =0

Поделим первое и второе уравнения на сомножители при X₂  (первое делим на 17,33, второе на 12). Получим:

1,54X₁ +X₂  -29,62 =0

1,44X₁ +X₂  -27,28 =0

Вычтем из первого уравнения второе. Тогда получим:

X₁ =23,4

X₂  = -6,4

6) Умножаем единичные эпюры на найденные значения X_{1 ,}  X_2. 

Получим эпюры M₁x₁ и M₂x₂

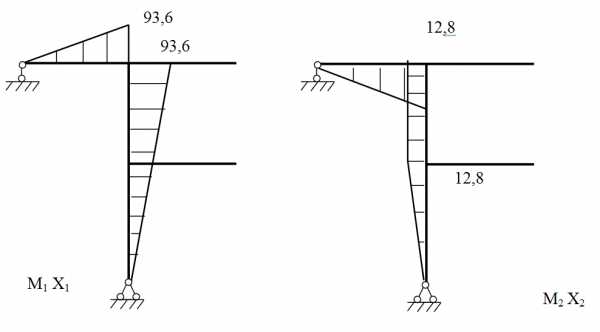
При построении эпюры M₂x₂  следует обратить внимание на то, что значение x₂  — отрицательное.

7) строим окончательную эпюру моментов, складывая эпюры:  

М_ок = M₁x₁+M₂x₂+M_F

M_F^л= 93,6 — 12,8 -100 = — 19,2  кНм  (сжатые волокна внизу)                      

M_F^пр= -40 кНм   (сжатые волокна внизу)

M_F^низ= 93,6 -12,80 – 60 = 20, 8 кНм       (сжатые волокна справа)     

M_E= 46,8 – 12,8 – 40 = -6 кНм  (сжатые волокна слева)  

Посчитаем так же момент в середине действия распределённой нагрузки

M_ср= 70,2 – 12,8 – 55 = 2,4 кНм (сжатые волокна справа)

8) Произведем проверки окончательной эпюры М

Статическая проверка (методом вырезания узлов рамы — они должны находиться в равновесии):

верно 

Деформационная проверка: заключается в определении перемещений по направлению отброшенных связей. Эти перемещения должны быть равны нулю. Ошибка может составлять не более 5%.

Эпюра M_s = M₁ + M₂     Это суммарная единичная эпюра: к основной системе  прикладываем одновременно Х₁=1 и  Х₂=1.

 

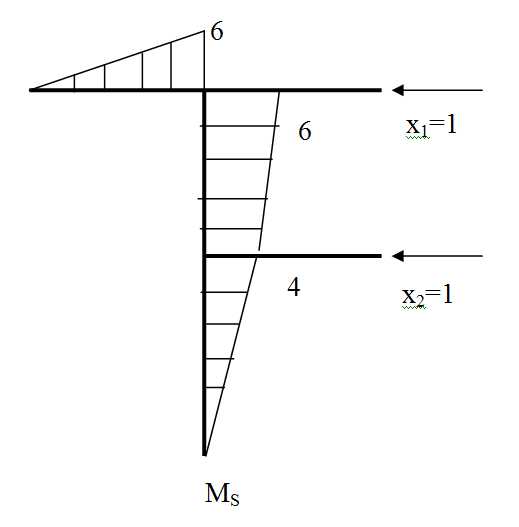
Сначала проверим коэффициенты канонических уравнений.

1  проверка.

Первая проверка заключается в равенстве: M_s ∙ M_s = ∑δ_ij

Произведение суммарной эпюры саму на себя должно равняться сумме единичных коэффициентов.

верно

Вторая проверка заключается в равенстве: M_s ∙ M_F = ∑Δ_iF

Произведение суммарной эпюры на грузовую эпюру должно равняться сумме грузовых коэффициентов.

Все проверки выполняются, значит, коэффициенты определены верно.

И наконец, третья, деформационная проверка.

Ошибка составляет: , что допустимо.

9) построим эпюру поперечной силы Q по М_ок:

где М^пр и М^лев – моменты с эпюры М_ок, соответственно с правой и с левой стороны участка. Моменты берутся со своими знаками, l— длина участка, q — распределенная нагрузка на участке. Если нагрузки на участке нет, и эпюра моментов представляет собой прямую линию, то в формуле полагаем q=0.

 Q_AF=(-19,2 — 0)/2= -9,6 кН

Q_FB=(0 – (-40))/2=20 кН

Q_DE=(0 — (-6))/2=3 кН

На участке EF приложена распределённая нагрузка. Рассмотрим этот участок отдельно.

М_прав  =   -20,8  , М_лев  =   6

Значение поперечной силы в точке E:

Значение в точке F найдём:

Строим эпюру Q

10) Построение эпюры N по Q методом вырезания узлов

Вырезаем узел, к узлу прикладываем известные поперечные силы с эпюры Q с соответствующим знаком  (+ по часовой стрелке), неизвестные продольные силы,   и рассматриваем равновесие данного узла.  Знаки у продольных сил —  от узла — растяжение.

Рассмотрим узел Е

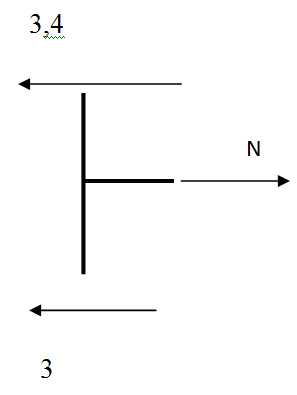
∑х = 0,    — 3 -3,4 + N = 0      N = 6,4 (растяжение)  

Рассмотрим узел F

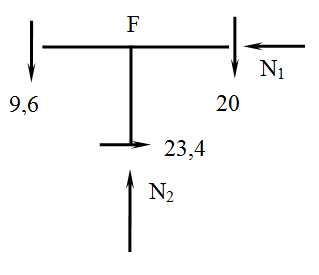
∑х = 0,    — N₁ + 23,4 = 0

              N₁ = 23,4 кН  (сжатие –к узлу)

 

     ∑у = 0 ,  N₂ – 9,6  – 20= 0

              N2 = 29,6 кН (сжатие –к узлу)

Строим эпюру N

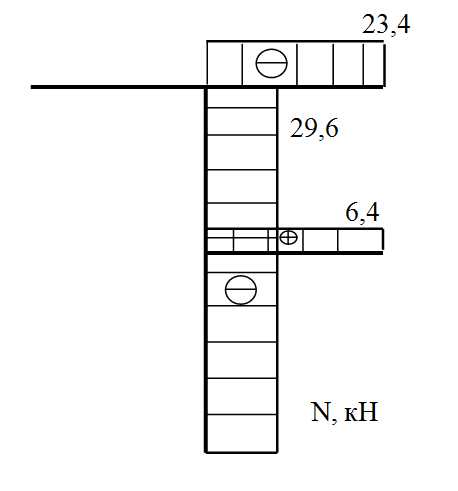
11) Общая статическая проверка: зарисовывается исходная рама, в опорах показываются все реакции (их числовые значения необходимо брать с построенных эпюр M, Q, N с учетом знаков),  и проверяется равновесие рамы в целом

 

 Все проверки выполняются.

   

prosopromat.ru

Различия настольной и мини версий он-лайн программы для расчет рам, фем, балок он-лайн. Расчет рамы, фермы, балки он-лайн (на прочность)!! СОПРОМАТ, СТРОЙМЕХ (СТРОИТЕЛЬНАЯ МЕХАНИКА)

Для чего нужна Mini версия?

Mini версия программы разработана специально для расчетов рам, ферм, балок он-лайн с использование мобильных устройств (например через браузер Opera Mini).

Mini версия учитывает специфику мобильных устройств. Главное — это отсутствие мышки. Поэтому в Mini версии графическое построение заменено на диалоговый ввод.

Различия

В целом и Нстольная и Mini версии имеют абсолютно одинаковый функционал. Единственное отличие Mini версии от Настольной в том, что графическое построение заменено на диалоговый ввод.

Построение схемы (добавление стержный) в Mini версии

Это важно!

Обратите внимание, что при вводе координат нового стержня в диалоге ось Y направлена вниз.

При вводе нагрузок, распределенных нагрузок, а так же при отображении реакций опор (т.е все остальное) ось Y направлена как полагается вверх!

Обязательно

Попробуйте Mini версию сначала на компьютере прежде чем рассчитывать на телефоне. Разберитесь что к чему в ней.

Вход

Новости сайта

01 июня 2010 г.

Добавлена возможность экспорта результатов в формат DXF

18 марта 2010 г.

Доработана Mini версия программы.

14 марта 2010 г.

Добавлено немного пояснений при выводе хода решения методом конечных элементов (МКЭ).

11 марта 2010 г.

По просьбам добавлен горизонтальный подвижный шарнир.

09 марта 2010 г.

Теперь масштаб сохраняется! и при загрузке расчета показывает в том масштабе, в котором сохраняли.

05 февраля 2010 г.

День Рождения проекта Рама.Сопромат.Орг

rama.sopromat.org

Расчет плоской статически неопределимой рамы методом сил

Для статически неопределимой рамы требуется построить эпюры изгибающих моментов, поперечных и продольных сил,  проверить правильность построения эпюр. Дано:  L=8 м, F=4кН, q=2 кН/м, h=8 м, соотношение жесткостей  I₁=2I, I₂=I

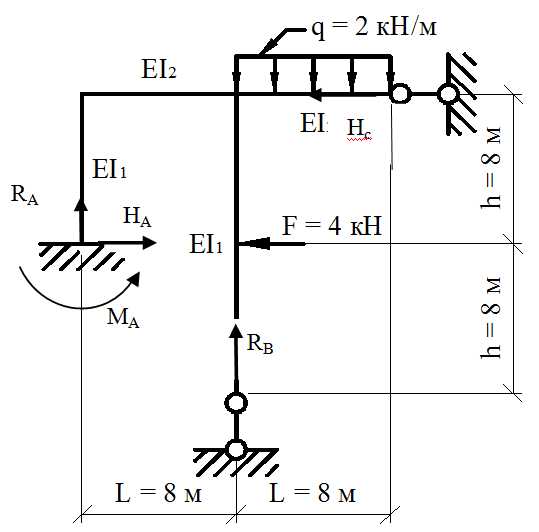
     Решение:

1. Определяем степень статической неопределимости:  n = R — Ш – 3 = 5 – 0 – 3 = 2,  где R – число всех неизвестных реакций,    Ш – число простых соединительных шарниров, в данной схеме их нет. Рама получилась дважды статически неопределима.

2. Выбираем основную систему путем отбрасывания лишних связей Основная система

3. Зарисовываем эквивалентную систему: к основной системе прикладываем всю внешнюю нагрузку и вместо отброшенных связей их неизвестные реакции Х₁, Х₂ 

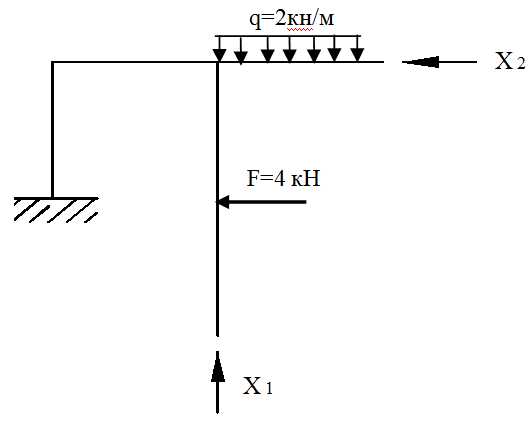Эквивалентная система

4. Составляем канонические уравнения:

δ₁₁x₁ + δ₁₂x₂ + Δ_1F = 0

               δ₂₁x₁ + δ₂₂x₂ + Δ_2F = 0 

 5. Строим единичные эпюры: к основной системе прикладываем сначала Х₁=1, затем Х₂=1. Эпюры моментов построим на растянутых волокнах.

а) Построение эпюры М₁ 

Строим эпюру

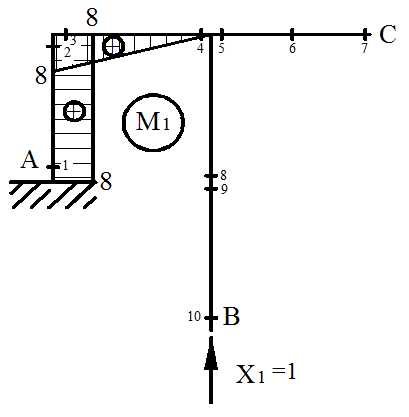
б) Построение эпюры М₂ 

Строим эпюру

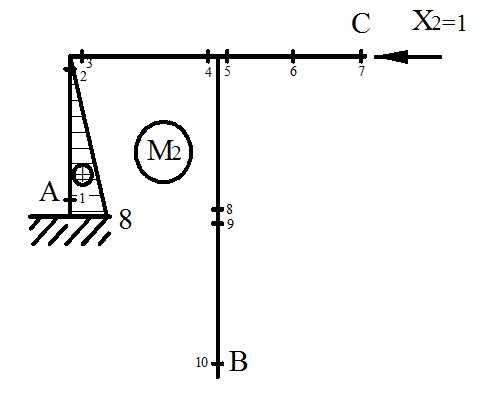
6. Строим грузовую эпюру моментов. К основной системе прикладываем всю заданную внешнюю нагрузку 

Строим эпюру

7. Определяем коэффициенты канонических уравнений по формуле Симпсона:

8. Проверяем коэффициенты канонических уравнений.

Для этого строим суммарную единичную эпюру : к основной системе  прикладываем одновременно Х₁=1 и  Х₂=1. Эпюра M_s = M₁ + M₂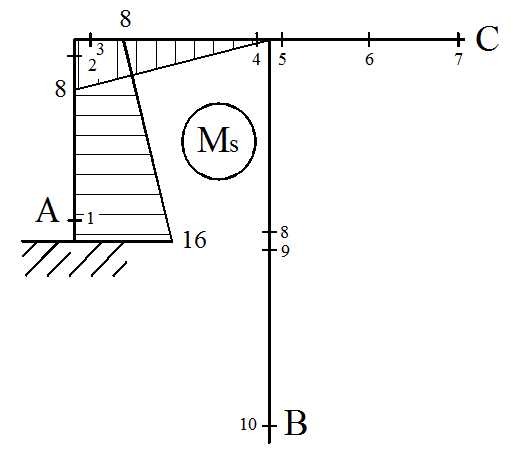

а) Первая проверка заключается в равенстве: M_s ∙ M_s = ∑δ_ij 

При умножении суммарной единичной эпюры саму на себя мы должны получить сумму единичных коэффициентов канонических уравнений

верно

б) Вторая проверка заключается в равенстве: M_s ∙ M_F = ∑Δ_iF

Умножая суммарную единичную эпюру на грузовую, мы должны получить сумму грузовых коэффициентов

верно

Все проверки выполняются, значит, коэффициенты определены верно.

9. Решаем систему канонических уравнений:

10. Строим окончательную эпюру моментов М_ок   по формуле:

         М_ок = M_F + M₁ ∙ x₁ + M₂ ∙ x₂

 

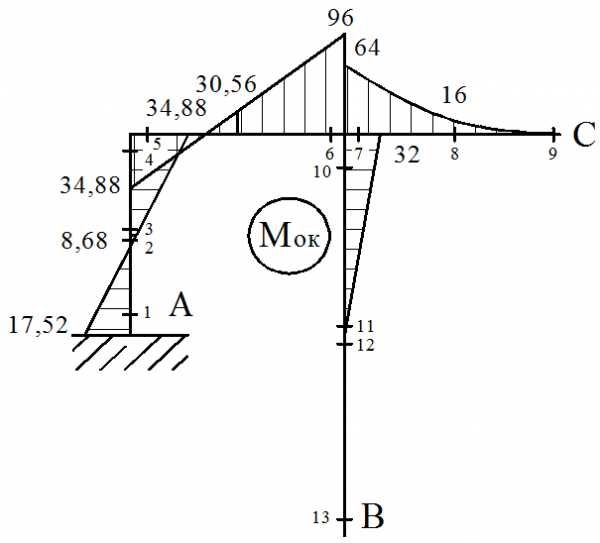
11. Проверки окончательной эпюры моментов М­_ОК:

а) Статическая проверка: заключается в проверке равновесия вырезанных узлов. Вырезается узел, пунктирной линией показываются растянутые волокна, прикладываются узловые моменты со стороны растянутых волокон и проверяется равновесие вырезанного узла

Выполним статическую проверку вырезанием узлов 

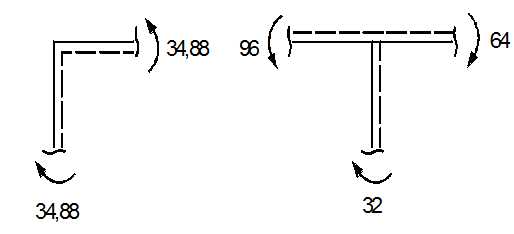
Узды находятся в равновесии

б) Деформационная проверка: заключается в определении перемещений по направлению отброшенных связей. Эти перемещения должны быть равны нулю. Ошибка может составлять не более 5%. Для выполнения этой проверки умножим окончательную эпюру моментов на суммарную эпюру единичных моментов.

Ошибка составляет: 

12. По эпюре М_ОК строим эпюру поперечных сил Q  с использованием формулы:  , где М^пр и М^лев – моменты с эпюры М_ок, соответственно с правой и с левой стороны участка . Моменты берутся со своими знаками,  l— длина участка, q — распределенная нагрузка на участке. Если нагрузки на участке нет, и эпюра моментов представляет собой прямую линию, то в формуле полагаем q=0.

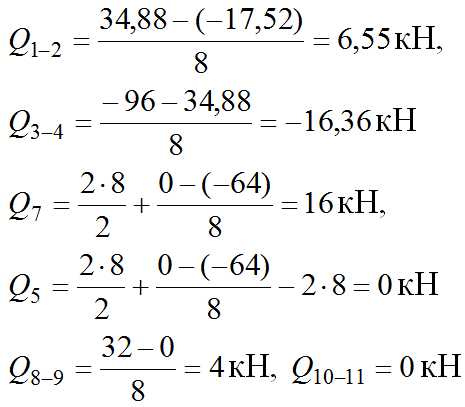
Строим эпюру

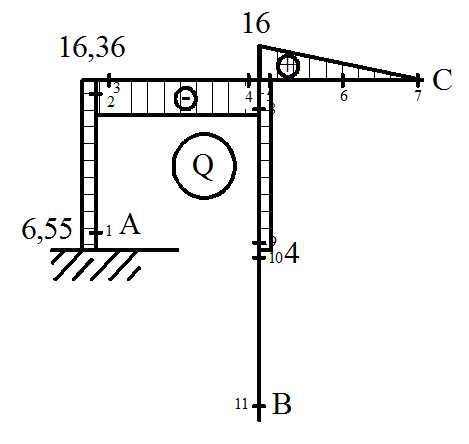
13. По эпюре Q  строим эпюру продольных сил N : вырезаем узел, к узлу прикладываем неизвестные продольные силы в положительном направлении (от узла — растяжение), затем известные поперечные силы с эпюры Q со своим знаком (+ по часовой стрелке) и рассматриваем равновесие данного узла.

Вырезаем узел 1

Вырезаем узел 2

Строим эпюру

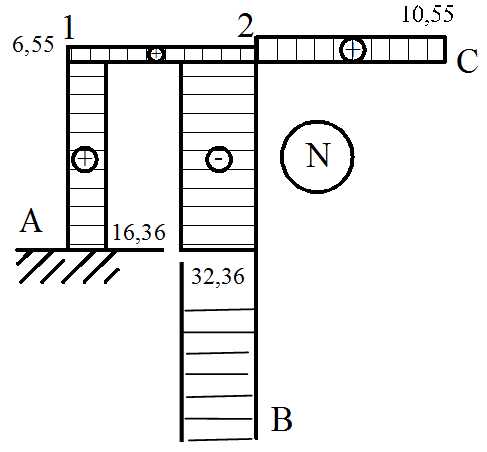
14. Общая статическая проверка: зарисовывается исходная рама, в опорах показываются все реакции (их числовые значения необходимо брать с построенных эпюр M, Q, N с учетом знаков), заданная нагрузка и проверяется равновесие рамы в целом

Составляем уравнения равновесия:

Все проверки выполняются.

 

 

 

 

prosopromat.ru

Задачи на метод сил | ПроСопромат.ру

Рассчитать статически неопределимую раму методом сил. Для рамы построить эпюры M_ок,Q, N со всеми проверками.

Дано: l=h=2 м, q=10 кН/м, F=20 кН, I₁/I₂=½

Зададимся соотношением моментов инерции. Пусть первый I₁=I  , тогда  второй I₂=2 I

1) определим степень статической неопределимости системы:

 λ=Соп-3=5-3=2

где Соп – число опорных реакций

3 – число  уравнений статики 

то есть, система дважды статически неопределима. т.е. для ее решения требуются два дополнительных уравнения. Это будут канонические уравнения метода сил.

Тогда система канонических уравнений будет:     

δ₁₁∙Х₁+ δ₁₂Х₂+ Δ_1F=0,

δ₂₁∙Х₁+ δ₂₂Х₂+ Δ_2F=0.

 2) построим основную систему, отбросив некоторое число опор, суммарное количество реакций которых должно соответствовать значению статической неопределимости (т.е. в нашем случае – 2 реакции). Отбросим опоры В и С. Действие опор заменим двумя неизвестными силами —  X_{1    ,}   X_2.

2) загружаем основную систему заданной нагрузкой, определяем реакции опор и строим эпюру изгибающих моментов — грузовую эпюру.

Построим грузовую эпюру моментов  (все значения откладываются на сжатых волокнах):

Посчитаем так же момент в середине действия распределённой нагрузки

3) По направлению предполагаемых реакций отброшенных опор к основной системе поочерёдно прикладываем единичные силы х₁=1 и  х₂=1, строим единичные эпюры М₁ и М₂  

Построим эпюру M₁   от действия x₁=1.

Сначала определим опорные реакции

 ∑X=0   -x₁ + H_D = 0       H_D=1

∑M_D:  R_A2-x₁4=0      R_A=2

∑M_А:  R_Д2- H_D4=0     R_D=2

Проверка  ∑Y=0    R_A— R_D= 0     верно

Теперь определим моменты в характерных точках

M_A=M_D=0 

M_F^лев=R_A2=22=4 (сжатые волокна сверху).  Строим эпюру M₁

Построим эпюру M₂   от действия x₂=1.

Сначала определим опорные реакции

 ∑X=0   -x₂ + H_D = 0       H_D=1

∑M_D:  R_A2-x₂2=0      R_A=1

∑M_А:  R_Д2- H_D4+x₂2=0     R_D=1

Проверка  ∑Y=0    R_A— R_D= 0     верно

Моменты в характерных точках

M_A=M_D=0 

M_F^лев=R_A2=12=2 (сжатые волокна сверху)

4) определяем коэффициенты канонических уравнений перемножением эпюр по формуле Симпсона. Следует помнить о соотношении жесткостей стержней.

Знак минус перед слагаемыми в грузовых коэффициентах ставим потому, что эпюры на грузовой и единичной эпюрах расположены по разные стороны стержней.

5) подставляем значения перемещений в канонические уравнения, сокращаем на EI, находим значения x₁ и x₂ :

26,7X₁ +17,33X₂  -513, 33=0

17,33X₁ +12X₂  -333 ,32 =0

Поделим первое и второе уравнения на сомножители при X₂  (первое делим на 17,33, второе на 12). Получим:

1,54X₁ +X₂  -29,62 =0

1,44X₁ +X₂  -27,28 =0

Вычтем из первого уравнения второе. Тогда получим:

X₁ =23,4

X₂  = -6,4

6) Умножаем единичные эпюры на найденные значения X_{1 ,}  X_2. 

Получим эпюры M₁x₁ и M₂x₂

При построении эпюры M₂x₂  следует обратить внимание на то, что значение x₂  — отрицательное.

7) строим окончательную эпюру моментов, складывая эпюры:  

М_ок = M₁x₁+M₂x₂+M_F

M_F^л= 93,6 — 12,8 -100 = — 19,2  кНм  (сжатые волокна внизу)                      

M_F^пр= -40 кНм   (сжатые волокна внизу)

M_F^низ= 93,6 -12,80 – 60 = 20, 8 кНм       (сжатые волокна справа)     

M_E= 46,8 – 12,8 – 40 = -6 кНм  (сжатые волокна слева)  

Посчитаем так же момент в середине действия распределённой нагрузки

M_ср= 70,2 – 12,8 – 55 = 2,4 кНм (сжатые волокна справа)

8) Произведем проверки окончательной эпюры М

Статическая проверка (методом вырезания узлов рамы — они должны находиться в равновесии):

верно 

Деформационная проверка: заключается в определении перемещений по направлению отброшенных связей. Эти перемещения должны быть равны нулю. Ошибка может составлять не более 5%.

Эпюра M_s = M₁ + M₂     Это суммарная единичная эпюра: к основной системе  прикладываем одновременно Х₁=1 и  Х₂=1.

 

Сначала проверим коэффициенты канонических уравнений.

1  проверка.

Первая проверка заключается в равенстве: M_s ∙ M_s = ∑δ_ij

Произведение суммарной эпюры саму на себя должно равняться сумме единичных коэффициентов.

верно

Вторая проверка заключается в равенстве: M_s ∙ M_F = ∑Δ_iF

Произведение суммарной эпюры на грузовую эпюру должно равняться сумме грузовых коэффициентов.

Все проверки выполняются, значит, коэффициенты определены верно.

И наконец, третья, деформационная проверка.

Ошибка составляет: , что допустимо.

9) построим эпюру поперечной силы Q по М_ок:

где М^пр и М^лев – моменты с эпюры М_ок, соответственно с правой и с левой стороны участка. Моменты берутся со своими знаками, l— длина участка, q — распределенная нагрузка на участке. Если нагрузки на участке нет, и эпюра моментов представляет собой прямую линию, то в формуле полагаем q=0.

 Q_AF=(-19,2 — 0)/2= -9,6 кН

Q_FB=(0 – (-40))/2=20 кН

Q_DE=(0 — (-6))/2=3 кН

На участке EF приложена распределённая нагрузка. Рассмотрим этот участок отдельно.

М_прав  =   -20,8  , М_лев  =   6

Значение поперечной силы в точке E:

Значение в точке F найдём:

Строим эпюру Q

10) Построение эпюры N по Q методом вырезания узлов

Вырезаем узел, к узлу прикладываем известные поперечные силы с эпюры Q с соответствующим знаком  (+ по часовой стрелке), неизвестные продольные силы,   и рассматриваем равновесие данного узла.  Знаки у продольных сил —  от узла — растяжение.

Рассмотрим узел Е

∑х = 0,    — 3 -3,4 + N = 0      N = 6,4 (растяжение)  

Рассмотрим узел F

∑х = 0,    — N₁ + 23,4 = 0

              N₁ = 23,4 кН  (сжатие –к узлу)

 

     ∑у = 0 ,  N₂ – 9,6  – 20= 0

              N2 = 29,6 кН (сжатие –к узлу)

Строим эпюру N

11) Общая статическая проверка: зарисовывается исходная рама, в опорах показываются все реакции (их числовые значения необходимо брать с построенных эпюр M, Q, N с учетом знаков),  и проверяется равновесие рамы в целом

 

 Все проверки выполняются.

   

prosopromat.ru

решение задач. Пример решения задачи. Расчет статически неопределимой рамы методом перемещений.

Меню сайта

Расчет геометрических характеристик сечений он-лайн ^NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.

Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!

Расчет рам, ферм балок он-лайн ^NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.

Лекции — теория, практика, задачи…

Примеры решения задач

Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.

Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).

Форум сопромата и механики

Книги — разная литература по теме.

Заказать задачу

Друзья сайта (ссылки)

WIKI^betta

Разработчикам (сотрудничество)

Веб-мастерам (партнёрка)

О проекте, контакты

Подпроекты

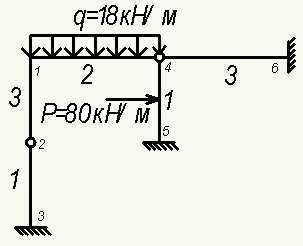
Пример №2. Расчет статически неопределимой рамы методом перемещений.

Необходимо построить эпюры внутренних силовых факторов, а так же найти реакции.

Решение.

1.Определяем число неизвестных метода перемещений.

n=1+1=2

V=2·6-5-6=1

2.Выбираем основную систему метода перемещений.

3.Записываем канонические уравнения метода перемещений.

r₁₁ + z₁ + r₁₂ + z₂ + R_1P = 0

r₂₁ + z₁ + r₂₂ + z₂ + R_2P = 0

4.Строим эпюры изгибающих моментов в основной системе от z₁=1, z₂=1 и от нагрузки.

5.Определяем реакции во вновь введённых связях.

6.Подставляем найденные значения реакций в уравнения.

15·z₁ + 2,25·z₂ — 81 = 0

2,25·z₁ + 0,75·z₂ + 0 = 0

z₁ = 9,8185 кН·м, z₁ = -29,4569 кН.

7.Определяем концевые моменты и поперечные силы в стержнях заданной системы.

8.Строим эпюры изгибающих моментов и поперечных сил в заданной системе от нагрузки.

9.Определяем продольные силы в стержнях рамы, используя способ вырезания узлов.

10.Строим эпюру продольных сил в заданной системе от нагрузки.

11.Выполняем статическую проверку.

Все.

Автор решения: cтудент гр.193 Шубочкин.А.В. (Нижегородский государственный архитектурно-строительный университет).

Копирование материалов допускается при наличии ссылки на первоисточник (на эту страницу).

Полезные ссылки

Программа для расчета любых рам, ферм он-лайн.

www.sopromat.org