Сопромат — Lurkmore
У этой страницы нет проверенных версий, вероятно, её качество не оценивалось на соответствие стандартам.| В эту статью нужно добавить как можно больше балок, статики и динамики. Также сюда можно добавить интересные факты, картинки и прочие кошерные вещи. |
| « | Cдал теормех — можно влюбиться. | » |
| — Распространенное студенческое заблуждение | ||
| « | Всё, что гнётся и ломается, — относится к сопромату и женщинам | » |
| — Анонимус | ||
Сопромат (сопротивление материалов, сопровождение матершинника) — инженерная дисциплина, изучаемая в вузах и ссузах технической направленности, раздел механики.
Использует уравнения механики сплошных сред и физики, вариационные принципы теормеха. По этой причине изучается, как правило, чуть позже оных, но при этом методами сопромата можно решать всякие хитрые задачи, от которых, например, теормех испытывает фууу и которые решить не должен.
Ещё более нелюбима студентами, чем матан, несмотря на то, что в сопромате в качестве математического аппарата в основном применяется обычная алгебра уровня 9-го класса школы, где самой трудной операцией является возведение в четвёртую степень. Строй-сопромат радует учащихся дифференциальными уравнениями первого и второго порядка и анализом имагинарных функций. Основной же сложностью является весьма специфичная техника расчетов, требующая аналитического мышления, а также построение эпюр, требующее пространственного воображения.
| Построение эпюры касательных напряжений |
Правда, если в алгебре уровня 9-го класса школы все эти уравнения имеют чисто абстрактный характер, то в сопромате они преследуют вполне конкретные цели, такие как расчет конструкции на сжатие, растяжение, изгиб, кручение, усталость металла, и прочую разъёбоустойчивость. Даже самое коротенькое уравнение редко влезает в три строки тетради, а решение его может затянуться листа на два.
С другой стороны, весь сабж умещается в трех истинах:
- Где тонко, там и рвется
- Была бы сила, момент найдется.
- Чуть менее, чем все былинные и не очень отказы IRL есть следствия хренового знания этой дисциплины.
| Резонанс, вызванный срывным флаттером (совпадение частоты срыва вихрей с кромки моста с собственной частотой колебаний) | Еще. |
По сопромату даже проводятся студенческие олимпиады уровнем вплоть до общегосударственного. Да и задачи не особо легче такового уровня по физике.
Радисты, прочие электронщики и программисты сопромата лишены. Поэтому представители других технических специальностей считают их неполноценными инженерами. Но не всегда… В ЛЭТИ дополнительно к теормеху существует дисциплина под названием «прикладная механика», примех, ПМ. На практике — тот же сопромат. В МИРЭА на факультете Кибернетики — та же петрушка. На ФРЭЛА МАИ даже последний кулхацкер проходит обстрел ядрёным курсом «несущие конструкции и механизмы ЭВА», слитым из сопромата, ТММ и теормеха, после которого не только шестерёнки принтера можно рассчитать, но и исполнительные механизмы ЧПУ вплоть до ОБЧР. Облегченным сопроматом забивают даже мозги химиков, в том же МИТХТ. Кстати, аналог сопромата у «любителей тока» — теория электроцепей и теория электрополей, так что собственное проклятье есть и у них. Сопромат они тоже учат, ибо всякие там микрические схемы и платы тоже нуждаются во всяких «сопротивлениях на изгиб» и прочей сопромататени — но не так сурово.
[править] Студенческие анекдоты по теме
Спросили нашего дорогого и любимого В. Е. Перельмана (сопромат), как он принимает экзамен. — Я задаю вопрос, если студент не отвечает, мне становится все ясно, ставлю ему неуд и выгоняю нахрен с экзамена. — А если отвечает? — Я задаю ему еще один вопрос, если он не отвечает, мне становится все ясно, я ставлю ему неуд и выгоняю нахрен с экзамена. — А если снова отвечает? — Я задаю ему третий вопрос, если он не отвечает, мне становится все ясно, я ставлю ему неуд и выгоняю нахрен с экзамена. — И как долго это продолжается? — Пока мне все не станет ясно! |
Защищал как-то американский студент свой дипломный проект по сопромату: «Пожароустойчивость высотных зданий». В нем он доказал, что из-за пожара небоскреб упасть не может. Через неделю полиция нашла его тело… |
Объявление в Челябинской Государственной Агроинженерной Академии: Рефераты, дипломные и курсовые работы по сопромату. Цена договорная. Если договоримся, то можете вообще ко мне на пару не ходить. |
При этом в реальной жизни все эти аналитические методы и системы уравнений десятки лет уже никто вручную не считает ввиду сложности анализируемых конструкций и наличия численных методов и соответствующего ПО.
А вместо этого вашего институтского сопромата на три листа тетрадочки вовсю используется так называемый метод конечных элементов, когда болван-компьютер разбивает расчет заданой детали на миллионы мелких подзадач, каждая из которых может быть решена теми самыми примитивными формулами, которые студенты осваивали в тетрадках целый семестр. То есть, считается не сама деталь целиком, а её кусочки, при этом результаты расчета напряжений предыдущего кусочка используются как входные данные для следующего и так далее.
Однако, стоит заметить, что такой подход работает лишь в случае с более или менее известными и распространёнными конструкциями типа хрущевок-брежневок. Как только надо строить что-либо нестандартное, горе-инженеры лезут из кожи вон, чтобы проект или хотя бы своё участие в нём слить, ибо там калькулятор не поможет, и надо ручками-ручками. В таком случае выясняется, что в сабже надо шарить вполне себе неиллюзорно, так как все методы «на отъебись» больше не прокатывают. А для того, чтобы 9-этажки во всяких CAD-ах рисовать, инженера и не нужно. Однако в строительстве фейл инженера (который может выявиться далеко не сразу, а через годы после приёмки объекта) чреват тем, что легко может убить пользователей этого здания, а это влечёт сопутствующие последствия для строителей, причём спектр применяемых статей начинается от «халатности со смертельным исходом», а заканчивается «убийством».
Есть ещё один способ решать подобные задачи необычным способом. Для этого из стекла или прозрачных пластиков строится моделька, которую затем хитро облучают плоскополяризованным лучом света (гугли полярископ, нерд). Нахрена? Прошедший через модельку луч в местах механических напряжений успел поменять поляризацию и позволяет при правильной обработке выявить как распределяются напряжения в модельке. Называется всё это безобразие «поляризационно-оптический метод исследования напряжений».
lurkmore.to
Что изучает сопротивление материалов и что это за наука
/ Сопротивление материалов онлайн/ 0 комментариев
Сопротивление материалов — это наука, которая занимается расчетом на прочность, жесткость и устойчивость — это те три вопроса, что изучает сопротивление материалов.
Да, всего три вопроса, а вот каково разнообразие этих расчетов, например на прочность:
- при растяжении-сжатии
- при изгибе
- при кручении
- при сдвиге
- при срезе
- при смятии
- сложное сопротивление (когда действует несколько деформаций одновременно)
После расчета на прочность нужно провести расчет на жесткость.
Что изучает сопротивление материалов — видео урок
Вот видео урок в котором объясняется что изучает сопротивление материалов, о чем предмет сопротивление материалов, что за наука — сопромат:
Расчет на прочность
При расчете на прочность мы даем ответ вопрос: выдержит ли, не разрушится ли (сломается) наша конструкция, тело, объект.
Расчет на жесткость
Дает ответ на второй вопрос: не будет ли прогиб, растяжение-сжатие, или другой вид деформации слишком большим. Конечно же не комфортно ходить по полу в доме, который прогибается под ногами. Или когда крыша над головой «висит». Это и есть не жесткая конструкция. Она прочная, выдерживает, не «ломается», но, при этом, не жесткая.
достаточно жесткая балка
Расчет на устойчивость
Расчет на устойчивость дает ответ на еще один вопрос. Часто, колонны, поддерживающие крыши, балконы и другие конструкции, бывают большой длины (высоты). В механических конструкциях тоже встречаются различные стержни, которые тонкие и длинные. Так вот, это и есть гибкость, такое понятие, которое определяется двумя показателями — длина и тонкое сечение. Ну линейка, например (только длинная сантиметров на 100). Если к ней приложить нагрузку на сжатие, то увеличивая ее все больше и больше в определенный момент времени, она изогнется. Это явление называют потеря устойчивости. Она еще не «сломалась», но уже не такая какой мы ее запроектировали в конструкции. А это мы должны заранее предусмотреть и рассчитать.
Какие бывают виды деформации
В нашей жизни, в природе, в строительных конструкциях, машинах и механизмах внешние воздействия: ветер, собственный вес объекта, вес других предметов и объектов вызывают различные изменения, которые мы называем деформацией. А деформации, которые возникают, разделяют на соответствующие виды:
- растяжение — сжатие
- изгиб
- кручение
Есть и другие, но пока остановимся на том, что названо. Так вот определение изменения усилий, вызывающих эти деформации, построение графиков этих изменений — называют построением эпюр внутренних усилий. Об этом сняты видео в соответствующих разделах. Так например при изгибе строят эпюры изгибающих моментов M и поперечных сил Q. При растяжении сжатии — строят эпюры продольных сжимающих и растягивающих внутренних усилий N. Пример решения такой задачи, на построение эпюр приведен по ссылке выше. Ну и в задачах на кручение — строят эпюры крутящих моментов.
Диграмма растяжения стали и вид образцов в каждой характерной точке диаграммы
вид образца для испытаний на растяжение
Сопротивление материалов — это… Что такое Сопротивление материалов?
 Внешние силовые линии увеличиваются около отверстия, в общем случае концентрации напряжений
Внешние силовые линии увеличиваются около отверстия, в общем случае концентрации напряженийСопротивление материалов (в обиходе — сопромат) — часть механики деформируемого твёрдого тела, которая рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности. Сопротивление материалов относится к фундаментальным дисциплинам общеинженерной подготовки специалистов с высшим техническим образованием, за исключением специальностей, не связанных с проектированием объектов, для которых прочность является важным показателем.
Определение
Сопротивление материалов базируется на понятии «прочность», что является способностью материала противостоять приложенным нагрузкам и воздействиям без разрушения. Сопротивление материалов оперирует такими понятиями как: внутренние усилия, напряжения, деформации. Приложенная внешняя нагрузка к некоторому телу порождает внутренние усилия в нём, противодействующие активному действию внешней нагрузки. Внутренние усилия, распределенные по сечениям тела называются напряжениями. Таким образом, внешняя нагрузка порождает внутреннюю реакцию материала, характеризующуюся напряжениями,которые в свою очередь прямо пропорциональны деформациям тела. Деформации бывают линейные такие как удлинение,укорочение, сдвиг и углы поворота сечений. Основные понятия сопротивления материалов оценивающие способность материала сопротивляться внешним воздействиям являются:
1. Несущая способность — способность материала воспринимать внешнюю нагрузку не разрушаясь;
2. Жесткость — способность материала сохранять свои геометрические параметры в допустимых пределах при внешних воздействиях
3. Устойчивость — способность материала сохранять в стабильности свою форму и положение при внешних воздействиях
Связь с другими науками
В теоретической части сопротивление материалов базируется на математике и теоретической механике, в экспериментальной части — на физике и материаловедении и применяется при проектировании машин, приборов и конструкций. Практически все специальные дисциплины подготовки инженеров по разным специальностям содержат разделы курса сопротивления материалов, так как создание работоспособной новой техники невозможно без анализа и расчета её прочности, жёсткости и надёжности.
Задачей сопротивления материалов, как одного из разделов механики сплошной среды, является определение деформаций и напряжений в твёрдом упругом теле, которое подвергается силовому или тепловому воздействию.
Эта же задача среди других рассматривается в курсе теории упругости. Однако методы решения этой общей задачи в том и другом курсах существенно отличаются друг от друга. Сопротивление материалов решает её главным образом для бруса, базируясь на ряде гипотез геометрического или физического характера. Такой метод позволяет получить, хотя и не во всех случаях, вполне точные, но достаточно простые формулы для вычисления напряжений. Также поведением деформируемых твёрдых тел под нагрузкой занимается теория пластичности и теория вязкоупругости.
Гипотезы и допущения
Расчет конструкций и их элементов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов существует модель идеализированного деформируемого тела.
- Гипотеза сплошности и однородности — материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела.
- Гипотеза об изотропности материала — физико-механические свойства материала одинаковы по всем направлениям.
- Гипотеза об идеальной упругости материала — тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.
- Гипотеза (допущение) о малости деформаций — деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.
- Допущение о справедливости закона Гука — перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения.
- Принцип независимости действия сил — принцип суперпозиции; результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.
- Гипотеза Бернулли о плоских сечениях — поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.
- Принцип Сен-Венана — в сечениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.
Эти положения ограниченно применимы к решению конкретных закдач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.
Теории прочности
Прочность конструкций определяется с использованием теории разрушения — науки о прогнозировании условий, при которых твердые материалы разрушаются под действием внешних нагрузок. Материалы, как правило, подразделяются на разрушающиеся хрупко и пластично. В зависимости от условий (например, температура, состояние напряжений, виды нагрузки) большинство материалов может быть отнесено к хрупким или пластичным или обоим видам одновременно. Тем не менее, для большинства практических ситуаций, материалы могут быть классифицированы как хрупкие или пластичные. Несмотря на то, что теория разрушения находится в разработке уже более 200 лет, уровень её приемлемости для механики сплошных сред, не всегда достаточен.
В математических терминах, теория разрушения выражается в виде различных критериев разрушения, которые справедливы для конкретных материалов. Критерием разрушения является поверхность разрушения, выраженная через напряжения или деформации. Поверхность разрушения разделяет «поврежденное» и «не поврежденное» состояния. Для «поврежденного» состояния трудно дать точное физическое определение. Поэтому это понятие следует рассматривать как рабочее определение, используемое в инженерном сообществе. Термин «поверхность разрушения», используемый в теории прочности, не следует путать с аналогичным термином, который определяет физическую границу между поврежденными и не поврежденными частями тела. Довольно часто феноменологические критерии разрушения одного и того же вида используются для прогнозирования хрупкого и пластичного разрушения.
Среди феноменологических теорий прочности наиболее известными являются следующие теории, которые принято называть «классическими» теориями прочности:
1. Теория наибольших нормальных напряжений.
2. Теория наибольших деформаций.
3. Теория наибольших касательных напряжений Треска (Tresca).
4. Теория наибольшей удельной потенциальной энергии формоизменения фон Мизеса (von Mises).
5. Теория Мора (Mohr).
Классические теории прочности имеют существенные ограничения для их применения. Так теории наибольших нормальных напряжений и наибольших деформаций применимы лишь для расчета прочности хрупких материалов, причём только для некоторых определённых условий нагружения. Поэтому эти теории прочности сегодня применяют весьма ограниченно. Из перечисленных теорий наиболее часто используют теорию Мора, которую также называют критерием Мора-Кулона. Кулон (Coulomb) в 1781 г. на основе выполненных им испытаний установил закон сухого трения, который использовал для расчета устойчивости подпорных стенок. Математическая формулировка закона Кулона совпадает с теорией Мора, если в ней выразить главные напряжения через касательные и нормальные напряжения на площадке среза. Достоинством теории Мора является то, что она применима к материалам, имеющим разные сопротивления сжатию и растяжению, а недостатком то, что она учитывает влияние только двух главных напряжений — максимального и минимального. Поэтому теория Мора не точно оценивает прочность при трехосном напряженном состоянии, когда необходимо учитывать все три главных напряжения. Кроме того, при использовании эта теория не учитывается поперечное расширение (дилатацию) материала при сдвиге. На эти недостатки теории Мора неоднократно обращал внимание А. А. Гвоздев, который доказал неприменимость теории Мора для бетона [2].
На смену «классическим» теориям прочности в современной практике пришли многочисленные новые новые теории разрушения. Большинство из них используют различные комбинации инвариантов тензора напряжений Коши (Cauchy) Среди них наиболее известны следующие критерии разрушения:
- Друкера-Прагера (Drucker-Prager).
- Бреслера-Пистера (Bresler-Pister) — для бетона.
- Вильяма-Варнке (Willam-Warnke) — для бетона.
- Хенкинсона (Hankinson)- эмпирический критерий, используемый для ортотропных материалов типа древесины.
- Хила (Hill) — для анизотропных тел.
- критерий Tsai-Wu — для анизотропных материалов.
- критерий Hoek-Brown -для скальных массивов.
Перечисленные критерии прочности предназначены для расчета прочности однородных (гомогенных) материалов. Некоторые из них используются для расчёта анизотропных материалов.
Для расчета прочности неоднородных (не гомогенных) материалов используется два подхода, называемые макро-моделированием и микро-моделированием. Оба подхода ориентированы на использование метода конечных элементов и вычислительной техники. При макро-моделировании предварительно выполняется гомогенизация — условная замена неоднородного (гетерогенного) материала на однородный (гомогенный). При микро-моделировании компоненты материала рассматриваются с учётом их физических характеристик. Микро-моделирование используют в основном в исследовательских целях, так как расчет реальных конструкций требует чрезмерно больших затрат машинного времени. Методы гомогенизации широко используются для расчета прочности каменных конструкций, в первую очередь для расчета стен-диафрагм жесткости зданий. Критерии разрушения каменных конструкций учитывают многообразные формы разрушения каменной кладки. Поэтому поверхность разрушения, как правило. принимается в виде нескольких пересекающихся поверхностей, которые могут иметь разную геометрическую форму.
Применение
Методы сопротивления материалов широко используются при расчете несущих конструкций зданий и сооружений, в дисциплинах связанных с проектированием деталей машин и механизмов.
Как правило, именно из-за оценочного характера результатов, получаемых с помощью математических моделей этой дисциплины, при проектировании реальных конструкций все прочностные характеристики материалов и изделий выбираются с существенным запасом (в несколько раз относительно результата, полученного при расчетах).
В студенческой среде сопротивление материалов считается одной из наиболее сложных общепрофессиональных дисциплин, что дало богатую пищу студенческому фольклору и породило целый ряд шуток и анекдотов.
См. также
Литература
1.^Старовойтов Э. И. Сопротивление материалов. — М.: ФИЗМАТЛИТ, 2008. — С. 384. — ISBN 978-5-9221-0883-6
2.^Гениев Г.А., Киссюк В.Н., Тюпин Г.А. Теория пластичности бетона и железобетона. — М.: Стройиздат, 1974.
dvc.academic.ru
Сопротивление материалов | ПроСопромат.ру
Сопромат – это предмет, который изучается во всех технических вузах, и вот почему. Дело в том, что этот предмет является основой для изучения всех без исключения конструкций – машиностроительных, строительных и др. Что же изучает сопромат? В старых учебниках ответ на этот вопрос таков – сопромат является наукой о прочности, которая занимается расчетом инженерных конструкций и определяет их надежные размеры. Это, безусловно, правильное определение, но не совсем полное. В учебниках нового поколения сопромат определяется как наука, занимающаяся расчетами конструкций на прочность, жесткость и устойчивость. Разберемся, что же это такое.
Прочность – это свойство конструкций не разрушаться под действием нагрузки. Жесткость – свойство конструкций получать предельно малые деформации под нагрузкой (крайне незначительно менять свою форму и размеры, в определенных пределах). Устойчивость – это свойство конструкций сохранять проектную, заданную форму равновесия. Таким образом, можно обобщить, что сопромат – это наука о расчетах элементов конструкций на механическую надежность (прочность, жесткость и устойчивость).
Требования к сооружениям – надежность, долговечность, экономичность, эстетичность. Надежность обеспечивается грамотными расчетами на перечисленные выше свойства. Долговечность вполне понятна, она гарантирует длительный период эксплуатации конструкции без разрушений. Экономичность заставляет подбирать такие варианты размеров элементов сооружений, при которых были бы обеспечены их прочность, жесткость и устойчивость, и не было лишнего расхода материалов. Кроме того, сооружение должно радовать взгляд, но это уже задача архитекторов и дизайнеров.
Для достижения этих требований определяются задачи сопромата – изучение методов расчета на прочность, жесткость и устойчивость элементов конструкций.
Сопромат дает теоретические основы для расчета инженерных конструкций, это азбука для технических специалистов.
prosopromat.ru
Что такое сопромат
В советские времена студенты шутили — сдал сопромат? Можешь жениться! Это свидетельствует о том, что это одна из наиболее сложных дисциплин, которую изучают будущие инженеры, строители и иные представители технических дисциплин.
Овладение данным предметом требует аналитического мышления, необходимо иметь пространственное воображение.
Если нет времени, чтобы решить задачи по сопромату, то я рекомендую обратиться к опытному специалисту. Это позволит получить допуск к зачёту или экзамену. В учебных заведениях очень строго подходят к срокам сдачи контрольных работ. Работающим студентам зачастую не хватает времени на решение и оформление заданий. Помимо работы и учёбы у них есть семья, личная жизнь, друзья. В этом случае обращаются к специалистам, которые за короткое время способны решить задачи и правильно их оформить. К ним обращаются студенты гуманитарных вузов, изучающие краткий курс технических дисциплин. Стоимость зависит от сложности заданий и срочности их выполнения. Если студент обращается за несколько дней до сдачи, то цена услуги будет выше. Отправить задание и получить готовое решение можно через интернет.
Что изучает сопромат
Это слово означает сопротивление материалов. Студенты изучают такие понятия, как жёсткость, устойчивость, напряжение, внутреннее усилие, прочность и сложное сопротивление. Под прочностью понимают способность материала сопротивляться внешнему воздействию и не разрушаться при этом. Жесткость — это способность материалов сохранять свои геометрические размеры при внешнем воздействии в прежнем размере. Будущим строителям, архитекторам, инженерам предстоит изучить, насколько будет изменяться материал при внешних воздействиях. От этого зависит безопасность человека, которому предстоит жить в построенном здании, лететь в самолёте или переходить через мост
Этот раздел механики появился в 17 веке. Впервые его рассмотрел Галилей. Подразделы были изучены в дальнейшем. Англичанин Гук рассмотрел способность материала к сопротивлению нагрузкам.
Студентам предстоит прослушать лекции по сопромату. На семинарах они решают задачи, которые им позволяют в дальнейшем конструировать безопасные здания, конструкции, технику. После курса сопромата студенты переходят к изучению узкоспециализированных дисциплин — теория упругости, динамика сооружений и ряд иных курсов.

anapa.net.ru
Сопротивление материалов — это… Что такое Сопротивление материалов?
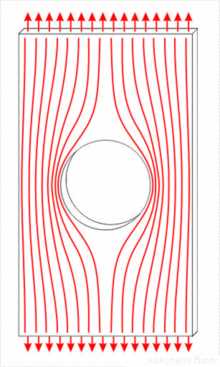 Внешние силовые линии увеличиваются около отверстия, в общем случае концентрации напряжений
Внешние силовые линии увеличиваются около отверстия, в общем случае концентрации напряженийСопротивление материалов (в обиходе — сопромат) — часть механики деформируемого твёрдого тела, которая рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности. Сопротивление материалов относится к фундаментальным дисциплинам общеинженерной подготовки специалистов с высшим техническим образованием, за исключением специальностей, не связанных с проектированием объектов, для которых прочность является важным показателем.
Определение
Сопротивление материалов базируется на понятии «прочность», что является способностью материала противостоять приложенным нагрузкам и воздействиям без разрушения. Сопротивление материалов оперирует такими понятиями как: внутренние усилия, напряжения, деформации. Приложенная внешняя нагрузка к некоторому телу порождает внутренние усилия в нём, противодействующие активному действию внешней нагрузки. Внутренние усилия, распределенные по сечениям тела называются напряжениями. Таким образом, внешняя нагрузка порождает внутреннюю реакцию материала, характеризующуюся напряжениями,которые в свою очередь прямо пропорциональны деформациям тела. Деформации бывают линейные такие как удлинение,укорочение, сдвиг и углы поворота сечений. Основные понятия сопротивления материалов оценивающие способность материала сопротивляться внешним воздействиям являются:
1. Несущая способность — способность материала воспринимать внешнюю нагрузку не разрушаясь;
2. Жесткость — способность материала сохранять свои геометрические параметры в допустимых пределах при внешних воздействиях
3. Устойчивость — способность материала сохранять в стабильности свою форму и положение при внешних воздействиях
Связь с другими науками
В теоретической части сопротивление материалов базируется на математике и теоретической механике, в экспериментальной части — на физике и материаловедении и применяется при проектировании машин, приборов и конструкций. Практически все специальные дисциплины подготовки инженеров по разным специальностям содержат разделы курса сопротивления материалов, так как создание работоспособной новой техники невозможно без анализа и расчета её прочности, жёсткости и надёжности.
Задачей сопротивления материалов, как одного из разделов механики сплошной среды, является определение деформаций и напряжений в твёрдом упругом теле, которое подвергается силовому или тепловому воздействию.
Эта же задача среди других рассматривается в курсе теории упругости. Однако методы решения этой общей задачи в том и другом курсах существенно отличаются друг от друга. Сопротивление материалов решает её главным образом для бруса, базируясь на ряде гипотез геометрического или физического характера. Такой метод позволяет получить, хотя и не во всех случаях, вполне точные, но достаточно простые формулы для вычисления напряжений. Также поведением деформируемых твёрдых тел под нагрузкой занимается теория пластичности и теория вязкоупругости.
Гипотезы и допущения
Расчет конструкций и их элементов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов существует модель идеализированного деформируемого тела.
- Гипотеза сплошности и однородности — материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела.
- Гипотеза об изотропности материала — физико-механические свойства материала одинаковы по всем направлениям.
- Гипотеза об идеальной упругости материала — тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.
- Гипотеза (допущение) о малости деформаций — деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.
- Допущение о справедливости закона Гука — перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения.
- Принцип независимости действия сил — принцип суперпозиции; результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.
- Гипотеза Бернулли о плоских сечениях — поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.
- Принцип Сен-Венана — в сечениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.
Эти положения ограниченно применимы к решению конкретных закдач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.
Теории прочности
Прочность конструкций определяется с использованием теории разрушения — науки о прогнозировании условий, при которых твердые материалы разрушаются под действием внешних нагрузок. Материалы, как правило, подразделяются на разрушающиеся хрупко и пластично. В зависимости от условий (например, температура, состояние напряжений, виды нагрузки) большинство материалов может быть отнесено к хрупким или пластичным или обоим видам одновременно. Тем не менее, для большинства практических ситуаций, материалы могут быть классифицированы как хрупкие или пластичные. Несмотря на то, что теория разрушения находится в разработке уже более 200 лет, уровень её приемлемости для механики сплошных сред, не всегда достаточен.
В математических терминах, теория разрушения выражается в виде различных критериев разрушения, которые справедливы для конкретных материалов. Критерием разрушения является поверхность разрушения, выраженная через напряжения или деформации. Поверхность разрушения разделяет «поврежденное» и «не поврежденное» состояния. Для «поврежденного» состояния трудно дать точное физическое определение. Поэтому это понятие следует рассматривать как рабочее определение, используемое в инженерном сообществе. Термин «поверхность разрушения», используемый в теории прочности, не следует путать с аналогичным термином, который определяет физическую границу между поврежденными и не поврежденными частями тела. Довольно часто феноменологические критерии разрушения одного и того же вида используются для прогнозирования хрупкого и пластичного разрушения.
Среди феноменологических теорий прочности наиболее известными являются следующие теории, которые принято называть «классическими» теориями прочности:
1. Теория наибольших нормальных напряжений.
2. Теория наибольших деформаций.
3. Теория наибольших касательных напряжений Треска (Tresca).
4. Теория наибольшей удельной потенциальной энергии формоизменения фон Мизеса (von Mises).
5. Теория Мора (Mohr).
Классические теории прочности имеют существенные ограничения для их применения. Так теории наибольших нормальных напряжений и наибольших деформаций применимы лишь для расчета прочности хрупких материалов, причём только для некоторых определённых условий нагружения. Поэтому эти теории прочности сегодня применяют весьма ограниченно. Из перечисленных теорий наиболее часто используют теорию Мора, которую также называют критерием Мора-Кулона. Кулон (Coulomb) в 1781 г. на основе выполненных им испытаний установил закон сухого трения, который использовал для расчета устойчивости подпорных стенок. Математическая формулировка закона Кулона совпадает с теорией Мора, если в ней выразить главные напряжения через касательные и нормальные напряжения на площадке среза. Достоинством теории Мора является то, что она применима к материалам, имеющим разные сопротивления сжатию и растяжению, а недостатком то, что она учитывает влияние только двух главных напряжений — максимального и минимального. Поэтому теория Мора не точно оценивает прочность при трехосном напряженном состоянии, когда необходимо учитывать все три главных напряжения. Кроме того, при использовании эта теория не учитывается поперечное расширение (дилатацию) материала при сдвиге. На эти недостатки теории Мора неоднократно обращал внимание А. А. Гвоздев, который доказал неприменимость теории Мора для бетона [2].
На смену «классическим» теориям прочности в современной практике пришли многочисленные новые новые теории разрушения. Большинство из них используют различные комбинации инвариантов тензора напряжений Коши (Cauchy) Среди них наиболее известны следующие критерии разрушения:
- Друкера-Прагера (Drucker-Prager).
- Бреслера-Пистера (Bresler-Pister) — для бетона.
- Вильяма-Варнке (Willam-Warnke) — для бетона.
- Хенкинсона (Hankinson)- эмпирический критерий, используемый для ортотропных материалов типа древесины.
- Хила (Hill) — для анизотропных тел.
- критерий Tsai-Wu — для анизотропных материалов.
- критерий Hoek-Brown -для скальных массивов.
Перечисленные критерии прочности предназначены для расчета прочности однородных (гомогенных) материалов. Некоторые из них используются для расчёта анизотропных материалов.
Для расчета прочности неоднородных (не гомогенных) материалов используется два подхода, называемые макро-моделированием и микро-моделированием. Оба подхода ориентированы на использование метода конечных элементов и вычислительной техники. При макро-моделировании предварительно выполняется гомогенизация — условная замена неоднородного (гетерогенного) материала на однородный (гомогенный). При микро-моделировании компоненты материала рассматриваются с учётом их физических характеристик. Микро-моделирование используют в основном в исследовательских целях, так как расчет реальных конструкций требует чрезмерно больших затрат машинного времени. Методы гомогенизации широко используются для расчета прочности каменных конструкций, в первую очередь для расчета стен-диафрагм жесткости зданий. Критерии разрушения каменных конструкций учитывают многообразные формы разрушения каменной кладки. Поэтому поверхность разрушения, как правило. принимается в виде нескольких пересекающихся поверхностей, которые могут иметь разную геометрическую форму.
Применение
Методы сопротивления материалов широко используются при расчете несущих конструкций зданий и сооружений, в дисциплинах связанных с проектированием деталей машин и механизмов.
Как правило, именно из-за оценочного характера результатов, получаемых с помощью математических моделей этой дисциплины, при проектировании реальных конструкций все прочностные характеристики материалов и изделий выбираются с существенным запасом (в несколько раз относительно результата, полученного при расчетах).
В студенческой среде сопротивление материалов считается одной из наиболее сложных общепрофессиональных дисциплин, что дало богатую пищу студенческому фольклору и породило целый ряд шуток и анекдотов.
См. также
Литература
1.^Старовойтов Э. И. Сопротивление материалов. — М.: ФИЗМАТЛИТ, 2008. — С. 384. — ISBN 978-5-9221-0883-6
2.^Гениев Г.А., Киссюк В.Н., Тюпин Г.А. Теория пластичности бетона и железобетона. — М.: Стройиздат, 1974.
dic.academic.ru
Сопротивление материалов — это… Что такое Сопротивление материалов?
наука о прочности и деформируемости элементов (деталей) сооружений и машин. Основные объекты изучения С. м. — стержни и пластины, для которых устанавливаются соответствующие методы расчёта на прочность, жёсткость и устойчивость при действии статических и динамических нагрузок. С. м. базируется на законах и выводах теоретической механики (См. Механика), но, помимо этого, учитывает способность материалов деформироваться под действием внешних сил. Физико-механические характеристики (предел текучести, предел прочности, модуль упругости и т.п.), необходимые для оценки прочности и деформативности материалов, определяются при помощи испытательных машин и специальных измерительных приборов — Тензометров. При испытаниях обеспечиваются требуемые условия загружения и высокая точность измерения деформаций испытываемых образцов материалов. Наиболее характерно испытание на растяжение образцов, представляющих собой стержни круглого сечения или полосы с сечением в виде узкого прямоугольника. По результатам этих испытаний строится т. н. диаграмма растяжения-сжатия (См. Растяжение-сжатие). Располагая диаграммой испытания и пользуясь разработанными в С. м. методами расчёта, можно предсказать, как будет вести себя реальная конструкция, изготовленная из того же материала.Основное содержание и методы С. м. При деформации твёрдого тела под нагрузкой изменяется взаимное расположение его микрочастиц, вследствие чего в теле возникают внутренние напряжения. В С. м. определяются наибольшие напряжения в элементах сооружений или деталях машин. Они сравниваются с нормативными величинами, т. е. с напряжениями, которые можно допустить, не опасаясь повреждения или разрушения этих элементов (деталей). Проверке подлежат также деформации тела и перемещения его отдельных точек. Помимо необходимой прочности, конструкция должна быть также устойчивой, т. е. обладать способностью при малых случайных кратковременных воздействиях, нарушающих её равновесие, лишь незначительно отклоняться от исходного состояния. Выполнение этого требования зависит от внешних сил, геометрии элемента (детали) и от физических констант материала.
Для расчёта элементов конструкций в С. м. разрабатываются приближённые инженерные методы, использующие кинематические и статические гипотезы, которые в большинстве случаев оказываются достаточно близкими к действительности. При выводе расчётных формул для определения напряжений и перемещений производится схематизация рассчитываемого элемента сооружения, его опорных закреплений и действующей нагрузки, иначе говоря, создаётся Расчётная схема (модель) объекта. При построении общей теории расчёта в С. м. рассматриваются т. н. идеализированные тела со свойствами, лишь приближённо отражающими поведение реальных объектов. Тела считаются однородными (со свойствами, одинаковыми во всех точках), сплошными (без пустот), обладающими упругостью (способностью восстанавливать свои размеры после снятия нагрузки), изотропными (с одинаковыми упругими свойствами по всем направлениям). На основе изучения простейших деформаций — растяжения-сжатия, кручения (См. Кручение), Изгиба в С. м. выводятся формулы, позволяющие для каждого из этих видов деформаций определять напряжения, перемещения и деформации в отдельных точках тела. При наличии одновременно двух или нескольких простейших деформаций, протекающих в упругой стадии (для которой справедлива линейная зависимость между напряжением и деформациями), напряжения и деформации, найденные отдельно для каждого вида, суммируются. Многие материалы (например, бетон) обладают свойством ползучести (см. Ползучесть материалов), вследствие которой деформации могут возрастать со временем при неизменной нагрузке. В С. м. устанавливаются законы развития ползучести и время, в течение которого она заметно проявляется, а также рассматривается воздействие на стержень ударной нагрузки, при которой возникают динамические напряжения; последние определяются по приближённым формулам, выведенным на основе ряда допущений. При расчёте элементов сложной формы, для которых аналитические формулы вывести не удаётся, применяют экспериментальные методы (например, оптический, лаковых покрытий, муаровых полос и др.), позволяющие получать наглядную картину распределения деформаций по поверхности исследуемого элемента (детали) и вычислять напряжения в его отдельных точках. Наибольшую трудность представляет определение т. н. остаточных напряжений, которые могут возникать в элементах конструкций, не несущих нагрузки (например, при сварке или в процессе прокатки стальных профилей).Одна из важных задач С. м. состоит в создании т. н. теорий прочности, на основе которых можно проверить прочность элементов в сложном напряжённом состоянии, исходя из прочностных характеристик, полученных опытным путём для простого растяжения-сжатия. Существует ряд теорий прочности; в каждом отдельном случае пользуются той из них, которая в наибольшей степени отвечает характеру нагружения и разрушения материала.
Историческая справка. История С. м., как и многих др. наук, неразрывно связана с историей развития техники (См. Техника). Зарождение науки о С. м. относится к 17 в.; её основоположником считается Галилей (См. Галилея), который впервые обосновал необходимость применения аналитических методов расчёта взамен эмпирических правил. Важным шагом в развитии С. м. явились экспериментальные исследования Р. Гука (60—70-е гг. 17 в.), установившего линейную зависимость между силой, приложенной к растянутому стержню, и его удлинением (закон Гука). В 18 в. большой вклад в развитие аналитических методов в С. м. был сделан Д. Бернулли, Л. Эйлером и Ш. Кулоном, сформулировавшими важнейшие гипотезы и создавшими основы теории расчёта стержня на изгиб и кручение. Исследования Эйлера в области продольного изгиба послужили основой для создания теории устойчивости стержней и стержневых систем. Т. Юнг ввёл (1807) понятие о модуле упругости при растяжении и предложил метод его определения. Важный этап в развитии С. м. связан с опубликованием (в 1826) Л. Навье первого курса С. м., содержавшего систематизированное изложение теории расчёта элементов конструкций и сооружений. Принципиальное значение имели труды А. Сен-Венана (2-я половина 19 в.). Им впервые были выведены точные формулы для расчёта на изгиб кривого бруса (См. Кривой брус) и сформулирован принцип, согласно которому распределение напряжений в сечениях, отстоящих на некотором расстоянии от места приложения нагрузки, не связано со способом её приложения, а зависит только от равнодействующей этой нагрузки. Большие заслуги в развитии С. м. принадлежат русскому учёным М. В. Остроградскому (См. Остроградский), исследования которого в области С. м., строительной механики, математики и теории упругости приобрели мировую известность, и Д. И. Журавскому (См. Журавский), впервые установившему (1855) наличие касательных напряжений в продольных сечениях бруса и получившему формулу для их определения (эта формула применяется и в современной практике инженерных расчётов). Всеобщее признание получили исследования Ф. С. Ясинского (См. Ясинский), разработавшего (1893) теорию продольного изгиба в упругой стадии и за её пределами (рекомендации Ясинского послужили основой для разработки современных нормативных документов в СССР и за рубежом). В начале 20 в. расширение масштабов применения железобетонных и стальных конструкций, появление сложных машин и механизмов обусловили быстрое развитие науки о С. м. Были опубликованы классические учебники С. П. Тимошенко по С. м. и строительной механике, труды А. Н. Динника по продольному изгибу, устойчивости сжатых стержней и др. Дальнейшему совершенствованию методов С. м. способствовало создание в СССР ряда научно-исследовательских учреждений для проведения исследований в области расчёта конструкций. Появились новые разделы С. м. Большое влияние на развитие С. м. оказали труды Н. М. Беляева в области пластических деформаций, А. А. Ильюшина по теории пластичности, Ю. Н. Работнова и А. Р. Ржаницына по теории ползучести. Значительным вкладом в науку о С. м. явилась созданная В. З. Власовым теория расчёта тонкостенных стержней и оболочек. Важные фундаментальные исследования выполнены советскими учёными Н. И. Безуховым, В. В. Болотиным, А. Ф. Смирновым, В. И. Феодосьевым и др.Современные тенденции развития науки о С. м. Одна из важнейших задач С. м. — установление причин и характера разрушения материалов, требующее всестороннего теоретического и экспериментального изучения процессов, происходящих в микрообъёмах тела, в частности характера возникновения и развития трещин. Установлено существование таких (предельных) напряжений, превышение которых влечёт за собой прогрессирующий рост уже появившихся трещин, приводящий в конечном счёте к разрушению тела. Если напряжения меньше указанного предела, то тело, имеющее трещины, находится в состоянии трещиноустойчивости. В некоторых случаях под действием нагрузки разрушения в микроэлементах распространяются на весь объём тела (особенно при высоких температурах). Исследование этих вопросов требует создания нового важного раздела механики деформируемого тела — механики разрушения. Ещё недостаточно изучен ряд вопросов т. н. усталостной прочности материалов, в частности прочность элементов (деталей) машин при их длительном циклическом нагружении.
В связи с появлением новых конструкционных материалов (См. Конструкционные материалы) (например, пластмасс, лёгких сплавов) возникла необходимость создания теорий прочности, отражающих специфические свойства этих материалов. Современные технологические процессы (например, с применением высоких давлений) позволяют получать материалы с весьма высокой прочностью, поведение которых под нагрузкой недостаточно изучено и требует целенаправленных исследований.Лит.: Тимошенко С. П., История науки о сопротивлении материалов с краткими сведениями из истории теории упругости и теории сооружений, М., 1957; Работнов Ю. Н., Сопротивление материалов, М.. 1962; Феодосьев В. И., Сопротивление материалов, М., 1974; Сопротивление материалов, М., 1975.
Под редакцией А. Ф. Смирнова.
dic.academic.ru