Изгиб | ПроСопромат.ру

При выводе формулы для вычисления нормальных напряжений рассмотрим такой случай изгиба, когда внутренние силы в сечениях балки приводятся только к изгибающему моменту, а поперечная сила оказывается равной нулю. Этот случай изгиба носит название чистого изгиба. Рассмотрим средний участок балки, подвергающийся чистому изгибу.

В нагруженном состоянии балка прогибается так,что ее нижние волокна удлиняются,а верхние укорачиваются.

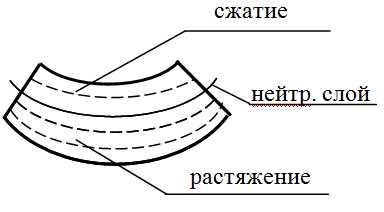
Поскольку часть волокон балки растягивается, а часть сжимается, причем переход от растяжения к сжатию происходит плавно, без скачков, в средней части балки находится слой, волокна которого только искривляются, но не испытывают ни растяжения, ни сжатия. Такой слой называют

нейтральным слоем. Линия, по которой нейтральный слой пересекается с поперечным сечением балки, называется нейтральной линией или нейтральной осью сечения. Нейтральные линии нанизаны на ось балки. Нейтральная линия — это линия, в которой нормальные напряжения равны нулю.

Линии, проведенные на боковой поверхности балки перпендикулярно оси, остаются плоскими при изгибе. Эти опытные данные позволяют положить в основу выводов формул гипотезу плоских сечений (гипотеза Бернулли). Согласно этой гипотезе сечения балки плоские и перпендикулярные к ее оси до изгиба, остаются плоскими и оказываются перпендикулярными изогнутой оси балки при ее изгибе.

Допущения для вывода формул нормального напряжения: 1)   Выполняется гипотеза плоских сечений.   2)   Продольные волокна друг на друга не давят (гипотеза о ненадавливании) и, следовательно, каждое из волокон находится в состоянии одноосного растяжения или сжатия.  3)   Деформации волокон не зависят от их положения по ширине сечения. Следовательно, и нормальные напряжения, изменяясь по высоте сечения, остаются по ширине одинаковыми.   4)   Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости.   5)   Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков.   6)   Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.

Рассмотрим балку произвольного сечения, но имеющую ось симметрии.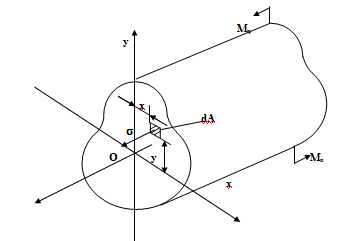Изгибающий момент представляет собой результирующий момент внутренних нормальных сил, возникающих на бесконечно малых площадках и может быть выражен в интегральном виде:  (1), где y — плечо элементарной силы относительно оси х

Формула (1) выражает статическую сторону задачи об изгибе прямого бруса, но по ней по известному изгибающему моменту нельзя определить нормальные напряжения, пока не установлен закон их распределения. 

Выделим на среднем участке балки и рассмотрим участок  длиной dz, подвергающийся изгибу. Изобразим его в укрупненном масштабе.

К выводу формул при изгибе: а) участок балки до деформации; б) участок балки после деформации

Сечения, ограничивающие участок dz, параллельны друг другу до деформации, а после приложения нагрузки повернутся вокруг своих нейтральных линий на угол . Длина отрезка волокон нейтрального слоя при этом не изменится и будет равна:, где  -это радиус кривизны изогнутой оси балки. А вот любое другое волокно, лежащее ниже или выше нейтрального слоя, изменит свою длину. Вычислим относительное удлинение волокон, находящихся от нейтрального слоя на расстоянии у.

Относительное удлинение — это отношение абсолютной деформации к первоначальной длине ,тогда:

 Сократим на и приведем подобные члены, тогда получим:(2) Эта  формула выражает геометрическую сторону задачи о чистом изгибе: деформации волокон прямо пропорциональны их расстояниям до нейтрального слоя. 

Теперь перейдем к напряжениям, т.е. будем рассматривать физическую сторону задачи. в соответствии с допущением о ненадавливании волокон используем закон Гука при осевом растяжении-сжатии:, тогда с учетом формулы (2) имеем (3),т.е.  нормальные напряжения при изгибе по высоте сечения распределяются по линейному закону. На крайних волокнах нормальные напряжения достигают максимального значения, а в центре тяжести сечения равны нулю. Подставим  

(3) в уравнение (1) и вынесем за знак интеграла дробь  как постоянную величину, тогда имеем. Но выражение  — это осевой момент инерции сечения относительно оси х  — I_х. Его размерность см⁴, м⁴

Тогда ,откуда (4) ,где — это кривизна изогнутой оси балки, а — жесткость сечения балки при изгибе.

Подставим полученное выражение кривизны (4) в выражение (3) и получим формулу для вычисления нормальных напряжений в любой точке поперечного сечения: (5) 

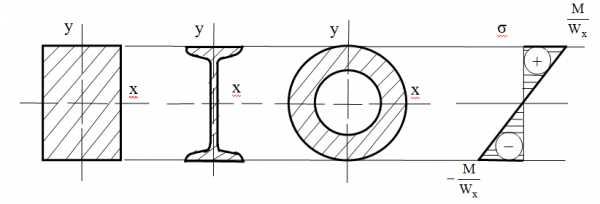
Т.о. максимальные напряжения возникают в точках, наиболее удаленных от нейтральной линии. Отношение  (6) называют осевым моментом сопротивления сечения. Его размерность см³, м³. Момент сопротивления характеризует влияние формы и размеров поперечного сечения на величину напряжений.

Тогда максимальные напряжения:  (7)

Условие прочности при изгибе: (8)

При поперечном изгибе действуют не только нормальные, но и касательные напряжения,т.к. имеется поперечная сила. Касательные напряжения усложняют картину деформирования, они приводят к искривлению поперечных сечений балки, в результате чего нарушается гипотеза плоских сечений. Однако исследования показывают, что искажения, которые привносят касательные напряжения, незначительно влияют на нормальные напряжения,подсчитанные по формуле (5). Таким образом ,при определении нормальных напряжений в случае поперечного изгиба теория чистого изгиба вполне применима.

Нейтральная линия. Вопрос о положении нейтральной линии. 

При изгибе отсутствует продольная сила, поэтому можно записать Подставим сюда формулу нормальных напряжений

(3) и получим Так как модуль продольной упругости материала балки не равняется нулю и изогнутая ось балки имеет конечный радиус кривизны, остается положить, что  этот интеграл представляет собой статический момент площади поперечного сечения балки относительно нейтральной линии-оси х , и, поскольку он равен нулю, то нейтральная линия проходит через центр тяжести сечения.

Условие  (отсутствие момента внутренних сил относительно силовой линии) даст или с учетом (3) . По тем же соображениям (см. выше) . В подынтегральном выражении — центробежный момент инерции сечения относительно осей х и у  равен нулю, значит, эти оси являются главными и центральными и составляют прямой угол. Следовательно, силовая и нейтральная линии пр  прямом изгибе взаимно перпендикулярны. 

Установив положение нейтральной линии, несложно построить эпюру нормальных напряжений по высоте сечения. Ее линейный характер определяется уравнением первой степени.

Характер эпюры σ для симметричных сечений относительно нейтральной линии, М<0

prosopromat.ru

Напряжения и прочность при изгибе

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.

Закон распределения нормальных напряжений по высоте сечения выражается формулой:

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2: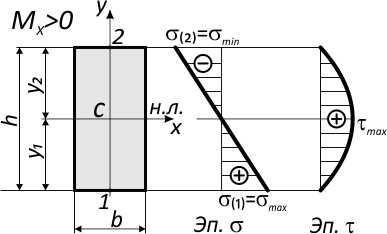

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2:

где:

W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.

Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[σ], [σ]_р, [σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]_с>[σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
3. Определение максимально допустимой нагрузки
   

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского

где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max:

где [τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

1. По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
2. По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
3. По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда M_max и Q_max действуют в одном и том же сечении балки).

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид:

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >

isopromat.ru

решение задач. Пример решения задачи. Расчет статически определимой балки.

Меню сайта Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления. Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. + Полное расписанное решение! Теперь и для статически неопределимых балок! Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты

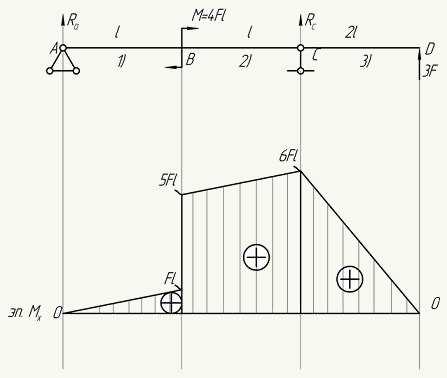
Пример №1. Расчет статически определимой балки, подбор сечения. Необходимо определить минимальный диаметр круглого сечения d балки в точке С. Решение. Определяем реакции опор в точках A и C. Для этого составляем уравнения моментов относительно этих точек: откуда: Делаем проверку: Проверка показала, что реакции опор найдены верно. Строим эпюру изгибающих моментов: 1) Участок 1 (от A до B) Mx = Ra · z; z = 0; Mx = 0; z = l; Mx = Fl; 2) Участок 2 (от B до C) Mx = Ra · (l + z) + M; z = 0; Mx = 5Fl; z = l; Mx = 6Fl; 3) Участок 3 (от D до C, подчеркиваю от D до С, т.к. балку на этом участке рассматривает справа налево): Mx = 3F · z; z = 0; Mx = 0; z = 2L; Mx = 6Fl; Находим минимальный диаметр d в точке С: где Мс – момент на эпюре моментов в точке С Все. Автор решения Алексей Большаков (The Боль). Копирование материалов допускается при наличии ссылки на первоисточник (на эту страницу). Полезные ресурсы 1. Он-лайн программа (версия 2004 года), которая выдаст расписанное решение любой балки. Пример результата. Кроме построения эпюр эта программа так же подбирает профиль сечения по условию прочности на изгиб, считает прогибы и углы поворота в балке. 2. Он-лайн программа (версия 2008 года), которая строит 4 вида эпюр и рассчитывает реакции для любых балок (даже для статически неопределимых).

Сообщество Вход Решение задач Расчет редукторов Для Android (рекомендую) NEW Mobile Beam 2.0 Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME

www.sopromat.org

Подбор сечения балки (сопромат)

Балка проверяется на прочность по наибольшим нормальным напряжениям, возникающие в поперечном сечении балки, где на эпюре наибольший по абсолютному значению изгибающий момент. При поперечном изгибе в балке возникают и касательные напряжения, но они невелики, и при расчете на прочность учитываются только для двутавровых балок.

Условие прочности при изгибе по нормальным напряжениям: ,

где допускаемое напряжение принимается, как и при растяжении (сжатии) стержня из такого же материала.

Формула условия прочности при изгибе по нормальным напряжениям позволяет осуществить подбор сечения балки при заданном материале и максимальном абсолютном значении изгибающего момента. Требуемый момент сопротивления балки при изгибе определяется из условия: .

При изменении положения сечения по отношению к действующей нагрузке прочность балки существенно изменяется, хотя площадь сечения и остается неизменной. Например, для балки прямоугольного поперечного сечения с отношением сторон , расположенной таким образом, что высота прямоугольника h перпендикулярна нейтральной оси x, прочнее той же самой балки повернутой на , в три раза, так как . В выражении для осевого момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален ( ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня».

Проверка прочности двутавров

Для тонкостенных балок, например балок двутаврового профиля, проверка прочности производится следующим образом:

в наиболее удаленных от нейтральной оси точках прочность проверяется по формуле ;

в точках, где полка соединяется со стенкой прочность определяется по главным напряжениям.

в точках, расположенных на нейтральной оси, прочность определяется по наибольшим касательным напряжениям:

sopromato.ru