Расчет балки. Общие положения — Доктор Лом. Первая помощь при ремонте

1 этап. Определение максимальных напряжений

Внешние силы, действующие на балку, называются нагрузками. Внутренние силы — напряжениями. Тем не менее с точки зрения физики никакой разницы между этими силами нет, поэтому согласно третьему закону Ньютона (сила действия равна силе противодействия и направлена в противоположную сторону) внешние силы можно рассматривать как внутренние и наоборот. На этом основан метод сечений, используемый при расчете балок.

Согласно этому методу, если отсечь часть балки, то для того, чтобы отсеченная часть находилась в состоянии статического равновесия, к полученному сечению балки, как правило поперечному (перпендикулярному нейтральной оси балки), нужно приложить внешние силы. При этом в рассматриваемом сечении будут возникать силы противодействия — напряжения, равные по значению внешним силам и направленные в противоположную сторону.

1.1. Определение видов и количества опор

Опоры у балки могут быть разные: шарнирные и(или) жесткие.

Рисунок 219.2

.

Например, у балки, показанной на рисунке 219.2 имеется две вертикальных шарнирных опоры, показанные фиолетовым цветом и одна горизонтальная шарнирная опора, показанная синим цветом.

Как правило опоры обозначаются латинскими литерами А, В, С, D и т.д.

1.2. Определение количества и длины пролетов

Балки могут иметь не только один пролет, но два, три и сколь угодно много. Количество пролетов n_п определить не сложно:

n_п = n_о — 1 (517.1)

где n_o — количество вертикальных шарнирных опор или жестких заделок.

Балка, показанная на рисунке 219.2, имеет один пролет. Длина пролета l равна расстоянию между вертикальными опорами. Так как действительные опоры балки имеют некоторую ширину, то пролет балки — это расстояние в свету между краями опор. Пролет измеряется в метрах (м).

Если у балки только одна опора — жесткое защемление на конце, то такая балка пролетов не имеет и называется консольной.

1.3. Система координат

При расчете балок используется стандартная система координат с осями х, у и z. Для упрощения расчетов балка рассматривается как стержень, нейтральная ось которого совпадает с осью координат х. При этом начало координат как правило совпадает с началом балки. Соответственно длина балки измеряется по оси х.

Геометрические размеры поперечных сечений балки, т.е. размеры относительно осей y и z, на первом этапе расчетов никакого значения не имеют. Более того именно эти параметры и нужно определить на втором этапе расчета балки на действующие нагрузки.

Таким образом на первом этапе балка рассматривается как некий стержень, размеры сечения которого пренебрежимо малы по сравнению с длиной.

1.4. Определение действующих нагрузок

Все нагрузки, действующие на балку, можно представить в виде:

1.4.1. Сосредоточенных сил

Могут обозначаться как Q, P, N и др. Измеряются в Ньютонах (Н) или килограмм-силах (кгс).

1.4.2. Нагрузок, распределенных по некоторой части длины или по всей длине балки

Как правило такие нагрузки обозначаются литерой q. Измеряются в Н/м или кгс/м.

В свою очередь распределенные нагрузки могут быть равномерно и неравномерно распределенными.

График, показывающий изменение значения распределенной нагрузки по длине балки, называется эпюрой нагрузки. Изменение значения распределенной нагрузки может описываться различными уравнениями. Например, для балки, на которую действует равномерно распределенная нагрузка, эпюра нагрузки имеет вид прямоугольника, а уравнение, описывающее изменение значений нагрузки, имеет следующий вид:

q = const (517.2)

Если одна или несколько нагрузок направлены не перпендикулярно оси х, а под некоторым углом

а, то для дальнейших расчетов такие нагрузки разбиваются на вертикальную и горизонтальную составляющие.

Вертикальные составляющие используются для расчета балки на поперечный изгиб. Горизонтальные составляющие используются для определения горизонтальных опорных реакций, а также при необходимости для расчетов на устойчивость сжатого стержня.

Определить значение вертикальных и горизонтальных составляющих нагрузки можно по следующим формулам:

Q_в = Qsina (517.3)

Q_г = Qcosa (517.4)

где а — угол между осью х и вектором приложения нагрузки. Для распределенных нагрузок используется тот же принцип определения вертикальной и горизонтальной составляющих.

1.4.3. Моментов

Внешний момент, действующий в любой точке по оси х, рассматривается как пара сил, равных по значению и направленных в противоположные стороны. Таким образом значение внешнего момента не зависит от расстояния до какой либо точки по оси

х, а только от расстояния между векторами двух противоположно направленных сил.

Примечание: иногда при расчете балок бывает известен угол поворота или перемещение поперечного сечения. По большому счету ни угол поворота, ни перемещение не являются нагрузками, а есть результат воздействия нагрузок. Поэтому в таких случаях перемещения или углы поворота поперечных сечений заменяются силами или моментами, которые вызывают эквивалентное рассматриваемому перемещение или угол поворота.

1.5. Степень статической неопределимости

Все балки с количеством пролетов более одного, являются статически неопределимыми. Но даже и однопролетные балки могут быть статически неопределимыми. Степень статической неопределимости s для балок с шарнирными опорами определяется следующим образом:

s_ш

= n_п — 1 (517.5) 

Например, для балки, показанной на рисунке 219.2, степень статической неопределимости равна s_ш = 1 — 1 = 0. Это означает, что такая балка является статически определимой и для ее расчета на первом этапе достаточно трех уравнений статического равновесия системы.

Каждая жесткая заделка добавляет одну степень статической неопределимости. При наличии жестких заделок статическая определимость s определяется следующим образом:

s_ж = n_п + n_ж — 1 (517.6)

где n_ж — количество жестких заделок.

Рисунок 145.3.1

Например, для балки, показанной на рисунке 145.3.1, степень статической неопределимости составит s_ж = 1 + 2 — 1 = 2. Это означает, что для расчета балки на первом этапе потребуется составить два дополнительных уравнения.

1.6. Замена опор опорными реакциями

На этом этапе расчета опоры, имеющиеся у балки, заменяются реактивными силами, получившими название «опорные реакции». Эти опорные реакции также являются внешними силами для балки. Главное отличие опорных реакций от нагрузок в том, что изначально опорные реакции в отличие от нагрузок не известны и их нужно вычислить.

1.7. Статическое равновесие системы

Таким образом, после замены опор на реактивные силы, балка рассматривается как некий стержень, на который действуют внешние силы — нагрузки и опорные реакции. А так как стержень остается в состоянии статического равновесия, то сумма нагрузок равна сумме опорных реакций.

Из этого следуют первые два уравнения статического равновесия системы:

∑F_у = 0 (249.5.1) — для внешних сил, действующих параллельно оси у.

∑F_х = 0 (249.5.2) — для внешних сил, действующих параллельно оси х.

В данном случае

F — это общее обозначение для внешних сил: и нагрузок и опорных реакций.

Третье уравнение статического равновесия применимо только для статически определимых балок с шарнирными опорами. Смысл его сводится к тому, что шарнирные опоры не препятствуют повороту стержня на опоре, а значит момент на такой опоре будет равен нулю, если балка бесконсольная. Если на консоль действует нагрузка, то момент на опоре определяется, как для обычной консольной балки.

Для бесконсольной балки третье уравнение статического равновесия будет иметь вид:

∑М_А = ΣМ_В = 0 (517.7).

Примечание: В данном случае моменты — это произведение рассматриваемых сил на плечо действия.

Если нагрузка распределена по длине балки, то сначала определяется суммарная нагрузка (площадь грузовой эпюры), при этом плечо действия равно расстоянию от центра тяжести эпюры нагрузки. Другими словами, сначала распределенная нагрузка приводится к сосредоточенной силе и эта условно сосредоточенная сила действует в центре тяжести эпюры нагрузки.

1.8. Определение опорных реакций

Используя уравнения статического равновесия системы, можно сразу определить опорные реакции для статически определимой балки. Сначала с помощью уравнения (517.7) определяется одна вертикальная опорная реакция, а потом с помощью уравнения (249.5.1) — вторая вертикальная опорная реакция. При наличии горизонтальных составляющих нагрузки при помощи уравнения (249.5.2) определяется горизонтальная опорная реакция.

При расчете статически неопределимых балок сначала определяются значения опорных реакций на промежуточных шарнирных опорах, если используется метод нулевых перемещений на опорах (метод сил) или моменты на промежуточных шарнирных или крайних жестких опорах, если используется метод определения углов поворота на опорах (уравнения трех моментов).

При использовании уравнений трех моментов значение реакции на крайней опоре А определяется, исходя из условия:

А = (М_В + М_н)/l (517.8)

где М_В — значение момента на опоре В, определенное с помощью уравнений трех моментов. М_н — значение момента на опоре В от действующей нагрузки. Для остальных опор уравнения составляются по такому же принципу и только для крайней опоры используется одно из уравнений статического равновесия.

1.9. Построение эпюр

После того, как определены значения опорных реакций, можно переходить непосредственно к определению напряжений в поперечных сечениях балки. Для этого строятся эпюры поперечных и продольных сил, эпюра моментов, углов поворота поперечных сечений и эпюра перемещений (прогибов).

Физический смысл эпюр в том, что они показывают изменение указанных параметров в поперечных сечениях по длине балки. Таким образом эпюры являются графиками, описывающими решение соответствующих уравнений. Примеры эпюр поперечных сил и изгибающих моментов при действии различных видов нагрузки для статически определимых балок можно посмотреть здесь, а для некоторых видов статически неопределимых балок — тут.

Затем по эпюре моментов определяется самое нагруженное поперечное сечение балки, в этой точке на эпюре моментов максимальное значение, отрицательное или положительное, в данном случае не имеет значения. Затем для этого сечения определяются значения поперечных и нормальных сил по соответствующим эпюрам.

2 этап. Подбор сечения

Так как разные материалы имеют разные значения расчетных сопротивлений, то соответственно и требуемые параметры сечения для балок из различных материалов будут разными.

2.1. Определение материала балки и расчетного сопротивления материала

После того, как выбран материал для балки, определяются расчетные сопротивления материала изгибу R_и, сжатию R_c, растяжению R_р и т.п. по действующим нормативным документам или по данным производителя, если балка будет из стали.

Для балок из разнородных материалов сначала определяются параметры приведенного сечения. Суть приведенного сечения состоит в том, что рассматривается некое условное сечение материала обладающего равным сопротивлением, при этом ширина сечения для материала, обладающего большим расчетным сопротивлением увеличивается во столько раз, во сколько расчетное сопротивление одного материала больше расчетного сопротивления другого материала. Поэтому такое сечение и называется приведенным. Другими словами, если бы балка изготавливалась из одного материала, то именно так и должно было бы выглядеть поперечное сечение.

Для железобетонных балок, являющихся также балками из разнородных материалов, как правило в процессе расчета требуется дополнительно определить сечение арматуры. Возможные варианты расчета железобетонных балок рассмотрены отдельно.

2.2. Определение требуемого момента сопротивления

Требуемый момент сопротивления определяется, исходя из следующего условия:

W_тр ≥ М/R_иγ_s (149.4.8)

где М — максимальное значение изгибающего момента, определенного по эпюре моментов, построенной относительно оси х. γ_s — коэффициент условий работы.

Момент сопротивления измеряется в см³.

2.3. Определение геометрических параметров сечения

2.3 Определение геометрических параметров сечения

Поперечное сечение балки может быть каким угодно: круглым, квадратным, прямоугольным, в виде швеллера, двутавра, круглой или прямоугольной трубы и т.д.

Как известно наиболее оптимальными являются сечения в виде двутавра, швеллера или квадратной трубы, именно такие сечения и принимаются для стальных балок.

Для деревянных балок чаще используются прямоугольные и круглые сечения. И хотя круглое сечение саме неэффективное с точки зрения использования материала, однако бревна — самый дешевый строительный материал, так как требуют минимум предварительной обработки при изготовлении балок. Тем не менее, при достаточно больших пролетах и нагрузках деревянные клеенные балки двутаврового сечения также имеют место.

Для железобетонных балок наиболее характерны прямоугольное и тавровое сечения. Впрочем, как уже говорилось, расчет железобетонных балок отличается от расчета обычных балок.

Для балок прямоугольного сечения требуемая высота сечения определяется по формуле:

 (147.4)

Для стальных балок все значительно проще — момент сопротивления принимаемого профиля, определяемой по соответствующему сортаменту, должен быть не меньше требуемого момента сопротивления, определенного по формуле (149.4.8)

2.4. Определение прогиба

Так как для однопролетных балках на шарнирных опорах значение прогиба часто является определяющим, то я рекомендую определять прогиб сразу после определения параметров сечения.

Формулы для определения прогиба и углов поворота сечения на опорах зависят от вида приложенной к балке нагрузки. Значение модуля упругости E для выбранного материала балки определяется по нормативным документам, здесь можно посмотреть примерные значения модулей упругости для некоторых строительных материалов. Значение момента инерции I определяется в зависимости от геометрической формы сечения или по сортаменту для стальных балок из прокатного профиля.

Если прогиб f, определенный по одной из вышеуказанных формул, меньше допустимого нормативными документами, в частности СП 20.13330.2011 «Нагрузки и воздействия», то можно продолжать расчеты. Если прогиб больше допустимого, то сначала следует подобрать сечение, обеспечивающее требования по прогибу. Например для балки, на которую действует равномерно распределенная нагрузка, значение момента инерции можно определить по следующей формуле:

I = 5ql⁴/(384Ef) (517.9)

2.5. Проверка на прочность опорных участков балки

Любая балка в отличие от показанной на рисунке 219.2 модели имеет опорные участки. На этих опорных участках действуют нормальные напряжения в сечениях, параллельных нейтральной оси балки. В общем случае (если балка прямоугольная и напряжения на опорном участке равномерно изменяются от максимума до нуля) эти напряжения определяются по следующей формуле:

σ_у = 2Q/(bl_оп) ≤ R_cγ_s (517.10)

где Q — значение поперечной силы согласно эпюры «Q», b — ширина балки, l_оп — длина опорного участка, 2 — коэффициент учитывающий неравномерность распределения напряжений на опорном участке. R_c — расчетное сопротивление сжатию.

2.5.1. Проверка на прочность в местах действия сосредоточенной нагрузки

Так как на балку может действовать не только распределенная нагрузка, но и одна или несколько сосредоточенных нагрузок, то места действия сосредоточенных нагрузок также следует проверить на прочность.

В данном случае формула для определения нормальных напряжений будет будет почти такой же как (517.10), вот только значение коэффициента, учитывающего неравномерность распределения нагрузки, будет зависеть от того, как именно сосредоточенная нагрузка передается рассчитываемой балке.

Например, если рассчитываемая балка будет находиться посредине помещения и на нее сверху будет опираться второстепенная балка, то значение коэффициента будет равно 1.

2.6. Проверка по касательным напряжениям

В поперечных сечениях, соответствующих опорным точкам балки, а также в сечениях, параллельных нейтральной оси балки, будут действовать касательные напряжения, которые не должны превышать расчетного сопротивления R_s сдвигу или сколу:

т = Q_yS_z^отс/bI_z ≤ R_sγ_s (270.2)

Подобная проверка особенно важна для стальных тонкостенных балок.

2.7. Определение максимальных напряжений

Если в рассматриваемой точке (точнее на грани параллелепипеда с рассматриваемой точкой на одной из граней) действуют и нормальные и касательные напряжения, то возникает плоское напряженное состояние.

В этом случае необходимо определить максимальное нормальное напряжение, действующее в этой точке, другими словами определить главные площадки напряжений. Для этого используется одна из теорий прочности. Так, согласно третьей теории прочности:

σ_пр =(σ² +4т²)^0.5 ≤ R (517.11)

Если на 4 из 6 главных площадок напряжений в области рассматриваемой точки действуют нормальные и касательные напряжения (например в местах приложения сосредоточенных нагрузок или на промежуточных опорах многопролетных балок), то значение максимальных нормальных напряжений составит:

σ_пр = ((σ_х — σ_у)² + 4т_ху²)^0.5 ≤ R (517.12)

Эта формула следует из общих положений теории сопротивления материалов, однако для стальных балок нормативные документы требуют проводить расчет по несколько другой формуле.

Кроме того в некоторых случаях, если отсутствуют опорные связи из плоскости балки (что в малоэтажном строительстве встречается крайне редко) тонкостенные стальные балки открытого профиля, а также деревянные балки любого сечения следует проверить на устойчивость в сжатой зоне сечения, но это уже совсем другая история.

Вот собственно и все, что имеет отношение к расчету балок.

doctorlom.com

Расчет балок перекрытий | ЗАО «Техстройпроект»

Деревянные балки перекрытий

Деревянные балки перекрытий часто являются наиболее экономичным вариантом. Деревянные балки легки в изготовлении и монтаже, имеют низкую теплопроводность по сравнению со стальными или железобетонными балками. Недостатки деревянных балок — более низкая механическая прочность, требующая больших сечений, низкая пожаростойкость и устойчивость к поражению микроорганизмами и термитами (если они водятся в вашей местности). Поэтому, деревянные балки перекрытий требуется тщательно обрабатывать антисептиками и антипиренами, например ХМ-11 или ХМББ производства фирмы Антисептик (С-Петербург).

Как расчитать необходимое сечение деревянной балки перекрытий?

Оптимальный пролет для деревянных балок — 2,5- 4 метра. Лучшее сечение для деревянной балки — прямоугольное с соотношением высоты к ширине 1,4:1. В стену балки заводят не менее чем на 12 см и гидроизолируют по кругу, кроме торца. Желательно закрепить балку анкером, заделанным в стену.

При выборе сечения балки перекрытия учитывают нагрузку собственного веса, которая для балок междуэтажных перекрытий, как правило стоставляет 190-220 кг/м2, и нагрузку временную (эксплуатационную), её значение принимают равной 200 кг/м2. Балки перекрытия укладывают по короткому сечению пролёта. Шаг монтажа деревянных балок рекомендуется выбирать равным шагу установки стоек каркаса.

Для расчета минимального и оптимального сечения деревянной балки перекрытия можно воспользоваться он-лайн калькулятором Романова для деревянных балок перекрытий

Ниже приведены несколько таблиц, со значениями минимальных сечений деревянных балок для различных нагрузок и длинн пролетов:

Таблица сечений деревянных балок перекрытия в зависимости от пролёта и шага установки, при нагрузке 400кг/м2. — рекомендуется расчитывать именно на эту нагрузку

Если вы не используете утеплитель или не планируете нагружать перекрытия (например, перекрытие необитаемого чердака), то можно использовать таблицу для меньших значений нагрузок деревянных балок перекрытий:

Таблица минимальных сечений деревянных балок перекрытия в зависимости от пролёта и нагрузки, при нагрузках от 150 до 350 кг/м2.

Если вы используете вместо балок прямоугольного сечения круглы бревна, можно пользоваться следующей таблицей:

Минимальный допустимый диаметр круглых бревен, используемых в качестве балок междуэтажных перекрытий в зависимости от пролета при нагрузке 400 кг на 1 м2

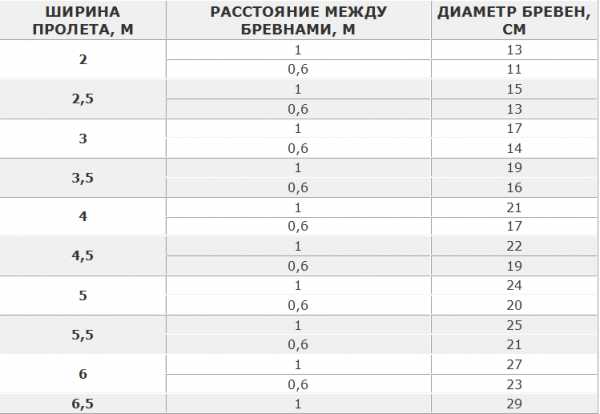
Если вы хотите перекрыть большие прогоны, то рекомендуем воспользоваться опытом с сайта Околоток.

Стальные (металлические) двутавровые балки перекрытий

Двутавровая металлическая балка перекрытий обладает рядом неоспоримых преимуществ, только при одном недостатке — высокой стоимости. Металлической двутавровой балкой можно перекрыть большие пролеты со значительной нагрузкой, металлическая стальная балка негорюча и устойчива к биологическим воздействиям. Однако, металлическая балка может корродировать при отсутствии защитного покрытия и наличия в помещении агрессивных сред.

Для расчета параметров двутавровой металлической балки можно воспользоваться хорошей программой расчета Beam

Вес одного метра двутавровой балки можно посмотреть в таблице веса двутавровых балок

В большинстве случаев в самодеятельном строительстве при расчетах в вышеуказанной программе или других ей подобных, следует считать, что металлическая балка имеет шарнирные опоры (то есть концы не фиксированы жестко — например, так как в каркасной стальной конструкции). Нагрузку на перекрытие со стальными двутавровыми металлическими балками с учетом собственного веса следует рассчитывать, как 350 (без стяжки) -500 (со стяжкой) кг/м2
Шаг между двутавровыми металлическими балками рекомендуется делать равным 1 метру. В случае экономии возможно увеличение шага между металлическими балками до 1200 мм.

Таблица для выбора номера двутавровой металлической балки при различном шаге и длине прогонов

Железобетонные балки перекрытий

При устройстве железобетонных балок нужно использовать следующие правила (по Владимиру Романову):

1. Высота железобетонной балки должна быть не менее 1/20 длины проема. Делим длину проема на 20 и получаем минимальную высоту балки. Например при проеме в 4 м высота балки должна быть не менее 0,2 м.
2. Ширину балки рассчитывают исходя из соотношения 5 к 7 (5 — ширина, 7 — высота).
3. Армировать балку следует минимум 4 прутками арматуры d12-14 (снизу можно толще) — по два сверху и снизу. Таблицы соотношения длины и массы арматуры различного сечения.
4. Бетонировать за один раз, без перерывов, чтобы ранее уложенная порция раствора не успела схватиться до укладки новой порции. С бетономешалкой бетонировать балки сподручнее, чем заказывать миксер. Миксер хорош для быстрой заливки больших объемов.

Вес строительной арматуры или сколько метров арматуры в тонне. Вес арматуры длиной 11,75 м. Вес арматуры диаметром от 5,5 до 32 мм. 

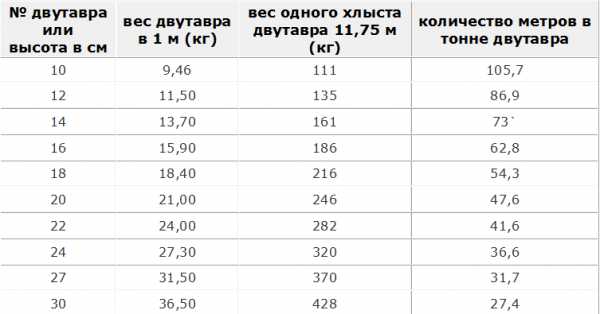
Вес двутавра и количество метров в тонне двутавра

 

Популярность: 21%

tsp76.ru

Методика расчета несущих конструкций из различных материалов

На балки перекрытия приходится значительная нагрузка, поэтому во избежание чрезмерного прогиба перекрытий и обрушения зданий необходимо выполнять расчет данных несущих конструкций. Балки изготавливаются из деревянного бруса, металлопроката и железобетона. Ниже приводятся простейшие методики расчетов и рекомендации по выбору балок из указанных материалов.

Расчет деревянных балок

Для расчета деревянных балок необходимо знать распределенную нагрузку на перекрытие, длину балок и расстояние между ними. Балки укладываются параллельно короткой стороне здания, распределенная нагрузка выбирается равной 400 кг/кв. метр для межэтажных и 200 кг/кв. метр для чердачных перекрытий. Для примера рассчитаем балки для комнаты размерами 6х4,5 метра, при этом длина балки будет равна около пяти метров, но расчет ведется исходя из расстояния между стенами — 4,5 метра. Расстояние между балками выбираем равным 0,8 метра.

Рассчитываем максимальный изгибающий момент:

М = (q х hхl2) / 8 = 400 х 0,8 х 4,52 / 8 = 810 кгм = 81000 кгсм;

где q — распределенная нагрузка, h — расстояние между балками; l — длина пролета.

Требуемый момент сопротивления балки равен:

W = М / R = 81000 / 142,71 = 567,6 куб. см;

где R — расчетное сопротивление древесины, для сосны равное 14 МПа или 142,71 кгс/кв. см.

Задавая ширину сечения бруса (10 см) определяем высоту балки:

h = √(6W/b) = √(6 х 567,6/10)= 18,5 см;

где h — высота, b — ширина балки. Результаты расчетов показывают, что можно применить брус 10х20 см.

Оптимальное соотношение ширины и высоты балки равняется 1:1,4. Подставляя в формулы разные значения расстояний между балками и их ширины подсчитываем расход материалов и выбираем наиболее экономичный вариант при оптимальном сечении.

Для выбора деревянных балок можно воспользоваться онлайн калькулятором Романова или таблицами, в которых по результатам расчетов приведены наиболее типичные варианты. Подобные материалы можно легко найти в интернете.

Прогиб деревянной балки должен быть менее 1/250 ее длины, для нашего случая 450/250 = 1,8 см. Он рассчитывается по формуле:

f=(5ql4)/(384EI) = 5 х 400 х 4,5 х 4,5 х 4,5 х 4,5 / 384 х 109 х 6666.6667 х 10 — 8 = 3,2 см;

где E — модуль упругости, для древесины равный 109 кгс/м2; I — момент инерции, для балки прямоугольного сечения равный:

I = b x h4 / 12 = 10 х 203 / 12 = 6666.6667 см4.

В данном случае прогиб больше допустимого, поэтому следует выбрать брус большего сечения или уменьшить расстояние между балками и повторить расчеты.

Расчет металлических балок

Методика определения максимального изгибающего момента и момента сопротивления одинакова для балок из любого материала. Металлические балки чаще всего изготавливаются из двутавра. Величину допустимого момента сопротивления для выбранного профиля можно узнать в справочнике по металлопрокату или вычислить на онлайн калькуляторе по геометрическим размерам. Расчеты значительно облегчаются при использовании программ, имеющихся в интернете. В таблице указаны рекомендуемые номера двутавров при распределенной нагрузке 400 кгс/кв. м.

Расстояние между балками (метров)	Двутавр при пролете 3 метра	Двутавр при пролете 4 метра	Двутавр при пролете 6 метров
1000	№10	№12	№20
1100	№10	№12	№20
1200	№10	№12	№20

• Как обеспечить правильное примыкание крыши к стене дома, читайте в нашей статье.
• Что представляет собой кровельный аэратор, Вы узнаете из данной публикации.
• О характеристиках и особенностях конструкции винилового сайдинга Хольцпласт мы рассказываем по этой ссылке.

Расчет железобетонных балок

Заводские балки выбираются по допустимому моменту сопротивления, который указывается в документации. Выбор конструкции монолитных балок затруднен тем, что железобетон является материалом, состоящим из нескольких компонентов и предусмотреть влияние всех факторов на несущую способность балки довольно сложно. Методику расчетов смогут осилить лишь специалисты, изучившие сопромат и имеющие практический опыт.

Общие рекомендации по выбору железобетонных балок сводятся к следующему:

• Бетон выдерживает значительные нагрузки на сжатие, а арматура — на растяжение, поэтому она устанавливается в растянутой зоне — нижней части балки.
• Высоту сечения балки выбирают большей 1/20 длины пролета, отношение высоты к ширине сечения — равным 7:5.
• Диаметр арматуры должен быть 12 мм и более, количество прутков — не менее 4, в нижней части сечения укладывается более толстая арматура (арматура в верхней части нужна, если балка изготавливается на почве и устанавливается на место подъемным краном).
• Бетонировка должна осуществляться в один прием, следующая порция бетона укладывается до схватывания предыдущей.
• Выбор балок упрощается при использовании программ, определяющих их сечение и количество арматуры.

Заключение

Приведенные формулы и рекомендации дают представление о методике расчетов и с большинстве случаев пригодны для выбора балок перекрытия. Более сложные методики учитывают все условия работы, при этом производится проверка на устойчивость к нагрузкам, действующим в разных направлениях.

Выбор балок упрощается при использовании программ и онлайн калькуляторов, которые имеются в интернете. Программы делаются людьми, а люди могут допустить ошибки, поэтому перед использованием программ нужно почитать отзывы, написанные пользователями.

okrovle.com